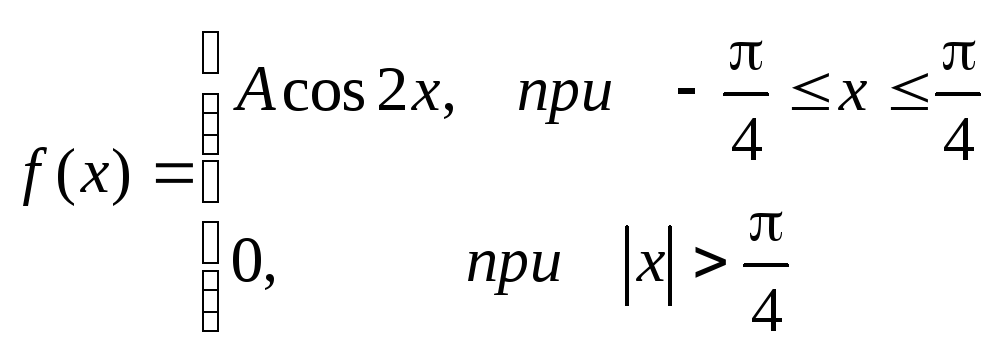Как найти средний квадрат случайной величины

Математическое ожидание, дисперсия, среднее квадратичное отклонение

Эти величины определяют некоторое
среднее значение, вокруг которого
группируются значения случайной
величины, и степень их разбросанности
вокруг этого среднего значения.

Математическое ожидание Mдискретной случайной величины – это
среднее значение случайной величины,
равное сумме произведений всех возможных
значений случайной величины на их
вероятности.

Свойства математического ожидания:

1. Математическое ожидание постоянной
   величины равно самой постоянной .

2. Постоянный множитель можно выносить
   за знак математического ожидания .

3. Математическое ожидание произведения
   двух независимых случайных величин
   равно произведению их математических
   ожиданий .

4. Математическое ожидание суммы двух
   случайных величин равно сумме
   математических ожиданий слагаемых

Для описания многих практически важных
свойств случайной величины необходимо
знание не только ее математического
ожидания, но и отклонения возможных ее
значений от среднего значения.

Дисперсия случайной величины— мера разброса случайной величины,
равная математическому ожиданию квадрата
отклонения случайной величины от ее
математического ожидания.

.

Принимая во внимание свойства
математического ожидания, легко показать
что

Казалось бы естественным рассматривать
не квадрат отклонения случайной величины
от ее математического ожидания, а просто
отклонение. Однако математическое
ожидание этого отклонения равно нулю.
Это объясняется тем, что одни возможные
отклонения положительны, другие
отрицательны, и в результате их взаимного
погашения получается ноль. Можно было
бы принять за меру рассеяния математическое
ожидание модуля отклонения случайной
величины от ее математического ожидания,
но как правило, действия связанные с
абсолютными величинами, приводят к
громоздким вычислениям.

Свойства дисперсии:

1. Дисперсия постоянной равна нулю.

2. Постоянный множитель можно выносить
   за знак дисперсии, возводя его в квадрат.

3. Если x и y независимые случайные величины
   , то дисперсия суммы этих величин равна
   сумме их дисперсий.

Средним квадратическим отклонением
случайной величины(иногда применяется
термин «стандартное отклонение случайной
величины») называется число равное.

Среднее квадратическое отклонение,
является, как и дисперсия, мерой рассеяния
распределения, но измеряется, в отличие
от дисперсии, в тех же единицах, которые
используют для измерения значений
случайной величины.

Решение задач:

1)Дана случайная величина Х:

xi	-3	-2	0	1	2
pi	0,1	0,2	0,05	0,3	0,35

Найти М(х), D(X).

Решение:

.

=9=2,31.

.

2) Известно, что М(Х)=5, М(Y)=2.
Найти математическое ожидание случайной
величиныZ=6X-2Y+9-XY.

Решение:М(Z)=6М(Х)-2М(Y)+9-M(X)M(Y)=30-4+9-10=25.

Пример:Известно, чтоD(Х)=5,D(Y)=2. Найти
математическое ожидание случайной
величиныZ=6X-2Y+9.

Решение:D(Z)=6²D(Х)-2²D(Y)+0=180-8=172.

Тема 7. Непрерывные случайные величины

Задача 14

Случайная
величина, значения которой заполняют
некоторый промежуток, называется
непрерывной.

Плотностью распределениявероятностей непрерывной случайной
величины Х называется функцияf(x)– первая производная от функции
распределенияF(x).

Плотность
распределения также называют
дифференциальной
функцией.
Для описания дискретной случайной
величины плотность распределения
неприемлема.

Зная плотность распределения, можно
вычислить вероятность того, что некоторая
случайная величина Х примет значение,
принадлежащее заданному интервалу.

Вероятность того, что непрерывная
случайная величина Х примет значение,
принадлежащее интервалу (a,
b), равна определенному
интегралу от плотности распределения,
взятому в пределах от a
до b.

Функция распределения может быть легко
найдена, если известна плотность
распределения, по формуле:

Свойства плотности распределения.

1) Плотность распределения – неотрицательная
функция.

2) Несобственный интеграл
от плотности распределения в пределах
от -доравен единице.

Решение задач.

1.Случайная величина подчинена
закону распределения с плотностью:

Требуется найти коэффициент а,
определить вероятность того, что
случайная величина попадет в интервал
от 0 до.

Решение:

Для нахождения коэффициента авоспользуемся свойством.

2 .Задана непрерывная случайная
величинахсвоей функцией распределенияf(x).

Требуется определить
коэффициент А, найти функцию распределения,
определить вероятность того, что
случайная величинахпопадет в
интервал.

Решение:

Найдем коэффициент А.

Найдем функцию распределения:

1) На участке
:

2) На участке

3) На участке

Итого:

Найдем вероятность попадания случайной
величины в интервал
.

Ту же самую вероятность можно искать
и другим способом:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Дисперсия и ее свойства.
Среднее квадратическое отклонение

• Краткая теория
• Примеры решения задач
• Задачи контрольных и самостоятельных работ

Краткая теория

---

Дисперсия и формула для ее вычисления

На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. Например, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели, которая должна быть поражена.

На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения случайной величины и затем найти их среднее значение. Однако такой путь ничего не даст, так как среднее значение отклонения, т. е. M[X-M(X)], для любой случайной величины равно нулю. Это свойство объясняется тем, что одни возможные отклонения положительны, а другие – отрицательны; в результате их взаимного погашения среднее значение отклонения равно нулю. Эти соображения говорят о целесообразности заменить возможные отклонения их абсолютными значениями или их квадратами. Так и поступают на деле. Правда, в случае, когда возможные отклонения заменяют их абсолютными значениями, приходится оперировать с абсолютными величинами, что приводит иногда к серьезным затруднениям. Поэтому чаще всего идут по другому пути, то есть вычисляют среднее значение квадрата отклонения, которое и называют дисперсией.

Дисперсией называется
математическое ожидание квадрата отклонения случайной величины

 от

:

Для того чтобы найти дисперсию, достаточно вычислить сумму произведений возможных значений квадрата отклонения на их вероятности.

Для вычисления дисперсии
на практике удобно пользоваться следующей формулой:

Свойства дисперсии

Свойство 1.

Дисперсия равна разности между
математическим ожиданием квадрата случайной величины

 и
квадратом ее математического ожидания.

Свойство 2.

Дисперсия константы
равна нулю:

Свойство 3.

Постоянный множитель
выносится из-под знака дисперсии в квадрате:

Свойство 4.

Дисперсия суммы
случайных величин:

где 

 –
ковариация  случайных величин

 и

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Следствия из свойств дисперсии.

В частности, если

 и

 независимы, то

Прибавление константы

 в
случайной величине не меняет ее дисперсии:

Дисперсия разности равна сумме дисперсий:

Среднеквадратическое отклонение

Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.

Стандартное (среднее
квадратичное) отклонение случайной величины

 определяется
как корень из дисперсии и обозначается

Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то ее размерность совпадает с размерностью X. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию. Например, если X выражается в линейных метрах, то среднее квадратичное отклонение X будет выражаться также в линейных метрах, a дисперсия X – в квадратных метрах.

Смежные темы решебника:

• Математическое ожидание и его свойства
• Дискретная случайная величина
• Непрерывная случайная величина

Примеры решения задач

---

Пример 1

В коробке 20 конфет, из которых 4 с
вареньем. Х – число конфет с вареньем среди двух случайно выбранных. Найти
дисперсию случайной величины Х.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Случайная
величина

 – число конфет с вареньем, может принимать
значения 0,1,2

Найдем
соответствующие вероятности:

Проверка:

Получаем
следующий закон распределения СВ

:

Математическое
ожидание:

Дисперсию
можно вычислить по формуле:

Искомая
дисперсия:

---

Пример 2

Даны
законы распределения независимых случайных величин X и Y:

и

Найти
закон распределения суммы (X+Y). Проверить равенство D(X+Y)=D(X)+D(Y).

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Распределение суммы

:

Окончательно получаем:

	2	3	4	Итого
	0.2	0.5	0.3	1

Вычислим математические ожидания:

Вычислим
дисперсии:

Проверим
равенство

:

Равенство
выполняется.

---

Пример 3

Вероятность
изготовления бракованной детали на первом станке составляет 3%, на втором
станке 5%. На первом станке было изготовлено 20 деталей, на втором 40 деталей.
Найти математическое ожидание и дисперсию числа бракованных деталей.

Решение

Математическое
ожидание биномиального распределения:

Дисперсия:

Математическое
ожидание величины

 – числа бракованных деталей на 1-м станке:

Дисперсия:

Математическое
ожидание величины

 – числа бракованных деталей на 2-м станке:

Дисперсия:

Математическое
ожидание числа бракованных деталей:

Дисперсия
числа бракованных деталей:

Ответ:

; 

.

---

Пример 4

Случайные
величины X,Y распределены по закону
Пуассона. Найдите M{(X+Y)²}, если M(X)=40 и
M(Y)=70, а коэффициент корреляции X и Yравен 0,8.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Поскольку
случайные величины

 и

 распределены по закону Пуассона и известны их
математические ожидания, соответствующие дисперсии равны:

Пользуясь
свойствами математического ожидания и дисперсии:

Подставляя
числовые значения, получаем:

Ответ:

.

Задачи контрольных и самостоятельных работ

---

Задача 1

Независимые случайные величины X и Y
заданы следующими законами:

x	2.3	2.5	2.7	2.9
p	0.4	0.3	0.2	0.1

Укажите
законы распределения случайной величины X+Y, X-Y и найдите их
математическое ожидание и дисперсию.

---

Задача 2

Найти
дисперсию, математическое ожидания, среднекваратическое отклонение ДСВ X,
заданной законом распределения.

x	-5	2	3	4
p	0,4	0,3	0,1	0,2

Написать F(x) и построить ее график.

---

Задача 3

Случайная
величина X имеет плотность вероятности

Требуется
найти дисперсию D_x.

---

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 4

Вероятность
того, что прибор исправен, равна 0,8. X – число исправных приборов
из двух выбранных. Найти дисперсию случайной величины X.

---

Задача 5

Случайные
величины X и Y независимы. Найти
дисперсию случайной величины Z=2X+3Y, если известно, что D(X)=4, D(Y)=5.

---

Задача 6

Найти
дисперсию дискретной случайной величины X – числа отказов элемента
некоторого устройства в десяти независимых опытах, если вероятность отказа
элемента в каждом опыте равна 0,9.

---

Задача 7

Дискретная
случайная величина X имеет только два возможных значения: x₁ и x₂, причем x₂>x₁. Вероятность того, что X
примет значение x₁, равна 0,6. Найти закон распределения величины X, если
математическое ожидание и дисперсия известны: M(X)=1,4; D(X)=0,24.

---

Задача 8

Закон
распределения случайной величины ξ имеет вид:

ξ	-1	2	3	5
P	1/4	1/2	1/8	1/8

Найти функцию распределения случайной величины ξ,
вычислить ее математическое ожидание, дисперсию и среднее квадратическое
отклонение. Вычислить вероятность P{5⁄2<ξ<5}.

---

Задача 9

Дискретная
случайная величины X принимает лишь два значения. Большее из значений 3
она принимает с вероятностью 0,4. Кроме того, известна дисперсия случайной
величины D(X)=6. Найти математическое
ожидание случайной величины.

---

Задача 10

Найти
дисперсию по заданному непрерывному закону распределения случайной величины X,
заданному плотностью вероятности

 при

 и

 в остальных точках.

• Краткая теория
• Примеры решения задач
• Задачи контрольных и самостоятельных работ

Числовые характеристики дискретной случайной величины

В этом разделе:

• Основная информация
• Онлайн калькулятор
• Полезные ссылки

Основная информация

Числовые характеристики дискретной случайной величины $X$, которые обычно требуется находить в учебных задачах по теории вероятностей, это математическое ожидание $M(X)$, дисперсия $D(X)$ и среднее квадратическое отклонение $sigma(X)$.

$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
$$
sigma(X) = sqrt{D(X)}.
$$

Подробные формулы и примеры расчета вы найдете по ссылкам в предыдущем абзаце, в этом же разделе вы сможете автоматически и бесплатно рассчитать эти значения с помощью онлайн-калькулятора, который даст не только ответ, но и продемонстрирует процесс вычисления.

Калькулятор: числовые характеристики случайной величины

• Введите число значений случайной величины К.
• Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -1.5 или 10.558). Введите нужные значения (убедитесь, что сумма вероятностей равна единице, то есть закон распределения задан верно).
• Нажмите на кнопку “Вычислить”.
• Калькулятор покажет процесс вычисления математического ожидания $M(X)$, дисперсии $D(X)$ и СКО $sigma(X)$.
• Нужны еще расчеты? Вводите новые числа и нажимайте на кнопку.

Видео. Полезные ссылки

Видеоролики об СКО

На закуску для продвинутых – какие формулы вычисления СКО для выборок бывают и для чего подходят.

Полезные ссылки

• Калькуляторы по теории вероятнстей
• Онлайн учебник по ТВ
• Примеры решений по теории вероятностей
• Контрольные по теории вероятностей на заказ

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро: