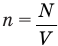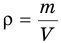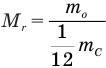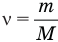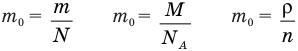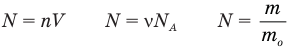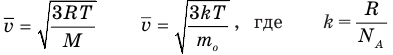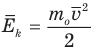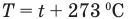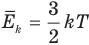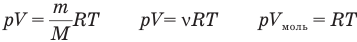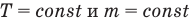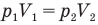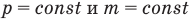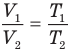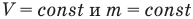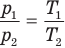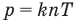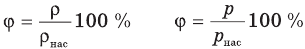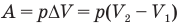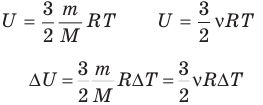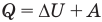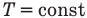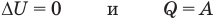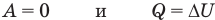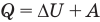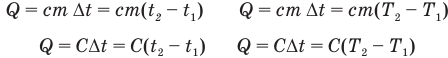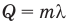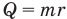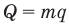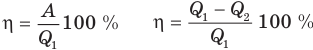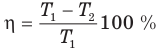|
|
Макеты страниц
Основная задача молекулярно-кинетической теории состоит в установлении количественных связей между макроскопическими свойствами физических систем (сжимаемостью, давлением, температурой и др.) и особенностями теплового движения образующих, систему молекул.
Механическое описание отдельно взятого тела как целого сводится к установлению зависимости его движения от действия внешних сил. В молекулярной же физике рассматривают явления, связанные с движением и взаимодействием колоссального числа частиц. Так, при нормальных условиях в 

Для решения задач молекулярной физики пользуются методами статистической физики. Статистическая физика оперирует средними значениями величин, характеризующих свойства отдельных молекул: средним размером молекул, средним расстоянием между ними и средней скоростью молекул.
В предыдущем параграфе отмечалось, что сложные молекулы имеют определенную структуру, форма многих молекул заведомо отличается от сферической. Для описания же усредненной картины столкновения частиц довольно сложные молекулы (такие, как молекулы бензола, гексана и др.) можно считать сферическими с диаметром 

Если известен объем системы V и число частиц в ней 



Плоская модель, иллюстрирующая нахождение межмолекулярных расстояний по (27.1), изображена на рисунке 3.3. На этом рисунке большой квадрат символизирует объем V, маленькие квадратики — элементарные объемы 
Следует отметить, что величина (27.1) не определяет каких-либо действительных расстояний между любыми двумя фиксированными частицами. Так, если взять газ и разбить его объем на 


Рис. 1.20.

Рис. 3.4.
объемов с течением времени будет меняться. Тем не менее величина (27.1) будет являться некоторой усредненной характеристикой распределения молекул в пространстве. Можно ставить более сложную задачу — отыскание возможного числа пустых элементарных объемов или заселенных по две или три молекулы. Такая задача позднее будет также рассмотрена (§ 39).
Из сопоставления свойств газов и жидкостей легко сделать заключение, что средние межмолекулярные расстояния в газах намного больше таких же расстояний в жидкостях, именно поэтому газы намного легче сжать, чем жидкости. В первом приближении будем полагать (а это в действительности так и есть), что молекулы жидкостей столь тесно примыкают друг к другу, что свободные промежутки между ними пренебрежительно малы. Тогда при разбиении жидкости на 


Рисунок 3.4 раскрывает содержание соотношения (27.2). Следует отметить, что, несмотря на грубое усреднение, картина, соответствующая рисунку 3.4, позволяет правильно оценить размеры молекул.
Плотность воды 





что близко к результатам других способов определения этой величины. Заметим, что молекулы обычных веществ (исключая полимеры) имеют размеры порядка 
Моль любого газа при нормальных условиях 



Выше отмечалась сложность детальной картины теплового движения. Скорости молекул могут резко различаться как по величине, так и по направлению, при этом распределение фиксированных молекул по скоростям с течением времени из-за столкновений меняется. Можно ввести среднюю скорость теплового движения молекул, которая в равновесных 
Если известны скорости всех молекул в данный момент времени, то среднее арифметическое значение скорости или просто средняя скорость 

где 

Кроме средней скорости, для характеристики теплового движения вводят еще среднюю квадратичную скорость молекул, квадрат которой согласно определению равен:

или

Для выяснения смысла соотношения (27.4) найдем энергию поступательного движения всех молекул. Искомая величина определяется как сумма кинетических энергий отдельных молекул системы:

где 

Используя (27.4), перепишем (27.5) в виде

Таким образом, суммарная энергия поступательного движения всех молекул выражается через среднюю квадратичную скорость их теплового движения. Из (27.6) следует также, что

т. е. средняя кинетическая энергия поступательного движения молекулы 
Для более детального усредненного описания теплового движения ансамбля частиц рассматривают три составляющие скорости каждой молекулы по трем взаимно перпендикулярным осям 


где 

Это выражение представляет собой сумму вида:

Введем обозначения

Величины 


Отметим, что в правой части (27.11) стоят величины, которые не являются компонентами каких-либо скоростей, они характеризуют усредненное движение молекул по осям 

Полученные результаты позволяют доказать возможность представления сложного теплового движения упорядоченным, что упрощает рассмотрение многих конкретных задач молекулярной физики. Из (27.12) и (27.6) легко получить:

Левая часть (27.13) характеризует тепловое движение относительно одной из осей прямоугольной системы координат. Согласно последнему выражению сложное тепловое движение молекул в условиях равновесия можно рассматривать как упорядоченное, при этом молекулам приписывается одна и та же скорость, равная средней квадратичной скорости, и все они движутся по трем взаимно перпендикулярным осям так, что по одной из осей (в обоих направлениях) движется третья часть всех частиц.
Как показывает исследование диффузии и броуновского движения, средние скорости движения молекул зависят от температуры. Раскрытие этой зависимости возможно только с использованием более сложных методов статистической физики.
Оглавление
- ПРЕДИСЛОВИЕ
- Глава I. ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПОНЯТИЯ И СВОЙСТВА ИДЕАЛЬНЫХ ГАЗОВ
- § 1 О ДВУХ МЕТОДАХ ИССЛЕДОВАНИЯ ФИЗИЧЕСКИХ ЯВЛЕНИЙ
- § 2. ОСНОВНЫЕ ПОНЯТИЯ И ПРЕДСТАВЛЕНИЯ ТЕРМОДИНАМИЧЕСКОГО ОПИСАНИЯ СИСТЕМ
- § 3 ТЕРМИЧЕСКОЕ УРАВНЕНИЕ СОСТОЯНИЯ. РАВНОВЕСНЫЕ ПРОЦЕССЫ
- § 4. ИЗОПРОЦЕССЫ
- § 5. МЕЖДУНАРОДНАЯ ПРАКТИЧЕСКАЯ ТЕМПЕРАТУРНАЯ ШКАЛА
- § 6. МЕТОДЫ ИЗМЕРЕНИЯ ТЕМПЕРАТУРЫ
- § 7. СВОЙСТВА ИДЕАЛЬНЫХ ГАЗОВ
- § 8. РАБОТА РАСШИРЕНИЯ СИСТЕМЫ И ФИЗИЧЕСКИЙ СМЫСЛ УНИВЕРСАЛЬНОЙ ГАЗОВОЙ ПОСТОЯННОЙ
- § 9. УРАВНЕНИЕ СОСТОЯНИЯ СМЕСИ ИДЕАЛЬНЫХ ГАЗОВ
- § 10. ИЗМЕРЕНИЕ ДАВЛЕНИЙ
- § 11. БАРОМЕТРИЧЕСКАЯ ФОРМУЛА
- Глава II. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- § 12. О ЗАКОНЕ СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ ЭНЕРГИИ
- § 13. РАБОТА КАК МАКРОСКОПИЧЕСКИЙ СПОСОБ ПЕРЕДАЧИ ЭНЕРГИИ
- § 14. ТЕПЛОТА КАК МИКРОФИЗИЧЕСКИЙ СПОСОБ ПЕРЕДАЧИ ЭНЕРГИИ. ТЕПЛОЕМКОСТЬ
- § 15. ИЗМЕРЕНИЕ ТЕПЛОЕМКОСТИ
- § 16. ВНУТРЕННЯЯ ЭНЕРГИЯ КАК ФУНКЦИЯ СОСТОЯНИЯ СИСТЕМЫ
- § 17. ФОРМУЛИРОВКА ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ
- § 18. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ ДЛЯ ИДЕАЛЬНЫХ ГАЗОВ
- § 19. ИЗОБАРИЧЕСКИЙ ПРОЦЕСС В ИДЕАЛЬНОМ ГАЗЕ
- § 20. ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС В ИДЕАЛЬНОМ ГАЗЕ
- § 21. АДИАБАТИЧЕСКИЙ ПРОЦЕСС В ИДЕАЛЬНОМ ГАЗЕ
- § 22. ПОЛИТРОПИЧЕСКИЕ ПРОЦЕССЫ В ИДЕАЛЬНОМ ГАЗЕ
- § 23. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ Cp/Cv
- § 24. ТЕПЛОЕМКОСТЬ СМЕСИ ГАЗОВ
- § 18. ЭНТАЛЬПИЯ КАК ФУНКЦИЯ СОСТОЯНИЯ СИСТЕМЫ
- Глава III. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ И ЕЕ ПРИМЕНЕНИЕ К ИДЕАЛЬНЫМ ГАЗАМ
- § 26. ИСХОДНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНОЙ ТЕОРИИ
- § 27. СРЕДНИЕ ВЕЛИЧИНЫ В ОПИСАНИИ МОЛЕКУЛЯРНЫХ СИСТЕМ
- § 28. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- § 29. РАСПРЕДЕЛЕНИЕ ЧАСТИЦ ПО ЭНЕРГИЯМ (РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА)
- § 30. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО КОМПОНЕНТАМ СКОРОСТЕЙ ИХ ТЕПЛОВОГО ДВИЖЕНИЯ (РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА)
- § 31. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО СКОРОСТЯМ ИХ ТЕПЛОВОГО ДВИЖЕНИЯ (РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА)
- § 32. ОПЫТНАЯ ПРОВЕРКА РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
- § 33. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА ПО КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 34. ПЛОТНОСТЬ ПОТОКА МОЛЕКУЛ В ИДЕАЛЬНОМ ГАЗЕ
- § 35. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ИДЕАЛЬНОГО ГАЗА В ПОЛВ СИЛЫ ТЯЖЕСТИ
- § 36. БРОУНОВСКОЕ ДВИЖЕНИЕ. ОПРЕДЕЛЕНИЕ ПЕРРЕНОМ ЧИСЛА АВОГАДРО
- § 37. ТЕОРЕМА О РАВНОРАСПРЕДЕЛЕНИИ И ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНЫХ ГАЗОВ
- § 38. КВАНТОВАЯ ТЕОРИЯ ТЕПЛОЕМКОСТИ ГАЗОВ
- § 39. ТЕРМОДИНАМИЧЕСКАЯ ВЕРОЯТНОСТЬ И РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ИДЕАЛЬНОГО ГАЗА В ПРОСТРАНСТВЕ
- Глава IV. ЯВЛЕНИЯ ПЕРЕНОСА И ИХ ТЕОРИЯ ДЛЯ ИДЕАЛЬНЫХ ГАЗОВ
- § 40. ТЕПЛОПРОВОДНОСТЬ
- § 41. ВНУТРЕННЕЕ ТРЕНИЕ (ВЯЗКОСТЬ)
- § 42. ДИФФУЗИЯ
- § 43. СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
- § 44. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО ДЛИНАМ ИХ СВОБОДНЫХ ПРОБЕГОВ
- § 45. ОБЩЕЕ УРАВНЕНИЕ ДЛЯ ЯВЛЕНИИ ПЕРЕНОСА В ИДЕАЛЬНЫХ ГАЗАХ
- § 46. ДИФФУЗИЯ В ИДЕАЛЬНЫХ ГАЗАХ
- § 47. ВНУТРЕННЕЕ ТРЕНИЕ В ИДЕАЛЬНЫХ ГАЗАХ
- § 48. ТЕПЛОПРОВОДНОСТЬ ИДЕАЛЬНЫХ ГАЗОВ
- § 49. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТАМИ ПЕРЕНОСА
- Глава V. СИЛЬНО РАЗРЕЖЕННЫЕ ГАЗЫ
- § 50. ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ ВАКУУМА
- § 51. СИЛЫ ТРЕНИЯ в ВАКУУМЕ
- § 52. ТЕПЛОПЕРЕДАЧА В ВАКУУМЕ
- § 53. ДИФФУЗИЯ В ВАКУУМЕ
- Глава VI. РЕАЛЬНЫЕ ГАЗЫ
- § 54. ОТКЛОНЕНИЕ ОТ ЗАКОНА БОЙЛЯ—МАРИОТТА
- § 55. РАВНОВЕСИЕ СИСТЕМЫ ЖИДКОСТЬ — ПАР
- § 56. ЭКСПЕРИМЕНТАЛЬНЫЕ ИЗОТЕРМЫ. КРИТИЧЕСКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- § 57. ПОТЕНЦИАЛ ПАРНОГО ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ
- § 58. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- § 59. ИЗОТЕРМЫ ВАН-ДЕР-ВААЛЬСА. КРИТИЧЕСКИЕ ПАРАМЕТРЫ И ПОСТОЯННЫЕ ВАН-ДЕР-ВААЛЬСА
- § 60. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА. ЭФФЕКТ ДЖОУЛЯ — ТОМСОНА
- § 61. СЖИЖЕНИЕ ГАЗОВ
- § 62. УРАВНЕНИЕ СОСТОЯНИЯ РЕАЛЬНЫХ ГАЗОВ В ВИРИАЛЬНОЙ ФОРМЕ
- Глава VII. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- § 63. РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ ПРОЦЕССЫ
- § 64. ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫ
- § 65. ЦИКЛИЧЕСКИЕ (КРУГОВЫЕ) ПРОЦЕССЫ
- § 66. ЦИКЛ КАРНО
- § 67. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ ДЛЯ ОБРАТИМЫХ ПРОЦЕССОВ
- § 68. ЭНТРОПИЯ КАК ФУНКЦИЯ СОСТОЯНИЯ СИСТЕМЫ
- § 69. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ ДЛЯ НЕОБРАТИМЫХ ПРОЦЕССОВ
- § 70. НЕРАВЕНСТВО КЛАУЗИУСА. ПРИНЦИП ВОЗРАСТАНИЯ ЭНТРОПИИ
- § 71. ЭНТРОПИЯ И ВЕРОЯТНОСТЬ СОСТОЯНИЯ СИСТЕМЫ
- § 72. О ТАК НАЗЫВАЕМОЙ «ТЕПЛОВОЙ СМЕРТИ ВСЕЛЕННОЙ»
- § 73. ИЗОЭНТРОПИЧЕСКОЕ СОСТОЯНИЕ ТРОПОСФЕРЫ ЗЕМЛИ
- § 74. ПРИМЕРЫ ИДЕАЛЬНЫХ ТЕХНИЧЕСКИХ ЦИКЛОВ. СХЕМА ХОЛОДИЛЬНОЙ МАШИНЫ
- Глава VIII. ЖИДКОСТИ
- § 75. ТЕПЛОВОЕ ДВИЖЕНИЕ И СТРУКТУРА ЖИДКОСТЕЙ
- § 76. ОСНОВНЫЕ СВОЙСТВА ЖИДКОСТЕЙ
- § 77. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ
- § 78. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ ПОВЕРХНОСТНОГО СЛОЯ ЖИДКОСТИ
- § 79. СИЛЫ, ВОЗНИКАЮЩИЕ НА КРИВОЙ ПОВЕРХНОСТИ ЖИДКОСТЕЙ
- § 80. КРАЕВОЙ УГОЛ. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- § 81. КИПЕНИЕ ЖИДКОСТЕЙ
- § 82. ТЕПЛОТА ПАРООБРАЗОВАНИЯ ЖИДКОСТЕЙ
- § 83. УРАВНЕНИЕ КЛАПЕЙРОНА — КЛАУЗИУСА
- § 84. ВЯЗКОСТЬ ЖИДКОСТЕЙ
- § 85. ЖИДКИЕ РАСТВОРЫ. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ. ЗАКОН РАУЛЯ
- § 86. ЖИДКИЙ ГЕЛИЙ. СВЕРХТЕКУЧЕСТЬ
- Глава IX. ТВЕРДЫЕ ТЕЛА
- § 87. ОСНОВНЫЕ ОСОБЕННОСТИ ТВЕРДЫХ ТЕЛ
- § 88. СТРУКТУРА КРИСТАЛЛОВ
- § 89. ФИЗИЧЕСКИЕ ТИПЫ КРИСТАЛЛИЧЕСКИХ РЕШЕТОК
- § 90. ТЕПЛОВОЕ ДВИЖЕНИЕ В КРИСТАЛЛАХ
- § 91. МЕХАНИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ
- § 92. ДЕФЕКТЫ В ТВЕРДЫХ ТЕЛАХ
- § 93. ТЕПЛОВОЕ РАСШИРЕНИЕ ТВЕРДЫХ ТЕЛ
- § 94. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ
- § 95. ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ
- § 96. ДИАГРАММЫ СОСТОЯНИЙ. ТРОЙНАЯ ТОЧКА
- § 97. ТЕПЛОТА ПЛАВЛЕНИЯ ПРОСТЫХ КРИСТАЛЛИЧЕСКИХ СТРУКТУР
- Глава X. ПОЛИМЕРЫ
- § 98. ОБЩИЕ ПРЕДСТАВЛЕНИЯ
- § 99. ПОЛУЧЕНИЕ ПОЛИМЕРОВ
- § 100. НЕКОТОРЫЕ ТИПЫ ПОЛИМЕРОВ. РОЛЬ МЕЖМОЛЕКУЛЯРНЫХ ВЗАИМОДЕЙСТВИЙ
- § 101. ТРИ СОСТОЯНИЯ АМОРФНЫХ ПОЛИМЕРОВ И ТЕПЛОВОЕ ДВИЖЕНИЕ В НИХ
- § 102. ЭЛАСТИЧНОСТЬ ПОЛИМЕРОВ
- § 103. КРИСТАЛЛИЧЕСКИЕ ПОЛИМЕРЫ
- § 104. ПРИМЕНЕНИЕ ПОЛИМЕРНЫХ МАТЕРИАЛОВ
- Глава XI. ЭЛЕМЕНТЫ ТЕРМОДИНАМИКИ ТЕКУЧИХ СРЕД И РАКЕТНОЙ ТЕХНИКИ
- § 105. РАБОТА ПЕРЕМЕЩЕНИЯ В ТЕКУЧИХ СРЕДАХ
- § 106. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ ДЛЯ ПОТОКОВ ГАЗОВ И ЖИДКОСТЕЙ
- § 107. ЧАСТНЫЕ СЛУЧАИ ТЕЧЕНИЯ СРЕД
- § 108. ИСТЕЧЕНИЕ ГАЗОВ ИЗ СОПЕЛ. КРИТИЧЕСКАЯ СКОРОСТЬ
- § 109. ПРИНЦИП ДВИЖЕНИЯ РАКЕТ
- § 110. ЭЛЕМЕНТАРНАЯ ТЕРМОДИНАМИКА РАКЕТНОГО ДВИГАТЕЛЯ
- § 111. СХЕМЫ РАКЕТНЫХ ДВИГАТЕЛЕЙ
- § 112. МНОГОСТУПЕНЧАТЫЕ РАКЕТЫ
- § 113. ДВИЖЕНИЕ СО СВЕРХЗВУКОВОЙ СКОРОСТЬЮ. УДАРНЫЕ ВОЛНЫ
- § 114. О ГРАДИЕНТЕ ТЕМПЕРАТУРЫ В ТРОПОСФЕРЕ ЗЕМЛИ
Формулы молекулярной физики
Формула концентрации молекул
Здесь n — концентрация 

Формула плотности
Здесь 


Формула относительной молекулярной массы
Здесь 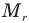

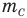
Формула количества вещества (количества молей)
Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).
Формулы массы одной молекулы
Здесь 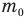
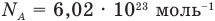



Формулы количества молекул
Здесь A — количество молекул (безразмерное), п — концентрация молекул 

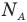
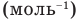

Формулы средней квадратичной скорости молекул
Здесь 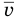
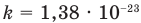

Основное уравнение кинетической теории идеального газа
Здесь р — давление газа (Па), 

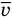

Формула средней кинетической энергии молекул
Здесь 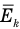
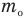
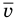
Связь шкал Цельсия и Кельвина
Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.
Связь средней кинетической энергии молекул идеального газа с абсолютной температурой
Здесь 
У равнение состояния идеального газа — уравнение Клапейрона — Менделеева
Здесь р — давление газа (Па), V — объем 
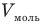
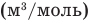
Объединенный газовый закон — уравнение Клапейрона
при
Здесь 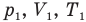

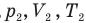

Закон Бойля — Мариотта (изотермический процесс)
при
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), 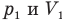

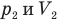

Закон Гей-Люссака (изобарный процесс)
при
Здесь р — давление газа (Па), m — масса газа (кг), 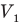
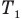

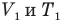

Закон Шарля
при
Здесь V — объем газа 
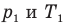
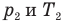
Связь давления идеального газа с концентрацией его молекул и температурой
Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа 
Формулы относительной влажности
Здесь 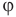
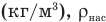
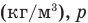
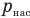
Работа при изобарном изменении объема газа
Здесь А — работа (Дж), р — давление газа (Па), 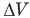
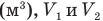

Внутренняя энергия идеального одноатомного газа
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), 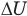
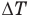
Первый закон термодинамики
Здесь Q — количество теплоты, переданное термодинамической системе (Дж), 
Применение первого закона термодинамики к термодинамическим процессам
к изотермическому: при
к изохорному: при V = const
к изобарному: при р = const
к адиабатному: при Q = 0
Здесь Т — абсолютная температура (К), 
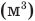
Формулы количества теплоты при нагревании или охлаждении тел
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), 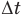
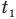
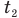
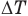
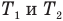
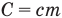
Формула количества теплоты при плавлении или кристаллизации
Здесь Q — количество теплоты (Дж), т — масса тела (кг), 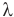
Формула количества теплоты при парообразовании или конденсации
Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).
Формула количества теплоты при сгорании топлива
Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).
Коэффициент полезного действия теплового двигателя
Здесь 
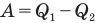
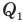
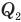
Коэффициент полезного действия идеального теплового двигателя
Здесь 
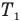
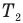
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:
Определение размеров молекул
1 способ. Основан на том, что молекулы вещества, когда оно находится в твердом или жидком состоянии, можно считать плотно прилегающими друг к другу. В таком случае для грубой оценки можно считать, что объем V некоторой массы m вещества просто равен сумме объемов содержащихся в нем молекул. Тогда объем одной молекулы мы получим, разделив объем V на число молекул N.
Число молекул в теле массой m равно, как известно, 
где М — молярная масса вещества NA — число Авогадро.
Отсюда объем V0 одной молекулы определяется из равенства
В это выражение входит отношение объема вещества к его массе.
Обратное же отношение
есть плотность вещества,
так что
Плотность практически любого вещества можно найти в доступных всем таблицах. Молярную массу легко определить, если известна химическая формула вещества.
Объем одной молекулы, если считать ее шариком, равен 
где r – радиус шарика.
Поэтому 
откуда мы и получаем выражение для радиуса молекулы:
Первый из этих двух корней — постоянная величина, равная ≈ 7,4 · 10-9 моль 1/3, поэтому формула для r принимает вид 
Например, радиус молекулы воды, вычисленный по этой формуле, равен rВ ≈ 1,9 · 10-10 м.
Описанный способ определения радиусов молекул не может быть точным уже потому, что шарики нельзя уложить так, чтобы между ними не было промежутков, даже если они соприкасаются друг с другом. Кроме того, при такой «упаковке» молекул – шариков были бы невозможны молекулярные движения. Тем не менее, вычисления размеров молекул по формуле, приведенной выше, дают результаты, почти совпадающие с результатами других методов, несравненно более точных.
2 способ. Метод Ленгмюра и Дево. В данном методе исследуемая жидкость должна растворяться в спирте (эфире) и быть легче воды, не растворяясь в ней. При попадании капли раствора на поверхность воды спирт растворяется в воде, а исследуемая жидкость образует пятно площадью S и толщиной d (порядка диаметра молекул).
Если допустить, что молекула имеет форму шара, то объем одной молекулы равен:

Необходимо определить диаметр молекулы d. В микропипетку набрать 0,5 мл раствора и, расположив ее над сосудом, отсчитать число капель n, содержащихся в этом объеме. Проделав опыт несколько раз, найти среднее значение числа капель в объеме 0,5 мл, а затем подсчитать объём исследуемой жидкости в капле: 
В ванну налить воду толщиной 1 – 2 см. Насыпать тальк тонким слоем на лист бумаги, ударяя слегка пальцем по коробочке. Расположив лист бумаги выше и сбоку от ванны на расстоянии 10 – 20 см, тальк сдуть с бумаги. На поверхность воды в ванне из пипетки капнуть одну каплю раствора. Линейкой измерить, средний диаметр образовавшегося пятна D и подсчитываю его площадь. Опыт повторить 2- 3 раза, а затем подсчитать диаметр молекул d.
3 способ. Определение диаметра молекулы. Будем считать, что капля масла растекается по воде до тех пор, пока толщина масляной плёнки не станет равной одной молекуле, тогда диаметр одной молекулы можно определить по формуле: d=V/S, где V – объём капли масла, S – площадь масленого пятна.
Объём капли масла можно определить следующим образом: накапать 100 капель из капилляра в сосуд и измерить массу масла в нём. После этого массу, выраженную в килограммах, поделить на плотность масла, которую можно взять из таблицы плотности некоторых веществ (плотность масла растительного 800 кг/м3).
Затем полученный результат поделить на количество капель. Объём капли можно определить также с помощью мерного цилиндра: накапать масло в цилиндр, измерить его объём в см3 и перевести в м3, для чего поделить на 1000000, затем на количество капель масла. После того, как объём капли стал известен нужно капнуть одну каплю масла на поверхность воды, которая налита в широкий сосуд.
Для ускорения реакции предварительно немного нужно нагреть воду – приблизительно до 400С. Масло начнёт растекаться, и в результате получится круглое пятно. После того, как пятно перестанет расширяться, с помощью линейки измерить его диаметр и рассчитать площадь пятна по формуле:
Практическое получение наночастиц
В современном мире в связи с общей тенденцией к миниатюризации большими темпами стала развиваться такая наука, как нанотехнология. Методы нанотехнологии позволяют получить принципиально новые устройства и материалы с характеристиками, значительно превосходящими их современный уровень, что весьма важно для интенсивного развития многих областей техники, биотехнологии, медицины, охраны окружающей среды и др.
Ход работы:
1) Определение объёма капли

2) Определение объёма капли путём взвешивания.
1. На весы накапали 10 капель растительного масла, измерили массу
mk=0,2 г
- Масса 1 капли m1=0,2 г/10=0,02 г
- Определение объёма капли V=m1/q=0,01г/0,8 г/см3=13 мм3
3) Определяем площадь пятна Sмасла=ПR2=11304 мм2
(Приложение 1,2,3,4,5)
4) Площадь пятна нефти Sнефти=20*16=32000 мм2
(Приложение 6,7,8,9)
5) Определяем толщину плёнки h=V/S
Для масла h=13/11304=1,2*10-7=120 нм
Для нефтиh=13/32000=4*10-8 м=40 нм
Вывод: В лабораторных условиях можно получать нанопленки
Заключение
Мы измерили толщину наноплёнок масла и нефти, изучили физические свойства плёнок и методы их получения, также ознакомились с физическими методами исследования микро- и наномасшатабных объектов.
К сожалению, из таких жидкостей как кислоты(уксусная, ортофосфорная, борная), моющие средства и мыло у нас не получилось сделать наноплёнки, потому что все эти жидкости гидрофобные(боятся воды).Мы пытались получить пленки с помощью скотча, но электронные весы позволяют измерять массу с точностью до десятых долей грамма
Список использованной литературы
- Анциферов Л.И. Самодельные приборы для физического практикума в средней школе. М.: Просвещение, 1985.
- Блудов М.И. Беседы по физике. М.: Просвещение, 1984.
- Буров В.А. Практикум по физике в средней школе. М.: Просвещение, 1973.
Приложения

Муниципальное общеобразовательное учреждение
«Снежногорская средняя общеобразовательная школа»
III муниципальная научно-практическая конференция
«На перекрёстке наук»
Определение размеров молекул
различных веществ
Автор:
Александрикова Татьяна Алексеевна,
10 класс
Руководитель:
Двойнова Марина Валерьевна,
учитель физики
п. Снежногорский
2012
Оглавление
- Введение ………………………………………………………………………………………3
- Глава I. Что такое молекула?……………………………………………………………………4
Глава II. Методы определения размеров молекул ….……………………………………5
Глава III. Определение диаметра молекул ……………………7
- Заключение ………………………………………………………………………………….8
- Список использованной литературы ………………………………………………………..9
Введение
Все тела, которые нас окружают, состоят из мельчайших частиц – молекул. Очень интересно узнать, каковы размеры молекул? Как их можно определить? Из-за очень малых размеров молекулы нельзя увидеть невооруженным глазом или с помощью обыкновенного микроскопа. Их можно увидеть только с помощью электронного микроскопа. Ученые доказали, что молекулы разных веществ отличаются друг от друга, а молекулы одного и того же вещества одинаковы. На практике измерить диаметр молекулы можно, но к сожалению, в школьной программе не предусмотрено изучение проблем такого рода.
Цель исследования: определить диаметр молекулы растительного масла.
Объект исследования: молекула растительного масла
Предмет исследования: диаметр молекулы.
Гипотеза: известно, из разных источников, что диаметр молекулы растительного масла может принять значение от 10-7 до 10-10м.
Задачи исследования:
- Изучение методов определения размеров молекул.
- Проведение эксперимента по определению размеров молекул.
- Анализ полученных результатов.
- Сравнение диаметра молекул полученных экспериментальным методом с статистическими данными.
Актуальность: работа относится к прикладным исследованиям и поможет лучше разобраться в вопросе определение размеров молекул.
Глава I. Что такое молекула?
Молекула в современном понимании – это наименьшая частица вещества, обладающая всеми его химическими свойствами. Молекула способна к самостоятельному существованию.
Различными способами было определено, что в 1 см3 любого газа при нормальных условиях содержится около 2,7×1019 молекул.
Чтобы понять, насколько велико это число, можно представить, что молекула – это «кирпич». Тогда если взять количество кирпичей, равное числу молекул в 1 см3 газа при нормальных условиях, и плотно уложить ими поверхность суши всего земного шара, то они покрыли бы поверхность слоем высотой 120 м, что почти в 4 раза превосходит высоту 10-этажного дома. Огромное число молекул в единице объёма указывает на очень малые размеры самих молекул. Например, масса молекулы воды m=29,9×10-27 кг. Соответственно малы и размеры молекул. Диаметром молекулы принято считать минимальное расстояние, на которое им позволяет сблизиться силы отталкивания. Однако понятие размера молекулы является условным, так как на молекулярных расстояниях представления классической физики не всегда оправданы. Средний размер молекул порядка 10-10м.
Если бы размер молекулы увеличить до размера точки в конце предложения в книге, то толщина человеческого волоса стала бы равна 40 м, а человек, стоя на поверхности Земли, упирался бы головою в Луну! Если из детского резинового шарика, надутого и наполненного водородом (массой 3г), каждую секунду выпускать по 1 миллиону молекул, то понадобится 30 миллиардов лет!
Молекула – это мельчайшая частица вещества, обладающая свойствами этого вещества. Так, молекула сахара – сладкая, а соли – соленая. Молекулы состоят из атомов. Размеры молекул ничтожно малы.
Как добыть молекулу из вещества? – механическим дроблением вещества. Каждому веществу соответствует определенный вид молекул. У разных веществ молекулы могут состоять из одного атома (инертные газы) или из нескольких одинаковых или различных атомов, или даже из сотен тысяч атомов (полимеры). Молекулы различных веществ могут иметь форму треугольника, пирамиды и других геометрических фигур, а также быть линейными.
Молекулы одного и того же вещества во всех агрегатных состояниях одинаковы.
Между молекулами в веществе существуют промежутки. Доказательствами существования промежутков служат изменение объема вещества, то есть расширение и сжатие вещества при изменении температуры, и явление диффузии. Молекулы вещества находятся в непрерывном тепловом движении.
Если удалить пространство из всех атомов человеческого тела, то все, что останется, сможет пролезть через игольное ушко.
Глава II. Методы определения размеров молекул
В молекулярной физике главные «действующие лица» — это молекулы, невообразимо маленькие частицы, из которых состоят все на свете вещества. Ясно, что для изучения многих явлений важно знать, каковы они, молекулы. В частности, каковы их размеры.
Когда говорят о молекулах, их обычно считают маленькими упругими твердыми шариками. Следовательно, знать размер молекул, значит знать их радиус или диаметр.
Несмотря на малость молекулярных размеров, физики сумели разработать множество способов их определения. В одном используется свойство некоторых (очень немногих) жидкостей растекаться в виде пленки толщиной в одну молекулу. В другом, размер частицы определяется с помощью сложного прибора – ионного проектора.
Строение молекул изучают различными экспериментальными методами. Электронография, нейтронография и рентгеновский структурный анализ позволяют получать непосредственную информацию о структуре молекул. Электронографии, метод, исследующий рассеяние электронов на пучке молекул в газовой фазе, позволяет рассчитать параметры геометрической конфигурации для изолированных сравнительно простых молекул. Нейтронография и рентгеновский структурный анализ ограничены анализом структуры молекул либо отдельных упорядоченных фрагментов в конденсированной фазе. Рентгенографические исследования кроме указанных сведений дают возможность получить количественные данные о пространственном распределении электронной плотности в молекулах.
Спектроскопические методы основаны на индивидуальности спектров химических соединений, которая обусловлена характерным для каждой молекулы набором состояний и отвечающих им энергетических уровней. Эти методы позволяют проводить качественный и количественный спектральный анализ веществ.
Разнообразную информацию о строении и свойствах молекул дает изучение их поведения во внешних электрических и магнитных полях.
Существуют, однако, очень простые способы определения размеров молекул:
1 способ. Основан на том, что молекулы вещества, когда оно находится в твердом или жидком состоянии, можно считать плотно прилегающими друг к другу. В таком случае для грубой оценки можно считать, что объем V некоторой массы m вещества просто равен сумме объемов содержащихся в нем молекул. Тогда объем одной молекулы мы получим, разделив объем V на число молекул N.
Число молекул в теле массой m равно, как известно, , где М — молярная масса вещества NA — число Авогадро. Отсюда объем V0 одной молекулы определяется из равенства
В это выражение входит отношение объема вещества к его массе. Обратное же отношение есть плотность вещества, так что
.
Плотность практически любого вещества можно найти в доступных всем таблицах. Молярную массу легко определить, если известна химическая формула вещества.
Объем одной молекулы, если считать ее шариком, равен , где r – радиус шарика. Поэтому
, откуда мы и получаем выражение для радиуса молекулы:
.
Первый из этих двух корней — постоянная величина, равная ≈ 7,4 · 10-9 моль1/3, поэтому формула для r принимает вид .
Например, радиус молекулы воды, вычисленный по этой формуле, равен rВ ≈ 1,9 · 10-10 м.
Описанный способ определения радиусов молекул не может быть точным уже потому, что шарики нельзя уложить так, чтобы между ними не было промежутков, даже если они соприкасаются друг с другом. Кроме того, при такой «упаковке» молекул – шариков были бы невозможны молекулярные движения. Тем не менее, вычисления размеров молекул по формуле, приведенной выше, дают результаты, почти совпадающие с результатами других методов, несравненно более точных.
2 способ. Метод Ленгмюра и Дево. В данном методе исследуемая жидкость должна растворяться в спирте (эфире) и быть легче воды, не растворяясь в ней. При попадании капли раствора на поверхность воды спирт растворяется в воде, а исследуемая жидкость образует пятно площадью S и толщиной d (порядка диаметра молекул).
Если допустить, что молекула имеет форму шара, то объем одной молекулы равен:
где d – диаметр молекулы.
Необходимо определить диаметр молекулы d. В микропипетку набрать 0,5 мл раствора и, расположив ее над сосудом, отсчитать число капель n, содержащихся в этом объеме. Проделав опыт несколько раз, найти среднее значение числа капель в объеме 0,5 мл, а затем подсчитать объём исследуемой жидкости в капле: , где n – число капель в объеме 0,5 мл, 1:400 – концентрация раствора.
В ванну налить воду толщиной 1 – 2 см. Насыпать тальк тонким слоем на лист бумаги, ударяя слегка пальцем по коробочке. Расположив лист бумаги выше и сбоку от ванны на расстоянии 10 – 20 см, тальк сдуть с бумаги. На поверхность воды в ванне из пипетки капнуть одну каплю раствора. Линейкой измерить, средний диаметр образовавшегося пятна D и подсчитываю его площадь. Опыт повторить 2- 3 раза, а затем подсчитать диаметр молекул d.
3 способ. Определение диаметра молекулы. Будем считать, что капля масла растекается по воде до тех пор, пока толщина масляной плёнки не станет равной одной молекуле, тогда диаметр одной молекулы можно определить по формуле: d=V/S, где V – объём капли масла, S – площадь масленого пятна. Объём капли масла можно определить следующим образом: накапать 100 капель из капилляра в сосуд и измерить массу масла в нём. После этого массу, выраженную в килограммах, поделить на плотность масла, которую можно взять из таблицы плотности некоторых веществ (плотность масла растительного 800 кг/м3). Затем полученный результат поделить на количество капель. Объём капли можно определить также с помощью мерного цилиндра: накапать масло в цилиндр, измерить его объём в см3 и перевести в м3, для чего поделить на 1000000, затем на количество капель масла. После того, как объём капли стал известен нужно капнуть одну каплю масла на поверхность воды, которая налита в широкий сосуд. Для ускорения реакции предварительно немного нужно нагреть воду – приблизительно до 400С. Масло начнёт растекаться, и в результате получится круглое пятно. После того, как пятно перестанет расширяться, с помощью линейки измерить его диаметр и рассчитать площадь пятна по формуле: .
Глава III. Определение диаметра молекулы
После изучения способов определения размера молекулы был выбран наиболее подходящий – третий способ.
ную массу растительного масла, а для этого необходимо знать химическую формулу растительного масла. Второй способ также невыполним, так как в данном методе исследуемая жидкость должна растворяться в спирте (эфире) и быть легче воды, не растворяясь в ней. Такой жидкостью может быть олеиновая кислота, которую сложно приготовить в школьной лаборатории.
Для проведения эксперимента был определён перечень лабораторного оборудования: шприц, лабораторная чашка, масляные вещества(вазелиновое масло, дизельное топливо, машинное масло), перманганат калия, линейка измерительная.
Цель работы: определить диаметр молекулы.
Ход эксперимента:
- Набираем исследуемую жидкость в мерный шприц.
- Определяем объём вещества по шкале нанесенной на шприц.
- Измеряем массу исследуемого вещества на электронных весах. Прежде чем, набрали вещество в шприц мы определили массу пустого шприца.
- Наливаем жидкость из шприца в воду, а затем наблюдаем, как расплывается пятно. Для того чтобы капля растекалась быстрее мы взяли воду нагретую примерно до 40 градусов, чтобы расплывшееся пятно было лучше видно мы добавили перманганат калия.
- Измеряем диаметр образовавшегося пятна мерной линейкой.
- Вычисляем площадь пятна. Образовавшееся пятно имеет форму круга, поэтому для определения его площади можно использовать формулу площади круга
.
- Вычисляем диаметр молекулы по формуле:
Все измерения и вычисления мы занесли в таблицу, по которой видно, что диаметры молекул исследуемых веществ подтверждают нашу гипотезу о том что диаметр молекул может принимать значения от 10-7 до 10-10м.
Определение объёма капли растительного масла.
В мерный цилиндр (мензурку) накапали 190 капель, общий объём которых составил 10 мл. Использую формулу для определения объём исследуемой жидкости в капле из метода Ленгмюра и Дево (2 способ), получаем .
- Определение площади масляного пятна.
Для того, чтобы получить масляное пятно провели несколько экспериментов.
В ванну размером 40×30 см необходимо налить воду и капнуть 1 каплю растительного масла, а затем наблюдать, как расплывается пятно, когда оно перестанет расплываться – измерить его диаметр.
Для определения площади пятна использовали формулу: .
Получаем: .
- Определение диаметра молекулы растительного масла.
Используем формулу: , получаем
.
Вывод: при расчёте диаметра молекулы растительного масла я получила значение , которое соответствует табличным данным.
Заключение
В результате работы я изучила литературу о молекулах, о методах определения диаметра
молекул. Используя полученные знания, я провела исследования по определению приблизительного диаметра молекулы растительного масла и получила следующий результат: .
Данный результат подтвердил моё предположение (гипотезу), что диаметр молекулы растительного масла может принять значение от 10-7 до 10-10м.
Цель моей работы достигнута, но изучение темы «Молекулы» ещё не закончено. На этом небольшом исследовании останавливаться не буду, так как есть много вопросов, на которые хочется найти ответы не только в книжках, но и убедиться самому, выполняя эксперимент. Например, ответить на вопросы: двигаются ли молекулы? Каковы размеры молекулы воды и как определить?
Список использованной литературы
- Анциферов Л.И. Самодельные приборы для физического практикума в средней школе. М.: Просвещение, 1985.
- Блудов М.И. Беседы по физике. М.: Просвещение, 1984.
- Буров В.А. Практикум по физике в средней школе. М.: Просвещение, 1973.
- http://medencped.ru/molekula/
- http://www.hemi.nsu.ru/text113.htm
- http://potomy.ru/world/2288.html
- http://www.alsak.ru/content/view/326/122/1/1
- http://marklv.narod.ru/mkt/str2.htm
- http://class-fizika.narod.ru/7_stroenie.htm
Лабораторная работа № 206
ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА
И ЭФФЕКТИВНОГО ДИАМЕТРА МОЛЕКУЛ ВОЗДУХА
Цель работы: 1) экспериментальное определение
средней длины свободного пробега молекул воздуха в
лаборатории;
2) определение эффективного диаметра молекул
воздуха.
Приборы и принадлежности:
стеклянный
баллон с краном,
мерный
стакан,
капиллярная
трубка,
линейка,
секундомер,
термометр,
барометр.
1. СРЕДНЯЯ ДЛИНА
СВОБОДНОГО ПРОБЕГА
МОЛЕКУЛ ГАЗА
Молекулы газа, находясь в
состоянии теплового хаотического движения, непрерывно сталкиваются друг с
другом. Термин «столкновение» применительно к молекулам не следует понимать
буквально и представлять себе этот процесс подобным соударению твердых шаров.
Под столкновением молекул подразумевают
процесс взаимодействия между молекулами, в результате которого молекулы
изменяют направление своего движения.
Рис. 1.
На рис. 1а представлен график зависимости
потенциальной энергии eп взаимодействия двух
молекул от расстояния r
между их центрами. Рассмотрим с помощью этого графика процесс сближения
(соударения) молекул. Мысленно поместим центр одной из молекул в начало
координат, а центр второй молекулы представим перемещающимся по оси r. Пусть вторая молекула
летит по направлению к первой из бесконечности, имея начальный запас
кинетической энергии. Приближаясь к
первой молекуле, вторая под действием силы притяжения движется со все
возрастающей скоростью. В результате кинетическая энергия молекулы eк также растет. Однако
полная энергия системы, равная e = eк+eп, остается неизменной
(система двух молекул замкнута), т.к. одновременно уменьшается потенциальная
энергия eп. При прохождении
молекулой точки с координатой r0
силы притяжения сменяются силами отталкивания, вследствие чего молекула
начинает быстро терять скорость (в области отталкивания кривая eп(r) идет очень круто). В
момент, когда потенциальная энергия eп становится равной полной
энергии системы e, скорость молекулы
обращается в нуль. В этот момент имеет место наибольшее сближение молекул
друг с другом. После остановки молекулы все явления протекают в обратной
последовательности: сначала молекула движется со все возрастающей скоростью
под действием силы отталкивания; миновав расстояние r0, молекула попадает под
действие замедляющей ее движение силы притяжения и, наконец, удаляется на
бесконечность, имея первоначальный запас кинетической энергии.
Минимальное расстояние,
на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис. 1b).
Величина
(1)
называется эффективным
сечением молекулы.
Значение d зависит от характера сил
взаимодействия, от энергии сближающихся молекул, т.е. от температуры. С
повышением температуры эффективный диаметр молекул уменьшается.
За секунду молекула
проходит в среднем путь, равный средней скорости . Если за секунду она претерпевает в среднем Z столкновений, то средняя
длина свободного пробега молекулы между двумя последовательными соударениями
будет равна
(2)
Рис. 2.
Для того чтобы подсчитать среднее число столкновений , предположим, что все молекулы газа представляют собой
упругие шарики радиуса r и все молекулы, кроме рассматриваемой, застыли
неподвижно на своих местах. Пусть молекула А движется со средней
скоростью (см. рис. 2). За
единицу времени она столкнется со всеми другими молекулами, центры которых
окажутся внутри цилиндра диаметром D
и высотой L, численно равной средней
скорости . Так молекула А не столкнется с молекулой С,
но испытает соударение с молекулой В. Так как средняя длина
свободного пробега молекул газа много больше, чем эффективный диаметр молекул,
то объем цилиндра можно считать равным
Умножив этот объем на число молекул в единице
объема n, получим среднее число
столкновений за единицу времени движущейся молекулы с неподвижными:
В действительности все
молекулы движутся, вследствие чего число соударений определяется средней
скоростью движения молекул по отношению друг к другу, а не средней скоростью молекул относительно
стенок сосуда:
Поэтому среднее число соударений должно быть
увеличено в раз:
(3)
Из соотношений (2) и (3) получим для средней
длины свободного пробега следующую формулу:
(4)
Из уравнения состояния идеального газа
следует, что концентрация молекул газа равна
Тогда формулу (4) можно записать
(5)
где k
– постоянная Больцмана, Т –
термодинамическая температура, Р –
давление, d – эффективный диаметр
молекул газа. Из формулы (5) видно, что при постоянной температуре с
увеличением давления Р средняя
длина свободного пробега молекул газа уменьшается.
Оценим среднюю длину
свободного пробега молекул газа. Молекулы имеют размеры порядка нескольких
десятых нанометра. Примем эффективный диаметр молекулы равным
Моль газа занимает при нормальных условиях (т.е.
при 0 °С и при Р = 1 атм = 1,013×105 Па) объем, равный
Число молекул в единице объема при этих условиях
равно
где NA – число Авогадро.
Подстановка этих чисел в формулу (4) дает
2. ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ И МЕТОДА
ИЗМЕРЕНИЙ
Молекулярно-кинетическая
теория позволила получить формулы, связывающие макроскопические параметры
газа (давление, объем, температура) с его микроскопическими параметрами
(размеры и масса молекулы, ее скорость, средняя длина свободного пробега).
Пользуясь этими формулами, можно на основании измеренных макроскопических
параметров газа найти его микроскопические параметры.
Для нахождения средней
длины свободного пробега молекул газа используют формулу,
выражающую зависимость коэффициента внутреннего трения (вязкости) h от :
(6)
где r – плотность газа.
Из теории Максвелла
следует, что средняя арифметическая скорость молекул газа равна
(7)
где R
– молярная газовая постоянная, Т –
термодинамическая температура, m – масса одного моля.
Состояние идеального газа
описывается уравнением Клапейрона-Менделеева:
Из последнего уравнения плотность газа
(8)
Подставив в формулу (6) значения и r из формул (7) и (8), получим:
(9)
В данной работе
используется зависимость коэффициента вязкости от радиуса r капиллярной трубки, через
которую проходит газ, ее длины l и
разности давлений DР,
возникающих на концах этой трубки. Эта зависимость выражается формулой
Пуазейля:
(10)
где V
– объем газа, в данном случае воздуха, проходящего через трубку за время t.
Из формул (9) и (10)
следует, что средняя длина свободного пробега молекул воздуха равна:
(11)
Из формулы (4)
эффективный диаметр молекулы
Учитывая, что
получим

где Р и
Т – давление и температура, при
которых проводится опыт (определяются по барометру и термометру, находящихся
в лаборатории).
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ОБРАБОТКА
РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1.
Наполняют баллон 1 на три четверти водой и плотно
закрывают пробкой 2, в которую вставлен капилляр 3.
2.
Линейкой замеряют первоначальный уровень воды h1. Открывают кран 4
(см. рис. 3) и одновременно включают секундомер.
3.
Когда в мерном стакане 5 будет 100 ¸ 200 мл воды (1 мл = 10–6 м3), закрывают кран и одновременно останавливают
секундомер.
4.
Замеряют уровень жидкости h2
в сосуде. Объем вытесненной из баллона воды в мерном стакане будет равен
объему воздуха V, вошедшего в баллон
через трубку 3.
5.
По формуле (11) рассчитывают среднюю длину свободного пробега молекул
воздуха. Разность давлений вычисляют по формуле:
(13)
где r – плотность воды. Расчет удобнее вести по
формуле (11), записанной в виде:
(14)
где А –
постоянная величина для данного опыта, которая равна
(15)
Рис. 3.
6.
Опыт повторяют три раза с одними и теми же значением V и h1.
7.
По формуле (12) рассчитывают эффективный диаметр молекулы воздуха d. Давление Р и
температуру Т воздуха в лаборатории
берут из показаний барометра и термометра.
8.
Методом расчета погрешностей косвенных измерений находят относительную
Е и абсолютную Dl погрешность средней
длины свободного пробега молекул воздуха. Для простоты расчетов используем
только формулы (14) и (13), считая, что вклад постоянной А (см. формулу (15)) в погрешность измерений незначителен, тогда

,
где и
абсолютные погрешности табличных величин;
и
абсолютные погрешности прямых однократных измерений,
зависящих от цены деления измерительных приборов; абсолютная погрешность прямых многократных измерений
времени.
9.
Данные измерений и вычислений занесите в таблицу.
Таблица
результатов
Температура воздуха Т = ……К, давление Р =……Па.
|
№ |
t, |
h1 |
h2 |
DР |
V |
|
|
Е |
|
|
|
п/п |
с |
м |
м |
Па |
м3 |
м |
м |
% |
м |
м |
Молярная
масса молекул воздуха m = 29×10–3 кг/моль, плотность воды r = 103 кг/м3,
постоянная Больцмана k
= 1,38×10–23 Дж/K,
молярная газовая постоянная R
= 8,31 Дж/(моль×К), 1 мм
рт.ст. = 133 Па.
4. ВОПРОСЫ
ДЛЯ ДОПУСКА К РАБОТЕ
- Сформулируйте цель
работы.
2.
Запишите рабочие формулы для расчета и d, поясните смысл всех
величин, входящих в эти формулы.
3.
Опишите рабочую установку и порядок выполнения работы.
5. ВОПРОСЫ
ДЛЯ ЗАЩИТЫ РАБОТЫ
1.
Что называется эффективным диаметром молекулы? Эффективным сечением?
2.
Дайте определение длины свободного пробега молекул газа.
3.
Выведите формулу для расчета (формулу (5)).
4.
Выведите рабочие формулы (11) и (12).
5.
Используя дифференциальный метод, получите формулу для расчета
относительной погрешности , т.е.