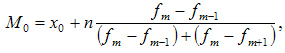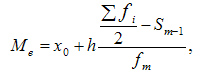Среднее арифметическое — статистический показатель, который демонстрирует среднее значение заданного массива данных. Такой показатель рассчитывается как дробь, в числителе которой стоит сумма всех значений массива, а в знаменателе — их количество. Среднее арифметическое — важный коэффициент, который находит применение в бытовых расчетах.
Смысл коэффициента
Среднее арифметическое — элементарный показатель для сравнения данных и подсчета приемлемого значения. К примеру, в разных магазинах продается банка пива конкретного производителя. Но в одном магазине она стоит 67 рублей, в другом — 70 рублей, в третьем — 65 рублей, а в последнем — 62 рубля. Довольно большой разбег цен, поэтому покупателю будет интересна средняя стоимость банки, чтобы при покупке товара он мог сравнить свои расходы. В среднем банка пива по городу имеет цену:
Средняя цена = (67 + 70 + 65 + 62) / 4 = 66 рублей.
Зная среднюю цену, легко определить где выгодно покупать товар, а где придется переплатить.
Среднее арифметические постоянно используется в статистических расчетах в случаях, если анализируется однородный набор данных. В примере выше — это цена банки пива одной марки. Однако мы не можем сравнить цену на пиво разных производителей или цены на пиво и лимонад, так как в этом случае разброс значений будет больше, средняя цена будет смазана и недостоверна, а сам смысл расчетов исказится до карикатурного «средняя температура по больнице». Для расчета разнородных массивов данных используется среднее арифметическое взвешенное, когда каждое значение получает свой весовой коэффициент.
Подсчет среднего арифметического
Формула для вычислений предельно проста:
P = (a1 + a2 + … an) / n,
где an – значение величины, n – общее количество значений.
Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.
К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.
Как считать средние для разнородных данных
В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12. Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.
Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.
Наша программа представляет собой простой и удобный калькулятор для расчета среднего арифметического. Для выполнения расчетов вам понадобится ввести только значения параметров.
Рассмотрим пару примеров
Расчет средней оценки
Многие учителя используют метод среднего арифметического для определения годовой оценки по предмету. Давайте представим, что ребенок получил следующие четвертные отметки по математике: 3, 3, 5, 4. Какую годовую оценку ему поставит учитель? Воспользуемся калькулятором и посчитаем среднее арифметическое. Для начала выберете соответствующее количество полей и введите значения оценок в появившиеся ячейки:
(3 + 3 + 5 + 4) / 4 = 3,75
Учитель округлит значение в пользу ученика, и школьник получит за год твердую четверку.
Расчет съеденных конфет
Давайте проиллюстрируем некоторую абсурдность среднего арифметического. Представим, что у Маши и Вовы было 10 конфет. Маша съела 8 конфет, а Вова — всего 2. Сколько конфет в среднем съел каждый ребенок? При помощи калькулятора легко вычислить, что в среднем дети съели по 5 конфет, что совершенно не соответствует действительности и здравому смыслу. Этот пример показывает, что показатель среднего арифметического важно считать для осмысленных наборов данных.
Заключение
Расчет среднего арифметического широко используется во многих научных сферах. Этот показатель популярен не только в статистических расчетах, но и в физике, механике, экономике, медицине или финансах. Используйте наши калькуляторы в качестве помощника для решения задач на вычисление среднего арифметического.
Средняя зарплата… Средняя продолжительность жизни… Практически каждый день мы с вами слышим эти словосочетания, используемые для описания множества одним единственным числом. Но как ни странно, «среднее значение» — достаточно коварное понятие, часто вводящее в заблуждение обычного, неискушенного в математической статистике, человека.
В чем проблема?
Под средним значением чаще всего подразумевается среднее арифметическое, которое очень сильно варьируется под воздействием единичных фактов или событий. И вы не получите реального представления о том, как именно распределены значения, которые вы изучаете.
Давайте обратимся к классическому примеру со средней зарплатой.
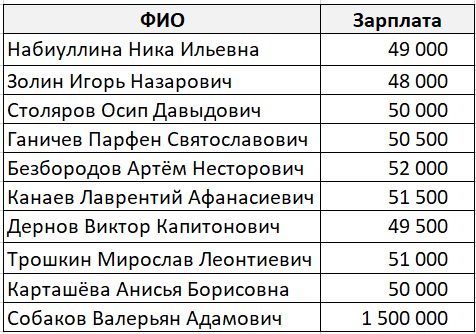
В какой-то абстрактной компании работает десять сотрудников. Девять из них получают зарплату около 50 000 рублей, а один 1 500 000 рублей (по странному совпадению он же является генеральным директором этой компании).
Средним значением в данном случае будет 195 150 рублей, что согласитесь, неправильно.
Какие способы вычисления среднего бывают?
Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.
Формула:
- x – среднее арифметическое;
- xn – конкретное значение;
- n – количество значений.
Плюсы:
- Хорошо работает при нормальном распределении значений в выборке;
- Легко вычислить;
- Интуитивно понятно.
Минусы:
- Не дает реального представления о распределении значений;
- Неустойчивая величина легко поддающаяся выбросам (как в случае с генеральным директором).
Вторым способом является вычисление моды, то есть наиболее часто встречающегося значения.
Формула:
- M0 – мода;
- x0 – нижняя граница интервала, который содержит моду;
- n – величина интервала;
- fm– частота (сколько раз в ряду встречается то или иное значение);
- fm-1 – частота интервала предшествующего модальному;
- fm+1 – частота интервала следующего за модальным.
Плюсы:
- Прекрасно подходит для получения представления об общественном мнении;
- Хорошо подходит для нечисловых данных (цвета сезона, хиты продаж, рейтинги);
- Проста для понимания.
Минусы:
- Моды может просто не быть (нет повторов);
- Мод может быть несколько (многомодальное распределение).
Третий способ — это вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. А если такого значения нет, то за медиану принимается среднее арифметическое между границами половин выборки.
Формула:
- Me – медиана;
- x0 – нижняя граница интервала, который содержит медиану;
- h – величина интервала;
- f i – частота (сколько раз в ряду встречается то или иное значение);
- Sm-1 – сумма частот интервалов предшествующих медианному;
- fm – число значений в медианном интервале (его частота).
Плюсы:
- Дает самую реалистичную и репрезентативную оценку;
- Устойчива к выбросам.
Минусы:
- Сложнее вычислить, так как перед вычислением выборку нужно упорядочить.
Мы рассмотрели основные методы нахождения среднего значения, называющиеся мерами центральной тенденции (на самом деле их больше, но это наиболее популярные).
А теперь давайте вернемся к нашему примеру и посчитаем все три варианта среднего при помощи специальных функций Excel:
СРЗНАЧ(число1;[число2];…)— функция для определения среднего арифметического;МОДА.ОДН(число1;[число2];...)— функция моды (в более старых версиях Excel использоваласьМОДА(число1;[число2];...));МЕДИАНА(число1;[число2];...)— функция для поиска медианы.
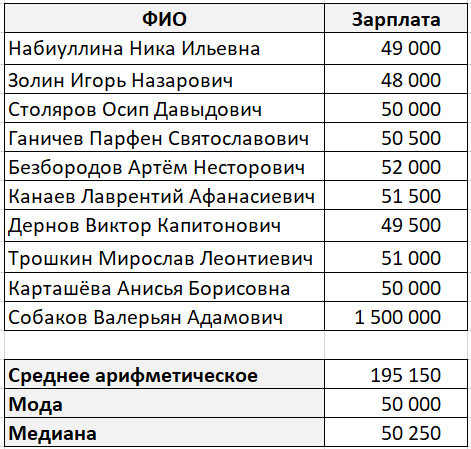
И вот какие значения у нас получились:
В данном случае мода и медиана гораздо лучше характеризуют среднюю зарплату в компании.
Но что делать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без проблем.
Вычисляем среднее арифметическое на SQL
Тут все достаточно просто, так как в SQL предусмотрена специальная агрегатная функция AVG.
И чтобы ее использовать достаточно написать вот такой запрос:
/* Здесь и далее salary - столбец с зарплатами, а employees - таблица сотрудников в нашей базе данных */ SELECT AVG(salary) AS 'Средняя зарплата' FROM employees
Вычисляем моду на SQL
В SQL нет отдельной функции для нахождения моды, но ее легко и быстро можно написать самостоятельно. Для этого нам необходимо узнать, какая из зарплат чаще всего повторяется и выбрать наиболее популярную.
Напишем запрос:
/* WITH TIES необходимо добавлять к TOP() если множество многомодально, то есть у множества несколько мод */ SELECT TOP(1) WITH TIES salary AS 'Мода зарплаты' FROM employees GROUP BY salary ORDER BY COUNT(*) DESC
Вычисляем медиану на SQL
Как и в случае с модой, в SQL нет встроенной функции для вычисления медианы, зато есть универсальная функция для вычисления процентилей PERCENTILE_CONT.
Выглядит все это так:
/* В данном случае процентиль 0.5 и будет являться медианой */
SELECT TOP(1) PERCENTILE_CONT(0.5)
WITHIN GROUP (ORDER BY salary)
OVER() AS 'Медианная зарплата'
FROM employees
Подробнее о работе функции PERCENTILE_CONT лучше почитать в справке Microsoft и Google BigQuery.
Какой способ все-таки использовать?
Из сказанного выше следует, что медиана лучший способ для вычисления среднего значения.
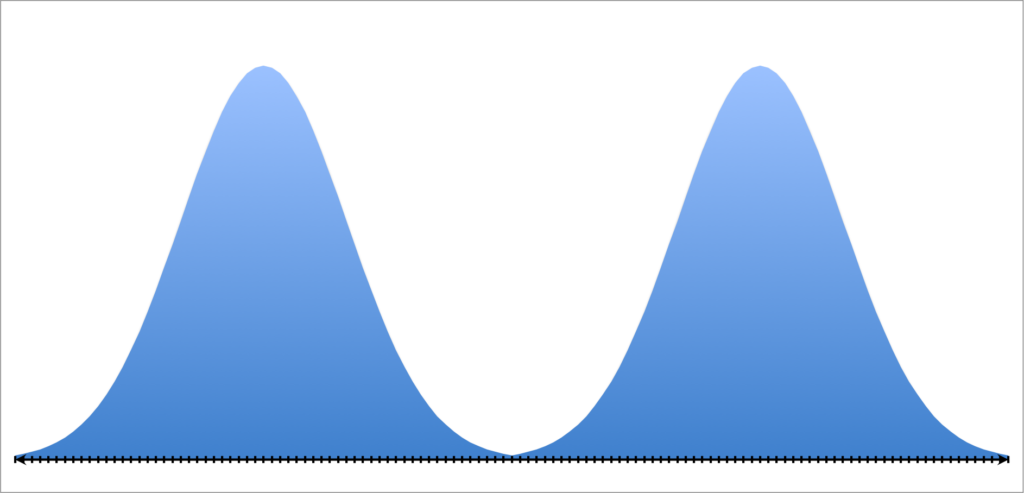
Но это не всегда так. Если вы работаете со средним, то остерегайтесь многомодального распределения:
На графике представлено бимодальное распределение с двумя пиками. Такая ситуация может возникнуть, например, при голосовании на выборах.
В данном случае среднее арифметическое и медиана — это значения, находящиеся где-то посередине и они ничего не скажут о том, что происходит на самом деле и лучше сразу признать, что вы имеете дело с бимодальным распределением, сообщив о двух модах.
А еще лучше разделить выборку на две группы и собрать статистические данные для каждой.
Вывод:
При выборе метода нахождения среднего нужно учитывать наличие выбросов, а также нормальность распределения значений в выборке.
Окончательный выбор меры центральной тенденции всегда лежит на аналитике.
Полезные ссылки:
- SQL и теория вероятностей (YouTube)
- Анализ нормальности распределения данных (YouTube)
- Меры центральной тенденции
- Об авторе
- Свежие записи
В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

Иногда при работе с данными нужно описать множество значений каким-то одним числом. Например, при исследовании эффективности сотрудников, уровня вовлеченности в аккаунте, KPI или времени ответа на сообщения клиентов. В таких случаях используют меры центральной тенденции. Их можно называть проще — средние значения.
Но в зависимости от вводных данных, находить среднее значение нужно по-разному. Основной набор задач закрывается с использованием среднего арифметического, медианы и моды. Но если выбрать неверный способ — выводы будут необъективны, а результаты исследования нельзя будет признать действительными. Чтобы не допустить ошибку, нужно понимать особенности разных способов нахождения средних значений.

Cтратег, аналитик и контент-продюсер. Работает с агентством «Палиндром».

Как считать среднее арифметическое
Использовать среднее арифметическое стоит тогда, когда множество значений распределяются нормально ― это значит, что значения расположены симметрично относительно центра. Как выглядит нормальное распределение на графике и в таблице, можно посмотреть на примере:


Если данные распределяются как в примерах — вам повезло. Можно без лишних заморочек считать среднее арифметическое и быть уверенным, что выводы будут объективны. Однако, нормальное распределение на практике встречается крайне редко, поэтому среднее арифметическое в большинстве случаев лучше не использовать.
Как рассчитать
Сумму значений нужно поделить на их количество. Например, вы хотите узнать средний ER за 4 дня при нормальном распределении значений и без аномальных выбросов. Для этого считаем среднее арифметическое: складываем ER всех дней и делим полученное число на количество дней.
Если хотите автоматизировать вычисления и узнать среднее арифметическое для большого числа показателей — используйте Google Таблицы:
- Заполните таблицу данными.
- Щелкните по пустой ячейке, в которую хотите записать среднее арифметическое.
- Введите «=AVERAGE(» и выделите ряд чисел, для которых нужно вычислить среднее арифметическое. Нажмите «Enter» после ввода формулы.
Когда можно не использовать
Если данные распределены ненормально, то наши расчеты не будут отражать реальную картину. На ненормальность распределения указывают:
- Отсутствие симметрии в расположении значений.
- Наличие ярко выраженных выбросов.
Как пример ненормального распределения (с выбросами) можно рассматривать среднее время ответа на комментарии по неделям:
Если посчитать среднее значение для такого набора данных с помощью среднего арифметического, то получится завышенное число. В итоге наши выводы будут более позитивными, чем реальное положение дел. Еще стоит учитывать, что выбросы могут не только завышать среднее значение, но и занижать его. В таком случае вы получите более скромный показатель, который не будет соответствовать реальности.
Например, в группе «Золотое Яблоко» во ВКонтакте иногда публикуют конкурсные посты. Они набирают более высокие показатели вовлеченности чем обычные публикации. Если посчитать средний ER с учетом конкурсов, мы получим 0,37%, а без учета конкурсов — только 0,29%. Аналогичная ситуация с числом комментариев. С конкурсами в среднем получаем 917 комментариев, а без конкурсов — всего лишь 503. Очевидно, что из-за розыгрышей средние показатели вовлеченности завышаются. В этом случае конкурсные посты следует исключить из анализа, чтобы объективно оценить эффективность контента в группе.
Еще часто бывает так, что данных очень много, заметны явные выбросы, но на их обработку и исключение аномальных значений не хватит ни времени, ни терпения. Тем более нет гарантий, что исключив выбросы, вы получите нормальное распределение. В таком случае лучше подсчитать средние значения, используя медиану.
Как найти медиану и когда ее применять
Если вы имеете дело с ненормальным распределением или замечаете значительные выбросы — используйте медиану. Так можно получить более адекватное среднее значение, чем при использовании среднего арифметического. Чтобы понять, как работать с медианой, рассмотрим аналогичный пример с ненормальным распределением времени ответов на комментарии.
Ниже в таблице уже введены данные из графика и рассчитано среднее время ответа с помощью среднего арифметического и медианы. Из расчетов видна наглядная разница между средним арифметическим и медианой ― она составляет 17 минут. Такое различие появляется из-за низкого темпа работы на выходных и в нестандартных ситуациях, когда к ответу на сообщения нужно относиться с особой ответственностью (события конца февраля). Подобные выбросы сильно завышают среднее арифметическое, а вот на медиану они практически не влияют. Поэтому если хотите посчитать среднее значение избегая влияния выбросов, — используйте медиану. Такие данные будут без искажений.
Как рассчитать
Разберем на примере. В аккаунте опубликовали семь постов и они набрали разное количество комментариев: 35, 105, 2, 15, 2, 31, 1. Чтобы вычислить медиану, нужно пройти два этапа:
- Расположите числа в порядке возрастания. Итоговый ряд будет выглядеть так: 1, 2, 2, 15, 31, 35, 105.
- Найдите середину сформированного ряда. В центре стоит число 15 — его и нужно считать медианой.
Немного сложнее найти медиану, если вы работаете с четным количеством чисел. Например, вы собрали количество лайков на последних шести постах: 32, 48, 36, 201, 52, 12. Чтобы найти медиану, выполните три действия:
- Расставьте числа по возрастанию: 12, 32, 36, 48, 52, 201.
- Возьмите два из них, наиболее близких к центру. В нашем случае — это 36 и 48.
- Сложите два этих числа и разделите на два: (36 + 48) / 2 = 42. Результат и есть медиана.
Чтобы вычислять медиану быстрее и обрабатывать большие объемы данных — используйте Google Таблицы:
- Внесите данные в таблицу.
- Щелкните по свободной ячейке, в которую хотите записать медиану.
- Введите формулу «=MEDIAN(» и выделите ряд чисел, для которых нужно рассчитать медиану. Нажмите «Enter», чтобы все посчиталось.
Когда можно не использовать
Если данные распределены нормально и вы не видите заметных выбросов — медиану можно не использовать. В этом случае значение среднего арифметического будет очень близким к медиане. Можете выбрать любой способ нахождения среднего, с которым вам работать проще. Результат от этого сильно не изменится.
Что такое мода и где ее использовать
Мода ― это самое популярное/часто встречающееся значение. Например, стоит задача узнать, сколько комментариев чаще всего набирают посты в аккаунте. В этом случае можно не высчитывать среднее арифметическое или медиану ― лучше и проще использовать моду.
Еще пример. Нужно узнать, в какое время аудитория чаще всего взаимодействует с публикациями. Для этого можно посчитать данные вручную или использовать готовую таблицу из LiveDune (вкладка «Вовлеченность» ― таблица «Лучшее время для поста»). По ее данным ― больше всего реакций пользователи оставляют в среду в 16 часов. Это время и есть мода. Таким образом, если вам нужно найти самое популярное значение, а не классическое среднее — проще использовать моду.
Как рассчитать
Чтобы найти наиболее часто встречающееся значение в наборе данных, нужно посмотреть, какое число встречается в ряду чаще всех. Например, для ряда 5, 4, 2, 4, 7 ― модой будет число 4.
Иногда в ряде значений встречается несколько мод. Например, ряду 7, 7, 21, 2, 5, 5 свойственны две моды — 7 и 5. В этом случае совокупность чисел называется мультимодальной. Также поиск моды можно упростить с помощью Google Таблиц:
- Внесите значения в таблицу.
- Щелкните по ячейке, в которую хотите записать моду.
- Введите формулу «=MODE(» и выделите ряд чисел, для которых нужно вычислить моду. Нажмите «Enter».
Однако важно иметь в виду, что табличная функция выдает только самую меньшую моду. Поэтому будьте внимательны — можно упустить из виду несколько мод.
Когда использовать не стоит
Моду нет смысла использовать, если вас не просят найти самое популярное значение. Там, где надо найти классическое среднее значение, про моду лучше забыть.
Памятка по использованию
Среднее арифметическое
Как находим: сумма чисел / количество чисел.
Используем: если данные распределены нормально и нет ярких выбросов.
Не используем: если видим явные выбросы или ненормальное распределение.
Медиана
Как находим: располагаем числа в порядке возрастания и находим середину сформированного ряда.
Используем: если работаем с ненормальным распределением или видим выбросы.
Не используем: если выбросов нет и распределение нормальное.
Мода
Как находим: определяем значение, которое чаще всего встречается в ряду чисел.
Используем: если нужно найти не среднее, а самое популярное значение.
Не используем: если нужно найти классическое среднее значение.
Только важные новости в ежемесячной рассылке
Нажимая на кнопку, вы даете согласие на обработку персональных данных.

Подписывайся сейчас и получи гайд аудита Instagram аккаунта
Маркетинговые продукты LiveDune — 7 дней бесплатно
Наши продукты помогают оптимизировать работу в соцсетях и улучшать аккаунты с помощью глубокой аналитики

Анализ своих и чужих аккаунтов по 50+ метрикам в 6 соцсетях.
Оптимизация обработки сообщений: операторы, статистика, теги и др.
Автоматические отчеты по 6 соцсетям. Выгрузка в PDF, Excel, Google Slides.
Контроль за прогрессом выполнения KPI для аккаунтов Инстаграм.
Аудит Инстаграм аккаунтов с понятными выводами и советами.
Поможем отобрать «чистых» блогеров для эффективного сотрудничества.
Как рассчитать средний показатель за год
Наиболее распространенной формой статистических показателей, используемых в социально-экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака статистической совокупности. Средние величины являются как бы «представителями» всего ряда наблюдений. Определить среднюю можно во многих случаях через исходное соотношение средней (ИСС) или ее логическую формулу:
Так, например, для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников:
Числитель исходного соотношения средней представляет собой ее определяющий показатель. Для средней заработной платы таким определяющим показателем является фонд заработной платы. Для каждого показателя, используемого в социально-экономическом анализе, можно составить только одно истинное исходное соотношение для расчета средней.
Следует еще добавить, что для того, чтобы более точно оценить стандартное отклонение для малых выборок (с числом элементов менее 30), в знаменателе выражения под корнем надо использовать не n, а n-1.
Понятие и виды средних величин
Средняя величина — это обобщающий показатель статистической совокупности, который погашает индивидуальные различия значений статистических величин, позволяя сравнивать разные совокупности между собой.
Существует 2 класса средних величин: степенные и структурные .
К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средние различных видов.
Степенные средние величины
Степенные средние могут быть простыми и взвешенными.
Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле средней степенной (при различной величине k (m)):
Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:
где x — средняя величина исследуемого явления;
xi – i -й вариант усредняемого признака ;
fi – вес i -го варианта.
где X – значения отдельных статистических величин или середин группировочных интервалов;
m — показатель степени, от значения которого зависят следующие виды степенных средних величин:
при m = -1 средняя гармоническая;
при m = 0 средняя геометрическая;
при m = 1 средняя арифметическая;
при m = 2 средняя квадратическая;
при m = 3 средняя кубическая.
Используя общие формулы простой и взвешенной средних при разных показателях степени m, получаем частные формулы каждого вида, которые будут далее подробно рассмотрены.
Средняя арифметическая
Средняя арифметическая – начальный момент первого порядка, математическое ожидание значений случайной величины при большом числе испытаний;
Средняя арифметическая — это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий вид:
где X — значения величин, для которых необходимо рассчитать среднее значение; N — общее количество значений X (число единиц в изучаемой совокупности).
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической простой: (3+4+4+5)/4 = 16/4 = 4.
Средняя арифметическая взвешенная имеет следующий вид:
где f — количество величин с одинаковым значением X (частота).
>Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической взвешенной: (3*1 + 4*2 + 5*1)/4 = 16/4 = 4.
Если значения X заданы в виде интервалов, то для расчетов используют середины интервалов X, которые определяются как полусумма верхней и нижней границ интервала. А если у интервала X отсутствует нижняя или верхняя граница (открытый интервал), то для ее нахождения применяют размах (разность между верхней и нижней границей) соседнего интервала X.
Например, на предприятии 10 работников со стажем работы до 3 лет, 20 — со стажем от 3 до 5 лет, 5 работников — со стажем более 5 лет. Тогда рассчитаем средний стаж работников по формуле средней арифметической взвешенной, приняв в качестве X середины интервалов стажа (2, 4 и 6 лет):
(2*10+4*20+6*5)/(10+20+5) = 3,71 года.
Функция СРЗНАЧ
Эта функция вычисляет среднее (арифметическое) своих аргументов.
Число1, число2, . — это от 1 до 30 аргументов, для которых вычисляется среднее.
Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа. Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения, учитываются.
Функция СРЗНАЧА
Вычисляет среднее арифметическое значений, заданных в списке аргументов. Помимо чисел в расчете могут участвовать текст и логические значения, такие как ИСТИНА и ЛОЖЬ.
Значение1, значение2. — это от 1 до 30 ячеек, интервалов ячеек или значений, для которых вычисляется среднее.
Аргументы должны быть числами, именами, массивами или ссылками. Массивы и ссылки, содержащие текст, интерпретируются как 0 (ноль). Пустой текст (“”) интерпретируется как 0 (ноль). Аргументы, содержащие значение ИСТИНА, интерпретируются как 1, Аргументы, содержащие значение ЛОЖЬ, интерпретируются как 0 (ноль).
Средняя арифметическая применяется чаще всего, но бывают случаи, когда необходимо применение других видов средних величин. Рассмотрим такие случаи далее.
Средняя гармоническая
Средняя гармоническая для определения средней суммы обратных величин;
Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:
Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf. В тех случаях, когда все w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:
Например, автомобиль ехал из пункта А в пункт Б со скоростью 90 км/ч, а обратно — со скоростью 110 км/ч. Для определения средней скорости применим формулу средней гармонической простой, так как в примере дано расстояние w1=w2 (расстояние из пункта А в пункт Б такое, же как и из Б в А), которое равно произведению скорости (X) на время (f). Средняя скорость = (1+1)/(1/90+1/110) = 99 км/ч.
Функция СРГАРМ
Возвращает среднее гармоническое множества данных. Среднее гармоническое — это величина, обратная к среднему арифметическому обратных величин.
Число1, число2, . — это от 1 до 30 аргументов, для которых вычисляется среднее. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.
Среднее гармоническое всегда меньше среднего геометрического, которое всегда меньше среднего арифметического.
Средняя геометрическая
Средняя геометрическая для оценки средних темпов роста случайной величин, нахождения значения признака, равноудаленного от минимального и максимального значения;
Средняя геометрическая применяется при определении средних относительных изменений. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.
Например, в период с 2005 по 2008 годы индекс инфляции в России составлял: в 2005 году — 1,109; в 2006 — 1,090; в 2007 — 1,119; в 2008 — 1,133. Так как индекс инфляции — это относительное изменение (индекс динамики), то рассчитывать среднее значение нужно по средней геометрической: (1,109*1,090*1,119*1,133)^(1/4) = 1,1126, то есть за период с 2005 по 2008 ежегодно цены росли в среднем на 11,26%. Ошибочный расчет по средней арифметической дал бы неверный результат 11,28%.
Функция СРГЕОМ
Возвращает среднее геометрическое значений массива или интервала положительных чисел. Например, функцию СРГЕОМ можно использовать для вычисления средних темпов роста, если задан составной доход с переменными ставками.
СРГЕОМ (число1; число2; . )
Число1, число2, . — это от 1 до 30 аргументов, для которых вычисляется среднее геометрическое. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.
Средняя квадратическая
Средняя квадратическая – начальный момент второго порядка.
Средняя квадратическая применяется в тех случая, когда исходные значения X могут быть как положительными, так и отрицательными, например при расчете средних отклонений.
Главной сферой применения квадратической средней является измерение вариации значений X.
Средняя кубическая
Средняя кубическая – начальный момент третьего порядка.
Средняя кубическая применяется крайне редко, например, при расчете индексов нищеты населения для развивающихся стран (ИНН-1) и для развитых (ИНН-2), предложенных и рассчитываемых ООН.
Как рассчитать средний заработок за год
При расчете многих видов выплат в пользу работников используется средняя заработная плата. Рассмотрим, как посчитать среднюю заработную плату за год и в каких случаях она требуется.
Для чего нужна средняя заработная плата
Трудовой кодекс предусматривает оплату «по среднему» во многих ситуациях. Их можно в целом охарактеризовать, как отклонения от обычного порядка работы. Наиболее распространенными вариантами, при которых необходимо знать, как рассчитать средний заработок за год, являются следующие:
- Выплата отпускных или компенсации за неиспользованный отпуск (ст. 114, 126, 127 ТК РФ).
- Обучение с отрывом от работы (ст. 167 ТК РФ)
- Нахождение в командировке (ст. 167 ТК РФ).
- Расчет суммы выходного пособия (ст. 178 ТК РФ).
Нормативная база и основные правила расчета
Общая информация о том, как посчитать среднюю зарплату за год, указана в ст. 139 ТК РФ.
Более подробный алгоритм расчета, учитывающий различные ситуации, приводится в постановлении Правительства РФ от 24.12.2007 № 922.
Главным правилом расчета является использование информации о доходах и отработанном времени за 12 месяцев, предшествующих расчетному периоду.
Расчет всех выплат, определяемых по среднему заработку, производится исходя из среднедневного заработка. Но порядок его определения отличается для разных категорий выплат. Существуют два подхода к расчету – для отпускных (компенсаций за отпуск) и во всех иных случаях.
Для выплаты отпускных, если отпуск предоставляется в календарных днях используется среднегодовое количество календарных дней в месяце – 29,3. Здесь тоже существуют два варианта:
- Если расчетный период (год) был отработан полностью, то доход за период (ФОТ) делится на установленное количество дней, умноженное на 12
СЗ = ФОТ / (12 х 29,3)
- Если период был отработан частично, то для определения количества дней складывается произведение 29,3 дней на количество «полных» месяцев (Мп) и сумма календарных дней, приходящихся на «неполные» месяца (Дн).
СЗ = ФОТ / (Мп х 29,3 + Дн)
Дни, приходящиеся на неполные месяцы, определяются как:
Дн = 29,3 / Км х Ко, где
Км – количество календарных дней в соответствующем месяце
Ко – количество календарных дней, соответствующее отработанному времени.
Если отпуск предоставляется в рабочих днях, то сумма дохода делится на количество рабочих дней, приходящихся на отработанный период, исходя из 6-ти дневной рабочей недели.
Во всех иных случаях расчета, не связанных с отпускными или компенсацией за отпуск, общий ФОТ за период делится на количество фактически отработанных дней или часов (при почасовом учете рабочего времени):
Пример 1
Инженер Иванов А.П. в феврале 2018 г. написал заявление на отпуск. Его доход за предшествующие 12 месяцев составил 520 тыс. руб. Предположим, что Иванов А.П. в течение этого периода не был в отпуске и не болел. Тогда вся сумма дохода будет использована для расчета и отпускные Иванова И.П. будут рассчитаны исходя из следующего среднедневного заработка:
СЗ = 520 000 / (12 х 29,3) = 1478,95 руб.
Пример 2
Теперь воспользуемся условиями предыдущего примера и предположим, что Иванов был на больничном две недели в течение июня 2017 г. и получил выплату по больничному листу в сумме 20 тыс. руб. Тогда сумма, используемая для расчета, будет равняться
ФОТ = 520 тыс. руб. – 20 тыс. руб. = 500 тыс. руб.
А количество дней нужно определить, как
Д = Дп + Дн = 11 мес. х 29,3 + 29,3 / 30 дн. х 15 дн. = 322 дн. + 15 дн. = 337 дней
Отсюда:
СЗ = 500 000 руб. / 337 дн. =1483,68 руб.
Аналогично производится расчет при нахождении работника в течение расчетного периода в очередном отпуске, в декрете и т.п.
Какие выплаты и в каком порядке включаются в расчет
Чтобы узнать, как рассчитать среднюю зарплату за год, нужно учесть все виды выплат – заработная плата со всеми надбавками, премии и иные аналогичные платежи.
Включение премиальных выплат связано с определенными особенностями и зависит от периода, за который начисляется премия:
- При месячном премировании в расчет включается не более одной премии каждого вида в месяц. Например, для менеджера по продажам это может быть премия за перевыполнение плана по выручке и за привлечение новых клиентов.
- Если период премирования больше месяца, но меньше или равен расчетному периоду (году), то премии учитываются аналогично месячным, т.е. в полном объеме. Это же относится к единовременной выплате за выслугу лет. Например, квартальная премия используется, чтобы определить, как рассчитать средний заработок за 3 месяца, а годовой бонус – чтобы узнать, как рассчитать среднемесячную зарплату за год.
- Если период, за который начислена премия, превышает расчетный, то учитывается месячная часть премии за каждый месяц расчетного периода.
В случае, когда расчетный период был отработан не полностью, включение премий зависит от порядка их начисления. Если премия начислялась пропорционально отработанному времени, то она включается в полном объеме. Если же порядок расчета премиальной выплаты не зависит от рабочего времени, то ее сумма входит в расчет пропорционально фактическому времени работы.
Если в течение расчетного периода или периода выплаты производилось повышение заработной платы, выплаты «по среднему» также подлежат индексации. Порядок того, как рассчитать среднюю заработную плату за год в этом случае, зависит от периода, когда повысилась заработная плата:
- Если повышение произошло во время отчетного периода, то индексируются доходы за каждый месяц периода. Коэффициент определяется, как отношение увеличенного оклада (тарифа) к соответствующим показателям расчетных месяцев.
- Если заработную плату повысили по окончании расчетного периода, но до начала времени выплаты «по-среднему», то индексируются не исходные данные, а итоговый показатель – заработок за день.
- Если повышение произошло после начала выплат «по-среднему», то также увеличивается дневной заработок, но не с начала периода выплаты, а с даты повышения.
Доходы, не включаемые в расчет и расчет при отсутствии доходов
В расчет не включаются следующие категории доходов:
- Различные выплаты социального характера (материальная помощь, компенсация питания и т.д.).
- Выплаты за период, когда работник по тем или иным причинам освобождается от работы с оплатой «по-среднему». В этом случае из расчета исключаются не только выплаты, но и период:
- нахождения в декретном отпуске или на больничном; ;
- дополнительные выходные дни по уходу за ребенком-инвалидом;
- другие случаи, когда за работником сохраняется средняя заработная плата в соответствии с ТК РФ.
Возможна ситуация, когда работник не получал зарплату в течение расчетного периода. В этом случае последовательно рассматриваются следующие варианты:
- Если работник имел доход за предыдущие 12 месяцев, то используется этот период. Порядок того, как рассчитать средний заработок за 2 года аналогичен расчету за год.
- Если ни в расчетном, ни в предыдущих периодах дохода не было, то берется доход за текущий месяц.
- Если же и доход за текущий период еще не начислен, то расчет оплаты «по-среднему» производится, исходя из оклада или тарифа.
Вывод
Средняя заработная плата рассчитывается в случаях, когда ТК РФ предусматривает выплаты в пользу сотрудников за неотработанное время либо при изменении режима работы. В стандартной ситуации она исчисляется на основе доходов и фактически отработанного времени за последние 12 месяцев.
CFA — Среднее арифметическое и меры центральной тенденции
Рассмотрим среднее арифметическое, — одну из наиболее распространенных мер центральной тенденции, используемых для анализа финансовых данных, — в рамках изучения количественных методов по программе CFA.
Меры центральной тенденции.
До сих пор мы обсуждали методы, которые мы можем использовать для организации и представления финансовых данных с целью того, чтобы они были более понятными.
Например, частотное распределение доходности класса активов показывает характер рисков, с которыми инвесторы могут столкнуться в конкретном классе активов. Гистограмма годовой доходности S&P 500 ясно показывает, что большие положительные и отрицательные значения годовой доходности являются обычной ситуацией.
Хотя таблицы частотных распределений и гистограммы предоставляют собой удобный способ обобщить серии наблюдений, эти методы являются лишь первым шагом к описанию финансовых данных.
В этом разделе мы обсудим использование количественных показателей, которые объясняют характеристики данных. Наше внимание сосредоточено на мерах центральной тенденции и других показателях (или параметрах), характеризующих положение данных.
Показатель или мера центральной тенденции (англ. ‘measure of central tendency’) указывает, насколько центрированы финансовые данные.
Меры центральной тенденции, вероятно, используются более широко, чем любые другие статистические показатели, потому что их легко рассчитать и применить. Меры положения (англ. ‘measures of location’) включают в себя не только меры центральной тенденции, но и другие показатели, которые иллюстрируют местоположение или распространение данных в рамках распределения.
Далее мы рассмотрим общепринятые меры центральной тенденции — среднее арифметическое, медиану, моду, взвешенное среднее и среднее геометрическое. Мы также объясняем другие полезные меры положения, включая квартили, квинтили, децили и процентили.
Среднее арифметическое.
Финансовые аналитики и портфельные менеджеры часто хотят получить одно число, которое репрезентативно описывает возможный исход инвестиционного решения. Среднее арифметическое — безусловно, наиболее часто используемая мера середины или центра данных.
Определение среднего арифметического.
Среднее арифметическое (англ. ‘arithmetic mean’) — это сумма наблюдений, деленная на количество наблюдений.
Мы можем вычислить среднее арифметическое как для совокупностей, так и для выборок. Эти показатели известны как среднее по совокупности и выборочное среднее значение соответственно.
Среднее значение для совокупности.
Среднее значение для совокупности (математическое ожидание или среднее по совокупности, от англ. ‘population mean’) — это среднее арифметическое значение, рассчитанное для совокупности.
Если мы можем адекватно определить совокупность, то мы можем рассчитать среднее значение для совокупности как среднее арифметическое всех наблюдений или значений в совокупности.
Например, аналитики, изучающие годовой рост продаж крупных оптовых клубов в США за 2013 финансовый год, могут определить интересующую совокупность, включив в нее только три компании: BJ’s Wholesale Club (частная компания с 2011 г.), Costco Wholesale Corporation. и Sam’s Club, входящую в группу Wal-Mart.
Оптовый клуб (англ. ‘wholesale club’) — это формат магазина, предназначенного в основном для оптовых продаж в торговых точках размером со склад для клиентов, которые платят членские взносы. По состоянию на начало 2010-х годов эти три оптовых клуба доминировали в данном сегменте в Соединенных Штатах.
В качестве другого примера можно привести портфельного менеджера, специализирующегося на индексе Nikkei 225. Интересующая его совокупность включает 225 акций из первой секции Токийской фондовой биржи, которые формируют индекс Nikkei.
Формула среднего значения для совокупности.
Среднее по совокупности, ( bf mu), является средним арифметическим значением совокупности.
Для конечной совокупности используется следующая формула среднего значения:
(large^X_i over N> >) (Формула 2)
- (N) — количество наблюдений во всей совокупности, а
- (X_i) — (i)-е наблюдение.
Среднее по совокупности является примером статистического параметра. Среднее значение для совокупности уникально; то есть, данная совокупность имеет только одно среднее значение.
Чтобы проиллюстрировать расчеты по приведенной формуле, мы можем найти среднее по совокупности для доли прибыли в выручке американских компаний, управляющих крупными оптовыми клубами за 2012 год.
В течение года прибыль в процентах от выручки для оптовых клубов BJ, Costco Wholesale Corporation, и Wal-Mart Stores составляли 0,9%, 1,6% и 3,5% соответственно, согласно списку Fortune 500 за 2012 год. Таким образом, среднее значение по совокупности для прибыли в процентах от выручки составило:
(mu) = (0,9 + 1,6 + 3,5)/3 = 6/3 = 2%
Выборочное среднее значение.
Среднее значение по выборке (выборочное среднее или выборочное среднее значение, от англ. ‘sample mean’) — это среднее арифметическое значение, вычисленное для выборки.
Очень часто мы не можем наблюдать каждый элемент множества данных; вместо этого мы наблюдаем подмножество или выборку из генеральной совокупности.
Концепция среднего значения может применяться к наблюдениям в выборке с небольшим изменением обозначений.
Формула выборочного среднего значения.
Выборочное среднее, ( overline ) (читается как «X-bar») — это среднее арифметическое значение по выборке:
(large = ^X_i over n> >) (Формула 3)
- (n) — количество наблюдений в выборке.
Формула 3 предписывает суммировать значения наблюдений (X_i) и делить эту сумму на количество наблюдений. Например, если выборка коэффициентов прибыли на акцию (P/E) для шести публичных компаний содержит значения 35, 30, 22, 18, 15 и 12, то среднее значение P/E для выборки будет 132/6 = 22. Среднее значение выборки также называется средним арифметическим (англ. ‘arithmetic average’).
Как отмечалось ранее, выборочное среднее значение является статистикой (то есть описательной мерой выборки).
Средние значения можно рассчитывать для отдельных статистических единиц или для временного отрезка.
В качестве примера можно привести рентабельность собственного капитала (ROE) за 2013 год для 100 компаний из FTSE Eurotop 100, индексе 100 крупнейших компаний Европы. В этом случае мы рассчитываем среднее значение ROE за 2013 год в среднем по 100 отдельным статистическим единицам (или элементам множества, от англ. ‘statistical unit’ или просто ‘unit’).
Когда мы изучаем характеристики некоторых статистических единиц в определенный момент времени (например, ROE для FTSE Eurotop 100), мы изучаем перекрестные данные (англ. ‘cross-sectional data’). Среднее этих наблюдений называется перекрестным средним значением (англ. ‘cross-sectional mean’).
С другой стороны, если наша выборка состоит из исторической месячной доходности по FTSE Eurotop 100 за последние 5 лет, то мы имеем дело с данными временного ряда (англ. ‘time-series data’). Среднее значение этих наблюдений называется средним временного ряда (англ. ‘time-series mean’).
Мы рассмотрим специализированные статистические методы, связанные с поведением временных рядов в следующих разделах, посвященных анализу временных рядов.
Ниже мы покажем пример определения выборочной средней доходности для 16 европейских фондовых рынков за 2012 г. В этом случае среднее значение является перекрестным, поскольку мы усредняем доходность по отдельным странам.
Пример вычисления перекрестного среднего значения.
Индекс MSCI EAFE (Европа, Австралия и Дальний Восток) — это индекс рыночной капитализации, скорректированный с учетом свободного обращения акций, предназначенный для оценки акций в развитых странах, за исключением США и Канады.
Термин «скорректированный с учетом свободного обращения акций» (англ. ‘free float-adjusted’) означает, что веса компаний в индексе отражают стоимость акций, фактически доступных для инвестиций.
По состоянию на сентябрь 2013 года EAFE состояла из 22 индексов стран развитых рынков, включая индексы для 16 европейских рынков, 2 австралийских рынков (Австралия и Новая Зеландия), 3 дальневосточных рынков (Гонконг, Япония и Сингапур) и Израиля.
Предположим, что мы заинтересованы в показателях динамики местной валюты на 16 европейских рынках EAFE в 2012 году. Мы хотим найти примерную среднюю общую доходность за 2012 год по этим 16 рынкам.
Ряды ставок доходности, представленные в Таблице 8, приведены в местной валюте (то есть доходность указана для инвесторов, проживающих в стране). Поскольку эта доходность не указывается в валюте каждого отдельного инвестора, она не является доходностью, которую мог бы получить отдельный инвестор. Это, скорее, средняя доходность для местных валют 16 стран.
Что такое средняя величина мы уже разобрали вот здесь. Сейчас поговорим о том, как рассчитывать среднюю величину.
В классическом виде общая теория статистики предлагает нам один вариант правил выбора средней величины.
Сначала необходимо составить правильно логическую формулу для расчета средней величины (ЛФС). Для каждой средней величины всегда есть только одна логическая формула ее расчета, поэтому ошибиться тут трудно. Но всегда надо помнить, что в числителе (это то, что сверху дроби) сумма всех явлений, а в знаменателе (то, что внизу дроби) общее количество элементов.
После того как составлена логическая формула можно пользоваться правилами (для простоты понимания упростим их и сократим):
1. Если в исходных данных (определяем по частоте) представлен знаменатель логической формулы, то расчет проводим по формуле средней арифметической взвешенной.
2. Если в исходных данных представлен числитель логической формулы, то расчет ведем по формуле средней гармонической взвешенной.
3. Если в задаче представлены сразу и числитель и знаменатель логической формулы (такое бывает редко), то расчет проводим по этой формуле или по формуле средней арифметической простой.
Это классическое представление о выборе верной формулы расчета средней величины. Далее представим последовательность действий при решении задач на расчет средней величины.
Алгоритм решения задач на расчет средней величины
А. Определяем способ расчета средней величины – простой или взвешенный. Если данные представлены в таблице то используем взвешенный способ, если данные представлены простым перечислением, то используем простой способ расчета.
Б. Определяем или расставляем условные обозначения – x – варианта, f – частота. Варианта это то, для какого явления требуется найти среднюю величину. Оставшиеся данные в таблице будут частотой.
В. Определяем форму расчета средней величины – арифметическая или гармоническая. Определение проводится по колонке частот. Арифметическая форма используется, если частоты заданы явным количеством (условно к ним можно подставить слово штук, количество элементов «штук»). Гармоническая форма используется, если частоты заданы не явным количеством, а сложным показателем (произведением осредняемой величины и частоты).
Самое сложное, это догадаться, где и какое количество задано, особенно неопытному в таких делах студенту. В такой ситуации можно воспользоваться одним из предлагаемых далее способов. Для некоторых задач (экономических) подходит наработанное годами практики утверждение (пункт В.1). В других же ситуациях придется пользоваться пунктом В.2.
В.1 Если частота задана в денежных единицах (в рублях), то используется для расчета средняя гармоническая, такое утверждение верно всегда, если выявленная частота задана в деньгах, в других ситуациях это правило не действует.
В.2 Воспользоваться правилами выбора средней величины указанными выше в этой статье. Если частота задана знаменателем логической формулы расчета средней величины, то рассчитываем по средней арифметической форме, если частота задана числителем логической формулы расчета средней величины, то рассчитываем по средней гармонической форме.
Рассмотрим на примерах использование данного алгоритма.
Задача 1. Рассчитать средний размер пенсии, если известны пенсии 12 пенсионеров – 8500, 7900, 11200, 9900, 8800, 8700, 9100, 9500, 7500, 8400, 10400, 10600 рублей.
А. Так как данные представлены в строчку то используем простой способ расчета.
Б. В. Имеем только данные по величине пенсий, именно они и будут нашей вариантой – х. Данные представлены простым количеством (12 человек), для расчета используем среднюю арифметическую простую.
Средний размер пенсии пенсионера составляет 9208,3 рубля.
Задача 2. Рассчитать средний размер детских выплат по следующим данным
А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
Б. Так как требуется найти средний размер выплаты на одного ребенка, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.
В. Частота (число детей) задана явным количеством (можно подставить слово штук детей, с точки зрения русского языка неверное словосочетание, но, по сути, очень удобно проверять), значит, для расчета используется средняя арифметическая взвешенная.
Эту же задачу модно решить не формульным способом, а табличным, то есть занести все данные промежуточных расчетов в таблицу.
В результате все, что нужно теперь сделать, это разделить два итоговых данных в правильно порядке.
Средний размер выплаты на одного ребенка в месяц составил 1910 рублей.
Задача 3. Рассчитать среднюю себестоимость единицы изделия
А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
Б. Так как требуется найти среднюю себестоимость единицы изделия, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.
В. Частота (себестоимость выпуска) задана неявным количеством (частота задана в рублях пункт алгоритма В1), значит, для расчета используется средняя гармоническая взвешенная. Вообще же, по сути, себестоимость выпуска это сложный показатель, который получается перемножение себестоимости единицы изделия на количество таких изделий, вот это и есть суть средней гармонической величины.
Чтобы эта задача могла решаться по формуле средней арифметической необходимо, чтобы вместо себестоимости выпуска стояло число изделий с соответствующей себестоимостью.
Обратите внимание, что сумма в знаменателе, получившаяся после расчетов 410 (120+80+210) это и есть общее количество выпущенных изделий.
Средняя себестоимость единицы изделия составила 314,4 рубля.
Задача 4. Рассчитать среднюю число пропусков одного студента
А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
Б. Так как требуется найти среднюю себестоимость единицы изделия, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.
В. Частота (общее число пропусков) задана неявным количеством (это произведение двух показателей числа пропусков и числа студентов, имеющих такое количество пропусков), значит, для расчета используется средняя гармоническая взвешенная. Будем использовать пункт алгоритма В2.
Чтобы эта задача могла решаться по формуле средней арифметической необходимо, чтобы вместо общего числа пропусков стояло число студентов.
Составляем логическую формулу расчета среднего числа пропусков одного студента.
Частота по условию задачи Общее число пропусков. В логической формуле этот показатель находится в числителе, а значит, используем формулу средней гармонической.
Обратите внимание, что сумма в знаменателе, получившаяся после расчетов 31 (18+8+5) это и есть общее количество студентов.
Среднее число пропусков одного студента 13,8 дня.