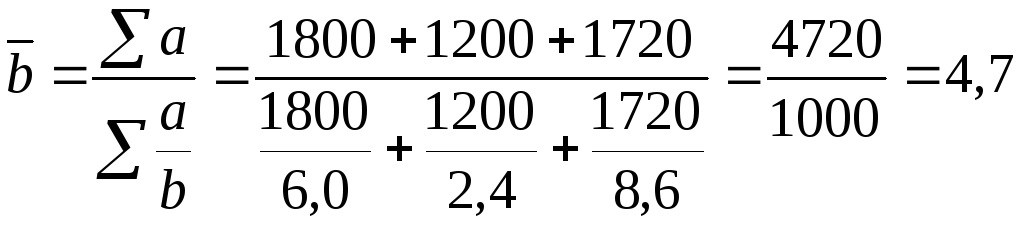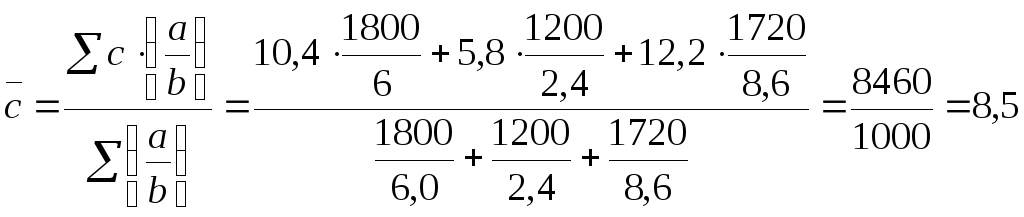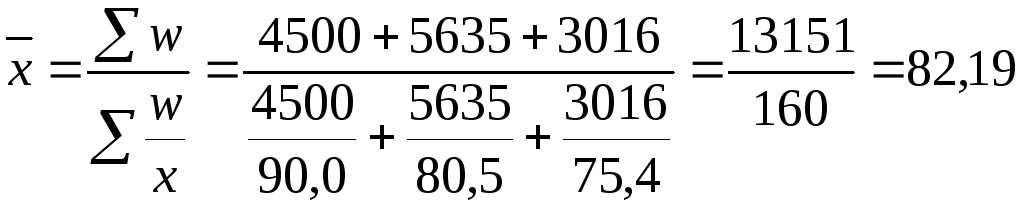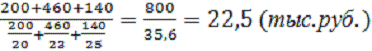Как найти средний процент бракованной продукции

32

№ 1

Средний стаж рабочего в 1-й бригаде
составил 6 лет, во 2-й – 8 лет, в 3-й – 10
лет. В 1-й бригаде работают 30 %, а во 2-й –
50% всех рабочих. Определить средний стаж
рабочих по трем бригадам.

Решение.

По данным задачи составим таблицу.

№ бригады	Средний стаж рабочего, лет	Число рабочих, в % к итогу
1 2 3	6 8 10	30 50 20
Итого	–	100

Средний стаж рабочих по трем бригадам
определим по формуле средней арифметической
взвешенной:

лет.

Ответ: г) 7,8.

№2

Доля бракованной продукции в 1 партии
изделий составила 1%, во 2 партии – 1,5%, а
в третьей – 2%. Первая партия составляет
35% всей продукции, вторая – 40%. Определить
средний процент бракованной продукции.

Решение.

По данным задачи составим таблицу.

№ партии	Доля бракованной продукции, %	Удельный вес каждой партии в общем объеме продукции
1 2 3	1 1,5 2	0,35 0,40 0,25
Итого	–	1

Средний процент бракованной продукции
определим по формуле средней арифметической
взвешенной:

.

Ответ: б) 1,45%.

№3

Количество пряжи, выработанной поддельным
цехом фабрики, увеличилось по сравнению
с прошлым годом в полтора раза, а
количество пряжи, вырабатывавшейся за
1 чел/час, возросло на 10%. Определить, как
изменилось общее число отработанных
чел/часов.

Решение.

Общее количество выработанной пряжи

равно произведению количества пряжи,
выработанной за один человеко-час
,
на общее число отработанных человеко-часов
:

.

Следовательно, между соответствующими
им индексами существует аналогичная
взаимосвязь:

.

По условию,

;

.

или 136,4%,

то есть общее число отработанных
человеко-часов увеличилось в 1,36 раза.

Ответ: г) увеличилось в 1,36 раза.

№4

В отчетном году по городу розничный
товарооборот увеличился на 9%. Прирост
товарооборота за счет роста объема
продаж составил 3%. Определить, на сколько
процентов увеличился розничный
товарооборот за счет роста цен.

Решение.

По условию,

– индекс розничного товарооборота;

– индекс физического объема товарооборота.

Требуется определить индекс цен
.

Используем взаимосвязь индексов:

.

Находим

или 105,8%,

то есть в отчетном году за счет роста
цен розничный товарооборот увеличился
на 5,8% (105,8 – 100).

Ответ: в) 5,8%.

№ 5

По трем населенным пунктам имеются
следующие данные:

Населенные пункты	Число жителей всего, тыс. чел.	% лиц, старше 18 лет	% лиц, старше 18 лет, занятых в общественном производстве
a	b	c
1 2 3	100 60 85	60 69 54	70 75 83

Определить среднее значение каждого
признака.

Решение.

1)

Используем формулу средней арифметической
простой:

тыс. чел.

2)

Используем формулу средней арифметической
взвешенной:

тыс. чел.

3)

Используем формулу средней арифметической
взвешенной:

тыс. чел.

Ответ: г) 81,7; 60,1; 75,5.

№ 6

По трем предприятиям отрасли имеются
следующие данные;

Предприятие	Выпуск продукции, тыс. руб.	Производительность труда 1 рабочего, тыс. руб.	Энерговооруженность 1 рабочего, тыс. кВт/час
a	b	c
1 2 3	1800 1200 1720	6,0 2,4 8,6	10,4 5,8 12,2

Определить среднее значение каждого
признака.

Решение.

1)

Используем формулу средней арифметической
простой:

тыс. руб.

2)

Используем формулу средней гармонической
взвешенной:

тыс. руб.

3)

(тыс. кВт/ч)

Ответ: б) 1573,3; 4,7; 8,5.

№ 7

Имеются следующие данные по трем
предприятиям отрасли за 2 периода:

предприятия	Базисный период	Отчетный период
Объем произведенной продукции, тыс. руб.	Фондоотдача основных фондов, руб.	Стоимость основных фондов, тыс. руб.	Фондоотдача основных фондов, руб.
1	4500	90,0	52	95,0
2	5635	80,5	49	75,0
3	3016	75,4	36	80,0

Определить фондоотдачу в среднем по
предприятиям в базисном и отчетном
периоде.

Решение.

Фондоотдача

рассчитывается по формуле:

,

где

– объем произведенной в данном периоде
продукции;

– стоимость основных производственных
фондов.

1) Для вычисления среднего уровня
фондоотдачи в базисном периоде используем
формулу средней гармонической взвешенной:

руб.

2) Для вычисления среднего уровня
фондоотдачи в отчетном периоде используем
формулу средней арифметической
взвешенной:

руб.

Ответ: в) 82,19; 84,00.

№ 8

При
анализе себестоимости единицы продукции
получили
=25
руб.;

² = 640. Определите
коэффициент вариации себестоимости.

Решение.

По условию,

=25
руб. – средняя себестоимость единицы
продукции;

²
= 640 – средняя
из квадратов индивидуальных значений.

Требуется определить
коэффициент вариации себестоимости.

.

Среднее квадратическое
отклонение:

.

.

Ответ: а)16%.

№ 9

Средний возраст жителей одного из
регионов 30 лет. При этом сред­ний
возраст сельских жителей, которые
составляют 60% всех жителей, 32 года при
7
лет, а городских жителей 27 пет при

8 лет. Опре­делите общую дисперсию
возраста жителей региона.

Решение.

По условию,

лет – средний возраст жителей одного
из регионов;

года – средний возраст сельских жителей;

– удельный вес сельских жителей в общем
числе жителей региона;

лет – среднее квадратическое отклонение
(для сельских жителей);

лет – средний возраст городских жителей;

лет – среднее квадратическое отклонение
(для городских жителей).

Найдем удельный вес городских жителей
в общем числе жителей региона:

.

Вычислим общую дисперсию

по правилу сложения дисперсий:

,

где

– средняя из внутригрупповых дисперсий;

;

– дисперсия групповых средних;

.

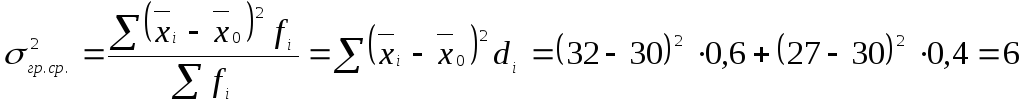
Отсюда, общая дисперсия будет:

.

Ответ: б) 61,0.

№ 10

Средний дневной удой молока по хозяйствам
области 18 кг при

3 кг. При этом средний дневной удой молока
по хозяйствам мясомолочного направления,
которые составляют 40% всех хозяйств,
равен 15 кг, а средний дневной удой молока
по хозяйствам молочного направ­ления
– 20 кг. Определить среднюю из групповых
и остаточную диспер­сию.

Решение.

По условию,

кг – средний дневной удой молока по
хозяйствам области;

кг – среднее квадратическое отклонение;

кг – средний дневной удой молока по
хозяйствам мясо-молочного направления;

– доля мясо-молочных хозяйств в общем
числе хозяйств;

кг – средний дневной удой молока по
хозяйствам молочного направления;

– доля молочных хозяйств в общем числе
хозяйств.

Определим дисперсию групповых средних
(межгрупповую дисперсию):

.

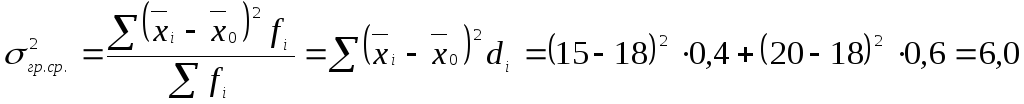
Общая дисперсия:

.

Отсюда, остаточная дисперсия:

.

Ответ: г) 6,0; 3,0.

№ 11

Ряд
динамики, характеризующий изменение
себестоимости товара А
на предприятии аналитически можно
представить уравнением:

у = 120 — 1,2t.

Это
значит, что себестоимость товара А
уменьшается ежегодно в среднем на: а)
1,2%; б) 118,8 руб.; в) 101,2%; г) 1,2 руб.

Решение.

Коэффициент
линейной регрессии, равный 1,2,
означает, что себестоимость товара А
уменьшается ежегодно в среднем на 1,2
руб.

Ответ: г).

№ 12

Имеются данные об объеме строительно-монтажных
работ и числен­ности рабочих по 2-м
строительным предприятиям:

Предприятие	Базисный период	Отчетный период
Объем строительных работ, тыс. руб.	Среднее списочное число рабочих, чел.	Объем строительных работ, тыс. руб.	Среднее списочное число рабочих, чел.
№ 1	450	200	450	230
№ 2	550	300	700	270
	1000	500	1150	500

Исчислить общий индекс динамики
производительности труда перемен­ного
состава (в %).

Решение.

Общий индекс производительности труда
переменного состава:

::
или 115%.

Следовательно, средний уровень
производительности труда по двум
предприятиям повысился в отчетном
периоде по сравнению с базисным на 15%
(115 – 100).

Ответ: в) 115%.

№ 13

Месячный план строительно-монтажных
работ был выполнен по СМУ на 108%. Выполнение
плана за этот период по среднесписочному
числу рабочих – 96%, числу дней работы на
одного рабочего – 102%, по средней
продолжительности рабочего дня – 94%.
Определить степень вы­полнения плана
по среднечасовой выработке рабочих.

Решение.

По условию,

– индекс выполнения плана СМР;

– индекс выполнения плана по среднесписочному
числу рабочих;

– индекс выполнения плана по среднесписочному
числу дней работы на одного рабочего;

– индекс выполнения плана по средней
продолжительности рабочего дня.

Требуется определить индекс выполнения
плана по среднечасовой выработке рабочих
.

.

Годовая производительность труда

зависит от часовой производительности
труда
,
средней продолжительности рабочего
дня

и средней продолжительности рабочего
года
.
Следовательно,

.

Отсюда,

или 117,3%.

Таким образом, план по среднечасовой
выработке рабочих был выполнен за данный
период на 117,3%.

Ответ: а) 117,3%.

№ 14

Производительность труда во II квартале
выросла по сравнению с I на 3%, в III квартале
по сравнению со II – на 5%, в IV квартале по
сравне­нию с III – на 6%. Определите, как
изменилась производительность тру­да
в IV квартале по сравнению с I (в %).

Решение.

По условию,

– темп роста производительности труда
по 2-ом квартале по сравнению с 1-ым;

;

.

Воспользуемся взаимосвязью между
цепными и базисными темпами роста:
произведение соответствующих цепных
темпов роста равно базисному (если
только они выражены в коэффициентах):

или 114,6%.

Это означает, что производительность
труда в 4-ом квартале по сравнению с 1-ым
выросла на 14,6% (114,6 – 100).

Ответ: б) 14,6.

№ 15

Имеются следующие данные о заготовке
древесины в двух лесопилках
(в тыс.м³)
и численности рабочих (чел.):

Лесопилка	Базисный период	Отчетный период
Добыча леса	Численность рабочих	Добыча леса	Численность рабочих
№ 1	160	40	126	30
№ 2	200	40	275	80

Исчислить общий индекс производительности
труда постоянного состава (в %).

Решение.

Общий индекс производительности труда
постоянного состава:

:.

Вычислим уровни производительности
труда:

● для лесопилки №1:

;

;

● для лесопилки №2:

;

.

или 77,1%,

то есть производительность труда
снизилась в отчетном периоде по сравнению
с базисным на 22,9% (77,1 – 100).

Ответ: 77,1% (ни один из предложенных
четырех вариантов не подходит).

№ 16

Производительность труда в отчетном
периоде по сравнению с базисным возросла
на 12%. Определить, как изменились в
отчетном периоде по сравнению с базисным,
затраты рабочего временя на единицу
про­дукции (в %).

Решение.

Затраты рабочего времени на единицу
продукции (трудоемкость изготовления
единицы продукции) – это обратный
показатель производительности труда.

Если индивидуальный индекс производительности
труда равен

или 112%,

то индивидуальный индекс трудоемкости:

или 89,3%.

Следовательно, затраты рабочего времени
на единицу продукции снизились на 10,7%
(89,3 – 100).

Ответ: б) снизились на 10,7%.

№ 17

В базисном году на производство 1000 тонн
продукции было затрачено
500 чел/часов,
а в отчетном году на производство уже
1800 тонн продукции было затрачено 600
чел/часов. Определите, сколько тонн
общего при­роста продукции получено
за счет роста производительности труда.

Решение.

По условию,

тонн – объем произведенной продукции
в базисном году;

чел/часов – затрачено в базисном году;

тонн – объем произведенной продукции
в отчетном году;

чел/часов – затрачено в отчетном году.

Вычислим уровни производительности
труда, то есть выработку продукции за
один человеко-час:

– в базисном году:

;

– в отчетном году:

.

Прирост объема произведенной продукции
за счет роста производительности труда:

тонн.

Ответ: а) 600.

№ 18

Средние затраты времени библиотекарями
на обслуживание одного посетителя
составляют 10 мин., при среднем квадрате
индивидуальных зна­чений 116. Определите
коэффициент вариации.

Решение.

По условию,

=10
мин. – средние затраты времени
библиотекарями на обслуживание одного
посетителя;

²
= 116 – средняя
из квадратов индивидуальных значений.

Требуется определить
коэффициент вариации.

.

Среднее квадратическое
отклонение:

.

.

Ответ: б) 40%.

№ 19

Обследовано 100 счетов вкладчиков в
банках города. Средний размер вклада в
государственных банках (60% всех счетов)
260 руб. при дис­персии вкладов равной
12, а средний размер вклада в коммерческих
банках 250 при дисперсии 22. Определите
коэффициент детерминации.

Решение.

По условию,

– число счетов вкладчиков в банках
города;

руб. – средний размер вклада в
государственных банках;

– доля вкладов в государственные банки
в общем числе всех вкладов;

 Готовое решение: Заказ №9701

 Тип работы: Задача

Статус:  Выполнен (Зачтена преподавателем ВУЗа)

 Предмет: Экономика

 Дата выполнения: 23.10.2020

 Цена: 229 руб.

Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Задача 1

Определите средний процент брака в среднем по предприятию.

Вид продукции	Процент брака	Стоимость бракованной продукции (тыс.руб.)
А	1,3	2 135
В	0,9	3 560
С	2,4	980
Д	1,7	1 896

Сделайте соответствующие выводы. Укажите, какой метод средней и почему был использован в данном случае.

Решение:

Логическая формула расчета процента брака следующая:

%б=Стоимость бракованной продукцииСтоимость всей продукции*100%

Средние величины

СРЕДНИЕ
ВЕЛИЧИНЫ

ЗАДАНИЕ 1.
ГРУППИРОВКА СТАТИСТИЧЕСКИХ ДАННЫХ

статистическая
группировка индекс вариация

Задача 1.1

Построить ряд распределения 25 предприятий по
стоимости основных производственных фондов, выделить 5 групп с равными интервалами.
Результаты показать в форме таблицы с расчетом частот и удельного веса каждой
группы в процентах к итогу.

Построить группировочную таблицу, в которой для
каждой группы по стоимости основных производственных фондов рассчитать
суммарную и среднюю на одно предприятие выручку от продаж, суммарную и среднюю
на одно предприятие численность рабочих. Дать краткий анализ данных
группировочной таблицы.

Показатели работы 25 предприятий

Номер п/п	Стоимость основных производственных фондов, млн.руб.	Средняя численность рабочих, чел.	Выручка от продаж, млн.руб.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25	30 70 20 39 33 28 65 66 20 47 27 33 30 31 31 35 31 56 35 40 10 70 45 49 65	360 380 220 460 395 280 580 200 270 340 200 250 310 410 635 400 310 450 300 350 330 260 435 505 600	32 96 15 42 64 28 94 119 25 35 23 13 14 30 25 79 36 80 25 28 16 129 56 44 110

Решение

Построим ряд распределения 25 предприятий по
стоимости основных производственных фондов с равными закрытыми интервалами.

Размах интервалов R = Xmax-Xmin- число
интервалов- наибольший элементнаименьший элемент

∆x = R / k – приближенная длина каждого
интервала

∆x = (70-10) /5 =60/5= 12

Удельный вес = (число предприятий в группе /
итог) * 100 %

Группы предприятий по стоимости основных производственных фондов	Частота (число предприятий в группе)	Удельный вес каждой группы в %  к итогу
10-22	3	12
22-34	9	36
34-46	5	20
46-58	3	12
58-70	5	20
Итого 25 100

Построим группировочную таблицу

Но-мер п/п	Группы предприятий по стоимости основных производственных фондов	Суммарная выручка от продаж предприятий, млн руб.	Средняя на одно предприятие выручка от продаж, млн руб.	Суммарная численность рабочих на предприятиях, чел.	Средняя численность рабочих на одно предприя-тие, чел.
1	10-22	56	18,7	820	273
2	22-34	265	29,4	3150	350
3	34-46	230	46	1945	389
4	46-58	159	53	1295	432
5	58-70	548	109,6	2020	404

Вывод: Самая большая суммарная выручка от продаж
предприятий принадлежит 5 группе предприятий по стоимости основных
производственных фондов от 58 до 70 млн руб.; самая меньшая – группе от 10-22.
Самая большая средняя на одно предприятие выручка от продаж принадлежит 5-ой
группе предприятий. Самая большая суммарная численность рабочих на предприятиях
– во 2-ой группе от 22 до 34; а самая большая средняя численность рабочих на
одно предприятие – в 4-ой группе от 46 до 58.

ЗАДАНИЕ 2. СРЕДНИЕ
ВЕЛИЧИНЫ

Задача 2.1

Найти среднюю
себестоимость единицы однородной продукции для трех производств

Производства	Суммарная величина затрат производства, млн. руб.	Себестоимость единицы продукции, тыс. руб.
1 2 3	200 460 140	20 23 25

Решение.

Используем формулу средней гармонической
простой:

х = ∑ω / ∑(ω/х)

х =

Ответ: средняя себестоимость единицы
однородной продукции для трех производств равна 22, 5 тыс. рублей.

Задача 2.2 Найти
среднюю цену поставок сырья приобретенного у двух поставщиков

Поставщики	Дата закупок	Объем закупок тонн	Закупочные цены тыс. руб./тонну
1 2	10.09 10.10	120 100	6 7

Решение.

Используем формулу средней арифметической
взвешенной:

х = ∑x*f / ∑ f

 х = (тыс. руб.)

Ответ: средняя цена поставок сырья,
приобретенного у двух поставщиков, равна 6,5 тыс. руб.

Задача 2.3

Найти среднюю
величину ставки за кредит по трем заемщикам банка

Заемщик	Величина кредита, млн. руб.	Срок кредита, мес.	Годовая процентная ставка, %
1 2 3	30 80 200	3 9 24	14 16 20

Решение.

Найдем процентную ставку за кредит по трем
заемщикам банка:

/12 * 3 = 3,5 (%) – 1- го заемщика,

/12 * 9 = 12 (%) – 2 -го заемщика,

/12 * 24 = 40 (%) – 3 -го заемщика.

Найдем среднюю величину ставки за кредит по трем
заемщикам банка, используя формулу средней арифметической взвешенной:

х = ∑x*f / ∑ f

х = (3,5*30 + 12*80 + 40*200) / (30 + 80 + 200)
= 9065/310 = 29 (%)

Ответ: средняя величина ставки за кредит по трем
заемщикам банка равна 29 %. 

Задача 2.4

Найти средний
процент выполнения плана прибыли по трем коммерческим организациям

Организации	Фактическая прибыль, млн. руб.	Выполнение плана %
1  2  3	18 28 20	115 95 102

Решение.

Найдем средний процент выполнения плана прибыли,
используя формулу средней арифметической взвешенной:

х = ∑x*f / ∑ f

= (115*18 + 95*28 + 102*20) / (18+28+20) = (2070
+ 2660 + 2040) / 66 =

= 6770 / 66 = 103 (%)

Ответ: средний процент выполнения плана прибыли
по трем коммерческим организациям равен 103 %.

Задача 2.5

Найти средний
уровень рентабельности продаж по группе коммерческих фирм, если известно, что
45% всех фирм имеют рентабельность равную 30%, 25% всех фирм работают с
рентабельностью 15%, а остальные – убыточные, с рентабельностью – 5%

Решение.

– (45 + 25) = 30 (%) – остальные фирмы с
рентабельностью = (-5) %

Найдем средний уровень рентабельности:

х = (30 * 0,45 + 15*0,25 + (-5) * 0,3) / 1 =
(13,5 + 3,75 -1,5) / 1 = 15,75 (%)

Ответ: средний уровень рентабельности продаж по
группе коммерческих фирм равен 15,75 %.

Задача 2.6

Найти среднюю норму
амортизационных отчислений по двум группам внеоборотных активов

Группы внеоборотных активов	Годовая сумма амортизации, млн. руб.	Норма амортизации, %
1  2	100 40	20 33

Решение.

Используем формулу средней арифметической
взвешенной:

х =  (%)

Ответ: средняя норма амортизационных
отчислений по двум группам внеоборотных активов= 23,7 %.

Задача 2.7

Найти средний
уровень затрат производства на единицу реализации по ряду распределения

Затраты производства на 1000 руб. реализованной продукции	Выручка от реализации, млн. руб.
до 800  800 – 900  900 – 1000	140 180 60

Решение

Затраты производства на 1000 руб. реализованной продукции	Середина интервала затрат производства	Выручка от реализации, млн. руб.
до 800  800 – 900  900 – 1000	750 850 950	140 180 60

Найдем средний уровень затрат производства на
единицу реализации, используя формулу средней арифметической взвешенной:

х = ∑x*f / ∑ f

х = (750*140 + 850*180 + 950*60) / (140+180+60)
= (105000+153000+57000) / 380 = 828,95 (руб.)

Ответ: средний уровень затрат производства на
1000 руб. реализованной продукции по ряду распределения составляет 828,95 руб.

Задача 2.8. Портфель ценных бумаг сформирован по
40% из гособлигаций, на 30% из корпоративных облигаций и на 30% из акций ОАО.
Найти потенциальную доходность портфеля, если доходность гособлигаций
составляет 6%, доходность корпоративных облигаций 8% и доходность акций равна
15%.

Решение.

х = .(0,4 * 6 + 0,3 * 8 + 0,3 * 15) / 1 = 9,3
(%)

Ответ: потенциальная доходность портфеля ценных
бумаг составляет 9,3 %.

Задача 2.9

Найти средний
уровень рентабельности продукции по каждому предприятию, выпускающему два вида
продукции, объяснить различие в величинах средней рентабельности

Виды	Предприятие 1	Предприятие 2
	Рентабельность продукции, %	Доля затрат на  производство продукции	Рентабельность продукции, %	Доля затрат на производство продукции
1 2	20 12	15 85	18 13	20 80

Решение

Найдем средний уровень рентабельности продукции
по первому предприятию:

х1 = (0,2 * 15 + 0,12*85) / 1 = 13,2 (%)

Найдем средний уровень рентабельности продукции
по второму предприятию:

х2 = (0,18*20 + 0,13*80) / 1 = 14 (%)

Ответ: 13,2 %, 14 %.

Задача 2.10

Найти средний
процент бракованной продукции

Виды продукции	Плановый выпуск, млн. руб.	Процент выполнения плана, %	Доля брака, %
1 2	350 650	98 105	1,0 0,5

Решение.

Найдем фактический выпуск продукции:

*0,98 = 343 (млн. руб.) – 1-й вид продукции,

*1,05 = 682,5 (млн. руб.) – 2-й вид продукции.

Найдем средний процент бракованной продукции:

х = (1,0 *343 + 0,5*682,5) / (343 +682,5) = 0,67
(%)

Ответ: средний процент бракованной продукции
составляет 0,67 %.

Задача 2.11

Найти средний
процент прироста цен на товары и услуги в 2004 г.

Виды товаров и услуг	Приросты цен в 2004 г, %	Доля в расходах населения, %
1. Продовольственные товары 2. Непродовольственные товары 3. Разные платные услуги	12 9 25	55 30 15

Решение.

Найдем средний процент прироста цен, используя
формулу средней арифметической взвешенной:

х = ∑x*f / ∑ f

х =  (%)

Ответ: средний процент прироста цен
на товары и услуги в 2004 г. составил 13,05 %.

Задача 2.12

Найти среднюю
заработную плату работников на каждом из двух предприятий

Категории персонала	Предприятие 1	Предприятие 2
	Средняя з/п, тыс. руб.	Доля категории в общей численности персонала, %	Средняя з/п, тыс. руб.	Доля категории в общей численности персонала, %
Руководители Специалисты Рабочие	20 12 7	4 21 75	18 13 8	5 25 70

Решение.

Используем формулу средней арифметической
взвешенной:

х = ∑x*f / ∑ f

 СЗП на 1-ом предприятии,

СЗП на 2-ом предприятии.

Ответ: 8,57 тыс. руб.; 9,75 тыс.
руб.

Задача 2.13

Найти средний
процент выполнения норм выработки по трем рабочим бригадам

Бригады рабочих	Нормы выработки продукции, ед.	Средний процент выполнения норм, %
1 2 3	20 21 23	115,0 100,0 98,5

Решение.

х =  (%)

Ответ: средний процент выполнения
норм выработки по трем рабочим бригадам составляет 104 %.

Задача 2.14

Определить среднюю
численность работников на одном предприятии

Группы предприятий работников	Интервалы по численности в группе	Количество предприятий
1  2  3  4	20 – 50 50 – 90 90 – 150 150 – 250	20 26 10 4

Решение

Группы предприятий работников	Интервалы по численности в группе	Середины интервала х	Количество предприятий	x*f
1  2  3  4	20 – 50 50 – 90 90 – 150 150 – 250	35 70 120 200	20 26 10 4	700 1820 1200 800
Итого		60	4520

х =

Ответ: средняя численность
работников на одном предприятии = 75 чел.

ЗАДАНИЕ 3.
ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ

Задача 3.1

Финансирование
организации складывается на 40% от коммерческой деятельности и на 60% из
госбюджета. Как изменится общая сумма финансирования, если бюджетное
финансирование сократится на 5%, а коммерческое увеличится на 10%

Решение.

Относительные показатель динамики вычисляется по
формуле

где . – уровень показателя в базисном
периоде, – уровень
показателя в отчетном периоде.

=1,25 (раза) – ОПД от коммерческой
деятельности

 от бюджетного финансирования

,25 + 0,91 = 2,16 (раза)

Ответ: в 2,16 раза увеличится сумма
финансирования организации.

Задача 3.2

Как изменится
фактический выпуск продукции в октябре в сравнении с сентябрем по каждому предприятию
и в среднем по всем предприятиям?

Предприятия	Сентябрь	Октябрь
	План выпуска продукции, млн. руб.	Выполнение плана, %	Фактический выпуск, млн. руб.
1 2 3	200 400 300	105 93 107	224 378 318

Решение.

Найдем фактический выпуск в сентябре по трем
предприятиям:

*1,05 = 210 (млн. руб.) – 1-го предприятия,

* 0,93 = 372 (млн. руб.) – 2-го предприятия,

*107 = 321 (млн. руб.) – 3-го предприятия,

Сравним его с фактич. выпуском в октябре:

) 224 – 210 = 14 (млн. руб.) – увеличится,

) 378 – 372 = 6 (млн.руб.) – увеличится,

) 318 – 321 = -3 (млн. руб.) – уменьшится.

Найдем среднее изменение фактического выпуска
продукции, используя среднюю арифметическую простую:

х = (14 + 6 -3) / 3 = 5,6 (млн. руб.)

Ответ: на 14 увеличится, на 6 увеличится, на 3
уменьшится; среднее изменение фактического выпуска продукции равно 5,6 млн.
руб.

Задача 3.3

Как изменятся
реальные доходы, если номинальная заработная плата увеличится на 12%, а цены
вырастут в 1,2 раза

Решение

∆Д – изменение реальных доходов

∆Д = 1 – ЗП / Ц, где

ЗП – коэффициент изменения номинальной
заработной платы,

Ц – коэффициент изменения цены

∆Д = 1-12 / 1,2 = – 9

Вывод: реальные доходы уменьшатся на 9 %.

Задача 3.5

Как изменится сумма налога, если налоговая база
вырастет на 6%, а ставка налога снизится на 2%?

Решение.

х – налоговая база ((1,00 + 0,06)х = 1,06х ),

у – ставка налога ((1,00 – 0,02)у = 0,98у)

налог – (х*у)

длина налога = 1,06х * 0,98у = 1,0388ху

Изменение суммы налога = (1,06 * 0,98)ху / ху =
1,0388 (раз)

Ответ: сумма налога увеличится на 3,88 %.

Задача 3.6

Доходы госбюджета
формируются как сумма налоговых и неналоговых поступлений. В базисном периоде
соотношение этих частей 4 к 1. Как изменится общая сумма доходов бюджета, если
налоговые доходы снизить на 1%, а неналоговые поступления увеличить на 4%

Решение.

а – налоговые поступления ((1,00 – 0,01)а =
0,99а)

в – неналоговые поступления (1,00 + 0,04)в =
1,04в

а/в = 4/1 – соотношение этих частей

(а + в) – доходы бюджета

Изменение доходов бюджета = (1,04в + 0,99а) / (а
+ в) = (1,04 + 0,99а/в) / (а/в + 1) = (1,04 + 0,99*4) / (4 + 1) = 5 / 5 = 1, 00

Ответ: общая сумма доходов бюджета не изменится.

ЗАДАНИЕ 4. РЯДЫ
ДИНАМИКИ

Задача 4.1

За полгода средние
размеры пенсий выросли с 2100 до 2300 руб.в месяц. Найти средний месячный
прирост пенсий за этот период ( в % )

Решение.

– конечный уровень ряда,- начальный уровень
ряда.

∆ = (2300-2100) / (6-1) = 200/5 = 40 / 100
= 0,4 (%)

Ответ: средний месячный прирост пенсий за
полгода составил 0,4 %.

Задача 4.2

По данным ежемесячным
приростам выручки от продаж, найти средний месячный прирост за период май –
август

Месяцы	май	июнь	июль	август
прирост выручки %	1,5	2,1	4,0	4,1

Решение.

∆= ∑∆ / (n – 1), где

∑∆ – сумма показателей прироста
выручки

∆1 = 2,1 – 1,5 = 0,6 9%),

∆2 = 4,0 – 2,1 = 1.9 (%),

∆3 =4,1 – 4,0 = 0,1 (%), – число месяцев =
4

∆ = (0,6 + 1,9+ 0,1)/ (4 – 1) = 2,6 / 3 =
0,9 (%)

Ответ: средний месячный прирост выручки за
период май – август составляет 0,9 %.

Задача 4.3

Найти
среднемесячный темп роста объема продаж торговой организации

Месяцы	июнь	июль	август	сентябрь	октябрь
Объем продаж, млн. руб.	2,5	3,0	3,8	4,2	4,5

Решение.

Кр= √Кр1 * Кр2 * …* Кр (n – 1)

средний коэффициент роста по формуле средней
геометрической, n – число уровней ряда,

Кр1= 3,0 / 2,5 = 1,2

Кр2= 3,8 / 3,0 = 1,27

Кр3= 4,2/3,8 = 1,1

Кр4=4,5 / 4,2 = 1,07

Кр = √1,2 * 1,27 * 1,1 * 1,07 = √1,79
= 1,156

Tр = Kр * 100 % – средний темп роста,

Tр = 1,156 * 100 = 115,6 (%)

Ответ: среднемесячный темп роста объема продаж
торговой организации равен 115,6 %.

Задача 4.4 Какой из двух показателей растет в
большей мере и на сколько

Показатели	Кварталы
	1	2	3	4
1. Выручка от продаж, млн. руб.	67,8	70,1	72,8	77,3
2. Валовая прибыль, млн. руб.	5,7	6,0	6,3	6,0
3. Рентабельность продаж в среднем в течение года растет / снижается?

Решение.

Найдем средний темп роста выручки от продаж:

Тр1= √(70,1 / 67,8) * (72,8 / 70,1) *
(77,3 / 72,8) * 100 = 104,5 (%)

Найдем средний темп роста валовой прибыли:

Тр2 = √(6,0 / 5,7) * (6,3 / 6,0) * (6,0 /
6,3) * 100 = 101,6 (%)

Найдем рентабельность продаж в среднем в течение
года:

Тр2 – Тр1= 101,6 – 104, 5 = – 2,9 (%) –
снизилась рентабельность

Ответ: выручка от продаж растет больше валовой
прибыли на 2,9 %, рентабельность продаж в среднем в течение года снижается.

ЗАДАНИЕ 5.
ПОКАЗАТЕЛИ ВАРИАЦИИ

Задача 5.1

Рассчитайте
коэффициент вариации производственного стажа работников предприятия

Стажевые группы, лет	Середина интервала стажевых групп	Количество работников в стажевых группах, чел.
До 5 5 – 10 10 – 15 15 – 20 свыше 20	2,5 7,5 12,5 17,5 22,5	50 150 320 100 80

Решение.

= S / x * 100 % – коэффициент вариации, где

-среднее квадратическое отклонение, х – мат.
ожидание

х = (2,5 * 50 + 7,5 * 150 + 12,5 * 320 + 17,5 *
100 + 22,5 * 80) / (50 + 150 + 320 + 100 + 80) = (125 + 1125 + 4000 + 1750 +
1800) / 700 = 12,57

= √ ∑(хi – х)2 ni / ∑ni

= √ ((2,5 – 12,57)2 * 50 + ( 7,5 – 12,57)
2 * 150 + (12,5 – 12,57) 2 * 320 + (17,5 – 12,57) 2 * 100 + (22,5 – 12,57) 2 *
80) / 700 = √(5070,2 + 3855,7 + 1,568 + 2430,49 + 7888,392) / 700 = √19246,35
/ 700 = √27,5 = 5,24= 5,24 / 12,57 * 100 = 41,69 (%)

Ответ: коэффициент вариации производственного
стажа работников предприятия равен 41,69 %.

ЗАДАНИЕ 6. ИНДЕКСЫ

Задача 6.4

По приведенным
данным определите:

1) индекс
физического объема продукции;

2) индекс
производительности труда;

3) экономию
(перерасход) затрат труда в зависимости от изменения производительности труда

Виды продукции	Производство продукции	Затраты времени на всю продукцию, чел. дни
	январь	февраль	январь	февраль
А Б	123 348	148 374	17400 11200	17350 10450

Решение.

Найдем индексы физического объема
продукции:ф.об.1 = 148 / 123 = 1,2ф.об.2 = 374 / 348 = 1,07

Затраты на производство:

Янв. Февр.

А х1 =17400 / 123 = 141,46 х2 = 17350 / 148 =
117,23

В у1 = 11200 / 348 = 32,18 у2= 10450 / 374 =
27,94

Найдем индекс производительности труда:пр.т.1 =
х2 / х1 = 117,23 / 141,46 = 0,83пр.т.2= у2 / у1 = 27,94 / 32,18 = 0,87

Найдем экономию (перерасход) затрат труда:

– 17400 = – 50 (чел.дн.) – А,

– 11200 = -750 (чел.дн.) – В. Экономия

Ответ: 1,2; 1,07; 0,83; 0,87; 50 чел. дн.; 750
чел. дн..

Задача 6.5

По данным таблицы
определить: общий индекс себестоимости; общий объем издержек производства;
сумму экономии (или перерасхода) издержек производства, полученную за счет
изменения себестоимости

Затраты на производство трех видов изделий

Виды изделий	Общая сумма затрат на производство в периоде, тыс. руб.	Изменение себестоимости продукции в отчетном периоде, по сравнению с базисным
	Базисном	Отчетном
А Б В	16 180 60	28 254 67	– 5  + 1 – 2

Решение.

Себестоимость: А а – 0,05а = 0,95а

В b + 0,01b = 1,01b

С с-0,02с = 0,98с

Общий индекс себестоимости:

сб. = ∑iq′ * p′ / ∑q0 *
p0

сб. =(28 / 0,95а * 0,95а + 254 / 1,01b * 1,01b +
67 / 0,98с * 0,98с) / (28 / 0,95а * а + 254 / 1,01b * b + 67 / 0,98с * с) = 349
/ (29,5 + 251,5 + 68,37) = 349 / 349,4 = 1

Общий объем издержек производства:

в базисн. пер. = 16 + 180 + 60 = 256 (тыс.
руб.),

в отчетн. пер.= 28 + 254 + 67 = 349 (тыс. руб.).

Сумма экономии (или перерасхода) издержек
производства:

– 256 = 93 (тыс. руб.) – перерасход

Ответ: 1; 256 тыс. руб.; 349 тыс.руб;93 тыс.
руб.

Задача 7.6

Выручка от продаж в розничной торговле в текущем
периоде составляет 1000 тыс. руб. Из-за роста цен в сравнении с базисным
периодом покупателем товаров переплатили 200 тыс. руб. Найдите индекс цен.

Решение.

Выручка = цена * кол – во

Цена = Выручка / кол-во (n)

Найдем индекс цен:

iц = цена тек. / цена баз.

Цена баз. = 1000 – 200 = 800 (тыс. руб.)ц =(1000
/ n ) / (800 / n) = 1000 / 800 = 1,25

Ответ: индекс цен равен 1,25.

ЗАДАНИЕ 7.
ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ

Задача 7.4

Найти необходимую
численность выборки при определении среднего размера срочных вкладов в отделении
Сбербанка с точностью 5000 рублей (ошибка выборки), если среднее квадратическое
отклонение по размеру вклада составляет 10 тыс. руб. и вероятность выбора 0,954

Решение.

х = (10000 ± 5000)*0,954 = 4770 и 14310, т. е.
численность выборки составляет от 4770 до 14310 руб.

Ответ: численность выборки при определении
среднего размера срочных вкладов в отделении Сбербанка при заданной ошибке
составляет от 4770 до 14310 руб.