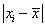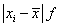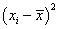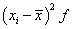2. С вероятностью 0,954 возможные пределы среднего процента влажности.
Сделайте
выводы.
1.
Определим средний процент влажности
(для расчета построим таблицу)
|
Влажность % |
Число |
f |
– |
(-) |
(-)f |
||
|
6 |
5 |
5 |
30 |
-4,6 |
21,16 |
105,8 |
|
|
6-8 |
25 |
7 |
175 |
-2,6 |
6,76 |
169,0 |
|
|
8-10 |
32 |
9 |
288 |
-0,6 |
0,36 |
11,52 |
|
|
10-12 |
19 |
11 |
209 |
1,4 |
1,96 |
37,24 |
|
|
12-14 |
13 |
13 |
169 |
3,4 |
11,56 |
150,28 |
|
|
14 |
6 |
14 |
84 |
4,4 |
19,36 |
116,16 |
|
|
Итого |
100 |
– |
955 |
– |
– |
590,0 |
|
=
/N – средняя арифметическая,
например:
= 6+8/2 = 7
=
8+10/2 = 9 и т.д.
2)
средний процент влажности определим
по формуле
=
?x*t/?f
=
955/100 = 9,6%
Определим
дисперсию и среднее квадратическое
отклонение по формулам:
среднее
квадратическое отклонение
• –
значения изучаемого признака (варианты);
• –
объем статистической совокупности;
• –
средняя арифметическая величина.
=
590,0/100 = 5,9% – дисперсия
=
2,43
3)
V = /*100% – коэффициент вариации
V
= 2,43/9,6 = 25,3%
Вывод:
данная совокупность считается однородной,
т. к. коэффициент вариации составляет
25,3%, что меньше 33%.
4.
Определим с вероятностью 0,954 возможные
пределы значения влажности продукции
для всей партии товара.
Сначала
определим численность генеральной
совокупности:
По
условию задачи выборочная совокупность
() составляет 100 единиц проб, что составляет
5% генеральной совокупности (N), составим
пропорцию:
100
ед. проб -5%
N
– 100%
N
= 100*100/5 = 2 000 ед. проб.
=
9,6% – средний% влажности в выборочной
совокупности
=
5,9%
t
= 2 – коэффициент доверия, соответствует
0,954
–
коэффициент доверия;
–
дисперсия количественно варьирующего
признака выборочной совокупности;
–
численность выборки;
–
численность единиц генеральной
совокупности.
^
= 2*v5,9/100*(1-100/2000) = 2v0,059*(1-0,05) = 2v0,0056= 2*(-+0,24)
=-+ 0,48%
Полученные
значения и ^X подставим в формулу
предельного выбора для количественных
признаков:
=
+^X
=
9,6% -+0,48
Вывод:
с вероятностью 0,954 можно утверждать,
что средний% влажности в генеральной
совокупности (во всей партии) будет
заключаться в пределах от 9,12 до 10,08
4)
С вероятностью 0,997 которой соответствует
коэффициент доверия 3, необходимо
определить возможный% нестандартной
продукции во всей партии, если известно,
что из 100 проб, попавших в выборку 25 ед.
отнесены к некачественной продукции.
Итак,
запишем, что дано:
m
= 25 ед. – отнесены к нестандартной
продукции;
n
= 100 ед. – численность выборочной
совокупност;
N
= 2000 ед. численность генеральной
совокупности;
t
= 3 – коэффициент доверия
Определим
^w
Так
как необходимо определить пределы доли
качественного признака используем
формулу: Р = w -+^w
Генеральная
доля равна выборочной доли -+ предельная
ошибка выборки
w = m /n –
выборочная доля
w =
25/100 = 0,25
Если
коэффициент умножить на 100%, то получим
25%, т.е. в выборочной совокупности
количество проб соответствующее
нестандартной продукции составляет
25%.
По
формуле предельной ошибки определим
её значение:
^w =t *v w (1_w)/n *
(1_n/N)
^w = 3*
v0,25*(1-0,25)/100 *(1-100/2000) = 3*v0,00188*0,95 = 3*v0,00178 =
3*0,042 =-+ 0,13
Полученные
значения w^w подставим
в формулу Р = w -+^w
Р
= 0,25
-+ 0,013 или результат выразим в%: 25 -+1,3
Следовательно
с вероятностью 0,997 возможный процент
нестандартной продукции во всей партии
будет составлять от 23,7% до 26,3%
Задача №4
Имеются
следующие данные о товарообороте
торговой фирмы и среднем изменении цен:
|
Месяцы |
Январь |
Февраль |
Март |
Апрель |
Май |
|
|
Товарооборот |
1920 |
1980 |
2215 |
2318 |
2620 |
|
|
Индекс |
100,0 |
104,2 |
105,3 |
110,2 |
116,1 |
|
1.
Для анализа динамики физического объема
товарооборота пересчитайте товарооборот
за соответствующие месяцы из фактических
цен в сопоставимые.
2.
Определите: абсолютные, относительные
и средние показатели динамики физического
объема товарооборота (интенсивность
динамики изобразите графически).
3.
Произведите анализ общей тенденции
физического объема товарооборота
методом аналитического выравнивания
(фактические и теоретические уровни
изобразите на графике).
Полученные
результаты оформите в виде статистической
таблицы. Сделайте выводы.
Решение:
1.
Определим изменение товарооборота в
сопоставимых ценах, данные сведем в
таблицу:
|
Месяцы |
Январь |
Февраль |
Март |
Апрель |
Май |
|
|
Товарооборот |
1920 |
1980 |
2215 |
2318 |
2620 |
|
|
Индекс |
100,0 |
104,2 |
105,3 |
110,2 |
116,1 |
|
|
Товарооборот |
1920 |
2000,6 |
2084,9 |
2440,9 |
2691,2 |
|
1)
При вычислении общего индекса цен по
формуле средней гармонической (1) важно
правильно определить индивидуальные
индексы .
,
следовательно
Товарооборот
в сопоставимых ценах будет равен:
январь
– 1920 *4,2% = 2000,6 тыс. руб.
февраль
– 1980*5,3% = 2084,9 тыс. руб. и т.д.
2)
Определим абсолютные, относительные и
средние показатели динамики физического
объема товарооборота относительные и
средние показатели динамики физического
объема товарооборота
|
месяцы |
Т/о |
Абсолютный |
Коэффициент |
Темпы |
Темп |
Абсол. |
||||||
|
цеп. |
баз. |
цеп. |
баз. |
цеп. |
баз. |
цеп. |
баз. |
цеп. |
баз. |
|||
|
январь |
1920 |
– |
– |
– |
1 |
– |
100 |
– |
– |
– |
19,2 |
|
|
февраль |
1980 |
60 |
60 |
1,03 |
1,03 |
103 |
103 |
3 |
3 |
19,8 |
19,2 |
|
|
март |
2215 |
235 |
295 |
1,12 |
1,15 |
112 |
115 |
12 |
15 |
22.2 |
19,2 |
|
|
апрель |
2318 |
103 |
398 |
1,05 |
1,21 |
105 |
121 |
5 |
21 |
23,2 |
19,2 |
|
|
май |
2620 |
302 |
700 |
1,13 |
1,36 |
113 |
136 |
13 |
36 |
26,2 |
19,2 |
|
1.
Абсолютный прирост на базисной основе
рассчитывается по формуле:
,
где
–
абсолютный прирост;
–
текущий уровень ряда динамики;
–
базисный уровень ряда динамики.
а)
На основании вышеуказанной формулы
рассчитаем абсолютный прирост на цепной
и базисной основе, взяв за базисный
уровень январь (01 месяц):
^уц01
= 1980-1920 = 60 тыс. руб.
^уц
02 = 2215-1980= 235 тыс. руб. и. т. д.
Базисный
прирост
^уб01
= 1980-1920 = 60 тыс. руб.
^уб02
= 2215-1920= 295 тыс. руб. и т.д.
б)
Коэффициент роста (Кр)
цепной:
Кр = уi /уi_1
Кр
= 1980/1920 = 1,03
Кр
= 2215/1980 = 1,12 и т.д.
базисный:
Кр = уi /у0
Кр
= 1980/1920 = 1,03
Кр
= 2215/ 1920= 1,15 и т.д.
в)
Темпы роста (Тр):
цепной:
Тр цеп = Кр цепн *100%
Тр
цеп = 1,03 *100% = 103%
Тр
цеп = 1,12 *100% = 112% и т.д.
Тр
баз = Кр баз *100%
Тр
баз = 1,03 *100% = 103%
Тр
баз = 1,15 *100% = 115%
г)
Темпы прироста (Тпр)
Тпр
цеп = Тцеп – 100
Тпр
цеп = 103 – 100 = 3
Т
пр баз = Т баз – 100
Т
пр баз = 112 – 100 = 12
Т
пр баз = 115 – 100 = 15 и т.д.
д)
Абсолютное значение 1% прироста
цепной:
Ац = уi_1 /100
Ац
= 1920/100 = 19,2
Аб
= у0 /100 = 1920/100 = 19,2
Определим
средний уровень ряда динамики по формуле:
?
= ?у /n
Так
как данный ряд является интервальным,
то
?
= (1920+1980+2215+ 2318 +2620) /5 = 11053/5 = 2210,6 тыс. руб.
Вывод:
средний показатель товарооборота
торгового предприятия за 5 месяцев
составил 2210,6 тыс. руб.
Среднегодовые
темпы роста определим по формуле (.)
–
средний темп роста.
=(5v2620/1920)*100%
=
5v1,365 *100% = 1,009 *100% = 109%
Вывод:
среднегодовые темпы роста товарооборота
с января по май месяц составили 109%
Средний
темп прироста получим. вычтя из среднего
темпа роста 100%:
–
средний темп прироста.,
=
109,0 – 100 = 9%
Среднегодовой
абсолютный прирост ()
–
средний абсолютный прирост;
–
конечный уровень ряда динамики;
–
число периодов.
=
2620-1920 / 5 = 140,0 тыс. руб.
Построим
график динамики товарооборота торгового
предприятия на рис 1.
Рис. 1
– товарооборот торгового предприятия
за 5 месяцев
Задача №5
Имеются
следующие данные о продаже продукта
«М»
на рынке города за два периода:
|
Продавцы |
Количество |
Цена |
|||
|
декабрь, |
март, |
декабрь, |
март, |
||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
10,5 |
12,0 |
38,5 |
33,3 |
|
|
2 |
36,6 |
10,6 |
30,4 |
39,2 |
|
|
3 |
18,6 |
18,4 |
32,2 |
38,0 |
|
|
4 |
24,0 |
20,2 |
30,9 |
36,7 |
|
|
Итого |
89,7 |
61,2 |
132 |
147,2 |
|
Для
анализа динамики средней цены реализации
продукта «М»
определите:
1.
Индексы цен: переменного и постоянного
состава.
2.
Индекс структурных сдвигов.
3.
Изменение средней цены (в абсолютных
величинах) в марте по сравнению с
декабрем: общее и за счет действия
отдельных факторов.
4.
Покажите взаимосвязь исчисленных общих
индексов.
Сделайте
выводы по полученным результатам.
Решение:
1)
Определим индекс цен переменного
состава:
Jп.с/
Р1/Р0 = (?p1g1/?g1)/ (?p0g0/? p0)
Jп.с.=
?(147,2*61,2/61,2)/(132*89,7/132) = (10661,04/61,6)/(11840,4/132) =
147,2/89,7 = 1,25 (т.е. увеличился на 25%)
Вывод:
в среднем цены на продукцию увеличились
на 25%, в результате изменения товарного
потока.
2)
Индекс цен постоянного состава:
Jф.с.
Р1/Р0 = (?p1g1/?g1)/ (?p0g0/? p1)
Jф.с.
= 147,2/132,0 = 1,12% (т.е. увеличился на 12%)
Вывод:
средняя цена увеличилась на 12% за счет
изменения индивидуальных цен каждого
продавца.
3)
Индекс структурных сдвигов:
Jстр.
= (?p0g1/?g1)/ (?p0g0/? p0)
Jстр.
= 132/132 = 1 (т.е. остался без изменений).
Вывод:
в среднем цены не изменились, т.е. влияние
структурных сдвигов в реализованной
продукции несущественно.
4)
Рассчитаем среднее изменение цены в
марте по сравнению с декабрем, в общем:
|
Продавцы |
Цена |
Цена |
Отклонение |
|
|
1 |
декабрь, |
март, |
||
|
1 |
38,5 |
33,3 |
-5,2 |
|
|
2 |
30,4 |
39,2 |
+7,8 |
|
|
3 |
32,2 |
38,0 |
+5,8 |
|
|
4 |
30,9 |
36,7 |
+5,8 |
|
|
Итого |
132 |
147,2 |
+15,2 |
|
,
где
–
абсолютный прирост;
–
текущий уровень ряда динамики;
–
базисный уровень ряда динамики.
=38,5-33,3
= -5,2 тыс. руб.
5)
за счет действия отдельных факторов:
Взаимосвязь
индексов выражается формулой:
Jстр.
= Jп. с. Jф. с. 125,4/112 = 1,12, что соответствует
вышеизложенным расчетам.
Задача №6
Имеются
данные о товарообороте в сопоставимых
ценах и изменении цен на товары по
торговому предприятию за два периода:
|
Товарные |
Товарооборот |
Среднее |
||
|
1_й |
2_й |
|||
|
1 |
2 |
3 |
4 |
|
|
А |
46,8 |
48,4 |
+10 |
|
|
Б |
85,4 |
100,8 |
-16 |
|
|
В |
74,2 |
70,0 |
без |
|
|
Г |
56,6 |
54,1 |
+20 |
|
Определите:
1.
Индивидуальные и общие индексы: цен,
товарооборота в фактических ценах и
физического объема товарооборота;
покажите их взаимосвязь.
2.
Изменение покупательной способности
рубля во 2_м периоде по сравнению с 1_м
периодом.
3.
Прирост товарооборота в фактических
ценах во 2_м периоде по сравнению с 1_м
периодом в целом и в том числе за счет
влияния отдельных факторов.
Сделайте
выводы по полученным результатам.
Решение:
Для
удобства решения данной задачи построим
вспомогательную таблицу (табл. 6), которую
будем заполнять в ходе решения:
Таблица
6. Вспомогательная таблица
|
Товарные |
Товарооборот |
Среднее |
ip |
p1g1/ |
||
|
1_й |
2_й |
|||||
|
А |
46,8 |
48,4 |
+10 |
1,1 |
53,24 |
|
|
Б |
85,4 |
100,8 |
-16 |
0,84 |
84,67 |
|
|
В |
74,2 |
70,0 |
без |
1,00 |
70,0 |
|
|
Г |
56,6 |
54,1 |
+20 |
1,2 |
64,92 |
|
|
Итого |
263,0 |
273,3 |
+14 |
1,14 |
311,56 |
|
Теперь
рассчитаем индивидуальные индексы для
каждой товарной группы и сделаем выводы
на основании полученных данных:
1.
Индивидуальный индекс физического
объёма рассчитаем по формуле:
–
индивидуальный индекс физического
объёма;
–
физический объём в отчётном периоде;
–
физический объём в базисном периоде.
Индивидуальный
индекс физического объема товарооборота:
iga
= 48,4/46,8 = 1,03
Индивидуальный
индекс физического объема товара А во
втором периоде по сравнению с первым
составил%. За изучаемый период цена на
данный вид товара уменьшилась на 3%.
igб
= 100,8/85,4 = 1,18
Индивидуальный
индекс физического объема товара Б во
втором периоде по сравнению с первым
составил 1,18. За изучаемый период цена
на данный вид товара увеличилась на
18%.
Igв
= 70,0/74,2 = 0,94
Индивидуальный
индекс физического объема товара В во
втором периоде по сравнению с первым
составил 94%. За изучаемый период цена
на данный вид товара уменьшилась на 6%.
Igг
= 54,1/56,6 = 0,96
Индивидуальный
индекс физического объема товара Г во
втором периоде по сравнению с первым
составил 96%. За изучаемый период цена
на данный вид товара уменьшилась на 4%.
Индивидуальный индекс товарооборота
в фактических ценах:
–
индивидуальный индекс товарооборота;
–
товарооборот в отчётном периоде;
–
товарооборот в базисном периоде.
Рассчитаем
индивидуальные индексы товарооборота
в фактических ценах в разрезе каждого
из товаров:
А
= 53,24/51,48 = 1,03
Б
= 84,67/ 71,74 = 1,18
В
= 70/ 74,2 = 0,94
Г
= 64,92/67,92 = 0.96
2.
Общий индекс цен рассчитывается по
формуле:
–
общий индекс цен.
В
нашем случае общий индекс цен на товары
составит:
I
p = 273,3/311,56 = 0,88
Общий
индекс цены составил 0,88%. Цены на всю
группу товаров в отчётном периоде по
сравнению с базисным снизились на 12%.
3.
Общий индекс физического объёма найдём
по формуле:
–
общий индекс физического объёма.
|
Товарные |
Товарооборот |
Среднее |
ip |
p1g1/ |
||
|
1_й |
2_й |
|||||
|
А |
46,8 |
48,4 |
+10 |
1,1 |
53,24 |
|
|
Б |
85,4 |
100,8 |
-16 |
0,84 |
84,67 |
|
|
В |
74,2 |
70,0 |
без |
1,00 |
70,0 |
|
|
Г |
56,6 |
54,1 |
+20 |
1,2 |
64,92 |
|
|
Итого |
263,0 |
273,3 |
+14 |
1,14 |
311,56 |
|
Общий
индекс физического объёма составит:
51,48/46,8
= 1,1
Общий
индекс физического объёма реализации
товаров за изучаемый период вырос в 1,1
раза, и составил 110%. В январе по сравнению
с сентябрем было реализовано товаров
больше на 10%.
4.
Общий индекс товарооборота в фактических
ценах:
–
общий индекс товарооборота в фактических
ценах.
Рассчитаем
общий индекс товарооборота в фактических
ценах:
=
53,24/46,8= 1,14
Общий
индекс товарооборота в фактических
ценах составил 14%. За изучаемый период
индекс товарооборота в связи со
значительным увеличением цен (12%)
увеличился на 14%.
5.
Между рассчитанными индексами существует
следующая взаимосвязь:
Используя
взаимосвязь индексов, проверим
правильность вычислений:
121,1
= 14,0
6.
Изменение покупательной способности
рубля во 2_м периоде по сравнению с 1_м
периодом.
7.
Прирост товарооборота в фактических
ценах во 2_м периоде по сравнению с 1_м
периодом в целом и в том числе за счет
влияния отдельных факторов.
|
Товарные |
Товарооборот |
Отклонения,+- |
Прирост |
||
|
1_й |
2_й |
||||
|
А |
46,8 |
48,4 |
+1,6 |
+3,4 |
|
|
Б |
85,4 |
100,8 |
+15,4 |
+18,0 |
|
|
В |
74,2 |
70,0 |
-4,2 |
-5,7 |
|
|
Г |
56,6 |
54,1 |
-2,5 |
-4.4 |
|
|
Итого |
263,0 |
273,3 |
+10,3 |
+3,9 |
|
Выводы:
за счет изменения покупательской
способности денег товарооборот товарных
групп В и Г сократился, соответственно
на 5,7% и 4,4%, а товары группы А и Б увеличились
за счет максимального увеличения
товарооборота 3,4% и 18% соответственно.
Задача №7
Имеется
следующая информация о производстве
товара «А» предприятием за 2001-2005 гг.:
|
Годы |
2001 |
2002 |
2003 |
2004 |
2005 |
|
|
Объём |
132 |
140 |
150 |
156 |
164 |
|
1.
Для анализа погодовой динамики
производства товара «А» определите
следующие показатели динамики:
1.1.
абсолютные приросты (цепные и базисные);
1.2.
темпы роста и прироста (цепные и базисные);
1.3.
средний абсолютный прирост и средний
темп прироста.
Постройте
график, характеризующий интенсивность
динамики и сделайте выводы.
Решение:
2.
Абсолютный прирост на базисной основе
рассчитывается по формуле:
,
где
–
абсолютный прирост;
–
текущий уровень ряда динамики;
–
базисный уровень ряда динамики.
На
основании вышеуказанной формулы
рассчитаем абсолютный прирост на
базисной основе, взяв за базисный уровень
2001 год:
=
140 – 132 = 8 тыс. шт.
=
150 – 132 = 18 тыс. шт.
=
156 – 132 = 24 тыс. шт.
=
164 – 132 = 32 тыс. шт.
3.
Абсолютный прирост на цепной основе
рассчитывается по формуле:
,
где
–
абсолютный прирост на цепной основе;
–
уровень ряда динамики, предшествующий
изучаемому периоду.
Таким
образом, показатели абсолютного прироста
на цепной основе будут следующими:
=
140 – 132 = 8 тыс. шт.
=
150 – 140 = 10 тыс. шт.
=
156 – 150 = 6 тыс. шт.
=
164 – 156 = 8 тыс. шт.
4.
Темп роста на базисной основе рассчитывается
следующим образом:
–
темп роста на базисной основе.
За
базисный возьмём 2001 год:
5.
Темп роста на цепной основе рассчитывается
следующим образом:
–
темп роста на цепной основе.
6.
Темп прироста на базисной основе
находится по формуле:
–
темп прироста на базисной основе.
Рассчитаем
темп прироста, взяв за базисный период
– 2001 год:
=
106,06% – 100%= 6,06%
=
113,64% – 100%= 13,64%
=
118,18% – 100%= 18,18%
=
124,24% – 100%= 24,24%
7.
Темп прироста на цепной основе:
–
темп прироста на цепной основе.
=
106,06 – 100% = 6,06%
=
107,14% – 100% = 7,14%
=
104% – 100% = 4%
=
105,13% – 100% = 5,13%.
8.
Средний абсолютный прирост мы можем
найти по следующей формуле:
–
средний абсолютный прирост;
–
конечный уровень ряда динамики;
–
число периодов.
Таким
образом, в нашей задаче средний абсолютный
прирост составит:
9.
Средний темп роста рассчитаем по формуле:
–
средний темп роста.
Средний
темп прироста получим. вычтя из среднего
темпа роста 100%:
–
средний темп прироста.
Таким
образом средний темп прироста составит:
На
основании полученных данных, построим
график (рис. 1), характеризующий
интенсивность динамики.
Рис. 1.
Интенсивность динамики
Из
данного графика видно, что наибольший
абсолютный прирост производства товара
«А» приходится на 2005 год.
Список
используемой литературы
1.
Башина О.Э., Спирина А.А. Общая
теория статистики. – М.: Финансы и
статистика, 2005.
2.
Шмойлова Р.А., Минашкин В.Г.,
Садовникова Н.А. Практикум по
теории статистики. – М.: Финансы и
статистика, 2005.
3.
Статистика. Под ред. В.М. Симчеры. –
М.: Финансы и статистика, 2006.
4.
Методические указания и задания для
выполнения контрольных работ по
дисциплине «Статистика» – М., 2007
Средние величины и показатели вариации
Задача за 100 руб.
Для контроля за качеством поступившей партии товара произведено 5%-ное выборочное обследование. При отборе в выборку образцов по схеме механического отбора получены следующие данные о содержании влаги:
|
Влажность, % |
Количество образцов |
|
До 14 |
20 |
|
14-16 |
30 |
|
16-18 |
25 |
|
18-20 |
20 |
|
20 и выше |
5 |
|
Итого |
100 |
Определите:
1. Средний процент товара влажности.
2. Показатели вариации (абсолютные и относительные).
3. Моду и медиану.
4. При условии, что к нестандартной относится продукция с влажностью до 14 %, установите для всей партии с вероятностью 0,954 возможные пределы удельного веса нестандартной продукции.
5. Установите с вероятностью 0,997 возможные пределы среднего процента влажности для всей партии товара.
6. Постройте гистограмму распределения.
7. Сделайте выводы.
Решение
Средняя арифметическая взвешенная вычисляется по формуле:
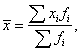
где xi – значение влажности,
fi – количество образцов.
Среднее линейное отклонение определяется из отношения суммы, взятых по абсолютной величине отклонений всех вариант от средней арифметической, к объему всей совокупности:
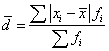
Дисперсией называется средний квадрат отклонений индивидуальных значений признака от их средней величины:
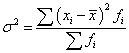
Среднее квадратическое отклонение – это показатель вариации, характеризующий величину, на которую все варианты в среднем отклоняются от средней арифметической. Равно корню квадратному из суммы квадратов отклонений индивидуальных значений признака от их средней, т.е. из дисперсии:
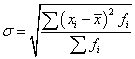
Произведем дополнительные расчеты в таблице для получения средних величин.
|
xi |
fi |
xifi |
|
|
|
|
|
|
1 |
13 |
20 |
260 |
3,2 |
64 |
10,24 |
204,8 |
|
2 |
15 |
30 |
450 |
1,2 |
36 |
1,44 |
43,2 |
|
3 |
17 |
25 |
425 |
0,8 |
20 |
0,64 |
16 |
|
4 |
19 |
20 |
380 |
2,8 |
56 |
7,84 |
156,8 |
|
5 |
21 |
5 |
105 |
4,8 |
24 |
23,04 |
115,2 |
|
85 |
100 |
1620 |
12,8 |
200 |
43,2 |
536 |
В результате получим следующие значения:
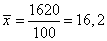
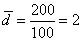
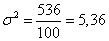
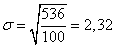
Вычислим относительные показатели вариации.
Коэффициент осцилляции: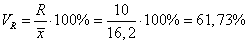
Линейный коэффициент вариации: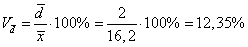
Коэффициент вариации: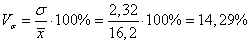
3. Мода – значение признака, наиболее часто встречающееся в исследуемой совокупности.
Для интервального вариационного ряда определяется по формуле:
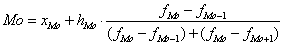
где xMo – нижняя граница значения интервала, содержащего моду;
hMo – величина модального интервала;
fMo – частота модального интервала;
fMo – 1 – частота интервала, предшествующего модальному ;
fMo + 1 – частота интервала, следующего за модальным ;
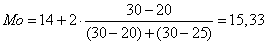
Медиана – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.
Для интервального вариационного ряда определяется по формуле:
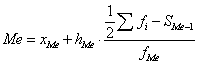
где xMe – нижняя граница значения интервала, содержащего медиану;
hMe – величина медианного интервала;
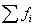– сумма частот;
SMe – 1 – сумма накопленных частот, предшествующих медианному интервалу;
fMe – частота медианного интервала.
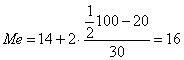
4. При условии, что к нестандартной относится продукция с влажностью до 14 %, установите для всей партии с вероятностью 0,954 возможные пределы удельного веса нестандартной продукции.
Возможные пределы, в которых ожидается доля нестандартной продукции с влажностью до 14% определим по формуле
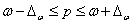
где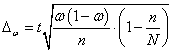 
– предельная ошибка выборочной доли.
t – нормированное отклонение, зависящее от вероятности,
n – объем выборки,
N – объем генеральной совокупности.
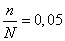
Доля продукции с влажностью до 14 %,. равна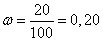 
, вероятность равна 0,954, тогда t = 2
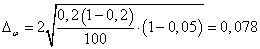
С помощью предельной ошибки выборочной доли определим границы для доли образцов:
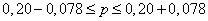
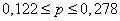
с вероятностью 0,954 можно ожидать, что доля нестандартной продукции с влажностью до 14%. будет в пределах от 0,122 до 0,278.
5. Установите с вероятностью 0,997 возможные пределы среднего процента влажности для всей партии товара
Предельную ошибку выборки рассчитаем по формуле
,
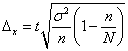где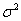 
– дисперсия выборочной совокупности.
Т.к. вероятность равна 0,997, то t = 3, тогда предельная ошибка выборки равна
.
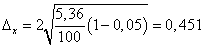Следовательно, с вероятностью 0,954 можно утверждать, что разность между выборочными (обследованные образцы) и генеральными показателями не превысит 0,451%.
С помощью предельной ошибки выборки определим границы для среднего процента влажности для всей партии товара:
.
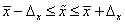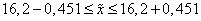
с вероятностью 0,997 можно ожидать, что средний процент влажности для всей партии товара будет в пределах от 15,7% до 16,7%.
- Главная
- Экономика
-
ПОМОГИТЕ!!!
Исч…
-
Предмет:
Экономика
-
Автор:
jeterp3de
-
Создано:
3 года назад
Ответы 2
-
Автор:
jadynharding
-
Оценить ответ:
0
Решение:
Средняя арифметическая взвешенная процента влажности всей
партии пшеницы определяется по формуле:
Х = (∑XiFi) / ∑Fi
где Fi – значение частоты повторения признака.
Х = [(15,9*700) + (14,8*620) + (14,2*328)] / (700+620+328) = (11130+9176+4657,6) / 1948 = 12,8%.
-
Автор:
riley22
-
Оценить ответ:
0
Знаешь ответ? Добавь его сюда!
Последние вопросы
-
Физика2 часа назад
Оценить число молекул воздуха в земной атмосфере, если давление воздуха вблизи поверхности Земли на уровне моря равно 760 мм рт.ст., молярная масса воздуха 29 г/моль. Радиус Земли 6400 км. Ускорение свободного падения считать постоянным и равным 9,8 м/с2 .
-
Математика3 часа назад
умоляю помогите
-
Математика5 часов назад
Помогите пожалуйста от этой оценки зависит годовая оценка
-
Информатика13 часов назад
3 вариант
-
Информатика13 часов назад
Помогите
-
Физика16 часов назад
Реохорд. какая электрическая величина меняется в цепи при изменении длины включенного реохорда
-
Математика17 часов назад
Представить в виде степенного ряда решение дифференциального уравнения, удовлетворяющее данным начальным условиям (для уравнения пер- вого порядка найти четыре ненулевых члена ряда, для уравнения второго по- рядка – пять членов).
y”=ye^x+1 y(0)=2; y'(0)=1.
-
Математика17 часов назад
1. Случайная величина распределена равномерно на отрезке [−2; 5]. Найти математическое ожидание и дисперсию. Что вероятнее: в результате ис- пытания случайная величина окажется в интервале (2,5; 3) или вне его?
-
Математика17 часов назад
1. В цехе работают 8 мужчин и 12 женщин. По табельным номерам отбира- ют 6 человек. Какова вероятность того, что среди них будут только 2 женщины?
-
Физика17 часов назад
определи фокусное расстояние лупы с точностью до сантиметра если её оптическая сила равна d 5.3 дптр.
-
Алгебра19 часов назад
-6x^2+x+2>0.Решение квадратных неравенств
-
Физика19 часов назад
2.3. Блок укреплен на вершине двух наклонных плоскостей, составляющих с горизонтом углы а = 30° и (3 = 45°. Гири равной массы
(т
х = т2 = 2 кг) соединены нитью, перекинутой через блок. Считая нить и блок невесомыми, принимая коэффициенты трения гирь о наклонные плоскости равными f1= f2= =0,1 и пренебрегая трением в блоке, определите: 1) ускорение, с которым движутся гири; 2) силу натяжения нити. [1) 0,24 м/с2; 2) 12 Н]
-
История1 день назад
ПЖ помогите КТО ЭТО Я НЕЗНАЮ
-
Алгебра1 день назад
Негр и мексиканец падают с небоскрёба. Кто упадёт первым?
-
Математика1 день назад
В машине сидят негр и мексиканец. Кто за рулём?
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Преподаватель который помогает студентам и школьникам в учёбе.
Определите средний процент влажности по способу моментов; среднеквадратическое отклонение тем же способом; коэффициент вариации, моду, медиану
 |
 |
Экономика |
 |
 |
Решение задачи |
 |
 |
18 февраля 2021 |
 |
 |
Выполнен, номер заказа №17342 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
245 руб. |
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!
Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):
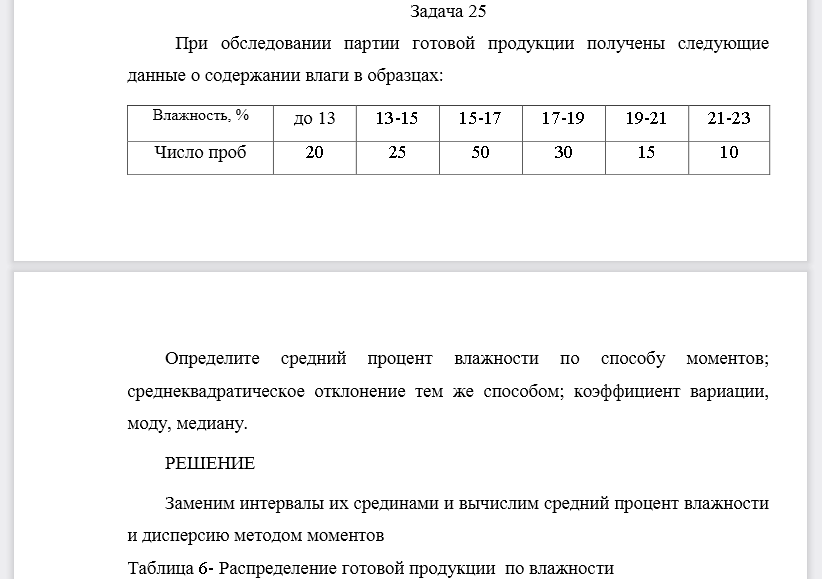
Задача 25 При обследовании партии готовой продукции получены следующие данные о содержании влаги в образцах:
Определите средний процент влажности по способу моментов; среднеквадратическое отклонение тем же способом; коэффициент вариации, моду, медиану.
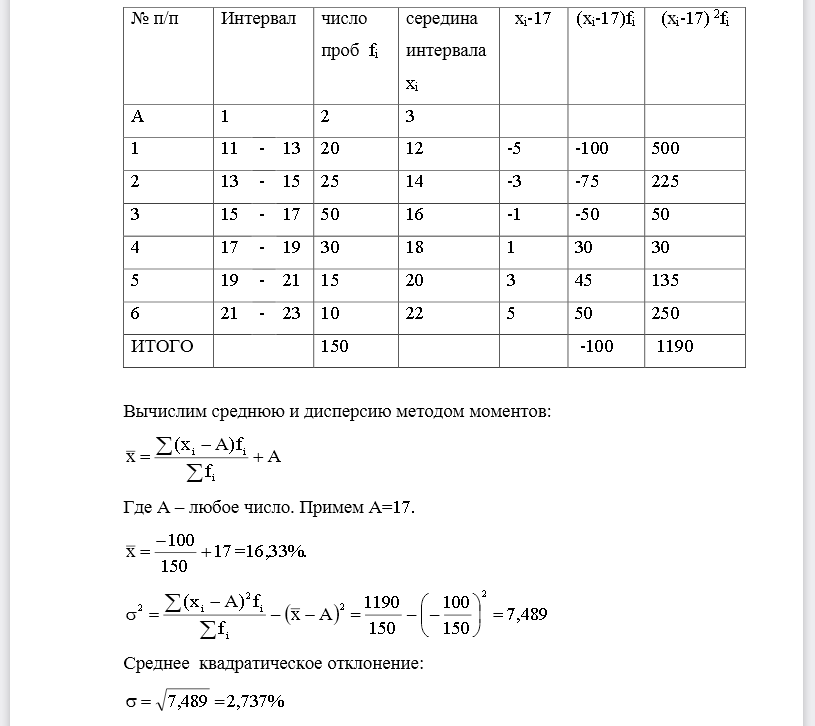
РЕШЕНИЕ Заменим интервалы их срединами и вычислим средний процент влажности и дисперсию методом моментов Таблица 6-Распределение готовой продукции по влажности Вычислим среднюю и дисперсию методом моментов: Где А –любое число. Примем Среднее квадратическое отклонение: Коэффициент вариации: Мода определяется по формуле: Где fМ0–минимальная граница модального интервала , hМ0–ширина модального интервала, fМ0-1–частота интервала, предшествующего модальному,fМ0–частота модального интервала, fМ0+1–частота интервала, следующего за модальным.Определим модальный интервал (имеющий наибольшую частоту): Для нахождения медианы будем пользоваться формулой: fMe–начальное значение медианного интервала, hMe–ширина медианного интервала, SMe–1 –сумма накопленных частот в интервалах, предшествующих медианному, fMe–частота медианного интервала По данным таблицы 1 медианный интервал 15-17(т.к. 20+25+50=95>150/2)50452150215Me16,2%Выводы: средняя влажность в данной совокупности составляла 16,33%. Показатель вариации позволяет сделать вывод, что данные выборки однородны (так как вариация менее 0,17). Вычисление моды показало, что наиболее типичная влажность в выборке 15,91%., а медиана, показывает, что в половине проб в выборке влажность менее 16,2%., а на другой половине более 16,2%.
Похожие готовые решения по экономике:
- Имеются следующие данные о товарных остатках торгового предприятия (тыс. руб.): Определите изменение товарных остатков по годам в тыс. руб. и в
- По одному из предприятий промышленности стройматериалов имеются следующие данные: Определите общий индекс цен и сумму роста или снижения объема
- Определите коэффициент корреляции, а также выровняйте ряд по прямой на основе следующих данных о рабочем стаже и выполнении сменных норм
- Из 2500 деталей в порядке механической выборки отобрано 500 штук деталей для определения среднего веса детали. Результаты получены такие
- По данным таблицы 1: 1.произведите группировку 30 коммерческих банков РФ (в зависимости от вашего варианта) по величине активов. К каждой выделенной группе
- На основании данных, приведенных в задаче 3, составьте по группам таблицу зависимости выпуска продукции от величины заводов по размеру основных фондов
- Определите изменение общей численности всего персонала по годам в процентах (на постоянной и переменной базах сравнения); удельный вес
- Определите план выпуска продукции по каждому заводу на первое полугодие, средний процент выполнения плана за полугодие по промышленной компании в целом
- Отразить приведенную ниже сделку на счетах бухгалтерского учета, сделав записи в Журнале регистрации хозяйственных операций. Российская
- Отразить предложенную ниже сделку по импорту товаров без посредников, записав все операции в Журнал регистрации хозяйственных операций.
- Определите среднюю списочную численность рабочих организации за сентябрь, если известны следующие данные
- Отразить на счетах бухгалтерского учета операции, связанные с получением и возвратом кредитных средств и процентов по их использованию. По договору
Работа добавлена на сайт samzan.net: 2016-01-17
Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой – мы готовы помочь.
Предоплата всего
от 25%
Подписываем
договор
Тема 4. СРЕДНИЕ ВЕЛИЧИНЫ
Основные вопросы
- Сущность средних величин. Требования к их использованию.
- Средняя арифметическая величина: методика расчета и условия применения.
- Применение величин средней гармонической, средней хронологической, средней геометрической.
- Сущность средних величин. Требования к их использованию
Средняя величина – это обобщающая, типическая характеристика совокупности исторически конкретных общественных явлений (процессов) по одному количественному признаку, показывающая уровень признака в расчете на единицу совокупности.
Основное назначение средней состоит в том, чтобы одним числом дать представление о совокупности различающихся между собой величин.
Средние величины должны вычисляться:
- на основе массовых данных;
- для качественно однородной совокупности;
- при наличии больших колебаний по группам общие средние должны дополняться групповыми средними.
При подборе формы средней величины следует исходить из экономического содержания осредняемого показателя. Например:
Признак, по которому рассчитывают среднюю величину, называют осредняемым и обозначают . Отдельные значения признака называют вариантами и обозначают 1, 2, 3…n , среднюю величину – .
Число вариант обозначают n, число повторений вариант обозначают f и называют частотой, весом или первичным носителем признака.
В статистике наиболее часто применяются следующие виды средних величин: средняя арифметическая простая и взвешенная, средняя гармоническая взвешенная, средняя хронологическая и средняя геометрическая.
- Средняя арифметическая величина:
методика расчета и условия применения
Средняя арифметическая простая – частное от деления суммы индивидуальных значений признака у всех единиц совокупности на число единиц данной совокупности n:
Применяется она в тех случаях, когда отдельные значения признака встречаются по одному разу или одинаковое число раз и когда первичные данные не сгруппированы.
При наличии большого числа единиц совокупности первичные данные целесообразно систематизировать, сгруппировав повторяющиеся варианты значений признака. Для расчета средней величины значения признака (i) умножают на число повторений вариантов (веса fi), суммируют полученные произведения и делят их на сумму весов (частот):
Эта формула носит название средней арифметической взвешенной.
В качестве весов могут выступать не только абсолютные, но и относительные величины (удельные веса в числе единиц совокупности).
Средняя арифметическая взвешенная применяется при наличии данных первичных значений признака и числа единиц совокупности, например, заработной платы отдельных рабочих и количества рабочих, себестоимости единицы продукции и количества продукции, урожайности отдельных культур и количества посевных площадей, выработки одного продавца и численности продавцов, процента продукции первого сорта и количества произведенной продукции.
Рассмотрим методику расчета средней величины по формуле средней арифметической взвешенной по данным дискретного ряда в таблице 1 для исчисления средней заработной платы.
Таблица 1
Заработная плата работников магазинов за отчетный период
|
Номер магазина |
Заработная плата одного продавца, тыс. р. (i) |
Количество продавцов, чел. (fi) |
Фонд заработной платы, тыс. р. (i fi) |
|
А |
1 |
2 |
3 |
|
1 |
16 |
5 |
80 |
|
2 |
13 |
8 |
104 |
|
3 |
11 |
7 |
77 |
|
Итого |
– |
20 |
261 |
Средняя заработная плата одного продавца ар.взв. определяется отношением фонда заработной платы всех продавцов i fi к численности продавцов трех магазинов fi, т. е. по формуле
Чтобы определить фонд заработной платы всех продавцов, необходимо сложить произведения заработной платы продавцов на количество продавцов по каждому магазину ( табл. 1, графа 3)
Промежуточные расчеты оформим в графе 3 таблицы 1. Количество продавцов известно по условию задачи ( fi = 20, табл. 1, гр. 2). Зная показатели числителя и знаменателя формулы, определяем среднюю заработную плату одного продавца:
При вычислении средней заработной платы применялась формула средней арифметической взвешенной, где в качестве весов выступало количество продавцов, т. е. первичный носитель признака.
Статистические данные часто могут быть представлены в виде интервальных вариационных рядов с закрытыми и открытыми интервалами.
Рассмотрим методику расчета средней величины в интервальном ряду. На основании исходных данных, которые приводятся в графах А, 1, таблицы 2, определяется средний процент влажности муки.
Таблица 2
Расчет среднего процента влажности муки
|
Группы образцов по влажности муки, % |
Число проб (fi) |
Фактическая влажность муки, % |
Середина интервала (i) |
Влажность муки во всех пробах, % (i fi) |
|
А |
1 |
2 |
3 |
4 |
|
До 13,0 |
10 |
12,8 – 13,0 |
12,9 |
129 |
|
13,0 – 13,2 |
20 |
13,0 – 13,2 |
13,1 |
262 |
|
13,2 – 13,4 |
40 |
13,2 – 13,4 |
13,3 |
532 |
|
Свыше 13,4 |
30 |
13,4 –13,6 |
13,5 |
405 |
|
Итого |
100 |
— |
— |
1328 |
В примере значения осредняемого признака: «влажность муки» – представлены в виде интервалов, причем в первой и последней группах интервалы открытые. В таком случае величина интервала первой группы условно принимается равной величине интервала последующей, а величина интервала последней группы равной величине интервала предыдущей.
В данном примере интервалы второй и третьей группы равные (13,2 – 13,0 = 0,2;
13,4 – 13,2 = 0,2). Нижняя граница интервала в первой группе определяется вычитанием из верхней границы размера интервала последующей группы (13,0 – 0,2 = 12,8), а верхняя граница в последней группе вычисляется прибавлением к нижней границе размера интервала предыдущей группы (13,4 + 0,2 = 13,6).
Занесем расчетные показатели влажности в гр. 2 таблицы 2.
Для нахождения среднего значения признака необходимо преобразовать интервальный ряд в дискретный, вычислив центр интервала в каждой группе.
Центр интервала определяем по формуле средней арифметической простой. Так, центры интервалов будут равны:
Занесем расчетные показатели в гр. 3 таблицы 2 и введем условные обозначения исходных данных. Влажность муки обозначаем символом i , число проб – символом fi. Дальнейший расчет аналогичен изложенному в таблице 1.
Для определения среднего процента влажности ( следует влажность муки во всех пробах ( i fi) разделить на число проб в партии ( fi), т. е. по формуле средней арифметической взвешенной
Число проб в партии известно по условию ( fi = 100, табл. 2, гр. 1). Влажность муки во всех пробах рассчитаем как сумму произведений показателей влажности муки на число проб в каждой группе:
i fi = 12,9 10 + 13,1 20 + 13,3 40 + 13,5 30 = 129 + 262 + 532 + 405 = 1328 (%).
Промежуточные расчеты оформим в гр. 4 таблицы 2. Зная показатели числителя и знаменателя, найдем средний процент влажности муки во всех пробах:
Средний процент влажности в 100 пробах составил 13,28 %.
- Применение величин средней гармонической, средней хронологической, средней геометрической
Средняя гармоническая величина применяется в тех случаях, когда известны не первичные, а вторичные носители признака (i fi), например, фонд заработной платы и заработная плата отдельных работников, затраты производства на всю продукцию и себестоимость единицы продукции, валовой сбор и урожайность отдельных культур, выработка всех продавцов и выработка одного продавца, количество продукции первого сорта и процент продукции первого сорта. В этих случаях отсутствуют данные о частотах. Средняя гармоническая взвешенная имеет вид:
где Мi = i fi , т. е. Мi – вес, который по своему значению является произведением варианты на частоту. Например, фонд заработной платы Мi – это произведение варианты (i – заработная плата отдельных рабочих) на частоту (fi – число рабочих), т. е. Мi – вторичный носитель признака.
Если надо найти среднюю заработную плату, имея данные о вторичном носителе признака – фонде заработной платы ( i fi) и заработной плате работников отдельных предприятий (i), необходимо предварительно вычислить количество работников, разделив фонд заработной платы на заработную плату продавцов каждого магазина.
Рассмотрим методику расчета средней величины по формуле средней гармонической взвешенной по данным таблицы 3 (гр. А, 1, 2).
Таблица 3
Данные о заработной плате работников магазинов
за отчетный период
|
Номер магазина |
Заработная плата одного продавца, тыс. р. (i) |
Фонд заработнойплаты, тыс. р. (i fi) |
Количество продавцов, чел. () |
|
А |
1 |
2 |
3 |
|
1 |
15 |
105 |
7 |
|
2 |
12 |
48 |
4 |
|
3 |
14 |
126 |
9 |
|
Итого |
– |
279 |
20 |
Вводим условные обозначения исходных данных. Осредняемый признак – заработную плату одного продавца – обозначим символом i, фонд заработной платы – вторичный носитель признака – символом i fi.
Чтобы определить количество продавцов, необходимо фонд заработной платы (i fi) разделить на заработную плату одного продавца (i) по каждому магазину. Промежуточные расчеты оформим в гр. 3 таблицы 3. Средняя заработная плата составит:
В этом случае при определении средней заработной платы применялась формула средней гармонической взвешенной.
Для расчета средней величины по данным на несколько дат при равных промежутках между датами применяется средняя хронологическая величина.
Средняя хронологическая – это частное от суммы индивидуальных значений признака, из которых первое и последнее значения взяты в половинном размере, на число единиц данной совокупности без одного (n–1), и рассчитывается по формуле
Среднюю хронологическую применяют для расчета среднего уровня моментного равноотстоящего динамического ряда, например, для расчета средних товарных запасов за квартал, полугодие, год; средних цен по данным о цене на несколько дат, когда отсутствуют данные о количестве товаров; средней численности высших учебных заведений (тема 7 «Ряды динамики»).
В тех случаях, когда отсутствуют данные о количестве проданных товаров, средняя цена по данным о цене на несколько дат (за квартал, полугодие, год) рассчитывается по формуле средней хронологической (табл. 4).
Таблица 4
Данные о ценах товара Б на рынке города
|
Наименование товара |
Цена за 1 кг (р.) на дату |
|||
|
22.03 |
22.04 |
22.05 |
22.06 |
|
|
Б |
28 |
26 |
29 |
32 |
Так, во втором квартале средняя цена товара Б равна :
Средняя геометрическая величина – это корень n – й степени из произведения значений признаков:
,
где n – число сомножителей.
Средняя геометрическая применяется для вычисления среднего темпа роста явления за отдельные периоды его развития. В качестве значений признака выступают цепные темпы роста, выраженные в коэффициентах (пример расчета показан в теме 7 «Ряды динамики»).
