На прошлых уроках мы познакомились с определением механического движения, узнали, каким бывает движение, изучили его свойства и характеристики. Теперь нам известны формулы для расчета скорости при равномерном движении ($upsilon = frac{S}{t}$) и средней скорости при неравномерном ($upsilon_{ср} = frac{S}{t}$).
На данном уроке мы посмотрим на эти формулы с другой стороны — научимся использовать их для расчета пути и времени движения, а также рассмотрим графики скорости и пути для равномерного движения.
Формулы для расчета пути и времени движения при равномерном движении тела
Скорость тела при равномерном движении вычисляется по формуле $upsilon = frac{S}{t}$. Отсюда, если мы знаем скорость и время, то можем найти пройденный путь:
$S = upsilon t$.
Чтобы определить путь, пройденный телом при равномерном движении, нужно скорость тела умножить на время его движения.
Выразим время:
$t = frac{S}{upsilon}$.
Чтобы рассчитать время при равномерном движении, нужно путь, пройденный телом, разделить на скорость его движения.
Формулы для расчета пути и времени движения при неравномерном движении тела
При неравномерном движении мы используем определение средней скорости, которую можем найти по формуле:
$upsilon_{ср} = frac{S}{t}$.
Чтобы определить путь при неравномерном движении, нужно среднюю скорость движения умножить на время:
$large S = upsilon_{ср} t$.
Также мы можем рассчитать время, разделив путь, пройденный телом, на среднюю скорость его движения:
$t = frac{s}{upsilon_{ср}}$.
График скорости равномерного движения
Так как скорость – это векторная величина, она характеризуется и модулем, и направлением. В зависимости от выбранного направления скорость по знаку может быть как положительной, так и отрицательной.
На рисунке 1 изображен динозавр, автомобиль и дом. Зададим ось координат $x$.
Если динозавр начнет двигаться к дому, то его скорость будет положительной, так как направление движения совпадает с направлением оси $x$. Если же динозавр направится к автомобилю, то его скорость будет отрицательной, так как направление движения противоположно направлению оси $x$.
Итак, график скорости равномерного движения имеет вид, представленный на рисунке 2.
Из графика видно, что скорости с течением времени не изменяется – они постоянны в любой выбранный момент времени. Если мы посмотрим на график положительной скорости, то увидим, что $upsilon = 6 frac{м}{с}$, на график отрицательной — $upsilon = -4 frac{м}{с}$.
Зная скорость и время, мы можем рассчитать пройденный путь за определенный промежуток времени. Рассчитаем какой путь пройдет тело с положительной скоростью за $4 space с$.
$S = upsilon t = 6 frac{м}{с} cdot space 4 c = 24 space м$.
График пути равномерного движения
Пример графика зависимости пути равномерного движения представлен на рисунке 3.
Здесь $S$ — ось пройденных путей, $t$ — ось времени. По этому графику мы можем найти путь, пройденный телом за определенный промежуток времени. Например, за 1 с тело проходит путь длиной 2 м, за 2 с – 4 м, за 3 с – 6 м.
Зная путь и время, мы можем рассчитать скорость. Для удобства расчета возьмем самый первый отрезок пути: $t = 1 space с$, $S = 2 space м$. Тогда,
$upsilon = frac{S}{t} = frac{2 space м}{1 space с} = 2 frac{м}{с}$.
Задачи
Задача №1
Самым быстрым животным на Земле считается гепард. Он способен развивать скорость до $120 frac{км}{ч}$, но сохранять ее способен в течение короткого промежутка времени. Если за несколько секунд он не настигнет добычу, то, вероятнее всего, уже не сможет ее догнать. Найдите путь, который пробежит гепард на максимальной скорости за $3$ секунды.
Переведем единицы измерения скорость в СИ и решим задачу.
$120 frac{км}{ч} = 120 cdot frac{1000 space м}{3600 space с} approx 33 frac{м}{с}$.
Дано:
$upsilon = 120 frac{км}{ч}$
$t = 3 space c$
СИ:
$upsilon = 33 frac{м}{с}$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Гепард двигается равномерно в течение 3 с.
Путь, который он проходит за это время:
$S = upsilon t$,
$S = 33 frac{м}{с} cdot 3 с approx 100 space м$
Ответ: $S = 100 space м$.
Задача №2
Колибри – самые маленькие птицы на нашей планете. При полете они совершают около 4000 взмахов в минуту. Тем не менее, они способны пролетать очень большие расстояния. Например, некоторые виды данной птицы перелетают Мексиканский залив длиной $900 км$ со средней скоростью $40 frac{км}{ч}$. Сколько времени у них занимает такой полет?
Переведем единицы измерения скорость в СИ и решим задачу.
$40 frac{км}{ч} = 40 cdot frac{1000 м}{3600 с} approx 11 frac{м}{с}$,
$900 space км = 900 space 000 м$.
Дано:
$upsilon_{ср} = 40 frac{км}{ч}$
$S = 900 space км$
CИ:
$upsilon_{ср} = 11 frac{м}{с}$
$S = 900 space 000 space м$
$t-?$
Показать решение и ответ
Скрыть
Решение:
Полет колибри будет примером неравномерного движения. Зная среднюю скорость и путь, рассчитаем время перелета:
$t = frac{s}{upsilon_{ср}}$,
$t = frac{900 space 000 space м}{11 frac{м}{с}} approx 82 space 000 space с$.
Переведем время в часы:
$1 space ч = 60 space мин = 60 cdot 60 space c = 3600 space c$.
Тогда:
$t = frac{82 space 000 space c}{3600 space c} approx 23 space ч$.
Ответ: $t = 23 space ч$.
Больше задач на расчет пути и времени движения с подробными решениями смотрите в отдельном уроке.
Упражнения
Упражнение №1
Пользуясь таблицей 1 из прошлого урока, найдите скорости страуса, автомобиля, искусственного спутника Земли. Определите пути, пройденные ими за $5 space с$.
Дано:
$upsilon_1 = 22 frac{м}{с}$
$upsilon_2 = 20 frac{м}{с}$
$upsilon_3 = 8000 frac{м}{с}$
$t = 5 space с$
$S_1 — ?$
$S_2 — ?$
$S_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Путь, пройденный страусом:
$S_1 = upsilon_1 t$,
$S_1 = 22 frac{м}{с} cdot 5 space с = 110 space м$.
Путь, пройденный автомобилем:
$S_2 = upsilon_2 t$,
$S_2 = 20 frac{м}{с} cdot 5 space с = 100 space м$.
Путь, пройденный искусственным спутником Земли:
$S_3 = upsilon_3 t$,
$S_3 = 8000 frac{м}{с} cdot 5 space с = 40 space 000 space м = 40 space км$.
Ответ: $S_1 = 110 space м$, $S_2 = 100 space м$, $S_3 = 40 space км$.
Упражнение №2
На велосипеде можно без особого напряжения ехать со скоростью $3 frac{м}{с}$. На какое расстояние можно уехать за $1.5 space ч$?
Дано:
$t = 1.5 space ч$
$upsilon = 3 frac{м}{с}$
СИ:
$t = 5400 space с$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем путь, который можно проехать на велосипеде с указанной скоростью:
$S = upsilon t$,
$S = 3 frac{м}{с} cdot 5400 space с = 16 space 200 space м = 16.2 space км$.
Ответ: $S = 16.2 space км$.
Упражнение №3
На рисунке 4 показан график зависимости пути равномерного движения тела от времени ($S$ — ось пройденного пути, $t$ — ось времени). По этому графику найдите, чему равен путь, пройденный телом за $2 space ч$. Затем рассчитайте скорость тела.
Определим из графика путь, пройденный телом за $2 space ч$. Этому времени на графике соответствует значение пути, равное $200 space км$. Запишем условие задачи и решим ее.
Дано:
$S = 200 space км$
$t = 2 space ч$
$upsilon — ?$
Показать решение и ответ
Скрыть
Решение:
Скорость равномерного движения рассчитываем по формуле:
$upsilon = frac{S}{t}$.
$upsilon = frac{200 space км}{2 space ч} = 100 frac{км}{ч}$.
Ответ: $upsilon = 100 frac{км}{ч}$.
Упражнение №4
График зависимости скорости равномерного движения тела от времени представлен на рисунке 5. По этому графику определите скорость движения тела. Рассчитайте путь, который пройдет тело за $2 space ч$, $4 space ч$.
Из графика видно, что скорость тела равна $8 frac{м}{с}$. Этот график представляет собой прямую, параллельную оси времени, потому что движение равномерное, и скорость тела не изменяется с течением времени. Запишем условие задачи и решим ее.
Дано:
$t_1 = 2 space ч$
$t_2 = 4 space ч$
$upsilon = 8 frac{м}{с}$
СИ:
$t_1 = 7200 space с$
$t_2 = 14 space 400 space с$
$S_1 — ?$
$S_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Путь рассчитаем по формуле: $S = upsilon t$.
За $2 space ч$ тело пройдет путь:
$S_1 = upsilon t_1$,
$S_1 = 8 frac{м}{с} cdot 7200 space с = 57 space 600 space м = 57.6 space км$.
За $4 space ч$ тело пройдет путь:
$S_2 = upsilon t_2$,
$S_2 = 8 frac{м}{с} cdot 14 space 400 space с = 115 space 200 space м = 115.2 space км$.
Ответ: $S_1 = 57.6 space км$, $S_2 = 115.2 space км$.
Упражнения №5
По графикам зависимости путей от времени (рисунок 6) двух тел, движущихся равномерно, определите скорости этих тел. Скорость какого тела больше?
Для того, чтобы рассчитать скорость тела, нам нужно знать путь и время, за которое этот путь был пройден. Возьмем эти значения для двух тел из их графиков. Первое тело (I) проходит путь, равный $4 space м$, за $2 space с$. Второе тело (II) проходит путь, равный $4 space м$, за $4 space с$. Запишем условие задачи и решим ее.
Дано:
$S = 4 space м$
$t_1 = 2 space с$
$t_2 = 4 space с$
$upsilon_1 — ?$
$upsilon_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем скорость первого тела:
$upsilon_1 = frac{S}{t_1}$,
$upsilon_1 = frac{4 space м}{2 space с} = 2 frac{м}{с}$.
Рассчитаем скорость второго тела:
$upsilon_2 = frac{S}{t_2}$,
$upsilon_2 = frac{4 space м}{4 space с} = 1 frac{м}{с}$.
Получается, что скорость первого тела больше скорости второго.
Ответ: $upsilon_1 = 2 frac{м}{с}$, $upsilon_2 = 1 frac{м}{с}$, $upsilon_1 > upsilon_2$.
Оглавление:
- Основные теоретические сведения
- Система СИ
- Путь и перемещение
- Средняя скорость
- Равноускоренное прямолинейное движение
- Свободное падение по вертикали
- Горизонтальный бросок
- Бросок под углом к горизонту (с земли на землю)
- Сложение скоростей
- Равномерное движение по окружности
Основные теоретические сведения
Система СИ
К оглавлению…
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины – метр (1 м),
- времени – секунда (1 с),
- массы – килограмм (1 кг),
- количества вещества – моль (1 моль),
- температуры – кельвин (1 К),
- силы электрического тока – ампер (1 А),
- Справочно: силы света – кандела (1 кд, фактически не используется при решении школьных задач).
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Таблица дольных и кратных приставок в физике:

Путь и перемещение
К оглавлению…
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
К оглавлению…
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:

где: Lполн – весь путь, который прошло тело, tполн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
К оглавлению…
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:

В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):

С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:

Свободное падение по вертикали
К оглавлению…
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:

Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:

Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):


Горизонтальный бросок
К оглавлению…
При горизонтальном броске с начальной скоростью v0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:

При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали. Тогда этот угол будет находиться из соотношения:


Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:

Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:

При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:

Бросок под углом к горизонту (с земли на землю)
К оглавлению…
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):

Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
К оглавлению…
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:

Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
К оглавлению…
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.

Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:

Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:

При равномерном вращении скорость тела будет определяется следующим образом:
где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt. Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:

Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:

Связь между модулем линейной скорости v и угловой скоростью ω:

При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).

Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:

Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.
Средняя скорость считается так: весь путь поделить на всё время движения. Формула одна и очень простая, но почему-то школьники часто путаются в задачах на среднюю скорость. Разберу три характерные задачи и основные ошибки. Возможно, статья будет полезна учителям и репетиторам, а также школьникам.
1. Половина пути
Первую половину пути поезд ехал со скоростью 60 км/ч, а вторую – 90 км/ч. С какой средней скоростью ехал поезд на всём пути?
Первым делом школьник захочет сложить эти две скорости и поделить пополам. Логично? Да. Но, к сожалению, неправильно.
Объясняю, почему. Поскольку первую половину пути поезд ехал с меньшей скоростью, то времени было затрачено больше, чем на вторую. А значит, вклад отдельных скоростей неравнозначен, и нельзя так просто делить пополам.
Тут школьник может впасть в панику. Что делать? Умножать? Делить? Непонятно. Воспользоваться напрямую формулой “расстояние поделить на время” не получится – ни расстояние, ни время нам неизвестно.
Для школьников, только начинающих изучать основы физики, бывает трудно оперировать с неизвестными величинами. Нам не дано ничего, кроме скоростей, как же быть? В качестве маленькой ступеньки к освоению неизвестности могу предложить следующий ход – сначала додумать неизвестные данные. Возьмём и сами решим, пусть поезд пройдет 180 километров, цифру возьмем так, чтобы легко делилась.
Тогда половина пути будет 90 километров. Поезд пройдет её за 1,5 часа. Вторую половину пути – за 1 час. Это легко посчитает любой школьник. Значит, общее время в пути будет 2,5 часа. Делим общее расстояние 180 километров на 2,5 часа, и получаем 72 км/ч.
Это просто и понятно, но учитель такую задачу не примет. Откуда мы взяли 180 километров, когда это неизвестно? Тем не менее, дав себе эти неизвестные данные, мы продумали алгоритм и довели задачу до ответа. Осталось формализовать это решение, так чтобы не использовать то, что не дано. Обозначим наши 180 километров за S, и опишем всё, что мы делали раньше, только вместо цифр используем буквы.
Получается, что зная ход решения “в цифрах”, мы переводим его в буквенные обозначения. И тут главное не остановиться на полдороги, не смущаться, что нам неизвестно расстояние. Ведь оно в конце сократилось, и средняя скорость оказалась независящей от расстояния (что вполне логично). И от школьника здесь требуются уже алгебраические умения – складывать дроби, переворачивать их.
Если подобная задача встретилась в тесте, где требуется только ответ, можно вообще не заморачиваться – так как средняя скорость в данной задаче не зависит от расстояния, можно посчитать при любом удобном расстоянии. По крайней мере, это лучше, чем сидеть и ломать голову, не зная, как подступиться к решению. Если же требуется оформление – тут числовое решение может помочь как переходный этап, чтобы понять, что именно делать с формулами, как их крутить-вертеть.
Школьникам часто бывает трудно переходить на новый уровень абстракции – от чисел к переменным, которые могут принимать разные числовые значения. В алгебре это тренируют, но там одна переменная икс, и иногда игреки встречаются. А в физике этих переменных пруд пруди, в каждой задаче они разные, и если ученик не освоил этот уровень, то физика кажется ему супер-трудной. Кроме того, в школе переход от чисел к переменным часто упускают, в программе отдельных навыков работы с формулами нет.
2. Средняя скорость по графику пути
Пусть нам дан график зависимости координаты от времени. Требуется определить среднюю скорость.
По графику видно, что движение состоит из четырех этапов:
- Тело стартует в нуле и через 2 секунды оказывается на координате 2 м.
- Тело останавливается, и в течение 4 секунд покоится в точке с координатой 2 м.
- Тело начинает движение, и через 2 секунды оказывается в точке 6 м.
- Тело движется в обратном направлении, и через 2 секунды оказывается в точке 5 м.
Проговорить, понять все эти этапы – важная часть решения. А дальше многие школьники начинают вычислять скорости движения на каждом этапе: На первом – 1 м/с, на втором – 0, на третьем – 2 м/с, на четвертом – 0,5 м/с. Вот это действие как раз лишнее. Для того, чтобы вычислить среднюю скорость, вовсе не обязательно знать скорости на каждом этапе!
Вспомним определение средней скорости – это весь путь, поделить на всё время. Поэтому просто по графику считаем весь путь – 6 метров “туда” и 1 метр “обратно”, в сумме 7 метров. Общее время движения – 10 секунд. Делим 7 метров на 10 секунд, получаем 0,7 м/с.
3. Средняя скорость по графику скорости
Бывает так, что нам дан график зависимости скорости от времени, и требуется определить среднюю скорость. Вот, к примеру, такой график.
Читаем график. Движение состоит из трёх этапов
- С начала движения до момента времени 2 с тело движется с постоянной скоростью 2 м/с
- От 2 до 6 с тело движется со скоростью 6 м/с
- В последние 4 секунды от 6 до 10 с тело замедляется, снижая свою скорость до нуля.
Попытки что-то сделать со значениями скорости самими по себе здесь обречены на провал. Опять надо найти весь путь и всё время движения. Путь по графику скорости определяется как площадь под графиком, причем если график идет ниже нуля, то соответствующие участки складываются.
Считаем площадь фигуры – два прямоугольника на первых двух этапах и треугольник на третьем. Первый этап – 4 м, второй этап – 24 м, третий этап – 12 м. Значит, весь путь будет 40 метров. Всё время 10 секунд, значит, средняя скорость 4 м/с.
Общие рекомендации для решения задач на среднюю скорость
1. Средняя скорость – это всегда весь путь делить на всё время. Данные об отдельных скоростях сами по себе не дадут полной информации о средней скорости. Используем только эту формулу.
2. Следует проанализировать конкретную ситуацию и понять, как можно применить формулу. Если кажется, что не хватает данных – не смущаться.
3. Данные по скоростям на отдельных этапах могут быть полезны для проверки готового ответа: средняя скорость должна лежать между минимальной и максимальной.
Спасибо, что прочитали до конца! Желаю школьникам хорошей учёбы, учителям – понятливых и любопытных учеников, родителям – чтобы дети радовали. Буду рада лайкам и новым подписчикам!
Содержание:
Как описывают механическое движение:
Хотя каждый имеет определенное представление о движении, сначала нужно договориться о точных терминах, которые мы будем употреблять, описывая разнообразные движения тел.
Абсолютно твердое тело
Телом в физике принято называть такой предмет, который имеет массу, форму и способ-но двигаться как единое целое. Это может быть камень, столб, автомобиль, мяч, планета, само-лет и тому подобное. Но что делать, когда форма тела несколько изменяется? При этом понятно, что мяч легче деформируется, чем камень.
Рассмотрим колесо железнодорожного вагона (рис. 9.1) и для простоты представим себе, что оно вообще недеформирующееся. Расстояние между любыми точками такого тела не изменяется, и его называют абсолютно твердым телом. Понятно, что в действительности таких тел не существует, это просто удобное упрощение.
Материальная точка
Бывает так, что в процессе движения размеры, форма и внутреннее строение тела не имеют большого значения. Например, если автомобиль длиной 10 м должен преодолеть расстояние 100 км, то его собственной длиной можно пренебречь, условно считая автомобиль просто точкой. При этом допускают, что масса данной точки равна массе автомобиля, а саму точку называют материальной. Следовательно, материальная точка – это тело, размерами которого в некоторых обстоятельствах можно пренебречь. Самолет, который летит в небе (рис. 9.1), или спутник на космической орбите можно рассматривать как материальные точки.
Такие упрощения, как материальная точка, часто используют в физике
и называют физической моделью.
Пример №1
Рассмотрим, какой путь должен преодолеть автомобиль длиной 10 м, чтобы переехать мост длиной 40 м. Очевидно, что для этого нужно проехать путь 40 м + 10 м = 50 м. То есть в данном случае автомобиль нельзя рассматривать как не имеющий размеров. Для человека, который двигается по мосту, это расстояние будет мало отличаться от 40 м.
Механическое движение
Механическим движением называют изменение положения тела относительно других тел в пространстве со временем.
Движение тела проще описать, если тело рассматривать как материальную точку. Линию, описываемую материальной точкой во время движения, называют траекторией. Иногда можно увидеть, где пролегает траектория движения. След, тянущийся за реактивным самолетом (рис. 9.2), или рельсы железной дороги (рис. 9.5) дают некоторое представление о траектории движения этих тел.
Орбиты, по которым двигаются планеты вокруг Солнца, то есть их траектории, были рассчитаны в ХVІІ в. немецким астрономом И. Кеплером, который доказал, что они являются эллипсами (рис. 9.3).
Тело в своем движении вдоль траектории может еще и вращаться. Такое движение описать сложнее, потому что разные точки тела могут двигаться по-разному. Например, красная точка на колесной паре (рис. 9.1) двигается по прямой, желтая точка описывает окружность вокруг центра колеса, а белая точка в данный момент вообще не двигается.
Но и здесь существует простой случай. Рассмотрим движение кабин колеса обозрения (рис. 9.6). Ось, к которой они прикреплены, двигается по окружности, но сами кабины передвигаются так, что их пол остается горизонтальным. В таком случае все точки кабины описывают одинаковые траектории, и нет необходимости заменять ее материальной точкой.
Если тело двигается так, что любая прямая на нем остается параллельной самой себе, то такое движение называют поступательным. В дальнейшем, где это не суть важно, будем употреблять термин «тело», имея в виду материальную точку.
 Рис. 9.5. Рельсы железной дороги указывают траекторию движения поезда Рис. 9.5. Рельсы железной дороги указывают траекторию движения поезда |
|
Тело отсчета
Когда мы едем на автомобиле, то изменяем свое положение относительно дороги, деревьев, домов или других автомобилей – мы движемся относительно этих тел. Однако мы не изменяем свое положение относительно собственного автомобиля, то есть относительно него мы не движемся.
Объекты, относительно которых мы определяем свое движение, называют телами отсчета.

Рис. 9.7. Космонавтам на МКС кажется, будто они зависли в пространстве, хотя в действительности их скорость составляет 8 км/с
Понятно, что скорость и траектория тела существенно зависят от выбора тела отсчета. Если такого тела нет или оно очень далеко, то вообще трудно установить, движемся мы или находимся в состоянии покоя. Космонавтам на международной космической станции МКС (рис. 9.7) кажется, будто они завис-ли в пространстве, хотя в действительности их скорость очень большая и составляет 8 км/с относительно Земли. То же самое ощущают пассажиры само-лета, летящего на значительной высоте.
Сидя в комнате, мы не чувствуем, что двигаемся вместе с Землей относи-тельно Солнца с огромной скоростью – 30 км/с. Следовательно нужно сделать вывод, что механическое движение – относительно.
Система отсчета
Если мы хотим точнее описать движение, то одного тела отсчета мало, ну-жен еще способ определения положения подвижного объекта в пространстве и часы для отсчета времени. Причем необходимо иметь по крайней мере двое часов, которые «идут» одинаково (то есть синхронизированы) – одни, связанные с подвижным объектом, а вторые – с телом отсчета. Все это вместе называют системой отсчета.
Система отсчета – это тело отсчета, связанная с ним навигационная система (например, GPS), которая позволяет определить положение подвижного объекта в пространстве в любой момент времени.
Путь и перемещение
Независимо от того, как двигается тело – по прямой или по кривой – пройденный им путь равен длине траектории (рис. 9.9). Величина пройденного пути не зависит от направления движения. Куда бы ни двигалось тело – вперед или назад – пройденный им путь только возрастает. Путь помечают буквой «s» и измеряют в СИ в метрах.
Нас может также интересовать, насколько далеко переместилось тело в своем иногда до-вольно запутанном движении. Например, на рис. 9.9 нижняя линия может изображать траекторию мяча, который ведет баскетболист, ударяя его о пол. Верхняя линия – мяч, брошенный верхом другому игроку, а средняя траектория образуется, когда игрок просто несет с собой мяч. Но во всех случаях перемещение мяча одинаковое.
Чтобы найти перемещение баскетбольного мяча, брошенного в кольцо (рис. 9.10), соединяем начало и конец движения направленным от-резком прямой, при этом стрелка указывает на конечную точку.
Перемещением называют направленный отрезок прямой, который соеди-няет начальное и конечное положение тела. Такие «направленные» отрезки в математике называют векторами. Следовательно, перемещение – вектор.
На рисунке 9.10 желтая пунктирная линия изображает траекторию мяча, длина которой обозначена «s». Синяя стрелка изображает вектор перемещения мяча. Перемещения, в отличие от пути, помечают «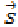 », где стрелка над бук-вой значит, что это «вектор». Величину перемещения измеряют в метрах, как и путь, однако их числовые значения, как видим, не всегда совпадают.
», где стрелка над бук-вой значит, что это «вектор». Величину перемещения измеряют в метрах, как и путь, однако их числовые значения, как видим, не всегда совпадают.
Если физическая величина характеризуется только числовым значением и нет необходимости указывать ее направление, то она называется скалярной физической величиной, или скаляром. Когда для полного определения величины нужно указать не только числовое значение, но и направление, то ее называют векторной физической величиной, или просто вектором.
Например, перемещение – это вектор, а путь и время – скаляры.
СЛОЖЕНИЕ ПЕРЕМЕЩЕНИЙ – ЭТО УМЕНИЕ ПРАВИЛЬНО РИСОВАТЬ СТРЕЛКИ
На рисунках, как вы уже видели, векторы изображают стрелками (рис. 9.11). Условимся, что длина стрелки в определенном масштабе равна величине вектора. Пусть перемещение материальной точки (желтая точка) из А в В (синяя Рис. 9.11 стрелка) составляет 4 м вправо, а из В в С (черная стрелка) 1 м вправо. Тогда общее перемещение из А в С (красная стрелка) будет составлять 5 м вправо (рис. 9.12).
В векторной форме последовательные перемещения точки из А в В, а потом в С записывают так: 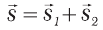 (9.1)
(9.1)
Если движение происходит по прямой в одну сторону, то пройденный путь совпадает с величиной перемещения, то есть s1 + s2 = s и общий путь также составляет 5 м. В этом случае величина общего перемещения не совпадает с пройденным точкой путем.
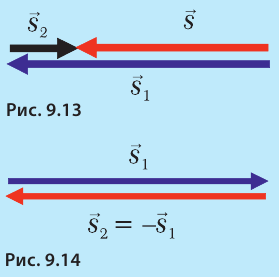
Два вектора считаются одинаковыми, если их величины и направления одинаковы. Вектор, противоположный данному, но равный ему по величине, помечают знаком «–» и записывают так 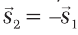 (рис. 9.14).
(рис. 9.14).
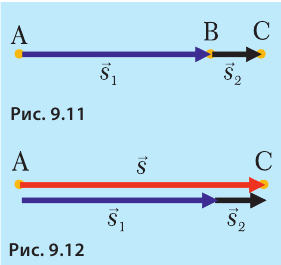
Если точка двигается в определенной плоскости из А в В, а потом из В в С (рис. 9.15), общее перемещение и здесь обозначают как 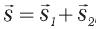 , но теперь расчет общего перемещения сложнее. В данном случае можно, например, длину стрелок изобразить в определенном масштабе, а затем линейкой измерить длину общего перемещения и по масштабу определить его настоящую величину (смотрите пример 9.2).
, но теперь расчет общего перемещения сложнее. В данном случае можно, например, длину стрелок изобразить в определенном масштабе, а затем линейкой измерить длину общего перемещения и по масштабу определить его настоящую величину (смотрите пример 9.2).
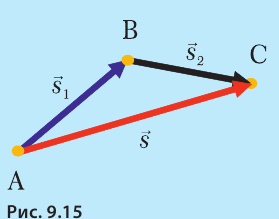
Подобно перемещениям другие векторные величины (скорость, ускорение, сила) складываются так же. Правило сложения векторов можно сформулировать следующим образом:
Чтобы сложить два вектора, нужно из конца стрелки первого вектора провести второй вектор. Вектор суммы соединяет начало первого вектора с концом второго.
Порядок (алгоритм) сложения векторов изображен на рисунке 9.16.
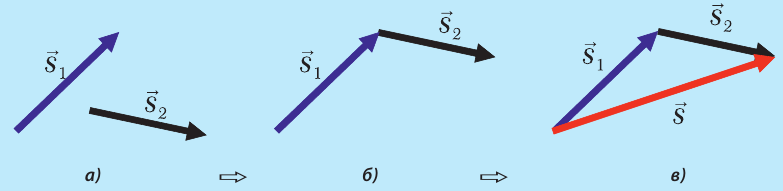
Рис. 9.16. а) Чтобы сложить два вектора 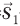 и
и 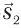 , нужно
, нужно  6) вектор
6) вектор 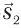 параллельно перенести так, чтобы его начало совпало с концом вектора
параллельно перенести так, чтобы его начало совпало с концом вектора 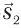
 в) затем соединить начало первого вектора с концом второго и получить вектор суммы
в) затем соединить начало первого вектора с концом второго и получить вектор суммы 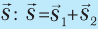
Пример №2
Перемещения, изображенные на рис. 9.17, состоялись последовательно из точки А в точку В, а затем в точку С. Нужно определить все перемещения, если известно, что одной клеточке соответствует 1 м.
Решение. Очевидно, что s1 содержит четыре клеточки, следовательно, s1 = 4 м. Аналогично s2 = 3 м. Общее перемещение АС ( 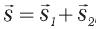 ) является гипотенузой треугольника АВС и по величине равно 5 м.
) является гипотенузой треугольника АВС и по величине равно 5 м.
В этом можно убедиться, измерив линейкой длину отрезка АС – она составляет ровно 5 клеточек. Второй способ заключается в расчете длины гипотенузы по теореме Пифагора: 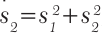 , откуда следует s2 = 25, следовательно s = 5 м.
, откуда следует s2 = 25, следовательно s = 5 м.
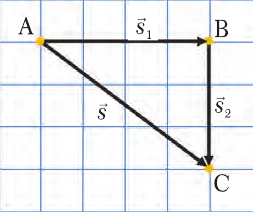
Рис. 9.17
Итоги
- Материальная точка – это тело, размерами которого при определенных условиях можно пренебречь.
- Механическим движением называют изменение положения тела относительно других тел со временем.
- Система отсчета позволяет определить положение тела в пространстве и описать его движение.
- Путь измеряют вдоль траектории – это скалярная физическая величина.
Равномерное прямолинейное движение
Равномерным называют движение вдоль прямой в одном направлении, при котором движущаяся точка совершает одинаковые перемещения за любые одинаковые промежутки времени. То есть мы должны следить за тем, чтобы перемещения были одинаковыми – как за большие, так и за насколько угодно малые (но одинаковые) промежутки времени.
Пример №3
«Хитрый жук» летит по прямой в одном направлении и каждую секунду преодолевает 1 м пути. Можно ли утверждать, что он двигается равномерно?
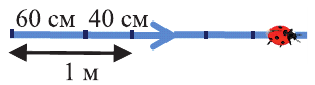
Для этого нужно посмотреть, одинаковы ли также его перемещения за каждые 0,5 с. Может случиться так, что за первые 0,5 с каждой секунды он пролетает 60 см, а за следующие 0,5 с – только 40 см. В таком случае движение жука не является равномерным.
Скорость
Скорость – это векторная физическая величина, которая характеризует скорость перемещения и направление движения материальной точки относительно выбранной системы отсчета. Она равна отношению перемещения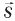 , которое прошло тело, ко времени, в течение которого происходило это перемещение:
, которое прошло тело, ко времени, в течение которого происходило это перемещение:
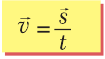
Во время равномерного движения скорость тела одинакова по величине и направлению независимо от того, какой по величине отрезок времени или пути мы выбрали.
Можно сказать и так: движение с постоянной по значению и направлению скоростью является равномерным и прямолинейным.
Поскольку скорость – это вектор, то ее обозначают буквой 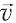 и чаще всего измеряют в м/с или км/ч. Если нас интересует только величина скорости, то ее обозначают |
и чаще всего измеряют в м/с или км/ч. Если нас интересует только величина скорости, то ее обозначают | 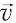 | (читают «модуль вэ») или просто
| (читают «модуль вэ») или просто 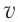 .
.
В английском языке эта скорость имеет специальное название «speed», от которого происходит слово «спидометр» – измеритель скорости. Скорость как вектор в английском языке называют «velocity» – отсюда и обозначение вели-чины буквой «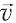 » и название «велосипед».
» и название «велосипед».
Поскольку при равномерном движении величина (модуль) перемещения |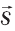 | совпадает с величиной пройденного пути s, то мы для начала будем рассматривать скорость по пути. Чтобы более кратко выражать свои мысли, физики пользуются языком математики, то есть представляют физические закономерности или понятия в виде формул. Скоростью по пути будем называть физическую величину, которая равна отношению пройденного пути ко времени, за которые этот путь был пройден. То есть, чтобы найти модуль скорости «
| совпадает с величиной пройденного пути s, то мы для начала будем рассматривать скорость по пути. Чтобы более кратко выражать свои мысли, физики пользуются языком математики, то есть представляют физические закономерности или понятия в виде формул. Скоростью по пути будем называть физическую величину, которая равна отношению пройденного пути ко времени, за которые этот путь был пройден. То есть, чтобы найти модуль скорости «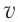 » тела, нужно модуль перемещения (то есть пройденный путь «s») разделить на затраченное время «t»:
» тела, нужно модуль перемещения (то есть пройденный путь «s») разделить на затраченное время «t»:
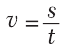 (10.1)
(10.1)
Такой способ определения скорости впервые предложил известный швейцарский математик Леонард Эйлер. Согласно формуле (10.1) путевая скорость точки показывает расстояние, которое прошло тело за единицу времени.
Зная скорость и затраченное время, из (10.1) можем найти пройденный те-лом путь:
s = v ∙ t (10.2)
Затраченное время, зная пройденный путь и скорость движения, можно найти при помощи формулы:
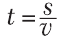 (10.3)
(10.3)
За единицу скорости в Международной системе единиц (СИ) принята скорость такого равномерного движения, при котором материальная точка за 1 с перемещается на 1 м:
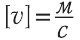
Напомним: если нас интересует единица измерения физической величины, а не ее числовое значение, то эту величину пишут в квадратных скобках. Например:  = 54 км/ч, а
= 54 км/ч, а 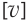 = км/ч.
= км/ч.
Конвертация единиц скорости
Если автомобиль двигается, например, со скоростью 54 км/ч, а нам надо узнать, какой путь он проходит за одну секунду, необходимо 54 км разделить на количество секунд в 1 часу. Один час равен 60 мин, а 1 мин – 60 с. Таким образом, за 1 с автомобиль преодолеет расстояние 54 км : 3600 = 0,015 км. Поскольку 1 км равен 1000 м, то это значит, что за 1 с автомобиль проходит 15 м, или, другими словами, его скорость – 15 м/с.
И наоборот, если нам нужно узнать, сколько км/ч составляет скорость 10 м/с (скорость спринтера-рекордсмена), нужно это число умножить на 3600 и разделить на 1000. Получим 36 км/ч.
Пример №4 «Автомобиль»
С какой скоростью двигается автомобиль по автостраде, если за три часа он, двигаясь равномерно, проехал 270 км?
Сокращенная запись задачи и решения:
Ответ: Скорость автомобиля равняется 90 км/ч.
Пример №5 «Автобус на мосту» (рис. 10.1)

Рис. 10.1. Автобус на мосту
Какое время затратит автобус длиной l = 10 м, который двигается со скоростью  = 72 км/ч, чтобы переехать мост длиной L = 100 м? Решите задачу в двух случаях: а) считая автобус материальной точкой, б) не считая автобус материальной точкой. Определите относительную погрешность, допущенную при применении модели материальной точки.
= 72 км/ч, чтобы переехать мост длиной L = 100 м? Решите задачу в двух случаях: а) считая автобус материальной точкой, б) не считая автобус материальной точкой. Определите относительную погрешность, допущенную при применении модели материальной точки.
б) Решим задачу точнее, не считая автобус материальной точкой. Авто-бус находится на мосту (рис. 10.2) от момента, когда только коснулся его передними колесами, и до момента, когда съехал с него задними колеса-ми. Для этого ему придется пройти путь L + l = 110 м.
Тогда: 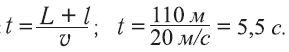
Абсолютная погрешность при приближенном решении составляет 5,5 с – 5 с = 0,5 с.
Относительная погрешность составляет: 0,5 с / 5 с = 0,1, или 0,1·100% = 10%.
Ответ. Автобус проедет мост за 5,5 с. Если считать его материальной точ-кой, то приближенный ответ составляет 5 с. При использовании модели материальной точки погрешность равняется 10%.
Итоги:
- Движение с постоянной по значению и направлению скоростью называют равномерным.
- Скоростью по пути называют отношение пройденного пути к затраченному на это времени (при равномерном движении).
- Физический смысл скорости – она показывает пройденный за единицу времени путь.
- Скорость, путь или время движения можно вычислить, пользуясь формулой
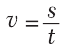
Относительность движения
Движение и спокойствие – понятия относительные
Когда говорят, что движение относительно, то имеют в виду, что перемещение, скорость и траектория тела зависят от того, относительно каких тел отсчета определяется движение.
Мало сказать, что тело двигается, следует еще указать, относительно какого тела отсчета происходит это движение. В зависимости от того, где находится наблюдатель, мы получим разные ответы.
Самолет-истребитель может дозаправиться в воздухе лишь в том случае, если его скорость совпадает по направлению и равна по значению скорости самолета-заправщика (рис. 11.1). Хотя самолеты движутся очень быстро, относительно друг друга они находятся в состоянии спокойствия.
Иногда, сидя в поезде, который еще не отправился (рис. 11.2) и посмотрев в окно на соседний поезд, вы можете подумать, что уже поехали. Но выглянув в противоположное окно, замечаете, что вокзал на месте. Так двигались вы или нет? – такой вопрос не имеет смысла. Относительно вокзала не двигались, а относительно соседнего поезда – двигались (как и он относительно вас).
В задачах «на относительность движения» надо уметь представить себя либо на месте одного наблюдателя, либо на месте другого. Такая манера раз-мышления похожа на работу актера, который играет разные роли в фильмах или спектаклях и должен каждый раз «вживаться» в чужой образ. В повседневной жизни также очень важно уметь представить себя на месте другого чело-века и проанализировать ход его мыслей.
Пример №6
Если стоять на эскалаторе (рис. 11.3), который движется со скоростью 2 м/с, то мы будем двигаться относительно стен вместе с эскалатором со скоростью 2 м/с. Если мы идем в направлении движения эскалатора со скоростью 0,5 м/с, то двигаемся относительно стен уже со скоростью 2,5 м/с. Если пойти в том же темпе против движения эскалатора, то он повезет нас назад со скоростью 1,5 м/с.

Рис. 11.3. Эскалатор
Пример №7
Вы едете на автомобиле со скоростью 40 км/ч, а вас догоняет другой автомобиль, скорость которого 60 км/ч (рис. 11.4). Хотя скорость догоняющего автомобиля относительно Рис. 11.3. Эскалатор
дороги довольно большая, вы замечаете, что сближение идет медленно. Скорость автомобиля, который догоняет вас, с вашей точки зрения всего 20 км/ч. Обозначим скорость второго автомобиля относительно первого  21 = 20 км/ч (читают «вэ два-один»). Если бы задний автомобиль ехал с такой же скоростью, как ваш, он вообще не мог бы вас перегнать.
21 = 20 км/ч (читают «вэ два-один»). Если бы задний автомобиль ехал с такой же скоростью, как ваш, он вообще не мог бы вас перегнать.

Рис. 11.4. Во время обгона скорость сближения этих автомобилей составляет:
 21= 20 км/ч
21= 20 км/ч
Пример №8
Рассмотрим ситуацию, когда вы едете на автомобиле со скоростью 40 км/ч, а второй автомобиль движется вам навстречу (рис. 11.5). Теперь скорость сближение большая:  21 = 100 км/ч. Почему так получается?
21 = 100 км/ч. Почему так получается?

Рис. 11.5. Во время движения навстречу скорость сближения увеличивается:
 21= 100 км/ч
21= 100 км/ч
а) Сначала рассмотрим движение с точки зрения наблюдателя, который находится на неподвижной дороге. Он может рассуждать так. За один час первый автомобиль проедет 40 км, а второй навстречу первому 60 км. Таким образом, за один час они сблизятся на 100 км. Следовательно, скорость их взаимного сближения составляет 100 км/ч.
б) А вот как рассуждали бы вы как наблюдатель, который находится в первом автомобиле. Движение относительно, потому вы с таким же успехом можете считать, что ваш автомобиль не движется, а дорога вместе со встречным автомобилем движется навстречу вам со скоростью 40 км/ч. Встречный автомобиль, кроме того, движется относительно дороги со скоростью 60 км/ч в том же направлении. Если к скорости дороги прибавить скорость второго автомобиля, то получим 100 км/ч.
Итоги:
- Перемещение, скорость и траектория тела зависят от того, относительно каких тел отсчета определяется движение.
- Если одно тело догоняет другое, то они сближаются медленно.
- Если тела двигаются навстречу друг другу, то они сближаются быстро.
Закон сложения скоростей
Скорость движения с точки зрения подвижной и неподвижной системы отсчета:
Проведем «воображаемый эксперимент». Рассмотрим случай, когда вы плывете в моторной лодке по озеру со скоростью 4 м/с. Представим, что в другой раз в той же лодке вы плывете вниз по течению реки (рис. 12.1). Пусть скорость течения составляет 1 м/с (конечно, относительно берега). Проплывая мимо дерева, вы включаете секундомер. На каком расстоянии от дерева вы окажетесь через 10 с?

Рис. 12.1. Скорость лодки относительно плота и берегов разная
В озере вы проплыли бы за это время 40 м. В реке же, даже с выключенным мотором, течение снесло бы вас на 10 м. В итоге вы оказываетесь на расстоянии 50 м от дерева: вы переместились на 40 м за счет работы двигателя и еще на 10 м вас снесло течение. Следовательно, скорость вашей лодки относительно берега равняется 5 м/с. Чтобы найти скорость лодки относительно берега, нужно к скорости лодки относительно воды (то есть в стоячей воде) прибавить скорость течения относительно берега.
Закон сложения скоростей
Если перемещение лодки относительно воды вниз по течению обозначить 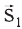 , а перемещение вместе с водой –
, а перемещение вместе с водой – 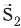 , то общее перемещение относительно
, то общее перемещение относительно 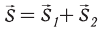 .
.
В этом случае 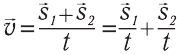 , откуда следует:
, откуда следует:
 (12.1)
(12.1)
Уравнение (12.1) называют законом сложения скоростей. Физический смысл закона такой: скорость лодки (рис. 12.2) относительно берега (красная стрелка) равна скорости лодки относительно воды (синяя стрелка) плюс скорость течения (переносная скорость) относительно берега (черная стрелка). В нашем примере скорость лодки относительно воды составляет 4 м/с, переносная скорость равна 1 м/с, а скорость лодки относительно берега составляет 5 м/с.
Посмотрим, какой будет скорость лодки относительно берега, если лодка плывет против течения. За те же 10 с в стоячей воде вы проплыли бы 40 м. Вода снесла вашу лодку вниз по течению на 10 м. В итоге вы сместились относительно дерева лишь на 30 м. Ваша скорость относительно берега теперь составляет 3 м/с, то есть 4 м/с – 1 м/с = 3 м/с. Но векторные скорости опять складываются (рис. 12.3): скорость лодки относительно берега (красная стрелка) равна скорости лодки относительно воды (относительная скорость – синяя стрелка) плюс (согласно правилам движения векторов) скорость течения (переносная скорость) относительно берега (черная стрелка).
Оба случая мы рассматривали с точки зрения наблюдателя, который находится на берегу.
Скорость движения лодки относительно воды не зависит от направления движения.
Теперь представим себе, что каждый раз, когда наша лодка проплывает мимо дерева, там находится еще и плот. Плот не имеет двигателя и двигается вниз по течению со скоростью течения. Выясним, какой будет ваша скорость относительно наблюдателя, находящегося на плоту. В первом случае, когда вы плывете вниз по течению, через 10 с вы окажетесь на расстоянии 50 м от дерева и 40 м от плота, поскольку за те же 10 с течение снесло его на 10 м вниз.
Во втором случае, двигаясь мимо дерева вверх против течения, вы опять окажетесь на расстоянии 40 м от плота, поскольку сместились против течения на 30 м относительно берега, а плот течение снесло на 10 м вниз.
Оказывается, что, двигаясь вниз по течению или вверх против течения, за 10 с вы перемещаетесь относительно плота одинаково. Это значит, что ваша скорость относительно плота одна и та же, куда бы вы ни двигались. В этом нет ничего удивительного. Ведь для того, чтобы двигаться, лопасти двигателя должны отталкиваться от воды и двигать лодку. Скорость этого движения относительно воды не зависит от того, движется вода (как в реке) или она стоячая (как в озере).
Подвижная и неподвижная системы отсчета равноправны.
Движение лодки с точки зрения наблюдателя на берегу и с точки зрения наблюдателя на плоту выглядит по-разному. Но оба они по-своему правы. Правда, при расчетах может оказаться удобнее наблюдать за лодкой с плота, а не с берега или наоборот. Решая задачи, вы научитесь выбирать «выгодные» тела отсчета.
Пример №9 «Вертолет»
Пролетая над пунктом А, пилот догнал воздушный шар, который сносило ветром по курсу вертолета (рис. 12.4). Через 0,5 часа пилот повернул назад и позже встретил воздушный шар на расстоянии 30 км от пункта А. Какой была скорость ветра?
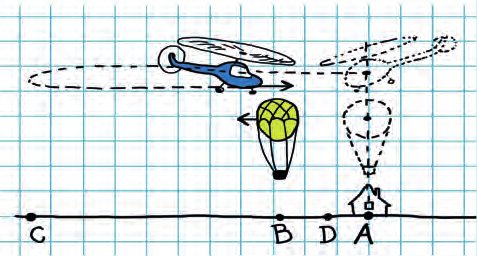
Рис. 12.4. Относительно шара вертолет движется с одинаковой скоростью
а) Решение в системе отсчета «земля». Пусть точка С – место разворота вертолета через tAC = 0,5 ч после встречи с воздушным шаром над пунктом А, а точка В – место повторной встречи вертолета и шара через время tСВ после разворота вертолета в точке С. Пусть u – скорость ветра,  – скорость вертолета относительно воздуха. Тогда
– скорость вертолета относительно воздуха. Тогда  + u – скорость вертолета относительно земли в направлении АВС,
+ u – скорость вертолета относительно земли в направлении АВС,  – u – скорость вертолета относительно земли в направлении СВ (против ветра):
– u – скорость вертолета относительно земли в направлении СВ (против ветра):
SAC = ( + u) · tAC; SCB = (
+ u) · tAC; SCB = ( – u) · tCB; SAB = u · (tAC + tCB).
– u) · tCB; SAB = u · (tAC + tCB).
В тот момент времени, когда вертолет был в точке С, шар находился в некоторой промежуточной точке D. За то время, пока вертолет долетел из точки С в точку В, шар переместился из D в В. Скорость воздушного шара равна скорости ветра u. Очевидно, что SAC – SCB = SAB. Подставив сюда выражения для SAC, SCB и SAB, получим: ( + u) · tAC – (
+ u) · tAC – ( – u) · tCB = u · (tAC + tCB). После несложных преобразований находим, что tAC = tCB. Тогда (tAC + tCB)= 1 час, а скорость ветра равна u = 30 км/ч.
– u) · tCB = u · (tAC + tCB). После несложных преобразований находим, что tAC = tCB. Тогда (tAC + tCB)= 1 час, а скорость ветра равна u = 30 км/ч.
Ответ: Скорость ветра равна 30 км/ч.
Соотношение tAC = tCB кажется довольно странным. Но его содержание становится понятным, если решить задачу иначе.
б) Решение с точки зрения тела отсчета «воздушный шар». Относительно воздуха шар не двигается. Скорость вертолета относительно шара одна и та же в произвольном направлении (то есть равна  ), поэтому время отдаления вертолета от шара (0,5 ч) равна времени его приближения к нему. Все время полета шара от А до В равна 1 час, и решение задачи очевидно.
), поэтому время отдаления вертолета от шара (0,5 ч) равна времени его приближения к нему. Все время полета шара от А до В равна 1 час, и решение задачи очевидно.
Эта задача показывает, насколько удобным может быть удачный выбор системы отсчета.
Итоги:
- Векторная скорость равна отношению перемещения ко времени движения:
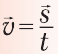 .
. - Скорость тела относительно неподвижной системы отсчета равняется сумме относительной и переносной скоростей тела:

График скорости
В физике и математике применяют три способа представления информации о связи между разными величинами: а) в виде формулы, например, s =  ∙ t; б) в виде таблицы; в) в виде графика (рисунка).
∙ t; б) в виде таблицы; в) в виде графика (рисунка).
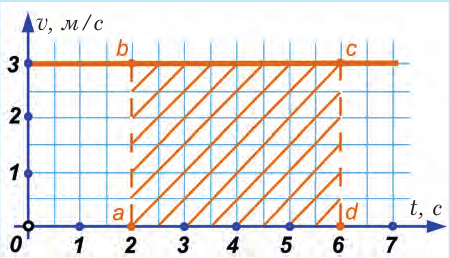
Рис. 13.1. График скорости тела, которое равномерно движется со скоростью 3 м/с. Путь, пройденный телом со 2-й по 6-ю секунды, численно равен площади заштрихованного прямоугольника abcd
График скорости отображает зависимость скорости от времени  (t) и изображается с помощью двух взаимно перпендикулярных осей. Вдоль горизонтальной оси будем откладывать время, а вдоль вертикальной – скорость (рис. 13.1). Нужно заранее продумать масштаб, чтобы рисунок не был слишком большим или слишком маленьким. На конце оси указывают букву, которая обозначает величину, откладываемую на ней. Около буквы ставят единицу измерения этой величины. Например, около оси времени указывают t, с, а около оси скорости –
(t) и изображается с помощью двух взаимно перпендикулярных осей. Вдоль горизонтальной оси будем откладывать время, а вдоль вертикальной – скорость (рис. 13.1). Нужно заранее продумать масштаб, чтобы рисунок не был слишком большим или слишком маленьким. На конце оси указывают букву, которая обозначает величину, откладываемую на ней. Около буквы ставят единицу измерения этой величины. Например, около оси времени указывают t, с, а около оси скорости –  (t), м/с. Выбирают масштаб и наносят деления на каждую ось.
(t), м/с. Выбирают масштаб и наносят деления на каждую ось.
Рассмотрим равномерное движение тела со скоростью 3 м/с, то есть число-вое значение скорости будет постоянным на протяжении всего времени движения. Сокращенно это записывают так:  = const (константа, то есть постоянная величина). В нашем примере она равна трем:
= const (константа, то есть постоянная величина). В нашем примере она равна трем:  = 3 м/с. Вы уже знаете, что информацию о зависимости одной величины от другой можно представить в виде таблицы (массива, как говорят в информатике):
= 3 м/с. Вы уже знаете, что информацию о зависимости одной величины от другой можно представить в виде таблицы (массива, как говорят в информатике):
| t, c | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
 , м/с , м/с |
3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
Из таблицы видно, что во все указанные моменты времени скорость равняется 3 м/с. Пусть масштаб оси времени 2 кл. = 1 с, а оси скорости 2 кл. = 1 м/с. График зависимости скорости от времени (сокращенно говорят: график скорости) приведен на рисунке 13.1.
С помощью графика скорости можно находить путь, который тело проходит за определенный интервал времени. Для этого надо сопоставить два факта: с одной стороны, путь можно найти, умножив скорость на время, а с другой – произведение скорости на время, как видно из рисунка, – это площадь прямо-угольника со сторонами t и  .
.
Например, со второй до шестой секунды тело двигалось на протяжении четырех секунд и прошло 3 м/с · 4 с = 12 м. Это площадь прямоугольника аbcd, длина которого равна 4 с (отрезок ad вдоль оси времени) и высота 3 м/с (отрезок аb вдоль вертикали). Площадь, правда, несколько непривычная, поскольку измеряется не в м2, а в м. Следовательно, площадь под графиком скорости численно равна пройденному пути за определенное время.
График пути
График пути s(t) можно изобразить, пользуясь формулой s =  ∙ t, то есть в нашем случае, когда скорость составляет 3 м/с : s = 3 ∙ t. Построим таблицу:
∙ t, то есть в нашем случае, когда скорость составляет 3 м/с : s = 3 ∙ t. Построим таблицу:
| t, c | 0 | 1 | 2 | 3 | 4 | 5 |
| s, м | 0 | 3 | 6 | 9 | 12 | 15 |
Вдоль горизонтальной оси опять откладывают время (t, с), а вдоль вертикальной – путь. Около оси пути пишем: s, м (рис. 13.2).
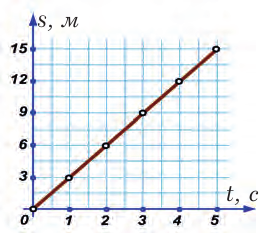
Рис. 13.2. График пути. Остальные точки, кроме шести, указанных в таблице, поставлены, исходя из предположения, что движение на протяжении всего времени было равномерным
Определение скорости на графике пути
Изобразим теперь на одном рисунке два графика, которые будут соответствовать движению со скоростями 3 м/с (прямая 2) и 6 м/с (прямая 1) (рис. 13.3). Видно, что, чем больше скорость тела, тем круче линия точек графика.
Существует и обратная задача: имея график движения, нужно определить скорость и за-писать уравнение пути (рис. 13.3). Рассмотрим прямую 2. От начала движения и до момента времени t = 2 с тело прошло путь s = 6 м. Следовательно, его скорость: 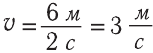 . Выбор другого интервала времени ничего не изменит, например, на момент t = 4 с путь, пройденный телом от начала движения, составляет s = 12 м. Отношение опять равняется 3 м/с. Но так и должно быть, поскольку тело двигается с постоянной скоростью. Поэтому проще всего было бы выбрать интервал времени 1 с, ведь путь, пройденный телом за одну секунду, численно равен скорости. Путь, пройденный первым телом (график 1) за 1 с равен 6 м, то есть скорость первого тела – 6 м/с. Соответствующие зависимости пути от времени у этих двух тел будут:
. Выбор другого интервала времени ничего не изменит, например, на момент t = 4 с путь, пройденный телом от начала движения, составляет s = 12 м. Отношение опять равняется 3 м/с. Но так и должно быть, поскольку тело двигается с постоянной скоростью. Поэтому проще всего было бы выбрать интервал времени 1 с, ведь путь, пройденный телом за одну секунду, численно равен скорости. Путь, пройденный первым телом (график 1) за 1 с равен 6 м, то есть скорость первого тела – 6 м/с. Соответствующие зависимости пути от времени у этих двух тел будут:
s1 = 6 ∙ t і s2 = 3 ∙ t.
Итоги:
- В физике применяют три способа представления информации: графический, аналитический (формулами) и таблицей (массивом). Третий способ больше приспособлен для решения на компьютере.
- Путь численно равен площади под графиком скорости.
- Чем круче график s (t), тем больше скорость.
Неравномерное движение
Тела двигаются равномерно прямолинейно только в том случае, когда они двигаются прямолинейно, с постоянной скоростью и в одном направлении, а это происходит редко. Преимущественно скорость движения по разным причинам меняется. Движение, при котором скорость тела изменяется, называют неравномерным.
Средняя скорость движения
Для описания неравномерного движения используют понятие средней скорости  cр. Чтобы найти среднюю путевую скорость за данный интервал времени (t), нужно весь пройденный телом путь (s) разделить на все затраченное время (включая время остановок).
cр. Чтобы найти среднюю путевую скорость за данный интервал времени (t), нужно весь пройденный телом путь (s) разделить на все затраченное время (включая время остановок).
Формула для расчета средней скорости  cр та же, что и для равномерного движения:
cр та же, что и для равномерного движения:
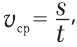 (14.1)
(14.1)
но смысл величин s и t другой: s – это весь пройденный телом путь, а t – все затраченное на это время.
Среднюю скорость движения необходимо знать, если мы хотим оценить общее время, необходимое для путешествия. Если бы тело двигалось равномерно со скоростью, равной средней скорости, то оно прошло бы весь путь за все время неравномерного движения.
Если в формулу (14.1) вместо пройденного пути «s» подставить вектор перемещения 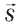 , то получим среднюю скорость перемещения:
, то получим среднюю скорость перемещения: 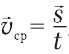 , которая по величине всегда меньше, чем средняя скорость пройденного пути, кроме случая, когда движение проходит по прямой и постоянно направлено в одну и ту же сторону. Тогда эти скорости равны.
, которая по величине всегда меньше, чем средняя скорость пройденного пути, кроме случая, когда движение проходит по прямой и постоянно направлено в одну и ту же сторону. Тогда эти скорости равны.
Пример №10 «Машинист»
Представьте себя машинистом, который ведет 12-вагонный поезд из пункта А в пункт В со средней скоростью  cр = 60 км/ч. Поезд делает 8 остановок, на которые затрачивает в целом t1 = 40 мин. Расстояние между пунктами А и В: s = 240 км. а) Сколько времени t поезд будет находиться в движении? б) За какое время t2 пройдены первые 120 км? в) Сколько лет машинисту?
cр = 60 км/ч. Поезд делает 8 остановок, на которые затрачивает в целом t1 = 40 мин. Расстояние между пунктами А и В: s = 240 км. а) Сколько времени t поезд будет находиться в движении? б) За какое время t2 пройдены первые 120 км? в) Сколько лет машинисту?
Решение.
а) Чтобы найти полное время путешествия, нужно весь пройденный путь – 240 км – разделить на среднюю скорость – 60 км/ч. Следовательно, полное время путешествия составляет 4 часа. От этого значения надо отнять время, которое было затрачено на остановки. В итоге получим: 3 часа и 20 мин.
б) Информации, приведенной в условии, недостаточно, чтобы ответить на этот вопрос. Мы не можем узнать, сколько времени займет половина дороги, поскольку средняя скорость на этом отрезке может быть другой, и она нам неизвестна. Отрицательный ответ в физике, если он достаточно аргументирован, также имеет ценность.
в) Сколько лет машинисту?
Подсказка. Третий вопрос и сложнее, и проще других. Он не требует числовых расчетов, а только вашего внимания.
Пример № 11 «Улитка на столбе»
Улитка начинает ползти вверх по столбу, высота которого 6 м. За 12 дневных часов она равномерно продвигается вверх на 2 м, а ночью, во время сна, равномерно съезжает вниз на 1 м.
а) За какое наименьшее время улитка достигнет вершины столба?
б) Определите перемещение и путь улитки за 4 суток, скорость преодоления пути и скорость перемещения.
Решение.
а) Быстрый и неправильный ответ – за 6 суток. На самом деле улитка достигает вершины быстрее. За 4 суток она окажется на высоте 4 м. Этой высоты она достигнет на рассвете пятого дня после ночного отдыха. За пятый день она поднимется на 2 м и, следовательно, достигнет вершины. Всего ей нужно для преодоления этого пути 4 ∙ 24 +12 = 108 часов.
б) За сутки улитка перемещается на 2 м вверх и на 1 м вниз, то есть общий путь составляет 3 м. Весь путь за 4 суток составит s = 12 м, а перемещение –лишь 4 м. Вектор перемещения соединяет начало столба и точку на высоте 4 м и направлен вверх. Средняя скорость преодоления улиткой пути составляет 3 м в сутки (2 м вверх и 1 м вниз:  cр = 3 м/сутки). Средняя скорость перемещения за сутки равна 1 м/сутки.
cр = 3 м/сутки). Средняя скорость перемещения за сутки равна 1 м/сутки.
Пример №12 «Маршрутный автобус»
Между двумя городами курсирует автобус. Из города А в город В он едет с постоянной скоростью 40 км/ч, а назад возвращается с постоянной скоростью 60 км/ч. Считая время разворота очень малым, найдите среднюю скорость движения на всем пути А-В-А.
Подсказка. Ответ 50 км/ч неправильный. Средняя скорость определяется как отношение всего пройденного пути к полному времени движения. Сложность этой задачи заключается еще и в том, что в условии не дано ни времени движения, ни расстояния между городами. Будьте смелее и введи-те их в решение.
Решение. Обозначим расстояние между городами А и В буквой «s». Скорость движения из А в В обозначим  1, время – t1, а скорость и время при возвращении В в А – как
1, время – t1, а скорость и время при возвращении В в А – как  2 и t2 соответственно. Согласно условию:
2 и t2 соответственно. Согласно условию:
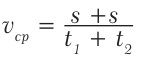
Подставим время t1 и t2 в формулу 14.2:
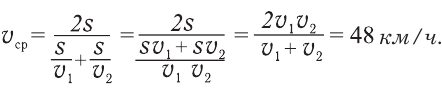
Ответ. Средняя скорость автобуса на всем маршруте составляет 48 км/ч.
Итоги:
- Движение с переменной скоростью называют неравномерным.
- Средней скоростью
 cр за некоторое время называют отношение всего пройденного пути ко всему затраченному времени t (включительно с остановками)
cр за некоторое время называют отношение всего пройденного пути ко всему затраченному времени t (включительно с остановками) - Если двигаться равномерно со средней скоростью, то за все время движения будет пройден весь путь.
Равномерное движение по окружности
Обращение искусственного спутника по круговой орбите вокруг Земли можно рассматривать как вращение материальной точки. Вращение стрелок часов (рис. 15.1) и колеса велосипеда (рис. 15.2) можно рассматривать как вращение абсолютно твердого тела вокруг оси. Многие детали машин и механизмов осуществляют вращательное движение, потому что его очень просто реализовать.
Тело может вращаться вокруг оси, которая лежит вне его пределов (например, обруч) или вокруг нескольких осей: наша планета Земля вращается одновременно вокруг собственной оси и вокруг Солнца.

Рис. 15.1. Разные стрелки вращаются с разным периодом

Рис. 15.2. Колесо велосипеда вращается вокруг оси и одно-временно движется вперед
Период вращения
Рассмотрим равномерное вращение тела, когда каждый оборот осуществляется за одно и то же время. Время, на протяжении которого тело осуществляет один оборот, называют периодом вращения и обозначают буквой T. Период измеряют в единицах времени: секундах, минутах, часах, сутках, месяцах, годах. Например, период вращения Земле вокруг собственной оси равен одним суткам, тогда как период вращения секундной стрелки часов составляет 60 с (рис. 15.1), или 1 мин. Если за время t тело сделало N оборотов, то его период вращения T определяется так:
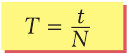 (15.1)
(15.1)
Каждая точка тела, которая вращается вокруг неподвижной оси, описывает окружнoсть.
Длина траектории, которую проходит точка за один оборот, – это длина окружности (рис. 15.3). Отношение длины окружности l к ее диаметру d является постоянным числом, то есть не
зависит от диаметра. Отношение 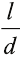 обозначают греческой буквой π (читается «пи»):
обозначают греческой буквой π (читается «пи»):
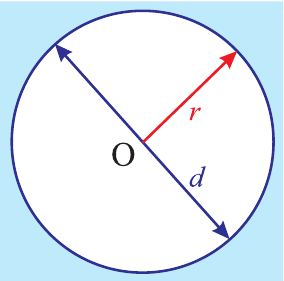
Рис. 15.3. О – центр окружности, r – ее радиус, d – диаметр, d = 2r
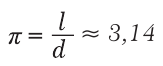 (15.2)
(15.2)
Исходя из определения числа π, можно записать формулу для вычисления длины окружности, описанной точкой:
l = π ∙ d (15.3)
Поскольку d = 2r, длину окружности можно выразить через радиус:
l = 2π ∙ r (15.4)
Скорость материальной точки во время движения по окружности
Скорость материальной точки при равномерном движении по окружности (ее еще называют линейной скоростью) можно вычислить, если разделить путь, пройденный точкой за период (длину окружности) на соответствующее время движения (период):
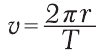 (15.5)
(15.5)
Пример №13
Определите линейную скорость точек экватора при вращении Земли вокруг своей оси. Радиус земного шара R = 6 400 км, период вращения 24 часа.
Ответ. Скорость движения точек экватора составляет 1 675 км/ч. Отметим, что это вдвое больше, чем скорость авиалайнера.
Частота вращения
Количество оборотов за единицу времени называют частотой вращения и обозначают буквой «n». Чаще всего частоту вращения измеряют в оборотах в секунду или оборотах в минуту. Если за время t тело сделало N оборотов, то частота равна:
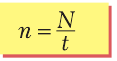
Сравнив формулы (15.1) и (15.6), видим, что частота и период – взаимно обратные величины:

Пример №14
За 5 с колесо велосипеда радиусом 50 см сделало 20 оборотов. Чему равны его: а) период вращения; б) частота вращения; в) скорость точек обода?
| Дано: t = 5 c R = 50 см N = 20 |
Решение: б) Формула Читают: 4 оборота в секунду. Слово «оборот» в формулах не пишут – нужно догадаться самому в) Применяя вместе формулы
v = 2πR · n = 2 · 3,14 · 0,5 м · 4 (1/с) = = 12,56 м/с ≈ 12,6 м/с |
 =? =? |
Ответ: а) T = 0,25 c; б) n = 4 (1/c); в) v = 12,56 м/с ≈ 12,6 м/с. |
Интересно:
Вал автомобильного двигателя может вращаться с частотой 500–5000 оборотов в минуту, в зависимости от того, насколько сильно водитель жмет на педаль акселератора (педаль «газа»). В автомобиле есть устройство, которое измеряет частоту – тахометр.
Вал турбины реактивного двигателя делает 30 000 оборотов за минуту, центрифуга стиральной машины – несколько сотен оборотов в минуту, а ультрацентрифуга в биологических лабораториях – до полумиллиона оборотов в минуту.

Рис. 15.4. Вал турбины реактивного двигателя делает 30 000 оборотов в минуту
Окружность и эллипс
Окружность – это плоская замкнутая кривая, все точки которой равноудалены от некоторой заданной точки, которая называется центром окружности. Расстояние от любой точки окружности до центра называют радиусом окружности r. Отрезок, который соединяет две точки на окружности и проходит через ее центр, называется диаметром – d. Окружность можно начертить циркулем.
Пример №15
Другой способ начертить окружность заключается в том, что вы, воткнув в плоскую поверхность булавку, набрасываете на нее петлю (рис. 15.5) и, натягивая ее заточенным кончиком карандаша, проводите им по поверхности, получая окружность. Центр окружности можно назвать его фокусом, а окружность – однофокусной фигурой.
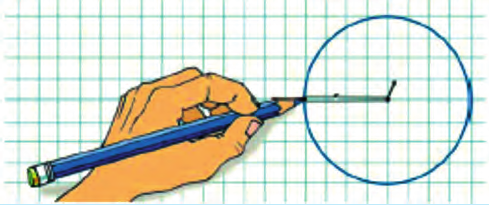
Рис. 15.5. Окружность можно рассматривать как однофокусную фигуру
История:
Можно ли в школьном возрасте сделать открытие?
Речь пойдет об английском физике Джеймсе Кларке Максвелле, который 150 лет тому назад открыл радиоволны.

Любуясь как-то в музее формой овальных ваз, которые сохранились от древних этрусков, четырнадцатилетний Максвелл задумался над тем, нельзя ли нарисовать эллипс так же просто, как и окружность. И вот что он придумал. Если, как в опыте 15.1, петлю накинуть на две иглы, воткнутые в бумагу на некотором расстоянии одна от другой, а длину нити сделать немного больше удвоенного расстояния между иглами и, натягивая концом карандаша нить, провести замкнутую кривую, то получим двухфокусную фигуру – эллипс (рис. 15.6). Точки, где находятся иглы (F1 и F2), и являются фокусами эллипса. Сумма расстояний r1 + r2 от произвольной точки эллипса до фокусов одинакова для всех точек данного эллипса.
Эллипс имеет две взаимно перпендикулярных оси – малую и большую. Точка О – центр эллипса – лежит на пересечении его осей. Большая ось эллипса проходит через оба фокуса, а отрезок ОВ (или ОА) называют большой полуосью эллипса. Орбиты планет, спутников планет и большинства искусственных спутников Земли – эллипсы.
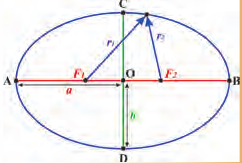
Рис. 15.6. а – большая полуось, b – малая полуось эллипса
Итоги:
Движение планет и луны
Солнечная система состоит из Солнца и восьми планет (рис. 16.1), которые вращаются вокруг него. Планеты подразделяются на две группы: планеты земной группы и планеты-гиганты. Планеты земной группы – Меркурий, Венера, Земля, Марс – имеют твердую оболочку и состоят преимущественно из тяжелых элементов. Внешние планеты – Юпитер, Сатурн, Уран, Нептун – состоят из газов, преимущественно водорода и гелия; их еще называют газовыми гигантами из-за огромных размеров. Внутренние и внешние планеты разделены поясом астероидов.

Рис. 16.1. Солнце – Меркурий – Венера – Земля – Марс. Пояс астероидов. Юпитер – Сатурн – Уран – Нептун – газовые гиганты
Состав солнечной системы
До 2006 года в состав Солнечной системы входила еще одна планета – Плутон. Но из-за того, что космические аппараты открыли за Плутоном еще несколько небесных тел приблизительно таких же размеров, было решено ограничить число планет до восьми. Кроме того, Плутон имеет вытянутую орбиту, которая сильно наклонена к плоскости вращения других планет.
На протяжении тысячелетий астрономы наблюдали за довольно сложным движением Солнца, Луны и планет на фоне звездного неба и считали, что все они движутся вокруг Земли. В 1543 году польский астроном Николай Коперник предложил выбрать телом отсчета Солнце, учитывая более простой способ описания движения планет. Согласно гелиоцентрической системе Коперника Земля и другие планеты вращаются вокруг Солнца. Траектория каждой из планет Солнечной системы является эллипсом, а Солнце находится в одном из фокусов этого эллипса.
Движение планет вокруг солнца
Орбиты большинства планет лежат практически в одной плоскости, которая называется плоскостью эклиптики (рис. 16.2), и вращаются в одну и ту же сторону. Солнце лежит в этой же плоскости и вращается вокруг собственной оси в том же направлении, что и планеты. Плоскость орбиты Плутона наклонена к плоскости эклиптики под углом 17°.
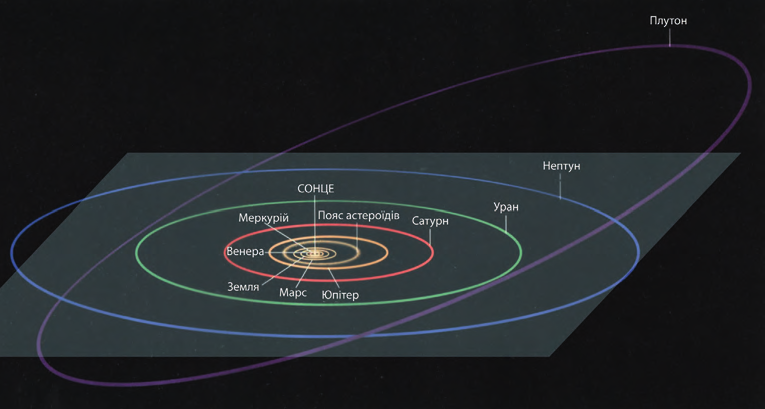
Рис. 16.2. Орбиты планет. Плоскость эклиптики выделена. Орбита Плутона явно выделяется наклоном и вытянутостью
Однако орбиты планет, кроме Плутона, настолько мало отличаются от окружностей, что только чрезвычайно кропотливые расчеты Кеплера, которые он завершил в 1609 году, дали возможность установить это отличие. История этого открытия такова.
История:
Датский астроном Тихо Браге достиг невиданной для своего времени точности измерений положения планет на небе. Он завещал результаты собственных астрономических наблюдений своему сотруднику, немецкому астроному И. Кеплеру. Анализируя данные о движении Марса, Кеплер определил, что планета движется по орбите неравномерно – если бы планета двигалась по окружности, то такого не могло бы быть. Первый закон Кеплера твердит: планеты движутся по эллипсам, в одном из фокусов которых находится Солнце. Ему понадобилось пять лет, чтобы вычислениями доказать этот факт.

В нижеприведенной таблице указаны основные данные о Солнечной системе.
Таблица 16.1 Основные данные о планетах Солнечной системы и Плутоне
| Радиусы небесных тел, км |
Длительность суток относительно звезд |
Большая полуось орбиты, км |
Период обращения вокруг Солнца |
|
| Меркурий | 2570 | 88 суток | 57,9 млн | 88 суток |
| Венера | 6310 | 243 сутки | 108 млн | 224,7 суток |
| Земля | 6380 | 23 ч 56 мин 4с | 149 млн | 365, 26 суток |
| Марс | 3430 | 24 ч 37 мин 23 с | 228 млн | 687 суток |
| Юпитер | 71800 | 9 ч 50 мин 30с | 778 млн | 11,9 лет |
| Сатурн | 60300 | 10 ч 14 мин | 1,43 млрд | 29,5 лет |
| Уран | 26700 | 11 ч | 2,87 млрд | 84 лет |
| Нептун | 24800 | 16 ч | 4,50 млрд | 164,8 лет |
| Плутон | 2743 | 6 суток 9 ч | 5,90 млрд | 247,7 лет |
Период обращения Земли вокруг собственной оси равняется 24 часам и называется солнечными сутками, или просто сутками. Периоды обращения других планет и Луны указаны в таблице в земных сутках.
Год – это период обращения планеты вокруг Солнца. Земной год равняется 365,26 земным суткам. Периоды обращения остальных планет указаны в земных сутках или в земных годах.
За миллиарды лет вращения Луны вокруг Земли она замедлила обращение вокруг своей оси настолько, что сейчас обращена к нам всегда одной своей стороной, и потому совершает один оборот вокруг собственной оси за один месяц.
Земля также замедляет свое суточное вращение (главным образом из-за вызываемых Луной приливов в океане и жидком ядре Земли), но происходит это очень медленно, хотя 3,5 млрд лет назад земные сутки составляли лишь 6 часов.
Луна – естественный спутник земли.
Кроме Меркурия и Венеры, все другие планеты Солнечной системы имеют естественные спутники. У Земли это Луна. Наблюдая за движением Луны, можно заметить, что за сутки она смещается на фоне звездного неба на восток приблизительно на 13°. Засекая минимальное время, через которое Луна опять займет свое предыдущее положение относительно звезд (позиция 2 на рис. 16.3), можно определить звездный период обращения Луны вокруг Земли: 27,3 суток (27 суток 7 часов и 43 мин). Надо понимать, что лучи от звезд идут практически параллельно, из-за огромного расстояния к ним.
Если определить промежуток времени между двумя последовательными одинаковыми фазами Луны (например полной и следующей полной Луной – позиция 3 на рис. 16.3), то получим ее солнечный период обращения, который длится приблизительно 29,5 суток (29 суток 12 ч 44 мин).
Солнечные и лунные затмения
Траекторию Луны вокруг Земли можно приближенно считать окружностью (рис. 16.4). Лучи света от Солнца идут практически параллельно, из-за огромного расстояния к нему.
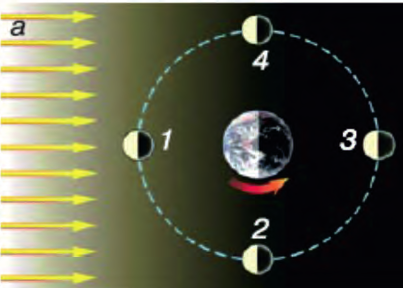

Рис. 16.4. Фазы Луны.
3 – полная Луна, 2 – первая четверть, 4 – последняя четверть, 1 – рождение новой Луны
Солнечные затмения возможны, когда Луна оказывается между Солнцем и Землей на одной линии. Угловые размеры Луны и Солнца практически одинаковы (то есть кажутся одинаковыми по размеру). Во время полного солнечного затмения Луна закрывает Солнце.
Лунное затмение возможно, когда Земля оказывается между Солнцем и Луной на одной линии. Казалось бы, что солнечные и лунные затмения должны происходить ежемесячно, но это не так. Плоскость орбиты Луны наклоне-на к плоскости эклиптики под углом 5°, поэтому в большинстве случаев, когда Луна оказывается между Солнцем и Землей, солнечного затмения не происходит, поскольку Луна находится выше или ниже плоскости эклиптики. Одна-ко в определенные моменты времени (попробуйте объяснить это с помощью рисунка) Земля, Луна и Солнце все же могут оказаться на одной прямой, которая лежит одновременно и в плоскости эклиптики, и в плоскости орбиты Луны. В таком случае можно наблюдать солнечное или лунное затмение.
Фазы луны
Интересно следить за фазами Луны. На рис. 16.4 а изображено положение Луны относительно Земли в разные моменты ее движения по околоземной орбите. Рисунок сделан с позиции наблюдателя, который находится в космосе выше плоскости орбиты Луны прямо над Северным полюсом Земли. Земля вращается вокруг своей оси против часовой стрелки (с запада на восток). В ту же сторону вращается по своей орбите и Луна. Рис. 16.4 б показывает Луну такой, какой ее видит земной наблюдатель. Полная луна наблюдается в положении 3, когда земной наблюдатель видит ее полностью освещенной. В этой же позиции можно наблюдать лунное затмение (если Луна лежит в пло-скости эклиптики). В положении 2 земной наблюдатель видит освещенной правую половину Луны – это первая четверть. В положении 4 земной наблюдатель видит освещенной левую половину Луны – это последняя четверть. В положении 1 диска Луны не видно, но уже на следующий день справа на диске появится узенький светящийся серп молодой луны. Если в положении 1 Луна будет находиться еще и в плоскости эклиптики, то в некоторых точках Земли можно наблюдать солнечное затмение.
Таблица 16.2 Основные данные о Луне
| Радиус Луны | Период обращения вокруг Земли | Радиус орбиты Луны | |
| Звездный период | Солнечный период | ||
| 1740 км | 27,3 суток | 29,5 суток | 380 000 км |
Итоги:
- Восемь планет Солнечной системы движутся вокруг солнца по эллипсам, которые мало отличаются от окружностей.
- Все планеты двигаются практически в одной плоскости (плоскости эклиптики).
- Солнечные и лунные затмения происходят, когда Солнце, Луна и Земля одновременно находятся на одной прямой и в одной плоскости.
Колебательное движение
Колебание часто можно наблюдать в природе и технике. Колеблются легкие при дыхании, колеблется маятник механических часов и поршни автомобильного двигателя.
Нитяной маятник
Удобнее всего наблюдать и изучать колебания при помощи устройства, которое называют нитяным маятником. Этот маятник состоит из нити, к которой прикреплен шарик (рис. 17.1), где L – длина нити маятника, 2 – положение равновесия – скорость шарика здесь наибольшая.
Пример №16
Прикрепим к одному концу тонкой нити длиной один метр пластилиновый шарик диаметром приблизительно 1 см, а второй конец привяжем, например, к люстре.
В состоянии равновесия нить вертикаль-на (положение 2 на рис. 17.1), то есть она совпадает с отвесной линией. Отклоним шарик вправо (положение 1 на рис. 17.1) на небольшое, сравнительно с длиной нити, расстояние (например, 10 см) и отпустим. Шарик начнет двигаться сначала медленно, а затем все быстрее в направлении к положению равновесия, проскочит это положение и начнет отклоняться влево, уменьшая свою скорость, пока не остановится в точке 3. Затем шарик начнет двигаться вправо,
опять пройдет положение равновесия и Рис. 17.1. Нитяной маятник остановится в крайней правой точке. Движения такого типа, которые периодически повторяются, называют колебаниями, а устройство, которое мы использовали, – маятником.
Движение шарика от крайнего правого положения до крайнего левого и назад называют одним полным колебанием (1-2-3-2-1 на рис. 17.1). Далее все повторится сначала. Если наблюдать за шариком достаточно долго, то мы заметим, что расстояния, на которые она отклоняется влево и вправо, постепенно уменьшаются. Причиной этого являются силы трения. В конце концов колебания прекратятся.
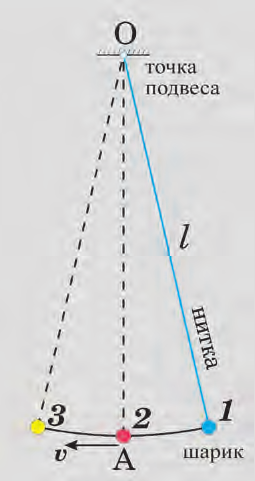
Рис. 17.1. Нитяной маятник
Амплитуда, период и частота колебаний
Траектория движения шарика – дуга окружности, центр которой находится в точке подвеса, а радиус равен расстоянию от точки подвеса к центру шарика. Наибольшее отклонение от положения равновесия называют амплитудой колебаний. Обозначим амплитуду буквой А. В нашем примере это длина дуги между точками 1 и 2.
Время, на протяжении которого шарик осуществляет одно полное колебание, называют периодом колебаний и обозначают буквой T. В СИ период измеряют в секундах. Если за время «t» шарик осуществил «N» полных колебаний, то период будет определяться так:
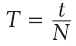 (17.1)
(17.1)
Количество полных колебаний, осуществляемых шариком за единицу времени, называют частотой и обозначают греческой буквой 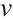 («ню»). Согласно этому определению
(«ню»). Согласно этому определению
Частоту измеряют в герцах (Гц). Один герц – это частота колебаний, при которой за одну секунду тело осуществляет одно полное колебание, то есть 1 Гц = одно колебание в секунду (пишут 1/с). Единица измерения частоты колебаний названа в честь немецкого физика Генриха Герца, который в 1887 году путем опытов доказал существование радиоволн.
- Заказать решение задач по физике
Пружинный маятник
Другая простая колебательная система – это пружинный маятник. Он состоит из пружины, к которой прикреплено тело. Такой маятник колеблется с определенной частотой и амплитудой (рис. 17.2), которые зависят от массы грузика и упругих свойств пружины.
Рис. 17.2. Пружинный маятник
Стробограмма
Колебания бывают не только механические, как у нитяного маятника, но и электрические. В электрической розетке, например, «колеблется» напряжение, то есть периодически изменяется с частотой 50 Гц.
На рис. 17.3 вы можете видеть фотографию странных траекторий насекомых в свете на-стольной лампы. Если внимательно присмотреться, то видно, что траектории не сплошные. Так случилось потому, что лампа, которая питается от источника переменного напряжения, ми-гает с частотой, равной двойной частоте напряжения, то есть 100 Гц. Такая частота незаметна для нашего глаза, но ее «замечает» фотокамера.
Сто раз в секунду лампа зажигается и столь-ко же раз гаснет. Пока света мало, насекомого на снимке не видно. Время экспозиции цифровой фотокамеры составляло несколько секунд, поэтому траектория и вышла «пунктирной». Такого вида фотографии называют стробоскопическими.
Есть специальные лампы-стробоскопы, частоту миганий которых можно менять. Вы, на-верное, видели их на дискотеках. Стробограммы используют спортивные тренеры (рис. 17.4), а при помощи стробоскопа настраивают частоту колебаний поршней автомобильного двигателя.
|
Рис. 17.3. Стробограмма траекторий насекомых |
 Рис. 17.4. Упражнение на турнике |
История:
В 1584 году двадцатилетний итальянец Галилео Галилей проделал чрезвычайно интересное наблюдение. Подвешивая к нити то кусок свинца, то кусок пробки, он до-казал, что маятники одинаковой длины колеблются с одинаковыми периодами не-зависимо от массы грузов. Он также заметил, что период колебаний маятника почти не зависит от амплитуды (по крайней мере, пока амплитуда мала по сравнению с длиной нити).
Поскольку период колебаний маятника не зависит ни от амплитуды малых колебаний, ни от массы шарика, то его, очевидно, можно применять для измерения времени. В старину координаты кораблей в морях и океанах определяли по солнцу и звездам, причем для определения долготы нужны точнейшие часы. Неточно измеренное время и, соответственно, ошибки в определении координат приводили к ошибкам в определении расстояний, а это, в свою очередь, могло спровоцировать аварии.
Потери торгового флота были настолько значительными, что во многих морских государствах обещали крупные денежные премии за создание точного морского хронометра.
В Голландии, например, была обещана премия 20 000 золотых гульденов, а в Великобритании – 20 000 фунтов стерлингов.
Двое ученых, независимо друг от друга, догадались, что маятник, благодаря постоянному периоду, может стать основной деталью точных часов. Это были уже упоминавшийся итальянец Галилео Галилей и голландец Кристиан Гюйгенс. Первые маятниковые часы по чертежам Гюйгенса были изготовлены в 1656 году.
Изобретателем морского хронометра стал англичанин Джон Гаррисон, который получил часть обещанной правительством премии (12 000 фунтов стерлингов).
Итоги
- Наибольшее отклонение от положения равновесия называют амплитудой колебаний.
- Время, на протяжении которого осуществляется одно полное колебание, называют периодом колебаний.
- Количество полных колебаний за единицу времени называет частотой.
- Период колебаний нитяного маятника не зависит ни от амплитуды малых колебаний, ни от массы шарика.
Что такое механическое движение
Механическое движение – это изменение положения тела относительно других тел в пространстве со временем.
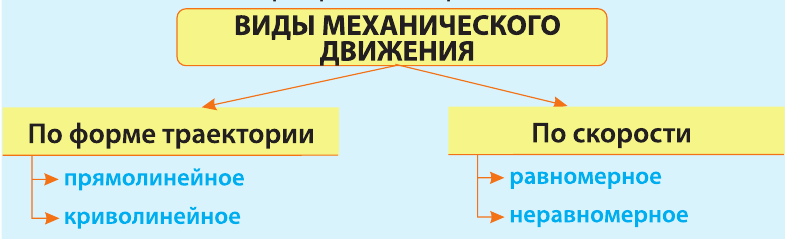
Перемещение, скорость, траектория зависят от того,
в какой СИСТЕМЕ ОТСЧЕТА изучается движение тела.
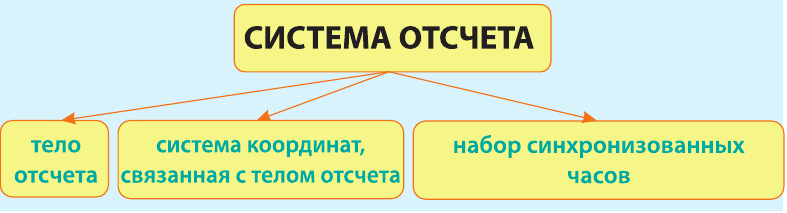
Закон сложения скоростей:
Скорость тела относительно неподвижной системы равна сумме скоростей тела в движущейся системе и скорости движущейся системы
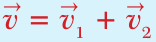
Равномерное прямолинейное движение:
| Форма траектории | Путь | Время | Скорость |
| Прямолинейное равномерное движение | |||
| Прямая линия | s =  · t · t |
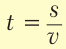 |
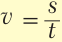 |
| Прямолинейное неравномерное движение | |||
| Прямая линия | s = s1 + s2 +…+sn | t = t1 + t2+…+ tn | 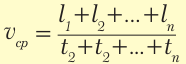 |
| Движение по окружности | |||
| Окружность | Движение за период l = 2πR, где R – радиус окружности |
Период T(c)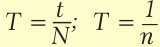 N – количество оборотов t – время |
Скорость при движении по окружности 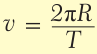 Оборотная частота n (1/c) 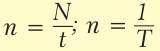 |
| Колебательное движение | |||
| Отрезок прямой, дуга окружности | l ≈ 4A, где A – амплитуда колебаний |
Период T (с)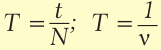 |
Частота 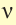 (Гц) (Гц)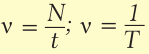 |
Подробное объяснение механического движения
Говоря, что автомобиль сначала ехал прямо, затем повернул направо и вскоре остановился, мы даем словесное описание того, как двигался автомобиль.
Для такой точной науки, как физика, этого недостаточно. Необходимо дать математически строгое, количественное описание движения тела. Этим занимается раздел физики кинематика.
В 7-м классе вы изучали самый простой вид движения — прямолинейное движение. Движение реальных тел может быть очень сложным. Понаблюдайте за самолетом, выполняющим фигуры высшего пилотажа (рис. 1, а), или за человеком, совершающим прыжок в воду (рис. 1, б). Как описать такие сложные движения?

Начнем описание с более простого движения — поступательного.
Если форма и размеры тела в процессе движения не изменяются, то тело называют абсолютно твердым. Движение таких тел мы и будем рассматривать в кинематике. При поступательном движении прямая, проходящая через любые две точки тела, остается параллельной своему первоначальному положению (рис. 2).
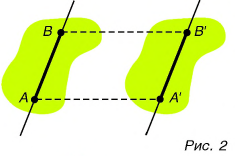
Поступательное движение может быть как прямолинейным, так и криволинейным (рис. 3). Траектории точек тела, движущегося поступательно, одинаковы. Они лишь смещены друг относительно друга.
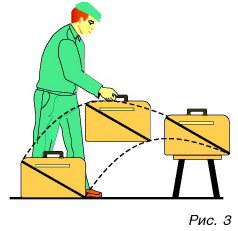
Любое движение абсолютно твердого тела сводится к поступательному перемещению и вращению.
Так как при поступательном движении все точки движутся одинаково, достаточно изучить движение только одной из точек тела, т. е. использовать модель материальной точки.
Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь.
Именно от поставленной задачи зависит, молено ли считать данное реальное тело материальной точкой. Например, если нас интересует движение крыльев бабочки (рис. 4), то бабочку нельзя рассматривать как материальную точку.

В то же время Землю можно считать материальной точкой, если рассматривать ее движение вокруг Солнца (рис. 5).
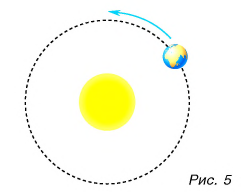
Главные выводы:
- Задача кинематики — математически строгое описание механического движения тел.
- При описании поступательного движения можно использовать модель материальной точки.
- Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь.
Основы кинематики
1. Основные понятия кинематики:
Механическим движением называется изменение положения в пространстве
или их частей друг относительно друга с течением времени.
Кинематика — раздел механики, изучающий механическое движение без выяснения причин, его вызывающих.
Телом отсчета называется условно неподвижное тело (или группа тел), отдельно которого (которых) рассматривается механическое движение других тел.
Слова «условно неподвижное тело» употребляются потому, что, читая : данное учебное пособие, вы неподвижны относительно, например, стола но движетесь вместе с Землей относительно Солнца со скоростью около 30 км/с.
Следовательно, покой любого тела, а значит, и тела отсчета — понятие иное, или относительное.
Системой отсчета называется система координат, жестко связанная с телом отсчета, вместе с выбранным устройством измерения времени.
Движение реального тела в пространстве чаще всего очень сложное, и по в физике вводятся модели реальных объектов, упрощенные представлены о теле или явлении, учитывающие только важнейшие его свойства и явления.
Материальной точкой называется модель реального тела, размерами которых можно пренебречь в данных условиях. Если размерами тела нельзя пренебречь, то используется модель абсолютно твердого тела.
Абсолютно твердым телом называется модель реального тела, изменением и размеров которого в данных условиях можно пренебречь, т. е. такое расстояние между любыми двумя точками которого остается постоянным.
Радиус-вектором называется вектор, проведенный из начала координат к положению материальной точки в некоторый момент времени (рис. 5).
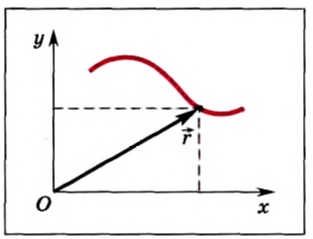
Рис. 5
Траекторией называется линия, вдоль которой материальная точка движется в пространстве (рис. 6) в данной системе отсчета, или линия, которую описывает в пространстве конец радиус-вектора точки (см. рис. 5).

Рис. 6
Уравнение траектории связывает координаты движущегося тела: y=ƒ(x) или x=ƒ(y) — при движении в плоскости, z =ƒ(x, у) — при движении в пространстве.
Например, при движении точки в плоскости, если координаты точки связаны уравнением y = kx + b, траектория точки — прямая линия, если уравнением y2+ x2 = R2, — окружность, если уравнением у = ах2 + bх + с, — парабола.
Вид траектории точки зависит от выбранной системы отсчета, так как механическое движение, как и покой, относительно.
По форме траектории движения разделяют на прямолинейные и криволинейные. Движение по окружности (или по дуге окружности) является простейшим из криволинейных движений. Любое сложное движение материальной точки по криволинейной траектории можно приближенно представить как движение по траектории, состоящей из плавно переходящих друг в друга дуг окружностей различного радиуса (рис. 7).
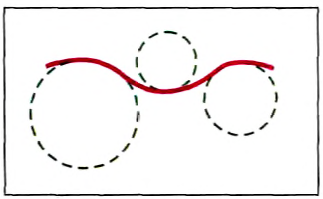
Рис. 7
Поступательным называется такое движение абсолютно твердого тела, при котором прямая, проведенная между двумя любыми точками тела, при его движении остается параллельной самой себе (рис. 8). Например, так движутся кабины колеса обозрения (рис. 9).
|
|
 Рис. 9 |
Если тело движется поступательно, то достаточно изучать движение только одной из его точек.
Вращательным называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения тела (рис. 10). Например, так движутся все точки кабинок карусели (рис. 11).
|
Рис. 8 |
 Рис. 9 |
Путь s материальной точки за некоторый промежуток времени равен длине участка траектории, пройденного точкой за это время. Путь — скалярная физическая величина.
Перемещением 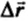 материальной точки за данный промежуток времени называется вектор, соединяющий ее начальное положение с конечным.
материальной точки за данный промежуток времени называется вектор, соединяющий ее начальное положение с конечным.
Если начальное положение точки задано радиус-вектором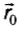 , а в некоторый момент времени радиус-вектор точки равен
, а в некоторый момент времени радиус-вектор точки равен 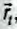 , то вектор перемещения представляет собой изменение радиус-вектора:
, то вектор перемещения представляет собой изменение радиус-вектора: 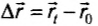 (рис. 12).
(рис. 12).
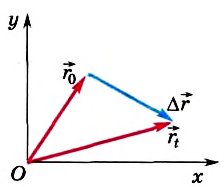
Рис. 12
Указание промежутка времени при определении вектора перемещения важно именно потому, что перемещение — вектор, модуль и направление которого зависят от выбранного промежутка времени.
Как хорошо видно из рисунка 13, путь, в общем случае, не совпадает с модулем перемещения.
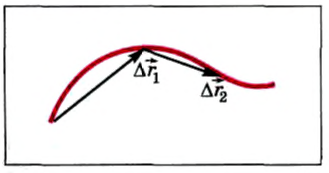
Рис. 13
Модуль вектора перемещения равен длине пути только при движении тела по прямолинейной траектории без изменения направления движения.
Например, модуль перемещения равен пути при движении тела из точки 1 в точку 2 в случае, изображенном на рисунке 14, а, и эти величины не равны в случае, изображенном на рисунке 14, б. Модуль перемещения всегда меньше или равен пути: 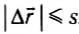 .
.
Путь и модуль перемещения в СИ измеряются в метрах (м).
Средней скоростью перемещения называется вектор, равный отношению вектора перемещения к тому промежутку времени, за который это перемещение произошло:
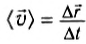
Средней скоростью пути называется отношение пройденного пути к тому промежутку времени, за который этот путь проделан. При выбранном способе отсчета времени средняя скорость пути равна:
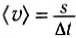
Единица скорости в СИ — 1 метр в секунду (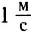 ).
).
Мгновенной скоростью называется вектор, определяющий направление и модуль скорости точки в данный момент времени.
Вектор мгновенной скорости точки в любой момент времени направлен по касательной, проведенной к траектории (рис. 15).
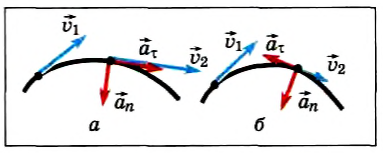
Рис. 15
Модуль и направление мгновенной скорости в общем случае движения тела по криволинейной траектории изменяются. Для характеристики быстроты изменения скорости вводится вектор ускорения.
Ускорением называется векторная физическая величина, равная отношению изменения скорости к промежутку времени, за который это изменение произошло:
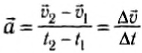
За единицу ускорения в СИ принят 1 метр на секунду в квадрате (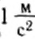 ).
).
Вектор ускорения  в общем случае не совпадает с направлением вектора скорости, а составляет с ним некоторый угол.
в общем случае не совпадает с направлением вектора скорости, а составляет с ним некоторый угол.
При движении по криволинейной траектории скорость точки непрерывно изменяется по модулю и направлению, поэтому вектор ускорения представляют в виде суммы двух векторов: 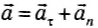 , причем
, причем 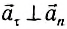 и
и 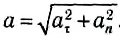 .
.
Вектор 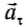 направлен по касательной к траектории и называется тангенциальным ускорением, а модуль этого вектора характеризует изменение скорости по модулю:
направлен по касательной к траектории и называется тангенциальным ускорением, а модуль этого вектора характеризует изменение скорости по модулю: 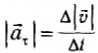 ∙ Если модуль скорости возрастает, то тангенциальное ускорение параллельно вектору скорости (см. рис. 15, я), если модуль скорости убывает, то оно направлено противоположно вектору скорости (см. рис. 15, б).
∙ Если модуль скорости возрастает, то тангенциальное ускорение параллельно вектору скорости (см. рис. 15, я), если модуль скорости убывает, то оно направлено противоположно вектору скорости (см. рис. 15, б).
Вектор 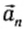 всегда направлен перпендикулярно мгновенной скорости и поэтому называется нормальным (нормаль — перпендикуляр) или центростремительным ускорением. Последнее название обозначает, что если точка движется по окружности, то это ускорение направлено к центру окружности.
всегда направлен перпендикулярно мгновенной скорости и поэтому называется нормальным (нормаль — перпендикуляр) или центростремительным ускорением. Последнее название обозначает, что если точка движется по окружности, то это ускорение направлено к центру окружности.
При движении точки по сложной криволинейной траектории ее можно представить в виде последовательных плавно переходящих друг в друга дуг. В этом случае вектор центростремительного ускорения в любой момент времени направлен к центру кривизны дуги, которой можно заменить отрезок траектории, по которой движется точка. Модуль нормального (центростремительного) ускорения равен: 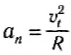 , где υt — мгновенная скорость, R — радиус дуги, совпадающей с траекторией точки в данный момент времени.
, где υt — мгновенная скорость, R — радиус дуги, совпадающей с траекторией точки в данный момент времени.
Простейшие виды механического движения
I. Равномерным прямолинейным движением называется движение, при котором тело за одинаковые промежутки времени совершает одинаковые перемещения, т. е. движется с постоянной по модулю и направлению скоростью:
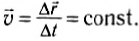
Пусть 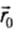 — радиус-вектор точки в начальный момент времени t1 = 0,
— радиус-вектор точки в начальный момент времени t1 = 0, 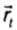 — радиус-вектор точки в момент времени t2 = t,
— радиус-вектор точки в момент времени t2 = t, 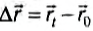 , ∆t = t (рис. 17).
, ∆t = t (рис. 17).
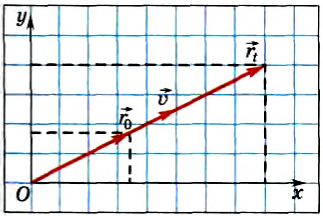
Рис. 17
Тогда 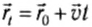 — векторное соотношение, представляющее собой кинематическое уравнение (закон) равномерного прямолинейного движения.
— векторное соотношение, представляющее собой кинематическое уравнение (закон) равномерного прямолинейного движения.
Соответственно, xt=x0 + υxt; yt=y0 + υyt — кинематические уравнения для координат при равномерном прямолинейном движении точки на плоскости хОу, где υx= const и υy = const — проекции вектора скорости на оси координат, x0 и у0— координаты точки в начальный момент времени.
Необходимо подчеркнуть, что в кинематических уравнениях для координат начальные координаты и проекции скорости на оси могут быть положительными, отрицательными и равными нулю.
Так как движение прямолинейное, то модуль вектора перемещения равен пути: 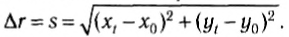
При движении точки вдоль одной оси, например Ох, путь и перемещение точки можно рассчитать по площади между графиком зависимости проекции скорости от времени и осью времени (рис. 18).
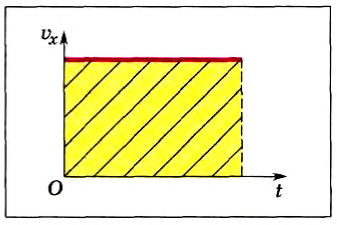
Рис. 18
II. Движение тела в двух системах отсчета. Механическое движение относительно, и одно и то же тело может двигаться одновременно относительно покоящихся или движущихся других тел, например моторная лодка при переправе через реку перемещается относительно воды и берега (рис. 19).

Рис. 19
В этом случае для описания движения тела вводят подвижную и неподвижную системы отсчета и используют классический закон сложения скоростей: 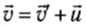 — скорость тела
— скорость тела  относительно неподвижной системы отсчета равна векторной сумме скорости тела
относительно неподвижной системы отсчета равна векторной сумме скорости тела  , относительно подвижной системы отсчета и скорости
, относительно подвижной системы отсчета и скорости  подвижной системы отсчета относительно неподвижной (рис. 20).
подвижной системы отсчета относительно неподвижной (рис. 20).
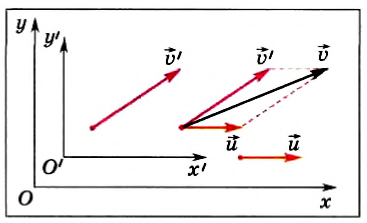
Рис. 20
III. Равноускоренным прямолинейным движением называется движение, при котором за любые равные промежутки времени скорость тела изменяется на одну и ту же величину, т. е. оно движется по прямолинейной траектории с постоянным ускорением:
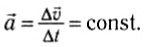
Уравнение для мгновенной скорости точки при равноускоренном движении: 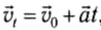 , где
, где 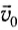 – скорость тела в начальный момент времени,
– скорость тела в начальный момент времени, 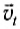 — скорость тела в любой момент времени с начала отсчета.
— скорость тела в любой момент времени с начала отсчета.
Для проекции на ось Ох, направленной вдоль траектории тела: 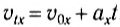 .
.
Координата тела в любой момент времени: 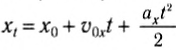 , где х0 — координата в начальный момент времени; перемещение
, где х0 — координата в начальный момент времени; перемещение 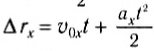 .
.
Модуль средней скорости перемещения при прямолинейном равноускоренном движении:
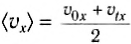
При решении задач часто удобно использовать формулу 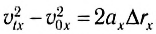 .
.
IV. При вращательном движении траектория точки представляет собой окружность (рис. 21). Линейной скоростью 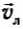 называется мгновенная скорость точки. При движении точки с постоянной по модулю линейной скоростью:
называется мгновенная скорость точки. При движении точки с постоянной по модулю линейной скоростью: 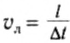 , где l — длина дуги, пройденной точкой за время Δt.
, где l — длина дуги, пройденной точкой за время Δt.
Пусть точка при движении по окружности радиуса R с постоянной по модулю скоростью за время t совершила N полных оборотов.
Периодом обращения T называется время одного полного оборота: 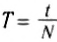 . В СИ единица периода обращения —1 секунда (1 с).
. В СИ единица периода обращения —1 секунда (1 с).
Частота v определяется числом оборотов в единицу времени: 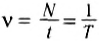 . Единицей частоты в СИ является 1 герц (1 Гц). 1 Гц = 1 с-1.
. Единицей частоты в СИ является 1 герц (1 Гц). 1 Гц = 1 с-1.
При движении точки по окружности ее радиус-вектор непрерывно поворачивается.
Угловой скоростью точки называется физическая величина, модуль которой численно равен отношению угла поворота радиус-вектора к промежутку времени, за который этот поворот произошел: 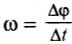 (см. рис. 21, а).
(см. рис. 21, а).
В СИ угол поворота измеряется в радианах (рад). Угол в 1 рад — это центральный угол, опирающийся па дугу, длина которой равна ее радиусу (см. рис. 21, о), тогда 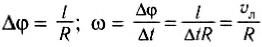 ∙
∙
Угловая скорость в СИ измеряется в радианах в секунду (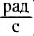 ).
).
При движении точки с постоянной по модулю скоростью по окружности радиуса 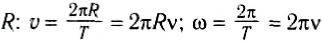 .
.
Если модуль скорости движения тела постоянная величина, то тангенциальное ускорение равно нулю: 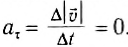 . Полное ускорение в любой момент времени равно нормальному, или центростремительному, ускорению:
. Полное ускорение в любой момент времени равно нормальному, или центростремительному, ускорению: 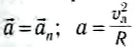 .
.
При неравномерном движении точки по окружности ее угловая скорость изменяется. Если угловая скорость за любые равные промежутки времени изменяется на одну и ту же величину, то угловым ускорением называют величину 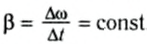 .
.
Если движение происходит с угловым ускорением, то модули тангенциального и нормального ускорений можно рассчитать по формулам: 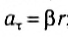 ;
; 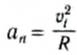 , где υt — скорость точки в данный момент времени.
, где υt — скорость точки в данный момент времени.
Виды механического движения
Существуют различные виды механического движения. Давайте вспомним их:
1. Прямолинейное равномерное движение. При таком движении траектория движения тела представляет собой прямую линию. Величина и направление скорости не изменяются. Пройденный путь определяется по формуле: 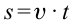 .
.
2. Прямолинейное неравномерное движение. При таком движении траектория движения тела представляет собой прямую линию. Величина скорости меняется, но направление остается неизменным. Пройденный путь определяется по формуле: 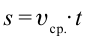 . Здесь
. Здесь 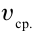 – средняя скорость тела.
– средняя скорость тела.
3. Прямолинейное равноускоренное (замедленное) движение. При таком движении траектория движения тела представляет собой прямую линию. Величина скорости равномерно увеличивается (уменьшается), т.е. за равные промежутки времени скорость увеличивается (уменьшается) на одинаковые величины, но направление не меняется. Пройденный
путь определяется по формуле: 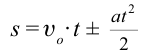 , знак (+) ставится в случае равноускоренного движения, когда
, знак (+) ставится в случае равноускоренного движения, когда 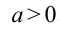 , знак (–) ставится при равнозамедленном движении, т.е. при
, знак (–) ставится при равнозамедленном движении, т.е. при 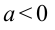 .
.
4. Криволинейное равномерное движение. Частным случем криволинейного движения можно считать равномерное движение по окружности. При таком движении направление скорости постоянно меняется и направляется по касательной к траектории. Основные параметры движения: 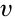 – линейная скорость;
– линейная скорость; 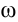 – угловая скорость;
– угловая скорость; 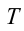 – период вращения;
– период вращения; 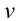 – частота вращения;
– частота вращения;  – длина дуги;
– длина дуги;  – пройденный путь.
– пройденный путь.
Нужно подчеркнуть, что вышеприведенные примеры описывают случаи, где тело участвует только в одном виде движения. В жизни чаще всего тела участвуют в нескольких видах движения
одновременно.
Например, плывущий по реке корабль, идущий по вагону поезда человек, выброшенный из летящего самолета груз и т.д. Плывущий корабль, благодаря силе двигателя движется в одном направлении со скоростью 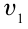 , а вода течет со скоростью
, а вода течет со скоростью 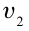 . Очевидно, что тело участвует сразу в двух видах движения.
. Очевидно, что тело участвует сразу в двух видах движения.
Возникает такой вопрос. Зависит ли скорость корабля, переданная силой тяги двигателя, от скорости течения воды в реке? Зависит ли время падения груза, выброшенного из самолета, от скорости самолета?
Опыты показывают, что скорость корабля не зависит от скорости течения воды, время падения груза, выброшенного из самолета, не зависит от скорости самолета!
Из этого вытекает следующий вывод.
Движения, в которых участвует тело, являются независимыми, их скорости (ускорения) не зависят друг от друга. Это называется принципом независимости движения.
Исходя из этого, любое сложное движение можно рассматривать как сумму простых движений. Эти движения не влияют друг на друга. Если одно из них изменяется или прекращается, это не влияет на другое движение. Именно на основе этого принципа мы можем в изучаемом процессе разделить их на отдельные составляющие векторных величин, т.е. этот принцип основан на проекции каждого движения на оси координат. Кроме того, этот принцип основан на получении результирующей скорости путем сложения векторов скоростей. На основе этого для движения тела, участвующего в нескольких движениях, делаем следующие выводы:
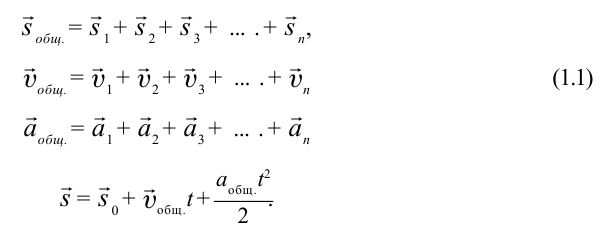
Соответственно проекции этих величин на оси х и у будут следующими:
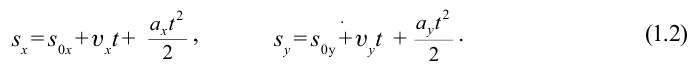
Пример №17
Скорость теплохода в воде в состоянии покоя составляет 70 км/час. За какое время он преодолеет расстояние между пристанями, расположенными по течению на расстоянии 36 км друг от друга? Скорость течения реки 2 км/час.
Дано:
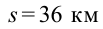
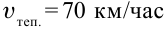
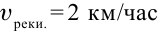
Найти:
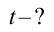
Формула и решения:
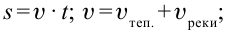
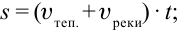
Отсюда: 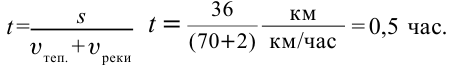
Ответ: 0,5 час.
Карта механического движения
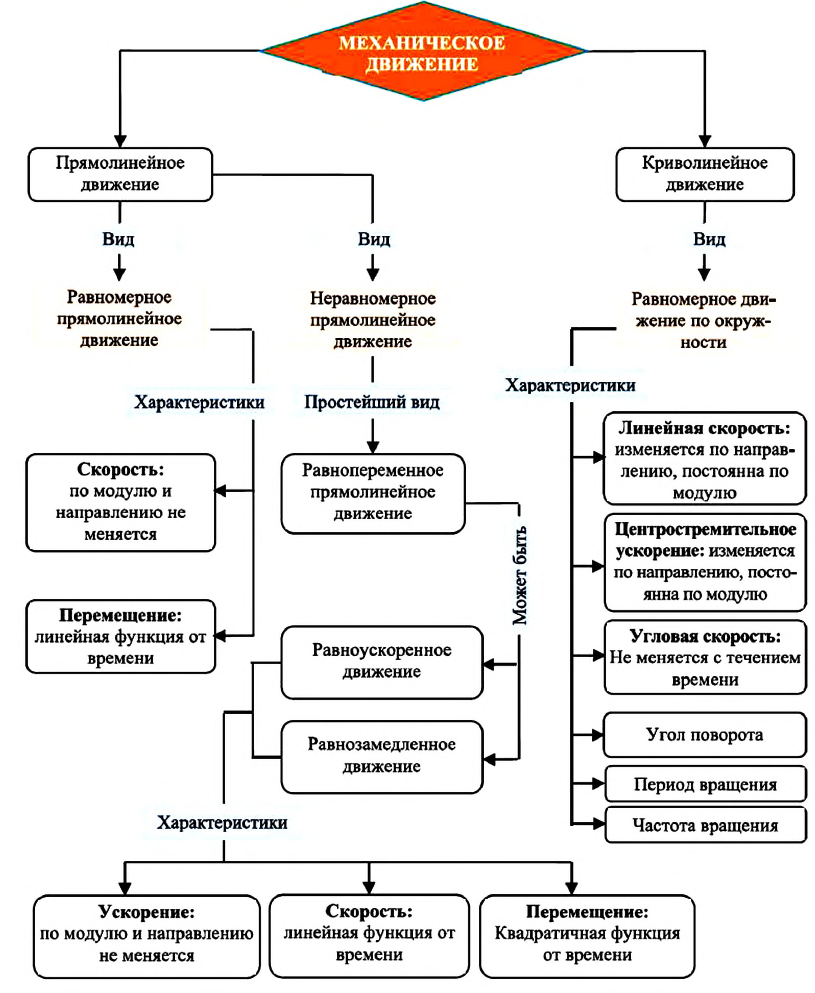
Механическое движение и его описание
Вероятно, вы слышали эти знаменитые выражения древнегреческого философа Гераклита Эфесского (554-483 гг. до н.э.): “Все течет, все изменяется”, “Невозможно дважды войти в одну и ту же реку”.

При отсутствии друга на месте заранее договоренной встречи вы, сразу позвонив ему по телефону, спрашиваете: “Где ты?”. Друг, представив себе место встречи, просит вас: “Стой на месте, иду”.
Движение является одним из основных свойств непрерывно изменяющейся материи в окружающем нас мире. Самой простой формой движения является механическое движение.
Механическое движение – это изменение положения тела относительно других тел в пространстве с течением времени.
Наука, изучающая закономерности механического движения и причины его возникновения, называется механика (от греческого слова mekhane — “машина”, “механизм”).
Основная задача механики — определение положения тела в произвольный момент времени.
Для решения основной задачи механики необходимо определить, как движется тело, как меняется его положение с течением времени. Другими словами, необходимо установить связь между физическими величинами, характеризующими механическое движение.
Раздел механики, изучающий механическое движение тел без учета причин возникновения этого движения, называется кинематикой (от греческого слова kinematos — “движение “).
Одним из самых простых видов механического движения является поступательное движение.
Поступательным называется движение тела, при котором все его точки движутся одинаково.
При поступательном движении тела прямая линия, проходящая через две его произвольные точки, остается параллельной своему первоначальному положению. Например, поступательным является движение чемодана, показанное на рисунке (b). Так как при поступательном движении все точки тела движутся одинаково, то такое движение тела можно представить как движение одной его точки. По этой причине в механике используют идеализированную физическую модель, называемую материальной точкой.
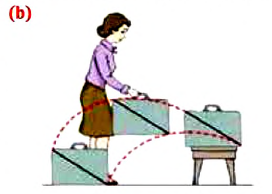
• Тело, размерами которого в данных условиях можно пренебречь, называют
Внимание! Здесь слова “в данных условиях” означают, что одно и то же тело в одних условиях можно принять за материальную точку, а в других нельзя. Например, так как радиус Земли в 24 ООО раз меньше расстояния от Земли до Солнца, то Землю при движении вокруг Солнца можно принять за материальную точку. Однако при изучении движения самолета, автомобиля, космического корабля и других относительно поверхности Земли, земной шар нельзя считать материальной точкой.
Для определения положения материальной точки в произвольный момент времени выбирается тело отсчета.
• Телом отсчета называется тело, относительно которого изучается движение материальной точки.
Тело отсчета выбирается произвольно, и оно условно считается неподвижным. Например, за тело отсчета можно принять Солнце, Землю, видимые звезды, вагон поезда, в котором вы едете, и другие.
Если тело отсчета выбрано, то положение материальной точки относительно него можно определить при помощи метода координат, или метода радиус-вектора.
Определение положения материальной точки при помощи метода координат. После выбора тела отсчета какая-либо точка этого тела принимается за начало отсчета, проводятся координатные оси, и положение любой материальной точки определяется этими координатами. Как это делается, вы изучали на уроках математики. Например, определим положение автомобиля на прямой дороге (с).
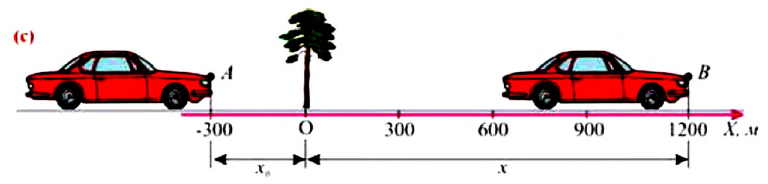
Для этого достаточно провести вдоль дороги одну координатную ось ОХ. За начальную точку отсчета на координатной оси (точка О) возьмем дерево, растущее на обочине дороги. В этом случае положение автомобиля определяется по его координате 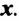 Вправо от начала координат вычисляемая координата положительна, а влево – отрицательна. Предположим, что в начальный момент времени
Вправо от начала координат вычисляемая координата положительна, а влево – отрицательна. Предположим, что в начальный момент времени 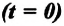 автомобиль находился в точке с координатой -300 м. Это его начальная координата
автомобиль находился в точке с координатой -300 м. Это его начальная координата 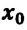 (точка А):
(точка А): 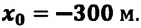 Автомобиль, двигаясь вдоль оси
Автомобиль, двигаясь вдоль оси 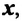 в момент времени
в момент времени 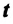 окажется в координате
окажется в координате 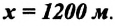 Положение автомобиля в любой момент времени можно определить, зная зависимость координаты от времени
Положение автомобиля в любой момент времени можно определить, зная зависимость координаты от времени 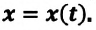
Если тело движется на плоскости (например, кончик ручки по бумаге, лодка по озеру), то через выбранное тело отсчета проводятся две координатные оси ОХ и OY. Положение точки на плоскости определяется координатами 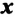 и
и 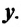 Например, координаты точки
Например, координаты точки 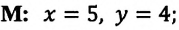 координаты же точки
координаты же точки 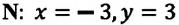 (d)
(d)
Таким образом, зависимость координат движущегося тела от времени 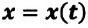 и
и 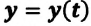 описывает движение материальной точки на плоскости.
описывает движение материальной точки на плоскости.
Для определения положения тела в пространстве (например, рыбы в воде, самолета в небе) с телом отсчета связывают трехмерную систему координат. В такой системе положение тела определяется тремя координатами – 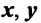 и
и 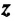 (е).
(е).
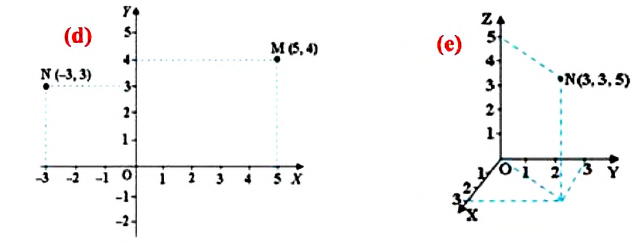
Определение положения материальной точки методом радиус-вектора.
Вектор, соединяющий начало координат с материальной точкой, называется радиус-вектором.
Радиус-вектор обозначается буквой 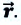 Его длина (модуль) определяется расстоянием от начала координат до материальной точки (f). Радиус-вектор используется, если известен его модуль и направление в пространстве. Зависимость радиус-вектора от времени
Его длина (модуль) определяется расстоянием от начала координат до материальной точки (f). Радиус-вектор используется, если известен его модуль и направление в пространстве. Зависимость радиус-вектора от времени 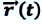 описывает движение материальной точки.
описывает движение материальной точки.
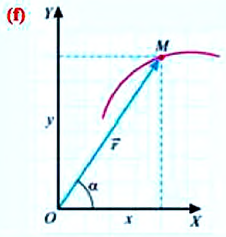
Чтобы иметь полное представление о механическом движении материальной точки (по прямой линии, на плоскости или в пространстве), необходимо установить, как изменяются его координаты с течением времени. Для этого необходим прибор, измеряющий время (часы, обычно используется секундная стрелка часов), при помощи которого определяются координаты материальной точки в начальный момент  в последующие моменты времени
в последующие моменты времени  и др.
и др.
Таким образом, механическое движение материальной точки изучается относительно выбранной системе отсчета:
Тело отсчета, система координат, связанная с этим телом, и прибор для отсчета времени образуют вместе системы отсчета.
Всё о механическом движение
Вспомните: вы сидите в вагоне поезда и смотрите на поезд, стоящий рядом. Вдруг вам показалось, что ваш поезд тронулся с места, ведь за окном начали проплывать вагоны соседнего поезда. И тут вы смотрите в окно напротив и… понимаете, что ваш поезд попрежнему стоит на перроне, а движется поезд, который стоял рядом. А если бы окна напротив не было, смогли бы вы определить, какой поезд тронулся — ваш или соседний?
Все в мире находится в движении (рис. 6.1): миллиарды лет, которые существует Вселенная, разлетаются в разные стороны галактики; Земля вращается вокруг Солнца, делая один оборот за год; за несколько часов самолет перелетает из Киева в Мадрид; в капле воды множество микробов ежесекундно передвигаются с места на место; все время движутся молекулы.
Несмотря на разнообразие примеров движения, у них есть общее: во-первых, все движущиеся тела изменяют свое положение в пространстве относительно других тел; во-вторых, изменение положения тел происходит с течением времени. Простейшей разновидностью движения является механическое движение.
Механическое движение — это изменение со временем положения тела или частей тела в пространстве относительно других тел.
Определение системы отсчета
Когда тело движется, его положение в пространстве изменяется. Для определения положения тела в пространстве используют систему координат, которую связывают с телом отсчета.
Тело отсчета — это тело, относительно которого рассматривают положение движущегося тела. Выбор тела отсчета является произвольным. За тело отсчета можно взять любое тело исходя из соображений удобства. Это может быть как вагон поезда, так и платформа вокзала, как дерево на обочине дороги, так и мчащийся автомобиль. Телом отсчета могут быть и планета Земля, и Солнце, и далекая галактика.

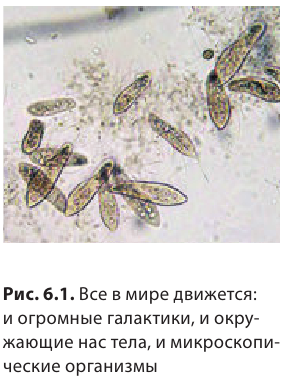
Какое тело, по вашему мнению, целесообразно принять за тело отсчета, исследуя ваше движение на перемене; на уроке физкультуры; во время путешествия? После того как тело отсчета выбрано, с ним связывают систему координат, которую задают с помощью одной, двух или трех координатных осей. Вдоль осей откладывают расстояния в выбранном масштабе, например в километрах или метрах (рис. 6.2, 6.3). Изменение положения тела происходит не мгновенно, а в течение некоторого времени, поэтому для исследования механического движения необходим прибор для отсчета времени — часы. Тело отсчета, связанная с ним система координат и часы образуют систему отсчета.
Когда тело можно считать материальной точкой
Обычно во время движения тела каждая его точка движется поразному. На практике исследовать движение всех точек тела довольно сложно и, как правило, нет необходимости.
Описывая движение тела, размеры которого намного меньше, чем расстояния, которые оно преодолевает, тело заменяют физической моделью — материальной точкой. Материальная точка не имеет размеров, а ее масса равна массе данного тела.
Материальная точка — это физическая модель тела, размерами которого в условиях данной задачи можно пренебречь. Одно и то же тело в условиях одной задачи можно считать материальной точкой, а в условиях другой — нельзя.
Представьте автомобиль, который движется по трассе из Одессы в Киев, и этот же автомобиль, когда он паркуется на автостоянке. В первом случае, исследуя движение автомобиля, его размерами можно пренебречь.
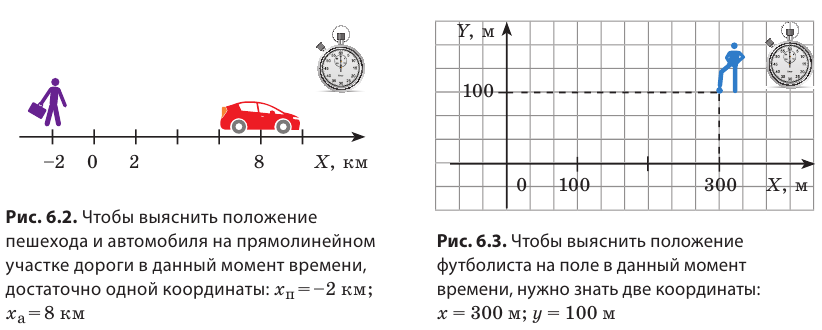
То есть можно не учитывать, что при движении автомобиля его отдельные точки двигались поразному, ведь расстояние, которое проехал автомобиль, было намного больше, чем, скажем, его длина. А вот во втором случае пренебречь размерами автомобиля нельзя. Попробуйте привести аналогичные примеры, взяв в качестве исследуемых тел человека, Землю, карандаш, дерево. Обратите внимание! Когда мы определяем координаты тела, то считаем это тело материальной точкой. Далее, когда будем говорить о движении тела, будем считать, что речь идет о движении материальной точки.
Относительность движения и покоя
То, что тело отсчета выбирается произвольно, означает, что состояние движения и состояние покоя относительны. Представьте пассажира, который сидит в вагоне движущегося поезда (рис. 6.4). Относительно сиденья и вагона пассажир не изменяет своего положения со временем, то есть находится в состоянии покоя, а относительно деревьев за окном — движется. Читая этот текст, вы, скорее всего, сидите в классе за партой или дома за столом. Назовите тела, относительно которых вы движетесь, и тела, относительно которых вы пребываете в состоянии покоя. Относительность движения дает возможность «остановить» движущийся автомобиль. Для этого нужен еще один автомобиль, который будет ехать рядом с первым, не отставая и не обгоняя его. В таком случае автомобили относительно друг друга будут пребывать в состоянии покоя. Вспомните, как каскадеры пересаживаются с одного мчащегося автомобиля на другой, который движется рядом! Тот же принцип используют и для заправки самолета топливом во время полета (рис. 6.5).
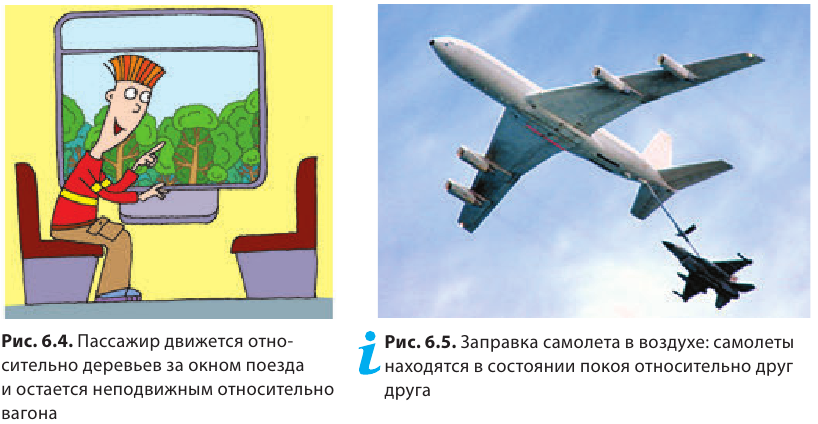
Итоги:
Механическое движение — изменение со временем положения тела или частей тела в пространстве относительно других тел. Тело, относительно которого рассматривают положение движущегося тела, называется телом отсчета. Тело отсчета, связанная с ним система координат и часы образуют систему отсчета. Состояния движения и покоя зависят от выбора системы отсчета, то есть являются относительными. В физике для упрощения описания движения тела используют физическую модель — материальную точку. Материальная точка — это тело, размерами которого в условиях данной задачи можно пренебречь.
- Движение и взаимодействие
- Относительность движения
- Поступательное движение
- Равномерное и неравномерное движение
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Что изучает механика в физике

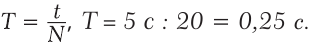
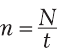 дает: n = 20 : 5 c = 4 (1/с).
дает: n = 20 : 5 c = 4 (1/с).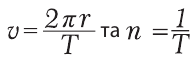 , получаем:
, получаем: