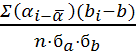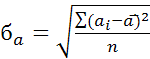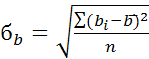Как найти средний угол наклона

Средний уклон поверхности.

Средний уклон
поверхности также можно определить
точечным способом.

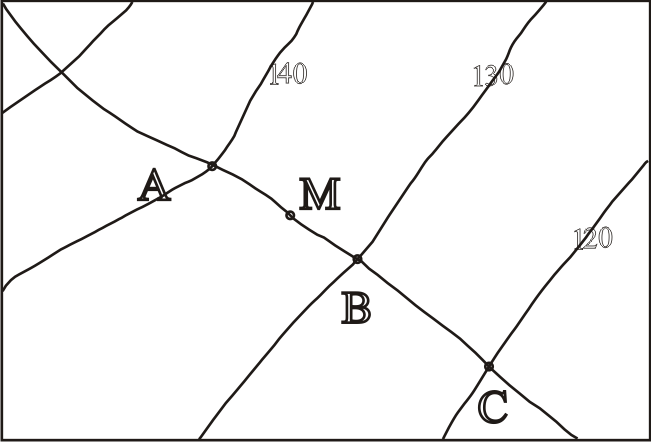
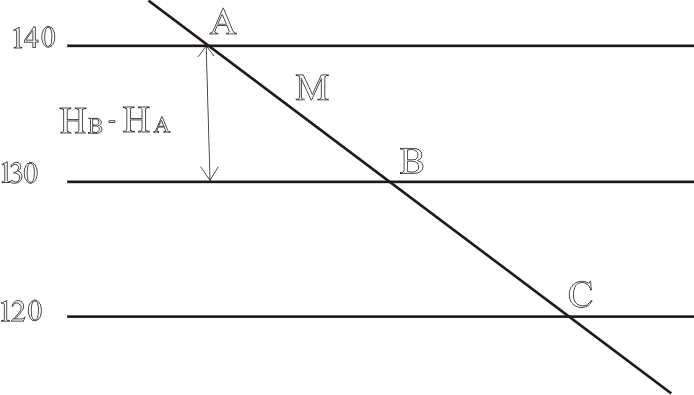
Для определения
значения уклона в точке М проводится
линия АВ, пересекающая горизонтали под
прямым углом.

Отношение разности
высот горизонталей к длине соответствующего
горизонтального положения АВ будет
являться средним уклоном линии АВ,
значение которого принимается за частный
уклон в точке М:

Средний же уклон
поверхности для области

определяется как:

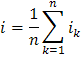
Показатели расчленения поверхности.

Существует
горизонтальное и вертикальное расчленение
поверхности. В горизонтальном
расчленении к расчленяющим линиям
относятся оси максимумов и минимумов
поверхности. Если речь идет о рельефе,
то расчленяющими будут линии тальвегов
и водоразделов.
Для геолого-структурных поверхностей
– оси прогибов и синклиналей. Для
барического поля – оси циклонов и
антициклонов.

Горизонтальное
расчленение подсчитывается по природным
районам, ландшафтам, элементарным
бассейнам или по квадратным сеткам.

Горизонтальное
расчленение бывает слабым и сильным.
Степень горизонтального расчленения
можно охарактеризовать следующими
показателями:

• густота эрозионной
  сети

Где L
– общая протяженность тальвегов и
водотоков в рассматриваемой области;

Р – площадь области.

• средняя удаленность
  водоразделов от тальвегов (средняя
  длина склонов)

Вертикальное
расчленение рельефа характеризуется:

• амплитудой высот
  в пределах какого-либо участка

• cредним
  превышением водоразделов над тальвегами

№5 Использование
топокарт для определения количественных
характеристик.

Количественные
характеристики явлений с последующей
оценкой точности получаемых результатов
определяются при помощи картометрических
исследований.

Картометрия
– дисциплина, изучающая способы и средства
измерений по картам для определения
количественных характеристик различных
географических объектов – длины, площади,
объема, извилистости и др.

При измерении на
картах длин прямых линий пользуются
линейным масштабом.

Длины кривых линий
(рек, горизонталей) измеряют циркулем
с малым растворением (1-2 мм). Измерение
выполняется по участкам в прямом и
обратном направлении. В данном случае
извилистая линия заменяется на ломаную.

Если река
имеет много мелких извилин, которые не
могут быть учтены при измерениях, вводят
поправку за извилистость. Полученная
величина умножается на коэффициент
извилистости К . Этот коэффициент
определяют путем сравнения измеряемой
кривой с эталонами извилистости
(1,00-1,28).

Измерение площадей
выполняется при помощи палеток или
планиметра.

Работа с палеткой
несложная, но требует большого количества
времени.

Планиметр – прибор,
используемый для определения площади
на картах крупных и средних масштабов.

Ошибка
измерения площади планиметром зависит
от размеров измеряемой площади и
вычисляется по формуле:

Чем больше площадь,
тем меньше относительная ошибка
измерений. Следовательно, при измерении
площади контуров небольшого размера
лучше применять палетки, а при определении
площади участков значительных размеров
– планиметр.

Для характеристики
реки измеряют ее длину L_KM
, длину притоков

и вычисляют общую длину речной сети в
бассейне –
.

Кроме длины
реки находят ее извилистость, которая
складывается из извилистости долины τ
(орографическая извилистость), извилистости
реки в длине

(гидрографическая извилистость) и общей
извилистости реки
.

Извилистость
долины:

t- длина долины;

q
– длина замыкающей (линия, соединяющая
точки истока и устья

реки).

Извилистость
реки в долине:

Общая извилистость:

Средний угол
падения реки
находят по формуле:

Средняя ширина
бассейна реки
равна отношению площади этого бассейна
к максимальной длине долины:

Густота речной
сети:

Бассейн реки
характеризуется не только особенностями
самой реки (извилистость), но и особенностями
рельефа бассейна.

Глубина расчленения
рельефа h max:

–
наибольшая высота в пределах бассейна,
которая берется около водораздельной
линии.

–
наименьшая высота, соответствующая
урезу воды в устье реки.

Средняя высота
рельефа:

№6. Показатели
извилистости кривых линий и изрезанности
контуров.

Разработка способов
оценки извилистости линий принадлежит
к давним и нерешенным до конца задачам
морфологии. Объективные трудности в
выборе подходящего показателя связаны
с тем, что извилистые линии имеют самую
различную природу. Так, например,
извилистость русла реки не похожа на
извилистость долины, изрезанность
участка берега моря не идентична
изрезанности замкнутой береговой линии
озера.

Говоря о большей
или меньшей извилистости кривых, имеют
в виду либо их визуальное сравнение,
либо сравнение некоторых количественных
характеристик извилистости.

Большинство таких
характеристик выражается соотношением
длин оцениваемой линии, и ее плавной
огибающей или прямолинейной замыкающей.

1 – извилистая
линия;

S
– плавная окаймляющая;

D
– прямолинейная замыкающая.

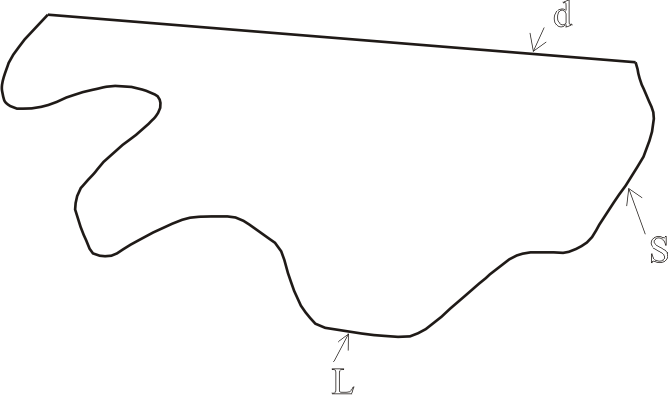
В этом случае
извилистость участка кривой может быть
оценена тремя показателями, отражающими
соотношение 1, S,
d:

• относительной
  извилистостью

  

• извилистостью
  общих очертаний (т.е. извилистостью
  огибающей)

• абсолютной
  извилистостью

Нетрудно заметить,
что последний показатель является
произведением первых двух:

В гидрологии
извилистость рек оценивают двумя
показателями

и β.

– гидрографическая извилистость, т.е.
извилистость реки в ее долине.

– орографическая извилистость, т.е.
извилистость оси долины.

Если все
извилины замкнутого или незамкнутого
контура имеют примерно один и тот же
размер, т.е. нет резко выделяющихся
изгибов большого радиуса или мелких
извилин, то удобно воспользоваться
сравнительно простым показателем
извилистости, который показывает
отклонение числа извилин (n) к общей
длине линии

Еще проще взять
отношение числа извилин к длине плавной
огибающей (S)

Определение
показателей извилистости связано с
поведением плавной огибающей.

Но эта огибающая
может быть проведена по-разному, т.е.
она несет элемент субъективности.
Поэтому рассмотрим показатели
извилистости, построенные на осреднении
характеристик отдельных извилин.

Извилиной
считается дуга кривой, заключенная
между 2-мя соседними точками перегиба
А и В.Её можно оценить тремя величинами:
длиной
,
угловой величиной

и средней кривизной

№7 Влияние
картографической генерализации на
результаты количественных определений
по картам. Эталонирование характеристик.

Генерализация
проводится по нескольким направлениям:
обобщается легенда карты, устанавливаются
цензы и нормативы отбора, упрощаются
очертания контуров. Все эти операции
преследуют 2 цели: во-первых, соблюсти
по возможности геометрическую точность
изображения, во-вторых, сохранить
географическое правдоподобие, что
приводит к противоречию. Так, на
генерализованной карте геометрическая
точность часто нарушается в угоду
географическому правдоподобию. Например,
при генерализации гипсометрического
изображения на картах средних и мелких
масштабов для сохранения географического
правдоподобия изображаемых форм рельефа
при редком сечении изолиний допускается
сдвиг отдельных горизонталей вверх или
вниз по склону, что искажает уклон
рельефа. Но, с другой стороны, мелкомасштабная
гипсометрическая карта удобна для
выявления региональных неотектонических
поднятий и опусканий.
Можно привести пример и с речной сетью
при отборе и обобщении элементов
гидрографии на топокартах средних
масштабов. Генерализация в этом случае
ведёт к изменению количества и общей
длины водотоков. Происходит так называемая
“потеря густоты” речной сети, что
отражено в следующей таблице:

Масштаб	Кол-во водотоков	в % к 1:100000	Длина водотоков	в % к 1:100000	Густота речной сети	в % к 1:100000
1:100000	81	100	450.1	100	0.39	100
1:200000	56	70	387.6	86	0.33	85
1:500000	34	42	304.5	67	0.26	67
1:1000000	15	18	219.0	49	0.19	49

Для учёта влияния
генерализации и выявления погрешностей,
вносимых генерализацией, применяются
следующие способы:

-сравнение с
крупномасштабными картографическими
источниками;

-сопоставление
объектов, изображённых на карте, с их
фактическим положением в действительности;

-изучение проявлений
генерализации на эталонных, заведомо
точно составленных картах разных
масштабов.

Наилучшими являются
первые 2 способа, позволяющие непосредственно
оценить качество генерализации, однако
они очень трудоёмки. Также следует
учесть, что крупномасштабные источники
многих тематических карт в ряде случаев
вообще отсутствуют, а точное положение
некоторых объектов в действительности
установить крайне затруднительно.

Универсальным же
способом учёта картографической
генерализации является эталонирование
количественных характеристик, определённых
по картам.

Эталонирование
означает исправление значений
характеристик, полученных по картам
определённого масштаба, на основе их
выборочного сравнения с соответствующими
эталонными значениями. Эти значения
определены с высокой точностью по
крупномасштабным картам или аэрофотоснимкам,
для которых влияние генерализации
являются незначительным.

Пусть определено
значение некоего показателя K
для N
территориальных единиц по карте мелкого
или среднего масштаба. Выберем из этих
N
единиц совокупность в n
единиц, для которых определим эталонные
значения Kэ.
Выведем эмпирическую формулу зависимости
Kэ
от K
и оценим ср.кв. ошибку расчёта Kэ
по K-mк.
По полученной эмпирической формуле
можно перейти от измерённых
значений
показателя к соответствующим эталонным
для всех N
территориальных единиц.

Рассмотрим вывод
эмпирической формулы связи в виде
параболы 2-го порядка:

ax²+bx+c
(1)

где под x
будем понимать значение K,а
под Y-Kэ.

а,b,c-параметры
формулы, определяемые по опытным данным
,т.е. по выборке соответствующих X

и Y

(
=1,2,…n).В
основу нахождения параметров а,b,c
положим принцип наименьших квадратов,
в соответствии с которым сумма квадратов
уклонений
,вычисляемых
по формуле(1) и действительных (эталонных),
д.б минимальной, т.е. должно выполняться
условие:

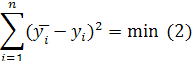
Эта сумма для
конкретной выборке является функцией
параметров a,b,c
и достигает минимума, когда частные
производные этой суммы по параметрам
a,b,c
обращаются в нуль.

Запишем формулу
(2) в развёрнутом виде :

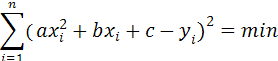
и найдём производные
суммы по параметрам:

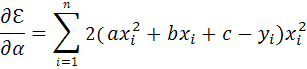
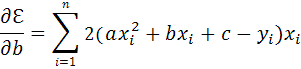
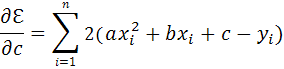
Приравняем правые
части к 0,вынесем параметры a,b,c
за знак суммы:

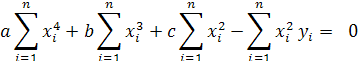
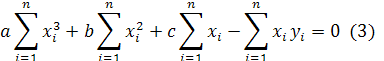
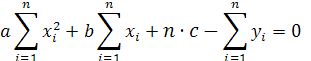
Коэффициенты при
неизвестных a,b
и c
подсчитываются по данным выборки, после
чего остаётся решить систему относительно
этих неизвестных и подставить полученные
их значения в формулу эталонирования
(1).

Среднеквадратическая
ошибка эталонирования вычисляется по
формуле:

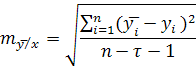
-число
параметров формулы эталонирования
(эмпирической формулы).

Рассмотренная
методика вывода эмпирических формул и
оценка её точности может быть распространена
на параболу любого порядка .В большинстве
случаев ограничиваются параболой
второго порядка (1).Иногда используют
линейную связь

ax+b
(4) ,

что упрощает
процесс эталонирования.

№8 Изучение по
картам взаимосвязей и зависимости
явлений.

Методика исследования
данного процесса многообразна .На неё
влияют не только способы изучения
связей, но и особенности используемых
карт, цели исследования и т.д. Очень
ценны карты, фиксирующие фактический
материал непосредственных наблюдений
в действительности. К таким картам
принадлежат топокарты, по которым легко
изучать взаимосвязи между гидрографией,
рельефом и растительностью.

Так же показательно
сопоставление топокарт с отраслевыми
математическими картами: геологическими,
почвенными и т.д. Например, анализ
природных взаимосвязей по топокарте
и почвенной картам Алтайского края
позволяет установить приуроченность
многих почвенных контуров к элементам
рельефа: солонцов и солончаков – к
приозёрным понижениям, аллювиальных
почв – к речным поймам и т.д. И подобных
примеров можно привести множество.

Для количественной
характеристики зависимостей используют
методы математической статистики с
целью вычисления корреляционных
зависимостей. Например, в случае
прямолинейной связи между двумя
исследуемыми явлениями сила связи
определяется вычислением коэффициента
корреляции:

r=

-конкретные
значения исследуемых явлений в некоторой
точке

n
– общее число точек ,и, следовательно
величин, измерённых для каждого явления.

=

;
=

– средние значения.

;

–дисперсия (рассеивание).

Среднеквадратическая
ошибка коэффициента корреляции
вычисляется по формуле:

Когда коэффициент
корреляции r=1(100%),между
явлениями существует функциональная
зависимость. Если коэффициент=0.9-0.7(90%-70%),то
существует тесная связь между явлениями.
Формула среднеквадратической ошибки
показывает, что ошибка корреляции
зависит от общего объёма выборки n.
В математической статистике считается,
что связь, выражаемая коэффициентом
корреляции, надёжна при
.Следовательно,
в каждом конкретном случае нетрудно
установить объём выборки, обеспечивающий
желаемую точность.

№9 Основные
принципы картометрии. Понятие
картографической , технической и
картометрической ошибок.

К сфере картометрии
относятся измерения
по картам плановых координат объектов,
длин, расстояний, площадей плоских
поверхностей, объёмов, горизонтальных
и вертикальных углов и т.д.

В задачи картометрии
входит также оценка
точности
измерений с учётом масштаба и проекции
карты.

Кроме этого
изучаются способы измерения количественных
характеристик объектов и явлений.

Основной принцип
картометрии – получение результатов,
имеющих место в действительности. При
этом необходимо выполнение 2-х задач:

1. Определение
количественных характеристик изображений,
объектов и явлений на картах. Достигается
это при помощи технических средств и
способов измерений без учёта свойств
карты.

2. Переход от
полученных значений количественных
характеристик к значениям, имеющим
место в действительности. При этом
учитывается искажение картографической
проекции, деформация картографической
бумаги, влияние картографической
генерализации на размеры объекта. Также
осуществляется переход от размеров
проекции объектов на эллипсоиде к их
размерам на физической земной поверхности.

Картометрические
измерения всегда приводят к приближённым
результатам. Поэтому необходима оценка
точности этих результатов(для определения
степени соответствия действительности).

Существуют
картографическая, техническая и
картометрическая ошибки.

1.Картографическая
ошибка. Это
разновидность значений характеристик
объектов на карте и в действительности.

К картографическим
относятся ошибки, обусловленные
искажениями картографической проекции,
генерализацией изображения объектов,
деформацией бумаги. Эти составляющие
могут быть с той или иной степенью
точности определены и учтены, т.е. в
результаты измерений могут быть введены
соответствующие поправки.

За счёт погрешностей
определения поправок получается
случайная картографическая ошибка.
Значение её не может быть определено в
конкретном случае, но оно может установить
степень соответствия полученных
результатов действительности. Этой
степенью являются среднеквадратическая
ошибка, средняя ошибка.

2. Техническая
ошибка. Это
ошибка измерений, без учёта свойств
карты. Её можно представить как разность
размера объекта (
,S,…)
на карте и результата его измерения.

Способы измерений
предлагают определённые методики
выполнения измерений и их обработки,
исключающие систематические ошибки.
Случайная же техническая ошибка зависит
от средств измерений и от некоторых
параметров измеряемых объектов.

Понятие
картографической и технической ошибок
относится к измерениям по картам размеров
объектов, показанных масштабными и
линейными условными знаками (измерение
площадей и длин кривых).

3.Картометрическая
ошибка возникает
в процессе выполнения и обработки
измерений. Например, если численность
населённых пунктов показана на карте
пунсоном при помощи непрерывной шкалы
отображения, то значение численности
определяется как функция диаметра
пунсона.

В этом случае
технической ошибкой является ошибка
измерения диаметра пунсона.

Соответствующая
же ошибка в численности, имеющая смысл
разности её значений, показанных пунсоном
на карте и рассчитанного по измерённому
диаметру пунсону, называется
картометрической ошибкой.

№10 Измерение
длин кривых линий.

6.1. Определение отметок горизонталей

Возникают три основных случая решения этой задачи.

На одной из горизонталей подписана отметка её. Тогда на основании свойств горизонталей отметка в любой точке её будет равна подписанному числу.

Подписана одна из ближайших горизонталей. Отметка искомой горизонтали определяется с учётом высоты сечения рельефа h_с и направления ската местности. Повышение или понижение рельефа определяется по бергштрихам или форме написания значения отметки горизонтали. Отметка искомой горизонтали Н_иск будет равна

где Н_исх — отметка исходной горизонтали, n – число интервалов между подписанной и определяемой горизонталями, знак + или — ставится с учётом повышения или понижения рельефа.

Подписана отметка земли. Отметка близлежащей горизонтали будет равна ближайшему к отметке земли числу, кратному высоте сечения рельефа с учётом повышения или понижения местности.

6.2. Определение отметок точек

Здесь также возможные различные варианты.

Точка лежит на горизонтали. Тогда отметка точки равна отметке данной горизонтали.

Точка лежит между одноимёнными горизонталями или внутри замкнутой горизонтали. В этом случае точно определить отметку точки нельзя. Возможно отметить, что отметка точки больше (или меньше) отметки горизонтали на величину, не превышающую половины высоты сечения рельефа.

Точка расположена между разноимёнными горизонталями. Тогда её отметку определяют в следующей последовательности:

определяют отметки соседних горизонталей;

определяют превышение h точки над горизонталью с меньшей отметкой;

вычисляют отметку точки по формуле

Для определения превышения точки над горизонталью через неё проводят нормаль к соседним горизонталям. Превышение в этом случае будет пропорционально горизонтальному проложению от точки до горизонтали, то есть, в каком отношении точка делит нормаль между горизонталями, в таком же отношении точка делит высоту сечения рельефа. Эта пропорция решается точно по формуле (20) или с некоторой погрешностью «на глаз». Пользоваться тем или иным приёмом следует с учётом того фактора, что при аналитическом определении отметок их значения всё равно округляют до 1 м при высоте сечения рельефа h_c = 5 м, до 0,5 м при h_c = 2,5 м.

7. Определение уклонов линий и крутизны скатов

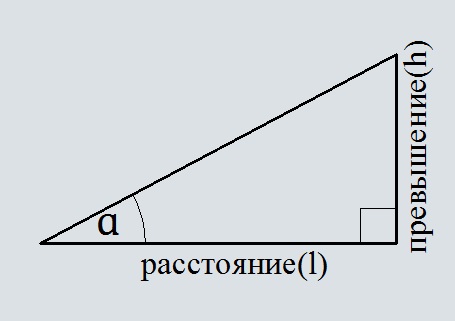
Уклон – это угол наклона линии к горизонту. На местности этот угол может быть измерен специальным угломерным прибором. При работе с картой такой возможности нет. Однако при наличии на карте горизонталей появляется возможность решения этой задачи косвенным путём

Если рассматривать прямую линию местности в вертикальной плоскости и через одну из точек её концов провести линию горизонта, а через другую точку отвесную линию, то путь определения искомого угла совершенно очевиден (см. рис. 25-26): искомый угол в прямоугольном треугольнике равен круговой функции тангенса отношения одного катета к другому. Так как катеты этого треугольника есть не что иное, как превышение между концами этой линии и горизонтальное проложение её, то ν = аrctg = arctg 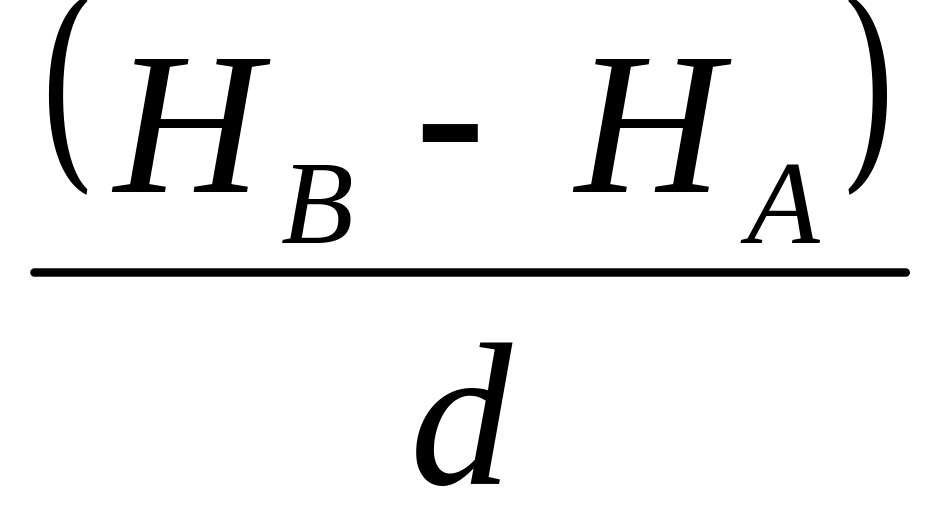. (35)

Величина угла наклона чаще всего характеризует рельеф местности, им определяют крутизну скатов рельефа (см. табл.5). В инженерной же практике применяют понятие просто уклон i, который равен отношению превышения между концами прямой к горизонтальному проложению её

Уклоны выражаются десятичной дробью с вычислением до 0,0001 и округлением окончательного результата до 0,001.

i = .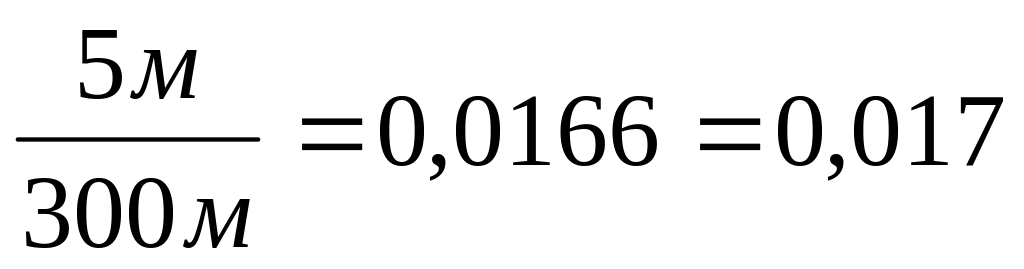

Часто уклоны выражаются в процентах % или промилях ‰. Например, i = 17 = 1,7% = 17‰.

Между уклоном и углом наклона существует известная зависимость (см. формулы 32-33)

Чтобы определить уклон линии местности, отмеченной на карте отрезком АВ, вычисляют превышение между концами его как разность отметок Н_В и Н_А, найденных по отметкам горизонталей. Затем, используя поперечный или линейный масштаб, находят горизонтальное проложение этого отрезка. Величину уклона вычисляют по формуле (33). Если есть необходимость выразить его в градусной мере, то следует использовать формулу (32). Здесь необходимо отметить, что полученная величина уклона характеризует положение только линии АВ (рис.34). Действительно, на участке А-1 или 2-В линия не совпадает с поверхностью земли и с характеристикой рельефа никак не связана. Вот на участке 1-2 линия совпадает с поверхностью земли и полученная величина уклона для всей линии будет характеризовать рельеф на этом участке местности.

Физическая поверхность местности на участке 1-2

Рис. 34. Схема прямой линии АВ на местности

Для характеристики рельефа необходимо вычислять превышения и горизонтальные проложения для линий, совпадающих с земной поверхностью, как это показано на рис. 34 (участок 1-2). При работе же с картой крутизну скатов определяют по отрезкам, концы которых лежат непосредственно на соседних горизонталей. Тогда уклон этого отрезка и крутизна ската вычисляется по тем же формулам, но превышение равно высоте сечения рельефа, а горизонтальное проложение заложению между горизонталями по заданному направлению. На практике поступают ещё проще. Так как при определении крутизны ската участвует превышение, равное высоте сечения рельефа, проще построить график (масштаб) заложений и использовать его при решении задач, подобных задаче по определению крутизны скатов рельефа. Подробное описание способа построения графиков заложений и методики их использования дано выше (см. разд. 3.4.2.3 с. 46-48 и рис.28). При несовпадении фиксированного измерителем заложения (см. рис.28, M-N) с подписанными на графиках значениями уклонов или углов наклона их величина определяется интерполированием «на глаз».

8. ТРАССИРОВАНИЕ ЛИНИИ

Эта задача выполняется при проектировании дорог на участках, где средние уклоны местности превышают допустимые для данной категории дорог. Для этого измерителем по шкале графика заложений фиксируют величину заложения, соответствующую максимально допустимому уклону. Затем из начальной точки трассы измерителем делают засечку на соседней горизонтали (возможны две засечки при наличии нескольких вариантов трассирования) и из полученной точки тем же раствором измерителя снова делают засечку уже на следующей горизонтали. В результате получают ломаную линию с заданным уклоном. При этом следует помнить, если расстояние между соседними горизонталями больше раствора измерителя, то проектную линию проводят по кратчайшему направлению. Подробное описание методики трассирования представлено в разделе «Проведение на картах и планах линий заданного уклона» (см. рис.29).

Источник

Калькулятор уклонов

Онлайн калькулятор

Посчитать уклон

Расстояние L =
Превышение h =

Посчитать превышение

Уклон α =
Расстояние L =

Посчитать расстояние

Уклон α =
Превышение h =

Теория

Как посчитать уклон

Для того чтобы посчитать уклон вам, для начала, необходимо знать расстояние (L) и превышение (h). Далее следуйте формулам:

В процентах:

Уклон в % = h / L ⋅ 100

В промилле:

Уклон в ‰ = h / L ⋅ 1000

В градусах:

Уклон в ° = arctg ( h /_L)

Пример

Для примера рассчитаем уклон дороги в процентах: на дистанции в L = 500 м дорога поднимается на h = 30 м:

Уклон дороги = 30/500 ⋅ 100 = 6%

Как посчитать превышение

Чтобы вычислить превышение (h), надо знать расстояние (L) и уклон (в процентах, в промилле или в градусах).

Если уклон в процентах (%):

h = L ⋅ Уклон в % /₁₀₀

Если уклон в промилле (‰):

h = L ⋅ Уклон в ‰ /₁₀₀₀

Если уклон в градусах (°):

h = L ⋅ tg(α) , где α — уклон в градусах

Пример

Для примера найдём превышение h, если расстояние L= 5м, а угол уклона α=45°:

h = 5 ⋅ tg(45) = 5 ⋅ 1 = 5 м

Как посчитать расстояние

Для того чтобы посчитать расстояние (L) необходимо знать превышение (h) и уклон (в процентах, в промилле или в градусах).

Если уклон в процентах (%):

L = h / _{Уклон в %} ⋅ 100

Если уклон в промилле (‰):

L = h / _{Уклон в ‰} ⋅ 1000

Если уклон в градусах (°):

L = h / tg(α) , где α — уклон в градусах

Пример

Для примера посчитаем расстояние (L), которое потребуется железной дороге, чтобы подняться на (h =) 6 м при угле подъёма 30‰:

Источник

Определение масштаба плана, среднего уклона местности и проектной глубины осушителей

Страницы работы

Фрагмент текста работы

1 Определение масштаба плана, среднего уклона местности и проектной глубины осушителей

1.1 Определение масштаба плана

Масштаб плана определяется для получения топографического плана местности из эскизного плана осушаемого участка в горизонталях. Масштаб М определяется как отношение действительной площади осушаемого участка F_б, к площади осушаемого участка на плане F_п.

. (1)

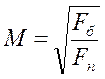
Параметры, входящие в формулу (1), должны иметь одинаковую размерность. Полученный результат округляют до ближайшего целого числа.

F_б = 16,8 км 2 = 16,8*1000000 = 16800000 м 2

F_п = 17 * 22 = 374/10000 см 2 = 0,0374 м 2

Отсюда .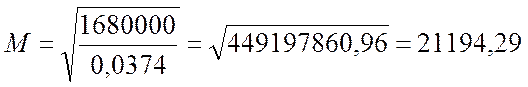

После округления получаем масштаб равный 1:20000.

1.2 Определение среднего уклона поверхности осушаемого участка

Для определения среднего уклона на плане выбирают три участка с различными уклонами, характеризующиеся разными расстояниями между соседними горизонталями, и на каждом участке определить уклон i как отношение превышения между горизонталями ∆h к расстоянию между ними по перпендикуляру l_г (горизонтальное проложение)

. (2)

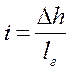
Средний уклон i_ср определяется как отношение арифметической суммы значений уклонов i_n к количеству замеров n

. (3)

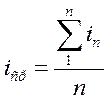
Уклон в точке А:

Уклон в точке Б:

i₂ = 0,5/(3,2 * 200) = 0,00078

Уклон в точке В:

i_ср = (0,002 + 0,00078 + 0,001) / 3 = 0,0039

1.3 Проектная глубина осушителей

Глубина осушительных каналов после осадки торфа Т_о принимает значение, зависящее от глубины торфа.

При глубине торфа = 1,6 м, Т_о = 1,2 м

После осушения болота происходит осадка торфа, поэтому проектную глубину каналов Т_пр определяют как:

Коэффициент m зависит от плотности торфа и типа болота.

Болота низинного типа, торф плотный, коэффициент m принимает значение равное 1,2

Исходя из формулы (4), получаем что:

Т_пр = 1,2 * 1,2 = 1,44 м.

Проектировочная глубина осушительных каналов равна 1,44м.

2 Требование к осушительной сети и выбор расчетных параметров

Лесоосушительной системой называется комплекс инженерных сооружений, устройств и мероприятий, которые обеспечивают создание оптимального водного режима переувлажненных земель с учетом выращиваемых пород и культур. Лесоосушительная система состоит из регулирующей, ограждающей и проводящей сети; водоприемника, гидротехнических сооружений; осушаемых земель и проводимых на них мелиоративных мероприятий.

Осушение земель производится в основном двумя способами: открытыми каналами (канавами) и дренажем; лесные земли обычно осушаются открытыми канавами.

Расчет, элементов осушительной системы начинают с расположения па плане проводящей (транспортирующей), оградительной и регулирующей сетей. При этом учитывают ряд факторов: рельеф поверхности, глубину торфа, причины избыточного увлажнения, цель осушения, экономические и хозяйственные требования. С учетом этих факторов при расположении осушительной сети нужно руководствоваться следующими основными указаниями.

2.1 Проводящая сеть

Проводящая сеть при любом типе водного питания служит для своевременного отвода всех избыточных вод и состоит из магистральных каналов и транспортирующих собирателей. Сеть в основном прямолинейная, с минимальным числом поворотов. Проводят ее по минимальным отметкам местности с учетом минерального дна болот. Если на плане нет явно выраженных лощин, проводящие каналы располагают в зависимости от удобства расположения осушителей. Каналы глубиной до 3 м делают обычно трапецеидальными, что облегчает их крепление. Минимальный уклон дна — 0,0005. Магистральные каналы должны проводиться по наибольшим глубинам торфа (если это возможно) так, чтобы глубина торфа по линии канала была оди­наковой или увеличивалась бы к устью. Проводящая сеть должна быть короткой и без холостых участков.

Магистральные каналы должны сопрягаться с водоприемником под углом около 60°. Также сопрягаются транспортирующие собиратели с магистральным каналом.

2.2 Регулирующая сеть

Регулирующая сеть (открытые осушители) — сеть параллельных каналов, расположенных поперек потока поверхностных и грунтовых вод или параллельно им. Минимальный уклон дна — 0,0005, длина — до 1500 м, ширина по дну — от 0,2 до 0,4 м, глубина от 0,6 до 1,5 м. Заложение откосов зависит от типа грунта и глубины канала. Расстояние между ними зависит от нормы осушения и района работ.

2.3 Ограждающая сеть

Ограждающая сеть включат в себя нагорные, ловчие, тальвеговые и защитные каналы.

Нагорные каналы служат дня перехвата поверхностных вод, стекающих с вышележащего водосбора. Глубина обычно до 1-1,2 м, длина — от 200- 500 м до нескольких километров, уклон — не менее 0,0005, одинаковый по всей длине. Кавальеры устраивают только с низовой стороны. Верхний откос более пологий — от 1:5 до 1:10. Нагорные каналы иногда совмещают с ловчими, образующими нагорно-ловчие каналы.

Ловчие каналы устраивают для перехвата поступающих на осушаемую территорию грунтовых вод в зоне наиболее высокого их стояния. Дно и откосы обычно крепят. При наличии подстилающего водоупора дно ловчего канала врезают в него. При глубине 2-2,5 м и слабых грунтах применяют параболическую форму поперечного сечения, в остальных случаях — трапецеидальную.

Тальвеговые каналы устраивают вдоль лощин (тальвегов) и других понижений, имеющих локальный характер. Они должны далее соединяться с магистральными или транспортирующими каналами.

Источник

Калькулятор уклонов

Чтобы посчитать уклон кровли, крыши, трубопровода, пандуса, лестницы, дороги, реки и т.п. воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Посчитать уклон

Посчитать превышение

Посчитать расстояние

Просто введите значения и выберите единицы измерения уклона.

Теория

Как посчитать уклон

Как посчитать превышение

Как посчитать расстояние

См. также

Расчёт уклона по расстоянию и превышению

Похожие калькуляторы