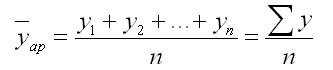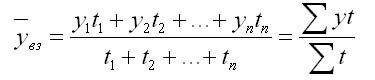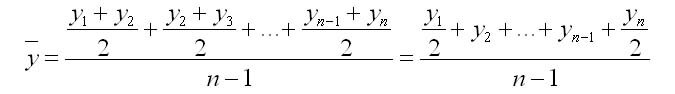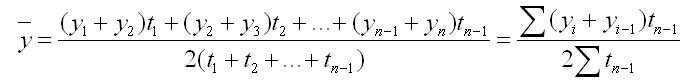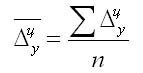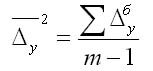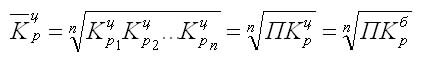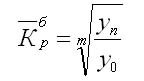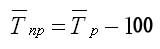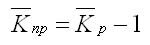Расчет средних показателей динамического ряда
Для
обобщающей характеристики динамики
исследуемого явления
определяют средние показатели: средние
уровни ряда и средние показатели
изменения уровней ряда.
Средний
уровень ряда
характеризует обобщённую величину
абсолютных
уровней. Он рассчитывается по средней
хронологической, т.е. по
средней исчисленной из значений,
изменяющихся во времени.
Методы
расчета среднего уровня интервального
и моментного рядов
динамики различны.
Для
интервальных рядов динамики из абсолютных
уровней средний за период времени
определяется по формуле средней
арифметической:
а)
при равных интервалах применяется
средняя
арифметическая простая:
,
где у1,…,уn– абсолютные уровни ряда;n– число уровней ряда.
б) при неравных
интервалах – средняя арифметическая
взвешенная:
,
где у1,…,уn– уровни ряда динамики, сохраняющиеся
без изменения в течение промежутка
времени,t;t1,…,
tn– веса, длительность интервалов времени
(дней, месяцев) между смежными датами.
Средний уровень
производства электроэнергии за 1989-1994
гг.:
.
Средний
уровень моментного ряда динамики с
равноотстоящими уровнями определяется
по формуле средней хронологической
моментного
ряда:
,
где у1,…,уn– уровни периода, за который делается
расчет;n– число
уровней;n–1 –
длительность периода времени.
Обобщающий
показатель скорости изменения уровней
во времени
– средний
абсолютный прирост (убыль),
представляющий собой обобщенную
характеристику
индивидуальных абсолютных приростов
ряда динамики.
По цепным данным об абсолютных приростах
за ряд лет можно
рассчитать средний годовой абсолютный
прирост как среднюю арифметическую
простую:
,
где n– число цепных абсолютных приростоввизучаемом
периоде.
Используя
данные табл.
5 о цепных абсолютных приростах
производства электроэнергии,
млрд кВт-ч:
(5
– 14 – 60 – 51 – 81) : 5 = ‑201 : 5 = ‑40,2
Средний
абсолютный прирост определим через
накопленный (базисный)
абсолютный прирост.
Для случая равных интервалов применим
следующую формулу:
,
где т
– число
уровней ряда динамики в изучаемом
периоде, включая базисный.
Для нашего примера,
млрд кВт-ч:
т.е. получен тот
же результат.
Сводной
обобщающей характеристикой интенсивности
изменения уровней
ряда динамики служит средний темп роста
(снижения), показывающий во сколько раз
в среднем за единицу времени изменяется
уровень
ряда динамики.
Средний
темп роста (снижения)
– обобщенная характеристика индивидуальных
темпов роста ряда динамики. В качестве
основы и критерия
правильности исчисления среднего темпа
(снижения) применяется
определяющий показатель – произведение
цепных темпов роста, равное
темпу роста за весь рассматриваемый
период. Следовательно, если значение
признака образуется как произведение
отдельных вариантов,
то нужно применять среднюю геометрическую.
Поскольку средний темп роста представляет
собой средний коэффициент роста,
выраженный
в процентах,
,
то для равностоящих рядов динамикирасчеты
по средней геометрической сводятся к
исчислению средних
коэффициентов роста из цепных коэффициентов
роста (по цепному способу):
,
где n– число цепных коэффициентов роста;‑
цепные коэффициенты роста;‑
базисный коэффициент роста за весь
период.
В
нашем примере среднегодовой темп
изменения производства электроэнергии
с 1990 по 1994г.:
;
Следовательно,
с 1990 по 1994г. производство электроэнергии
в России
снижалось в среднем на 4 % в год, т.е. (0,96
* 100) – 100.
Если
известны уровни динамического ряда, то
расчет среднего коэффициента
роста упрощается. Так как произведение
цепных коэффициентов
роста равно базисному, то в подкоренное
выражение подставляется
базисный коэффициент роста. Базисный
коэффициент, как известно,
получается непосредственно как частное
от деления уровня последнего
периода уп
на
уровень базисного периода у0.
Тогда
формула для расчета среднего коэффициента
роста для равностоящих
рядов динамики (по “базисному способу”)
выглядит следующим образом:
,
где т
– число
уровней ряда динамики в изучаемом
периоде, включая базисный.
Для
расчета средних коэффициентов роста
не нужно
знать годовые темпы. Для нашего примера:
Получен тот же
результат, расчеты упрощены.
Средние
темпы прироста (сокращения)
рассчитываются на основе
средних темпов роста, вычитанием из
последних 100%. Соответственно
при исчислении средних коэффициентов
прироста из значений
коэффициентов роста вычитается единица:
;
,
где
‑ средний темп прироста.
Если
уровни ряда динамики снижаются, то
средний темп роста будет
меньше 100 %, а средний темп прироста –
отрицательной величиной.
Отрицательный темп прироста
представляет собой средний
темп сокращения и характеризует среднюю
относительную скорость снижения
уровня.
При
анализе развития явлений, отражаемых
двумя динамическими рядами,
представляет интерес сравнение
интенсивностей изменения во
времени обоих явлений. Такое сопоставление
интенсивностей изменения
производится при сравнении динамических
рядов одинакового
содержания, но относящихся к разным
территориям (странам, республикам,
районам и т.п.), или к различным организациям
(министерствам,
предприятиям, учреждениям), или при
сравнении рядов разного
содержания, но характеризующих один и
тот же объект. Например,
сравнение рядов динамики, характеризующих
производство важнейших
видов продукции в Российской Федерации
и других странах.
Сравнение
интенсивности изменений уровней рядов
во времени возможно
с помощью коэффициентов
опережения (отставания),
представляющих
собой отношение базисных темпов роста
(или прироста) двух
рядов динамики за одинаковые отрезки
времени:


где
‑базисные
темпы роста и прироста первого и второго
рядов динамики (соответственно).
Коэффициенты
опережения (отставания) могут быть
исчислены на основе
сравнения средних темпов роста (или
прироста) двух динамических
рядов за одинаковый период времени:

где
‑средние
темпы роста первого и второго рядов
динамики
соответственно; n– число лет в периоде.
Коэффициент
опережения (отставания) показывает, во
сколько раз быстрее
растет (отстает) уровень одного ряда
динамики по сравнению с другим. При этом
сравнении темпы должны характеризовать
тенденцию
одного направления.
Статистика
населения
-
Понятие
статистики населения, ее объект
предмет изучения -
Население как
объект исследования
1. Статистика
населения —
отрасль статистической науки, изучающая
население и процессы, связанные с его
динамикой, с
количественной
стороны в конкретных условиях общественного
развития и
разрабатывающая
методы
статистического учета и
анализа
демографических
явлений и процессов.
Объект
изучения
–
население в целом, отдельные группы
населения (трудоспособные, инвалиды,
мужчины, женщины и др.), молодые
семьи, родившиеся (умершие) за определенный
промежуток времени.
Предмет
статистики населения –
население и закономерности его развития.
Основные
задачи статистики населения:
-
определение
численности населения; -
анализ размещения
населения по территории страны; -
характеристика
состава населения; -
изучение процессов
воспроизводства населения; -
определение
перспективной численности и состава
населения.
Единица
наблюдения – отдельный
человек как индивидуум, семья,
домохозяйство,
населенный пункт.
При
этом источниками информации являются:
текущий учет; единовременный
учет (микропереписи; выборочные переписи;
сплошные переписи).
2. Население
– совокупность
людей, проживающих в пределах
определенной
территории:
-
части страны;
-
всей страны;
-
группы стран;
-
всего земного
шара.
Также
это социальная
категория, т.е.
совокупность лиц, проживающих
на определенной территории, и одновременно
экономическая
категория, т.
е. совокупность участников процесса
производства
и потребителей его результатов.
Различаются
следующие группировки
населения:
-
п
о
полу; -
национальному
составу; -
возрасту;
-
уровню
образования; -
размещению;
-
доходу;
-
семейному положению.
Рис. Возрастно-половая
пирамида населения РФ на 01.01.1998
Соседние файлы в папке Статистика
- #
- #
- #
Показатели ряда динамики
Примеры решения задач
Задача 1
По АО
«Керамик» имеются данные о производстве кирпича за год. Рассчитайте все
недостающие в таблице уровни ряда и цепные показатели анализа динамики.
Рассчитайте средний уровень ряда, средние абсолютный прирост и темп роста.
| Месяцы |
Произведено кирпича, тыс.р. |
Цепные показатели | |||
| абсолютный | темп роста, % | темп прироста, % |
абсолютное значение 1% прироста |
||
| Январь | 450 | ||||
| Февраль | 100 | ||||
| Март | 80 | ||||
| Апрель | -30 | ||||
| Май | 250 | ||||
| Июнь | -30 | ||||
| Июль | |||||
| Август | 300 | 5,0 | |||
| Сентябрь | 150 | ||||
| Октябрь | 80 | ||||
| Ноябрь | -60 | ||||
| Декабрь | 300 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Формулы цепных показателей динамики
Абсолютный цепной прирост можно
найти по формуле:
-уровень ряда;
-предыдущий
уровень ряда
Цепной темп роста:
Темп прироста:
Абсолютное
содержание 1% прироста:
Расчет недостающих уровней ряда динамики
Исходя из формул, заполним
недостающие показатели:
Февраль:
Март:
Апрель:
Май:
Июнь:
Июль:
Август:
Сентябрь:
Октябрь:
Ноябрь:
Декабрь:
Вычисление цепных показателей динамики
|
Абсолютные приросты цепные: |
Темпы роста цепные: |
|
Темпы прироста цепные: |
Абсолютное содержание 1% прироста: |
Показатели динамики производства кирпича
| Месяцы |
Произведено кирпича, тыс.р. |
Цепные показатели |
|||
| абсолютный |
темп роста, % |
темп прироста, % |
абсолютное значение 1% прироста |
||
| Январь | 450 | —- | 100 | —- | —– |
| Февраль | 900 | 450 | 200 | 100 | 4.5 |
| Март | 720 | -180 | 80.0 | -20.0 | 9,0 |
| Апрель | 690 | -30 | 95.8 | -4.2 | 7.2 |
| Май | 1725 | 1035 | 250.0 | 150.0 | 6.9 |
| Июнь | 1208 | -517 | 70.0 | -30.0 | 17.25 |
| Июль | 500 | -708 | 41.4 | -58.6 | 12.08 |
| Август | 800 | 300 | 160.0 | 60.0 | 5,0 |
| Сентябрь | 1200 | 400 | 150.0 | 50.0 | 8,0 |
| Октябрь | 2160 | 960 | 180.0 | 80.0 | 12,0 |
| Ноябрь | 2100 | -60 | 97.2 | -2.8 | 21.6 |
| Декабрь | 6300 | 4200 | 300 | 200 | 21,0 |
Расчет средних уровней ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Вывод к задаче
Среднемесячный
показатель производства составил 1562,8 тыс.р. В среднем за месяц показатель
увеличивался на 531,8 тыс.р. или на 27,1% в относительном выражении.
Задача 2
Для
изучения динамики товаропотока рассчитайте:
- Абсолютные и относительные показатели динамики по годам периода (абсолютные
приросты – базисные и цепные; темпы роста – базисные и цепные). - Динамические средние за период в целом – среднегодовой уровень ряда,
среднегодовой абсолютный прирост, среднегодовой темп роста. Объясните их смысл. - Выполните прогнозы уровня ряда на следующий год, используя среднегодовой
абсолютный прирост и среднегодовой темп роста. Сделайте выводы о развитии
изучаемого процесса. - Постройте график динамики изучаемого процесса.
Динамика
экспорта РФ в Португалию, млрд. долл. США
| Годы | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Экспорт | 0.62 | 1.14 | 1.38 | 1.25 | 0.21 | 0.13 | 0.20 |
Решение
1)
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики экспорта 2004-2010 гг.
| Годы |
Экспорт, млрд.долл |
Абсолютные приросты, млрд.долл |
Темпы роста, % |
Темпы прироста, % |
|||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2004 | 0.62 | —– | —– | 100.0 | 100.0 | —– | —– |
| 2005 | 1.14 | 0.52 | 0.52 | 183.9 | 183.9 | 83.9 | 83.9 |
| 2006 | 1.38 | 0.24 | 0.76 | 121.1 | 222.6 | 21.1 | 122.6 |
| 2007 | 1.25 | -0.13 | 0.63 | 90.6 | 201.6 | -9.4 | 101.6 |
| 2008 | 0.21 | -1.04 | -0.41 | 16.8 | 33.9 | -83.2 | -66.1 |
| 2009 | 0.13 | -0.08 | -0.49 | 61.9 | 21.0 | -38.1 | -79.0 |
| 2010 | 0.20 | 0.07 | -0.42 | 153.8 | 32.3 | 53.8 | -67.7 |
2)
Средний уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Таким
образом в среднем за исследуемый период экспорт
составлял 0,704 млрд. долл. в год. В среднем показатель уменьшался на 0,07 млрд.долл. в год или на 17,2% в
относительном выражении.
3)
Прогноз на 2011 год с помощью среднего абсолютного прироста:
Прогноз
на 2011 год с помощью среднегодового темпа роста:
На
2011 год показатель, прогнозируемый с помощью среднего
абсолютного прироста составил 0,13 млрд. долл., а с помощью
среднегодового темпа роста – 0,166 млрд. долл.
4)
График динамики экспорта 2004-2010 гг.
Средние показатели динамики: уровень ряда, абсолютный прирост, темп роста
Средний уровень ряда в статистике
Средний уровень ряда определяет обобщенную величину абсолютных уровней. Он определяется по средней, исчисленной из значений, меняющихся во времени. Методы расчета среднего уровня интервального и моментного рядов динамики разные.
Средний уровень из абсолютных уровней для интервальных рядов динамики рассчитывается по формуле средней арифметической:
1. При равных интервалах используют среднюю арифметическую простую:
где у — абсолютные уровни ряда;
n — число уровней ряда.
2. При неравных интервалах используют среднюю арифметическую взвешенную:
где у1,…,уn — уровни ряда динамики;
t1,… tn — веса, длительность интервалов времени.
Средний уровень моментного ряда динамики рассчитывается по формуле:
1. С равностоящими уровнями рассчитывается по формуле средней хронологической моментного ряда:
где у1,…,уn — уровни периода, за который делается расчет;
n — число уровней;
n-1 — длительность периода времени.
2. С неравностоящими уровнями рассчитывается по формуле средней хронологической взвешенной:
где у1,…,уn — уровни рядов динамики;
t — интервал времени между смежными уровнями
Средний абсолютный прирост в задачах статистики
Средний абсолютный прирост определяется как среднее из абсолютных приростов за равные промежутки времени одного периода. Он рассчитывается по формулам:
1. По цепным данным об абсолютных приростах за ряд лет рассчитывают средний абсолютный прирост как среднюю арифметическую простую:
где n — число степенных абсолютных приростов в исследуемом периоде.
2. Средний абсолютный прирост рассчитывают через базисный абсолютный прирост в случае равных интервалов
где m — число уровней ряда динамики в исследуемом периоде, включая базисный.
Средний темп роста
Средний темп роста есть свободная обобщающая характеристика интенсивности изменения уровней ряда динамики и показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.
В качестве основы и критерия правильности вычисления среднего темпа роста (снижения) применяется обобщающий показатель, который рассчитывается как произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Если значение признака образуется как произведение отдельных вариантов, то используют среднюю геометрическую.
Так как средний темп роста представляет собой средний коэффициент роста, выражен в процентах, то для равностоящих рядов динамики расчеты по средней геометрической сводятся к вычислению средних коэффициентов роста из цепных по «цепному способу»:
где n — число цепных коэффициентов роста;
Кц — цепные коэффициенты роста;
Кб — базисный коэффициент роста за весь период.
Определение среднего коэффициента роста может быть упрощено, если будут ясны уровни динамического ряда. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляют базисный коэффициент роста.
Формула для определения среднего коэффициента роста для равностоящих рядов динамики по «базисному способу» будет такая:
Средний темп прироста
Средние темпы прироста рассчитываются на основе средних темпов роста (Тр) вычитанием из последних 100%:
Для того чтобы определить средний коэффициент прироста (Кпр), нужно из значений коэффициентов роста (Кр) вычесть единицу.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
Пример решения задачи. Ряд динамики
Условие задачи
Определить
вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные
абсолютные приросты, темпы
роста, темпы прироста, средний уровень ряда, средний темп роста, средний
темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По
расчетам сделать выводы. Графически изобразить полученный ряд динамики.
| Годы |
Объем производства, млн.р. |
| 2011 | 12 |
| 2012 | 10 |
| 2013 | 11 |
| 2014 | 10 |
| 2015 | 9 |
Решение задачи
Данный
ряд динамики – интервальный, так как значение показателя заданы за определенный
интервал времени.
Определяем цепные и базисные показатели ряда динамики
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики объема производства 2011-2015 гг
| Годы |
Объем производства, млн.р. |
Абсолютные приросты, млн.р. | Темпы роста, % | Темпы прироста, % | |||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2011 | 12 | —– | —– | 100.0 | 100.0 | —– | —– |
| 2012 | 10 | -2 | -2 | 83.3 | 83.3 | -16.7 | -16.7 |
| 2013 | 11 | 1 | -1 | 110.0 | 91.7 | 10.0 | -8.3 |
| 2014 | 10 | -1 | -2 | 90.9 | 83.3 | -9.1 | -16.7 |
| 2015 | 9 | -1 | -3 | 90.0 | 75.0 | -10.0 | -25.0 |
Определяем средние показатели ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Строим график
График динамики объема производства 2011-2015 гг
Таким образом на протяжении всего исследуемого
периода за исключением 2013 года объем производства продукции на предприятиях
снижался. В среднем предприятия производили продукции на 10,4 млн.р. в год. В
среднем показатель снижался на 0,75 млн.р. в год или на 6,9% в относительном
выражении.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
 о
о