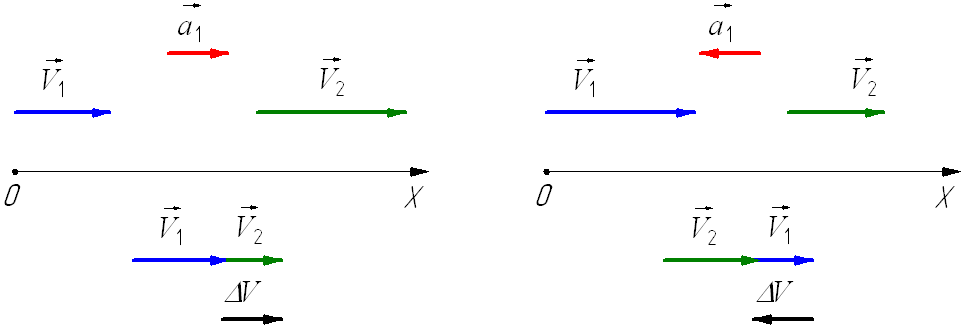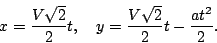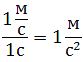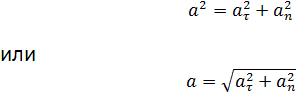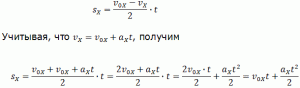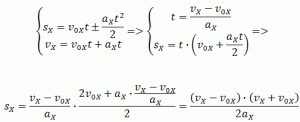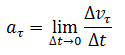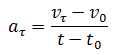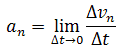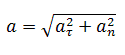Коллоквиум.
1. Механическое движение. Относительность
механического движения.
Механическое движение – это изменение
положения тела в пространстве относительно
других тел.
Относительность механического движения
Все тела во Вселенной движутся, поэтому
не существует тел, которые находятся в
абсолютном покое. По той же причине
определить движется тело или нет, можно
только относительно какого-либо другого
тела.
Например, автомобиль движется по дороге.
Дорога находится на планете Земля.
Дорога неподвижна. Поэтому можно измерить
скорость автомобиля относительно
неподвижной дороги. Но дорога неподвижна
относительно Земли. Однако сама Земля
вращается вокруг Солнца. Следовательно,
дорога вместе с автомобилем также
вращается вокруг Солнца. Следовательно,
автомобиль совершает не только
поступательное движение, но и вращательное
(относительно Солнца). А вот относительно
Земли автомобиль совершает только
поступательное движение. В этом
проявляется относительность механического
движения.
Относительность механического движения
– это зависимость траектории движения
тела, пройденного пути, перемещения и
скорости от выбора системы отсчёта.
2. Перемещение и скорость.
Перемещение
– это вектор, соединяющий начальное и
конечное положение точки. Направление
и величина перемещения определяются
отрезком прямой между начальной и
конечной точками движения.
Скорость.
Механическое
движение характеризуется еще и тем,
насколько быстро движется точка (тело).
Эта характеристика называется скорость
движения.
Скорость – величина векторная. Для того,
чтобы полностью задать ее, надо задать
собственно величину скорости и
направление, вдоль которого она измерена.
Обычно рассматривается скорость тела
вдоль траектории его движения. Тогда
величина скорости определяется как
путь, пройденный в единицу времени.
Иначе говоря, для того, чтобы найти
скорость вдоль траектории движения
надо путь разделить на время, за которое
он был пройден.
Формулы
для решения:
Пусть
v
–
скорость, s
–
путь, t
– время. Скорость
измеряется вдоль траектории движения.
Тогда:
Перемещение
определяется как геометрическая сумма
отрезков пути. Для простейшего случая,
когда один участок пути направлен
перпендикулярно другому решается
прямоугольный треугольник:
3. Виды движения. Ускорение.
В современной механике движение тела
подразделяется на виды, и существует
следующая классификация видов движения
тела:
1. Поступательное движение,
при котором любая прямая линия, связанная
с телом, остается при движении параллельной
самой себе.
2. Вращательное движение
или вращение тела вокруг своей оси,
считающейся неподвижной.
3. Сложное
движение тела, состоящее из
поступательного и вращательного
движений.
Ускорение – это величина,
которая характеризует быстроту изменения
скорости.
Среднее ускорение
Среднее
ускорение> – это отношение
изменения скорости к промежутку времени,
за который это изменении произошло.
Определить среднее ускорение можно
формулой:
где
–
вектор ускорения.
Направление
вектора ускорения совпадает с направлением
изменения скорости Δ
=
–
0
(здесь
0
– это начальная скорость, то есть
скорость, с которой тело начало
ускоряться).
В
момент времени t1 (см. рис 1.8) тело имеет
скорость
0.
В момент времени t2 тело имеет скорость
.
Согласно правилу вычитания векторов
найдём вектор изменения скорости Δ
=
–
0.
Тогда определить ускорение можно так:
Рис.
1.8. Среднее ускорение.
В
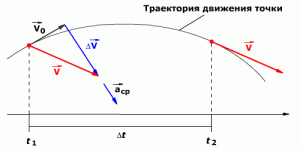
СИ единица ускорения – это 1
метр в секунду за секунду (или метр на
секунду в квадрате), то есть
Метр
на секунду в квадрате равен ускорению
прямолинейно движущейся точки, при
котором за одну секунду скорость этой
точки увеличивается на 1 м/с. Иными
словами, ускорение определяет, насколько
изменяется скорость тела за одну секунду.
Например, если ускорение равно 5 м/с2,
то это означает, что скорость тела каждую
секунду увеличивается на 5 м/с.
Мгновенное ускорение
Мгновенное
ускорение тела (материальной точки)
в данный момент времени – это физическая
величина, равная пределу, к которому
стремится среднее ускорение при
стремлении промежутка времени к нулю.
Иными словами – это ускорение, которое
развивает тело за очень короткий отрезок
времени:
Направление
ускорения также совпадает с направлением
изменения скорости Δ
при очень малых значениях промежутка
времени, за который происходит изменение
скорости. Вектор ускорения может быть
задан проекциями на соответствующие
оси координат в данной системе отсчёта
(проекциями аХ, aY, aZ).
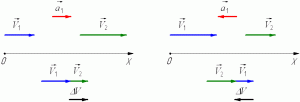
При
ускоренном прямолинейном движении
скорость тела возрастает по модулю, то
есть
v2
> v1
а направление вектора ускорения совпадает
с вектором скорости
2.
Если
скорость тела по модулю уменьшается,
то есть
v2
< v1
то направление вектора ускорения
противоположно направлению вектора
скорости
2.
Иначе говоря, в данном случае происходит
замедление движения, при этом
ускорение будет отрицательным (а < 0).
На рис. 1.9 показано направление векторов
ускорения при прямолинейном движении
тела для случая ускорения и замедления.
Рис.
1.9. Мгновенное ускорение.
При
движении по криволинейной траектории
изменяется не только модуль скорости,
но и её направление. В этом случае вектор
ускорение представляют в виде двух
составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное
(касательное) ускорение – это
составляющая вектора ускорения,
направленная вдоль касательной к
траектории в данной точке траектории
движения. Тангенциальное ускорение
характеризует изменение скорости по
модулю при криволинейном движении.
Рис.
1.10. Тангенциальное ускорение.
Направление
вектора тангенциального ускорения
τ
(см. рис. 1.10) совпадает с направлением
линейной скорости или противоположно
ему. То есть вектор тангенциального
ускорения лежит на одной оси с касательной
окружности, которая является траекторией
движения тела.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение
Средним ускорением $leftlangle arightrangle $ называется отношение приращения скорости $triangle v=vleft(t+triangle tright)-vleft(tright) $ к длительности промежутка времени $triangle t$, в течение которого оно произошло: $leftlangle arightrangle =frac{triangle v}{triangle t}$
Мгновенным ускорением $overrightarrow{a}$ (или просто ускорением) тела называют предел отношения малого изменения скорости $triangle overrightarrow{v}$ малому
промежутку времени $Delta $t, в течение которого происходило изменение скорости:
[overrightarrow{a}={mathop{lim}_{triangle tto 0} frac{triangle overrightarrow{v}}{triangle t} }=frac{d}{dt}left(frac{doverrightarrow{r}}{dt}right)=
frac{d^2r}{dt^2}=ddot{r}]
В декартовых координатах это уравнение эквивалентно системе трёх уравнений:
[left{ begin{array}{c}
a_x=dot{v_x}=ddot{x} \
a_y=dot{v_y}=ddot{y} \
a_z=dot{v_z}=ddot{z} end{array}
right.]
Модуль вектора ускорения
[a=sqrt{a^2_x+a^2_y+a^2_z}=sqrt{{dot{v}}^2+{dot{v}}^2_y+{dot{v}}^2_z}=sqrt{{ddot{x}}^2+{ddot{y}}^2+{ddot{z}}^2}]
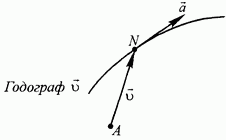
Конец вектора скорости $overrightarrow{v}$ при движении материальной точки описывает кривую, называемую годографом скорости (рис.2).
Рисунок 1. Годограф скорости
Ускорение в каждой точке годографа скорости направлено по касательной к годографу в этой точке. Следовательно, направление вектора ускорения $overrightarrow{a}$ в
случае криволинейного движения не совпадает с направлением вектора скорости $overrightarrow{v}$.
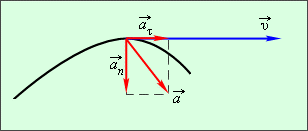
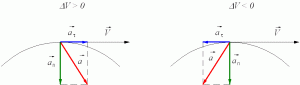
Вектор мгновенного ускорения $overrightarrow{a}$ можно представить как векторную сумму двух векторов, один из которых направлен по касательной к траектории в данной её точке, а другой — перпендикулярен ему и направлен к центру кривизны траектории в этой точке.
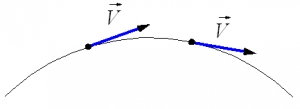
Рисунок 2. Касательное и нормальное ускорения
Эти составляющие вектора ускорения $overrightarrow{a}$ называют касательным (тангенциальным) $overrightarrow{a_{tau }}={mathop{lim}_{tto 0} frac{triangle
overrightarrow{v_{tau }}}{triangle t} }$ и нормальным $overrightarrow{a_n}={mathop{lim}_{tto 0} frac{triangle overrightarrow{v_n}}{triangle t} }$
ускорениями:
[overrightarrow{a}=overrightarrow{a_{tau }}+overrightarrow{a_n}]
Касательное ускорение $overrightarrow{a_{tau }}$ указывает, насколько быстро изменяется скорость тела по модулю, а нормальное ускорение $overrightarrow{a_n}$
указывает, насколько быстро скорость тела изменяется по направлению.
Из рис. 2 видно, что модуль полного ускорения $a=sqrt{a^2_{tau }+a^2_n}$
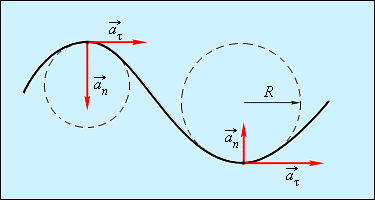
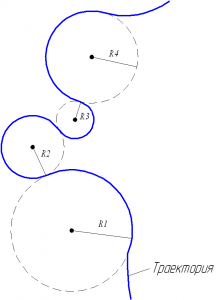
Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).
Рисунок 3. Движение по дугам окружностей
Нормальное ускорение $overrightarrow{a_n}$ зависит от модуля скорости $upsilon $ и от радиуса R окружности, по дуге которой тело движется в данный момент: $a_n=
frac{v^2}{R}$. Вектор $overrightarrow{a_n}$ всегда направлен к центру окружности.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Задача 1
Определить скорость, ускорение и координату x точки в момент времени, равный 10 c, если уравнение движения материальной точки имеет вид $x=A+Bt+Ct^2$ , где
А= 8 м, В = 5 м/c, С = 2 м/c2.
Дано: $x=A+Bt+Ct^2$;
А = 8 м; В = 5 м/с; С = 2 м/с2; t = 10 c. Найти: v — ?, a — ?, x — ?
Решение:
Определяем координату x в заданный момент времени, подставив в уравнение движения материальной точки значения коэффициентов:
[x=A+Bt+Ct^2=8+3times 10+2times {10}^2=238 м ]
Определяем мгновенную скорость v материальной точки, как первую производную координаты по времени, и находим скорость материальной точки в заданный момент времени:
$v=dot{x}=B+2Ct=5+2times 2times 10=45 м/с$
Определяем ускорение a материальной точки, как первую производную от скорости по времени и находим ускорение материальной точки в заданный момент времени:
[a=dot{v}=2C=2times 10=20 м/с^2]
Ответ: В момент времени t = 10 c координата материальной точки х = 238 м, скорость материальной точки v = $45 м/с$ , ускорение материальной точки а = $20 м/с^2$
«Ускорение» 👇
Задача 2
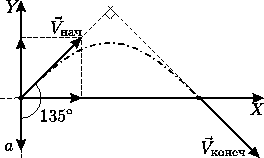
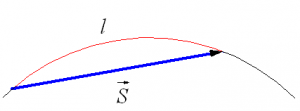
Космический корабль движется в открытом космосе со скоростью $overrightarrow{V}$. Требуется изменить направление скорости на 90 градусов, оставив величину скорости неизменной. Найдите минимальное время, необходимое для такого манёвра, если двигатель может сообщать кораблю в любом направлении ускорение, не превышающее $a$. По какой траектории будет при этом двигаться корабль?
Решение:
Перейдём в инерциальную систему отсчёта, движущуюся с постоянной скоростью $overrightarrow{V}$. Так как во всех инерциальных системах отсчёта при одинаковых начальных условиях все
механические явления протекают одинаково (принцип относительности Галилея), то ограничение, наложенное в условии задачи на ускорение корабля, не изменится. В новой системе отсчёта начальная скорость космического корабля равна нулю, а конечная скорость по модулю равна $vsqrt{2}$ и направлена под углом к первоначальному
направлению движения.
Теперь ясно, что для совершения манёвра нужно включить двигатели так, чтобы при развороте корабля его ускорение было всё время направлено в сторону конечной скорости корабля, то есть под углом 45 градусов к первоначальному направлению движения. Тогда минимальное время манёвра будет равно $tau =frac{triangle v}{a}=frac{Vsqrt{2}}{a}$.
Выясним, по какой траектории будет двигаться корабль при манёвре. Для этого вернёмся в исходную систему отсчёта и направим координатную ось декартовой системы
координат в направлении, обратном ускорению, а ось $X$ — перпендикулярно к ней, так, как показано на рисунке. Тогда закон движения в проекциях на эти оси примет вид:
Выражая из первого уравнения время и подставляя его во второе, получим уравнение траектории корабля: $y=x-frac{ax^2}{V^2}$ , то есть корабль будет двигаться по
параболе, аналогично телу, брошенному по углом к горизонту.
Ответ: минимальное время, необходимое для манёвра $tau =frac{Vsqrt{2}}{a}$. Корабль в ходе манёвра будет двигаться по параболе.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
v2 > v1
а направление вектора ускорения совпадает с вектором скорости
Если скорость тела по модулю уменьшается, то есть
v2 < v1
то направление вектора ускорения противоположно направлению вектора скорости Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а < 0). На рис. 1.9 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
Квантовые постулаты Бора – это два основных допущения, введённые Н.Бором для объяснения устойчивости атома и спектральных закономерностей (в рамках модели атома Резерфорда).
Планетарная модель атома Резерфорда позволила объяснить результаты опытов по рассеянию α-частиц вещества, но она не способна объяснить факт существования атома и его устойчивость.
В соответствии с планетарной моделью электроны атома должны двигаться вокруг неподвижного ядра. Двигаясь вокруг ядра с центростремительным ускорением под действием силы притяжения к ядру, электрон должен, как и всякий ускоренно движущийся электрический заряд, излучать электромагнитные волны с частотой, равной частоте обращения электрона вокруг ядра.
Энергия электрона в атоме должна при этом непрерывно уменьшаться за счёт излучения. Сам электрон должен с каждым оборотом приближаться по спирали к ядру и упасть на него под действием электрической силы притяжения. При этом атом потеряет всю электронную оболочку, а также присущие ему физические и химические свойства. Кроме того, атом должен потерять спектр излучения частоты, то есть атом должен давать излучение с непрерывным (сплошным) спектром частот.
Эти результаты, полученные с помощью классической механики и электродинамики, находятся в резком противоречии с опытом, который показывает, что
- Атомы являются весьма устойчивыми системами и в невозбуждённом состоянии могут существовать неограниченно долго, не излучая при этом электромагнитные волны
- Спектр излучения атома является линейчатым (дискретным) – образованным из отдельных линий (от латинского discretus – прерывистый, состоящий из отдельных значений)
Всё это свидетельствует о том, что законы классический физики применить к электронам в атомах нельзя, поэтому необходимы новые представления о механизме излучения и поглощения атомами электромагнитных волн. В основе современной теории атома лежитквантовая механика – теория, устанавливающая способ описания и законы движения микрочастиц (элементарных частиц, атомов, молекул, атомных ядер) и их систем (например, кристаллов), а также связь величин, которые характеризуют частицы и системы, с физическими величинами, измеряемыми опытным путём.
В 1913 году датский физик Нильс Бор (1885 – 1962) ввёл идеи квантовой теории в ядерную модель атома Резерфорда и разработал теорию атома водорода, которая подтвердилась всеми известными тогда опытами. Бор сформулировал в виде постулатов основные положения новой теории, которые налагали лишь некоторые ограничения на допускаемые классической физикой движения. Однако последовательной теории атома Бор не дал. Впоследствии теория Бора была включена как частный случай в квантовую механику. В основе теории Бора лежат два постулата.
Первый постулат Бора: постулат стационарных состояний
Атомная система может находиться только в особых стационарных, или квантовых, состояниях, каждому из которых соответствует определённая энергия En. В стационарном состоянии атом не излучает.
Второй постулат Бора: правило частотe
Излучение света происходит при переходе атома из стационарного состояния с большей энергией Ek в стационарное состояние с меньшей энергией En. Энергия излученного фотона равна разности энергий стационарных состояний:
hvkn = Ek — En
Частота излучения равна:
vkn = (Ek — En) / h = (Ek / h) — (En / h)
Или, длина волны излучения λ равна:
1 / λkn = (1 / hc) (Ek — En)
Где h – постоянная Планка, с – скорость света в вакууме.
Если Ek > En, то происходит излучение фотона, если Ek < En, то происходит поглощение фотона, при котором атом переходит из стационарного состояния с меньшей энергией в стационарное состояние с большей энергией. Таким образом, для каждого атома имеется ряд строго определённых дискретных значений энергии, которыми он может обладать. Физические величины, например энергия и импульс, которые могут принимать лишь дискретные (квантовые) значения, носят название квантованные физические величины (квантование физических величин). При этом энергетические уровни атома – это возможные значения энергии атома.
Правило квантования орбит позволяет определить радиусы стационарных орбит:
mvnrn = nh’
где n = 1, 2, 3…, m – масса электрона, rn – радиус n-ой орбиты, vn – скорость электрона на этой орбите.
Число n – положительное число, которое называется главное квантовое число.
Величина (mvn)rn – момент импульса электрона.
h’ – это величина, которая равна:
h’ = h/2π = 1,05445887•10-34 Дж•с
где h – постоянная Планка.
Главное квантовое число указывает номер орбиты, по которой может обращаться электрон.
Свои постулаты Н.Бор применил для построения теории простейшей атомной системы – атома водорода, состоящего из ядра – протона, и одного электрона. Эта теория также применима для водородоподобных ионов, то есть атомов с зарядом ядра Ze и потерявших все электроны, кроме одного (например, Li2+, Be3+ и т.п.). В предположении, что электрон движется по круговой орбите, постулаты Бора позволяют найти радиусы rn стационарных, возможных орбит электрона. На электрон действует кулоновская сила:
Fk = (1 / 4πε0) (ε2 / rn2)
Где е – модуль заряда электрона, равный заряду ядра, ε0 = 8,85418782 * 10-12 Ф/м – электрическая постоянная в единицах СИ.
Кулоновская сила сообщает электрону на орбите центростремительное ускорение:
aцс = (vn2) / rn
Согласно второму закону Ньютона:
Fk = maцс
Поэтому
(mvn2) / rn = e2 / (4πε0rn2)
Или
mvn2rn = e2 / (4πε0)
Используя правило квантования орбит mvnrn = nh’, можно получить выражения для возможных радиусов орбит. Исключая скорость vn из предыдущего выражения, получим:
rn = 4πε0n2h’ / me2 (так как h’ = h / 2π)
Таким образом, радиусы орбит электрона в атоме водорода прямо пропорциональны квадратам главного квантового числа n.
Наименьший радиус орбит при n = 1, то есть радиус первой орбиты в атоме водорода равен:
r1 = 4πε0h’ / me2 = 0,528 * 10-10 м = 0,528 Å
Радиус первой орбиты в атоме водорода носит название первый Боровский радиус и служит единицей длины в атомной физике.
Полная энергия Е электрона в атоме водорода, согласно механике Ньютона, равна сумме кинетической энергии Еk и потенциальной энергии П взаимодействия электрона с ядром:
E = Еk — П = (mvn2 / 2) — (e2 / 4πε0rn)
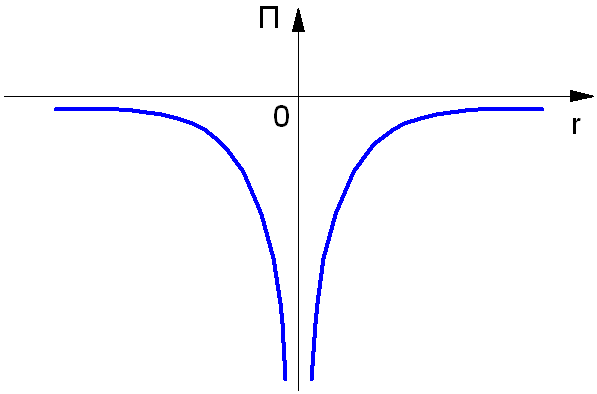
Потенциальная энергия электрона в атоме отрицательна:
П = — (e2 / 4πε0rn)
Так как нулевой уровень отсчёта берётся на бесконечности (рис. 1.3), а по мере приближения электрона к ядру его потенциальная энергия уменьшается. Взаимодействующие частицы – ядро и электрон – имеют заряды противоположных знаков.
Рис. 1.3. Потенциальная энергия электрона в атоме.
Подставляя значение скорости
vn2 = — e2 / 4πε0mrn
в выражение полной энергии, получим:
E = (m / 2) (e2 / 4πε0mrn) — (e2 / 4πε0rn)
Подставляя в эту формулу выражение для радиусов орбит, получим энергетические уровни электрона в атоме водорода (значения энергий стационарных состояний атома):
En = -(1 /(4πε0)2) me4 / 2h’2n2 = — (me4 / 8h2ε02) * (1 / n2), n = 1,2,3…
Энергия Еn электрона в атоме водорода зависит от главного квантового числа n, которое определяет энергетические уровни электрона в атоме водорода.
Основное энергетическое состояние атома (нормальное состояние атома) – это энергетический уровень при n = 1.
Значение энергии, соответствующее первому (низшему) энергетическому уровню в атоме водорода равно:
E1 = -(1 /(4πε0)2) me4 / 2h’2λ = -2,485 * 10-19 Дж = -13,53 эВ
В этом состоянии атом может находиться сколько угодно долго. Для того чтобы ионизировать атом водорода, ему нужно сообщить энергию 13,53 эВ, которая называется энергия ионизации.
Энергетические уровни при n > 1 – это возбуждённые энергетические состояния (возбуждённые состояния атома). Возбуждённое состояние атома является менее устойчивым, чем основное состояние. Время жизни атома в этом состоянии имеет порядок 10-8 секунд. За это время электрон успевает совершить около ста миллионов оборотов вокруг ядра.
При переходе электрона с удалённой от ядра стационарной k-орбиты на ближайшую n-ую орбиту атом излучает фотон, энергия которогоhvnk согласно второму постулату Бора определяется:
hvkn = Ek — En = -(1 / (4πε0)2) * (me4 / 2h’2) * [(1 / n2) — (1 / k2)] = (me4 / 8h2ε02) * [(1 / n2) — (1 / k2)]
Частота излучения атома водорода:
vkn = (1 / (4πε0)2) * (me4 / h’3) * [(1 / n2) — (1 / k2)] = R[(1 / n2) — (1 / k2)]
Где
R = (me4 / (4πε0)2) * 4πh’3) = (me4 / 8h3ε02) = 3,288 * 1015 c-1— постоянная Ридберга
Постоянная Ридберга определяется через постоянную Планка, массу и заряд электрона.
Длина волны излучения определяется соотношением:
1 / λnk = vnk / c = (me4 / 8ε02h3c) * [(1 / n2) — (1 / k2)] = Rc[(1 / n2) — (1 / k2)]
Где
Rc = R / c = 1,0974 * 107 м-1 — также постоянная Ридберга
с = 3*108 м/с – скорость света в вакууме.
Теоретическое значение R совпадает с экспериментальным значением, полученным из спектроскопических измерений.
Энергия обычно измеряется в электронвольтах (эВ). Электронвольт– это значение энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов в 1 В:
1 эВ = 1,6 * 10-19 Кл * 1В = 1,6 * 10-19 Дж
Равномерное прямолинейное движение – это частный случай неравномерного движения.
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
vcp = s / t
Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
Проекция вектора скорости на ось ОХ:
vx = x’
это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
vx = v0x ± axt
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
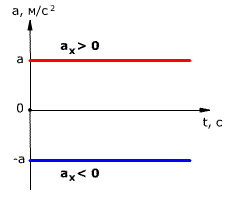
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
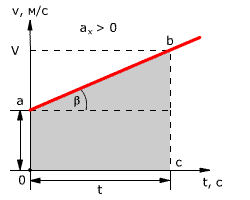
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
0a = v0 bc = v
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
Общая формула для определения проекции перемещения:
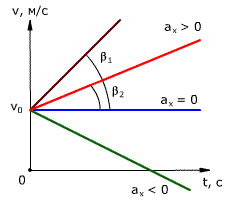
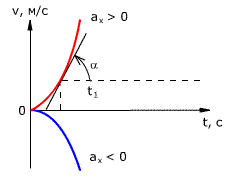
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При аx < 0 и х0 = 0 ветви параболы направлены вниз (рис. 1.18).
Свободное падение тел – это падение тел на Землю в вакууме при отсутствии помех. Движение тела под действием силы тяжести при отсутствии сопротивления воздуха можно считать свободным падением. Например, в свободном падении находится спортсмен, прыгающий в воду с вышки или мяч, выпущенный из руки.
В 1583 году итальянский учёный Галилео Галилей (1564-1642) установил, что при отсутствии сопротивления воздуха все тела, независимо от их массы, падают на землю с одинаковым ускорением g, которое направлено вертикально вниз. Это ускорение называется ускорение свободного падения. При свободном падении тела с небольшой высоты h от поверхности Земли (причём h намного меньше радиуса Земли RЗ, где радиус Земли RЗ ~ 6000 км) сила притяжения остаётся практически постоянной, поэтому ускорение свободного падения также остаётся постоянным.
Это заключение подтверждает опыт с падением тел в стеклянной трубке, из которой выкачан воздух (рис. 1.24). Кусочек свинца, лёгкое пёрышко и дробинка достигают дна трубки одновременно. Следовательно, они падают с одинаковым ускорением.
Свободное падение можно рассматривать как частный случай равноускоренного движения. Ускорение свободного падения зависит от высоты над уровнем моря и от географической широты места. Оно изменяется примерно от 9,83 м/с2 на полюсе и до 9,78 м/с2 на экваторе. На широте Москвы ускорение свободного падения принимается равным g = 9,8 м/с2. Поэтому в большинстве случаев при решении задач по физике ускорение свободного падения принимается равным 9,8 м/с2.
Различие в значении ускорения объясняется суточным вращением Земли и формой Земли – Земля сплюснута у полюсов, поэтому полюсный радиус Земли меньше экваториального радиуса.
Рис. 1.24. Свободное падение тел.
Зависимость ускорения свободного падения от высоты над уровнем моря можно получить, применяя второй закон Ньютона и закон всемирного тяготения. Модуль ускорения свободного падения равен:
g = G(M /(R + h)2)
где G – гравитационная постоянная (или постоянная всемирного тяготения), G = (6,673 ± 0,003)*10-11 н*м2 / кг2 М – масса Земли, M = 5,9736*1024 кг R – радиус Земли, средний радиус Земли RЗ.СР = 6371 км, h – высота тела над уровнем моря (над поверхностью Земли).
Из этого уравнения видно, что при подъёме тела ускорение свободного падения уменьшается. Это становится заметным при подъёме на высоту более 300 км.
В некоторых районах земного шара ускорение свободного падения может отличаться от значения ускорения на данной широте. Такие отклонения наблюдаются в местах, где имеются залежи полезных ископаемых.
Движение тел по вертикали (вверх или вниз) вблизи поверхности Земли без учёта сопротивления воздуха является прямолинейным равноускоренным движением. При описании такого движения выбирают координатную ось OY, направленную вверх или вниз. Независимо от направления оси OY вектор ускорения свободного падения направлен вертикально вниз.
Формулы для вычисления координат (или высот) и скоростей примут следующий вид.
Скорость тела в любой момент времени
vy = ± voy ± gyt
Перемещение тела
sy = ± voyt ± (gyt2) / 2
Координаты тела (высота тела)
y = h = h0 ± voyt ± (gyt2) / 2
Скорость тела в любой точке пути
vy2 = voy2 + 2gy(h — h0)
Если ось OY направлена вниз, то проекция ускорения свободного падения gy на эту ось положительна. Если ось OY направлена вверх, то проекция gy отрицательна. Например, мяч, подброшенный вертикально вверх, до верхней точки подъёма движется равнозамедленно, а его движение вниз будет равноускоренным.
Проекции начальной voy и конечной vy скоростей положительны, если направление скоростей совпадает с направлением оси OY, и отрицательны, если направления оси OY и скоростей противоположны.
Равномерное движение по окружности – это простейший пример криволинейного движения. Например, по окружности движется конец стрелки часов по циферблату. Скорость движения тела по окружности носит название линейная скорость.
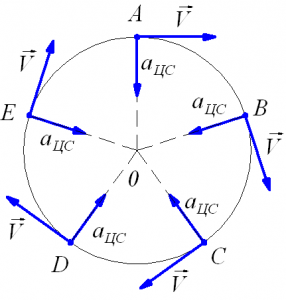
При равномерном движении тела по окружности модуль скорости тела с течением времени не изменяется, то есть v = const, а изменяется только направление вектора скорости Тангенциальное ускорение в этом случае отсутствует (ar = 0), а изменение вектора скорости по направлению характеризуется величиной, которая называется центростремительное ускорение (нормальное ускорение) an или аЦС. В каждой точке траектории вектор центростремительного ускорения направлен к центру окружности по радиусу.
Модуль центростремительного ускорения равен
aЦС=v2 / R
Где v – линейная скорость, R – радиус окружности
Рис. 1.22. Движение тела по окружности.
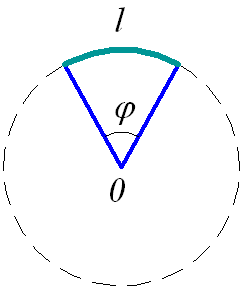
Когда описывается движение тела по окружности, используется угол поворота радиуса – угол φ, на который за время t поворачивается радиус, проведённый из центра окружности до точки, в которой в этот момент находится движущееся тело. Угол поворота измеряется в радианах. Радиан равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу окружности (рис. 1.23). То есть если l = R, то
1 радиан= l / R
Так как длина окружности равна
l = 2πR
то
360о = 2πR / R = 2π рад.
Следовательно
1 рад. = 57,2958о = 57о18’
Угловая скорость равномерного движения тела по окружности – это величина ω, равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершён этот поворот:
ω = φ / t
Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени t:
v= l / t
Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина l дуги окружности, пройденной точкой, связана с углом поворота φ выражением
l = Rφ
где R – радиус окружности.
Тогда в случае равномерного движения точки линейная и угловая скорости связаны соотношением:
v = l / t = Rφ / t = Rω или v = Rω
Рис. 1.23. Радиан.
Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности.Частота обращения – это величина, обратная периоду обращения – число оборотов в единицу времени (в секунду). Частота обращения обозначается буквой n.
n = 1 / T
За один период угол поворота φ точки равен 2π рад, поэтому 2π = ωT, откуда
T = 2π / ω
То есть угловая скорость равна
ω = 2π / T = 2πn
Центростремительное ускорение можно выразить через период Т и частоту обращения n:
aЦС = (4π2R) / T2 = 4π2Rn2
Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению.
Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).
Рис. 1.19. Траектория и вектор перемещения при криволинейном движении.
При движении по криволинейной траектории вектор перемещения направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).
Рис. 1.20. Мгновенная скорость при криволинейном движении.
Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение:
или
Где vτ, v0 – величины скоростей в момент времени t0 + Δt и t0соответственно.
Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.
Нормальное ускорение — это изменение скорости по направлению за единицу времени:
Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.
Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности.
Полное ускорение при равнопеременном криволинейном движении тела равно:
Движение тела по криволинейной траектории можно приближённо представить как движение по дугам некоторых окружностей (рис. 1.21).
Рис. 1.21. Движение тела при криволинейном движении.
Механическое движение – это изменение положения тела в пространстве относительно других тел.
Например, автомобиль движется по дороге. В автомобиле находятся люди. Люди движутся вместе с автомобилем по дороге. То есть люди перемещаются в пространстве относительно дороги. Но относительно самого автомобиля люди не движутся. В этом проявляется относительность механического движения. Далее кратко рассмотрим основные виды механического движения.
Поступательное движение – это движение тела, при котором все его точки движутся одинаково.
Например, всё тот же автомобиль совершает по дороге поступательное движение. Точнее, поступательное движение совершает только кузов автомобиля, в то время как его колёса совершают вращательное движение.
Вращательное движение – это движение тела вокруг некоторой оси. При таком движении все точки тела совершают движение по окружностям, центром которых является эта ось.
Упоминавшиеся нами колёса совершают вращательное движение вокруг своих осей, и в то же время колёса совершают поступательное движение вместе с кузовом автомобиля. То есть относительно оси колесо совершает вращательное движение, а относительно дороги – поступательное.
Колебательное движение – это периодическое движение, которое совершается поочерёдно в двух противоположных направлениях.
Например, колебательное движение совершает маятник в часах.
Поступательное и вращательное движения – самые простые виды механического движения.
Относительность механического движения
Все тела во Вселенной движутся, поэтому не существует тел, которые находятся в абсолютном покое. По той же причине определить движется тело или нет, можно только относительно какого-либо другого тела.
Например, автомобиль движется по дороге. Дорога находится на планете Земля. Дорога неподвижна. Поэтому можно измерить скорость автомобиля относительно неподвижной дороги. Но дорога неподвижна относительно Земли. Однако сама Земля вращается вокруг Солнца. Следовательно, дорога вместе с автомобилем также вращается вокруг Солнца. Следовательно, автомобиль совершает не только поступательное движение, но и вращательное (относительно Солнца). А вот относительно Земли автомобиль совершает только поступательное движение. В этом проявляется относительность механического движения.
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.
Материальная точка
Во многих случаях размером тела можно пренебречь, так как размеры этого тела малы по сравнению с расстоянием, которое походит это тело, или по сравнению с расстоянием между этим телом и другими телами. Такое тело для упрощения расчетов условно можно считать материальной точкой, имеющей массу этого тела.
Материальная точка – это тело, размерами которого в данных условиях можно пренебречь.
Многократно упоминавшийся нами автомобиль можно принять за материальную точку относительно Земли. Но если человек перемещается внутри этого автомобиля, то пренебрегать размерами автомобиля уже нельзя.
Как правило, решая задачи по физике, рассматривают движение тела как движение материальной точки, и оперируют такими понятиями, как скорость материальной точки, ускорение материальной точки, импульс материальной точки, инерция материальной точки и т.п.
Система отсчёта
Материальная точка движется относительно других тел. Тело, по отношению к которому рассматривается данное механическое движение, называется телом отсчёта. Тело отсчёта выбирают произвольно в зависимости от решаемых задач.
С телом отсчёта связывается система координат, которая представляет из себя точку отсчёта (начало координат). Система координат имеет 1, 2 или 3 оси в зависимости от условий движения. Положение точки на линии (1 ось), плоскости (2 оси) или в пространстве (3 оси) определяют соответственно одной, двумя или тремя координатами. Для определения положения тела в пространстве в любой момент времени также необходимо задать начало отсчёта времени.
Система отсчёта – это система координат, тело отсчета, с которым связана система координат, и прибор для измерения времени. Относительно системы отсчёта и рассматривается движение тела. У одного и того же тела относительно разных тел отсчёта в разных системах координат могут быть совершенно различные координаты.
Траектория движения также зависит от выбора системы отсчёта.
Виды систем отсчёта могут быть различными, например, неподвижная система отсчёта, подвижная система отсчёта, инерциальная система отсчёта, неинерциальная система отсчёта.
Вектор – среднее ускорение
Cтраница 1
Вектор среднего ускорения направлен параллельно вектору изменения скорости и образует с касательной к траектории некоторый угол а. Легко заметить, что вектор среднего ускорения при прочих равных условиях зависит от кривизны траектории. Увеличив кривизну участка АгАг траектории ( рис. 1.105, б), оставив неизменными время А.
[1]
Вектор среднего ускорения равен изменению скорости, деленному на величину интервала времени, в течение которого произошло это изменение.
[2]
На рис. 95 штриховыми линиями показаны векторные диаграммы скорости по рис. 94, а сплошными линиями – составляющие вектора среднего ускорения Дср при криволинейном движении. Направление вектора йср т всегда совпадает с направлением Айт, а направление вектора аср.
[4]
Отсюда следует вывод, что представляя вектор изменения скорости Аи в виде двух составляющих Аут и АУ, мы одновременно представляем вектор среднего ускорения аср тоже в виде двух составляющих аср.
[6]
Построив годограф скорости CD ( рис. 225, б), отложим там же скорости v и иь приращение вектора скорости Аи, а также вектор среднего ускорения аср, направленный по хорде Л годографа скорости.
[7]
Вектор среднего ускорения направлен параллельно вектору изменения скорости и образует с касательной к траектории некоторый угол а. Легко заметить, что вектор среднего, ускорения при прочих равных условиях зависит от кривизны траектории.
[8]
Вектор среднего ускорения направлен параллельно вектору изменения скорости и образует с касательной к траектории некоторый угол а. Легко заметить, что вектор среднего ускорения при прочих равных условиях зависит от кривизны траектории. Увеличив кривизну участка АгАг траектории ( рис. 1.105, б), оставив неизменными время А.
[9]
Как видно из рисунка, вектор Ли направлен в сторону вогнутости траектории. Туда же будет направлен и вектор среднего ускорения аср.
[10]
Вектор среднего ускорения равен изменению скорости, деленному на величину интервала времени, в течение которого произошло это изменение. Вектор среднего ускорения конца стрелки равен 0 30: 150 02 см / с2 и направлен под углом 45 налево вниз.
[11]
Среднее ускорение ср точки за какой-либо промежуток времени зависит от этого промежутка. Если, выбрав какой-либо промежуток времени At, мы будем затем его уменьшать, то среднее ускорение точки аср Дг / А будет изменяться как по модулю, так и по направлению. Однако по мере приближения А / к нулю вектор среднего ускорения точки стремится к некоторому определенному пределу. Этот предел называется истинным ускорением точки в данный момент времени или, чаще, просто ускорением точки.
[12]
Автор: Рассмотрим равномерное движение тела по окружности. Там же даны соответствующие векторы скорости ( tTj и – v3); они одинаковы по модулю, но различны по направлению. Взяв отношение этого вектора к промежутку времени А / / 2 – /, получим согласно (1.5) вектор среднего ускорения за промежуток времени А.
[13]
Страницы:
1
Базовые понятия кинематики
Для применения теории кинематики необходимо понимать базовые определения. Ниже будут описаны основные
термины, используемые в кинематике.
Материальная точка
Материальная точка (М.Т.) – идеализированный объект, объём которого считается нулевым в условиях
рассматриваемой задачи, например:
-
Машина едет из Москвы в Санкт-Петербург — обозначаем машину
материальной точкой, поскольку её размеры не имеют значения для решения задач кинематики -
Луна вращается вокруг земли — обозначим луну и землю материальными точками, поскольку их
размеры не имеют значения для решения задач кинематики
Под материальной точкой можно воспринимать любой объект в рамках решения задачи по кинематике.
Движение
Если система координат, в которой рассматривается положение м.т., действительно неподвижна, то такое
движение м.т. называется абсолютным. Когда система координат подвижна, то движение м.т. называется относительным.
В реальности, в мире не существует неподвижных точек, следовательно, любое движение относительно,
поэтому при описании движения всегда необходимо указывать систему координат в которой ведётся расчёт.
Почему так важно указывать точку отсчёта? Представьте, что к вам на встречу идёт кот: если Вы
выберете в качестве точки отсчёта кота — Вы идёте к нему навстречу, в то время, как кот стоит на месте.
Точку отсчёта можно выбирать абсолютно любой, но от выбранной точки отсчёта зависит насколько сложными
будут уравнения движения и решение задачи.
Радиус-вектор
Поскольку мы имеем установленную систему координат, положение материальной точки в пространстве может быть
однозначно описано вектором r. Радиус-вектор – это вектор, проложенный из начала координат.
Для того, что бы описать движение материальной точки, необходимо установить связь между положением
материальной точки и временем, за которое положение изменилось. Если мы говорим о скорости, то нас
интересует зависимость положения от времени, а значит это будет функция. Математически, положение точки в
любой момент времени можно описать функцией радиус-вектора:
r = r (t)
Если вести расчёты общим уравнением, то нам придётся работать с комплексными уравнениями, включающими большое
количество переменных в высоких степенях, что бы упростить расчёты, мы можем разложить радиус-вектор на
компоненты, таким образом, мы получим параметрические уравнения, зависящие от времени. Суть уравнений –
проекции радиус-вектора на координатные оси, в зависимости от системы координат мы будем иметь различное
количество уравнений:
Для R1:
ri = ri(t)Для R2:
ri = ri(t)
rj = rj(t)Для R3:
ri = ri(t)
rj = rj(t)
rk = rk(t)
Количество уравнений не обязательно обозначает привычные нам одно-, двух-, трёх-остные декартовы системы
координат, это могут быть цилиндрические, сферические и другие системы координат.
Траектория
Траектория — кривая, представляющая множество точек по которой движется материальная точка. Любая геометрическая
фигура может являться траекторией.
Аналитическое выражение
Аналитически, геометрическое место точек (Г.М.Т.) траектории в трёхмерном пространстве может быть задано
пересечением двух плоскостей, уравнения плоскостей, соответственно, могут быть выражены в параметрических
зависимостях:
f1 (i, j, k) = 0 плоскость 1
f2 (i, j, k) = 0 плоскость 2
f1 = f2 уравнение траектории
Траектория обозначается буквой s. Рассматривая движения, мы задаём положение материальной точки на траектории
через зависимость от времени:
s = s (t)
Данная функция траектории позволяет нам найти длину пройденной траектории в любой момент времени в заданном
направлении. Формула длины кривой выбирается исходя из выбранной системы координат и решаемой задачи. В общем
случае, задача решается через интеграл:
l = t0t1∫ s(t) dt
Перемещение
Рассмотрим перемещение материальной точки из положения r0 в положение r1 за время Δt,
обозначим за Δi, Δj, Δk соответствующие перемещения по координатам i, j k, тогда изменение радиус-вектора будет:
Δr = Δi•i + Δj•j + Δk•k
Учитывая, что r1 = r0 + Δr, новые координаты будут соответственно:
i1 = i0 + Δi
j1 = j0 + Δj
k1 = k0 + Δk
Таким образом, вектор перемещения можно выразить через начальные и конечные координаты движения, либо через
начальные координаты и перемещения по осям системы отсчёта.
Скорость
Скорость – это вектор, который показывает направление перемещения исследуемой точки, величина данного вектора
равна производной радиус-вектора по времени.
∨ = dr/dt
Вектор средней скорости
Вектор средней скорости определяется как отношение вектора перемещения ко времени
v = Δr / Δt
Вектор мгновенной скорости
Используя знания о средней скорости, мгновенную скорость можно получить когда временной интервал стремится к нулю:
v = lim (Δt → 0)(Δr/Δt) = dr/dt = r’
Единичный вектор в направлении вектора мгновенной скорости:
Δ = lim (Δt → 0)(Δr/Δs)
Тогда вектор мгновенной скорости выражается так:
v = v · dr = ds/dt = r’
Ускорение
Изменение вектора скорости в течение бесконечно малого интервала времени Δt называется мгновенным вектором
ускорения, или просто вектором ускорения:
a = lim (Δt → 0)(Δv/Δt) = dv/dt = v’ = d/dt · dr/dt = d2r/dt2 = r”
Вектор среднего ускорения
Вектор среднего ускорения это отношение изменения вектора скорости ко времени, в течение которого произошло
изменение:
a = [v(t + Δt) – v(t)]/Δt = Δv/Δt
в отличие от вектора скорости, который всегда направлен по касательной к траектории, вектор ускорения может
иметь любое направление.
Вам понравилась статья?
/
Просмотров: 1 194