Средняя гармоническая величина
Задача
2.5
Имеются данные об
удельном весе бракованной продукции
(табл. 2.5). Потери от брака (стоимость
бракованной продукции) одинаковы по
всем видам продукции.
Таблица 2.5
Удельный вес бракованной продукции
|
Вид |
Удельный |
|
А |
2,0 |
|
Б |
1,0 |
|
В |
2,5 |
|
Г |
4,0 |
Определить средний
удельный вес бракованной продукции.
Решение
1. Средний удельный
вес бракованной продукции рассчитывается
по формуле (исходное соотношение средней)
![]()
где
![]()
стоимость бракованной продукции i-го
вида;
![]() стоимость
стоимость
изготовленной продукции i-го
вида.
2.
Стоимость
изготовленной продукции i-го
вида может быть определена из удельного
веса бракованной продукции
![]()
![]()
3.
Средний
удельный вес бракованной продукции
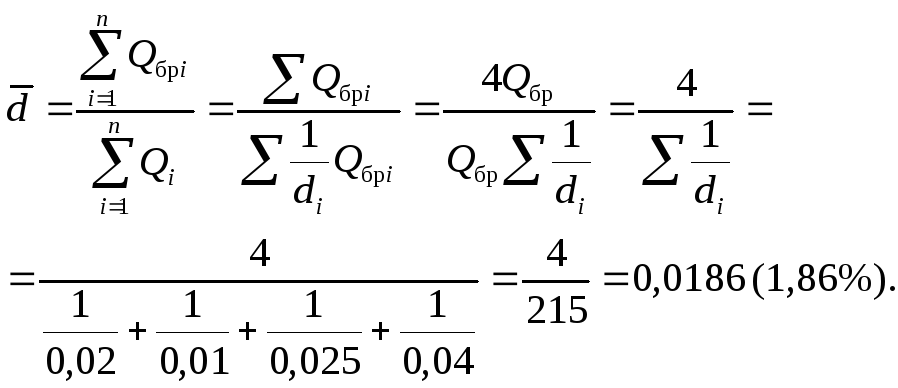
Задача
2.6
Имеются
данные по трем предприятиям о суммарных
затратах на весь выпуск продукции и
затратах на рубль произведенной продукции
(табл. 2.6).
Таблица 2.6
Затраты на производство продукции
|
Номер |
Затраты продукции, |
Затраты |
|
1 2 3 |
400 200 360 |
0,75 0,80 0,82 |
|
Итого |
960 |
|
Определить по трем
предприятиям средние затраты на рубль
товарной продукции.
Решение
1.
Средние затраты на рубль произведенной
продукции определяются по формуле
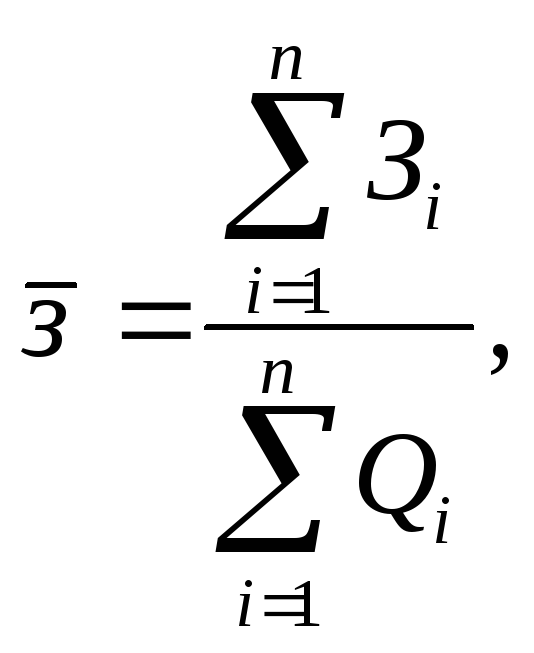
где
![]()
число предприятий;
![]() стоимость
стоимость
изготовленной продукции на i-м
предприятии.
2.
Стоимость
изготовленной продукции на i-м
предприятии может быть определена из
затрат на рубль товарной продукции
![]()
![]()
3. Средние
затраты на рубль товарной продукции

Задача
2.7
Имеются
данные о средних процентных ставках и
доходах коммерческих банков (табл. 2.7).
Таблица 2.7
Процентные ставки и доходы банков
|
Номер |
Средняя
|
Доход
|
|
1 2 3 |
15 20 12 |
600 400 360 |
|
Итого |
|
1360 |
Определить
среднюю процентную ставку по трем
коммерческим банкам.
Решение
1.
Исходное соотношение средней процентной
ставки

где
![]()
число банков;
![]() сумма
сумма
кредитов, выданных банком.
2.
Из формулы процентной ставки в i-м
коммерческом банке можно определить
сумму кредитов, выданных банком
![]()
![]()
3. Средняя процентная
ставка определяется по формуле средней
гармонической взвешенной

Задача
2.8
Имеются
данные об экспортной продукции предприятия
(табл. 2.8).
Таблица 2.8
Процентные ставки и доходы банков
|
Вид |
Доля |
Стоимость |
|
A |
40 |
120 |
|
Б |
30 |
150 |
|
В |
10 |
80 |
|
Итого |
|
350 |
Определить
среднюю долю экспортной продукции.
Решение
1.
Исходное соотношение средней доли
экспортной продукции
![]()
где
![]()
стоимость изготовленной продукции
i-го
вида.
2.
Из формулы удельного веса экспортной
продукции i-го
вида можно определить стоимость
изготовленной продукции
![]()
![]()
3.
Средний удельный вес экспортной продукции
определяется по формуле средней
гармонической взвешенной

Загрузить PDF
Загрузить PDF
Вычислить средневзвешенную величину, также известную как среднее взвешенное, не так просто, как найти среднее арифметическое. Среднее взвешенное — это величина, вычисляемая на основе чисел, «ценность» или «вес» которых не равнозначны. Например, если нужно вычислить среднее взвешенное оценки, помните, что оценки за разные задания составляют определенные проценты от финальной оценки. Метод вычисления зависит от того, равна ли сумма всех весов 1 (100 %) или нет.
-

1
Запишите все числа, среднее взвешенное которых нужно вычислить. Например, если нужно найти среднее взвешенное оценок, сначала запишите все оценки.[1]
- Например, вы получили 82 балла за тесты, 90 баллов за экзамен и 76 баллов за курсовую работу.
-

2
Определите вес (или «ценность») каждого числа. Например, оценка за тест составляет 20 % от финальной оценки, оценка за экзамен — 35 %, оценка за курсовую работу — 45 %. В этом случае сумма весов равна 1 (или 100 %).[2]
- Чтобы использовать проценты в вычислениях, необходимо преобразовать их в десятичные дроби. Полученные числа называются «весовыми коэффициентами».
Совет: чтобы преобразовать проценты в десятичную дробь, добавьте десятичную запятую в конец процентов, а затем переместите ее на 2 позиции влево. Например, 75 % = 0,75.
-

3
Умножьте каждое число (х) на соответствующий весовой коэффициент (w). Затем сложите полученные значения, чтобы вычислить среднее взвешенное.[3]
- Например, если за тест вы получили 82 балла, а оценка за тест составляет 20 % от финальной оценки, умножьте 82 x 0,2. В этом случае х = 82 и w = 0,2.
-

4
Сложите полученные значения, чтобы найти среднее взвешенное. Формула для вычисления среднего взвешенного, когда сумма весов равна 1: x1(w1) + x2(w2) + x3(w3) + …, где x1, ч2, … — это числа, w1, w2, … — это соответствующие весовые коэффициенты.[4]
Чтобы найти среднее взвешенное, просто умножьте каждое число на его весовой коэффициент, а затем сложите полученные значения.- В нашем примере: 82(0,2) + 90(0,35) + 76(0,45) = 16,4 + 31,5 + 34,2 = 82,1. Это означает, что за предмет вы получили 82,1%.
Реклама
-

1
Запишите все числа, среднее взвешенное которых нужно вычислить. Помните, что сумма весов не всегда равна 1 (или 100 %), но в любом случае сначала запишите все нужные числа.[5]
- Например, нужно вычислить среднюю продолжительность вашего ежедневного сна в течение 15 недель, причем продолжительность сна менялась — вы спали 5, 8, 4, 7 и так далее часов в сутки.
-

2
Определите вес (или «ценность») каждого числа. Например, допустим, что в течение 15 недель было несколько недель, когда вы спали дольше. Такие недели имеют больший вес (потому что вы спали дольше, чем обычно). В качестве весового коэффициента используйте количество недель, связанное со средней продолжительностью сна. Например:[6]
- 9 недель, в течение которых продолжительность сна в среднем составляла 7 часов в сутки.
- 3 недели, в течение которых продолжительность сна в среднем составляла 5 часов в сутки.
- 2 недели, в течение которых продолжительность сна в среднем составляла 8 часов в сутки.
- 1 неделя, в течение которой продолжительность сна в среднем составляла 4 часа в сутки.
- Количество недель, связанное с количеством часов, является весовым коэффициентом. В нашем примере вы спали 7 часов в сутки в течение большинства недель, а бо́льшая или меньшая продолжительность сна приходится на меньшее число недель.
-

3
Вычислите сумму весов. Для этого просто сложите все веса. В нашем примере сумма весов f = 15, потому что вы исследуете продолжительность сна в течение 15 недель. [7]
- Общее количество недель, которые вы рассматриваете, складывается следующим образом: 3 недели + 2 недели + 1 неделя + 9 недель = 15 недель.
-

4
Умножьте числа на соответствующие веса, а затем сложите результаты. В нашем примере умножьте среднюю продолжительность сна на соответствующее число недель. Вы получите:[8]
- 5(часов в сутки)*3(недели) + 8(часов в сутки)*2(недели) + 4(часа в сутки)*1(неделя) + 7(часов в сутки)*9(недель) = 5(3) + 8(2) + 4( 1) + 7(9) = 15 + 16 + 4 + 63 = 98
-

5
Разделите полученный результат на сумму весов, чтобы найти среднее взвешенное. В нашем примере:[9]
- 98/15 = 6,53. Это означает, что средняя продолжительность вашего ежедневного сна в течение 15 недель составила 6,53 часа.
Реклама
Об этой статье
Эту страницу просматривали 94 930 раз.
Была ли эта статья полезной?
Как вычислить среднее взвешенное
Соавтор(ы): Mario Banuelos, PhD. Марио Бануэлос — преподаватель математики в Университете штата Калифорния во Фресно. Имеет более восьми лет преподавательского опыта, специализируется на математической биологии, оптимизации, статистических моделях эволюции генома и науке о данных. Получил степень бакалавра по математике в Университете штата Калифорния во Фресно и PhD по прикладной математике в Калифорнийском университете в Мерседе. Преподавал как на уровне вуза, так и старшей школы.
Расчет средней массы
Средняя масса — это среднее значение массы, измеренное весами или иным измерительным прибором несколько раз.
Формула расчета средней массы:
Mср = (M1 + M2 + M3) / 3
Mср — средняя масса
M1 — первое измерение
M2 — второе измерение
M3 — третье измерение
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета средней массы (по результатам трех измерений) и формула для расчета средней массы. С помощью этого калькулятора вы в один клик сможете вычислить среднюю массу.
Как определить средний удельный вес
Каждая наука, которую можно назвать точной, прежде всего собирает данные для исследований путем наблюдений, выборки, экспериментов и опросов. Огромный поток информации в процессе кропотливой работы перерабатывается, чтобы получить средние данные. Они высчитываются и потом используются в физике, математике, статистике и других науках.
- Как определить средний удельный вес
- Как рассчитать удельный вес в процентах
- Как рассчитать удельный вес продукции
Огромная подготовительная работа проделана, поэтому теперь остается выполнить одно простое арифметическое действие: первую сумму поделить на вторую и умножить на сто. В числах это выглядит нагляднее, поэтому снова обратимся к нашему случаю. Если сумма зарплат составила 120, а себестоимость продукции – 400 (цифры условны), то средний удельный вес зарплаты рабочих в себестоимости консервной продукции по стране составит 30%.
- Что такое удельный вес затрат
- Как определить удельный вес
- Как вычисляется удельный вес
Как определить средний удельный вес
Каждая наука, которую можно назвать точной, прежде всего собирает данные для исследований путем наблюдений, выборки, экспериментов и опросов. Огромный поток информации в процессе кропотливой работы перерабатывается, чтобы получить средние данные. Они высчитываются и потом используются в физике, математике, статистике и других науках.
Инструкция
Займитесь подготовкой к расчетам. Соберите как можно больше сведений, необходимых для получения конечного числа. Чем точнее и полнее будет информация, тем более точной будет и итоговая цифра. Например, нужно определить средний удельный вес зарплаты рабочих в себестоимости выпускаемой продукции на заводах определенной категории (предположим, консервных) в нашей стране. Вы не сможете наверняка узнать точное число таких заводов, их очень много, но тем не менее собрать данные необходимо. Поэтому составьте максимально возможный их список и для каждого выясните общую сумму заработной платы рабочих и общую сумму себестоимости.
Информацию берите за определенный промежуток времени: за месяц, за квартал, за год. Учтите, что дать материал вам смогут только тогда, когда данный период уже закрыт в бухгалтерском учете. Текущие сведения вам дать не смогут по причине их постоянного изменения. Поэтому выбирайте только минувшие сроки, но все же не очень давние, чтобы информация не была устаревшей.
Такая масштабная работа отпадает, если вам нужен средний удельный вес на трех определенных заводах. В этом случае вы просто сужаете круг исследования, взяв цифры только этих предприятий.
Если конкретные цифры отсутствуют, высчитайте их сами на основе тех сумм, которые вам сможет дать компания. Помните, что при обработке данных одна сумма всегда логически вытекает из некоторых других и наоборот. Так, вам могут дать зарплаты рабочих по цехам – и вы их только суммируете. Или, напротив, сообщат общую сумму зарплаты, но при этом добавят штатное расписание, где видна специальность работника, и расчетную ведомость по зарплате. Тогда путем выборки ищите только рабочих.
Суммируйте все числа, которые удалось получить. На выходе вы будете иметь две цифры. В нашем примере это общая сумма зарплат всех рабочих на всех заводах и общая себестоимость консервной продукции.
Огромная подготовительная работа проделана, поэтому теперь остается выполнить одно простое арифметическое действие: первую сумму поделить на вторую и умножить на сто. В числах это выглядит нагляднее, поэтому снова обратимся к нашему случаю. Если сумма зарплат составила 120, а себестоимость продукции – 400 (цифры условны), то средний удельный вес зарплаты рабочих в себестоимости консервной продукции по стране составит 30%.
120/400*100=30.
Если же вы проведете это нехитрое действие еще и по каждому предприятию в отдельности, то сможете сопоставить, насколько процент удельного веса на каждом заводе будет отличаться от среднего в ту или другую сторону
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
ВЕСА в статистике, коэффициенты, используемые для вычисления среднего значения (средневзвешенного) элемента в совокупности; сумма коэффициентов равна единице. Взвешивание – фундаментальный методический приём, предназначенный для корректного сопоставления количественных значений показателей с учётом их качественной значимости.
Например, если в спортивной команде 10 человек имеют возраст 20 лет, а 1 человек – 30 лет, то средний возраст этой команды составит:
20 лет·(10/11) + 30 лет·(1/11) = 20,9 года.
В этом случае весами выступают значения долей, которые имеют группы соответствующего возраста в общем количестве людей, для которого рассчитывается средний возраст.
Если известны цены Р1(t), Pi(t), Pn(t) на товары и услуги в году t и аналогичные показатели для года t + 1, для каждого товара индекс цены за период от года t до года t + 1 можно рассчитать как IPi(t+ 1/t) =Pi(t+ 1)/Рi(t). Однако интерес представляет оценка индекса цен в целом, т. е. совокупное изменение цен по всем товарам. Например, для ответа на вопрос о росте стоимости жизни ключевое значение имеет обобщающий, средний индекс цен на потребительские товары и услуги – индекс потребительских цен. При этом нельзя просто использовать среднее арифметическое индексов по отдельным товарам (услугам), поскольку вклад каждого из них в общий рост цен не одинаков, а пропорционален объёму продаж данного товара (услуги). В этой связи каждому индексу цены отдельного товара (услуги) приписывается удельный вес ki, измеряемый в долях единицы и отражающий долю каждого товара (услуги) в общем росте цен. В итоге общий индекс цен IP(t+1/t) рассчитывается как средневзвешенное:
Реклама
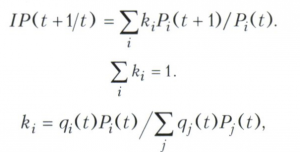
где qi(t) – количество товара в натуральном исчислении в году t.
При расчёте индекса в качестве весов можно использовать структуру продаж первого (t) или второго (t+ 1) из сопоставляемых периодов. Поскольку эти две структуры могут различаться, то результат расчёта зависит от того, структура какого периода используется для взвешивания. Если взвешивание опирается на структуру первого (базового) периода, как в приведённом примере, то такой индекс называется индексом Ласпейреса, если на структуру второго периода – то индексом Пааше.
А. Е. Косарев.
