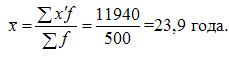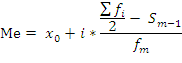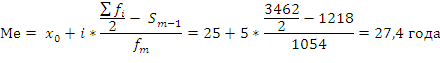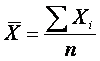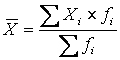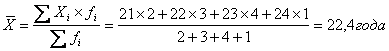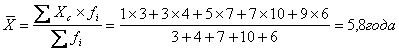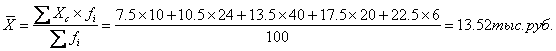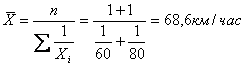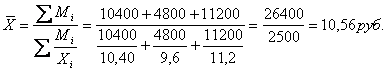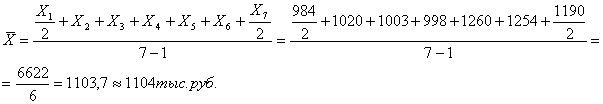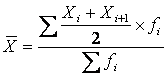Например, средняя арифметическая для интервального ряда
При расчете средней арифметической для
интервального вариационного ряда
сначала определяют среднюю для каждого
интервала, как полусумму верхней и
нижней границ, а затем — среднюю всего
ряда. В случае открытых интервалов
значение нижнего или верхнего интервала
определяется по величине интервалов,
примыкающих к ним.
Пример
3. Определить
средний возраст студентов вечернего
отделения.
|
Возраст |
Число |
Среднее |
Произведение |
|
до |
65 |
(18 + |
1235 |
|
20 — |
125 |
(20 + |
2625 |
|
22 — |
190 |
(22 + |
4560 |
|
26 — |
80 |
(26 + |
2240 |
|
30 и |
40 |
(30 + |
1280 |
|
Итого |
500 |
11940 |
Средние, вычисляемые из интервальных
рядов являются приближенными.
-
Структурные средние величины
Кроме степенных средних в статистике
для относительной характеристики
величины варьирующего признака и
характеристики рядов распределения
пользуются структурными средними: модой
и медианой.
Мода
Мода— это наиболее часто
встречающийся вариант ряда. Мода
применяется, например, при определении
размера одежды, обуви, пользующейся
наибольшим спросом у покупателей.
Модой для дискретного ряда является
варианта, обладающая наибольшей частотой.
При вычислении моды для интервального
вариационного ряда необходимо:
-
сначала определить модальный интервал
(по максимальной частоте), -
затем — значение модальной величины
признака по формуле:
где:
-
—
значение моды -
—
нижняя граница модального интервала -
i —
величина интервала -
—
частота модального интервала -
—
частота интервала, предшествующего
модальному -
—
частота интервала, следующего за
модальным
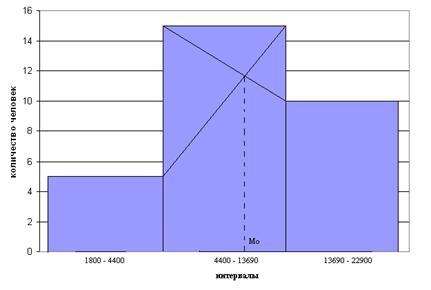
Определение моды графически:
Мода определяется по гистограмме
распределения. Для этого
правую вершину модального
прямоугольника соединяют с правым
верхним углом предыдущего прямоугольника
, а левую
вершину модального прямоугольника –
с левым верхним углом
последующего прямоугольника. Абсцисса
точки пересечения этих прямых и будет
модой распределения.
Медиана
Медиана — это значение признака,
который делит вариационный ряд на две
равные по численности части.
Медиана для дискретного ряда.
Для определения медианы в дискретном
рядус нечетнымколичеством
единиц наблюдения сначалапорядковый
номер медианыпо формуле: ,
а затем определяют, какое значение
варианта обладает накопленной частотой,
равной номеру медианы.
Если ряд содержит четное
число элементов, то
медиана будет равна средней из двух
значений признака, находящихся в
середине. Номер первого из этих признаков
определяется по формуле: ,
для второго – .
= n
(количество элементов в ряду).
Медиана для интервального ряда
При вычислении медианы для
интервального вариационного ряда сначала
определяют медианный интервал, в пределах
которого находится медиана.
Для этого:
-
определяется номер медианы
по формуле:,
полученное значение округляется до
целого большего числа. -
затем по
накопленной частоте определяется
интервал, в который входит элемент с
таким номером, -
затем — значение медианы по формуле:
где:
-
—
искомая медиана -
—
нижняя граница интервала, который
содержит медиану -
i
— ширина интервала -
—
сумма частот или число членов ряда -
–
накопленная частота интервала,
предшествующего медианному -
—
частота медианного интервала
Пример.
Найти моду и медиану для интервального
ряда.
|
Возрастные |
Число |
Сумма |
|
До 20 |
346 |
346 |
|
20 — 25 |
872 |
1218 |
|
25 |
1054 |
2272 |
|
30 — 35 |
781 |
3053 |
|
35 — 40 |
212 |
3265 |
|
40 — 45 |
121 |
3386 |
|
45 лет |
76 |
3462 |
|
Итого |
3462 |
Решение:
-
Определим моду
В
данном примере модальный интервал
находится в пределах возрастной группы
25-30 лет, так как на этот интервал приходится
наибольшая частота (1054).
Рассчитаем
величину моды:
Это значит, что модальный
возраст студентов равен 27 годам.
-
Определим медиану.
Медианный интервал
находится в возрастной группе 25-30 лет,
так как в пределах этого интервала
расположена варианта, которая делит
совокупность на две равные части (Σfi/2
= 3462/2 = 1731). Далее подставляем в формулу
необходимые числовые данные и получаем
значение медианы:
Это значит, что одна половина студентов
имеет возраст до 27,4 года, а другая свыше
27,4 года.
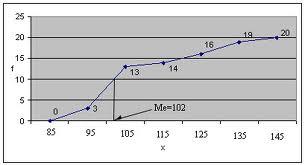
Графически медиана
определяется по кумуляте. Для ее
определения высоту наибольшей ординаты,
которая соответствует сумме всех частот,
делят пополам. Через полученную точку
проводят прямую,
параллельную оси абсцисс,
до
пересечения ее с кумулятой. Абсцисса
точки пересечения является медианой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Расчет средней величины в интервальных вариационных рядах немного отличается от расчета в рядах дискретных. Как рассчитать среднюю арифметическую и среднюю гармоническую в дискретных рядах можно посмотреть вот ЗДЕСЬ. Такое различие вполне объяснимо – это связано с особенностью интервальных рядов, в которых изучаемый признак приведен в интервале от и до.
Итак, посмотрим особенности расчета на примере.
Пример 1. Имеются данные о дневном заработке рабочих предприятия.
| Дневной заработок рабочего, руб. | Число рабочих, чел. |
| 500-1000 | 15 |
| 1000-1500 | 30 |
| 1500-2000 | 80 |
| 2000-2500 | 60 |
| 2500-3000 | 25 |
| Итого | 210 |
Нам необходимо рассчитать среднедневную заработную плату рабочего.
Начало решения задачи будет аналогичным правилам расчета средней величины, которые можно посмотреть в этой статье.
Начинаем мы с определения варианты и частоты, поскольку ищем мы средний заработок за день, то варианта это первая колонка, а частота вторая. Данные у нас заданы явным количеством, поэтому расчет проведем по формуле средней арифметической взвешенной (так как данные приведены в табличном виде). Но на этом сходства заканчиваются и появляются новые действия.
| Дневной заработок рабочего, руб. х | Число рабочих, чел. f |
| 500-1000 | 15 |
| 1000-1500 | 30 |
| 1500-2000 | 80 |
| 2000-2500 | 60 |
| 2500-3000 | 25 |
| Итого | 210 |
Дело в том, что интервальный рад представляет осредняемую величину в виде интервала. 500-1000, 2000-2500 и так далее. Чтобы решить эту проблему необходимо провести промежуточные действия, и только потом подсчитать среднюю величину по основной формуле.
Что же требуется в данном случае сделать. Все достаточно просто, чтобы провести расчет нам нужно, чтобы варианта была представлена одним числом, а не интервалом. Для получения такого значения находят так называемое ЦЕНТРАЛЬНОЕ ЗНАЧЕНИЕ ИНТЕРВАЛА (или середину интервала). Определяется оно путем сложение верхней и нижней границ интервала и делением на два.
Проведем необходимые расчеты и подставим данные в таблицу.
И так далее по всем интервалам рассчитываем центральное значение. В итоге получаем следующие результаты.
| Дневной заработок рабочего, руб. х | Число рабочих, чел. f | х’ | |
| 500-1000 | 15 | 750 | |
| 1000-1500 | 30 | 1250 | |
| 1500-2000 | 80 | 1750 | |
| 2000-2500 | 60 | 2250 | |
| 2500-3000 | 25 | 2750 | |
| Итого | 210 | — |
После того как мы рассчитали центральные значения далее проведем расчеты в таблицы и подставим итоговые данные в формулу, аналогично тому как мы уже рассматривали ранее.
| Дневной заработок рабочего, руб. х | Число рабочих, чел. f | х’ | x’f |
| 500-1000 | 15 | 750 | 11250 |
| 1000-1500 | 30 | 1250 | 37500 |
| 1500-2000 | 80 | 1750 | 140000 |
| 2000-2500 | 60 | 2250 | 135000 |
| 2500-3000 | 25 | 2750 | 68750 |
| Итого | ∑f = 210 | — | ∑ x’f = 392500 |
В итоге получаем, что среднедневная заработная плата одного рабочего составляет 1869 рублей.
Это пример решения, если интервальный ряд представлен со всеми закрытыми интервалами. Но достаточно часто бывает, когда два интервала открытые, первый и последний. В таких ситуациях прямой расчет центрального значения невозможен, но есть два варианта как это сделать.
Пример 2. Имеются данные о продолжительности производственного стажа персонала предприятия. Рассчитать среднюю продолжительность стада одного сотрудника.
| Длительность производственного стажа, лет | Число сотрудников, человек |
| до 3 | 19 |
| 3-6 | 21 |
| 6-9 | 15 |
| 9-12 | 10 |
| 12 и более | 5 |
| Итого | 70 |
В данном случае принцип решения останется точно таким же. Единственно, что поменялось в этой задаче, так это первый и последний интервалы. До 3 лет и 12 лет и более это и есть те самые открытые интервалы. Именно тут возникнет вопрос, а как же найти центральное значение интервала для таких интервалов.
Поступить в этой ситуации можно двумя способами:
- Предположить какой бы мог быть интервал, учитывая, что нам приведены интервалы равные, то это вполне возможно. Интервал до 3 мог бы выглядеть как 0-3, и тогда его центральное значение будет (0+3)/2 = 1,5 года. Интервал 12 и более мог бы выглядеть как 12-15, и тогда его центральное значение было бы (12+15)/2 = 13,5 года. Все оставшиеся центральные значения интервала рассчитываются аналогично. В результате получаем следующее.
| Длительность производственного стажа, лет х | Число сотрудников, человек f | х’ | x’f |
| до 3 | 19 | 1,5 | 28,5 |
| 3-6 | 21 | 4,5 | 94,5 |
| 6-9 | 15 | 7,5 | 112,5 |
| 9-12 | 10 | 10,5 | 105,0 |
| 12 и более | 5 | 13,5 | 67,5 |
| Итого | ∑f = 70 | — | ∑ x’f = 408,0 |
Средняя продолжительность стажа 5,83 года.
- Принять за центральное значение, то данное которое имеется в интервале, без дополнительных расчетов. В нашем случае в интервале до 3 это будет 3, а в интервале 12 и более это будет 12. Такой способ больше подходит для ситуаций, когда интервалы неравные и предположить какой интервал мог бы быть сложно. Рассчитаем нашу задачу по таким данным далее.
| Длительность производственного стажа, лет х | Число сотрудников, человек f | х’ | x’f |
| до 3 | 19 | 3 | 57,0 |
| 3-6 | 21 | 4,5 | 94,5 |
| 6-9 | 15 | 7,5 | 112,5 |
| 9-12 | 10 | 10,5 | 105,0 |
| 12 и более | 5 | 12 | 60,0 |
| Итого | ∑f = 70 | — | ∑ x’f = 429,0 |
Средняя продолжительность стажа 6,13 года.
Домашнее задание
- Рассчитать средний размер посевной площади на одно фермерское хозяйство по следующим данным.
| Размер посевной площади, га | Количество фермерских хозяйств |
| 0-20 | 64 |
| 20-40 | 58 |
| 40-60 | 32 |
| 60-80 | 21 |
| 80-100 | 12 |
| Итого | 187 |
- Рассчитайте средний возраст работника предприятия по следующим данным
| Возраст персонала, лет | Число сотрудников, человек |
| до 18 | 7 |
| 18-25 | 68 |
| 25-40 | 79 |
| 40-55 | 57 |
| 55 и старше | 31 |
| Итого | 242 |
Теперь Вы умеете рассчитывать среднюю в интервальном вариационном ряду!
Может еще поучимся? Загляни сюда!
В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

Иногда при работе с данными нужно описать множество значений каким-то одним числом. Например, при исследовании эффективности сотрудников, уровня вовлеченности в аккаунте, KPI или времени ответа на сообщения клиентов. В таких случаях используют меры центральной тенденции. Их можно называть проще — средние значения.
Но в зависимости от вводных данных, находить среднее значение нужно по-разному. Основной набор задач закрывается с использованием среднего арифметического, медианы и моды. Но если выбрать неверный способ — выводы будут необъективны, а результаты исследования нельзя будет признать действительными. Чтобы не допустить ошибку, нужно понимать особенности разных способов нахождения средних значений.

Cтратег, аналитик и контент-продюсер. Работает с агентством «Палиндром».

Как считать среднее арифметическое
Использовать среднее арифметическое стоит тогда, когда множество значений распределяются нормально ― это значит, что значения расположены симметрично относительно центра. Как выглядит нормальное распределение на графике и в таблице, можно посмотреть на примере:


Если данные распределяются как в примерах — вам повезло. Можно без лишних заморочек считать среднее арифметическое и быть уверенным, что выводы будут объективны. Однако, нормальное распределение на практике встречается крайне редко, поэтому среднее арифметическое в большинстве случаев лучше не использовать.
Как рассчитать
Сумму значений нужно поделить на их количество. Например, вы хотите узнать средний ER за 4 дня при нормальном распределении значений и без аномальных выбросов. Для этого считаем среднее арифметическое: складываем ER всех дней и делим полученное число на количество дней.
Если хотите автоматизировать вычисления и узнать среднее арифметическое для большого числа показателей — используйте Google Таблицы:
- Заполните таблицу данными.
- Щелкните по пустой ячейке, в которую хотите записать среднее арифметическое.
- Введите «=AVERAGE(» и выделите ряд чисел, для которых нужно вычислить среднее арифметическое. Нажмите «Enter» после ввода формулы.
Когда можно не использовать
Если данные распределены ненормально, то наши расчеты не будут отражать реальную картину. На ненормальность распределения указывают:
- Отсутствие симметрии в расположении значений.
- Наличие ярко выраженных выбросов.
Как пример ненормального распределения (с выбросами) можно рассматривать среднее время ответа на комментарии по неделям:
Если посчитать среднее значение для такого набора данных с помощью среднего арифметического, то получится завышенное число. В итоге наши выводы будут более позитивными, чем реальное положение дел. Еще стоит учитывать, что выбросы могут не только завышать среднее значение, но и занижать его. В таком случае вы получите более скромный показатель, который не будет соответствовать реальности.
Например, в группе «Золотое Яблоко» во ВКонтакте иногда публикуют конкурсные посты. Они набирают более высокие показатели вовлеченности чем обычные публикации. Если посчитать средний ER с учетом конкурсов, мы получим 0,37%, а без учета конкурсов — только 0,29%. Аналогичная ситуация с числом комментариев. С конкурсами в среднем получаем 917 комментариев, а без конкурсов — всего лишь 503. Очевидно, что из-за розыгрышей средние показатели вовлеченности завышаются. В этом случае конкурсные посты следует исключить из анализа, чтобы объективно оценить эффективность контента в группе.
Еще часто бывает так, что данных очень много, заметны явные выбросы, но на их обработку и исключение аномальных значений не хватит ни времени, ни терпения. Тем более нет гарантий, что исключив выбросы, вы получите нормальное распределение. В таком случае лучше подсчитать средние значения, используя медиану.
Как найти медиану и когда ее применять
Если вы имеете дело с ненормальным распределением или замечаете значительные выбросы — используйте медиану. Так можно получить более адекватное среднее значение, чем при использовании среднего арифметического. Чтобы понять, как работать с медианой, рассмотрим аналогичный пример с ненормальным распределением времени ответов на комментарии.
Ниже в таблице уже введены данные из графика и рассчитано среднее время ответа с помощью среднего арифметического и медианы. Из расчетов видна наглядная разница между средним арифметическим и медианой ― она составляет 17 минут. Такое различие появляется из-за низкого темпа работы на выходных и в нестандартных ситуациях, когда к ответу на сообщения нужно относиться с особой ответственностью (события конца февраля). Подобные выбросы сильно завышают среднее арифметическое, а вот на медиану они практически не влияют. Поэтому если хотите посчитать среднее значение избегая влияния выбросов, — используйте медиану. Такие данные будут без искажений.
Как рассчитать
Разберем на примере. В аккаунте опубликовали семь постов и они набрали разное количество комментариев: 35, 105, 2, 15, 2, 31, 1. Чтобы вычислить медиану, нужно пройти два этапа:
- Расположите числа в порядке возрастания. Итоговый ряд будет выглядеть так: 1, 2, 2, 15, 31, 35, 105.
- Найдите середину сформированного ряда. В центре стоит число 15 — его и нужно считать медианой.
Немного сложнее найти медиану, если вы работаете с четным количеством чисел. Например, вы собрали количество лайков на последних шести постах: 32, 48, 36, 201, 52, 12. Чтобы найти медиану, выполните три действия:
- Расставьте числа по возрастанию: 12, 32, 36, 48, 52, 201.
- Возьмите два из них, наиболее близких к центру. В нашем случае — это 36 и 48.
- Сложите два этих числа и разделите на два: (36 + 48) / 2 = 42. Результат и есть медиана.
Чтобы вычислять медиану быстрее и обрабатывать большие объемы данных — используйте Google Таблицы:
- Внесите данные в таблицу.
- Щелкните по свободной ячейке, в которую хотите записать медиану.
- Введите формулу «=MEDIAN(» и выделите ряд чисел, для которых нужно рассчитать медиану. Нажмите «Enter», чтобы все посчиталось.
Когда можно не использовать
Если данные распределены нормально и вы не видите заметных выбросов — медиану можно не использовать. В этом случае значение среднего арифметического будет очень близким к медиане. Можете выбрать любой способ нахождения среднего, с которым вам работать проще. Результат от этого сильно не изменится.
Что такое мода и где ее использовать
Мода ― это самое популярное/часто встречающееся значение. Например, стоит задача узнать, сколько комментариев чаще всего набирают посты в аккаунте. В этом случае можно не высчитывать среднее арифметическое или медиану ― лучше и проще использовать моду.
Еще пример. Нужно узнать, в какое время аудитория чаще всего взаимодействует с публикациями. Для этого можно посчитать данные вручную или использовать готовую таблицу из LiveDune (вкладка «Вовлеченность» ― таблица «Лучшее время для поста»). По ее данным ― больше всего реакций пользователи оставляют в среду в 16 часов. Это время и есть мода. Таким образом, если вам нужно найти самое популярное значение, а не классическое среднее — проще использовать моду.
Как рассчитать
Чтобы найти наиболее часто встречающееся значение в наборе данных, нужно посмотреть, какое число встречается в ряду чаще всех. Например, для ряда 5, 4, 2, 4, 7 ― модой будет число 4.
Иногда в ряде значений встречается несколько мод. Например, ряду 7, 7, 21, 2, 5, 5 свойственны две моды — 7 и 5. В этом случае совокупность чисел называется мультимодальной. Также поиск моды можно упростить с помощью Google Таблиц:
- Внесите значения в таблицу.
- Щелкните по ячейке, в которую хотите записать моду.
- Введите формулу «=MODE(» и выделите ряд чисел, для которых нужно вычислить моду. Нажмите «Enter».
Однако важно иметь в виду, что табличная функция выдает только самую меньшую моду. Поэтому будьте внимательны — можно упустить из виду несколько мод.
Когда использовать не стоит
Моду нет смысла использовать, если вас не просят найти самое популярное значение. Там, где надо найти классическое среднее значение, про моду лучше забыть.
Памятка по использованию
Среднее арифметическое
Как находим: сумма чисел / количество чисел.
Используем: если данные распределены нормально и нет ярких выбросов.
Не используем: если видим явные выбросы или ненормальное распределение.
Медиана
Как находим: располагаем числа в порядке возрастания и находим середину сформированного ряда.
Используем: если работаем с ненормальным распределением или видим выбросы.
Не используем: если выбросов нет и распределение нормальное.
Мода
Как находим: определяем значение, которое чаще всего встречается в ряду чисел.
Используем: если нужно найти не среднее, а самое популярное значение.
Не используем: если нужно найти классическое среднее значение.
Только важные новости в ежемесячной рассылке
Нажимая на кнопку, вы даете согласие на обработку персональных данных.

Подписывайся сейчас и получи гайд аудита Instagram аккаунта
Маркетинговые продукты LiveDune — 7 дней бесплатно
Наши продукты помогают оптимизировать работу в соцсетях и улучшать аккаунты с помощью глубокой аналитики

Анализ своих и чужих аккаунтов по 50+ метрикам в 6 соцсетях.
Оптимизация обработки сообщений: операторы, статистика, теги и др.
Автоматические отчеты по 6 соцсетям. Выгрузка в PDF, Excel, Google Slides.
Контроль за прогрессом выполнения KPI для аккаунтов Инстаграм.
Аудит Инстаграм аккаунтов с понятными выводами и советами.
Поможем отобрать «чистых» блогеров для эффективного сотрудничества.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3.
Расчёт степенных средних величин.
Студент должен:
знать:
– область применения и методику расчёта
степенных средних величин;
уметь:
– исчислять
степенные средние
величины;
– формулировать вывод по полученным
результатам.
Методические указания
Средней величиной называется обобщающая величина
статистической совокупности, выражающая типический уровень изучаемого признака.
Она выражает величину признака, отнесённую к единице совокупности.
К степенным средним
относятся средняя арифметическая, средняя
гармоническая, средняя хронологическая, средняя геометрическая, средняя квадратическая, средняя кубическая.
Средняя величина всегда
обобщает количественную вариацию признака, т. е. в средних величинах погашаются
индивидуальные различия признака у отдельных единиц совокупности, обусловленные
случайными обстоятельствами. Средняя величина позволяет сравнивать значения
признака у единиц, относящихся к разным совокупностям.
Принципы применения средних величин:
1)
Необходим
обоснованный выбор признака у единиц совокупности, для которого рассчитывается
средняя.
2)
При
определении средней величины в каждом конкретном случае следует исходить из
качественного содержания осредняемого признака,
учитывать взаимосвязь изучаемых признаков и особенность имеющихся исходных
данных;
3)
Средняя
величина должна, прежде всего, рассчитываться по однородной совокупности.
Однородную совокупность позволяет получить метод группировки.
4)
Общие
средние должны подкрепляться групповыми средними.
5)
Средняя
величина не может быть меньше минимального значения и больше максимального
значения признака в совокупности.
Область применения и методика расчёта степенных
средних величин:
1. Средняя арифметическая
1.1 Средняя
арифметическая простая.
При небольшом объёме
исходной информации, когда исходные данные не сгруппированы, применяется средняя
арифметическая простая,которая рассчитывается по формуле:
где ΣXi – сумма
значений;
n– число
значений.
Например: В
бригаде четверо рабочих в возрасте 21,
22, 23 и 24 года. Средний возраст рабочего бригады составляет
1.2 Средняя арифметическая взвешенная.
Когда исходные данные сгруппированы,
то расчёт средней производится по
формуле средней арифметической
взвешенной:
где fi –
частота ряда распределения, с которой отдельные варианты встречаются в
совокупности (или удельный вес отдельных значений во всей совокупности).
Например: Рабочие бригады по возрасту распределились следующим
образом:
|
Возраст рабочих, лет (X) |
21 |
22 |
23 |
24 |
|
Численность рабочих, чел. (fi) |
2 |
3 |
4 |
1 |
Средний возраст рабочего
бригады составляет
Если
исходная информация представлена в виде
интервального ряда распределения,
то средняя арифметическая взвешенная определяется по формуле:
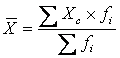
где Xc –
центральное (серединное) значение признака в интервале.
Например: По
имеющимся данным определить средний стаж рабочего бригады:
|
Стаж работы, лет |
0 – 2 |
2 – 4 |
4 – 6 |
6 – 8 |
8 – 10 |
|
Численность рабочих, чел. (fi) |
3 |
4 |
7 |
10 |
6 |
Для расчёта средней
арифметической взвешенной интервального ряда распределения определим центральное
(серединное) значение признака в каждом интервале. Среднее значение интервала
находится как полусумма нижней границы данного
интервала и нижней границы следующего интервала:
|
Стаж работы, лет |
0 – 2 |
2 – 4 |
4 – 6 |
6 – 8 |
8 – 10 |
|
(Xc ) |
|
|
|
|
|
Оформим исходные данные
а следующем виде:
|
Стаж работы, лет |
0 – 2 |
2 – 4 |
4 – 6 |
6 – 8 |
8 – 10 |
|
(Xc ) |
1 |
3 |
5 |
7 |
9 |
|
Численность |
3 |
4 |
7 |
10 |
6 |
Средний стаж рабочего бригады
составляет
Если в интервальном ряду
распределения имеются «открытые» интервалы, то для установления центральных
(серединных) значений «открытых» интервалов на каждый из них условно
распространяется величина смежного «закрытого» интервала.
Например: Работники организации по величине заработной платы за январь 2010 года
распределились следующим образом:
|
Группы работающих по заработной платы за январь 2010 года, тыс.руб. |
Численность работников, в % к |
|
До 9 |
10 |
|
9 – 12 |
24 |
|
12 – 15 |
40 |
|
15 – 20 |
20 |
|
20 и выше |
6 |
|
Итого: |
100 |
Определить по имеющимся данным
среднюю зарплату работников организации.
Для расчёта средней
арифметической взвешенной интервального ряда распределения определим центральное
(серединное) значение признака в каждом интервале. На каждый открытый интервал
условно распространим величину смежного закрытого интервала:
|
Группы |
Численность в % к |
Центральное (Xc), руб |
|
До 9 |
10 |
|
|
9 – 12 |
24 |
|
|
12 – 15 |
40 |
|
|
15 – 20 |
20 |
|
|
20 и выше |
6 |
|
|
Итого: |
100 |
Частоты
при расчете средних арифметических могут быть выражены
не только абсолютными величинами, но и относительными величинами – частостями Результаты применительно к одинаковым
вариантам будут совпадать. В данном примере численность работников
выражена не частотами, а частостями – удельными
весами численности отдельных групп во всей совокупности, что не влияет на
порядок расчёта средней.
Средняя зарплата работников
организации составляет:
Необходимо небольшое
пояснение применительно к расчету средней в
интервальных рядах распределения. В действительности распределение отдельных
вариантов в пределах интервала может оказаться неравномерным. В этом случае
середина интервала будет в той или иной степени отличаться от
фактической средней по интервалу. Это в свою очередь может повлиять на
правильность общей средней, исчисленной по данным интервального ряда. Степень
расхождения зависит от ряда причин. Во-первых, от числа вариант, чем больше
число вариант, тем вероятнее, что середина интервала будет мало отличаться от групповой средней. Во-вторых, от величины интервала. Если
интервал невелик, то ошибка будет незначительной, т.к. групповая средняя будет
мало отличаться от середины интервала. В-третьих, от характера распределения.
Чем симметричнее распределение, тем ошибка меньше. В-четвертых, размер ошибки
зависит от принципа построения интервального ряда. При равных интервалах
середина интервала будет ближе к средней по данной
группе. При наличии открытых интервалов расхождение, как правило, взрастает
из-за условного обозначения неизвестных границ. Общая
средняя равна средней из частных (групповых) средних, взвешенных по численности
соответствующих частей совокупности. Это правило имеет большое значение для
всей статистики – организации сбора и обработки данных, их анализа.
Свойства средней арифметической:
1. Произведение средней на сумму частот всегда равно сумме
произведений вариант на частоты. Другими словами, постоянный
множитель может быть вынесен за знак средней.
2. Если от каждой варианты отнять (прибавить) какое-либо
произвольное число, то новая средняя уменьшится (увеличится) на то же число:
3. Если каждую варианту умножить (разделить) на какое-то произвольное
число, то средняя арифметическая увеличится
(уменьшится) во столько раз
4. Если все частоты (веса) разделить или умножить на
какое-либо число, то средняя арифметическая от этого не изменится. Дело в том,
что веса при исчислении средней арифметической выполняют роль
удельного веса (соотношений между группами по количеству единиц). Поэтому
замена частот частостями не меняет значения средней.
5. Сумма отклонений отдельных вариантов от средней
арифметической всегда равняется нулю.
Перечисленные свойства могут быть использованы для того,
чтобы облегчить технику исчисления средней арифметической.
Например. Можно из всех значений признака вычесть произвольную
постоянную величину (лучше значение серединной варианты или варианты с
наибольшей частотой), полученные разности сократить на общий множитель (лучше
на величину интервала), а частоты выразить частостями
(в процентах) и исчисленную среднюю умножить на общий множитель и прибавить
произвольную постоянную величину. Иногда этот способ расчета средней
арифметической также называется способом расчета от условного нуля. Широкое
применение для обработки статистических материалов современных ЭВМ сужает
необходимость исчисления средних по упрощенным схемам.
2. Средняя гармоническая
2.2 Средняя гармоническая простая. Если объёмы явлений, т.е. произведения Хi ×fi по каждой
единице равны, то для расчёта средней применяется формула средней гармонической простой:
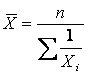
Например: Две
автомашины прошли один и тот же путь: первая со скоростью 60 км/ч, вторая со
скоростью 80 км/ч.
Определить среднюю скорость движения автомашины.
2.2 Средняя гармоническая взвешенная. Учитывая, что средние выражают
качественные свойства изучаемых явлений, важно правильно выбрать вид средней исходя из
взаимосвязей явлений и признаков. Когда статистическая информация не содержит
частот (fi ) у отдельных вариант (X), а представлена как их произведение Mi=(Xi × fi), то для
расчёта средней применяется формула средней гармонической взвешенной:
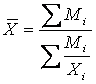
Например: По
имеющимся данным о продаже хлеба «Дарницкий»
определить среднюю цену одной булки хлеба
|
№ |
Цена одной булки хлеба «Дарницкий» 0,5 кг, руб. (Xi) |
Сумма выручки от продажи хлеба «Дарницкий», |
Количество проданных булок |
|
1 |
10,40 |
10400 |
1000 |
|
2 |
9,60 |
4800 |
500 |
|
3 |
11,20 |
11200 |
1000 |
|
Итого: |
26400 |
2500 |
Средняя цена одной булки хлеба может
быть определена делением общей суммы выручки от продажи хлеба на общее
количество проданных булок
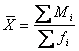
проданных булок в каждом торговом павильоне неизвестно, его можно выразить,
учитывая особенность исходных данных, делением суммы выручки от продажи хлеба
на цену одной булки (2). Подставим
значение (fi) – формулу (2) в формулу (1) и
получим

Средняя цена одной булки хлеба
составляет:
Используя для расчёта
средней цены формулу средней арифметической простой, получим , что является неверным результатом, так как не учтено
количество проданных булок.
Средняя гармоническая представляет собой
обратную величину средней арифметической из обратных значений осредняемого признака. Если определить частоты ряда
распределения, то можно использовать формулу средней арифметической взвешенной,
но формула средней гармонической взвешенной позволяет избежать промежуточных расчётов.
3.Средняя геометрическая
3.1 Средняя
геометрическая простая применяется для характеристики средних темпов роста в рядах динамики с
равноотстоящими уровнями и исчисляется по формуле:
где Хi – цепной коэффициент роста уровня ряда динамики.
n –
число цепных коэффициентов роста в ряду динамики.
3.2 Средняя
геометрическая взвешенная применяется для характеристики средних темпов роста в рядах динамики с неравноотстоящими уровнями и исчисляется по формуле:
где fi – промежуток времени между датами.
4. Средняя хронологическая
4.1 Средняя хронологическая простая
Средний уровень моментного ряда
динамики с равноотстоящими уровнями характеризует средняя хронологическая простая,
которая исчисляется по
формуле:
где Xi – значение уровня моментного ряда
динамики;
n – число
уровней моментного ряда динамики.
Например: По
имеющимся данным определить средний товарный запас за первое полугодие
|
Дата |
1 января |
1 февраля |
1 марта |
1 апреля |
1 мая |
1 июня |
1 июля |
|
Товарный |
984 |
1020 |
1003 |
998 |
1260 |
1254 |
1190 |
|
обозначение |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
п=7
Средний товарный запас за
полугодие составляет
4.2 Средняя хронологическая взвешенная
Средний уровень моментного ряда
динамики с неравноотстоящими уровнями характеризует средняя
хронологическая взвешенная, которая исчисляется по формуле:
Xi и Xi+1
– значение
уровня моментного ряда динамики и уровня, следующего за ним;.
где fi – промежуток времени между датами.
Например: Известна списочная численность персонала организации на некоторые даты 2009 года. Определить
среднесписочную численность персонала за год.
|
Дата |
1.01.2009 |
1.03.2009 |
1.06.2009 |
1.09.2009 |
1.01.2010 |
|
Численность |
1200 |
1100 |
1250 |
1500 |
1350 |
Среднесписочная
численность персонала за 2009 год составляет
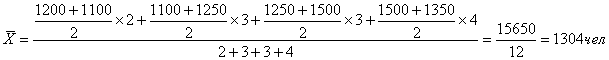
5. Средняя квадратическая
5.1 Средняя квадратическая простая применяется, когда возникает
потребность расчета среднего размера признака, выраженного в квадратных
единицах измерения, для несгруппированных данных. Она
исчисляется как квадратный корнень
из частного от деления суммы квадратов отдельных значений признака на их число
по формуле:
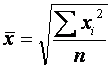
где fi –
частота ряда распределения или удельный вес в совокупности.
5.2. Средняя квадратическая взвешенная применяется,
когда возникает потребность расчета среднего размера признака, выраженного в
квадратных единицах измерения, для сгруппированных данных. Исчисляется по
формуле:

где fi –
частота ряда распределения или удельный вес в совокупности.
6. Средняя кубическая
6.1 Средняя кубическая простая применяется, когда возникает потребность расчета
среднего размера признака, выраженного в кубических единицах измерения, для несгруппированных данных. Исчисляется по формуле:
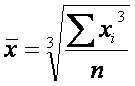
6.2 Средняя кубическая взвешенная применяется, когда возникает потребность расчета
среднего размера признака, выраженного в кубических единицах измерения, для
сгруппированных данных. Исчисляется по формуле:
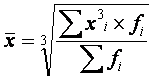
Правило мажорантности
средних величин
Если
рассчитать все виды средних для одних и тех же исходных данных, то значения их
окажутся неодинаковыми. Здесь действует правило мажорантности
средних: с
увеличением показателя степени m увеличивается и
соответствующая средняя величина:
В статистической практике чаще, чем
остальные виды средних взвешенных, используются
средние арифметические и средние гармонические взвешенные.