Запомните!
![]()
Чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму
на их количество.
Пример:
Найти среднее арифметическое 2, 3 и 4.
Обозначим среднее арифметическое буквой «m». По определению выше найдем сумму всех чисел.
2 + 3 + 4 = 9
Разделим полученную сумму на количество взятых чисел. У нас по условию три числа.
В итоге мы получаем формулу среднего арифметического:

Для чего нужно среднее арифметическое?
Кроме того, что его постоянно предлагают найти на уроках, нахождение среднего арифметического весьма полезно и в жизни.
Например, вы решили продавать футбольные мячи. Но так как вы новичок в этом деле, совершенно непонятно по какой
цене вам продавать мячи.
Тогда вы решаете узнать, по какой цене в вашем районе уже продают футбольные мячи конкуренты. Узнаем цены
в магазинах и составим таблицу.
| Магазин | Цена футбольного мяча |
|---|---|
|
«Спорт-товары» |
290 руб. |
| «Adidas» | 360 руб. |
| «Все для футбола» | 310 руб. |
Цены на мячи в магазинах оказались совсем разные. Какую цену для продажи футбольного мяча нам лучше выбрать?
Если выбрать самую низкую (290 руб.), то мы будем продавать
товар себе в убыток. Если выбрать самую высокую (360 руб.), то покупатели не будут приобретать футбольные мячи у нас.
Нам нужна средняя цена. Здесь на помощь приходит среднее арифметическое.
Вычислим среднее арифметическое цен на футбольные мячи:
Средняя цена = =
= 320 руб.
Таким образом, мы получили среднюю цену (320 руб.), по которой мы можем продавать футбольный мяч не слишком дёшево и не
слишком дорого.
Средняя скорость движения
Со средним арифметическим тесно связано понятие средней скорости движения.
Наблюдая за движением транспорта в городе, можно заметить, что машины, то
разгоняются и едут с большой скоростью, то замедляются и едут с
маленькой скоростью.
Таких участков на пути следования автотранспорта бывает много. Поэтому
для удобства расчётов, используют понятие средней скорости движения.
Запомните!
![]()
Средняя скорость движения — это весь пройденный путь разделить на всё время движения.
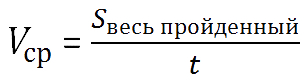
Рассмотрим задачу на среднюю скорость.
Разбор примера
Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем
1,5 ч по
грунтовой дороге со скоростью 45 км/ч, наконец
0,3 ч по просёлочной дороге со скоростью 30 км/ч.
Найдите среднюю скорость движения автомобиля на всём пути.
Для расчёта средней скорости движения нужно знать весь путь, пройденный автомобилем,
и всё время, которое автомобиль двигался.
S1 = V1t1
S1 = 90 · 3,2 = 288 (км)
— шоссе.
S2 = V2t2
S2 = 45 · 1,5 = 67,5 (км)
— грунтовая дорога.
S3 = V3t3
S3 = 30 · 0,3 = 9 (км)
— просёлочная дорога.
S = S1 + S2 + S3
S = 288 + 67,5 + 9 = 364,5 (км)
— весь путь, пройденный автомобилем.
t = t1 + t2 + t3
t = 3,2 + 1,5 + 0,3 = 5 (ч)
— всё время.
Vср = S : t
Vср = 364,5 : 5 = 72,9
(км/ч) — средняя скорость движения автомобиля.
Ответ: Vср = 72,9 (км/ч) — средняя скорость движения автомобиля.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
10 апреля 2015 в 18:52
Дарья Некрасова

Профиль
Благодарили: 0
Сообщений: 3

Дарья Некрасова
Профиль
Благодарили: 0
Сообщений: 3
Автомобиль проехал 180 км за 3 ч с одинаковой скоростью. Из-за гололёда на обратном пути он уменьшил скорость на 15 км/ч. Сколько времени затратил автомобиль на обратный путь.
0
Спасибо
Ответить
10 апреля 2015 в 18:55
Ответ для Дарья Некрасова
Дарья Некрасова

Профиль
Благодарили: 0
Сообщений: 3

Дарья Некрасова
Профиль
Благодарили: 0
Сообщений: 3
180: 3=60
60 ?15=45
180 :45=4
0
Спасибо
Ответить
14 апреля 2015 в 17:11
Ответ для Дарья Некрасова
Asel Talantbekovna

Профиль
Благодарили: 0
Сообщений: 8

Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
сама себе отвечает? ![]()
0
Спасибо
Ответить
Сегодня разберем с вами очередной сложный момент, который ломает мозг не только ученикам 9-11 класса, но и студентам, которые запустили тему кинематики и подзабыли основные определения…
Средняя скорость в физике — один из подвохов, на котором попадаются учащиеся. По аналогии со средним арифметическим школьники и студенты частенько просто берут, складывают, делят пополам. Но в задачах по физике и математике на среднюю скорость так работает далеко не всегда. Предлагаю вам подумать над тем, почему не всегда работает среднее арифметическое двух скоростей, если у нас есть первая половина пути, где тело двигалось с постоянной скоростью v₁ и есть вторая половина пути, на которой тело двигалось с постоянной скоростью v₂. Почему средняя скорость на всём пути не равна среднему арифметическому ? Свой ответ напишите в комментариях. А сегодня мы рассматрим более интересную и редко встречающуюся задачку.
А пока прошу вас подписаться на мой канал в telegram IT mentor. Там я делюсь более короткими постами, рассказываю некоторые интересные случаи из жизни, непосредственно связанные с физикой, математий и IT.
Задача
Двигаясь равноускорено по прямой из состояния покоя, тело проходит некоторый путь. Чему равно отношение средней скорости тела на второй половине пути к средней скорости на первой половине пути?
Попробуйте на этом этапе остановиться, взять черновик с карандашом и решить задачку самостоятельно. Ваши ответы, комментарии, идеи и мнение о задаче обязательно напишите в комментариях. Так я лучше понимаю что интересно моим дорогим читателям
Решение:
Сделаем небольшой рисунок, уточняющий что происходит в задаче:
Для начала определим средние скорости на каждой части. Уже в этой части задачи нужно кое-что понимать. Обычно, под средней скоростью подразумевают именно среднюю путевую скорость. В то же время есть и просто средняя скорость. И две эти величины, в общем случае, отличаются. Давайте вспоминать определения.
Средняя путевая скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.
Средняя скорость — это скорость, определяемая отношением перемещения (S) при неравномерном движении к промежутку времени, за который это перемещение произошло.
Чувствуете подвох? Просто средняя скорость вполне может обнулиться, если вы попадете в момент, когда перемещение становится нулевым. В круговом движении или периодических колебаниях это реализуемо. А вот средняя путевая скорость всегда величина ненулевая, если тело прошло хоть какое-то расстояние. В нашей задаче будем иметь в виду именно среднюю путевую скорость.
1 способ
Средняя скорость на первой половине пути:
Здесь учитывается, что тело стартует с нулевой начальной скоростью.
Средняя скорость на второй половине пути:
Здесь уже учитывается, что начальная скорость для этого участка ненулевая. И находится она из времени разгона на предыдущем участке. Конечная скорость первого участка есть начальная скорость для второго участка. В полученном квадратном уравнении относительно нужного нам момента времени, корень будем выбирать заведомо положительный, т.к. нелогично предполагать, что время получится отрицательной величиной):
Отсюда средняя скорость на данном участке получается:
А теперь мы можем посчитать конечное отношение средней скорости на второй части пути к средней скорости на первой части пути:
Итак, у нас появился первый ответ на задачу. Логичный ли он? Похож ли на правду? А может нам второй способ бахнуть?
2 способ
Хотите второй способ решения задачи? Для любителей хардкорных формул математического анализа я приведу альтернативное решение.
Мы помним общую формулу скорости для движения с постоянным ускорением:
Интегральное обобщенное определение средней скорости можно записать в виде:
Определим моменты времени t₁ и t₂ :
Получили точно такой же ответ, какой был в первом способе решения задачи. Задача решена. И похоже, что решена верно
Краткое решение двумя способами
Какой способ решение вам больше понравился? Напишите в комментариях!
Понравилась статья? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в telegram
Средняя скорость
- Главная
- /
- Физика
- /
- Средняя скорость
Чтобы найти среднюю скорость воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Средняя скорость на протяжении всего пути
Расстояние (путь)
S =
Время
t =
Средняя скорость
Vср =
0
/
Округление ответа:
Средняя скорость через несколько скоростей
Средняя скорость
Vср =
0
Округление ответа:
Просто введите значения скоростей на разных участках пути и получите среднюю скорость. Для того чтобы добавить в ряд более двух чисел воспользуйтесь зелёной кнопкой “+”.
Теория
Как найти среднюю скорость зная расстояние (путь) и время
Чему равна средняя скорость Vср если известны путь S и время t за которое этот путь преодолён?
Формула
Vср = S⁄t
Пример
К примеру, поезд преодолел расстояние в 1000 км за 16 часов. Посчитаем с какой средней скоростью он двигался:
Vср = 1000/16 = 62.5 км/ч
Как найти среднюю скорость зная скорости на участках пути
Чтобы найти среднюю скорость Vср на протяжении всего пути, зная показатели скорости на его участках (V1 , V2 , … Vn), следует найти среднее гармоническое этих скоростей.
Формула
| Vср | = | n |
| 1⁄V1 + 1⁄V2 + … + 1⁄Vn |
Пример
Средняя скорость через две скорости
Автомобиль проехал некий путь, при этом первые полпути он ехал со скоростью 80 км/ч, а вторые полпути – со скоростью 20 км/ч. Определим среднюю скорость этого автомобиля:
| Vср | = | 2 | = | 2 | = 32 |
| 1⁄80 + 1⁄20 | 0.0125 + 0.05 |
Средняя скорость автомобиля равна 32 км/ч.
Нередко, при решении задач по физике, ученики путают (а если точнее не знают вообще отличий) среднюю и среднеарифметическую скорости. Сегодня внесём ясность в эти определения, выучим их и будем применять при решении задач.
Вспомним определение, которое вводится ещё при изучении математики в 5 классе – среднее арифметическое. Среднее арифметическое чисел Х1 , Х2 , Х3, … Хn – есть отношение суммы этих чисел к числу слагаемых.
Хср = (Х1 + Х2 +Х3 + ….. + Хn)/n.
Задача 1.
Гоночную трассу первый автомобиль прошёл со скоростью 120 км/ч, второй – со скоростью 131 км/ч, а третий – со скоростью 115 км/ч. Рассчитайте среднеарифметическую скорость команды.
Решение.
ϑср = (120 км/ч + 131 км/ч + 115км/ч)/3 = 122 км/ч.
Ответ: ϑср = 122 км/ч.
Теперь перейдём к понятию средняя скорость движения.
Средняя скорость – физическая величина, численно равная отношению всего пути, пройденного телом ко всему времени движения.
<ϑ> = весь путь / все время
Задача 2.
Путешественник проехал 8 км со скорость 16 км/ч, затем, у него был 30 минут привал, а оставшиеся 15 км он проехал со скорость 10 км/ч. Рассчитайте среднюю скорость путешественника на всём участке пути.
Решение.
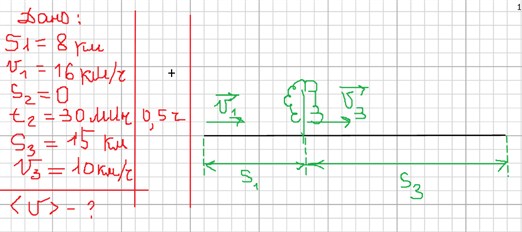 Предварительно надо рассчитать время t1 и t3 .
Предварительно надо рассчитать время t1 и t3 .
t1 = S1/ϑ1 = 8 км / 16 км/ч = 0,5 ч, t3 = S3/ϑ3 = 15 км / 10 км/ч = 1,5 ч.
<ϑ> = (S1 + S2 + S3 ) / t1 + t2 + t3 = (8 км + 0 + 15 км) / 0,5 ч + 0,5 ч + 1,5 ч = 23 км / 2,5 ч = 9,2 км/ч.
Ответ: <ϑ>= 9,2 км/ч.
Как видим, нет ничего сложного в этих определениях и формулах. Необходимо только внимательно прочитать статью и выучить эти формулы и определения. Удачи!
Остались вопросы? Не знаете, как решить задачу по физике?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.

В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.
Определение средней скорости
Средней скоростью движения ![]() тела называется отношение пути
тела называется отношение пути ![]() , пройденного телом, ко времени
, пройденного телом, ко времени ![]() , в течение которого двигалось тело:
, в течение которого двигалось тело:
![]()
Научимся ее находить на примере следующей задачи:
Тело двигалось 3 мин. со скоростью 5 м/с, после чего 7 мин. двигалось со скоростью 3 м/с. Найти среднюю скорость движения тела.
Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей ![]() и
и ![]() , которое равно:
, которое равно:
![]() м/с.
м/с.
Частные случаи нахождения средней скорости
1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью ![]() , а вторую половину пути — со скоростью
, а вторую половину пути — со скоростью ![]() . Требуется найти среднюю скорость движения тела.
. Требуется найти среднюю скорость движения тела.
![Rendered by QuickLaTeX.com [ upsilon_{cp} = frac{s}{t_1+t_2} = frac{s}{frac{s}{2upsilon_1}+frac{s}{2upsilon_2}} = frac{2upsilon_1upsilon_2}{upsilon_1+upsilon_2}. ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-7360def65faa837f59240afaf124708c_l3.png)
2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью ![]() в течение некоторого промежутка времени, а затем стало двигаться со скоростью
в течение некоторого промежутка времени, а затем стало двигаться со скоростью ![]() в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.
в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.
![]()
Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей ![]() и
и ![]() на двух участках пути.
на двух участках пути.
Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.
Пройденный телом путь составляет: ![]() м. Можно найти также путь, который прошло тело за последние
м. Можно найти также путь, который прошло тело за последние ![]() с своего движения:
с своего движения: ![]() м. Тогда за первые
м. Тогда за первые ![]() с своего движения тело преодолело путь в
с своего движения тело преодолело путь в ![]() м. Следовательно, средняя скорость на этом участке пути составила:
м. Следовательно, средняя скорость на этом участке пути составила:
![]() м/с.
м/с.
Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!
Репетитор по физике на Юго-Западной
Сергей Валерьевич




