Как найти среднюю арифметическую скорость молекул газа

Наиболее вероятная, среднеквадратичная и средняя арифметическая скорости молекул газа

Рассмотрим, как изменяется с абсолютной
величиной скорости число частиц,
приходящихся на единичный интервал
скоростей, при единичной концентрации
частиц.

График функции распределения Максвелла

,

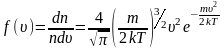
приведен
на рисунке 2.6.

Рис.
2.6

Из
графика видно, что при «малых» υ,
т.е. при

,
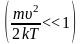
имеем

;
затем

достигает максимума А
и далее экспоненциально спадает

.

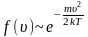
Величину
скорости, на которую приходится максимум
зависимости

,
называют
наиболее вероятной скоростью.

Найдем
эту скорость из условия равенства
производной

.

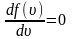
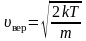
, (2.3.6)

– наиболее
вероятная скорость одной молекулы.

Для
одного моля газа:

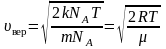
. (2.3.7)

Среднюю
квадратичную скорость
найдем, используя соотношение

:

– для одной молекулы. (2.3.8)

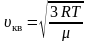
– для одного моля газа. (2.3.9)

Средняя
арифметическая скорость:

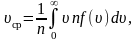
где

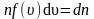
– число молекул со скоростью от υ
до

.
Если подставить сюда f(υ)
и вычислить, то получим:

–
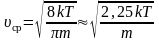
для одной молекулы. (2.3.10)

–
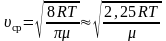
для одного моля газа. (2.3.11)

Все
три скорости незначительно отличаются
друг от друга множителем порядка единицы,
причем

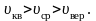
Формула Максвелла для относительных скоростей

Для
решения многих задач удобно использовать
формулу Максвелла, где скорость выражена
в относительных единицах.

Относительную
скорость обозначим через u:

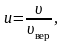
(2.3.13)

где

.
Тогда из (2.3.3), получим

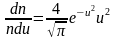
. (2.3.14)

Это
уравнение универсальное. В
таком виде функция
распределения
не зависит ни от рода газа, ни от
температуры.

На
рисунке 2.7 показано максвелловское
распределение частиц f(υ),
имеющих скорости от υ до

За единицу скорости здесь взята наиболее
вероятная скорость.

Полезно
знать, что

.

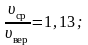
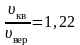
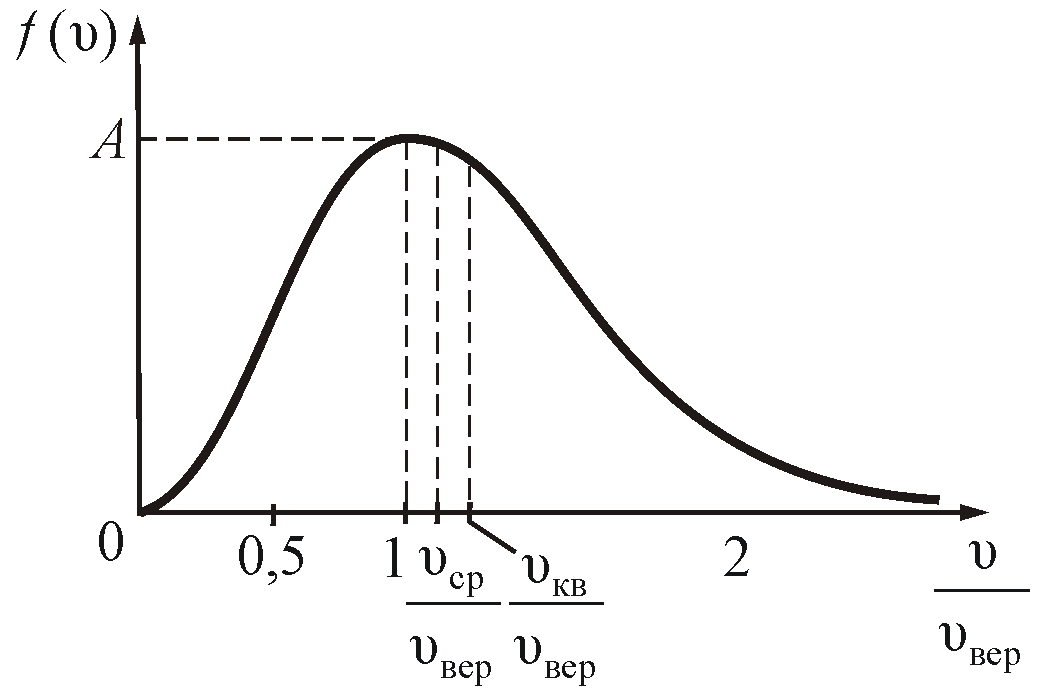
Рис.
2.7

Зависимость функции распределения Максвелла от массы молекул и температуры газа

На
рисунке 2.8 показана зависимость

при различных температурах и массах
молекул газа.

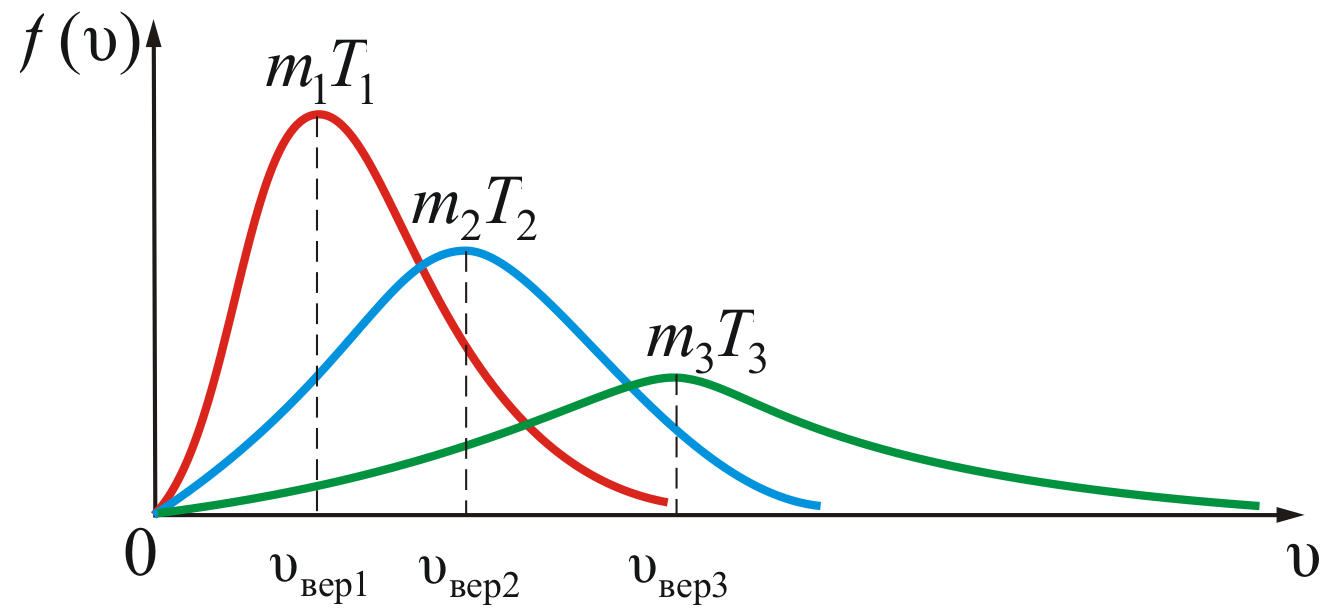
Рис.
2.8

Из
рисунка 2.8 можно проследить за изменением

при изменении m
и T.
В данном случае

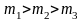
(при

)
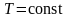
или

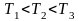
(при

).
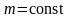
Площадь
под кривой величина постоянная,
равная единице (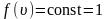
),
поэтому важно знать как будет изменяться
положение максимума кривой:

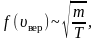
кроме
того

Максвелловский
закон распределения по скоростям и все
вытекающие следствия справедливы только
для газа в равновесной системе. Закон
статистический, и выполняется тем лучше,
чем больше число молекул.

Барометрическая формула

Рассмотрим
ещё один очень важный закон.

Атмосферное
давление на какой-либо высоте h
обусловлено весом слоёв газа, лежащих
выше. Пусть P
– давление на высоте h,
а


–
на высоте

(рис. 2.9).

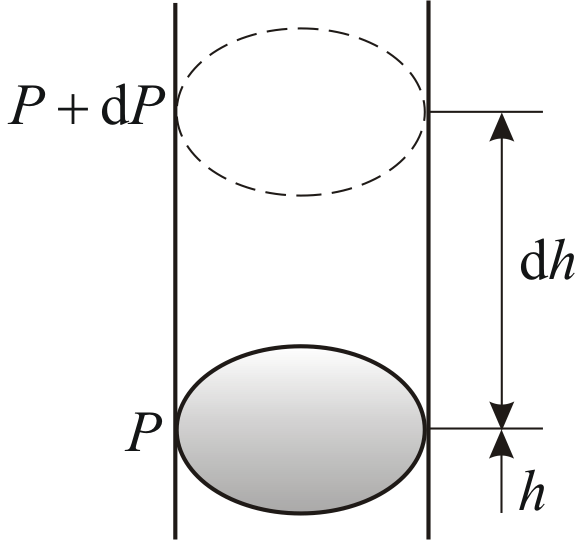
Рис.
2.9

Причём

,
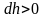
а dР
< 0, так как на большей высоте давление
меньше. Разность давления

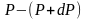
равна весу газа, заключённого в объёме
цилиндра с площадью основания равного
единице и высотой dh.

Т.к.

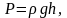
где


плотность газа на высоте h,
медленно убывающая с высотой, то можно
записать:

.

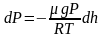
или

.

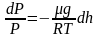
Проинтегрировав
это выражение, получим:

,

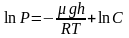
где
С
– произвольная постоянная.

В
силу произвольности, примем, что С
= Р₀
– давление на высоте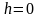
.
Отсюда, после потенцирования, получаем
барометрическую формулу:

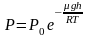
(2.4.1)

Из
формулы (2.4.1) следует, что P
убывает с высотой тем быстрее, чем
тяжелее газ (чем больше μ) и чем ниже
температура (например, на больших высотах
концентрация легких газов Не и Н₂
гораздо больше, чем у поверхности Земли).

На
рисунке 2.10 изображены две кривые, которые
можно трактовать, либо как соответствующие
разным μ (при одинаковой Т),
либо как отвечающие разным Т,
при одинаковых μ.

Таким
образом, чем тяжелее
газ (больше μ) и чем ниже
температура, тем быстрее
убывает давление.

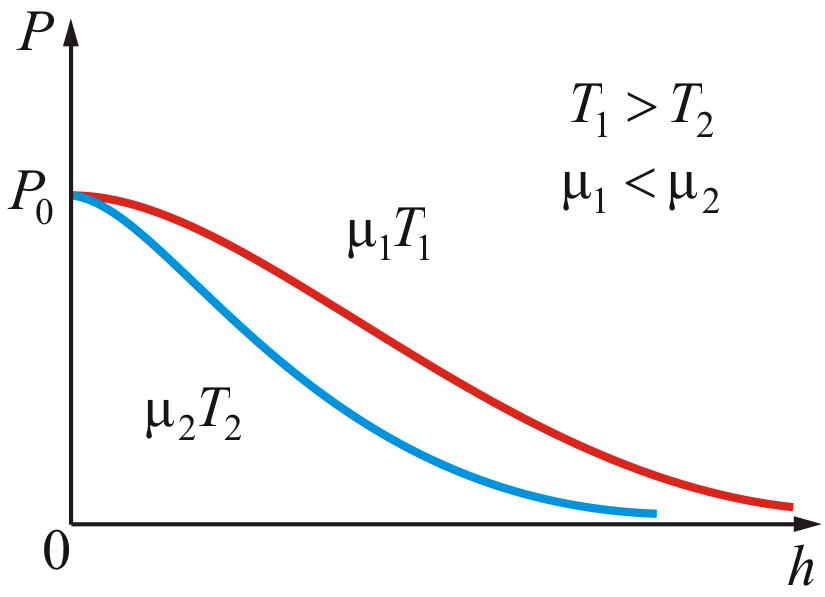
Рис.
2.10

Пусть идеальный газ находится в поле
консервативных сил в условиях теплового
равновесия. При этом концентрация газа
будет различной в точках с различной
потенциальной энергией, что необходимо
для соблюдения условий механического
равновесия. Так, число молекул в единичном
объеме n убывает с
удалением от поверхности Земли, и
давление, в силу соотношения

,
падает.

Если известно число молекул в единичном
объеме, то известно и давление, и наоборот.
Давление и плотность пропорциональны
друг другу, поскольку температура в
нашем случае постоянна. Давление с
уменьшением высоты должно возрастать,
потому что нижнему слою приходится
выдерживать вес всех расположенных
сверху атомов.

Исходя
из основного уравнения молекулярно-кинетической
теории:

,
заменим P
и P₀
в барометрической формуле (2.4.1) на n
и n₀
и получим распределение
Больцмана
для молярной массы газа:

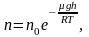
(2.5.1)

где
n₀
и n

число молекул в единичном объёме на
высоте h
= 0 и h.

Так
как

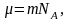
а

,
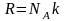
то (2.5.1) можно представить в виде

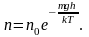
(2.5.2)

С
уменьшением температуры число молекул
на высотах, отличных от нуля, убывает.
При

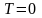
тепловое движение прекращается, все
молекулы расположились бы на земной
поверхности. При высоких температурах,
наоборот, молекулы оказываются
распределёнными по высоте почти
равномерно, а плотность молекул медленно
убывает с высотой. Так как

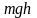
– это потенциальная энергия U,
то на разных высотах

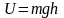
– различна. Следовательно, (2.5.2)
характеризует распределение частиц по
значениям потенциальной энергии:

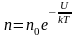
, (2.5.3)

– это
закон распределения частиц по потенциальным
энергиям – распределение Больцмана.
Здесь n₀
– число молекул в единице объёма там,
где

.

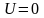
На
рисунке 2.11 показана зависимость
концентрации различных газов от высоты.
Видно, что число более тяжелых молекул
с высотой убывает быстрее, чем легких.

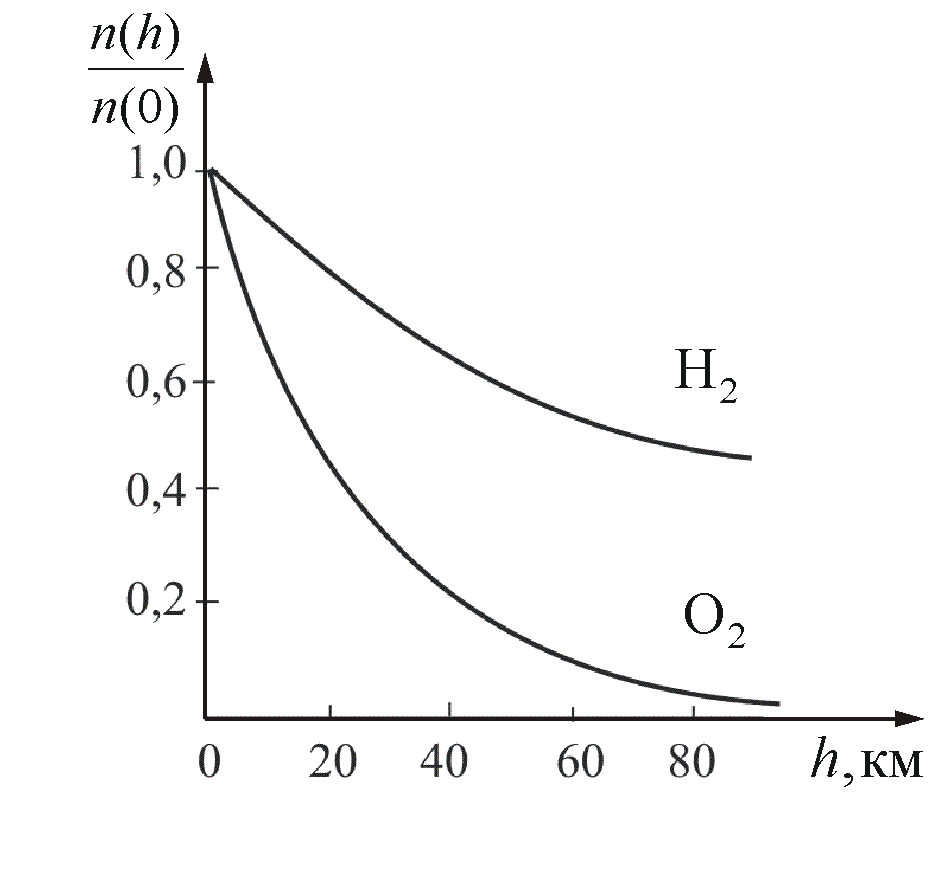
Рис.
2.11

Из
(2.5.3) можно получить, что отношение
концентраций молекул в точках с U₁
и U₂
равно:

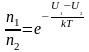
. (2.5.4)

Больцман
доказал, что соотношение (2.5.3) справедливо
не только в потенциальном поле сил
гравитации, но и в любом потенциальном
поле, для совокупности любых одинаковых
частиц, находящихся в состоянии
хаотического теплового движения.

В
п. 2.3 мы получили выражение для распределения
молекул по скоростям (распределение
Максвелла):

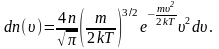
Из
этого выражения легко найти
распределение молекул газа по значениям
кинетической энергии
K.
Для этого перейдём от переменной υ
к переменной

:

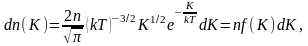
где
dn(K)
– число молекул, имеющих кинетическую
энергию поступательного движения,
заключённую в интервале от K

до

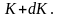
Отсюда получим функцию
распределения молекул по энергиям
теплового движения:

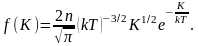
(2.6.1)

Средняя
кинетическая энергия

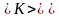
молекулы идеального газа:

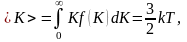
то
есть получаем результат, совпадающий
с прежним результатом, полученным в п.
1.3.

Итак,
закон Максвелла даёт распределение
частиц по значениям кинетической
энергии, а закон Больцмана – распределение
частиц по значениям потенциальной
энергии. Оба распределения можно
объединить в единый закон
Максвелла – Больцмана:

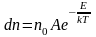
. (2.6.2)

Здесь
n₀
– число молекул в единице объёма в той
точке, где

,

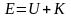
– полная энергия.

В
последнем выражении, потенциальная и
кинетическая энергии, а следовательно
и полная энергия Е,
могут принимать непрерывный ряд значений.
Если же энергия частицы может принимать
лишь дискретный ряд значений Е₁,
Е₂…,
(как это имеет место, например, для
внутренней энергии атома), то в этом
случае распределение Больцмана имеет
вид:

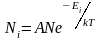
, (2.6.3)

где
N_i
– число частиц, находящихся в состоянии
с энергией Е_i,
а А
– коэффициент пропорциональности,
который должен удовлетворять условию

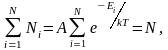
где
N
– полное число частиц в рассматриваемой
системе.

Тогда
окончательное выражение распределения
Максвелла – Больцмана для случая
дискретных значений энергий
будет иметь вид:

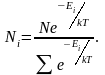
(2.6.4)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

0 Пользователей и 1 Гость просматривают эту тему.

---

---

Для характеристики движения молекул в физике используют две скорости: среднюю и среднюю квадратичную скорость молекул.

Важно. Следует обязательно понимать, что в реальных условиях мы не можем точно знать ни конкретное число молекул в системе, ни тем более скорость каждой из них в конкретный момент времени. Это обусловлено неимоверно гигантским числом частиц в реальных и даже сколько-нибудь приближенных к ним системах. Например, в 1 см³ при давлении 200 мм. рт. ст. содержится 4,18*1018 молекул водорода. Говоря более понятными категориями, это более чем 4 миллиарда миллиардов. Заметим, что указанное давление меньше атмосферного почти в 4 раза. Последнее в среднем равняется 760 мм. рт. ст. Разрежённый водород по своим свойствам наиболее близок к идеальному газу. В данном случае физика вынуждена иметь дело с распределениями скоростей и энергий частиц.

Что такое средняя скорость движения молекул

Среднюю скорость движения молекул часто именуют скоростью их теплового движения.

Как определить среднюю квадратичную скорость движения молекул

Если обе её части возвести в квадрат и проинтегрировать, то получим выражение:

[langlemathrm{VKB}rangle^{2}=int_{0}^{infty} v^{2} F(v) d v]

Ещё одно выражение для среднеквадратичной скорости:

[leftlangle V_{K B}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]

Именно она присутствует в уравнении, именуемом основным уравнением молекулярно-кинетической теории

P = (1/3)nm*<Vкв>

Где n – концентрация молекул, которая вычисляется делением их общего числа на объём.

Пример. 1.

Рассмотрим простейший случай, чтобы использование интегрирования не затруднило понимание сути явления и помогло лучше понять материал. Вычислим как меняется средняя скорость движения молекул в идеальном газе при линейном увеличении его давления. График следующий:

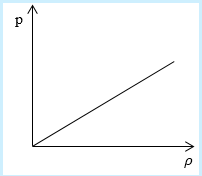
Напомним, что средняя скорость частиц:

[mathrm{Vcp}=sqrt{frac{8 R T}{pi m_{0}}}]

Если присмотреться к представленному графику, то можно заметить, что P приблизительно равно ρ‎. Эти две величины можно связать соотношением

P=C*ρ‎

Где С – некоторая постоянная величина, константа.

Далее считаем m₀= ρ/n, p = n*k*T = C* ρ. Отсюда следует, что k*T = (C*ρ)/n.

Нужно лишь подставить эти значения в формулу для средней скорости:

[V c p=sqrt{8 mathrm{kT} / pi mathrm{m}}=sqrt{(8 mathrm{C} rho / pi mathrm{n})(mathrm{n} / rho)}=sqrt{8 mathrm{C} / pi}]

В полученном выражении нет ни одной переменной величины, т. е. при увеличении давления, вопреки ожиданиям, скорость оказалась неизменной.

Ответ: В процессе, который был дан нам на графике, при увеличении давления средняя скорость молекул никак не меняется.

Пример. 2.

Определим среднюю квадратичную скорость молекул газа при условии, что нам известны его давление (P), молярная масса (M) и концентрация частиц (n).

Воспользуемся формулой:

[leftlanglemathrm{V}_{kappa в}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]

Также нам потребуется уравнение Менделеева-Клайперона

Здесь мы воспользовались тем, что:

m/μ = N/N_a

PV = (m/μ)*RT = (N/N_a)*RT

Если обе части этого уравнения поделить на V и принять во внимание, что

(N/V) = n, то можно получить

P = (n/N_a)*RT. Отсюда находим, что RT = (p*N)/n

Если мы это подставим в выражение для среднеквадратичной скорости [leftlangle V_{K B}rightrangle=sqrt{3 mathrm{kT} / mathrm{m}_{0}}=sqrt{3 mathrm{RT} / mu}], получим, что средняя квадратичная скорость движения молекул газа: [leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]

Ответ: Формула средней квадратичной скорости молекул исходя из данный нам условий следующая:

[leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]

Значительная часть явлений молекулярной физики определяется скоростями молекул. Несмотря на это, нахождение скоростей молекул газа приобретает как теоретического, так и практического значения.

Виды скоростей молекул газа

Скорости газовых молекул в результате их хаотического движения отличаются как по величине, так и по направлению. Скорость данной молекулы газа в данный момент времени есть величина случайная. В молекулярно-кинетической теории газов пользуются понятиями средней (vv), средней квадратичной (vквv_{кв}) и наиболее вероятной (νHν_H) скоростей. Эти скорости задаются для равновесных состояний газа.

Средняя (или среднеарифметическая) скорость определяется уравнением

v=1n∑i=1nviv=frac{1}{n}sumlimits_{i=1}^{n}{{{v}_{i}}}

где viv_i – скорость ii-й молекулы;

nn –количество молекул.

Средняя квадратичная скорость определяется как:

vкв=v2=3kTm{{v}_{кв}}=sqrt{{{v}^{2}}}=sqrt{frac{3kT}{m}}

По этой формуле можно вычислить также скорость броуновских частиц. Конечно, при этом mm –масса броуновской частицы.

Выражению vквv_{кв} можно придать более удобный вид, умножив числитель и знаменатель под корнем на число Авогадро и учитывая, что kN=RkN = R и mN=МmN = М,

vкв=3RTM{{v}_{кв}}=sqrt{frac{3RT}{M}}

Среднюю квадратичную скорость называют еще тепловой. Значение vкв для газов достаточно велики. Так, для водорода при комнатной температуре vкв=1,9⋅103v_{кв} = 1,9 · 10^3 м/с, то есть около 2 км/с.

Тепловая скорость, как видно из уравнения, пропорциональна корню температуры и обратно пропорциональна корню массы. Это обстоятельство определяет, что тепловое движение– достаточно интенсивно для молекул, заметно для микроскопически малых частиц, которые осуществляют броуновское движение, и совершенно незаметно для тяжелых тел.

Экспериментальное определение скоростей газовых молекул

Большой интерес представляет непосредственное экспериментальное определение скоростей газовых молекул. Оно является прямым подтверждением многих результатов и положений молекулярно-кинетической теории. Впервые такое исследование провел А. Штерн в 1920 г. Источником атомов, скорость которых измерялась, в опыте Штерна был молекулярный пучок атомов серебра Ag. Схема установки приведены на рис. 1. На оси системы двух коаксиальных цилиндрических поверхностей натянуто платиновый провод, покрытый слоем серебра.

Примечание

В других опытах использовали также висмут, кадмий, цезий.

Проволока разогревается электрическим током. Так, при температуре около 1300°С серебро с поверхности проволоки испаряется. Таким образом создавался линейный источник «Ag-лучей» и в камере цилиндров, воздух из которой предварительно откачивался при давлении 1,3 · 10^-4 Па, образовывался одноатомный газ серебра. Часть атомов серебра через диафрагмы s₁ и s₂ проходила, образуя молекулярный пучок, к поверхности внешнего цилиндра, где оседала на прозрачной пластинке, создавая слой в виде узкой полосы.

Рис. 1

На первой стадии опыта Штерна установка находится в состоянии покоя. При достижении равновесного состояния (температура проволоки достигала определенного значения, которое определяли по её свечению) атомы серебра оседали у точки а₁. На второй стадии опыта оба цилиндра приводились в достаточно быстрое вращение с частотой 41,7 с^-1.

При этом атомы серебра, двигаясь в вакууме прямолинейно, оседали у точки b. Смещение полосы объясняется тем, что пока атомы серебра пролетают по инерции путь r, внешний цилиндр успевает вернуться на угол φ=ωtφ = ωt, то есть каждая точка внешнего цилиндра смещается на расстояние Δs=ωrtΔs = ωrt, где ωω –угловая скорость его вращения; tt –время, за который атомы серебра проходят путь r. Таким образом,

t=rv=Δsωrt=frac{r}{v}=frac{Delta s}{omega r}

где vv – скорость атомов серебра.

Отсюда

v=ωr2Δsv=frac{omega {{r}^{2}}}{Delta s}

Измеряя смещение полос атомов серебра ΔsΔs и угловую скорость вращения прибора, можно определить скорость атомов серебра. Она приблизительно описывалась выражением

(3,5kTm)12{{left( 3,5frac{kT}{m} right)}^{frac{1}{2}}}

что согласуется со средней скоростью молекул, которые определяются по формуле

v=8kTπmv=sqrt{frac{8kT}{pi m}}

Результаты опытов Штерна показали, что на самом деле картина структуры полосы сложнее.

Смещенная возле точки b полоса была не резко ограниченной, а размытой (рис. 2).

Рис. 2

Несмотря на то, что атомы серебра имеют разные скорости, более быстрым атомам должны соответствовать меньшие смещения, а тем более медленным – большие. Таким образом, результаты опыта Штерна вполне передают реальную картину теплового движения молекул.

Тест по теме «Скорость движения молекул»