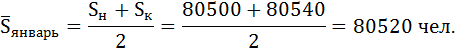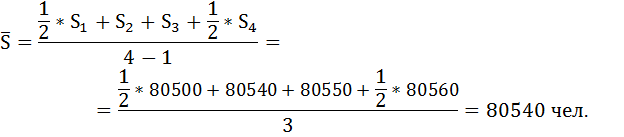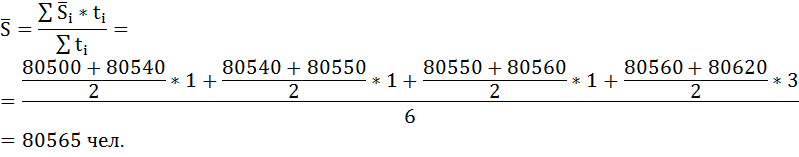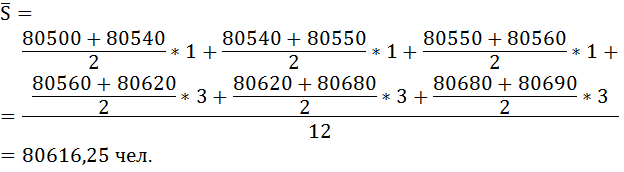Численность населения города составляла:
на 1 января – 80500 чел.,
на 1 февраля – 80540 чел.,
на 1 марта – 80550 чел.,
на 1 апреля – 80560 чел.,
на 1 июля – 80620 чел.,
на 1 октября – 80680 чел.,
на 1 января следующего года – 80690 чел.
Определите среднюю численность населения города за январь, в первом квартале, в первом полугодии и за год в целом.
Решение:
На примере данной задачи разберём все методы определения средней численности населения.
Найдём среднюю численность населения города за январь по формуле средней арифметической простой:
Найдём среднюю численность населения города за первый квартал.
Так как даты, на которые приходятся данные о численности, равны между собой, расчёт выполним по формуле средней хронологической:
В первом полугодии средняя численность населения будет определяться по формуле средней арифметической взвешенной, так как промежутки между датами не равные:
Среднюю численность за год в целом определим также по формуле средней арифметической взвешенной:
Постоянное
население – те, кто на момент переписи
постоянно проживает в данном городе,
включая временно отсутствующих, если
их отсутствие за пределами города не
превышает 1 года к моменту переписи.
Наличное
население – те, кто на момент переписи
оказался в городе на лицо, включая
временно проживающих иногородних, если
их временное проживание здесь не
превышает 1 год.
ПН
– численность постоянного населения,
НН
– наличного населения,
ВО
– временно отсутствующих,
ВП
– временно проживающих.
ПН=НН+ВО-ВП.
Юридическое
(приписное) население – лица, связанные
с данной территорией существующими
правилами регистрации.
Если
данные о численности населения разделены
между собой равными периодами времени,
то средняя определяется по методу
средней хронологической невзвешенной
xср(с
чертой)=((1/2)Х1+Х2+ … + Хn-1 + (1/2)Хn)/(n – 1)
Х
– значение уровней ряда – численность
населения на каждую дату ,
n
– число имеющихся показателей.
Если
же между отдельными значениями численности
лежат неравные промежутки времени, то
есть мы имеем дело с рядом динамики с
неравными интервалами, то рассчитывается
средняя хронологическая взвешенная:
xср=(сумма((Yi+Yi+1)*Ti))/(2*сумма(Ti))
Состав
изучается по признакам:
1.Место
проживания – городское и сельское,
2.Род
занятий – сельскохозяйственное и
несельскохоз.,
3.Пол
и возраст.
По
другим признакам (образование, наличие
детей, состав в браке) население изучают
только по данным переписи.
3.Источники данных о численности населения. Методика расчета средней численности населения.
Основным
источником информации о населении
является сплошная перепись населения,
который, как правило, проводится раз в
десять лет. Отдельные сведения собираются
на основе выборочной переписи населения.
При переписи населения учитываются две
категории населения: наличное население
– лица, фактически находящиеся на момент
переписи в данном населенном пункте,
включая временно проживающих и постоянное
население – лица, для которых данный
населенный пункт является местом
постоянного проживания, включая временно
отсутствующих.
Еще
используют данные органов ЗАГС, данные
ОВД о регистрации прибытия и выбытия,
Эти методы позволяют измерять население
между переписями.
Средняя
числен.населения м. определяться разными
способами:
Средняя
арифметическая- если известна численность
населения на начало и конец года.
Нср=
(Н1+Н2)/2 , где, Н1 и Н2 — численность
населения на начало и конец периода.
Простая
хронологическая средняя – если интервалы
между наблюдениями расположены через
равные промежутки времени — то формуле
простой хронологической средней:
где
Нi— численность населения на каждую
дату.
Нср=
(Н1/2+Н2+…+Нn-1+Нn/2)/(n-1)
Хронологическая
взвешенная – если замеры численности
населения проводились через неравные
промежутки времени то — по формуле
хронологической взвешенной:
Hср=(сумма(Нi*Ti))/сумма(Ti)
Нi-
полусумма двух соседних уровней ряда
динамики;
Ti—
промежуток между двумя уровнями ряда,
выраженный в днях, неделях или месяцах.
Например
возьмём промежутки равными месяцам.
СЧН
=
(((4836+4800)/2)*3+((4800+4905)/2)*3+((4905+4890)/2)*3+((4890+4805)/2)*3)/12=4854
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Формула для расчета среднего значения населения
Средние значения населения — это среднее или среднее всех значений в данной совокупности. Он рассчитывается как сумма всех значений в совокупности, обозначаемая суммой X, деленной на количество значений совокупности, обозначаемых как N.
Он получается путем суммирования всех наблюдений в группе и деления суммы на количество наблюдений. Когда для вычисления статистического параметра используется весь набор данных, набор данных представляет собой совокупность. Например, доходность всех акций, котирующихся на фондовой бирже NASDAQ, среди населения этой группы. Таким образом, для этого примера совокупность означает, что среднее значение означает среднее математическое значение, рассчитанное для двух или более значений. В основном есть два способа: среднее арифметическое, когда все числа складываются и делятся на их веса, и среднее геометрическое, когда мы умножаем числа вместе, берем корень N и вычитаем из него единицу. акций, котирующихся на фондовой бирже NASDAQ, будет средней доходностью всех акций, котирующихся на этой бирже.
Чтобы вычислить среднее значение совокупности для группы, нам сначала нужно найти сумму всех наблюдаемых значений. Итак, если общее количество наблюдаемых значений обозначить через X, то сумма всех наблюдаемых значений будет равна ∑X. И пусть число наблюдений в популяции равно N.
Формула представлена следующим образом,
µ= ∑X/N
- µ = среднее значение населения
Оглавление
- Формула для расчета среднего значения населения
- Примеры
- Пример №1
- Пример #2
- Пример №3
- Актуальность и использование
- Рекомендуемые статьи
- Примеры
Примеры
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон формулы Excel для среднего населения здесь — Формула средней численности населения Шаблон Excel
Пример №1
Давайте проанализируем доходность акции XYZ за последние двенадцать лет. А доходность акций за последние двенадцать лет составляет 12%, 25%, 16%, 14%, 40%, 15%, 13%, 17%, 23%, 13%, 17% и 19%. Чтобы вычислить среднее значение для всего населения, мы должны сначала найти сумму всех наблюдаемых значений. Таким образом, в этом примере ∑X составляет 224%, а количество наблюдаемых значений для совокупности равно 12, поскольку оно включает в себя доход от акций за 12-летний период.
С этими двумя переменными мы можем рассчитать среднее значение доходности акций с помощью формулы.
Приведены следующие данные:
Следовательно, используя приведенную выше информацию, среднее значение можно рассчитать как
- µ= 224%/12
Пример показывает, что средний или средний доход для наблюдаемого значения составляет 19%.
Пример #2
Проанализируем доходность тематического паевого фонда за последние восемь лет. А доходность акций за последние двенадцать лет составляет 25%, 16%, 14%, 15%, 13%, 23%, 33% и 27%. Чтобы вычислить среднее значение для всего населения, мы должны сначала найти сумму всех наблюдаемых значений. Таким образом, в этом примере ∑X составляет 166%, а количество наблюдаемых значений для населения равно 8, поскольку оно включает доход взаимного фонда за 8 лет.
С этими двумя переменными мы можем рассчитать среднее значение доходности акций с помощью формулы.
Ниже приведены данные для расчета:
Следовательно, среднее значение можно рассчитать как
- µ= 166%/8
Пример показывает, что средний или средний доход для наблюдаемого значения составляет 21%.
Пример №3
Найдем среднее значение веса 15 учеников в классе. Вес каждого ученика в классе из 15 человек в кг составляет 35, 36, 42, 40, 44, 45, 38, 42, 39, 42, 44, 45, 48, 42 и 40. среднее значение для всего населения, мы должны сначала найти сумму всех наблюдаемых значений. Таким образом, в этом примере ∑X составляет 622 кг, а количество наблюдаемых значений для населения равно 15, поскольку оно включает в себя вес 15 учащихся.
С этими двумя переменными мы можем рассчитать среднее значение доходности акций с помощью формулы.
Ниже приведены данные для расчета:
Следовательно, используя приведенную выше информацию, среднее значение населения можно рассчитать как
- мк = 622/15
Пример показывает, что средний или средний доход для наблюдаемого значения составляет 41,47.
Актуальность и использование
Средняя численность населения является очень важным статистическим параметром. Это помогает узнать среднее значение параметров населения. Среднее значение важно, поскольку его можно использовать для расчета ряда других статистических параметров, таких как дисперсия, стандартное отклонение и другие. Его можно рассчитать, используя понятие формулы среднего арифметического. Формула среднего арифметического. Среднее арифметическое обозначает среднее значение всех наблюдений ряда данных. Это совокупность всех значений в наборе данных, деленная на общее количество наблюдений. Подробнее. Он представляет собой среднее или среднее значение, на основе которого можно сделать вывод, является ли наблюдение высоким или низким во всей совокупности наблюдений.
Рекомендуемые статьи
Эта статья была руководством по формуле средней численности населения. Здесь мы обсуждаем расчет средних значений населения вместе с практическими примерами и загружаемым шаблоном Excel. Вы можете узнать больше о финансировании из следующих статей: –
- Среднее геометрическое и среднее арифметическое Среднее геометрическое и среднее арифметическое Среднее геометрическое — это расчет среднего или среднего значения ряда значений продукта, который учитывает эффект начисления сложных процентов и используется для определения эффективности инвестиций, тогда как среднее арифметическое — это расчет среднего значения по сумме значения, разделенные на количество значений.Подробнее
- Примеры среднего Примеры среднего Примеры Примеры среднего включают различные ситуации, когда мы можем применять арифметические, взвешенные, геометрические и гармонические средние значения для измерения центральной тенденции. Кроме того, мы используем среднее арифметическое в нашей повседневной жизни, чтобы найти процент, набранный студентом в учебе, или стоимость вечеринки на человека.Подробнее
- Mean vs MedianMean Vs MedianMean — это среднее значение заданных чисел. Он суммирует числа и делит их на количество чисел, которое дает нам среднее значение. С другой стороны, медиана возвращает среднее число из всего набора данных.Подробнее
- Формула выборочного распределенияФормула выборочного распределенияВыборочное распределение — это вероятностное распределение подробной статистики. Это помогает рассчитать средние значения, диапазон, стандартное отклонение и дисперсию для взятой выборки. Для размера выборки более 30 используется формула: µ͞x =µ и σ͞x =σ / √n читать дальше
- Аннуитет против единовременной суммыАннуитет против единовременной суммыАннуитет относится к серии частых платежей, сделанных через равные промежутки времени в течение определенного периода. В то время как единовременная выплата означает выплату причитающейся суммы сразу, т. е. расчет всей суммы одним платежом. читать далее
Изучение состава населения
Состав населения изучается с помощью группировок. При этом производят группировки населения по полу, возрасту, национальности, месту жительства, семейному положению, уровню образования как в целом по стране, так и по ее отдельным регионам.
Группировка населения по возрасту помогает решать различные задачи при определении контингентов дошкольников, школьников, численности трудоспособного населения и населения старше трудоспособного возраста. Группировка по возрасту строится как для всего населения, так и раздельно для мужчин и женщин, для городского и сельского населения.
Например, на 1 января 2001 г. из общей численности населения страны 144,8 млн. чел. численность мужского населения составляла 67,8 млн. чел. (47%), женского — 77,0 млн. чел. (53%); численность городского населения составляла 105,6 млн. чел. (73%); сельского — 39,2 млн. чел. (27%). Из общей численности населения России удельный вес лиц в возрасте моложе трудоспособного составлял 19,20%, в трудоспособном возрасте — 60,15%, старше трудоспособного — 20,65%.
Изучение численности населения и его размещения по территории страны
Численность населения РФ составляла на начало года:
| Год | Численность населения млн.чел |
| 1995 | 147,9 |
| 1996 | 147,6 |
| 1997 | 147,1 |
| 1998 | 146,7 |
| 1999 | 146,3 |
| 2000 | 145,6 |
| 2001 | 144,8 |
В российской статистике численность населения учитывается не только по стране в целом, но и по отдельным административно-территориальным единицам. В составе РФ 21 республика, 6 краев, 49 областей, 2 города федерального значения, 1 автономная область, 10 автономных округов.
Динамика численности населения характеризуется с помощью аналитических и средних показателей динамики (абсолютного прироста, темпа роста, темпа прироста, среднего абсолютного прироста за период, среднего темпа роста за период).
Средняя численность населения за период времени
Для расчета ряда показателей необходимо знать среднюю за период численность населения.
Среднюю численность населения можно рассчитать различными методами.
Средняя арифметическая
Если известна численность населения на начало и конец года, то средняя годовая численность населения рассчитывается как средняя арифметическая из этих двух чисел.
где, и
— численность населения на начало и конец периода.
Пример
- На начало года 200 тыс.чел.
- На конец года 260 тыс.чел.
СЧН = тыс.чел.
Среднехронологические величины используются для усреднения моментных показателей. Дело в том, что в экономическом анализе и экономической статистике используются как интервальные (за определенный период), так и моментные (на определенную дату) показатели. Чтобы найти средние величины интервальных показателей (выручка от продаж, прибыль и др.) как правило, используютсреднеарифметические величины. Для нахождения средних величин моментных показателей (об основных фондах, о численности работников на какую либо-дату, о населении) применяют среднехронологические величины. Их определяют по формуле:
— это ряд моментных показателей
Простая хронологическая средняя
Если интервалы между наблюдениями расположены через равные промежутки времени — то формуле простой хронологической средней:
где, ,
, и
— численность населения на каждую дату.
Пример
Численность населения:
- на 1 января 2008 года — 4836 тыс.чел.
- на 1 апреля 2008 года — 4800 тыс.чел.
- на 1 июля 2008 года — 4905 тыс.чел.
- на 1 октября 2008 года — 4890 тыс.чел.
- на 1 января 2009 года — 4805 тыс.чел.
Определить среднюю численность населения за год.
Решение
1. Сумму крайних интервалов поделенных на два и внутренних интервалов делим на количество дат отчетности минус один.
СЧН =
Хронологическая взвешенная
В случае если замеры численности населения проводились через неравные промежутки времени то — по формуле хронологической взвешенной:
где:
Например возьмём промежутки равными месяцам.
СЧН =
Ответ: 4854 чел.
Статистика помогает исследователям провести оценку процессов, которые происходят в системе. Различные факторы допускается группировать, сравнивать с другими подобными категориями. Население и процессы, происходящие в социальной сфере, исследуются статистикой довольно тщательно. Ведь это отражает на глобальном уровне существующую демографическую ситуацию.
Среднегодовая численность населения участвует во многих экономических исследованиях на макроуровне. Поэтому эту важную категорию данных постоянно контролируют, проводят пересчеты. Важность показателя, а также методики проведения анализа рассмотрены в статье.
Население
Чтобы иметь возможность определить среднегодовую численность населения города, района или страны, необходимо понимать суть предмета исследования. Демографическая ситуация может рассматриваться под разными углами зрения.
Населением называют всю численность людей, которые проживают в границах определенной территории. Для проведения анализа демографической ситуации этот показатель рассматривают в разрезе естественного воспроизводства (рождаемости и смертности) и миграции. Также исследуют структуру населения (по возрасту, полу, экономическому и социальному уровню и т. д.). Также данные о демографии показывают, как менялось расселение людей по территории.
Население исследуется статистикой при помощи общих и специальных методов. Это позволяет сделать полноценные, глубокие выводы о развитии демографических показателей.
Направления анализа
Среднегодовая численность населения оценивается с применением разных признаков группировки в зависимости от целей анализа. Демографическая картина, сложившаяся за определенный период времени на конкретно взятой территории, может рассматриваться в разрезе динамики общей численности населения.
Чтобы понимать, почему произошли те или иные изменения, необходимо оценить естественное движение, миграцию людей. Для этого в анализе принимают участие соответствующие данные. Чтобы иметь полное представление о группировании населения, формировании общей численности людей, их классифицируют по определенным признакам.
Например, исследование показывает, сколько на определенной территории проживает женщин и мужчин, какого они возраста, сколько людей из трудоспособного населения имеет квалификацию, высший уровень образования.
Формула расчета
Чтобы сделать пересчет населения, применяются различные формулы. Но порой расчет усложняется собором данных за несколько временных интервалов. Если есть информация на начало и конец периода, среднегодовая численность населения (формула) имеет такой вид:
ЧНсред. = (ЧНн.п. + ЧНк.п.) / 2, где ЧНсред. – средняя численность населения, ЧНн.п. – число населения на начало периода, ЧНк.п. – численность на конец периода.
Если статистические данные собирались за каждый месяц исследуемого периода, формула будет такой:
ЧНсред. = (0,5ЧН1 + ЧН2 … ЧНп-1 + 0,5ЧНп)(п-1), где ЧН1, ЧН2 … ЧНп-1 – число населения в начале месяца, п – количество месяцев.
Данные для анализа
Среднегодовая численность населения, формула которой была представлена выше, берет для расчета ряд данных. Необходимо вычислять постоянное количество населения, проживающее на этой территории (ПН). В него входит наличное количество людей, которые фактически проживают в районе исследования (НН).
Помимо этого показателя, для изучения демографического состояния страны берут во внимание категорию временно проживающего здесь населения (ВП). Также временно отсутствующие люди (ВО) принимают участие в подсчете. Только этот показатель отнимают из общей суммы. Формула постоянно проживающего населения выглядит так:
ПН = НН + ВП – ВО.
Чтобы различать показатель ВП и НН, берут во внимание интервал времени 6 месяцев. Если группа людей проживает на исследуемой территории больше полгода, их относят к наличному, а меньше полгода – к временному населению.
Перепись населения
Среднегодовая численность постоянного населения рассчитывается на основе данных переписи населения. Но этот процесс требует значительных затрат времени, сил и средств. Поэтому проводить перепись каждый месяц или даже год не представляется возможным.
Поэтому в промежутках между пересчетом количества людей на определенной территории применяют систему логических расчетов. Собирают статистические данные о рождении и смертности, миграционном движении. Но со временем накапливается определенная погрешность в показателях.
Поэтому для правильного определения среднегодовой численности населения все-таки требуется проводить периодически перепись.
Применение данных анализа
Расчет среднегодовой численности населения проводится с целью дальнейшего исследования демографических процессов. Результат анализа применяют при исчислении коэффициентов смертности и рождаемости, естественного воспроизводства. Их рассчитывают в разрезе каждой возрастной группы.
Также средняя численность применима при оценке количества трудоспособного и экономически активного населения. При этом могут рассматривать совокупность людей, выбывших или прибывших на территорию страны или области путем миграции. Это дает возможность оценить потенциал всей рабочей силы, сконцентрированной здесь.
Правильное распределение трудовых ресурсов является залогом экономического развития государства. Поэтому важность подсчета количества населения трудно переоценить.
Естественное движение населения
Среднегодовая численность населения, формула расчета которой была рассмотрена выше, участвует в оценке различных демографических показателей. Одним из них выступает естественное движение населения. Оно обусловлено природными процессами рождаемости и смертности.
За год среднее количество населения увеличивается на число новорожденных детей и уменьшается на число умерших людей. Это природный ход жизни. Относительно среднего количества населения находят коэффициенты естественного движения. Если показатель рождаемости превышает показатель смертности, наблюдается прирост (и наоборот).
Также при проведении подобного анализа выполняется разбивка населения по возрастным категориям. Так определяется, в какой группе была большая смертность. Это позволяет сделать вывод об уровне жизни на исследуемой территории, социальной защищенности граждан.
Миграция
Меняться показатель количества жителей может не только вследствие естественных процессов. Люди уезжают на заработки или, наоборот, приезжают с целью трудоустройства. Если такие переселенцы находятся или отсутствуют на исследуемом объекте более 6 месяцев, это обязательно учитывают при анализе.
Значительные миграционные потоки влияют на экономику. Рынок рабочей силы меняется как при уменьшении, так и при увеличении численности трудоспособных жителей.
Среднегодовая численность населения поможет найти как коэффициент роста, так и уменьшения предложения рабочей силы в регионе. Если слишком большой поток эмигрантов приедет в страну, будет повышаться уровень безработицы. Уменьшение количества трудоспособного населения ведет к дефициту бюджета, снижению пенсий, зарплат врачей, педагогов и т. д. Поэтому для контроля миграционного движения также крайне необходим представленный показатель.
Экономическая активность
Помимо изменений в количественном отношении всего населения страны или района, обязательно проводится структурный анализ. Обычно по уровню дохода различают три класса населения.
Среднегодовая численность экономически активного населения позволяет оценить покупательную способность жителей, их уровень жизни. В развитых странах большую часть социума составляют люди со средним достатком. Они могут приобретать необходимые продукты питания, вещи, периодически совершать крупные приобретения, путешествовать.
В таких государствах есть небольшой процент очень богатых и бедных людей. Если количество жителей с низким достатком значительно увеличивается, большая финансовая нагрузка падает на бюджет. При этом снижается совокупный уровень жизни.
Все группы экономически активного населения представляют в виде коэффициентов относительно среднегодовой численности населения.
Вероятностные таблицы
Чтобы определить среднегодовую численность населения без переписи, применяется метод построения вероятностных таблиц. Дело в том, что большинство демографических процессов можно предсказать заранее. Это касается естественного движения населения.
Таблица строится на основе нескольких утверждений. Естественное движение необратимо, ведь нельзя умереть и родиться дважды. Только один раз можно родить первого ребенка. Определенная очередность событий обязательно учитывается. Например, нельзя вступить во второй брак, если не было зарегистрировано первого.
Население разбивается на возрастные группы. Для каждой из них вероятность наступления того или иного события разная. Далее анализируется количество человек, входящих в каждую категорию.
С течением времени люди с определенной долей вероятности переходят в ту или иную группу. Так делается прогноз. Например, та категория населения, которая находится в трудоспособном возрасте, станет пенсионерами. Поэтому аналитики в силах предсказать, какое количество человек вольется в следующую группу.
Планирование
Планирование на макроэкономическом уровне невозможно произвести без статистических данных. Среднегодовая численность активного населения учитывается при изучении уровня жизни, покупательной способности, а также при разработке главного экономического документа страны (бюджета).
Количество его доходов и расходов нельзя спрогнозировать без учета количества и структуры жителей страны. Чем больше людей работает в небюджетной сфере, чем выше уровень их дохода, тем значительнее будут вливания в бюджетные фонды.
Если аналитики определяют падение входных потоков в будущем, необходимо разрабатывать мероприятия по улучшению ситуации. У каждого государства существует свой аппарат рычагов управления демографическими ресурсами. Создавая новые рабочие места, проводя грамотную социальную политику, повышая уровень жизни населения, можно сделать страну процветающей.
Анализ и планирование демографической ситуации производят с обязательным применением среднегодовых показателей численности населения, а также прочих структурных коэффициентов. Поэтому от правильности сбора данных и их изучения зависит адекватность планирования бюджета страны.
Рассмотрев такое понятие, как среднесписочная численность населения, можно понять важность этого показателя для макроэкономического анализа и планирования. Многие прогнозы на будущее страны, региона или города строятся после правильного сбора и обработки соответствующей информации. Это является необходимым действием при составлении плана бюджета и множества других важных финансовых документов.