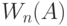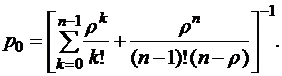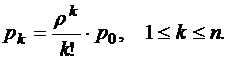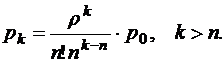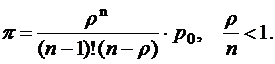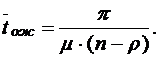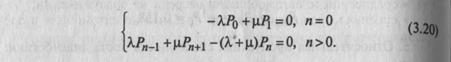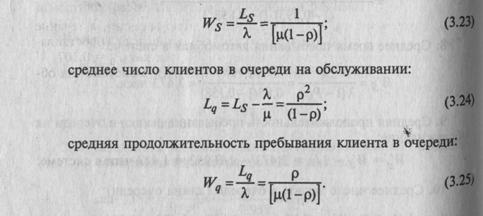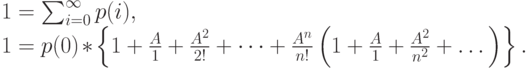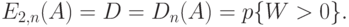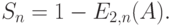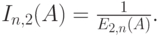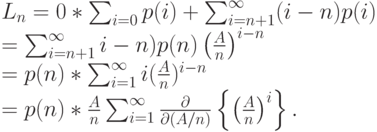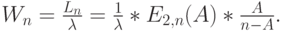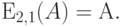Как найти среднюю длину очереди - Сайт, где вы сможете решить свои вопросы

СМО с ожиданием (очередью)

Системы с ожиданием при неограниченном входящем потоке

На n одинаковых каналов поступает простейший поток заявок интенсивностью λ. Если в момент поступления заявки все каналы заняты, то эта заявка становится в очередь и ждет начала облуживания. Время обслуживания каждой заявки является случайной величиной, которая подчиняется экспоненциальному закону распределения с параметром μ.

Расчетные формулы

Вероятность того, что все каналы свободны

Вероятность того, что занято kканалов, при условии, что общее число заявок, находящихся на обслуживании, не превосходит числа каналов,

Вероятность того, что в системе находится k заявок, в случае, когда их число больше числа каналов,

Вероятность того, что все каналы заняты,

Среднее время ожидания заявкой начала обслуживания в системе

Средняя длина очереди

Среднее число свободных от обслуживания каналов

Пример

Автозаправочная станция с двумя колонками обслуживает пуассоновский поток машин с интенсивностью λ=0,8 машин в минуту. Время обслуживания одной машины подчиняется показательному закону со средним значением 2 минуты. В данном районе нет другой АЗС, так что очередь перед АЗС может расти практически неограниченно. Найдите:

1) среднее число занятых колонок;

2) вероятность отсутствия очереди у АЗС;

3) вероятность того, что придется ждать начала обслуживания;

4) среднее число машин в очереди;

5) среднее время ожидания в очереди;

6) среднее время пребывания машины на АЗС;

7) среднее число машин на АЗС.

Решение. По условию задачи n=2, λ=0.8; μ=1/t_обсл=0.5; ρ=λ/μ=1.6

Поскольку ρ/n=0,8<1, то очередь не растет безгранично и имеет смысл говорить о предельном стационарном режиме работы системы массового обслуживания.

Находим вероятности состояний СМО:

Среднее число занятых колонок:

N_зан=n-N₀ = 2-(2·p₀+1·p₁) = 2-2·0.1111 – 0.1778 = 1.6

Вероятность отсутствия очереди у АЗС:

p₀+p₁+p₂ = 0.1111+0.1778+0.1422 = 0.4311

Вероятность того, что придется ждать начала обслуживания равна вероятности того, что все колонки заняты:

p₀+p₁+p₂ = 0.1111+0.1778+0.1422 = 0.4311

Среднее число машин в очереди:

Среднее время ожидания в очереди:

Среднее время пребывания машины на АЗС:

t_преб=t_обсл+t_ож = 2+3.5556 = 5.5556 мин.

Среднее число машин на АЗС:

N_зан+L_оч = 1.6+2.8444 = 4.4444

Рассмотрим одноканальную СМО с ожиданиями, в которой число каналов равно единице n = 1, интенсивность поступления заявок – λ, интенсивность обслуживания равна μ. Заявка, поступившая в тот момент времени, когда канал занят, становится в очередь и ждет обслуживания. Количество мест в очереди ограничено и равно m. Если все места в очереди заняты, то заявка покидает очередь не обслуженной. Проанализируем состояние системы:

S₀ – канал свободен;
S₁ – канал занят;
S₂ – канал занят, одна заявка в очереди;
S_k – канал занят, (k–1) заявок в очереди;
S_m_{+ 1} – канал занят, в очереди m заявок.

Изобразим граф состояний такой СМО (рис. 25).

Рис. 25

По формулам Эрланга найдем вероятности событий, состоящих в том, что СМО находится в состоянии S₁, S₂, …, S_m+1:

(28)

При этом вероятность того, что заявка, прибывшая в систему, найдет ее свободной, равна

. (29)

Отношение интенсивности поступления заявок λ к интенсивности обслуживания заявок μ есть приведенная интенсивность μ, т.е.

ρ=λ/μ

Произведем замену в формулах (28) и (29) отношения λ/&mu на ρ, тогда выражения примут вид:

(30)

Вероятность Р₀ будет вычисляться по следующей формуле:

p₀=[1+ρ+ρ²+ … +ρ^m+1]^-1. (31)

Выражение для вероятности P₀ есть геометрическая прогрессия, сумма которой будет равна

.

Таким образом, формулы (30) и (31) позволяют определить вероятность любого события, которое может произойти в системе, т. е. определить вероятность нахождения системы в любом состоянии.

Формула для P₀ справедлива для случая, когда ρ ≠ 1. В случае, когда ρ = 1, т. е. интенсивность поступления заявок равна интенсивности их обслуживания, используется другая формула для вычисления вероятности того, что система свободна:

,

где m – это количество заявок, находящихся в очереди.

Определим характеристики эффективности одноканальной СМО:

вероятность того, что очередная заявка, прибывшая в систему, получит отказ Р_отк;
абсолютную пропускную способность А,
относительную пропускную способность Q,
число занятых каналов k,
среднее число заявок в очереди r,
среднее число заявок, связанных с СМО, z.

Очередная заявка, поступившая в систему, получает отказ в том случае, когда занят канал, т. е. идет обслуживание другой заявки, и все m мест в очереди также заняты. тогда вероятность этого события можно вычислить по следующей формуле:

. (32)

Вероятность того, что заявка придет в систему и либо немедленно будет обслужена, либо будут места в очереди, т. е. относительную пропускную способность, можно найти по формуле

. (33)

Среднее число заявок, которые могут быть обслужены в единицу времени, т. е. абсолютную пропускную способность, рассчитывают следующим образом:

A=Q·λ (34)

Таким образом, по формулам (32), (33), (34) можно вычислить основные показатели эффективности для любой системы массового обслуживания. теперь выведем выражения для вычисления характеристик, присущих лишь данной СМО.

Среднее число заявок в очереди r определим как математическое ожидание дискретной случайной величины, где R – число заявок в очереди.

♦ Р₂ – это вероятность того, что в очереди на обслуживание находится одна заявка;

♦ Р₃ – вероятность того, что в очереди две заявки;

♦ Р_k – вероятность того, что в очереди (k–1) заявка;

♦ Р_m_{+ 1} – вероятность того что в очереди m заявок.

Тогда среднее число заявок в очереди можно вычислить следующим образом:

r=1·P²+2·P³+ … +(k-1)·P^k+ … +m·P^m+1. (35)

Подставим в формулу (35) найденные ранее значения вероятностей, вычисленные в формуле (30):

r=1·ρ²·p₀+2·ρ³·p₀+ … +(k-1)·ρ^k·p₀+ … +m·ρ^m+1·p₀. (35)

Вынесем за скобку вероятность P₀ и Р², тогда получим итоговую формулу для вычисления среднего числа заявок в очереди на обслуживание:

r=ρ²·p₀(1+2·ρ+ … +(k-1)·ρ^k-2+ … +m·ρ^m-1)

Выведем формулу для среднего числа заявок, связанных с СМО, z, т. е. число заявок в очереди, находящихся на обслуживании. Рассмотрим общее число заявок, связанных с СМО, z как сумму двух величин среднего числа заявок в очереди r и числа занятых каналов k:

z = r+k.

Так как канал один, то число занятых каналов k может принимать значения 0 или 1. Вероятность того, что k = 0, т.е. система свободна, соответствует вероятности Р₀, значение которой можно найти по формуле (31). Если k= 1, т.е. канал занят обслуживанием заявки, но места в очереди еще есть, то вероятность этого события можно вычислить по формуле

.

Следовательно, z будет равно:

. (37)

Одноканальная СМО с ожиданием

Система массового обслуживания имеет один канал. Входящий поток заявок на обслуживание – простейший поток с интенсивностью l. Интенсивность потока обслуживания равна m (т. е. в среднем непрерывно занятый канал будет выдавать m. обслуженных заявок). Длительность обслуживания — случайная величина, подчиненная показательному закону распределения. Поток обслуживании является простейшим пуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.

Предположим, что независимо от того, сколько требований поступает на вход обслуживающей системы, данная система (очередь ⁺ обслуживаемые клиенты) не может вместить более N-требований (заявок), т. е. клиенты, не попавшие в ожидание, вынуждены обслуживаться в другом месте. Наконец, источник, порождающий заявки на обслуживание, имеет неограниченную (бесконечно большую) емкость.

Граф состояний СМО в этом случае имеет вид, показанный на Рис. 3.2.

Граф состояний одноканальной СМО с ожиданием (схема гибели и размножения)

Состояния СМО имеют следующую интерпретацию:

S₀ – канал свободен

S₁ – канал занят (очереди нет);

S₂ – канал занят (одна заявка стоит в очереди);

………………………………

S_n–канал занят (n – 1 заявок стоит в очереди);

……………………………

S_N – канал занят (N – 1 заявок стоит в очереди).

Стационарный провес в данной системе будет описываться следующей системой алгебраических уравнений:

п –номер состояния.

Решение приведенной выше системы уравнений (3.10) для нашей модели СМО имеет вид

Следует отметить, что выполнение условия стационарности для данной СМО необязательно, поскольку число допускаемых в обслуживающую систему заявок контролируется путем введения ограничения на длину очереди (которая не может превышать N— 1), а не соотношением между интенсивностями входного потока, т. е. не отношением

l/m = p

Определим характеристики одноканальной СМОс ожиданием и ограниченной длиной очереди, равной (N —1):

вероятность отказа в обслуживании заявки:
среднее время пребывания заявки в системе:
средняя продолжительность пребывания клиента (заявки) в очереди:

W_q=W_S-1/μ
среднее число заявок (клиентов) в очереди (длина очереди):

L_q=λ(1-P_N)·W_q

Рассмотрим пример одноканальной СМО с ожиданием.

Пример 3.2. Специализированный пост диагностики представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих проведения диагностики, ограничено и равно 3 [(N– 1) = 3]. Если все стоянки заняты, т. е. в очереди уже находится три автомобиля, то очередной автомобиль, прибывший на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, распределен по закону Пуассона и имеет интенсивность l= 0,85 (автомобиля в час). Время диагностики автомобиля распределено по показательному закону и в среднем равно 1,05 час.

Требуется определить вероятностные характеристики поста диагностики, работающего в стационарном режиме.

Решение

1. Параметр потока обслуживании автомобилей:

2. Приведенная интенсивность потока автомобилей определяется как отношение интенсивностей l и m, т. е.

3. Вычислим финальные вероятности системы:

P₁=ρ·P₀ = 0.893·0.248 = 0.221

P₂=ρ²·P₀ = 0.893²·0.248 = 0.198

P₃=ρ³·P₀ = 0.893³·0.248 = 0.177

P₄=ρ⁴·P₀ = 0.893²·0.248 = 0.158

4. Вероятность отказа в обслуживании автомобиля:

P_отк=P₄=ρ⁴·P₀ ≈ 0.158

5. Относительная пропускная способность поста диагностики:

q=1-P_отк = 1-0.158 = 0.842

6. Абсолютная пропускная способность поста диагностики

A=λ·q = 0.85·0.842 = 0.716 (автомобиля в час)

7. Среднее число автомобилей, находящихся на обслуживании и в очереди (т.е. в системе массового обслуживания):

8. Среднее время пребывания автомобиля в системе:

9. Средняя продолжительность пребывания заявки в очереди на обслуживание:

W_q=W_S-1/μ = 2.473-1/0.952 = 1.423 часа

10. Среднее число заявок в очереди (длина очереди): L_q= А,(1 – P_N) W_q= 0,85

L_q=λ(1-P_N)·W_q = 0.85·(1-0.158)·1.423 = 1.02

Работу рассмотренного поста диагностики можно считать удовлетворительной, так как пост диагностики не обслуживает автомобили в среднем в 15,8% случаев (Р_отк= 0,158).

В качестве показателей эффективности СМО с ожиданием, кроме уже известных показателей — абсолютной А и относительной Q пропускной способности, вероятности отказа P_отк., среднего числа занятых каналов (для многоканальной системы) будем рассматривать также следующие: L_сист. – среднее число заявок системе; Т_сист. — среднее время пребывания заявки в системе; L_оч. — среднее число заявок в очереди (длина очереди); Т_оч. — среднее время пребывания заявки в очереди; Р_зан.. — вероятность того, что канал занят (степень загрузки канала).

Одноканальная система с неограниченной очередью

На практике часто встречаются одноканальные СМО с неограниченной очередью (например, телефон-автомат с одной будкой).

Рассмотрим задачу.

Имеется одноканальная СМО с очередью, на которую не наложены никакие ограничения (ни по длине очереди, ни по времени ожидания). Поток заявок, поступающих в СМО, имеет интенсивность λ, а поток обслуживании — интенсивность μ. Необходимо найти предельные вероятности состояний и показатели эффективности СМО.

Система может находиться в одном из состояний S₀, S₁, S₂, …, S_k, по числу заявок, находящихся в СМО: S₀ — канал свободен; S₁ — канал занят (обслуживает заявку), очереди нет, S₂ — канал занят, одна заявка стоит в очереди; … S_k — канал занят, (k—1) заявок стоят в очереди и т.д.

Граф состояний СМО представлен на рис. 8.

Рис. 8

Это процесс гибели и размножения, но с бесконечным числом состояний, в котором интенсивность потока заявок равна λ, а интенсивность потока обслуживании μ.

Прежде чем записать формулы предельных вероятностей, необходимо быть уверенным в их существовании, ведь в случае, когда время t→∞, очередь может неограниченно возрастать. Доказано,
что если ρ<1, т.е. среднее число приходящих заявок меньше среднего числа обслуженных заявок (в единицу времени), то предельные вероятности существуют. Если ρ≥1, очередь растет до бесконечности.

Для определения предельных вероятностей состояний воспользуемся формулами (16), (17) для процесса гибели и размножении (здесь мы допускаем известную нестрогость, так как ранее эти формулы были получены для случая конечного числа состояний системы). Получим(32)

Так как предельные вероятности существуют лишь при ρ < 1, то геометрический ряд со знаменателем

ρ < 1, записанный в скобках в формуле (32), сходится к сумме, равной . Поэтому

p₀=1-ρ, (33)

и с учетом соотношений (17)

p₁=ρ·p₀; p₂=ρ²·p₀; … ; p_k=ρ^k·p₀; …

найдем предельные вероятности других состояний

p₁=ρ·(1-ρ); p₂=ρ²·(1-ρ); … ; p_k=ρ^k·(1-ρ); … (34)

Предельные вероятности p₀, p₁, p₂, …, p_k,… образуют убывающую геометрическую профессию со знаменателем р < 1, следовательно, вероятность р₀ — наибольшая. Это означает, что если СМО справляется с потоком заявок (при ρ < 1), то наиболее вероятным будет отсутствие заявок в системе.

Среднее число заявок в системе L_сист. определим по формуле математического ожидания, которая с учетом (34) примет вид

(35)

(суммирование от 1 до ∞, так как нулевой член 0·p₀=0).

Можно показать, что формула (35) преобразуется (при ρ < 1) к виду

(36)

Найдем среднее число заявок в очереди L_оч. Очевидно, что

L_оч=L_сист-L_об (37)

где L_об. — среднее число заявок, находящихся под обслуживанием.

Среднее число заявок под обслуживанием определим по формуле математического ожидания числа заявок под обслуживанием, принимающего значения 0 (если канал свободен) либо 1 (если канал занят):

L_оч=0·p₀+1·(1-p₀)

т.е. среднее число заявок под обслуживанием равно вероятности того, что канал занят:

L_оч=P_зан=1-p₀, (38)

В силу (33)

L_оч=P_занρ, (39)

Теперь по формуле (37) с учетом (36) и (39)

(40)

Доказано, что при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе (очереди) равна среднему числу заявок в системе (в очереди), деленному на интенсивность потока заявок, т.е.

(41)

(42)

Формулы (41) и (42) называются формулами Литтла.
Они вытекают из того, что в предельном, стационарном режиме среднее число заявок, прибывающих в систему, равно среднему числу заявок, покидающих
ее: оба потока заявок имеют одну и ту же интенсивность λ.

На основании формул (41) и (42) с учетом (36) и (40) среднее время пребывания заявки в системе определится по формуле:

(43)

а среднее время пребывания заявки в очереди

(44)

Одноканальная СМО с ожиданием без ограничения на вместимость блока ожидания

Стационарный режим функционирования данной СМО существует при t→∞ для любого п=0,1,2,… и когда l < m.Система алгебраических уравнений, описывающих работу СМО при t®¥ для любого n = 0, 1, 2…., имеет вид

Решение данной системы уравнений имеет вид

P_n=(1-ρ)·ρⁿ, n=0,1,2,… (3.21)

где ρ=λ/μ < 1

Характеристики одноканальной СМО с ожиданием, без ограничения на длину очереди, следующие:

среднее число находящихся в системе клиентов (заявок) на обслуживание:

средняя продолжительность пребывания клиента в системе:

Пример 3.3. Вспомним о ситуации, рассмотренной в пример 3.2, где речь идет о функционировании поста диагностики. Пусть рассматриваемый пост диагностики располагает неограниченны» количеством площадок для стоянки прибывающих на обслуживание автомобилей, т. е. длина очереди не ограничена.

Требуется определить финальные значения следующих вероятностных характеристик:

вероятности состояний системы (поста диагностики);
среднее число автомобилей, находящихся в системе (на обслуживании и в очереди);
среднюю продолжительность пребывания автомобиля в системе (на обслуживании и в очереди);
среднее число автомобилей в очереди на обслуживании;
среднюю продолжительность пребывания автомобиля в очереди.

Решение

1. Параметр потока обслуживания m и приведенная интенсивность потока автомобилей р определены в примере 3.2:

m = 0,952; p = 0,893.

2. Вычислим предельные вероятности системы по формулам

P₀=1-ρ = 1-0.893 = 0.107

P₁=(1-ρ)·ρ = (1-0.893)·0.893 = 0.096

P₂=(1-ρ)·ρ² = (1-0.893)²·0.893 = 0.085

P₃=(1-ρ)·ρ³ = (1-0.893)³·0.893 = 0.076

P₄=(1-ρ)·ρ⁴ = (1-0.893)⁴·0.893 = 0.068

P₅=(1-ρ)·ρ⁵ = (1-0.893)⁵·0.893 = 0.061

и т.д.

Следует отметить, что Р_о определяет долю времени, в течение которого пост диагностики вынужденно бездействует (простаивает). В нашем примере она составляет 10,7%, так как Р_о= 0,107.

3. Среднее число автомобилей, находящихся в системе (на обслуживании и в очереди):

4. Средняя продолжительность пребывания клиента в системе:

6. Средняя продолжительность пребывания автомобиля в очереди-

7. Относительная пропускная способность системы:

q=1,

т. е. каждая заявка, пришедшая в систему, будет обслужена.

8. Абсолютная пропускная способность: А= lq= 0,85·1 = 0,85

Следует отметить, что предприятие, осуществляющее диагностику автомобилей, прежде всего интересует количество клиентов, которое посетит пост диагностики при снятии ограничения на длину очереди.

Допустим, в первоначальном варианте количество мест для стоянки прибывающих автомобилей было равно трем (см. пример 3.2). Частота m возникновения ситуаций, когда прибывающий на пост диагностики автомобиль не имеет возможности присоединиться к очереди:

т= l P_N

В нашем примере при N = 3 + 1 = 4 и р = 0,893,

m = l Р_ор⁴ = 0,85·0,248·0,8934·0,134 автомобиля в час.

При 12-часовом режиме работы поста диагностики это эквивалентно тому, что пост диагностики в среднем за смену (день) будет терять 12·0,134 = 1,6 автомобиля.

Снятие ограничения на длину очереди позволяет увеличить количество обслуженных клиентов в нашем примере в среднем на 1,6 автомобиля за смену (12 ч. работы) поста диагностики. Ясно, что решение относительно расширения площади для стоянки автомобилей, прибывающих на пост диагностики, должно основываться на оценке экономического ущерба, который обусловлен потерей клиентов при наличии всего трех мест для стоянки этих автомобилей.

Многоканальная СМО с неограниченной очередью

Рассмотрим задачу. Имеется n-канальная СМО с неограниченной очередью. Поток заявок, поступающих в СМО, имеет интенсивность λ, а поток обслуживании — интенсивность μ. Необходимо найти предельные вероятности состояний СМО и показатели ее эффективности.

Система может находиться в одном из состояний S₀, S₁, S₂,…, S_k,…, S_n,…, — нумеруемых по числу заявок, находящихся в СМО: S₀ — в системе нет заявок (все каналы свободны); S₁ — занят один канал, остальные свободны; S₂ — заняты два канала, остальные свободны;…, S_k — занято k каналов, остальные свободны;…, S_n — заняты все n каналов (очереди нет); S_n+1 — заняты все n каналов, в очереди одна заявка;…, S_n+r — заняты все n каналов, r заявок стоит в очереди,….

Граф состояний системы показан на рис. 9. Обратим внимание на то, что в отличие от предыдущей СМО, интенсивность потока обслуживаний (переводящего систему из одного состояния в другое справа налево) не остается постоянной, а по мере увеличения числа заявок в СМО от 0 до n увеличивается от величины m до nm, так как соответственно увеличивается число каналов обслуживания.
При числе заявок в СМО большем, чем n, интенсивность потока обслуживании сохраняется равной nm.

Рис. 9

Можно показать, что при r/n < 1 предельные вероятности существуют. Если r/n > 1, очередь растет до бесконечности. Используя формулы (16) и (17) для процесса гибели и размножения, можно получить следующие формулы для предельных вероятностей состояний n-канальной СМО с неограниченной очередью

, (45)

, (46)

, (47)

Вероятность того, что заявка окажется в очереди,

, (48)

Для n-канальной СМО с неограниченной очередью, используя прежние приемы, можно найти:

среднее число занятых каналов

, (49)

среднее число заявок в очереди

, (50)

среднее число заявок в системе

L_сист=L_оч+ρ, (51)

Среднее время пребывания заявки в очереди и среднее время пребывания заявки в системе, как и ранее, находятся по формулам Литтла (42) и (41).

Замечание. Для СМО с неограниченной очередью при r < 1 любая заявка, пришедшая в систему, будет обслужена, т.е. вероятность отказа P_отк = 0, относительная пропускная способность Q=1, а абсолютная пропускная способность равна интенсивности входящего потока заявок, т.е. А=l.

СМО с ограниченной очередью

СМО с ограниченной очередью. СМО с ограниченной очередью отличаются от рассмотренных выше задач лишь тем, что число заявок в очереди ограничено (не может превосходить некоторого заданного т). Если новая заявка поступает в момент, когда все места в очереди заняты, она покидает СМО необслуженной, т.е. получает отказ.

Очевидно: для вычисления предельных вероятностей состояний и показателей эффективности таких СМО может быть использован тот же подход, что и выше, с той разницей, что суммировать надо не бесконечную прогрессию (как, например, мы делали при выводе формулы (33)), а конечную.

Среднее время пребывания заявки в очереди и в системе, как и ранее, определяем по формулам Литтла (44) и (43).

СМО с ограниченным временем ожидания. На практике часто встречаются СМО с так называемыми “нетерпеливыми” заявками. Такие заявки могут уйти из очереди, если время ожидания превышает некоторую величину. В частности, такого рода заявки возникают в различных технологических системах, в которых задержка с началом обслуживания может привести к потере качества продукции, в системах оперативного управления, когда срочные сообщения теряют ценность (или даже смысл), если они не поступают на обслуживание в течение определенного времени.

В простейших математических моделях таких систем предполагается, что заявка может находиться в очереди случайное время, распределенное по показательному закону с некоторым параметром υ, т.е. можно условно считать, что каждая заявка, стоящая в очереди на обслуживание, может покинуть систему с интенсивностью υ.

Соответствующие показатели эффективности СМО с ограниченным временем получаются на базе результатов, полученных для процесса гибели и размножения.

В заключение отметим, что на практике часто встречаются замкнутые системы обслуживания, у которых входящий поток заявок существенным образом зависит от состояния самой СМО. В качестве примера можно привести ситуацию, когда на ремонтную базу поступают с мест эксплуатации некоторые машины: понятно, что чем больше машин находится в состоянии ремонта, тем меньше их продолжает эксплуатироваться и тем меньше интенсивность потока вновь поступающих на ремонт машин. Для замкнутых СМО характерным является ограниченное число источников заявок, причем каждый источник “блокируется” на время обслуживания его заявки (т.е. он не выдает новых заявок). В подобных системах при конечном числе состояний СМО предельные вероятности будут существовать при любых значениях интенсивностей потоков заявок и обслуживании. Они могут быть вычислены, если вновь обратиться к процессу гибели и размножения.

Источник

СМО с ожиданием (очередью): определение и формулы

В качестве показателей эффективности СМО с ожиданием, кроме уже известных показателей — абсолютной и относительной пропускной способности, вероятности отказа $P_{text{otk}}$ , среднего числа занятых каналов к (для многоканальной системы) будем рассматривать также следующие:

1) $L_{text{sist.}}$ — среднее число заявок в системе;

2) $T_{text{sist.}}$ — среднее время пребывания заявки в системе;

3) $L_{text{och.}}$ — среднее число заявок в очереди (длина очереди);

4) $T_{text{och.}}$ — среднее время пребывания заявки в очереди;

5) $P_{text{zan.}}$ — вероятность того, что канал занят (степень загрузки канала).

Одноканальная система с неограниченной очередью

На практике часто встречаются одноканальные СМО с неограниченной очередью (например, телефон-автомат с одной будкой). Рассмотрим задачу.

Имеется одноканальная СМО с очередью, на которую не наложены никакие ограничения (ни по длине очереди, ни по времени ожидания). Поток заявок, поступающих в СМО, имеет интенсивность lambda , а поток обслуживании — интенсивность . Необходимо найти предельные вероятности состояний и показатели эффективности СМО.

Система может находиться в одном из состояний S_0,S_1,S_2,ldots,S_k , по числу заявок, находящихся в СМО: S_0 — канал свободен; S_1 — канал занят (обслуживает заявку), очереди нет; S_2 — канал занят, одна заявка стоит в очереди; — канал занят, (k-1) заявок стоят в очереди и т.д.

Граф состояний СМО представлен на рис. 8.

Граф состояний одноканальной СМО с неограниченной очередью

Это процесс гибели и размножения, но с бесконечным числом состояний, в котором интенсивность потока заявок равна lambda , а интенсивность потока обслуживании .

Прежде чем записать формулы предельных вероятностей, необходимо быть уверенным в их существовании, ведь в случае, когда время ttoinfty , очередь может неограниченно возрастать. Доказано, что если rho<1 , т.е. среднее число приходящих заявок меньше среднего числа обслуженных заявок (в единицу времени), то предельные вероятности существуют. Если rhogeqslant1 , очередь растет до бесконечности.

Для определения предельных вероятностей состояний воспользуемся формулами (16), (17) для процесса гибели и размножения (здесь мы допускаем известную нестрогость, так как ранее эти формулы были получены для случая конечного числа состояний системы). Получим:

$p_0=left[1+ frac{lambda}{mu}+ left(frac{lambda}{mu}right)^{2}+ldots+ left(frac{lambda}{mu}right)^{k}+ldotsright]^{-1}= left(1+rho+rho^2+ldots+rho^k+ldotsright)^{-1}.$

(32)

Так как предельные вероятности существуют лишь при rho<1 , то геометрический ряд со знаменателем rho<1 , записанный в скобках в формуле (32), сходится к сумме, равной $frac{1}{1-rho}$ . Поэтому

p_0=1-rho,

(33}

и с учетом соотношений (17)

p_1=rhocdot p_0,quad p_2=rho^2cdot p_0,quadldots,quad p_k=rho^kcdot p_0,quadldots

найдем предельные вероятности других состояний

p_1=rho(1-rho),quad p_2=rho^2(1-rho),quadldots,quad p_k=rho^k(1-rho),quad ldots

(34)

Предельные вероятности p_0,p_1,p_2,ldots,p_k,ldots образуют убывающую геометрическую профессию со знаменателем rho<1 , следовательно, вероятность p_0 — наибольшая. Это означает, что если СМО справляется с потоком заявок (при rho<1 ), то наиболее вероятным будет отсутствие заявок в системе.

Среднее число заявок в системе $L_{text{sist.}}$ определим по формуле математического ожидания, которая с учетом (34) примет вид

$L_{text{sist.}}= sum_{k=1}^{infty}kp_k=(1-rho)sum_{k=1}^{infty}krho^k$

(35)

(суммирование от 1 до infty , так как нулевой член 0cdot p_0=0 ).

Можно показать, что формула (35) преобразуется (при rho<1 ) к виду

$L_{text{sist.}}=frac{rho}{1-rho},.$

(36)

Найдем среднее число заявок в очереди $L_{text{och.}}$ . Очевидно, что

$L_{text{och.}}= L_{text{sist.}}- L_{text{ob.}},$

(37)

где $L_{text{ob.}}$ — среднее число заявок, находящихся под обслуживанием.

Среднее число заявок под обслуживанием определим по формуле математического ожидания числа заявок под обслуживанием, принимающего значения 0 (если канал свободен) либо 1 (если канал занят):

$L_{text{ob.}}=0cdot p_0+1cdot (1-p_0),$

т.е. среднее число заявок под обслуживанием равно вероятности того, что канал занят:

$L_{text{ob.}}=P_{text{zan.}}=1-p_0.$

(38)

В силу (33)

$L_{text{ob.}}=P_{text{zan.}}=rho.$

(39)

Теперь по формуле (37) с учетом (36) и (39)

$L_{text{och.}}=frac{rho^2}{1-rho},.$

(40)

Доказано, что при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе (очереди) равна среднему числу заявок в системе (в очереди), деленному на интенсивность потока заявок, т.е.

$T_{text{sist.}}=frac{1}{lambda}cdot L_{text{sist.}} ,$

(41)

$T_{text{och.}}=frac{1}{lambda}cdot L_{text{och.}}.$

(42)

формулы (41) и (42) называются формулами Литтла. Они вытекают из того, что в предельном, стационарном режиме среднее число заявок, прибывающих в систему, равно среднему числу заявок, покидающих ее: оба потока заявок имеют одну и ту же интенсивность lambda .

На основании формул (41) и (42) с учетом (36) и (40) среднее время пребывания заявки в системе определится по формуле:

$T_{text{sist.}}=frac{rho}{lambda(1-rho)},,$

(43)

а среднее время пребывания заявки в очереди —

$T_{text{och.}}=frac{rho^2}{lambda(1-rho)},.$

(44)

Пример 8. В порту имеется один причал для разгрузки судов. Интенсивность потока судов равна 0,4 (судов в сутки). Среднее время разгрузки одного судна составляет 2 суток. Предполагается, что очередь может быть неограниченной длины. Найти показатели эффективности работы причала, а также вероятность того, что ожидают разгрузки не более чем 2 судна.

Решение. Имеем $rho=frac{lambda}{mu}=lambdaoverline{t}_{text{ob.}}=0,!4cdot2=0,!8$ . Так как rho=0,!8<1 , то очередь на разгрузку не может бесконечно возрастать и предельные вероятности существуют. Найдем их.

Вероятность того, что причал свободен, по (33) p_0=1-0,!8=0,!2 , а вероятность того, что он занят, $P_{text{zan.}}=1-0,!2=0,!8$ . По формуле (34) вероятности того, что у причала находятся 1, 2, 3 судна (т.е. ожидают разгрузки 0, 1, 2 судна), равны

p_1=0,!8(1-0,!8)=0,!16;quad p_2=0,!8^2(1-0,!8)=0,!128;quad p_3=0,!8^3(1-0,!8)=0,!1024.

Вероятность того, что ожидают разгрузку не более чем 2 судна, равна

P=p_1+p_2+p_3=0,!16+0,!128+0,!1024=0,!3904.

По формуле (40) среднее число судов, ожидающих разгрузки, $L_{text{och.}}=frac{0,!8^2}{1-0,!8}=3,!2$ среднее время ожидания разгрузки по формуле (42) $T_{text{och.}}=frac{3,!2}{0,!8}=4$ (сутки).

По формуле (36) среднее число судов, находящихся у причала, $L_{text{sist.}}=frac{0,!8}{1-0,!8}=4$ (сутки) (или проще по (37) $L_{text{sist.}}=3,!2+0,!8=4$ (сутки), а среднее время пребывания судна у причала по формуле (41) $T_{text{sist.}}=frac{4}{0,!8}=5$ (сутки).

Очевидно, что эффективность разгрузки судов невысокая. Для ее повышения необходимо уменьшение среднего времени разгрузки судна $overline{t}_{text{ob.}}$ либо увеличение числа причалов.

Многоканальная СМО с неограниченной очередью

Рассмотрим задачу. Имеется n-канальная СМО с неограниченной очередью. Поток заявок, поступающих в СМО, имеет интенсивность lambda , а поток обслуживании — интенсивность . Необходимо найти предельные вероятности состояний СМО и показатели ее эффективности.

Система может находиться в одном из состояний S_0,S_1,S_2,ldots,S_k,ldots,S_n,ldots нумеруемых по числу заявок, находящихся в СМО: S_0 — в системе нет заявок (все каналы свободны); S_1 — занят один канал, остальные свободны; S_2 — заняты два канала, остальные свободны; ldots,S_k — занято каналов, остальные свободны; ldots,S_n — заняты все каналов (очереди нет); $S_{n+1}$ — заняты все каналов, в очереди одна заявка; $ldots,S_{n+r}$ — заняты все каналов, заявок стоит в очереди, и т.д.

Граф состояний системы показан на рис. 9. Обратим внимание на то, что в отличие от предыдущей СМО, интенсивность потока обслуживании (переводящего систему из одного состояния в другое справа налево) не остается постоянной, а по мере увеличения числа заявок в СМО от 0 до увеличивается от величины до nmu , так как соответственно увеличивается число каналов обслуживания. При числе заявок в СМО большем, чем , интенсивность потока обслуживании сохраняется равной nmu .

Граф состояний многоканальной СМО с неограниченной очередью

Можно показать, что при $frac{rho}{n}<1$ предельные вероятности существуют. Если $frac{rho}{n}geqslant1$ , очередь растет до бесконечности. Используя формулы (16) и (17) для процесса гибели и размножения, можно получить следующие формулы для предельных вероятностей состояний n-канальной СМО с неограниченной очередью

$p_0={left(1+ frac{rho^1}{1!}+ frac{rho^2}{2!}+ldots+frac{rho^n}{n!}+ frac{rho^{n+1}}{n!(n-rho)}right)!}^{-1},$

(45)

$p_1=frac{rho^1}{1!}cdot p_0,~ldots,~ p_k=frac{rho^k}{k!}cdot p_0,~ldots,~ p_n=frac{rho^n}{n!}cdot p_0,$

(46)

$p_{n+1}=frac{rho^{n+1}}{ncdot n!}cdot p_0,~ldots,~p_{n+r}=frac{rho^{n+r}}{n^rcdot n!}cdot p_0,~ldots$

(47)

Вероятность того, что заявка окажется в очереди,

$P_{text{och.}}=frac{rho^{n+1}}{n!(n-rho)}cdot p_0.$

(48)

Для n-канальной СМО с неограниченной очередью, используя прежние приемы, можно найти:

среднее число занятых каналов

$overline{k}=frac{lambda}{mu}=rho,$

(49)

среднее число заявок в очереди

$L_{text{och.}}=frac{rho^{n+1}cdot p_0}{ncdot n!}cdotleft(1-frac{rho}{n}right)^{-2},,$

(50)

среднее число заявок в системе

$L_{text{sist}}=L_{text{och.}}+rho.$

Среднее время пребывания заявки в очереди и среднее время пребывания заявки в системе, как и ранее, находятся по формулам Литтла (42) и (41).

Замечание. Для СМО с неограниченной очередью при rho<1 любая заявка, пришедшая в систему, будет обслужена, т.е. вероятность отказа $P_{text{otk.}}=0$ , относительная пропускная способность Q=1 , а абсолютная пропускная способность равна интенсивности входящего потока заявок, т.е. A=lambda .

Пример 9. В универсаме к узлу расчета поступает поток покупателей с интенсивностью lambda=81 чел. в час. Средняя продолжительность обслуживания контролером-кассиром одного покупателя $overline{t}_{text{ob.}}=2$ мин. Определить:

а. Минимальное количество контролеров-кассиров $n_{min}$ , при котором очередь не будет расти до бесконечности, и соответствующие характеристики обслуживания при $n=n_{min}$ .

б. Оптимальное количество $n_{text{opt.}}$ контролеров-кассиров, при котором относительная величина затрат $C_{text{otn.}}$ , связанная с издержками на содержание каналов обслуживания и с пребыванием в очереди покупателей, задаваемая, например, как $C_{text{otn.}}=frac{n}{lambda}+3T_{text{och.}}$ , будет минимальна, и сравнить характеристики обслуживания при $n=n_{min}$ и $n=n_{text{opt.}}$ .

в. Вероятность того, что в очереди будет не более трех покупателей.

Решение. а. По условию lambda=81 (1/ч) $=frac{81}{60}=1,!35$ (1/мин.). По формуле (24) $rho=frac{lambda}{mu}=lambdaoverline{t}_{text{ob.}}=1,!35cdot2=2,!7$ . Очередь не будет возрастать до бесконечности при условии $frac{rho}{n}<1$ , т.е. при n>rho=2,!7 . Таким образом, минимальное количество контролеров-кассиров $n_{min}=3$ .

Найдем характеристики обслуживания СМО при n=3 .

Вероятность того, что в узле расчета отсутствуют покупатели, по формуле (45)

$p_0={left(1+2,!7+ frac{2,!7^2}{2!}+ frac{2,!7^3}{3!}+ frac{2,!7^4}{3!(3-2,!7)}right)!}^{-1}=0,!025$

т.е. в среднем 2,5% времени контролеры-кассиры будут простаивать.

Вероятность того, что в узле расчета будет очередь, по (48)

$P_{text{och.}}=frac{2,!7^4}{3!cdot(3-2,!7)}cdot0,!025=0,!735.$

Среднее число покупателей, находящихся в очереди, по (50)

$L_{text{och.}}=frac{2,!7^4}{3cdot3!cdot(1-2,!7/3)^2}cdot0,!025=7,!35.$

Среднее время ожидания в очереди по (42)

$T_{text{och.}}=frac{7,!35}{1,!35}=5,!44$ (мин).

Среднее число покупателей в узле расчета по (51)

$L_{text{sist.}}= 7,!35+2,!7=10,!05.$

Среднее время нахождения покупателей в узле расчета по (41)

$T_{text{sist.}}=frac{10,!05}{1,!35}approx7,!44$ (мин).

Среднее число контролеров-кассиров, занятых обслуживанием покупателей, по (49) overline{k}=2,!7 .

Коэффициент (доля) занятых обслуживанием контролеров-кассиров $overline{k}_{text{otn.}}=frac{rho}{n}=frac{2,!7}{3}=0,!9$ .

Абсолютная пропускная способность узла расчета A=1,!35 (1/мин), или 81 (1/ч), т.е. 81 покупатель в час.

Анализ характеристик обслуживания свидетельствует о значительной перегрузке узла расчета при наличии трех контролеров-кассиров.

б. Относительная величина затрат при n=3

$C_{text{otn.}}=frac{n}{lambda}+3T_{text{och.}}=frac{3}{1,!35}+3cdot5,!44=5,!44.$

Рассчитаем относительную величину затрат при других значениях (табл. 2).

Расчёт относительных величин затрат

Как видно из табл. 2, минимальные затраты получены при $n=n_{text{opt.}}=5$ контролерах-кассирах.

Определим характеристики обслуживания узла расчета при $n=n_{text{opt.}}=5$ . Получим

$P_{text{och.}}=0,!091;~ L_{text{och.}}= 0,!198;~ T_{text{och.}}=0,!146;~ L_{text{sist.}}=2,!9;~ T_{text{sist.}}=2,!15;~ overline{k}=2,!7;~k_3=0,!54.$

Как видим, при n=5 по сравнению с n=3 существенно уменьшились вероятность возникновения очереди $P_{text{och.}}$ , длина очереди $L_{text{och.}}$ и среднее время пребывания в очереди $T_{text{och.}}$ , и соответственно среднее число покупателей $L_{text{sist.}}$ и среднее время нахождения в узле расчета $T_{text{sist.}}$ , а также доля занятых обслуживанием контролеров k_3 . Но среднее число занятых обслуживанием контролеров-кассиров overline{k} и абсолютная пропускная способность узла расчета естественно не изменились.

в. Вероятность того, что в очереди будет не более 3 покупателей, определится как

$P{rleqslant3}=p_1+p_2+p_3+p_4+p_5+p_{5+1}+p_{5+2}+p_{5+3}=1-P_{text{och.}}+p_{5+1}+p_{5+2}+p_{5+3},$

где каждое слагаемое найдем по формулам (45)–(48). Получим при n=5:

$P{rleqslant3}=1-frac{2,!7^6}{5!(5-2,!3)}cdot 0,!065+frac{2,!7^6}{5cdot5!}cdot0,!065 +frac{2,!7^7}{5^2cdot5!}cdot0,!065 +frac{2,!7^8}{5^3cdot5!}cdot0,!065=0,!986.$

(Заметим, что в случае n=3 контролеров-кассиров та же вероятность существенно меньше: P{rleqslant3}=0,!464 ).

Пример 10. Железнодорожная касса с двумя окошками продает билеты в два пункта и . Интенсивность потока пассажиров, желающих купить билеты, для обоих пунктов одинакова: $lambda_{A}=lambda_{B}=0,!45$ (пассажиров в минуту). На обслуживание пассажиров кассир тратит в среднем 2 мин. Рассматриваются два варианта продажи билетов: первый — билеты продаются в одной кассе с двумя окошками одновременно в оба пункта и , второй — билеты продаются в двух специализированных кассах (по одному окошку в каждой), одна только в пункт , другая — только в пункт . Необходимо:

а. Сравнить два варианта продажи билетов по основным характеристикам обслуживания.

б. Определить, как надо изменить среднее время обслуживания одного пассажира, чтобы по второму варианту продажи пассажиры затрачивали на приобретение билетов в среднем меньше времени, чем по первому варианту.

Решение.
а. По первому варианту имеем двухканальную СМО, на которую поступает поток заявок интенсивностью lambda=0,!45+0,!45=0,!9 ; интенсивность потока обслуживании $mu=frac{1}{2}=0,!5;$ $rho=frac{lambda}{mu}=1,!8$ . Так как $frac{rho}{n}=frac{1,!8}{2}=0,!9<1$ , то предельные вероятности существуют.

Вероятность простоя двух кассиров по (45)

$p_0={left(1+ frac{1,!8}{1!}+ frac{1,!8^2}{2!}+ frac{1,!8^3}{2!cdot(2-1,!8)}right)!}^{-1}approx0,!0526.$

Среднее число пассажиров в очереди по (50)

$L_{text{och.}}=frac{1,!8^3}{2cdot2!cdot(1-1,!8/2)^2}cdot0,!0526=7,!67.$

Среднее число пассажиров у кассы по (51)

$L_{text{sist.}}= 7,!67+1,!8=9,!47.$

Среднее время на ожидание в очереди и покупку билетов равно соответственно (по формулам (42) и (41)):

$T_{text{och.}}=frac{7,!67}{0,!9}=8,!52$ (мин) и $T_{text{sist.}}=frac{9,!47}{0,!9}=10,!5$ (мин).

По второму варианту имеем две одноканальные СМО (два специализированных окошка); на каждую поступает поток заявок с интенсивностью lambda=0,!45 . По-прежнему mu=0,!5; $rho=frac{lambda}{mu}=0,!9<1$ , предельные вероятности существуют. По формулам (40), (36), (42), (41)

$L_{text{och.}}=frac{0,!9^2}{1-0,!9}=8,!1;~ L_{text{sist.}}=frac{0,!9}{1-0,!9}=9;~ T_{text{och.}}=frac{8,!1}{0,!45}=18;~ T_{text{sist.}}=frac{9}{0,!45}=20.$

Итак, по второму варианту увеличились и длина очереди, и среднее время ожидания в ней и в целом на покупку билетов. Такое различие объясняется тем, что в первом варианте (двухканальная СМО) меньше средняя доля времени, которую простаивает каждый из двух кассиров: если он не занят обслуживанием пассажира, покупающего билет в пункт , он может заняться обслуживанием пассажира, покупающего билет в пункт , и наоборот. Во втором варианте такой взаимозаменяемости нет.

Можно заметить, что среднее время на покупку билетов по второму варианту увеличилось более чем в 2 раза. Такое значительное увеличение связано с тем, что СМО работает на пределе своих возможностей (rho=0,!9) : достаточно незначительно увеличить среднее время обслуживания $overline{t}_{text{ob.}}$ , т.е. уменьшить , и rho превзойдет 1, т.е. очередь начнет неограниченно возрастать.

б. Выше было получено, что по первому варианту продажи билетов при среднем времени обслуживания одного пассажира $overline{t}_{text{ob.}}=2$ (мин) среднее время на покупку билетов составит $T_{text{sist.1}}=10,!5$ (мин). По условию для второго варианта продажи $T_{text{sist.2}}<T_{text{sist.1}}$ , или с учетом (36) и (41): $frac{1}{lambda}frac{rho}{1-rho}< T_{text{sist.1}}$ .

Полагая $rho=frac{lambda}{mu}=lambdaoverline{t}_{text{ob.}}$ , получим $-frac{overline{t}_{text{ob.}}}{1-lambdaoverline{t}_{text{ob.}}}<T_{text{sist.1}}$ , откуда найдем $overline{t}_{text{ob.}}<frac{T_{text{sist.1}}}{1+lambda T_{text{sist.1}}}$ или $overline{t}_{text{ob.}}<frac{10,!5}{1+0,!45cdot10,!5}=1,!83$ (мин).

Итак, средние затраты времени на покупку билетов по второму варианту продажи уменьшатся, если среднее время обслуживания одного пассажира уменьшится более чем на 0,17 мин, или более чем на 8,5%.

СМО с ограниченной очередью

СМО с ограниченной очередью отличаются от рассмотренных выше задач лишь тем, что число заявок в очереди ограничено (не может превосходить некоторого заданного ). Если новая заявка поступает в момент, когда все места в очереди заняты, она покидает СМО необслуженной, т.е. получает отказ.

Очевидно: для вычисления предельных вероятностей состояний и показателей эффективности таких СМО может быть использован тот же подход, что и выше, с той разницей, что суммировать надо не бесконечную прогрессию (как, например, мы делали при выводе формулы (33)), а конечную. Соответствующие формулы сведем в табл. 3.

Среднее время пребывания заявки в очереди и в системе, как и ранее, определяем по формулам Литтла (44) и (43).

Таблица 3. Показатели одно- и многоканальной СМО с ограниченной очередью

Показатели одно- и многоканальной СМО с ограниченной очередью

Пример 11. По условию примера 8 найти показатели эффективности работы причала. Известно, что приходящее судно покидает причал (без разгрузки), если в очереди на разгрузку стоит более 3 судов.

Решение. По условию m=3 . Используем формулы, приведенные во второй графе табл. 3.

Вероятность того, что причал свободен:

$p_0=frac{1-0,!6}{1-0,!8^{3+2}}=0,!297.$

Вероятность того, что приходящее судно покинет причал без разгрузки:

$P_{text{otk.}}=0,!8^{3+1}cdot 0,!122.$

Относительная пропускная способность причала:

Q=1-0,!122=0,!878.

Абсолютная пропускная способность причала A=0,!4cdot0,!878=0,!351 , т.е. в среднем в сутки разгружается 0,35 судна.

Среднее число судов, ожидающих разгрузку

$L_{text{och.}}=frac{0,!8^2cdot[1-0,!8^3cdot(3+1-3cdot0,!8)]}{(1-0,!8^{3+2})(1-0,!8)}=0,!861,$

а среднее время ожидания разгрузки по (42)

$T_{text{och.}}=frac{0,!861}{0,!8}=1,!076$ (сутки).

Среднее число судов, находящихся у причала $L_{text{sist.}}=0,!861+(1-0,!297)=1,!564$ , а среднее время пребывания судна у причала по (41):

$T_{text{sist.}}=frac{1,!564}{0,!8}=1,!955$ (сутки).

СМО с ограниченным временем ожидания

На практике часто встречаются СМО с так называемыми “нетерпеливыми” заявками. Такие заявки могут уйти из очереди, если время ожидания превышает некоторую величину. В частности, такого рода заявки возникают в различных технологических системах, в которых задержка с началом обслуживания может привести к потере качества продукции, в системах оперативного управления, когда срочные сообщения теряют ценность (или даже смысл), если они не поступают на обслуживание в течение определенного времени.

Соответствующие показатели эффективности СМО с ограниченным временем получаются на базе результатов, полученных для процесса гибели и размножения.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

ρ(mρ)m

Для многоканальных СМО точный расчет характеристик возможен только при условии, что СМО является марковской, т.е. для СМО типа M/M/m. Для расчета характеристик таких СМО применяются следующие формулы.

Вероятность простоя:

	m−1	(mρ)	i		(mρ)	m	−1
P	= ∑		+		,	(8.23)
i!
0				m!(1 − ρ)
	i=0

где m – количество каналов (т.е. количество заявок, которые могут обслуживаться в СМО одновременно).

Средняя длина очереди:

q = m!(1 −ρ)2 P0 .

Вероятности пребывания в СМО j заявок:

	(mρ)	j			P ,	j =1,…, m,


		j!				0
Pj =				j
(mρ)			P ,	j > m.
		j−m
	m!	0
m

Формула (8.25) позволяет найти вероятности состояний СМО, при которых очередь отсутствует (количество заявок, обслуживаемых в СМО, не превышает количества каналов), а формула (8.26) – вероятности состояний при наличии очереди.

Примечание. Приведенные формулы могут применяться и для приближенного расчета характеристик немарковских многоканальных СМО (т.е. СМО типа M/G/m, G/M/m или

G/G/m).

Пример 8.3. В ремонтной службе предприятия выполняется наладка некоторых механизмов. На наладку поступает в среднем 10 механизмов в час (поток механизмов можно считать пуассоновским). Наладка одного механизма занимает в среднем 15 мин (время наладки инструмента можно считать экспоненциальной случайной величиной). В ремонтной службе работают три наладчика. Заработная плата наладчика составляет 30 ден.ед. в день.

В то время, когда механизм находится в ремонтной службе (т.е. налаживается или ожидает наладки), он не может использоваться для работы. Простой механизма в течение часа приносит предприятию убытки в размере 6 ден.ед.

Найти: а) характеристики работы ремонтной службы; б) потери предприятия в течение рабочей смены (8 часов), связанные с наладкой инструментов, включая затраты на содержание ремонтной службы и убытки от простоя меха-

107

низмов; в) вероятность того, что наладка механизма начнется сразу же после его поступления (без ожидания в очереди); г) вероятность того, что количество механизмов, ожидающих наладки, окажется свыше пяти; д) определить, целесообразно ли уменьшить количество наладчиков до двух; е) определить, целесообразно ли увеличить количество наладчиков до четырех.

а) Ремонтную службу можно рассматривать как СМО типа M/M/3 без ограничений на очередь. В этой СМО λ=10 механизмов/час = 0,167 механизма/мин, x =15 мин, μ=0,067 механизма/мин.

Найдем нагрузку на СМО: ρ=λ/(mμ) = 0,833. Найдем вероятность простоя по формуле (8.23):

		(3	0,833)	0		1		(3 0,833)	2		(3	0,833)	3	−1
P	=		+	(3 0,833)	+		+			= 0,046.
	0!		1!	2!		3!(1 − 0,833)
0

По формуле (8.24) определяем среднюю длину очереди (т.е. среднее количество механизмов, ожидающих наладки): q =3,43 механизма.

Ремонтная служба выполняет наладку всех поступающих механизмов. Поэтому Pотк=0, Pобсл=1. Найдем остальные характеристики по формулам

(8.4)-(8.11): U=0,833, S =2,49 механизма, k =5,92 механизма, γ=0,167 механизма/мин, w =20,5 мин, t =35,5 мин.

б) Затраты на содержание ремонтной службы составляют 30·3=90 ден.ед. Убытки предприятия, связанные с простоем механизмов, найдем по формуле

(8.18): Zпр = 5,92·6·8=284,16 ден.ед. за смену. Таким образом, полные потери предприятия, связанные с наладкой механизмов, составляют 90+284,16 = 374,16 ден.ед. за смену.

в) Найдем вероятность того, что наладка механизма начнется сразу же после его поступления. Это произойдет в случае, если в момент поступления механизма в ремонтную службу хотя бы один наладчик окажется свободным. Для этого требуется, чтобы количество механизмов, находящихся в ремонтной службе, не превышало двух. Вероятность такого состояния находится по фор-

муле (8.12): P(j ≤ 2) = P0+P1+P2. Вероятности P1 и P2 найдем по формуле

(8.25): P1=0,115, P2=0,144. Таким образом, P(j ≤ 2) = 0,046+0,115+0,144=0,305.

Это значит, что примерно в 30,5% случаев механизм, доставленный в ремонтную службу, сразу же поступит к наладчику.

г) Найдем вероятность того, что количество механизмов, ожидающих наладки, окажется свыше пяти. Такое состояние означает, что количество механизмов, находящихся в ремонтной службе, превышает восемь (три из них – на наладке, остальные – в очереди). Вероятность такого состояния находится по

формуле (8.13): P(j > 8) = 1-(P0+P1+…+P8). Вероятности P1, P2, P3 найдем по формуле (8.25): P1=0,115, P2=0,144, P3=0,12. Вероятности P4, P5,…,P8 найдем

по формуле (8.26): P4=0,1, P5=0,083, P6=0,069, P7=0,058, P8=0,048. Таким образом, P(j > 8) = 0,218.

108

д) Найдем нагрузку на СМО при m=2: ρ=λ/(mμ) = 1,25. Величина ρ>1 означает, что механизмы поступают в ремонтную службу с большей интенсивностью, чем она может их обслуживать. Таким образом, два наладчика “не справятся” с потоком заявок. Уменьшить количество наладчиков до двух нельзя.

е) Найдем характеристики СМО при m=4: ρ=0,623, P0=0,074, q =0,53 ме-

ханизма, Pотк=0, Pобсл=1, U=0,623, S =2,49 механизма, k =3,02 механизма, w =3,14 мин, t =18,14 мин, γ=0,167 механизма/мин.

Затраты на содержание ремонтной службы составляют 30·4=120 ден.ед. По формуле (8.18) найдем убытки предприятия, связанные с простоем меха-

низмов: Zпр = 3,02·6·8=144,96 ден.ед. за смену. Таким образом, полные потери предприятия, связанные с наладкой инструментов, составляют 120+144,96 = =264,96 ден.ед. за смену. Эти потери меньше, чем для трех наладчиков. Поэтому увеличение количества наладчиков до четырех следует признать выгодным.

8.9. СМО с ограничением на длину очереди

В СМО такого типа в очереди может находиться не более n заявок. Если заявка поступает в СМО в момент, когда в очереди уже находятся n заявок, то она не обслуживается (не допускается в очередь). Для расчета характеристик таких СМО применяются следующие формулы.

Вероятность простоя:

		m	(mρ)	i	(mρ)	m+1		1 − ρ	n −1
P	=	∑		+			,
i!		m m!
0					1 − ρ
	i=0

где m – количество каналов СМО;

n – максимально допустимое количество заявок в очереди. Вероятность отказа в обслуживании:

P		=	(mρ)m+n	P .

отк		mn m!		0

Средняя длина очереди:
	(mρ)m+1 P		1 − (n	+1)ρn + nρn+1
q =		0			.
			(1 − ρ)2
			m m!

Вероятности пребывания в СМО j заявок:

	(mρ)	j			P ,	j =1,…, m,


		j!				0
Pj =				j
(mρ)			P ,	j = m +1,…, m + n.
		j−m
	m!	0
m

(8.27)

(8.28)

(8.29)

(8.30)

(8.31)

109

Формула (8.30) позволяет найти вероятности состояний СМО, при которых очередь отсутствует (количество заявок, обслуживаемых в СМО, не превышает количества каналов), а формула (8.31) – вероятности состояний при наличии очереди.

При ρ=1 расчет вероятности простоя и средней длины очереди выполняется по следующим формулам:

= m (mρ)i P0 i∑=0 i!

q = (mρ)m P0 m!

+ n(mρ)m −1;

n(n +1) . 2

Пример 8.4. Предприятие выполняет заказы на переводы с иностранных языков. В среднем на предприятие поступает 8 заказов в день (поток заказов можно считать пуассоновским). Средний размер перевода – 5 страниц (размер перевода можно считать случайной величиной, распределенной по экспоненциальному закону). На предприятии работают 4 переводчика. Норма для переводчика – 7 страниц в день. Чтобы исключить невыполнение заказов в срок, предприятие не принимает новые заказы, если уже имеется 6 переводов, ожидающих выполнения.

Переводчику выплачивается 2 ден.ед. за каждую переведенную страницу, плюс 100 ден.ед. в месяц. Заказчик платит предприятию 4 ден.ед. за каждую переведенную страницу.

Найти а) характеристики работы предприятия; б) среднюю заработную плату переводчика за месяц (25 рабочих дней); в) среднюю прибыль предприятия за месяц; г) определить, выгодно ли предприятию принять на работу еще одного переводчика.

а) На предприятии работают 4 переводчика (m=4). Поток заказов – пуассоновский, время их выполнения – экспоненциальная случайная величина. Поэтому предприятие можно рассматривать как СМО типа M/M/4 с ограничением на длину очереди (n=6). В этой СМО λ=8 заказов/день. Так как переводчик может перевести в среднем 7 страниц в день, а средний размер перевода – 5 страниц, значит, производительность переводчика (интенсивность обслуживания заявок) составляет μ=7/5=1,4 заказа/день. Среднее время работы переводчика над заказом x =1/μ=0,71 дня.

Найдем нагрузку на СМО: ρ=λ/(mμ) = 1,43. Найдем вероятность простоя по формуле (8.27):

		0		1		(4 1,43)	2		3		(4 1,43)	4		5	6	−1
P =	(4 1,43)	+	(4 1,43)	+		+	(4 1,43)	+		+	(4 1,43)		1−1,43	=0,000827.
0!	1!	2!		3!	4!		4 4!	1−1,43
0

110

По формуле (8.28) определяем вероятность отказа в обслуживании:

Pотк=0,31. Это означает, что примерно 31% заказчиков, обращающихся на предприятие, получают отказ из-за перегруженности переводчиков. Вероят-

ность обслуживания составляет Pобсл=1-Pотк=0,69.

По формуле (8.29) найдем среднюю длину очереди (т.е. среднее количество заказов, ожидающих выполнения): q =4,1 заказа.

Найдем остальные характеристики по формулам (8.4)-(8.11): U=0,982,

S =3,93 заказа, k =8,03 заказа, γ=5,5 заказа/день, w =0,75 дня, t =1,46 дня.

б) Найдем заработную плату переводчика за месяц (25 рабочих дней). Переводчики, работающие на предприятии, выполняют в среднем 5,5 заказа в день (γ=5,5). Средний размер заказа – 5 страниц; за каждую страницу переводчику выплачивается 2 ден.ед. Таким образом, сумма, выплачиваемая всем переводчикам за выполнение заказов в течение месяца, составляет в среднем 5,5·5·2·25=1375 ден.ед. Заработная плата каждого из переводчиков составляет в среднем 1375/4 + 100 = 443,75 ден.ед. в месяц.

в) Найдем среднюю прибыль предприятия за месяц. Выручка предприятия от выполнения переводов за месяц составляет в среднем 5,5·5·4·25=2750 ден.ед. Переводчикам выплачивается 4·443,75 = 1775 ден.ед. Таким образом, прибыль предприятия составляет 2750 – 1775 = 975 ден.ед. в месяц.

г) Определим, выгодно ли предприятию принять на работу еще одного переводчика. Найдем характеристики работы предприятия для m=5: ρ=1,14, P0= =0,00154, Pотк=0,175, Pобсл=0,825, q =2,99 заказа, U=0,943, S =4,72 заказа,

k =7,71 заказа, γ=6,6 заказа/день, w =0,45 дня, t =1,16 дня. Выполнив расчеты, как показано выше, найдем, что выручка предприятия за месяц составит

6,6·5·4·25=3300 ден.ед., заработная плата переводчика – (6,6·2·4·25)/5+100=430

ден.ед., прибыль предприятия – 3300 – 5·430 = 1150 ден.ед.

Таким образом, прием на работу еще одного переводчика приведет к росту прибыли предприятия с 975 до 1150 ден.ед., т.е. на 175 ден.ед. в месяц. Рост прибыли достигнут за счет уменьшения количества отказов, в результате чего увеличивается пропускная способность предприятия. Снижение количества отказов также является положительным результатом, так как улучшает репутацию предприятия. Еще одним положительным результатом является сокращение среднего срока выполнения заказа (с 1,46 до 1,16 дня). Отрицательным результатом является некоторое снижение заработной платы переводчика (с 443,75 до 430 ден.ед. в месяц). Однако предприятие имеет возможность избежать этого, использовав часть дополнительной прибыли на повышение заработной платы переводчиков. Например, если предприятие будет выплачивать переводчикам дополнительно по 15 ден.ед., то заработная плата переводчиков не снизится (и даже увеличится с 443,75 до 445 ден.ед.), а дополнительная прибыль предприятия составит 175-5·15 = 100 ден.ед. Таким образом, прием на работу еще одного переводчика следует признать выгодным.

111

Источник

ИНФОРМАТИКА, ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА И УПРАВЛЕНИЕ

УДК 519.872

А. П. Кирпичников, Д. Б. Флакс, К. Н. Галямова

СРЕДНЯЯ ДЛИНА ОЧЕРЕДИ В СИСТЕМЕ МАССОВОГО ОБСЛУЖИВАНИЯ С ОГРАНИЧЕННЫМ СРЕДНИМ ВРЕМЕНЕМ ПРЕБЫВАНИЯ ЗАЯВКИ В СИСТЕМЕ

Ключевые слова: система массового обслуживания, поток требований, очередь, обслуживающее устройство.

Представлена математическая модель открытой многоканальной системы массового обслуживания с ограниченным средним временем пребывания заявки в системе и вычислено среднее число требований, одновременно находящихся в очереди в ожидании начала обслуживания.

Keywords: queuing system, flow of requirements, queue, serving device.

The mathematical model of multi-channel queuing system of open type with bounded mean residence time in the system is presented. The average number of requests simultaneously queued waiting for the first service is calculated.

Настоящая работа является продолжением цикла публикаций авторов, начатого в работах [1-7] и посвященного разработке математических основ функционирования системы массового обслуживания (СМО) с ограниченным средним временем пребывания заявки в этой системе. Напомним, что в этих работах рассмотрена система массового обслуживания, в которой на каждую заявку, находящуюся в системе (как в очереди, так и под обслуживанием), действует своего рода «поток уходов» с интенсивностью у_1/1. Интенсивность обслуживания заявки в системе при этом обозначается как ц, а интенсивность поступающего в систему потока заявок как X

Граф системы массового обслуживания такого рода изображён рис. 1. В этом случае приведённая интенсивность потока поступающих в систему заявок равна р = Х/ ц. Физический смысл этой величины заключается, очевидно, в том, что она показывает, какое число заявок в среднем поступило в систему за среднее время обслуживания в системе одной заявки.

В работе [2] были впервые получены формулы для вероятностных характеристик системы массового обслуживания такого рода, в частности, для вероятности полного простоя системы

Ро =i e

(1)

и вероятностей стационарных состоянии системы

Рь =Рт Ро при k * m; k!

Pk –

m (m p +1)

при k > m.

k-m

~ X X где p = —

f f + v 1 + p

~ v v

f f+V

1+p

ет(р) – неполная экспонента [1,2]. При этом Р = у/ц – приведённая интенсивность ухода «нетерпеливых» заявок из системы – величина, которая показывает, сколько в среднем заявок покидает систему необслуженными за среднее время обслуживания системой одной заявки. В этих соотношениях (г)к = г(г + 1)(а + 2) … (а + к-1); (я)0 = 1 – символ

Похгаммера [8], при этом (1)к =к!.

Рис. 1 – Граф системы массового обслуживания

-1

k -m

Величина a=p /р = Х/у

очевидно, показывает, ка-

кое среднее число заявок поступает в систему за среднее время пребывания в системе одной «нетерпеливой» заявки. В формуле (1) ^1(а;Ь^) – так

называемая вырожденная гипергеометрическая функцию Э. Куммера, определяемая соотношением [2, 3]

(a)k

1 U ^ Гп bk k!

(2)

k = п

Для упрощения записи в дальнейших расчётах мы будем пока опускать знак тильды в указанных выше обозначениях.

В работах [5, 6] была найдена вероятность ожидания обслуживания вновь поступившей в систему заявкой, то есть вероятность того, что поступающее требование найдёт все каналы занятыми (вне зависимости от того, будет оно дожидаться обслуживания или нет), которая имеет вид

пт- п г и

Рожид (т-1)! ^1 ^ тР;«)-! =

Рожид (0)^ [ 1 Fi (1; ml р; a)-1 ]

где

рожид(п):

m „

Р Рп

(m-1)! (m-p)

(3)

(4)

– это выражение для вероятности ожидания системы с неограниченной очередью и «терпеливыми» заявками, известное из модели М/М/т [9, 10]. Заметим, что хотя по форме это соотношение совпадает с аналогичным выражением модели М/М/т, однако, в отличие от него, содержит внутри себя ещё и зависимость от параметра Р, содержащуюся внутри вероятности полного отсутствия заявок в системе По =По (Р) согласно формуле (1).

В работе [7] было впервые получено выражение для такой важнейшей характеристики данного типа СМО, как среднее число требований, находящихся под обслуживанием (среднее число занятых каналов), которое имеет вид

т = р-(т – р)УПожид(0)-Пожид (5) Отсюда коэффициент загрузки СМО этого типа

к3 = т-(1-т)[Рожид(о)-Пожид ,

есть выражение для дисперсии числа занятых каналов, которое имеет вид

=p-p Рожид-(m-m)p-m).

При р=П m=p и a’m =р-ррожид(о) в соответствии с результатами [9, 10].

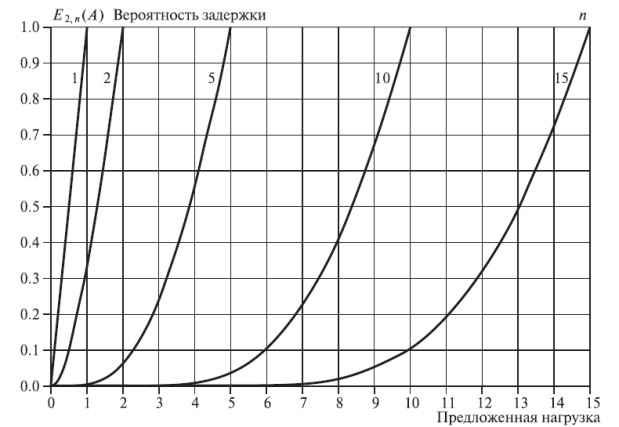
В настоящей работе мы покажем, как рассчитывается такая ключевая для понимания процессов, происходящих в СМО, величина, как среднее количество заявок, одновременно находящихся в очереди в ожидании начала обслуживания, говоря другими словами, средняя длина очереди. Заметим, что именно эта величина является основной характеристикой широкого класса систем массового обслуживания различных типов и именно эта величина дала название, принятого для подобного рода систем в англоязычной научной литературе – Queueing Systems.

Согласно общей формуле, среднее число требований в очереди (средняя длина очереди)

м pm м ^к-т

l = У (k – m)pk =- У (k – т)-.—–т-

k=m+1 m! k=m+1 (т/Р+1)ь

“Рп =

m „ м k m+1 _ j м

_p_р у k а =p_—d У

‘ m! k=1 (mP+1)k mfi day (m/p + 1)k

~m+1 „ 7 м __k _m+1 ,„ 7

p Ро d ^ a _p Р0 d т!р dak~0 (mjP + 1)k mp da

1F1(1; m/ p+1;a)

в силу соотношения (2). С другой стороны, из этой же формулы следует

7 м k м k-1 1 м

1 F1(1; b; z)=d у ^=У k * =1 у (k – ъ+ъ)^=

dz k=0 (b)k k=0 (ъ)

‘k ^ k=0

м k м k

УЬ + k)b”У z

(b)k

k=0

zk м zk

У b+k-1+0w-У (b)k

У b + k- 1)(b-1)

zk м zk м zk

(b+k-1)(b-1)k k (b)* (b)*

м м k

=1 b-1)[ 1F1(1;b-1;z)- 1F(1bz)].

соответственно коэффициент простоя

= |[1 + Рожид(п)”Рожид ].

Заметим, что к. 3.< к. з.(о) , соответственно к. п >к . п(о) . В работе [7] также было получено выражение для второго момента этой величины, то

Отсюда

т п г ■,

‘={т- %Р ^ 1 ^ (1; т р; «)-1F1 (1; т Р+1; «) .

Но согласно рекуррентному соотношению для вырожденных гипергеометрических функций Э. Куммера, полученному в работе [2], имеем

k=1

2 РРожид -(т-р)1 -.2 7 / =–I .

7 Р

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

и тогда, очевидно,

-трр^Мт/ р)-т^Мт! р)-1 ]}=

„—-1 -Р Ро

(т-1)! Р

т-1 ^ Р Ро

(т-1)! Р

[(Р- т) ^(а—р)+т]=

[т-(т-р) ^(а-т!р)]=

= трРР[Рожид{°)-Рожид ]. (6)

При малых значениях параметра Р в соответствии с приближённым решением [5, 6] отсюда имеем

РРожид (0)

т – р

1- т + 2 р р

(т -рУ

= 1(о)

1- т + 2 р р (т-рр

Дисперсия числа требований в очереди

Используя асимптотическую зависимость для вероятности ожидания заявкой обслуживания, полученную в работах [5, 6], легко проверить, что соотношения (6) и (7) при стремлении параметра Р к нулю после ряда простых преобразований), как и следовало ожидать, перейдут в соответствующие соотношения многоканальной модели без ограничений [9, 10]

7(0) = р Рожид20 ; 7-2(0)= (т + р) 110 – 7^(0) (т-р)2 7 т-р

(модель М/М/т.

Далее, как мы знаем, на каждую из заявок, стоящих в очереди, действует своего рода «поток уходов» с интенсивностью, а это, в свою очередь, означает, что из среднего числа I заявок в очереди в среднем будет уходить , не дождавшись обслуживания, V так называемых нетерпеливых заявок в единицу времени. Тем самым всего в единицу времени система обслужит

–Т2

((= у (к -1)2 рк – т2=рр0 у (к – т) а ч

к=т+1 т! к=т+1 (т/ Р + 1)

Найдем сначала осредненный квадрат величины к – т :

А= X-vТ

заявок. В этом случае относительная пропускная способность такой СМО, то есть доля обслуженных заявок среди всех поступивших в систему, будет, очевидно,

(( =У(к – т)2 рк =^ У (к – т)

2 а

т!

_^р_р0 А

т! (т/ Р + 1)к т!Р йа

(т/ Р+1)к

_ртР0^,.2 ак

(т/Р + 1)к

т+1 ^ л _р Р0 d

— !р dа

а— ^(1;—/р + 1;а) dа

_т+1 7

р Р0 й (т -1)!Р2 йа

[ ^(1;т/Р;а)- ^(1;т/Р + 1;а)]=

т+1 г. л

р Р0 —

— !р —’а

а-^(1;—/Р + 1;а)

А X-vI , V т q=—=-=1–I

XX X

или

9=1-7/а.

Среднее же число занятых каналов т, как обычно, можно получить путем деления абсолютной пропускной способности А на скорость обслуживания одной заявки откуда вытекает связь

– А Х^7 –

т=—=-=р-Р7,

ц ц

с помощью которой легко проверить полученные ранее авторами соотношения для среднего числа занятых каналов [7]

— = р-(т-р Рожид (0) – Рожид ]

1,(т – р)2

рР

т – р

рРожид

1,(—-р)2

рР )2

р- Р0 (—-р) __ — – 1)!Р2

р д ( -2 ^ _Рожид(0) Рожид]~~

рРожид -(—-р)7 р

и тогда

и соотношение (6) для средней длины очереди. Заметим, что полученную в работе [7] формулу для

7т

>=р-рРожид-(—- — )(р-—)

можно в этом случае переписать ещё и как

— = р-рРожид-р(—- т)7.

Литература

1. М.И. Бусарев, А.П. Кирпичников, Д.Б. Флакс // Вестник Казанского технологического университета, Т. 14,№ 22, С. 155-161, (2011);

к=т+1

2. А.П. Кирпичников, Д.Б. Флакс // Вестник Казанского технологического университета, Т. 17, № 24,С. 242-245, (2014);

3. А.П. Кирпичников, Д.Б. Флакс, Л.Р. Валеева // Theoretical & Applied Science. 2015. № 5 (25). С. 44-49.

4. А.П. Кирпичников, Д.Б. Флакс, Л.Р. Валеева // Фэн-наука. 2015. № 6 (45). С. 5-9.

5. А.П. Кирпичников, Д.Б. Флакс, К.Н. Галямова // Вестник технологического университета, . 19, № 11, С. 122-126, (2016).

6. А.П. Кирпичников, Д.Б. Флакс, К.Н. Галямова // Успехи современной науки. 2016. Т. 4. № 8. С. 176-178.

7. А.П. Кирпичников, ,Д.Б. Флакс, К.Н. Галямова // Вестник технологического университета. 2о16. Т. 19. № 22. С. 123-125.

8. А.П. Прудников, Ю.А. Брычков, О.И. Маричев, Интегралы и ряды. Дополнительные главы. М., Наука, 1985. 8оо с.

9. А.П. Кирпичников, Прикладная теория массового обслуживания. Казань, Изд-во Казанского гос. университета, 2оо8. 112 с.

10. А.П. Кирпичников, Методы прикладной теории массового обслуживания. Казань, Изд-во Казанского университета, 2о11. 2оо с.

© А. П. Кирпичников – д-р ф.-м. наук, проф., зав. кафедрой интеллектуальных систем и управления информационными ресурсами КНИТУ, e-mail: kirpichnikov@kstu.ru; Д. Б. Флакс – ст. препод. каф. сбора и обработки информации КНИТУ, e-mail: flaxdm@gmail.com; К. Н. Галямова – магистр каф. сбора и обработки информации КНИТУ, e-mail: galyamovakn@gmail.com.

© А. P. Kirpichnikov – Dr. Sci, Prof, Head of the Department of Intelligent Systems & Information Systems Control, KNRTU, e-mail: kirpichnikov@kstu.ru; D. B. Flax – Senior Lecturer of the Department of Automated Data Acquisition & Processing Systems, KNRTU, e-mail: flaxdm@gmail.com; K. N. Galyamova – Master of the Department of Automated Data Acquisition & Processing Systems, KNRTU, e-mail: galyamovakn@gmail.com.

Источник

Аннотация: В этой лекции мы рассматриваем нагрузку систем с n идентичными обслуживающими приборами и бесконечным числом мест ожидания. Когда все n обслуживающих приборов заняты, поступивший вызовов ставится в очередь и ждет, пока не освободится хотя бы один обслуживающий прибор. Когда хотя бы один обслуживающий прибор свободен, клиенты не могут оставаться в очереди (полная доступность).

Мы рассмотрим те же самые два случая потоков нагрузки, о которых говорили в Лекциях 7 и 8.

Пуассоновский поток вызовов (бесконечное число источников) и экспоненциально распределенное время обслуживания ( PCT-I ). Эта самая важная система организация очереди называется Эрланговская система с ожиданием. Используя систему обозначений, которую мы введем позже в секции 13.1, назовем Эрланговскую систему с ожиданием – . В этой системе обслуженная нагрузка равна предложенной нагрузке, поскольку попытки вызова не блокируются. Положительная вероятность времени ожидания означает необходимость вычисления:
- длины очереди;
- среднего времена ожидания;
- функции увеличения.
С этими параметрами мы будем иметь дело в секции 12.2. В секции12.3 будет показано, как для оптимизации системы может быть применен Принцип Мо. В секции 12.4. вычисляется распределение времени ожидания для основной дисциплины обслуживания – Первый Прибыл Первый обслужен ( FCFS * – First Come First Served).
Ограниченное число источников и экспоненциально распределенное время обслуживания ( PCT-II ). Эта модель Пальма, называемая моделью восстановления машин, рассмотрена в секции 12.5. (проблема взаимного влияния машин) и широко применяется для того, чтобы планировать сети, например, компьютерные сети, терминальные сети. Модель восстановления машин оптимизирована в секции 12.6.

Система с ожиданием Эрланга M/M/n

Рассмотрим систему с ожиданием M/M/n . Она обслуживает Пуассоновский поток вызовов ( ), имеет экспоненциальное время обслуживания ( ) и n обслуживающих приборов при бесконечном числе мест ожидания. Состояние системы определяется как общее количество пользователей в системе (или в обслуживании, или ожидающих в очереди).

Рис.
12.1.
Диаграмма переходов состояний M/M/n системы с ожиданием, имеющей n серверов и неограниченное число мест ожидания.

Нас интересуют вероятности устойчивых состояний системы. В секции 7.4 дана диаграмма переходов между состояниями (рис.12.1). Принимая, что диаграмма находится в статистическом равновесии, получаем:

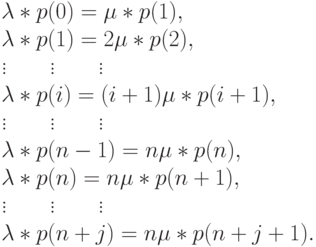$lambda *p(0)=mu *p(1),\ lambda *p(1)=2 mu *p(2),\ qquad qquad vdots qquad vdots qquad vdots\ lambda * p(i)=(i+1) mu * p(i+1),\ qquad qquad vdots qquad vdots qquad vdots\ lambda *p(n-1)=n mu *p(n),\ lambda*p(n)=n mu*p(n+1),\ qquad qquad vdots qquad vdots qquad vdots\ lambda*p(n+j)=n mu*p(n+j+1).$

(
12.1)

Если – это предложенная нагрузка, то мы имеем:

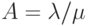
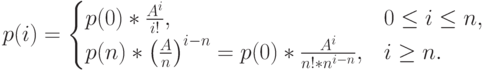$p(i)=begin{cases} p(0)*frac{A^i}{i!}, & 0 le i le n,\ p(n)*left ( frac An right )^{i-n}=p(0)*frac{A^i}{n!*n^{i-n}}, & i ge n. end{cases}$

(
12.2)

С помощью нормировки вероятностей состояний получаем:

$1=sum_{i=0}^{infty}p(i),\ 1=p(0)*left { 1+frac A1+frac{A^2}{2!}+ dots + frac{A^n}{n!} left (1+frac A1+ frac{A^2}{n^2}+dots right ) right }.$

Внутренние фигурные скобки содержат геометрическую прогрессию с коэффициентом прогрессии A/n . Условие нормализации может быть выполнено только для:

(
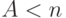12.3)

Статистическое равновесие получено лишь для A/n . Иначе очередь будет увеличиваться до бесконечности. Мы получаем значение p_0 :

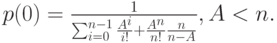$p(0)=frac{1}{sum_{i=0}^{n-1} frac{A^i}{i!}+frac{A^n}{n!} frac{n}{n-A}}, A < n.$

(
12.4)

Уравнения (12.2) и (12.4) показывают вероятности устойчивых состояний.

Характеристики нагрузки систем с ожиданием

Для оценки производительности и рабочих характеристик системы нужно рассмотреть несколько характеристик. Они отражают вероятности устойчивых состояний.

C-формула Эрланга

Когда Пуассоновский поток вызовов не зависит от состояния системы, вероятность того, что произвольный вызов должен будет ждать обслуживания в очереди, равна пропорции времени, когда заняты все обслуживающие приборы ( свойство PASTA ). Время ожидания – случайная величина, которая обозначается . Для произвольного поступления вызовов имеем:

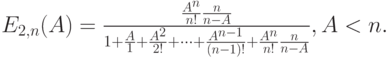$E_{2,n}(A)=frac{frac{A^n}{n!} frac{n}{n-A}}{1+frac A1+frac{A^2}{2!}+dots+frac{A^{n-1}}{(n-1)!}+frac{A^n}{n!} frac{n}{n-A}}, A < n.$

(
12.6)

Эта вероятность ожидания зависит только от , т.е.произведения lambda и . Формула имеет несколько названий: C-формула Эрланга, вторая формула Эрланга или формула Эрланга для систем с ожиданием. Она имеет различные обозначения в литературе:

$E_{2,n}(A)=D=D_n(A)=p{W > 0}.$

Клиенты либо обслуживаются немедленно, либо помещаются в очередь. Вероятность, что клиент обслуживается немедленно, равна:

$S_n=1-E_{2,n}(A).$

Обслуженная нагрузка равняется предложенной нагрузке , так как ни одному вызову не отказывается в обслуживании, а процесс поступления вызовов – Пуассоновский процесс:

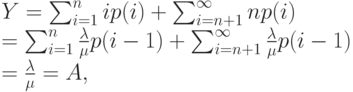$Y=sum_{i=1}^n ip(i)+sum_{i=n+1}^{infty}np(i)\ =sum_{i=1}^n frac{lambda}{mu}p(i-1)+sum_{i=n+1}^{infty} frac{lambda}{mu}p(i-1)\ =frac{lambda}{mu}=A,$

(
12.7)

Здесь применено уравнение равновесия.

Длина очереди – случайная величина . Вероятность наличия клиентов в очереди в случайной точке времени:

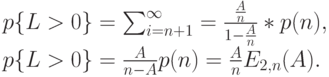$p{L > 0}=sum_{i=n+1}^{infty}=frac{frac An}{1-frac An}*p(n),\ p{L > 0}=frac{A}{n-A}p(n)=frac AnE_{2,n}(A).$

(
12.8)

Здесь использовалось (12.5).

Числовая оценка

Формула подобна B-формуле (7.10) Эрланга, за исключением коэффициента 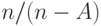n/(n-A) в последнем элементе. Поскольку существует очень точная рекурсивная формула для числовой оценки B-формулы Эрланга (7.29), можно использовать следующие отношения для того, чтобы получить числовые значения для C-формулы:

$E_{2,n}(A)=frac{n*E_{1,n}(A)}{n-A(1-E_{1,n}(A))}\ =frac{E_{1,n}(A)}{1-A{1-E_{1,n}(A)}/n}, quad A < n.$

(
12.9)

где элемент 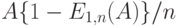$A{1-E_{1,n} (A)}/n$ – средняя обслуженная нагрузка на канал в соответствующей системе с потерями. Для A ge n мы имеем $E_{2,n} (A) = 1$ . Это – вероятность того, что все клиенты поставлены на ожидание. C-формула Эрланга может быть выражена B-формулой:

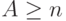
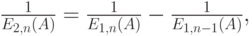$frac{1}{E_{2,n}(A)}=frac{1}{E_{1,n}(A)}-frac{1}{E_{1,n-1}(A)},$

(
12.10)

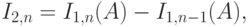$I_{2,n}=I_{1,n}(A)-I_{1,n-1}(A),$

(
12.11)

где – инверсия вероятности (7.30).

$I_{n,2}(A)=frac{1}{E_{2,n}(A)}.$

C-формула Эрланга была сведена в таблицу в Принципе Мо (Jensen, 1950 [50] ) и показана на рис.12.2.

Рис.
12.2.
C-формула Эрланга для системы с ожиданием M/M/n.

Вероятность 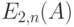$E_{2,n} (A)$ для положительного времени ожидания показана как функция предложенной нагрузки для различных значений числа обслуживающих приборов n.

Средняя длина очереди

Мы должны отличать длину очереди в произвольный момент времени и длину очереди, когда есть клиенты, стоящие в очереди.

Средняя длина очереди в произвольный момент времени

Длина очереди в произвольной момент времени называется виртуальной длиной очереди. Для произвольного клиента длина очереди определяется как свойство PASTA, т.е. Пуассоновский поток вызовов (математическое ожидание по времени = математическое ожидание по вызовам). Мы получаем среднюю длину очереди:

$L_n = E {L}$ в произвольный момент времени:

$L_n=0*sum_{i=0}p(i)+sum_{i=n+1}^{infty}(i-n)p(i)\ =sum_{i=n+1}^{infty}i-n)p(n) left (frac An right )^{i-n}\ =p(n)*sum_{i=1}^{infty}i (frac{A}{n})^{i-n}\ =p(n)*frac An sum_{i=1}^{infty} frac{partial}{partial (A/n)} left { left (frac An right)^i right }.$

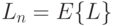
Поскольку , ряд является равномерно сходящимся, оператор дифференцирования может быть вынесен за сумму:

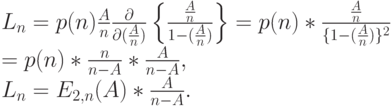$L_n=p(n) frac An frac{partial}{partial (frac An)} left { frac{frac An}{1-(frac An)} right }=p(n)*frac{frac An}{{1-(frac An)}^2}\ =p(n)*frac{n}{n-A}*frac{A}{n-A},\ L_n=E_{2,n}(A)*frac{A}{n-A}.$

(
12.12)

Средняя длина очереди может интерпретироваться как нагрузка, которую обслуживают места ожидания очереди, и поэтому она иногда называется нагрузкой времени ожидания.

Средняя длина очереди, со временем ожидания больше нуля

Математическое ожидание времени и в этом случае равно математическому ожиданию вызова. Условная средняя длина очереди будет:

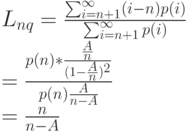$L_{nq}=frac{sum_{i=n+1}^{infty}(i-n)p(i)}{sum_{i=n+1}^{infty}p(i)}\ =frac{p(n)*frac{frac An}{(1-frac An)^2}}{p(n) frac{A}{n-A}}\ =frac{n}{n-A}$

(
12.13)

Применяя (12.8) и (12.12), получаем:

$L_{nq}=frac{L_n}{p{L > 0}},$

где – случайная переменная, обозначающая длину очереди.

Средние времена ожидания

Здесь представляют интерес две характеристики:

среднее время ожидания для всех клиентов;
среднее времени ожидания w для клиентов, для которых время ожидания имеет положительное значение.

Первая является индикатором уровня обслуживания целой системы, тогда как вторая относится к задержанным вызовам.

Математические ожидания времени будут равны математическим ожиданиям по вызовам из-за свойства PASTA.

Среднее время ожидания для всех вызовов

Формула Литла говорит, что средняя длина очереди равна интенсивности прибытия, умноженной на среднее время ожидания:

(
12.14)

где 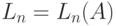и . Рассматривая процесс поступления вызовов, из (12.12) мы имеем:

$W_n=frac{L_n}{lambda}=frac {1}{lambda}*E_{2,n}(A)*frac{A}{n-A}.$

Поскольку 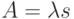, где – среднее время обслуживания, мы имеем:

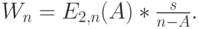$W_n=E_{2,n}(A)*frac{s}{n-A}.$

(
12.15)

Среднее время ожидания для задержанных вызовов

Полное время ожидания является постоянным и может быть вычислено либо в среднем по всем клиентам ( 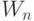W_n ), либо только по вызовам, для которых времена ожидания ( w_n ) имеют положительные значения (3.20):

$W_n=w_n*E_{2,n}(A),$

(
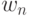
12.16)

$w_n=frac{s}{n-A}$

(
12.17)

Пример 12.2.1: Система организации очереди с одним обслуживающим прибором (M/M/1)

Эта система наиболее часто упоминается в литературе. Вероятности состояния (12.2) определяются рядом геометрической прогрессии:

(
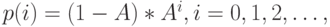12.18)

поскольку 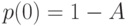. Вероятность задержки равна:

$Е_{2,1}(A)=А.$

Средняя длина очереди 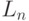L_n (12.12) и среднее время ожидания для всех вызовов W_n (12.15) :

$L_1=frac{A^2}{1-A},$

(
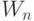
12.19)

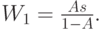$W_1=frac{As}{1-A}.$

(
12.20)

С помощью уравнений 12.12, 12.14, 12.17 мы можем установить, что увеличение нагрузки из-за большего количества вызовов лучше, чем увеличение нагрузки из-за более длинного времени обслуживания, поскольку увеличение времени обслуживания увеличивает величину всех показателей. Поэтому важно, чтобы времена обслуживания системы не увеличивались в момент перегрузки.

Пример 12.2.2: Среднее время ожидания, когда A -> 0

Заметьте, что если 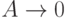A to 0 , мы получаем (12.17). Если клиент ожидает (что редко случается, когда A to 0 ), то этот клиент будет единственным в очереди. Клиент должен ждать, пока сервер освободится. Это случается в конце экспоненциально распределенного временного интервала со средней величиной s/n . Поэтому w_n никогда не может быть меньше, чем s/n .

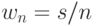
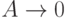
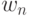
Функция увеличения для M/M/n

Предельное увеличение нагрузки, которую может обслуживать система, когда мы дополняем число обслуживающих приборов, может быть выражено несколькими способами. Уменьшение отношения нагрузки канала к полной нагрузке (пропорционально числу всех вызовов от клиентов) определяется как:

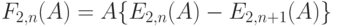$F_{2,n}(A)=A{E_{2,n}(A)-E_{2,n+1}(A)}$

(
12.21)

Уменьшение средней длины очереди (пропорционально нагрузке, которую обслуживают места ожидания) определяется формулой Литла (12.14):

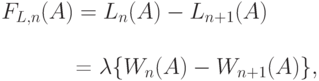$F_{L,n}(A)=L_n(A)-L_{n+1}(A)\ qquad = lambda {W_n(A)-W_{n+1}(A)},$

(
12.22)

где W_n(A) – среднее время ожидания для всех вызовов, когда предложенная нагрузка и число обслуживающих приборов – (12.15). Равенства (12.21) и (12.22) сведены в таблицу в Принципе Мо (Jensen, 1950 [50] ) и могут быть легко рассчитаны с помощью калькулятора или компьютера.

Источник

СМО с ожиданием (очередью)

Системы с ожиданием при неограниченном входящем потоке

Одноканальная СМО с ожиданием

Одноканальная система с неограниченной очередью

Одноканальная СМО с ожиданием без ограничения на вместимость блока ожидания

Многоканальная СМО с неограниченной очередью

СМО с ограниченной очередью

СМО с ожиданием (очередью): определение и формулы

Одноканальная система с неограниченной очередью

Многоканальная СМО с неограниченной очередью

СМО с ограниченной очередью

СМО с ограниченным временем ожидания

8.9. СМО с ограничением на длину очереди

Система с ожиданием Эрланга M/M/n

Характеристики нагрузки систем с ожиданием

C-формула Эрланга

Числовая оценка

Средняя длина очереди

Средние времена ожидания

Пример 12.2.1: Система организации очереди с одним обслуживающим прибором (M/M/1)

Пример 12.2.2: Среднее время ожидания, когда A -> 0

Функция увеличения для M/M/n

Вам также может понравиться

Как составить день овуляции

Как найти среднемесячную амплитуду температуры

Заговор как найти кольцо которое потеряла

Добавить комментарий Отменить ответ