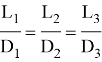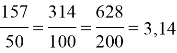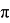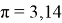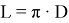Как посчитать длину окружности
Онлайн калькулятор
Как посчитать длину окружности зная диаметр
Какая длина у окружности если
Какова длина окружности (С) если её диаметр d?
Формула
С = π⋅d , где π ≈ 3.14
Пример
Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная радиус
Какая длина у окружности если
Какова длина окружности (С) если её радиус r?
Формула
С = 2⋅π⋅r , где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная её площадь
Какая длина у окружности если
Какова длина окружности (С) если её площадь S?
Формула
С = 2π⋅ √ S /π , где π ≈ 3.14
Пример
Если площадь круга равна 6 см 2 , то его длина примерно равна 8.68 см.
Нахождение длины окружности: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать длину/периметр окружности (круга) и разберем примеры решения задач.
Формула вычисления длины/периметра
1. Через радиус
Периметр круга или длина окружности (C) равняется удвоенному произведению ее радиуса на число π :
C = 2 * π * r
Радиус (r) – это отрезок, который соединяет центр окружности и любую точку на ней.
2. Через диаметр
Периметр/длина окружности считается как произведение ее диаметра на число π :
C = π * d
Диаметр (d) равен двум радиусам (d=2r). Это отрезок, соединяющий две противоположные точки на окружности.
Примечание: в расчетах значение числа π округляется до 3,14.
Примеры задач
Задание 1
Найдите длину окружности, если ее радиус равен 12 см.
Решение:
Воспользуемся первой формулой, в которой участвует значение радиуса: C = 2 * 3,14 * 12 см = 75,36 см.
Задание 2
Найдите периметр круга, если ее диаметр составляет 15 см.
Решение:
Применим формулу, в которой используется диаметр: C = 3,14 * 15 см = 47,1 см.
Длина окружности
О чем эта статья:
6 класс, 9 класс, ЕГЭ/ОГЭ
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так – l
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
r – радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
π – математическая константа, примерно равная 3,14
a – сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/dlina-okruzhnosti
[/spoiler]
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
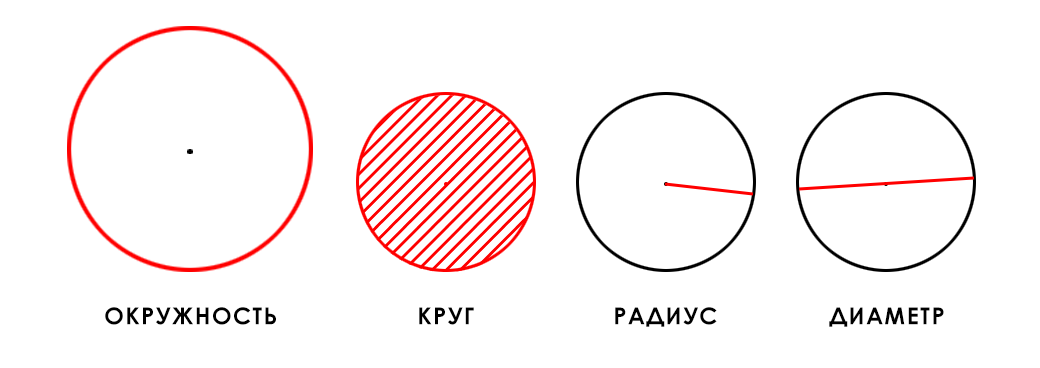
Что такое окружность?
Окружность – это замкнутая плоская кривая, ограничивающая круг.
Или, другими словами, окружность представляет собой множество точек, удаленных на одно и тоже расстояние от центра круга на длину радиуса этого круга. А длина окружности – это длина этой кривой, которую образует это множество точек и которая ограничивает собой круг. Это хорошо видно на иллюстрации выше.
Как найти длину окружности?
Чтобы вычислить длину окружности, нужно знать радиус, диаметр или площадь круга. Причём достаточно только чего-то одного из этих элементов.
По диаметру
Диаметр — это такой отрезок, который соединяет две точки на окружности и проходит через центр круга. Чтобы найти длину окружности через диаметр, просто умножаем диаметр окружности на число Пи и получаем длину окружности.
Формула будет такой:
L = π × d
Где L – длина окружности, π – константа, равная примерно 3,14, а d – это диаметр.
Например, нам нужно посчитать периметр канализационной трубы диаметром 100 мм. Окружность этой трубы можно найти весьма несложными расчётами:
L = 3,14 × 100 = 314 мм.
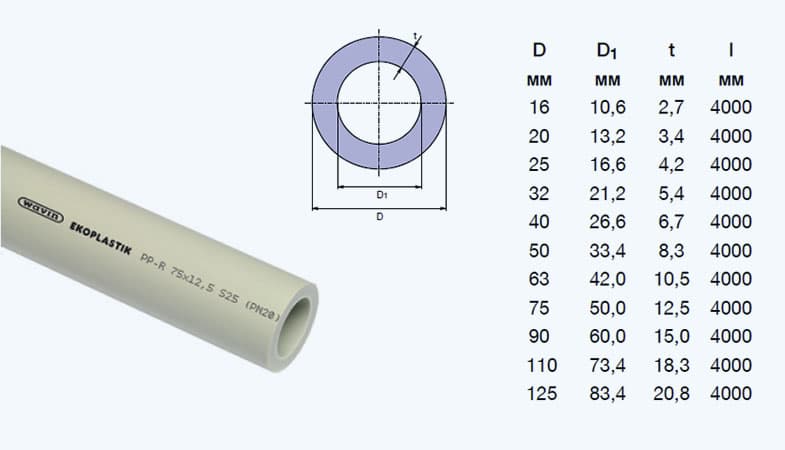
Кстати, у труб есть 2 окружности и 2 диметра: внутренние и внешние. Это хорошо показано на рисунке ниже.
Всегда обращайте внимание, какой именно диаметр известен и какую длину окружности вам требуется вычислить. Часто внутренний диаметр обозначается малой d или D1, а наружный просто – D или DN.
Зная радиус
Радиус окружности — это отрезок, который соединяет центр окружности с точкой на окружности. Радиус равен половине диаметра, поэтому вычисление длины окружности будет похоже на предыдущий случай: умножаем радиус на два и на число пи и получаем длину окружности.
Формула расчёта выглядит следующим образом:
L = 2π × R
Где L – длина окружности, π – константа (приблизительно 3,14), а r – это радиус.
К примеру, нужно посчитать длину внутренней окружности трубы, с внутренним радиусом 26 мм. В этом случае периметр получается следующим образом:
L = 2 × 3,14 × 26 = 163,28 мм.
Также обратите внимание, что в число Пи взято с точностью до двух знаков после запятой, и всегда расчёт через Пи идёт с округлением и является приблизительным.
Через площадь круга
И, пожалуй, самым редким случаем калькуляции периметра круга будет тот, когда нам известна только площадь этого круга. В этом случае, чтобы рассчитать длину окружности, можно воспользоваться следующей формулой:
L = (4Sπ)1/2
Где L – длина окружности, S – площадь круга, а π – константа, равная 3,14.
То есть длина окружности равна квадратному корню произведения площади круга, числу пи, умноженному на четыре. На всякий случай, корень и степень ½ – это одно и то же.
Возьмём пример, к нам прилетели инопланетяне и оставили круги на полях.
Площадь одного из этих кругов составила аж 1146,5 квадратных метра. Чтобы рассчитать длину окружности, нужно сделать следующее:
- Умножить 4 на 3,14, и полученное произведение умножить на площадь круга 1146,5. Получаем 14400,04.
- И теперь находим квадратный корень из этого числа и получаем примерно 120 метров. Это и есть длина окружности.
Как и в прошлых случаях из-за наличия числа Пи, которое является иррациональным, ответ будет считаться с округлением.
❓Вопросы и ответы
И наконец, предлагаем вам прочитать ответы на некоторые часто задаваемые вопросы относительно вычисления длины окружности.
Что что имеет большее значение радиус, диаметр, длина окружности или площадь круга?
Площадь круга. А если выставить всё это по мере убывания, то рейтинг будет таким:
- Площадь круга
- Длина окружности
- Диаметр
- Радиус
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разные калькуляторы, в частности калькуляторы: диаметра, площади круга и длины окружности. Для последней калькулятор находится наверху данной страницы.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Хватит ли чего-то одного (диаметра, радиуса, площади) для расчёта длины окружности?
Да, хватит. Формулы и примеры расчетов периметра круга, в которых используется что-то одно из перечисленного, есть выше на данной странице.
Что такое внутренняя и внешняя окружность? Чем они отличаются?
Внутренняя и внешняя окружность (а также диаметр) чаще всего используются для расчёта параметров труб, у которых есть стенки ненулевой ширины. Поэтому окружность внутри трубы всегда меньше окружности снаружи. Для окружности снаружи используется обозначение L или LN, а диаметра – D или DN. А для периметра и диаметра круга внутри добавляется нижний индекс «единица»: L1 и D1, или используются буквы в нижнем регистре (малые): l и d.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Как посчитать длину окружности
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать длину окружности
Чтобы посчитать длину окружности (круга) просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор

Как посчитать длину окружности зная диаметр
Какая длина у окружности если
её диаметр ?
Ответ:
0
Какова длина окружности (С) если её диаметр d?
Формула
С = π⋅d, где π ≈ 3.14
Пример
Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная радиус
Какая длина у окружности если
её радиус ?
Ответ:
0
Какова длина окружности (С) если её радиус r?
Формула
С = 2⋅π⋅r, где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная её площадь
Какая длина у окружности если
её площадь ?
Ответ:
0
Какова длина окружности (С) если её площадь S?
Формула
С = 2π⋅√S/π, где π ≈ 3.14
Пример
Если площадь круга равна 6 см2, то его длина примерно равна 8.68 см.
См. также
8 способов найти длину окружности
Выбирайте формулу, ориентируясь на известные величины.
1. Как найти длину окружности через диаметр
Просто умножьте диаметр на число пи.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d —диаметр окружности.
2. Как найти длину окружности через радиус
Умножьте число пи на два радиуса.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- r — радиус окружности.
3. Как вычислить длину окружности через площадь круга
Умножьте число пи на четыре площади круга.
Найдите корень из результата.
- O — искомая длина окружности.
- S – площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
4. Как найти длину окружности через диагональ вписанного прямоугольника
Умножьте число пи на диагональ.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d – любая диагональ прямоугольника.
5. Как вычислить длину окружности через сторону описанного квадрата
Умножьте число пи на сторону квадрата.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- a – любая сторона квадрата.
6. Как найти длину окружности через стороны и площадь вписанного треугольника
Перемножьте стороны треугольника.
Поделите результат на площадь и на два.
Умножьте полученное число на пи.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- a, b, c – стороны треугольника.
7. Как найти длину окружности через площадь и полупериметр описанного треугольника
Поделите площадь треугольника на его полупериметр.
Умножьте результат на число пи и на два.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- p – полупериметр треугольника (равен половине от суммы всех сторон).
8. Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разделите 180 градусов на количество сторон многоугольника.
Найдите синус полученного числа.
Разделите сторону многоугольника на результат.
Умножьте получившееся число на пи.
- O — искомая длина окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- π (пи) — константа, равная 3,14.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✏️🎓
- Как найти периметр прямоугольника
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым
В своей повседневной жизни мы часто сталкиваемся с задачами, которые связаны с вычислением периметра, то есть суммы длин сторон различных геометрических фигур. В случае, если геометрическая фигура — многоугольник, нахождение его периметра не составляет особого труда: для этого достаточно с помощью линейки измерить длину каждой из сторон и сложить полученные результаты. Что же делать, если необходимо узнать длину окружности? Ответу на этот вопрос посвящена данная статья.
Окружность является самой распространённой кривой практически во всех областях человеческой деятельности. Форму окружности или круга мы встречаем повсюду: это и колесо машины, и линия горизонта, и диск Луны. Многие вещи, окружающие нас, имеют круглую форму, например: обруч, кольцо, мяч, тарелка.
В свободное время я люблю заниматься моделированием из бумаги, пластилина и, особенно, из деталей конструктора Лего. Иногда, для того чтобы подготовить нужную заготовку для модели, необходимо знать длину сторон фигуры, которую хочешь получить. Никогда эта задача не вызывала у меня затруднений, пока я не столкнулся с определением длины окружности.
В учебнике по геометрии 7 класса рассматривается вопрос определения длины окружности. Существует формула, при помощи которой решается эта задача. Мне стало интересно, а как же раньше, в древности, люди находили длину окружности, можно ли ее найти экспериментальным путем без помощи известной формулы, какая существует связь между размером окружности (диаметром) и длиной окружности, и какое практическое применение может иметь решение этой задачи.
Ещё в давние времена люди сталкивались с практическими задачами, для решения которых необходимо было уметь находить длину окружности. Например, для того чтобы изготовить металлический обод для колеса телеги, определить вместительность сосуда, при строительстве зданий, для изготовления ювелирных изделий, при пошиве одежды.
В источниках [1, 4] сказано, что уже 4 тысячи лет назад люди знали, что длина окружности примерно равна трём его диаметрам. В дальнейшем, более 2 тыс. лет назад, большой вклад в развитие геометрии, в том числе в изучение геометрических фигур — окружности и круга — внесли древнегреческий математик Евклид, а позже — Архимед.
Целью исследования является изучение различных способов нахождения длины окружности и получение взаимосвязи между диаметром окружности и её длиной.
Гипотеза исследования: формулу длины окружности можно получить самостоятельно экспериментальным путем.
Основные понятия
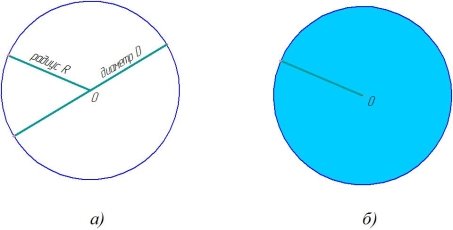
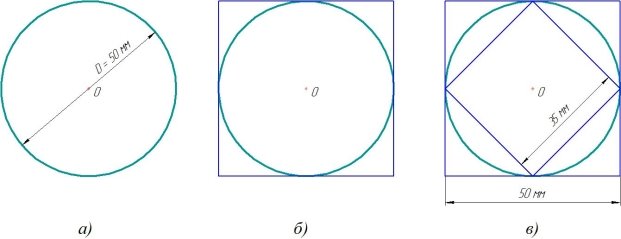
Окружность — это замкнутая плоская кривая линия, все точки которой находятся на одинаковом расстоянии от заданной точки О. Эта точка называется центром окружности (рисунок 1,а).
Круг — часть плоскости, ограниченная окружностью (рисунок 1,б).
Можно сказать, что окружность является границей круга.
Основные линии окружности — радиус и диаметр (рисунок 1,а).
Радиус R окружности — это отрезок, соединяющий центр О с любой точкой окружности.
Диаметр D окружности — отрезок, который соединяет две точки окружности и проходит через ее центр.
Рис. 1. Окружность и круг
Способы нахождения длины окружности
Рассмотрим некоторые возможные способы нахождения длины окружности.
Нахождение длины окружности с
помощью нити
Когда я впервые задумался над решением данной задачи, первое и самое простое, что пришло на ум — это приложить нить к окружности, а затем при помощи линейки измерить ее длину. Подготовиться к эксперименту мне помог папа: он вырезал на станке металлические круги разных диаметров.
Проведем измерение круга диаметром 50 мм. Я обернул круг нитью, шариковой ручкой сделал отметки и при помощи линейки измерил длину нити между отметками (рисунок 2).
Длина нити оказалась равной 158 мм. При измерении я обратил внимание на то, что результат получается приблизительным, так как зависит от силы натяжения нити и ее толщины. И самое главное — не каждую окружность можно измерить таким способом.
То есть данный экспериментальный способ не решает поставленной задачи. Необходимо получить универсальную формулу, при помощи которой можно было бы найти длину окружности любого диаметра.
Рис. 2. Нахождение длины окружности с помощью нити
Нахождение длины окружности с
помощью квадратов
Следующий способ, который я решил применить: представить окружность в виде квадрата (рисунок 3).
Продолжаем исследовать окружность диаметром 50 мм (рисунок 3,а).
Построим вокруг окружности квадрат так, чтобы он касался окружности в 4-х точках (рисунок 3,б), то есть сторона квадрата равна диаметру окружности.
Но на рисунке видно, что периметр квадрата явно больше длины вписанной окружности. А что, если внутри окружности построить еще один квадрат? Тогда, возможно, длина окружности будет средней величиной между периметрами двух квадратов.
Рис. 3
Измерим длины сторон квадратов с помощью линейки (рисунок 3,в). Длина стороны внутреннего квадрата равна 35 мм, наружного — 50 мм.
Найдем периметры квадратов:
Периметр внутреннего квадрата Р
внутр
= 35+35+35+35 = 435= 140 (мм);
Периметр внешнего квадрата Р
внешн
= 50+50+50+50= 450 = 200 (мм).
Предположим, что длина окружности — это средняя величина двух периметров. Найдём, чему она равна: (140+200):2 = 170 (мм).
Это значение намного отличается от длины окружности, полученной при измерении с помощью нити — 158 мм, что говорит о невысокой точности этого метода.
Нахождение длины окружности с
помощью многоугольников
Далее я предположил, что если внутри окружности построить многоугольник с большим количеством сторон, то его периметр будет больше приближен к длине описанной окружности.
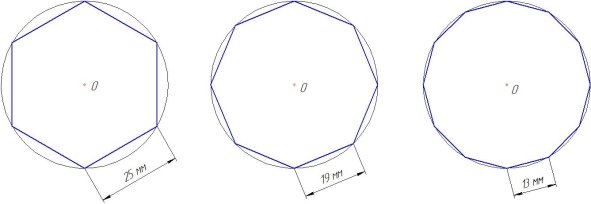
Для того чтобы подтвердить своё предположение, я решил исследовать несколько геометрических фигур: шестиугольник, восьмиугольник, двенадцатиугольник. Диаметр окружности — 50 мм (рисунок 4).
Рис. 4
Измерим линейкой длины сторон и с помощью калькулятора найдем периметры построенных фигур.
Периметр шестиугольника (обозначим его Р
6
) равен:
Р
6
= 25+25+25+25+25+25= 625 = 150 (мм).
Найдем периметры восьмиугольника Р
8
и
двенадцатиугольника Р
12
:
Р
8
= 19+19+19+19+19+19+19+19 = 819 = 152 (мм);
Р
12
= 13+13+13+13+13+13+13+13+13+13+13+13 = 1213 = 156 (мм).
Из полученных результатов можно сделать вывод, что чем больше сторон имеет многоугольник, тем больше его периметр будет приближен к реальной длине окружности, в которую он вписан.
Получение формулы длины окружности экспериментальным методом
От геометрических построений переходим к практическому исследованию и попробуем ответить на вопрос: существует ли связь между диаметром окружности и его длиной.
Экспериментальным способом найдём длины 3-х окружностей диаметром 50, 100 и 200 мм.
Для эксперимента нам понадобятся: 3 металлических круга диаметром 50, 100 и 200 мм, простой карандаш, цветные карандаши, лист ватмана, линейка, рулетка, корпус шариковой ручки, выполняющий роль оси вращения (рисунок 5).
Рис. 5. Подготовка к эксперименту
Для нахождения длины окружности мы будем катить металлический круг, как колесо, по прямой линии, проведенной на листе ватмана. На круге сделана насечка для того, чтобы можно было отметить, когда круг сделает полный оборот. Расстояние, которое пройдет круг за один оборот, и будет являться длиной окружности соответствующего диаметра (рисунок 6).
Рис. 6. Проведение эксперимента
В ходе эксперимента мы получили следующие результаты (рисунок 7).
Длина окружности, диаметр которой D
1
= 50мм, равна 157мм, то есть L
1
=157 мм.
Длина окружности диаметром D
2
=100 мм равна L
2
=314 мм.
Длина окружности диаметром D
3
=200 мм равна L
3
=628 мм.
Рис. 7. Результаты эксперимента
Представим полученные результаты в виде таблицы.
|
Диаметр окружности, мм |
50 |
100 |
200 |
|
Длина окружности, мм |
157 |
314 |
628 |
Сравним полученные результаты. Из таблицы видно, что при увеличении диаметра окружности в 2 раза, длина окружности увеличивается также в 2 раза. Отсюда можно сделать вывод, что отношение длины окружности к её диаметру — одинаковая величина для любой окружности, то есть:
С помощью калькулятора выполним расчет:
Экспериментальным методом мы определили, что отношение длины к диаметру окружности — постоянная величина, приблизительно равная 3,14.
Уже более 2 тыс. лет назад древнегреческий математик Архимед в своих научных трудах доказал, что отношение длины окружности к её диаметру является постоянной величиной, равной 3,14.
В 1706 году британский математик Уильям Джонс предложил это отношение обозначать греческой буквой
(пи), от первой буквы греческого слова “periferia (периферия)” — круг:
Зная отношение длины окружности к диаметру, получим формулу для нахождения длины окружности:
При помощи этой формулы можно вычислить длину любой окружности, насколько бы велика или мала она не была, или решить обратную задачу для нахождения радиуса окружности, если известна её длина.
Заключение
Таким образом, были исследованы различные способы нахождения длины окружности: с помощью нити, методом квадратов, с помощью многоугольников, в результате чего мы пришли к выводу, что метод многоугольников позволяет найти наиболее точное значение длины окружности.
Экспериментальным путем найдена взаимосвязь между диаметром окружности и её длиной и получена формула для нахождения длины окружности
, где
, что подтверждает нашу гипотезу.
Литература:
- Энциклопедический словарь юного математика/Сост. А. П. Савин. — М.: Педагогика, 1989. — 352 с.: ил.
- Что такое. Кто такой: В 3 т. Т. 1–4-е изд., перераб. и доп. — М.: Педагогика-Пресс, 1998. — 384 с.: ил.
- Что такое. Кто такой: В 3 т. Т. 2–4-е изд., перераб. И доп. — М.: Педагогика-Пресс, 1998. — 416 с.: ил.
- Окружность: история // ВикипедиЯ. URL: https://ru.wikipedia.org/wiki/ %D0 %9E %D0 %BA %D1 %80 %D1 %83 %D0 %B6 %D0 %BD %D0 %BE %D1 %81 %D1 %82 %D1 %8C (дата обращения: 11.12.2019).
Основные термины (генерируются автоматически): длина окружности, диаметр окружности, нахождение длины окружности, окружность, помощь линейки, помощь нити, диаметр, рисунок, отношение длины окружности, длина.