Как найти среднюю энергию хаотического теплового движения

Физика, 10 класс

Урок №19. Температура. Энергия теплового движения молекул

На уроке рассматриваются понятия: температура и тепловое равновесие; шкалы Цельсия и Кельвина; абсолютная температура как мера средней кинетической энергии теплового движения частиц вещества, зависимость давления от концентрации молекул и температуры.

Глоссарий по теме:

Макроскопические параметры – величины объём V, давление p и температура t, характеризующие состояние макроскопических тел без учёта их молекулярного строения.

Температура характеризует степень нагретости тела (холодное, тёплое, горячее).

Температура (от лат. temperatura — надлежащее смешение, соразмерность, нормальное состояние) – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.

Тепловым равновесием называют – такое состояние тел, при котором температура во всех точках системы одинакова.

Тепловым или термодинамическим равновесием, изолированной системы тел, называют состояние, при котором все макроскопические параметры в системе остаются неизменными.

Термометр — это прибор для измерения температуры путём контакта с исследуемым телом. Различают жидкостные, газовые термометры, термопары, термометры сопротивления.

Абсолютная температура Т прямо пропорциональна температуре Θ (тета), выражаемой в энергетических единицах (Дж).

Абсолютный нуль – предельная температура, при которой давление идеального газа обращается в нуль при фиксированном объёме или объём идеального газа стремится к нулю при неизменном давлении.

Абсолютный нуль – температура, при которой прекращается тепловое движение молекул.

Абсолютная шкала температур (Шкала Кельвина) – здесь нулевая температура соответствует абсолютному нулю, а каждая единица температуры равна градусу по шкале Цельсия.

Кельвин – единица абсолютной температуры в Международной системе измерений (СИ).

Постоянная Больцмана – коэффициент, связывает температуру Θ энергетических единицах (Дж) с абсолютной температурой Т (К).

Абсолютная температура есть мера средней кинетической энергии молекул.

Давление газа прямо пропорционально концентрации его молекул и абсолютной температуре Т.

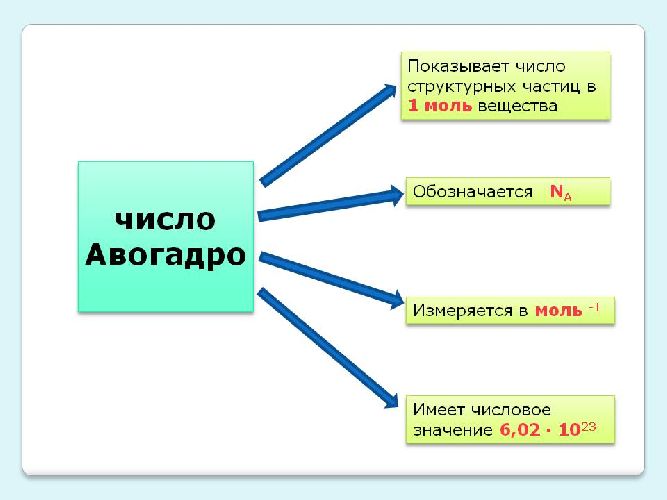
Закон Авогадро – в равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул

Обязательная литература:

1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 195 – 203.

Дополнительная литература:

1. Смородинский Я.А. Температура. – 3-е издание. – М.: Бюро Квантум, 2007. (Библиотечка «Квант». Вып. 103. Приложение к журналу «Квант» № 5/2007.) С. 5— 25.
2. Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. – С. 111-115.
3. Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. – С. 65 – 67.
4. Орлов В.А., Сауров Ю.А. Практика решения физических задач. 10-11классы. – М.: Вентана-Граф, 2014. – С. 98-99.
5. http://kvant.mccme.ru/1991/09/idealnyj_gaz_-_universalnaya_f.htm

Теоретический материал для самостоятельного изучения

Измеряя расположение звёзд на небе, расстояния на земле, время, люди знали, для чего они это делают и изобретали, телескопы, часы, прототипы современных линеек. О температуре такого же сказать было нельзя. О том, что такое тепловое равновесие и что означает степень нагрева тела (температура), существовали разные мнения. Но человек с незапамятных времен точно знал, что, когда два тела плотно соприкасаются, между ними устанавливается, выражаясь современным языком, тепловое равновесие.

Любое макроскопическое тело или группа макроскопических тел при неизменных внешних условиях самопроизвольно переходят в состояние теплового равновесия.

Тепловым равновесием называют такое состояние тел, при котором температура во всех точках системы одинакова.

Температура (от лат. temperatura — надлежащее смешение, соразмерность, нормальное состояние) – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.

К числу характеристик состояния макроскопических тел (твёрдых тел, жидкостей, газов) и процессов изменения их состояний, относят объём, давление и температуру. Эти величины описывают в целом тела, состоящие из большого числа молекул, а не отдельные молекулы. При этом микроскопические процессы внутри тела не прекращаются при тепловом равновесии: расположения молекул всё время меняются и меняются их скорости при столкновениях.

Величины объём, давление и температуру, характеризующие состояние макроскопических тел без учёта их молекулярного строения, называют макроскопическими параметрами.

Тепловым или термодинамическим равновесием, изолированной системы тел, называют состояние, при котором все макроскопические параметры в системе остаются неизменными.

Для точной характеристики нагретости тела, необходим прибор, способный измерить температуры тел и дать возможности их сравнения.

Термометр — это прибор для измерения температуры путём контакта с исследуемым телом. Различают жидкостные, газовые термометры, термопары, термометры сопротивления.

В 1597 году Галилей создал термоскоп, в собственных сочинениях учёного нет описания этого прибора, но его ученики засвидетельствовали этот факт. Аппарат представлял собой устройство для поднятия воды при помощи нагревания.

Изобретение термометра, данные которого не зависели бы от перепадов атмосферного давления, произошли благодаря экспериментам физика Э. Торричелли, ученика Галилея.

Во всех приборах, изобретённых в XVIII веке, измерение температуры было относительно расширению столбика воды, спирта или ртути и произвольности выбора начала отсчёта, т.е. нулевой температуры. Наполняющие их вещества замерзали или кипели и этими термометрами нельзя было измерять очень низкие или очень высокие температуры. Необходимо было изобрести такую шкалу, чтобы избавиться от зависимости выбранного вещества, на основе которого формировалось градуирование.

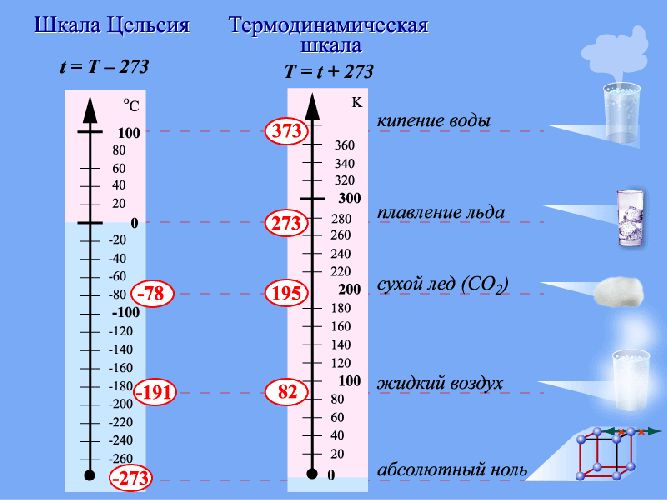
Шкала, предложенная шведским учёным Андерсом Цельсием в 1742 г., точно устанавливала положение двух точек: 0 и 100 градусов. По шкале Цельсия температура обозначается буквой t, измеряется в градусах Цельсия (ºС).

На территории Англии и США используется шкала Фаренгейта. Такая шкала была предложена немецким учёным Даниелем Габриелем Фаренгейтом в 1724 г.: 0 °F — температура смеси снега с нашатырём или поваренною солью, 96 °F —температура здорового человеческого тела, во рту или под мышкой.

Рене Антуан де Реомюр не одобрял применения ртути в термометрах вследствие малого коэффициента расширения ртути. В 1730 году изобрёл водно-спиртовой термометр и предложил шкалу от 0 до 80°.

Шкала Реомюра очень долго использовалась на родине учёного во Франции вплоть до настоящего времени.

Различные жидкости при нагревании расширяются не одинаково. Поэтому расстояния на шкале между нулевой отметкой 0 °C и 100 °C будут разными.

Однако существует способ создать тело, которое приближенно обладает нужными качествами. Это идеальный газ. Было замечено, что в отличие от жидкостей все разряжённые газы – водород, гелий, кислород – расширяются при нагревании одинаково и одинаково меняют своё давление при изменении температуры. Это свойство газов позволяет избавиться в термометрах от одного существенного недостатка шкалы Цельсия – произвольности выбора начала отсчёта, то есть нулевой температуры.

При тепловом равновесии, если давление и объём газа массой m постоянны, то средняя кинетическая энергия молекул газа должна иметь строго определённое значение, как и температура.

Практически такую проверку произвести непосредственно невозможно, но с помощью основного уравнения молекулярно-кинетической теории её можно выразить через макроскопические параметры:

; ; ; ;

Если кинетическая энергия действительно одинакова для всех газов в состоянии теплового равновесия, то и значение давления р должно быть тоже одинаково для всех газов при постоянном значении отношения объёма к числу молекул. Подтвердить или опровергнуть данное предположение может только опыт.

Возьмём несколько сосудов, заполненных различными газами, например, водородом, гелием и кислородом. Сосуды имеют определённые объёмы и снабжены манометрами, для измерения давления газов в сосудах. Массы газов известны, тем самым известно число молекул в каждом сосуде. Приведём газы в состояние теплового равновесия. Для этого поместим их в тающий лёд и подождём, пока не установится тепловое равновесие и давление газов перестанет меняться.

Здесь устанавливается тепловое равновесие и все газы имеют одинаковую температуру 0 °С. При этом показания манометра показывают разное давление р, объёмы сосудов V изначально были разными и число молекул N различно, так как газы, закаченные в баллоны разные. Найдём отношение для водорода всех параметров для одного моля вещества:

Такое значение отношения произведения давления газа на его объём к числу молекул получается для всех газов при температуре тающего льда. Обозначим это отношение через Θ₀ (тета нулевое):

Таким образом, предположение, что средняя кинетическая энергия, а также давление р в состоянии теплового равновесия одинаковы для всех газов, если их объёмы и количества вещества одинаковы или если отношение

Если же сосуды с газами поместить в кипящую воду при нормальном атмосферном давлении, то согласно эксперименту, отношение макроскопических параметров будет также одинаковым для всех газов, но значение будет больше предыдущего

Отсюда следует, что величина Θ растёт с повышением температуры и не зависит от других параметром, кроме температуры. Этот опытный факт позволяет рассматривать величину Θ тета как естественную меру температуры и измерять в энергетических единицах — джоулях.

А теперь вместо энергетической температуры введём температуру, которая будет измеряться в градусах. Будем считать величину тета Θ прямо пропорциональной температуре Т, где k- коэффициент пропорциональности

Так как , то тогда

По этой формуле вводится температура, которая даже теоретически не может быть отрицательной, так как все величины левой части этого равенства больше или равны нулю. Следовательно, наименьшим значением этой температуры является нуль, при любом другом параметре p, V, N равным нулю.

Предельную температуру, при которой давление идеального газа обращается в нуль при фиксированном объёме или при которой объём идеального газа стремится к нулю при неизменном давлении, называют абсолютным нулём температуры.

Тепловое движение молекул непрерывно и бесконечно, а при абсолютном нуле молекулы поступательно не двигаются. Следовательно, абсолютный нуль температур при наличии молекул вещества не может быть достигнут. Абсолютный нуль температур — это самая низкая температурная граница, верхней не существует, та «наибольшая или последняя степень холода», существование которой предсказывал М.В. Ломоносов.

В 1848 г. английскому физику Вильяму Томсону (лорд Кельвин) удалось построить абсолютную температурную шкалу (её в настоящее время называют шкалой Кельвина), которая имеет две основные точки 0 К (или абсолютный нуль) и 273К, точка в которой вода существует в трёх состояниях (в твёрдом, жидком и газообразном).

Абсолютная температурная шкала — шкала температур, в которой за начало отсчёта принят абсолютный нуль. Температура здесь обозначается буквой T и измеряется в кельвинах (К).

На шкале Цельсия, есть две основные точки: 0°С (точка, в которой тает лёд) и 100°С (кипение воды). Температура, которую определяют по шкале Цельсия, обозначается t. Шкала Цельсия имеет как положительные, так и отрицательные значения.

Из опыта мы определили значения величины Θ (тета) при 0 °С и 100 °С. Обозначим абсолютную температуру при 0 °С через Т₁, а при 100 °С через Т₂. Тогда согласно формуле:

Отсюда можно вычислить коэффициент k, который связывает температуру в Θ энергетических единицах (Дж) с абсолютной температурой Т (К)

k = 1,38 • 10^-23 Дж/К – постоянная Больцмана.

Зная постоянную Больцмана, можно найти значение абсолютного нуля по шкале Цельсия. Для этого найдём сначала значение абсолютной температуры, соответствующее 0°С:

значение абсолютной температуры.

Один кельвин и один градус шкалы Цельсия совпадают. Поэтому любое значение абсолютной температуры Т будет на 273 градуса выше соответствующей температуры t по Цельсию:

Теперь выведем ещё одну зависимость температуры от средней кинетической энергии молекул. Из основного уравнения молекулярно-кинетической теории и уравнения для определения абсолютной температуры

Здесь видно, что левые части этих уравнений равны, значит правые равны тоже.

Средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре.

Абсолютная температура есть мера средней кинетической энергии движения молекул.

Из выведенных формул мы можем получить выражение, которое показывает зависимость давления газа от концентрации молекул и температуры

Из этой зависимости вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же. Отсюда следует закон Авогадро, известный нам из курса химии.

Закон Авогадро: в равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.

Рассмотрим задачи тренировочного блока урока.

1. При температуре _______ (37⁰C; 283⁰C; 27⁰C) средняя кинетическая энергия поступательного движения молекул равна 6,21·10^-21Дж.

Дано:

k = 1,38 • 10-23 Дж/К – постоянная Больцмана

t -?

Решение:

Запишем значение средней кинетической энергии хаотического поступательного движения молекул с зависимостью от абсолютной температуры:

Отсюда выразим Т:

Соотношение между абсолютной температурой и температурой в градусах Цельсия:

Подставим значение абсолютной температуры:

Правильный вариант ответа:

2. При температуре 290 К и давлении 0,8 МПа, средняя кинетическая энергия молекул равна __________ Дж, а концентрация составляет молекул ___________ м^-3.

Дано:

Т = 290К

р = 0,8 МПа =0,8·10⁶ Па

k = 1,38 • 10^-23 Дж/К – постоянная Больцмана

Е_к -? n – ?

Решение:

Значение средней кинетической энергии хаотического поступательного движения молекул:

Подставив значение абсолютной температуры, найдём ответ:

Определим концентрацию газа из соотношения:

Правильный вариант ответа: 6·10^-21; 2·10²⁶ м^-3.

При решении задач этой главы используется формула (2.6), определяющая абсолютную температуру, формула (2.9), связывающая среднюю энергию хаотического движения с температурой, и формула (2.12) для средней квадратической скорости молекул. Некоторые задачи удобно решать, используя формулу (2.10), связывающую давление газа с концентрацией молекул и абсолютной температурой.

Кроме того, нужно знать значение постоянной Больцмана (2.7).

1. Чему равно отношение произведения давления газа на его объем к числу молекул при температуре t = 300°C?
Решение. Согласно формуле (2.6) 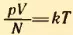, где k = 1,38*10^-23 Дж/К – постоянная Больцмана. Так как абсолютная температура n = t + 273 = 573 K, то

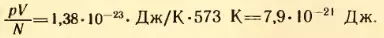
2. Определить среднюю квадратическую скорость молекулы газа при 0°C. Молярная масса газа M = 0,019 кг/моль.
Решение. Средняя квадратическая скорость молекул вычисляется по формуле (2.12), где следует положить 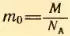и T = 273 К:

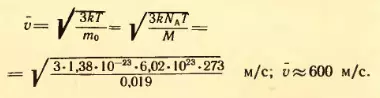
3. Некоторое количество водорода находится при температуре T₁ = 200 K и давлении p₁ = 400 Па. Газ нагревают до температуры T₂ = 10 000 K, при которой молекулы водорода практически полностью распадаются на атомы. Определить новое значение давления газа p₂, если его объем и масса остались без изменения.

Решение. Согласно формуле (2.10) давление газа при температуре T₁ равно: p₁ = n₁kT₁, где n₁ – концентрация молекул водорода.

При расщеплении молекул водорода на атомы число частиц в сосуде увеличивается в два раза. Следовательно, концентрация атомов водорода равна n₂ = 2n₁. Давление атомарного водорода p₂ = n₂kT₂ = 2n₁kT₂.

Разделив почленно второе уравнение на первое, получим: .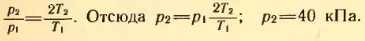

Упражнения

1. Какое значение имела бы постоянная Больцмана, если бы единица температуры в СИ – кельвин – была равна не 1°C, а 2°С?
2. Какова средняя кинетическая энергия молекул аргона, если температура газа 17°С?
3. Современные вакуумные насосы позволяют понижать давление до 1,3*10^-10 Па (10^-12 мм. рт. ст.). Сколько молекул газа содержится в 1 см³ при указанном давлении и температуре 27°С?
4. Где больше молекул: в комнате объемом 50 м³ при нормальном атмосферном давлении и температуре 20°С или в стакане воды объемом 200 см³?
5. Средняя квадратическая скорость молекулы газа, находящегося при температуре 100°С, равна 540 м/с. Определить массу молекулы.
6. На сколько процентов увеличивается средняя квадратическая скорость молекул воды в нашей крови при повышении температуры от 37 до 40°С?

Средняя кинетическая энергия теплового движения молекул газа.

Уравнение состояния
идеального газа в форме pV
= nRT
или p
= nkT может
быть обосновано и методами кинетической
теории газов. На основе кинетического
подхода сравнительно просто выводится
выражение для давления идеального газа
в сосуде, которое получается как результат
усреднения импульсов молекул, передаваемых
стенке сосуда при многочисленных
соударениях молекул со стенкой. Величина
получаемого при этом давления определяется
как

,

Где бv
²с – среднее
значение квадрата скорости молекул, m
– масса молекулы.

Средняя кинетическая
энергия молекул газа (в расчете на одну
молекулу) определяется выражением

Кинетическая
энергия поступательного движения атомов
и молекул, усредненная по огромному
числу беспорядочно движущихся частиц,
является мерилом того, что называется
температурой. Если температура T
измеряется в градусах Кельвина (К), то
связь ее с E_k
дается соотношением

Это соотношение
позволяет, в частности, придать более
отчетливый физический смысл постоянной
Больцмана

1. Внутренняя
   энергия идеального газа.

В теории идеального газа потенциальная
энергия взаимодействия молекул считается
равной нулю. Поэтому внутренняя энергия
идеального газа определяется кинетической
энергией движения всех его молекул.
Средняя энергия движения одной молекулы
равна

Так как в одном киломоле содержится
молекул,
то внутренняя энергия одного киломоля
газа будет

Учитывая,
что,
получим

Для любой массы m газа, т.е. для любого
числа киломолей
внутренняя
энергия

(10.12)

Из этого выражения следует, что внутренняя
энергия является однозначной функцией
состояния и, следовательно, при совершении
системой любого процесса, в результате
которого система возвращается в исходное
состояние, полное изменение внутренней
энергии равно нулю. Математически это
записывается в виде тождества

1. Распределение
   Максвелла

Распределение
Ма́ксвелла—распределение
вероятности, встречающееся вфизикеихимии.
Оно лежит в основаниикинетической
теории газов, которая объясняет
многие фундаментальные свойства газов,
включаядавлениеидиффузию.
Распределение Максвелла также применимо
для электронных процессов переноса и
других явлений. Распределение Максвелла
применимо к множеству свойств
индивидуальных молекул в газе. О нём
обычно думают как о распределении
энергий молекул в газе, но оно может
также применяться к распределению
скоростей, импульсов, и модуля импульсов
молекул. Также оно может быть выражено
как дискретное распределение по множеству
дискретных уровней энергии, или как
непрерывное распределение по некоторому
континууму энергии.

Распределение Максвелла может и должно
быть получено при помощи статистической
механики(см. происхождениестатсуммы).
Как распределение энергии, оно
соответствует самому вероятному
распределению энергии, в
столкновительно-доминируемой системе,
состоящей из большого количества
невзаимодействующих частиц, в которой
квантовые эффекты являются незначительными.
Так как взаимодействие между молекулами
в газе является обычно весьма небольшим,
распределение Максвелла даёт довольно
хорошее приближение ситуации, существующей
в газе.

Во многих других случаях, однако, даже
приблизительно не выполнено условие
доминирования упругих
соударенийнад всеми другими
процессами. Это верно, например, в физикеионосферыи космическойплазмы,
где процессы рекомбинации и столкновительного
возбуждения (то есть излучательные
процессы) имеют большое значение, в
особенности для электронов. Предположение
о применимости распределения Максвелла
дало бы в этом случае не только
количественно неверные результаты, но
даже предотвратило бы правильное
понимание физики процессов на качественном
уровне. Также, в том случае где квантоваяде
Бройлева длина волнычастиц
газа не является малой по сравнению с
расстоянием между частицами, будут
наблюдаться отклонения от распределения
Максвелла из-за квантовых эффектов.

Распределение энергии Максвелла может
быть выражено как дискретное распределение
энергии:

,

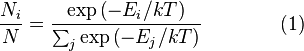где
является
числом молекул имеющих энергиюпри
температуре системы,является
общим числом молекул в системе и—постоянная
Больцмана. (Отметьте, что иногда
вышеупомянутое уравнение записывается
с множителем,
обозначающим степень вырождения
энергетических уровней. В этом случае
сумма будет по всем энергиям, а не всем
состояниям системы). Поскольку скорость
связана с энергией, уравнение (1) может
использоваться для получения связи
между температурой и скоростями молекул
в газе. Знаменатель в уравнении (1)
известен как каноническаястатистическая
сумма.

1. Распределение
   Больцмана.

Распределение Больцмана—
распределение вероятностей различных
энергетических состоянийидеальной
термодинамической системы (идеальный
газ атомов или молекул)в условияхтермодинамического
равновесия; открытоЛ.
Больцманомв1868—1871.

Согласно распределению Больцманасреднее число частиц с полной энергиейравно

где
—
кратность состояния частицы с энергией—
число возможных состояний частицы с
энергией.
Постояннаянаходится
из условия, что суммапо
всем возможным значениямравна
заданному полному числу частицв
системе (условие нормировки):

В случае, когда движение частиц подчиняется
классической механике, энергию
можно
считать состоящей из

• кинетической энергии
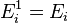  (кин)
  частицы (молекулы или атома),

• внутренней энергии
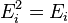  (вн)
  (например, энергии возбуждения электронов)
  и

• потенциальной энергии
  (пот)
  во внешнем поле, зависящей от положения
  частицы в пространстве:

1. Явление переноса.
   Диффузия

В термодинамически
неравновесных системах происходят
особые необратимые процессы, называемые
явлениями
переноса, в
результате которых осуществляется
пространственный перенос массы, импульса,
энергии. К явлениям переноса относятся
теплопроводность
(перенос энергии), диффузия
(перенос массы) и внутреннее
трение
(перенос импульса). Ограничимся одномерными
явлениями переноса. Систему отсчета
будем выберать так, чтобы ось х была
направлена в сторону в направления пер

Диффузия.
При происходит самопроизвольное
проникновение и перемешивание частиц
двух соприкасающихся газов, жидкостей
и даже твердых тел; диффузия есть обмен
масс частиц этих тел, при этом явление
возникает и продолжается, пока существует
градиент плотности. Во времена становления
молекулярно-кинетической теории по
вопросу явления диффузии возникли
противоречия. Поскольку молекулы
перемещаются в пространстве с огромными
скоростями, то диффузия должна происходить
очень быстро. Если же открыть в комнате
крышку сосуда с пахучим веществом, то
запах распространяется довольно
медленно. Но здесь нет противоречия.
При атмосферном давлении молекулы
обладают малой длиной свободного пробега
и, при столкновениях с другими молекулами,
приемущественно «стоят» на месте.

Явление диффузии для химически
однородного газа подчиняется закону
Фика:

(3)

где j_m
— плотность
потока массы
— величина, определяемая массой вещества,
диффундирующего в единицу времени через
единичную площадку, перпендикулярную
оси х, D — диффузия
(коэффициент
диффузии),
dρ/dx — градиент плотности, который равен
скорости изменения плотности на единицу
длины х в направлении нормали к этой
площадке. Знак минус говорит о том, что
перенос массы происходит в направлении
убывания плотности (поэтому знаки j_mи dρ/dx противоположны). Диффузия D численно
равна плотности потока массы при
градиенте плотности, равном единице.
Согласно кинетической теории газов,(4)

1. Явление переноса.
   Теплопроводность

В термодинамически
неравновесных системах происходят
особые необратимые процессы, называемые
явлениями
переноса, в
результате которых осуществляется
пространственный перенос массы, импульса,
энергии. К явлениям переноса относятся
теплопроводность
(перенос энергии), диффузия
(перенос массы) и внутреннее
трение
(перенос импульса). Ограничимся одномерными
явлениями переноса. Систему отсчета
будем выберать так, чтобы ось х была
направлена в сторону в направления
переноса.

Теплопроводность.
Если в первой области газа средняя
кинетическая энергия молекул больше,
чем во второй, то вследствие постоянных
столкновений молекул с течением времени
происходит процесс выравнивания средних
кинетических энергий молекул, т. е.,
выравнивание температур. Перенос энергии
в форме теплоты подчиняется закону
Фурье:

(1)

где j_E
— плотность
теплового потока
— величина, которая определяется
энергией, переносимой в форме теплоты
в единицу времени через единичную
площадку, перпендикулярную оси х, λ —
теплопроводность,
— градиент температуры, равный скорости
изменения температуры на единицу длины
х в направлении нормали к этой площадке.
Знак минус говорит о том, что во время
теплопроводности энергия перемещается
в направлении убывания температуры
(поэтому знаки j_E
и – противоположны). Теплопроводность
λ равна плотности теплового потока при
градиенте температуры, равном единице.

Можно показать, что

(2)

где с_V
— удельная
теплоемкость
газа при постоянном объеме (количество
теплоты, которое необходимо для нагревания
1 кг газа на 1 К при постоянном объеме),
ρ — плотность газа, <ν>
— средняя скорость теплового движения
молекул, <l>
— средняя длина свободного пробега.

1. Явление переноса.
   Вязкость

В термодинамически
неравновесных системах происходят
особые необратимые процессы, называемые
явлениями
переноса, в
результате которых осуществляется
пространственный перенос массы, импульса,
энергии. К явлениям переноса относятся
теплопроводность
(перенос энергии), диффузия
(перенос массы) и внутреннее
трение
(перенос импульса). Ограничимся одномерными
явлениями переноса. Систему отсчета
будем выберать так, чтобы ось х была
направлена в сторону в направления
переноса.

Внутреннее
трение
(вязкость).
Суть механизма возникновения внутреннего
трения между параллельными слоями газа
(жидкости), которые движущутся с различными
скоростями, есть в том, что из-за
хаотического теплового движения
осуществляется обмен молекулами между
слоями, в результате чего импульс слоя,
который движется быстрее, уменьшается,
который движется медленнее — увеличивается,
что приводит к торможению слоя, который
движется быстрее, и ускорению слоя,
который движется медленнее.

Как
известно, сила внутреннего трения между
двумя слоями газа (жидкости) подчиняется
закону
Ньютона:

(5)

где η — динамическая вязкость
(вязкость), dν/dx
— градиент скорости, который показывает
быстроту изменения скорости в направлении
х, перпендикулярном направлению движения
слоев, S — площадь, на которую действует
сила F.

Согласно второму закону
Ньютона взаимодействие двух слоев можно
рассматривать как процесс, при котором
в единицу времени от одного слоя к
другому передается импульс, который по
модулю равен действующей силе. Тогда
выражение (5) можно записать в виде

(6)

где j_p
— плотность
потока импульса
— величина, которая определяется
определяемая полным импульсом, переносимым
в единицу времени в положительном
направлении оси х через единичную
площадку, перпендикулярную оси х, dν/dx
— градиент скорости. Знак минус говорит
о том, что импульс переносится в
направлении убывания скорости (поэтому
знаки j_p
и dν/dx
противоположны).

Динамическая
вязкость η
численно равна плотности потока импульса
при градиенте скорости, равном единице;
она вычисляется по формуле

(7)

Из сопосавления формул (1), (3) и (6),
которые описывают явления переноса,
следует, что закономерности всех явлений
переноса сходны между собой. Эти законы
были известны еще задолго до того, как
они были обоснованы и получены из
молекулярно-кинетической теории, которая
позволила установить, что внешнее
сходство их математических выражений
является следствием общностью лежащего
в основе явлений теплопроводности,
диффузии и внутреннего трения молекулярного
механизма перемешивания молекул в
процессе их хаотического движения и
столкновений друг с другом.

Рассмотренные
законы Фурье, Фика и Ньютона не вскрывают
молекулярно-кинетической сути
коэффициентов λ, D и η. Выражения для
коэффициентов переноса получаются из
кинетической теории. Они записаны без
вывода, поскольку строгое и формальное
рассмотрение явлений переноса довольно
громоздко, а качественное — не имеет
смысла. Формулы (2), (4) и (7) дают связь
коэффициентов переноса и характеристики
теплового движения молекул. Из этих
формул следуют простые зависимости
между λ, D и η:и

1. Реальный газы.
   Уравнение Ван-дер-Ваальса. Изотермы
   реального газа.

Реальный газ—газ,
который не описывается уравнением
состояния идеального газа Клапейрона —
Менделеева.

Зависимости между
его параметрами показывают, что молекулы
в реальном газе взаимодействуют между
собой и занимают определенный объём.
Состояние реального газа часто на
практике описывается обобщённым
уравнением Менделеева — Клапейрона:

где p — давление;
V — объем; T — температура; Z_r
= Z_r
(p,T)  — коэффициент
сжимаемости
газа; m — масса; М — молярная
масса;
R — газовая
постоянная.

Уравнение
состояния газа Ван-дер-Ваальса—уравнение,
связывающее основные термодинамические
величины
в модели газа Ван-дер-Ваальса.

Хотя модель
идеального
газа
хорошо описывает поведение реальных
газов
при низких давлениях
и высоких температурах,
в других условиях её соответствие с
опытом
гораздо хуже. В частности, это проявляется
в том, что реальные
газы
могут быть переведены в жидкое
и даже в твёрдое
состояние,
а идеальные — не могут.

Для более точного
описания поведения реальных газов при
низких температурах была создана модель
газа Ван-дер-Ваальса, учитывающая силы
межмолекулярного взаимодействия. В
этой модели внутренняя
энергия
становится
функцией не толькотемпературы,
но и объёма.

Уравнение
Ван-дер-Ваальса — это одно из широко
известных приближённых уравнений
состояния, имеющее компактную форму и
учитывающее основные характеристики
газа с межмолекулярным взаимодействием^[1].

-Поскольку весь
процесс происходит при постоянной
температуре T,
кривую, что изображает зависимость
давления р от объёма V,
называют изотермой.
При объёме V₁
начинается конденсация
газа, а при объёме V₂
она заканчивается. Если V > V₁
то вещество будет в газообразном
состоянии, а при V < V₂ —
в жидком.

1. Твёрдое тело.
   Закон Дюлонга и Пти. Тепловое расширение
   твердых тел. Плавление.

Твёрдое тело —
это одно из четырёх агрегатных
состояний вещества,
отличающееся от других агрегатных
состояний (жидкости,
газов,
плазмы)
стабильностью формы и характером
теплового
движения
атомов,
совершающих малые колебания
около положений равновесия^[1].

Различают
кристаллические
и аморфные
твёрдые тела. Раздел физики,
изучающий состав и внутреннюю структуру
твёрдых тел, называется физикой
твёрдого тела.
То, как твёрдое тело меняет форму при
воздействиях и движении, изучается
отдельной дисциплиной — механикой
твёрдого (деформируемого) тела.
Движением абсолютно твёрдого тела
занимается третья наука — кинематика
твёрдого тела.

Технические
приспособления, созданные человеком,
используют различные свойства твёрдого
тела. В прошлом твёрдое тело применялось
как конструкционный материал и в основе
употребления лежали непосредственно
ощутимые механические свойства как то
твёрдость,
масса,
пластичность,
упругость,
хрупкость.
В современном мире применение твёрдого
тела основывается на физических
свойствах, которые зачастую обнаруживаются
только при лабораторных исследованиях.

Закон Дюлонга —
Пти
(Закон
постоянства теплоёмкости) —
эмпирический
закон,
согласно которому молярная
теплоёмкость
твёрдых тел при комнатной температуре
близка к 3R^[1]:

где R —
универсальная
газовая постоянная.

Закон выводится
в предположении, что кристаллическая
решетка тела состоит из атомов, каждый
из которых совершает гармонические
колебания
в трех направлениях, определяемыми
структурой решетки, причем колебания
по различным направлениям абсолютно
независимы друг от друга. При этом
получается, что каждый атом представляет
три
осциллятора
с энергией E,
определяемой следующей формулой:

Формула вытекает
из теоремы о равнораспределении энергии
по степеням свободы. Так как каждый
осциллятор имеет одну степень
свободы,
то его средняя кинетическая
энергия
равна
,
а так как колебания происходят
гармонически, то средняяпотенциальная
энергия
равна средней кинетической, а полная
энергия — соответственно их сумме.
Число осцилляторов в одном моле вещества
составляет
,
их суммарная энергия численно равна
теплоемкости тела — отсюда и вытекает
закон Дюлонга-Пти.

Приведем таблицу
экспериментальных значений теплоемкости
ряда химических элементов для нормальных
температур:

Элемент	, кал/(К·моль)	Элемент	, кал/(К·моль)
C	1,44	Pt	6,11
B	2,44	Au	5,99
Al	5,51	Pb	5,94
Ca	5,60	U	6,47
Ag	6,11	–	–

Тепловое
расширение—изменение
линейных размеров и формы тела при
изменении его температуры.
Количественно тепловое расширение
жидкостей и газов при постоянном давлении
характеризуется изобарным
коэффициентом
расширения
(объёмным коэффициентом теплового
расширения). Для характеристики теплового
расширения твёрдых тел дополнительно
вводят коэффициент линейного теплового
расширения.

Раздел физики
изучающий данное свойство называется
дилатометрией.

Тепловое расширение
тел учитывается при конструировании
всех установок, приборов и машин,
работающих в переменных температурных
условиях.

Основной закон
теплового расширения
гласит, что тело с линейным размером
в
соответствующем измерении при увеличении
его температуры нарасширяется
на величину,
равную:

,

где
—
так называемыйкоэффициент
линейного теплового расширения.
Аналогичные формулы имеются для расчета
изменения площади и объема тела. В
приведенном простейшем случае, когда
коэффициент теплового расширения не
зависит ни от температуры, ни от
направления расширения, вещество будет
равномерно расширяться по всем
направлениям в строгом соответствии с
вышеприведенной формулой.

Плавле́ние—это процесс перехода
тела из кристаллического
твёрдого состояния в жидкое, то есть
переход вещества из одного агрегатного
состояния
в другое. Плавление происходит с
поглощением удельной
теплоты плавления
и является фазовым
переходом
первого рода, которое сопровождается
скачкообразным
изменением теплоёмкости
в конкретной для каждого вещества
температурной точке превращения —
температура
плавления.

Способность
плавиться
относится к физическим
свойствам
вещества^[1]

При нормальном
давлении, наибольшей температурой
плавления
среди металлов
обладает вольфрам
(3422 °C), среди простых
веществ —
углерод
(по разным данным 3500 — 4500 °C^[2])
а среди произвольных веществ — карбид
тантала-гафния
Ta₄HfC₅
(4216 °C). Можно считать, что самой низкой
температурой плавления обладает гелий:
при нормальном давлении он остаётся
жидким при сколь угодно низких
температурах.

Многие вещества
при нормальном давлении не имеют жидкой
фазы. При нагревании они путем сублимации
сразу переходят в газообразное состояние.

1. Жидкости.
   Поверхностное плавление. Смачивание.

Жи́дкость—
вещество, находящееся в жидком агрегатном
состоянии,
занимающем промежуточное положение
между твёрдым и газообразным состояниями^[1].
Основным свойством жидкости, отличающим
её от веществ, находящихся в других
агрегатных состояниях, является
способность неограниченно менять форму
под действием касательных механических
напряжений, даже сколь угодно малых,
практически сохраняя при этом объём.

Поверхностные
явления,физико-химические
явления, которые обусловлены особыми
(по сравнению с объемными) свойствами
поверхностных слоев жидкостей
и твердых тел. Наиболее общее и важное
свойство этих слоев – избыточная свободная
энергия F = sS,
где s-поверхностное (межфазное) натяжение,
для твердых тел – удельная свободная
поверхностная
энергия.
S-площадь
поверхности раздела фаз. Поверхностные
явления протекают наиболее выраженно
в гетерогенных системах с сильно развитой
поверхностью раздела фаз, т. е. в дисперсных
системах. Изучение
закономерностей поверхностных явлений
является составной частью коллоидной
химии
и чрезвычайно важно для всех ее
практических приложений.

Самопроизвольные
поверхностные явления происходят
вследствие уменьшения поверхностной
энергии системы.
Они могут быть обусловлены уменьшением
общей поверхности системы либо уменьшением
поверхностного натяжения на границе
раздела фаз. К поверхностным явлениям,
связанным с уменьшением общей поверхности,
относят: 1) капиллярные
явления.
в частности приобретение каплями (в
туманах) и газовыми пузырьками (в жидкой
среде) сферич. формы, при которой
поверхность капли (пузырька) минимальна.
2) Коалесценция
– слияние капель в эмульсиях
(или газовых пузырьков в пенах)при
их непосредств. контакте. 3) Спекание
мелких твердых частиц в порошках
при достаточно высоких температурах.
4) Собирательная рекристаллизация –
укрупнение зерен поликристаллического
материала при повышении температуры.
5) Изотермическая перегонка
– увеличение объема крупных капель за
счет уменьшения мелких. При этом
вследствие повышенного давления
паров
жидкости с более высокой кривизной
поверхности происходит испарение
мелких капель и последующая их конденсация
на более крупных каплях. Для жидкости,
находящейся на твердой подложке,
существенная роль в переносе вещества
от мелких капель к крупным играет
поверхностная диффузия.
Изотермическая перегонка
твердых частиц может происходить через
жидкую фазу вследствие повышенной
растворимости более мелких частиц.

При определенных
условиях в системе могут происходить
самопроизвольные поверхностные явления,
сопровождающиеся увеличением общей
поверхности раздела фаз. Так,
самопроизвольное диспергирование и
образование устойчивых лиофильных
коллоидных
систем
(например, критических эмульсий)
происходит в условиях, когда увеличение
поверхностной энергии, вызываемое
измельчением
частиц, компенсируется их вовлечением
в тепловое движение и соответствующим
возрастанием энтропии
(см. Микроэмульсии).
При гомогенном
образовании зародышей новой фазы при
конденсации паров, кипении.
кристаллизации
из растворов и расплавов
увеличение энергии системы вследствие
образования новой поверхности
компенсируется уменьшением хим.
потенциала вещества при фазовом
переходе.
Критические размеры зародышей, при
превышении которых выделение новой
фазы идет самопроизвольно, зависят от
поверхностного натяжения, а также от
величины перегрева (переохлаждения,
пересыщения). Связь между этими параметрами
определяется уравнением Гиббса (см.
Зарождение
новой фазы).

Сма́чивание—физическое
взаимодействие жидкости
с поверхностью твёрдого
тела
или другой жидкости. Смачивание бывает
двух видов:

• Иммерсионное
  (вся поверхность твёрдого тела
  контактирует с жидкостью)

• Контактное
  (состоит из трёх фаз — твердая,
  жидкая, газообразная)

Смачивание зависит
от соотношения между силами сцепления
молекул
жидкости с молекулами (или атомами)
смачиваемого тела (адгезия)
и силами взаимного сцепления молекул
жидкости (когезия).

Если жидкость
контактирует с твёрдым телом, то
существуют две возможности:

1. молекулы жидкости
   притягиваются друг к другу сильнее,
   чем к молекулам твёрдого тела. В
   результате силы притяжения между
   молекулами жидкости собирают её в
   капельку. Так ведёт себя ртуть
   на стекле,
   вода
   на парафине
   или «жирной» поверхности. В этом случае
   говорят, что жидкость не
   смачивает
   поверхность;

2. молекулы жидкости
   притягиваются друг к другу слабее, чем
   к молекулам твёрдого тела. В результате
   жидкость стремится прижаться к
   поверхности, расплывается по ней. Так
   ведёт себя ртуть на цинковой
   пластине, вода на чистом стекле или
   дереве. В этом случае говорят, что
   жидкость смачивает
   поверхность.

Степень смачивания
характеризуется углом смачивания. Угол
смачивания (или краевой угол смачивания)
— это угол, образованный касательными
плоскостями к межфазным поверхностям,
ограничивающим смачивающую жидкость,
а вершина угла лежит на линии раздела
трёх фаз. Измеряется методом лежащей
капли^[1].
В случае порошков надёжных методов,
дающих высокую степень воспроизводимости,
пока (по состоянию на 2008 год) не разработано.
Предложен весовой метод определения
степени смачивания, но он пока не
стандартизован.

Измерение степени
смачивания весьма важно во многих
отраслях промышленности (лакокрасочная,
фармацевтическая, косметическая
и т. д.). К примеру, на лобовые стёкла
автомобилей наносят особые покрытия,
которые должны быть устойчивы против
разных видов загрязнений. Состав и
физические свойства покрытия стёкол и
контактных линз можно сделать оптимальным
по результатам измерения контактного
угла^[2].

К примеру, популярный
метод увеличения добычи нефти при помощи
закачки воды в пласт исходит из того,
что вода заполняет поры и выдавливает
нефть.
В случае мелких пор и чистой воды это
далеко не так, поэтому приходится
добавлять специальные ПАВ.
Оценку смачиваемости горных пород при
добавлении различных по составу растворов
можно измерить различными приборами.

Физическую величину, являющуюся мерой взаимодействия материи, то есть перехода из одного состояния в другое, называют энергией. Кинетическая средняя величина определяет перемещение материальной точки. Это понятие было введено Готфридом Вильгельмом Лейбницем, который и сформулировал закон сохранения силы. Фактически это работа движения, зависящая от направления и скорости. Важное значение здесь имеет выбранная система отсчёта.

Оглавление:

• Общие сведения
• Движение частиц
• Температура и энергия
• Решение задач

Общие сведения

В природе есть два закона сохранения: импульса и момента. Они являются следствием свойств пространства. Другими словами, описываются однородностью какого-либо выделенного места и изотропностью. Все направления в пространстве считаются равноправными.

В седьмом классе изучают силу, характеризующуюся работой. Если на тело оказывается воздействие, приводящее к движению, то возникает действие. Например, пусть имеется спица, на которую нанизана бусинка. Она может свободно перемещаться по ней, если к телу приложена сила. Её направление по касательной к спице можно обозначить как F1. Угол, образованный между направлением силы и движения, пусть будет J1.

Чтобы бусинка двигалась по прямой, на неё должны действовать другие силы. Это воздействие определяется реакцией спицы. Представить её можно в виде упругости F2 и трения F3. Углы, которые образуются после перемещения S, можно обозначить так: между F2 и вектором — J2, S и F3 — J3.

Второй закон Ньютона в векторной форме записывается как F1 + F2 + F3 = m * a. Это уравнение можно рассмотреть в проекции вдоль спицы на ось икс. Она имеет следующий вид: F1 * cos (J1) + F2 * cos (J2) + F3 * cos (J3) = m * ax. Пусть силы будут постоянные по направлению и модулю. Справа и слева стоит постоянное число, следовательно, движение будет равноускоренным.

Проекцию вектора перемещения можно записать так: Sa = (Vx2- Vox2) / 2ax. Отсюда: ax = (Vx2- Vox2) / 2 Sx, где Vx — конечная скорость, V0 — начальная. Полученную формулу можно подставить во второй закон Ньютона. В результате получится: F1 * cos (J1) + F2 * cos (J2) + F3 * cos (J3) = m * (Vx² — V0²) / 2 Sx.

Проекция перемещения равна модулю. Левую и правую часть можно умножить на него. В дроби равенства стоят квадраты проекции, поэтому: Sx = S; Vx² = V²; Vox² = V0². Учитывая соотношения и разбив дробь на слагаемые, умноженные на массу, можно получить выражение: F1 * cos (J1) + F2 * cos (J2) + F3 * cos (J3) = (m * Vx ²) / 2 — (mV0 ²) / 2.

В левой части есть три однотипных слагаемых F * S * cos (J). Эту физическую величину называют работой и обозначают буквой A. Но справедливо равенство только для постоянной силы. Измеряется она в ньютонах, умноженных на метр, или в джоулях. Справа стоит величина, которая является работой, связанной с движением тела. Следовательно, это какая-то средняя кинетическая энергия молекул, формула которой будет иметь вид Ech = mv² /2.

Движение частиц

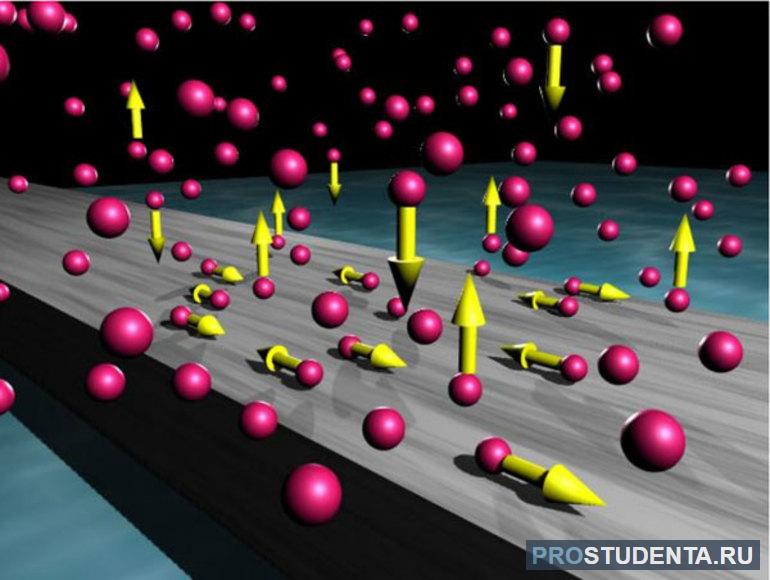
Молекулы — это частицы, которые подчиняются законам классической механики. В системе они совершают беспорядочное движение. Отсюда следует, что число микросостояний будет определяться интенсивностью перемещений. Для определения этого значения было введено понятие термодинамическая вероятность — мера хаотичности движения молекул (энтропия). Если рассматривать твёрдые тела, то величина параметра будет небольшой. Это связано с тем, что скорости атомов невелики, а сами частицы имеют устойчивые связи.

В газе же взаимодействие проявляется в короткие моменты при столкновении молекул. Этот процесс сопровождается резким изменением скорости. Все законы рассматривают для так называемой идеальной среды. Для неё предполагается, что расстояние между молекулами намного больше, чем радиус воздействия межмолекулярных сил.

Так, если размер частицы имеет примерное значение, равное d = 3·10^-8 см, то для идеального газа физики считают, что число молекул в единице объёма не должно превышать 3·10²² см^-3.

Для рассматриваемого состояния установлено три закона:

• произведение объёма на постоянную температуру определяется таким изменением давления, что выражение p * V будет постоянным значением;
• при определённом давлении величина объёма газа к его температуре является постоянной V / T = const;
• давление связано с температурой формулой pV = n RT, где R — газовая постоянная, n — число молей.

Последнее уравнение с учётом постоянной Больцмана (k = p / nT) является основой кинетической теории газов. Средняя величина давления находится как усреднённое значение квадрата скорости всех групп молекул: p = n * m (V²) / 3. Эта формула получена с учётом того, что каждая молекула имеет приблизительно одинаковую скорость. Её можно переписать так: p = (2 / 3) * n * Ek. Отсюда получается усреднённая кинетическая энергия молекул: Ek = 1 / 2 *(m * V²).

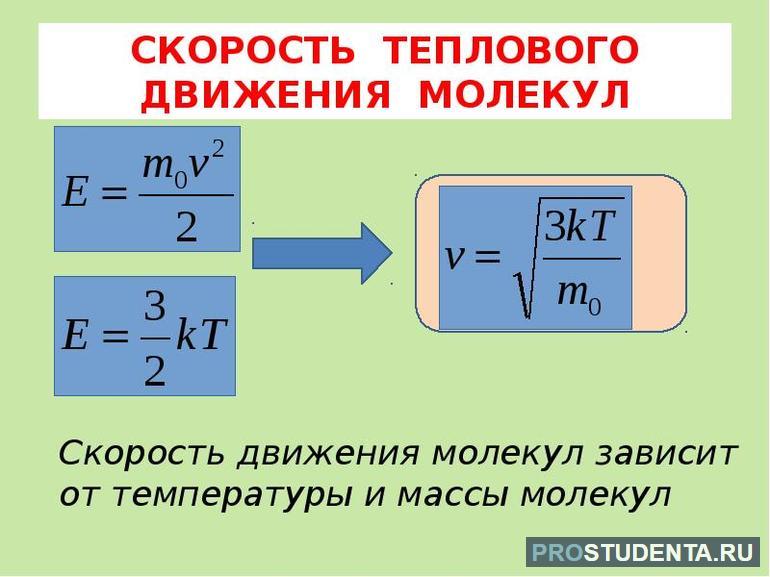
Поступательное движение атомов и молекул, взятое по большему числу хаотично перемещающихся частиц, является мерилом температуры. Если она измеряется в градусах Кельвина, то её связь c энергией описывается отношением Ek = (3 * k T) / 2.

Следует отметить, что выражение справедливо только при расчёте для одной частицы. Такой энергией обладает каждая молекула, так как она находится в тепловом хаотическом движении.

Температура и энергия

Если взять два тела с разной температурой и обеспечить между их поверхностями контакт, то через время произойдёт выравнивание температуры. Ранее считалось, что существует некая субстанция, которая, хаотично смешиваясь, уравновешивает показатели. Но на самом деле происходит просто изменение кинетической энергии. Именно она и определяет состояние равновесия.

Это свойство позволило связать энергию с температурой через коэффициент пропорциональности Больцмана: T = (2 * m 0 * V ²) / 3 * K * 2. Если при расчётах использовать это выражение, в ответе получится так называемая абсолютная температура. Её значение служит мерой кинетической энергии теплового движения молекул идеального газа. В качестве единиц измерения взят Кельвин.

Идеальный газ описывается уравнением Клайперона — Менделеева: p * V = (m * R * T) / µ. В то же время газовую постоянную можно определить как произведение постоянной Больцмана на число Авогадро (Na). Это значение равняется 6,02 * 10²³. Измеряется в молях и показывает количество структурных частиц на один моль вещества. Формулу для хаотического движения молекул можно вывести следующим образом:

1. Поскольку концентрация этих веществ определяется как (m * Na) / µ * V, выражение для давления легко представить в виде p = n * k * T.
2. Подставив в формулу давления для одноатомного газа полученное равенство, можно получить p = (1 / 3) ∗ (n ∗ m ∗ v²c) = (n ∗ k ∗ T).
3. После сокращения обеих частей на три вторых и концентрацию молекул получится равенство: m * V² / 2 = (3 * k * T) / 2.
4. В правой части стоит значение полной кинетической работы, поэтому формулу можно записать как Ek = (3 * k * T) / 2.

Таким образом, газовая температура зависит от среднекинетической энергии. Эти две величины связаны прямо пропорционально. Температура имеет абсолютное значение, поэтому её физический смысл заключается в определении средней кинетической энергии, приходящейся на молекулу. Но температура характеризует систему в целом. Значит, с помощью формулы можно установить связь параметров макромира и микромира.

Следует отметить, что средняя суммарная тепловая энергия перемещения молекул определяется только температурой газа. То есть кинетическая энергия поступательного хаотичного движения частиц не зависит от химического состава, массы, давления или занимаемого объёма.

Решение задач

Самостоятельное решение примеров позволяет закрепить теоретические знания. Существуют определённые типы заданий, с помощью которых можно проработать весь изученный материал и наглядно увидеть практическое применение знаний. Вот некоторые из них:

1. Выяснить, какова средняя кинетическая энергия поступательного движения молекулы газа неона, если созданное давление при концентрации 2, 65 * 10²⁵ м^-3 составляет 98,8 кПа. Решение примера следует начать с записи уравнения для идеального газа: p = (m 0 * n * V²) / 3. Так как энергию молекулы можно вычислить из выражения E = (m 0 V²) / 2, то нужная формула примет вид p = (2 * n * E) / 3. Отсюда искомая величина равняется E = 3 p / 2 n. Теперь нужно подставить исходные данные и выполнить количественный расчёт: Ek = (3 * 98,8 * 10³) / (2 * 2,65 * 10²⁵) = 5,6 * 10^-21 джоулей.
2. Средняя энергия поступательного движения частицы гелия равняется 60 Дж, а давление составляет 2 * 10⁵ Па. Необходимо найти концентрацию частиц газа. В основе решения лежит уравнение идеальной системы: p = n * k * T. Добавив к нему формулу связи движения и температуры E = (3 / 2) * kT, можно выразить искомую концентрацию: kT = (2 * E) / 3. Отсюда: n = 3p / 2E = 3 * 2 * 10⁵ / 2 * 60 = 6 * 10⁵ / 60 = 10⁵ / 10 = 10⁴ м^-3.
3. Найти работу, которая выполняется телом в течение трёх секунд после воздействия, если изменение энергии происходит по графику в виде параболы. Трем секундам соответствует энергия, равная 2 Дж, шести — 4 Дж. Для выяснения работы нужно воспользоваться определением кинетической энергии. Так как существует силовое взаимодействие, то А = ΔEk. В соответствии с графиком энергия изменяется от четырёх джоулей до двух. Значит, работа равна A = 2 — 4 = -2 Дж.

Решать задачи по исследованию кинетической работы несложно. Нужно лишь знать несколько формул и внимательно следить за размерностью величин при выполнении вычислений.