поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,655 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,944 -
разное
16,904
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Решение.
Т = (273 + 27) К = 300 К.
Температура газа связана с средней кинетической энергией движения молекулы соотношением:
[ {{E}_{K}}=frac{i}{2}cdot kcdot T (1). ]
Где: к – постоянная Больцмана, к = 1,38∙10-23 Дж/К, i – количество степеней свободы.
Определим среднее значение кинетической энергии вращательного движения всех молекул водорода (вращательному движению для двухатомной молекулы водорода соответствует количество степеней свободы i = 2)
[ begin{align}
& {{E}_{K}}({{H}_{2}})=Ncdot frac{2}{2}cdot kcdot T(2),N=frac{m}{M}cdot {{N}_{A}}(3),{{E}_{K}}({{H}_{2}})=frac{m}{M}cdot {{N}_{A}}cdot kcdot T(4). \
& {{E}_{K}}({{H}_{2}})=frac{0,2cdot {{10}^{-3}}}{2cdot {{10}^{-3}}}cdot 6,02cdot {{10}^{23}}cdot 1,38cdot {{10}^{-23}}cdot 300=249,228. \
end{align} ]
Где: N – количество всех молекул, M – молярная масса молекулы водорода, М(Н2) = 2∙10-3 кг/моль, NА число Авогадро, NА = 6,02∙1023 моль-1.
Ответ: 249,228 Дж.
Пример решения задач
Чему
равны средние кинетические энергии
поступательного и вращательного движения
молекул, содержащихся в 2 кг водорода
при температуре 400К?
Дано:![]() кг;
кг;
Т=400К;
М=![]() кг/моль.
кг/моль.
Найти:<Епост>,<Eвр>.
Решение.
Считаем водород
идеальным газом. Молекула водорода –
двухатомная. Связь между атомами считаем
жесткой. Тогда число степеней свободы
молекулы водорода равно
пяти. В среднем
на одну степень свободы приходится
энергия
![]() .
.
Поступательному
движению приписывается три (i=3),
а вращательному две (i=2)
степени свободы. Тогда энергия одной
молекулы
![]() пост>
пост>![]()
![]() вр>=
вр>=![]()
Число
молекул, содержащихся в массе газа ν,
![]()
где
ν
– число молей; NA
– постоянная Авогадро. Тогда средняя
кинетическая энергия поступательного
движения молекул водорода будет
<Епост>=![]()
(1)
где
![]()
– молярная газовая постоянная. Средняя
кинетическая энергия вращательного
движения молекул водорода:
<Eвр>=![]() .
.
(2)
Подставляя
числовые значения в формулы (1) и (2),
имеем:
<Епост>=![]() (Дж)=4986(кДж);
(Дж)=4986(кДж);
<Eвр>=![]() (Дж)=3324(кДж).
(Дж)=3324(кДж).
Глава 11. Реальные газы
Поведение
реальных газов довольно хорошо описывается
уравнением состояния Менделеева-Клапейрона
для идеальных газов
![]()
(1)
при
не слишком высоких давлениях и достаточно
высоких температурах. Вывод этого
уравнения основан на трех существенных
предположениях:
-
Между
молекулами отсутствуют силы взаимодействия,
т.е. молекулы газа взаимодействуют друг
с другом только в момент столкновения. -
Размеры
молекул пренебрежимо малы и собственный
объем молекул очень мал по сравнению
с объемом сосуда, в котором находится
газ. -
Молекулы
при столкновениях со стенками сосуда
и между собой взаимодействуют как
упругие шары.
При
повышении давления и уменьшении
температуры наблюдаются значительные
отступления от уравнения (1) . По оценкам
размер молекулы имеет величину порядка
10-8
см. Принимая радиус молекулы r
≅
10-8
см, ее объем будет равен V1![]() 4∙10-24
4∙10-24
cм3.
В
1 см3
при нормальных условиях содержится
![]() 2,7∙1019
2,7∙1019
молекул. Объем, занимаемый непосредственно
самими молекулами, примерно равен
V=4∙10-24∙2,7∙1019![]() 10-4
10-4
см3
и им можно пренебречь.
Если
же давление составит 5000 атм, то объем
молекул составит 0,5 см3.
Таким объемом пренебречь нельзя и на
объем, занимаемый самими молекулами,
необходимо вносить поправку в уравнение
состояния газа. Какого вида поправку –
будет сказано ниже.
Взаимодействие молекул реального газа
Рассмотрим силы
взаимодействия молекул.
Атомы и молекулы
– весьма устойчивые системы. В известном
смысле атомы “тверже” стальных шаров.
Стальные
шары, налетающие друг на друга со
скоростью 500 м/с, разрушатся, а атомы
даже при бо;´льших скоростях не
претерпевают изменений в структуре.

Суммарный
электрический заряд атома равен нулю.
Поэтому на больших расстояниях,
практически на расстоянии r,
равном 2-3 диаметрам молекулы (рис. 64а),
силовая характеристика электрического
поля, создаваемого атомами или молекулами,
равна нулю, а следовательно, равна нулю
и сила их электрического взаимодействия.
При сближении молекул начинает проявляться
взаимодействие зарядов. Мгновенное
распределение зарядов станет таким,
что возникнет сила притяжения (рис.
64б), которая возрастает по мере сближении
молекул. Однако, когда молекулы подойдут
“вплотную”друг к другу и “соприкоснутся“
своими электронными оболочками дальнейшее
сближение окажется невозможным. Между
электронными оболочками возникнут
огромные силы отталкивания (рис. 64в).
На рис. 65 даны примерные зависимости
силы взаимодействия F
и потенциальной энергии E от расстояния.

Значения
силы F<0
соответствуют притяжению, а значения
F
>0 соот-ветствуют отталкиванию
взаимодействующих молекул.
На
некотором расстоянии r0
эти силы уравновешивают друг друга и
равнодействующая их равна нулю. Выберем
начало отсчета для значения Еп
в бесконечности, т.е. Еп=0
при r=∞.
При постепенном сближении молекул между
ними появляются силы притяжения (F<0).
Эти силы совершают положительную работу
и потенциальная энергия постепенно
уменьшается (аналогично случаю свободно
падающего на Землю тела). При выбранном
начале отсчета потенциальная энергия
будет отрицательна и при некотором r=r0
достигнет наименьшего значения. При
переходе через положение равновесия
и дальнейшем
сближении молекул возникнут силы
отталкивания (F>0).
Совершаемая против этих сил работа
будет отрицательной и потенциальная
энергия будет резко возрастать.
Устойчивому
положению взаимодействующих молекул
соответствует:
-
Наименьшее значение
потенциальной энергии взаимодействия
молекул. Это – общее положение: система
устойчива, если она обладает минимальным
запасом энергии. -
Равенство
нулю сил взаимодействия молекул.
Уменьшение r
приводит к отталкиванию молекул, а
увеличение r
– к их притяжению.
Кинетическая
энергия Ек
пропорциональна kT.
Структура совокупности молекул и
агрегатное состояние вещества будут
зависеть от соотношения величин
минимальной потенциальной энергии Еп
min
и kT.
-
Если
kT << Еп
min
(в случае низких температур), то молекулы
притянутся друг к другу и расположатся
вплотную – вещество будет находиться
в твердом
состоянии. -
В
противоположном предельном случае
высоких температур (kT
>>Eп min)
интенсивное тепловое движение молекул
будет препятствовать соединению молекул
в агрегаты, При соударении молекул эти
агрегаты будут моментально разбиваться
и вещество будет находиться в
газообразном
состоянии. -
При
промежуточных температурах, когда kT
 Еп min
Еп min
, благодаря тепловому движению молекулы
будут непрерывно перемещаться в
пространстве, обмениваясь местами, но
не увеличивая взаимных расстояний на
величину, заметно превышающую r0.
Вещество в этом случае находится в
жидком
состоянии.
Над
твердым и жидким веществом всегда
присутствует небольшое ко- личество
того же вещества в газообразном состоянии.
Соседние файлы в папке физика
- #
- #
- #
- #
- #
- #
- #
- #
221. Определить внутреннюю энергию U водорода, а также среднюю кинетическую энергию молекулы этого газа при температуре T=300 К, если количество вещества ν этого газа равно 0,5 моль. |
| Задача из учебного пособия Чертов(методичка) |
|
Данная задача находится в разделе Решебник Чертов(методичка) на странице № 3 <<< Предыдущая задача из Чертов(методичка) |
Идеальный газ — газ, удовлетворяющий трем условиям:
- Молекулы — материальные точки.
- Потенциальная энергия взаимодействия молекул пренебрежительно мала.
- Столкновения между молекулами являются абсолютно упругими.
Реальный газ с малой плотностью можно считать идеальным газом.
Измерение температуры
Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.
Обозначение температуры
- По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 oC).
- По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).
Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:
∆t = ∆T
При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:
T = t + 273
Если особо важна точность, следует использовать более точную формулу:
T = t + 273,15
Пример №1. Температура воды равна oC. Определить температуру воды в Кельвинах.
T = t + 273 = 2 + 273 = 275 (К)
Основное уравнение МКТ идеального газа
Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).
Основное уравнение МКТ
Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
p=23n−Ek
p — давление идеального газа, n — концентрация молекул газа, −Ek — средняя кинетическая энергия поступательного движения молекул.
Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:
|
p=13m0n−v2 |
m0— масса одной молекулы газа; n — концентрация молекул газа; −v2 — среднее значение квадрата скорости молекул газа. Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости: v=√−v2 |
|
p=13ρ−v2 |
ρ — плотность газа |
|
p=nkT |
k — постоянная Больцмана (k = 1,38∙10–3 Дж/кг) T — температура газа по шкале Кельвина |
Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?
Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:
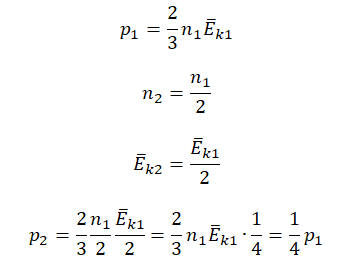
Следствия из основного уравнения МКТ идеального газа
Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):
v=√3kTm0=√3RTM
R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:
R=NAk=8,31 Дж/К·моль
Температура — мера кинетической энергии молекул идеального газа:
−Ek=32kT
T=2−Ek3k
Полная энергия поступательного движения молекул газа определяется формулой:
E=N−Ek
Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?
Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:
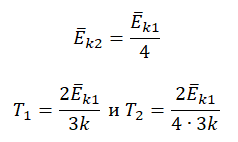
Следовательно:
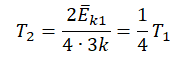
Составим систему уравнений:
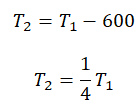
Отсюда:
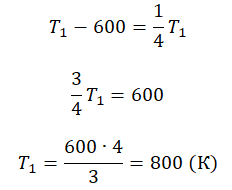
Задание EF19012
 На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
Алгоритм решения
1.Указать, в каких координатах построен график.
2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.
Решение
График построен в координатах (V;Ek). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
T=2−Ek3
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева — Клапейрона:
pV=νRT
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
νR=p1V1T1=p2V2T2
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.
Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.
Ответ:
• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.
• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17560
Первоначальное давление газа в сосуде равнялось р1. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р2 газа в сосуде стало равным
Ответ:
а) 13p1
б) 2p1
в) 23p1
г) 43p1
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для состояний 1 и 2.
4.Выразить искомую величину.
Решение
Исходные данные:
• Начальное давление: p0.
• Начальная концентрация молекул: n1 = 3n.
• Конечная концентрация молекул: n2 = n.
• Начальная средняя энергия хаотичного движения молекул: Ek1 = Ek.
• Конечная средняя энергия хаотичного движения молекул: Ek2 = 2Ek.
Основное уравнение МКТ:
p=23n−Ek
Составим уравнения для начального и конечного состояний:
p1=23n1−Ek1=233n−Ek=2n−Ek
p2=23n2−Ek2=23n2−Ek=43n−Ek
Отсюда:
n−Ek=p12=3p24
p2=4p16=23p1
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18416
Цилиндрический сосуд разделён неподвижной теплоизолирующей перегородкой. В одной части сосуда находится кислород, в другой – водород, концентрации газов одинаковы. Давление кислорода в 2 раза больше давления водорода. Чему равно отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода?
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для обоих газов.
4.Найти отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода.
Решение
Анализируя условия задачи, можно выделить следующие данные:
• Концентрации кислорода и водорода в сосуде равны. Следовательно, n1 = n2 = n.
• Давление кислорода вдвое выше давления водорода. Следовательно, p1 = 2p, а p2 = p.
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n−Ek1
p2=23n2−Ek2 или p=23n−Ek2
Выразим среднюю кинетическую энергию молекул газа из каждого уравнения:
−Ek1=3pn
−Ek2=3p2n
Поделим уравнения друг на друга и получим:
−Ek1−Ek2=3pn·2n3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18824
В одном сосуде находится аргон, а в другом – неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для обоих газов.
4.Найти отношение концентрации молекул аргона к концентрации молекул неона.
Решение
Анализируя условия задачи, можно выделить следующие данные:
• Средние кинетические энергии теплового движения молекул газов одинаковы. Следовательно, −Ek1=−Ek2=−Ek.
• Давление аргона в 2 раза больше давления неона. Следовательно, p1 = 2p, а p2 = p.
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n1−Ek
p2=23n2−Ek2 или p=23n2−Ek
Выразим концентрации молекул газа из каждого уравнения:
n1=3p−Ek
n2=3p2−Ek
Поделим уравнения друг на друга и получим:
n1n2=3p−Ek·2−Ek3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 10.8k

