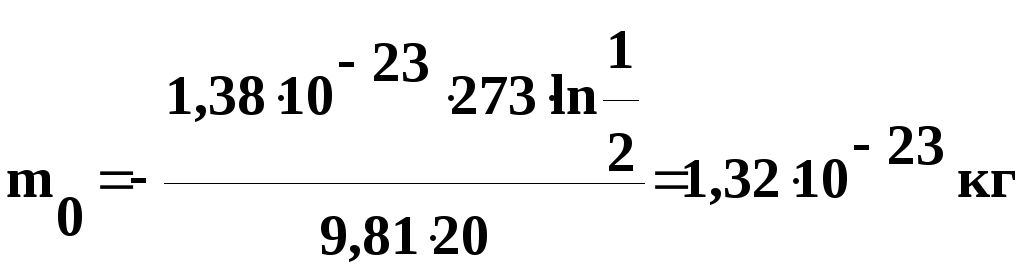Как найти среднюю кинетическую энергию молекулы кислорода

Как найти среднюю кинетическую энергию молекулы кислорода

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

  • Все категории
  • экономические
    43,655
  • гуманитарные
    33,653
  • юридические
    17,917
  • школьный раздел
    611,939
  • разное
    16,901

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Источник

Представляем формулу основного уравнения молекулярно-кинетической теории (МКТ) газов:

(где n=NV – это концентрация частиц в газе, N – это число частиц, V – это объем газа, 〈E〉 – это средняя кинетическая энергия поступательного движения молекул газа, υkv – это средняя квадратичная скорость, m0 – это масса молекулы) связывает давление – макропараметр, достаточно просто измеряющийся с такими микропараметрами, как средняя энергия движения отдельной молекулы (или в другом выражении), как масса частицы и ее скорость. Но находя только лишь давление, нельзя установить кинетические энергии частиц отдельно от концентрации. Поэтому для нахождения в полном объеме микропараметров нужно знать еще какую-то физическую величину, связанную с кинетической энергией частиц, составляющих газ. За данную величину можно взять термодинамическую температуру.

Газовая температура

Для определения газовой температуры нужно вспомнить важное свойство, которое сообщает о том, что в условиях равновесия средняя кинетическая энергия молекул в смеси газов одинаковая для различных компонентов данной смеси. Из данного свойства следует то, что если 2 газа в различных сосудах находятся в тепловом равновесии, тогда средние кинетические энергии молекул данных газов одинаковые. Это свойство мы и будем использовать. К тому же в ходе экспериментов доказано, что для любых газов (при неограниченном числе), которые находятся в состоянии теплового равновесия, справедливо следующее выражение:

С учетом вышесказанного, используем (1) и (2) и получаем:

Из уравнения (3) следует, что величина θ, которой мы обозначили температуру, вычисляется в Дж, в чем измеряется также и кинетическая энергия. В лабораторных работах температура в системе измерения вычисляется в кельвинах. Поэтому введем коэффициент, который уберет данное противоречие. Он обозначается k, измеряется в ДжК и равняется 1,38·10-23. Данный коэффициент называется постоянной Больцмана. Таким образом:

Определение 1

θ=kT (4), где T – это термодинамическая температура в кельвинах.

Связь термодинамической температуры и средней кинетической энергией теплового движения молекул газа выражается формулой:

E=32kT (5).

Из уравнения (5) видно, что средняя кинетическая энергия теплового движения молекул прямо пропорциональна температуре газа. Температура является абсолютной величиной. Физический смысл температуры заключается в том, что она, с одной стороны, определяется средней кинетической энергией, которая приходится на 1 молекулу. А с другой стороны, температура – это характеристика системы в целом. Таким образом, уравнение (5) показывает связь параметров макромира с параметрами микромира.

Определение 2

Известно, что температура – это мера средней кинетической энергии молекул.

Можно установить температуру системы, а затем рассчитать энергию молекул.

Абсолютный ноль температур

В условиях термодинамического равновесия все составляющие системы характеризуются одинаковой температурой.

Определение 3

Температура, при которой средняя кинетическая энергия молекул равняется 0, давление идеального газа равняется 0, называется абсолютным нулем температур. Абсолютная температура никогда не является отрицательной.

Пример 1

Необходимо найти среднюю кинетическую энергию поступательного движения молекулы кислорода, если температура T=290 K. А также найти среднюю квадратичную скорость капельки воды диаметра d=10-7 м, взвешенной в воздухе.

Решение

Найдем среднюю кинетическую энергию движения молекулы кислорода по уравнению, связывающему энергию и температуру:

E=32kT (1.1).

Поскольку все величины заданы в системе измерения, проведем вычисления:

E=32·1,38·10-23·10-7=6·10-21 Дж.

Перейдем ко второй части задания. Положим, что капелька, взвешенная в воздухе, – это шар (рисунок 1). Значит, массу капельки можно рассчитать как:
m=ρ·V=ρ·πd36.

Абсолютный ноль температур

Рисунок 1

Найдем массу капельки воды. Согласно справочных материалов, плотность воды в нормальных условиях равняется ρ=1000 кгм3, тогда:

m=1000·3,14610-73=5,2·10-19 (кг).

Масса капельки чрезмерно маленькая, поэтому, сама капелька сравнима с молекулой газа, и тогда можно использовать при расчетах формулу средней квадратичной скорости капли:

E=mυkυ22 (1.2),

где 〈E〉 мы уже установили, а из (1.1) понятно, что энергия не зависит от разновидности газа, а зависит только лишь от температуры. Значит, мы можем применить полученную величину энергии. Найдем из (1.2) скорость:

υkυ=2Em=6·2Eπρd3=32kTπρd3 (1.3).

Рассчитаем:

υkυ=2·6·10-215,2·10-19=0,15 мс

Ответ: Средняя кинетическая энергия поступательного движения молекулы кислорода при заданной температуре равняется 6·10-21 Дж. Средняя квадратичная скорость капельки воды при заданных условиях равняется 0,15 м/с.

Пример 2

Средняя энергия поступательного движения молекул идеального газа равняется 〈E〉, а давление газа p. Необходимо найти концентрацию частиц газа.

Решение

В основу решения задачи положим уравнение состояния идеального газа:

p=nkT (2.1).

Прибавим к уравнению (2.1) уравнение связи средней энергии поступательного движения молекул и температуры системы:

E=32kT (2.2).

Из (2.1) выражаем необходимую концентрацию:

n=pkT 2.3.

Из (2.2) выражаем kT:

kT=23E (2.4).

Подставляем (2.4) в (2.3) и получаем:

n=3p2E

Ответ: Концентрацию частиц можно найти по формуле n=3p2E.

Источник

• Основное уравнение
кинетической теории газов

,

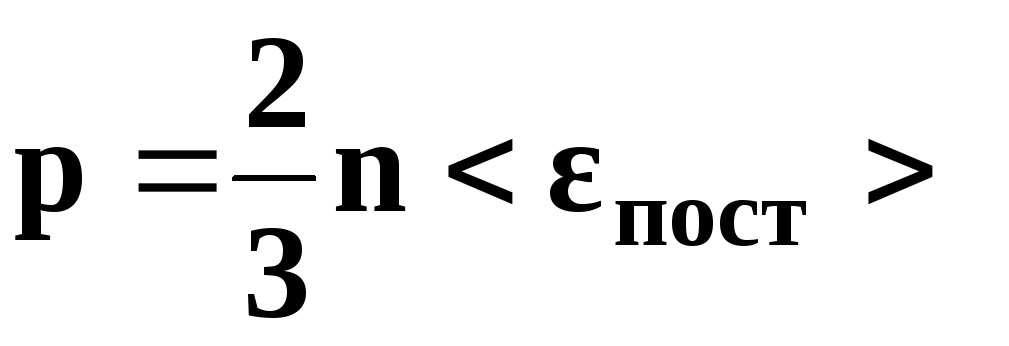
где
р – давление
газа, n
– концентрация
молекул (число молекул в единице объема),
–
средняя кинетическая энергия
поступательного движения одной молекулы,
угловые скобки обозначают осреднение
по

большому
ансамблю частиц, m0
– масса
молекулы,
–
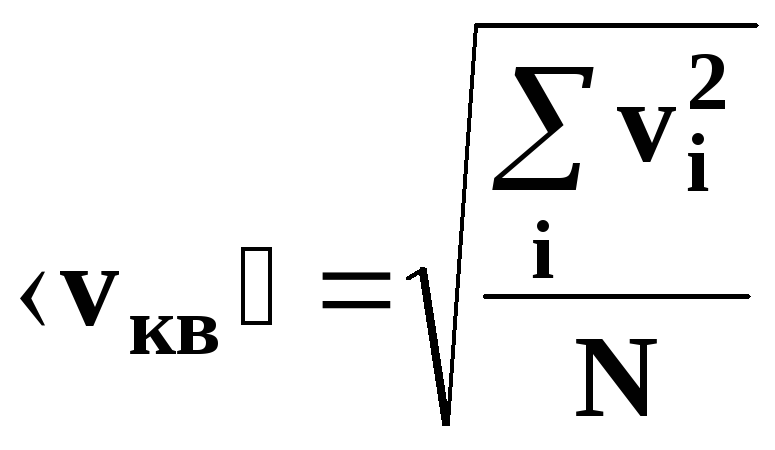
средняя квадратичная скорость движения
молекул.

• Средняя
кинетическая энергия поступательного
движения одной молекулы

,

где
k
=
1,38·10-23
Дж/К –
постоянная Больцмана, Т
– абсолютная температура.

•
Энергия теплового
движения молекул (внутренняя энергия
идеального газа):

,

где
i
– число степеней свободы молекулы, m
– масса газа, М
– молярная
масса данного вещества, R
= 8,31 Дж/(кг·К) –
универсальная газовая постоянная, Т
– абсолютная
температура.

• Числом степеней
свободы называется число независимых
координат полностью определяющих
положение тела в пространстве. Любая
молекула имеет 3 поступательных степени
свободы (iпост=3).
Молекулы,
кроме одноатомных, имеют еще вращательные
степени свободы (у двухатомных молекул
iвр
= 2, у
многоатомных iвр
= 3) и
колебательные степени свободы, которые
при невысоких (комнатных) температурах
не учитываются.

• В соответствии
с законом Больцмана о равномерном
распределении энергии по степеням
свободы, в
среднем на каждую степень свободы
молекулы приходится одинаковая энергия,
равная
.

• Средняя
кинетическая энергия вращательного
движения одной молекулы:

•
Средняя суммарная
кинетическая энергия одной молекулы:

,

где
i
– число степеней свободы молекулы
(i=iпост+
iвр).

• Средняя
квадратичная скорость молекулы:

• Средняя
арифметическая скорость (средняя
скорость теплового движения)молекулы:

,

где m0
– масса одной молекулы, М
– молярная масса вещества, причем
,

NA=
6,023·1023
1/моль –
число Авогадро.

• Барометрическая
формула характеризует изменение давления
газа с высотой в поле сил тяжести:

или
,

где
p
– давление
на высоте h
над уровнем
моря, p0
– давление на высоте h
= 0,
g
– ускорение
свободного падения. Эта формула
приближенная, так как температуру нельзя
считать постоянной для большой разности
высот.

•
Распределение
Больцмана для концентрации частиц в
силовом поле имеет вид:

,

где
n
– концентрация частиц, обладающих
потенциальной энергией Wп
, n0
– концентрация
частиц в точках поля с Wп
= 0.

Примеры
решения задач

Задача
1. Найти
среднюю кинетическую энергию
вращательного движения одной молекулы
кислорода при температуреТ
= 350 К, а также среднюю кинетическую
энергию
вращательного движения всех молекул
кислорода массойm
= 4 г.

Решение.
Согласно закону Больцмана о равном
распределении энергии по степеням
свободы на каждую степень свободы
приходится энергия равная
,
гдеk
– постоянная Больцмана, Т
– абсолютная
температура.

Так
как молекула кислорода двухатомная, у
нее две вращательных степени свободы,
поэтому средняя кинетическая энергия
вращательного движения выразится
формулой:

Подставим
в полученную формулу значения k
= 1,38·10-23
Дж/К, и Т
= 350 К, получим

Кинетическая
энергия всех N
молекул, содержащихся в 4 г кислорода
равна:

Число
всех молекул газа можно вычислить по
формуле:

,
где NA
– число
Авогадро,
–
количество вещества,m
– масса газа, М
– молярная
масса. Учтя приведенные выражения,
получим:

Подставляем
числовые значения: NA
= 6,023·1023
1/моль ; m
= 4 г = 4·10-3
кг ; М
= 32·10-3
кг/моль;
=
4,83·10-21
Дж:

Выведем
размерность полученной величины:

Задача
2. В
воздухе при нормальных условиях взвешены
одинаковые частицы. Известно, что
концентрация частиц уменьшается в два
раза на высоте h
= 20 м. Определить массу частицы.

Решение.
Воспользуемся формулой распределения
Больцмана:

,

где
Wп
= m0gh
– потенциальная
энергия частицы в поле сил тяжести.

Подставив
это выражение в формулу распределения
Больцмана, получим:

Логарифмируем
обе части уравнения по основанию е,
тогда:

,
откуда

Подставив
числовые значения в полученную формулу,
найдем

Выведем
размерность полученной величины:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

какова кинетическая энергия молекулы кислорода при нормальных условиях???

Ирина Шавлинская



Ученик

(166),
закрыт



12 лет назад

Marat

Просветленный

(25907)


12 лет назад

У молекулы О2 пять степеней свободы (три поступательные + две вращательные) . На каждую степень свободы приходится по k*T/2 – значит, СРЕДНЯЯ кинетическая энергия молекулы составляет (5/2)*k*T, или 0.0625 эВ при нормальных условиях (Т = 298 К) . Колебательную степень свободы можно не учитывать.

Источник

Задача. Определите среднюю кинетическую энергию поступательного движения молекул кислорода при нормальных условиях, если их концентрация displaystyle n=2,7cdot {{10}^{25}} м-3.

Дано:

displaystyle n=2,7cdot {{10}^{25}} м-3

Найти:
displaystyle <{{E}_{k}}> — ?

Решение

Думаем: средняя кинетическая энергия поступательного движения (впоследствии мы назовём её внутренней энергией) может быть связана с заданной концентрацией через соотношение

displaystyle P=frac{2}{3}n<{{E}_{k}}> (1)

Фраза «при нормальных условиях» говорит о ещё нескольких добавочных дано (нормальное давление — displaystyle T=273 Па, нормальная температура — displaystyle T=273 К).

Решаем: выразим из (1) искомую величину

displaystyle <{{E}_{k}}>=frac{3}{2}frac{P}{n} (2)

Фактически всё есть.

Считаем: 

displaystyle <{{E}_{k}}>=frac{3}{2}frac{1*{{10}^{5}}}{2,7*{{10}^{25}}}approx 5,6*{{10}^{-21}} Дж

Ответ: displaystyle <{{E}_{k}}>approx 5,6*{{10}^{-21}} Дж.

Ещё задачи на тему «Кинематические характеристики газа«.

Источник

Добавить комментарий