
Автор: .
Издательство:
Дрофа 2016
Тип: Задачник
Подробный решебник (ГДЗ) по Физике за 10‐11 (десятый‐одиннадцатый) класс задачник – готовый ответ номер – 476. Авторы учебника: Рымкевич. Издательство: Дрофа 2016.
Условие /
номер / 476
476. Найти среднюю кинетическую энергию молекулы одноатомного газа при давлении 20 кПа. Концентрация молекул этого газа при указанном давлении составляет 3- 1025м”3.
Решебник №1 / номер / 476

Видеорешение / номер / 476
Решебник №2 / номер / 476

Оцените решебник:
4.4/5

382
Молекулярная физика Основные формулы
1. Основы молекулярно-кинетической теории. Газовые законы
1.1 Количество вещества

m — масса;
μ — молярная масса вещества;
N — число молекул;
NA = 6,02·1023 моль-1 — число Авогадро
1.2 Основное уравнение молекулярно-кинетической теории идеального газа

p — давление идеального газа;
m — масса одной молекулы;
n = N/V — концентрация молекул;
V — объем газа;
N — число молекул;
 — среднее значение квадрата скорости молекул.
— среднее значение квадрата скорости молекул.
1.3 Средняя квадратичная скорость молекул идеального газа

k = 1,38·10-23 Дж/К — постоянная Больцмана;
R = kNA = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T = t+273 — абсолютная температура;
t — температура по шкале Цельсия.
1.4 Средняя кинетическая энергия молекулы одноатомного газа

1.5 Давление идеального газа

n — концентрация молекул;
k — постоянная Больцмана;
T — абсолютная температура.
1.6 Закон Бойля-Мариотта

p — давление;
V — объем газа.
1.7 Закон Шарля
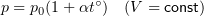
p0 — давление газа при 0 °С;
α = 1/273 °C-1 — температурный коэффициент давления.
1.8 Закон Гей-Люссака

V0 — объем газа при 0 °С.
1.9 Уравнение Менделеева-Клапейрона

1.10 Объединенный закон газового состояния (уравнение Клапейрона)

1.11 Закон Дальтона

pi — парциальное давление i-й компоненты смеси газов.
2. Основы термодинамики
2.1 Внутренняя энергия идеального одноатомного газа

ν — количество вещества;
R = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T — абсолютная температура.
2.2 Элементарная работа, совершаемая газом,
при изменении объема на бесконечно малую величину dV

p — давление газа.
При изменении объема от V1 до V2

2.3 Первый закон термодинамики

ΔQ — количество подведенной теплоты;
ΔA — работа, совершаемая веществом;
ΔU — изменение внутренней энергии вещества.
2.4 Теплоемкость идеального газа

ΔQ — количество переданной системе теплоты на участке процесса;
ΔT — изменение температуры на этом участке процесса.
Уравнение состояния идеального газа в форме (p=frac 13nm_0overline {v^2}) или (p=frac 23noverline E) может быть обосновано и методами кинетической теории газов. На основе кинетического подхода сравнительно просто выводится выражение для давления идеального газа в сосуде, которое получается как результат усреднения импульсов молекул, передаваемых стенке сосуда при многочисленных соударениях молекул со стенкой. Величина получаемого при этом давления определяется как
(p=frac 13nmbig (v^2big)),
где (v^2) – среднее значение квадрата скорости молекул, (m) – масса молекулы.
Средняя кинетическая энергия молекул газа (в расчете на одну молекулу) определяется выражением
(E_k=frac 12mbig (v^2big)).
Кинетическая энергия поступательного движения атомов и молекул, усредненная по огромному числу беспорядочно движущихся частиц, является мерилом того, что называется температурой. Если температура T измеряется в градусах Кельвина (К), то связь ее с (E_k) дается соотношением
(E_k=frac 32 kT).
Это соотношение позволяет, в частности, придать более отчетливый физический смысл постоянной Больцмана (k = 1,38·10^{–23}) Дж/K, которая фактически является переводным коэффициентом, определяющим, какая часть джоуля содержится в градусе.
Используя (6) и (7), находим, что (frac 13m v^2 = kT). Подстановка этого соотношения в формулу для энергии приводит к уравнению состояния идеального газа в форме
(p = nkT,) которое уже было получено из уравнения Клапейрона – Менделеева.
Также из уравнений можно определить значение среднеквадратичной скорости молекул:
((v)_{ке}=sqrt{(v^2)}=big (frac {3kT}{m}big )^{frac 12}=big (frac{3RT}Mbig )^{frac 12}).
Расчеты по этой формуле при (T = 273) K дают для молекулярного водорода (v_{кв} = 1838 ) м/с, для азота – (493 ) м/с, для кислорода – (461) м/с и т. д.
Напомним, что газообразное состояние возникает тогда, когда энергия теплового движения молекул вещества превышает энергию их взаимодействия. Молекулы вещества в этом состоянии приобретают прямолинейное поступательное движение, а индивидуальные свойства веществ теряются, и они подчиняются общим для всех газов законам. Газообразные тела не имеют собственной формы и легко изменяют свой объем при воздействии внешних сил или при изменении температуры.
-
Плотность идеального газа в сосуде – (1,2) кг/м(^3). Если средняя квадратичная скорость молекул газа равна (500) м/с, то газ находится под давлением
-
Давление кислорода и водорода при одинаковых концентрациях молекул и равных средних квадратичных скоростях их движения находятся в соотношении (М((O_2)) (= 0,032) кг/моль; М((H_2)) (= 0,002) кг/моль)
-
В вакуумном диоде электроны ускоряются до энергии (140) эВ. Их минимальная скорость у анода лампы равна
(e (= 1,6 ⋅ 10^{-19}) Кл; (m_e) (= 9 ⋅ 10^{-31}) кг; (1) эВ (= 1,6 ⋅ 10^{-19})Дж)
-
Объем одноатомного газа уменьшили в (2) раза, а среднюю кинетическую энергию молекул увеличили в (3) раза. Определите изменение давления.
-
Найдите среднюю кинетическую энергию атома аргона, если температура газа равна (117^{circ}C) ((k = 1,38 ⋅ 10^{-23})(frac{Дж}{К})).
-
Чему равна энергия покоя электрона? ((c = 3 ⋅ 10^8)м/с; (m = 9,1 ⋅ 10^{-31})кг)
-
Во сколько раз отличаются средние квадратичные скорости молекул диоксида серы и гелия при одинаковой температуре?
(M(_{SO_2}) (= 64 ⋅ 10^{-3})(frac{кг}{моль}); M(_{He}) (= 4 ⋅ 10^{-3})(frac{кг}{моль}))
-
Во сколько раз изменится среднеквадратичная скорость движения частиц одноатомного идеального газа (υ), если, не меняя его плотности, увеличить давление в (9) раз?
-
Среднеквадратичная скорость молекул идеального одноатомного газа, заполняющего закрытый сосуд, равна (0,25) км/с. Газ охладили, уменьшив при этом давление на (19%). Как и на сколько изменилась среднеквадратичная скорость молекул этого газа?
-
Одноатомный газ находится при давлении в (400) кПа. Чему будет равна средняя кинетическая энергия молекул этого газа, если в (1) м(^3) содержится примерно (2·10^{27}) молекул?
-
Маленькая частичка массой (19,2cdot10^{-12}) кг находится в воздухе. Во сколько раз ее средняя квадратичная скорость будет отличаться от средней квадратичной скорости движения молекул воздуха? (Молярная масса воздуха – (0,029) кг/моль)
-
Вычислите среднюю квадратичную скорость молекул газа, находящегося под давлением (10) кПа, если его масса равна (3) кг, объем – (16) м(^3).
-
Можно ли получить температуру ниже или равную абсолютному нулю?
-
При нагревании ртуть в градуснике расширилась. Что это означает?
-
Найдите давление углекислого газа в сосуде, если концентрация его молекул равна (2,7 · 10^{20}) м(^{–3}), а среднее значение квадрата их скорости – (3 · 10^4) м(^2)/с(^2). (Масса молекулы углекислого газа равна (7,3 · 10^{–26}) кг)
Светило науки – 138 ответов – 5608 раз оказано помощи
Дано:
Т=290К
р=0,8*10^6Па
k=1,38*10^-23Джк
найти:(Е) и n.
Решение:
Основное ур-ние молекулярно-кинетической теории газов
p=13n*m0*(Vкв)^2
где (Vкв)^2-средняя квадратичная скорость молекул, n-концентрация молекул, m0-масс одной молекулы.
p=23n*(m0* (Vкв)^22) =23n* (Е),
где (Е)-средняя кинетическая энегрия движения молекул.Отсюда
(Е)=23*pn (1)
другая формула для определениядавления газа
p=n*k*T (2)
где к-постаянная Больцмана,Т-абсалютная температура газа
определим из ур-ия 2 концентрацию молекул газа:
n=pk*T
n=0,8*10^61,38^-23*290 приблизительно равно 2*10^26(1м^3)
подставляя в ур-е 1 найденное значение,находим среднюю кинетическую энергию движения молекул:
(E)=32*0,8*10^62*10^26=0,6*10^-20 (Дж)
Cредняя кинетическая энергия молекул идеального одноатомного газа

E — энергия, Дж (Джоуль)
k = 1.38∙10-23Дж/К — константа Больцмана
T — температура, К (кельвин); 273 кельвина = 00 Цельсия

Температура — мера средней кинетической энергии молекул газа.
Для наглядного представления идеального газа, используется механическая модель Эйхенвальда. Модель состоит из прозрачного поля, на которое помещены упругие стальные шарики. Поле окружено электромагнитными вибраторами. При подачи напряжения на вибраторы, шарики начинают двигаться наподобие молекул идеального газа. Эта модель позволяет демонстрировать явления происходящие в газе.
Механическую модель идеального газа — модель Эйхенвальда, можно посмотреть в действии на этом видео.
Задача.
Как изменится средняя кинетическая энергия теплового движения молекул идеального газа при уменьшении абсолютной температуры в 4 раза?

Решение.
Согласно формуле: E=1.5kT — при уменьшении абсолютной температуры в 4 раза, также в 4 раза уменьшится энергия молекул. То есть задача решается в одно действие. Но, обратите внимание! В такого рода задачах нужно всегда уточнять в каких единицах измерения дана температура.
В этой задаче, уточнение «абсолютная температура» дает понять, что речь идет о кельвинах.
Если же в задаче будут числовые значения, то возможно придется переводить градусы цельсия в кельвины. И в этом случае уже нельзя будет решить задачу, уменьшив значение начальной энергии в 4 раза.
Ответ: уменьшиться в 4 раза.
Задача 22.
Определите среднекинетическую энергию молекул одноатомного идеального газа, при температуре 270С.
Нажмите сюда, чтобы раскрыть ответ.
Ответ: Eк = 6,21∙10-21 Дж
