Как найти среднюю квадратичную скорость его молекул

Как найти среднюю квадратичную скорость его молекул

Условие задачи:

Найти среднюю квадратичную скорость молекул газа, имеющего плотность 1,8 кг/м3 при давлении 152 кПа.

Задача №4.1.44 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(rho=1,8) кг/м3, (p=152) кПа, (upsilon_{кв}-?)

Решение задачи:

Запишем для начала основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:

[p = frac{1}{3}n{m_0}upsilon _{кв}^2]

Распишем в этой формуле концентрацию молекул (n) как отношение числа молекул (N) к объему газа (V):

[p = frac{1}{3}frac{{{m_0}N}}{V}upsilon _{кв}^2]

Произведение массы одной молекулы (m_0) на число молекул (N) равна массе газа (m), поэтому:

[p = frac{1}{3}frac{m}{V}upsilon _{кв}^2]

Отношение массы газа (m) к его объему (V) есть плотность газа (rho), значит:

[p = frac{1}{3}rho upsilon _{кв}^2]

Выразим отсюда искомую среднюю квадратичную скорость молекул (upsilon_{кв}):

[{upsilon _{кв}} = sqrt {frac{{3p}}{rho }} ]

Численное значение этой скорости равно:

[{upsilon _{кв}} = sqrt {frac{{3 cdot 152 cdot {{10}^3}}}{{1,8}}}  = 503,3;м/с = 1812;км/ч]

Ответ: 1812 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.1.43 Найдите отношение средних скоростей молекул O2 и H2 при одинаковой температуре
4.1.45 В баллоне находится кислород при давлении 4 МПа и температуре 42 C. Определить
4.1.46 В баллоне объемом 0,01 м3 находится газ, кинетическая энергия поступательного движения

Источник

Средняя квадратичная скорость молекул — среднее квадратическое значение модулей скоростей всех молекул рассматриваемого количества газа

Large vecupsilon =sqrt{frac{3kT}{m}}=sqrt{frac{3RT}{M}}


Таблица значений средней квадратичной скорости молекул некоторых газов

Средняя квадратичная скорость газа

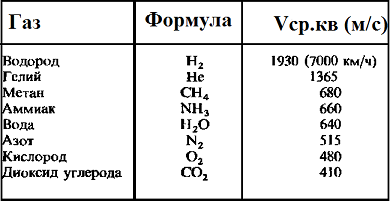
Для того чтоб понять, откуда же у нас получается эта формула, мы выведем среднюю квадратичную скорость молекул. Вывод формулы начинается с основного уравнения молекулярно кинетический теории (МКТ):

large PV=nu RT

Где nu у нас количество вещества, для более легкого доказательства, возьмем на рассмотрение 1 моль вещества, тогда у нас получается:

large PV=RT

Если посмотреть, то PV это две третьих средней кинетической энергии всех молекул (а у нас взят 1 моль молекул):

large PV=frac{2}{3}vec E_k

Тогда, если приравнять правые части, у нас получается, что для 1 моля газа средняя кинетическая энергия будет равняться:

large vec E_k =frac{3}{2}RT

Но средняя кинетическая энергия, так же находится, как :

large vec E_k =frac{1}{2}N_a m vecupsilon^2

А вот теперь, если мы приравняем правые части и выразим из них скорость и возьмем квадрат,Число Авогадро на массу молекулы , получается Молярная масса N_a m = M то у нас и получится формула для средней квадратичной скорости молекулы газа:

Large vecupsilon =sqrt{frac{3RT}{M}}

А если расписать универсальную газовую постоянную, как R=N_ak , и за одно молярную массу M=N_a m , то у нас получится?

Large vecupsilon =sqrt{frac{3kT}{m}}

В Формуле мы использовали :

vecupsilon — Средняя квадратичная скорость молекул

k=1.38cdot10^{-23} — Постоянная Больцмана

T — Температура

m — Масса одной молекулы

R=8.31 — Универсальная газовая постоянная

M — Молярная масса

nu — Количество вещества

vec E_k — Средняя кинетическая энергия молекул

N_a=6,02cdot10^{23} — Число Авогадро

Источник

Средняя скорость молекул

В физике выделяют 2 скорости, характеризующие движение молекул: средняя скорость движения молекул и средняя квадратичная скорость.

Средняя скорость движения молекул

Средняя скорость движения молекул называется также скоростью теплового движения молекул.

Определение 1

Формула средней относительной скорости молекул в физике представлена следующим выражением:

υotn=28kTπm0=2υ.

Средняя квадратичная скорость

Средняя квадратичная скорость движения молекул газа это следующая величина:

υkυ=1N∑i=1Nυi2

Формулу средней квадратичной скорости можно переписать так:

υkυ2=∫0∞υ2Fυdυ.

Проводя интегрирование, аналогичное интегрированию при получении связи средней скорости с температурой газа, получаем:

υkυ=3kTm0=3RTμ

Именно средняя квадратичная скорость поступательного движения молекул газа входит в состав основного уравнения молекулярно-кинетической теории:

p=13nm0υkυ,

где n=NV – это концентрация частиц вещества, N – это количество частиц вещества, V – это объем.

Пример 1

Необходимо определить, как изменяется средняя скорость движения молекул идеального газа с увеличением давления в процессе, изображенном на графике (рисунок 1).

Средняя квадратичная скорость

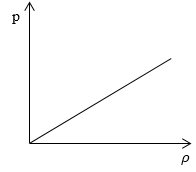
Рисунок 1

Решение

Запишем выражение для средней скорости движения молекул газа следующим образом:

υ=8kTπm0

Из графика видно, что p~ρ или p=Cρ,  где C – это некоторая константа.

m0=ρn, p=nkT=Cρ→kT=Cρn

Подставив m0=ρn, p=nkT=Cρ→kT=Cρn в υ=8kTπm0, получаем:

υ=8kTπm0=8Cρπnnρ=8Cπ

Ответ: В процессе, представленном на графике, с увеличением давления средняя скорость движения молекул не меняется.

Пример 2

Можно ли найти среднюю квадратичную скорость молекулы идеального газа, если известно: давление газа (p), молярная масса газа (μ), а также концентрация молекул газа (n)?

Решение

Применим выражение для υkυ:

υkυ=3RTμ

Помимо этого, из уравнения Менделеева-Клайперона и зная, что mμ=NNA:

pV=mμRT=NNART.

Поделим правую и левую части pV=mμRT=NNART на V, и зная NV=n, получаем:

p=nNART→RT=pNAn

Подставляем p=nNART→RT=pNAn в выражение для среднеквадратичной скорости υkυ=3RTμ, получаем:

υkυ=3pNAμn

Ответ: По заданным в условии задачи параметрам среднеквадратичная скорость движения молекул газа вычисляется при помощи формулы υkυ=3pNAμn.

Роман Адамчук

Источник

Для характеристики движения молекул в физике используют две скорости: среднюю и среднюю квадратичную скорость молекул.

Важно. Следует обязательно понимать, что в реальных условиях мы не можем точно знать ни конкретное число молекул в системе, ни тем более скорость каждой из них в конкретный момент времени. Это обусловлено неимоверно гигантским числом частиц в реальных и даже сколько-нибудь приближенных к ним системах. Например, в 1 см3 при давлении 200 мм. рт. ст. содержится 4,18*1018 молекул водорода. Говоря более понятными категориями, это более чем 4 миллиарда миллиардов. Заметим, что указанное давление меньше атмосферного почти в 4 раза. Последнее в среднем равняется 760 мм. рт. ст. Разрежённый водород по своим свойствам наиболее близок к идеальному газу. В данном случае физика вынуждена иметь дело с распределениями скоростей и энергий частиц.

Что такое средняя скорость движения молекул

Среднюю скорость движения молекул часто именуют скоростью их теплового движения.

Определение 1

Вид формулы средней относительной скорости молекул в физике можно представить выражением:

[text { Vотн }=sqrt{2} sqrt{frac{8 R T}{pi m_{0}}}]

Выражение под корнем – средняя скорость молекул идеального газа.

Как определить среднюю квадратичную скорость движения молекул

Определение 2

Средней квадратичной скоростью молекул идеального газа называют величину равную квадратному корню из среднего арифметического величины квадратов скоростей каждой из молекул.

Средняя скорость молекул равна:

[leftlanglemathrm{V}_{mathrm{KB}}rightrangle=sqrt{frac{1}{N} sum_{i=1}^{N} v_{i}^{2}}]

Если обе её части возвести в квадрат и проинтегрировать, то получим выражение:

[langlemathrm{VKB}rangle^{2}=int_{0}^{infty} v^{2} F(v) d v]

Ещё одно выражение для среднеквадратичной скорости:

[leftlangle V_{K B}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]

Именно она присутствует в уравнении, именуемом основным уравнением молекулярно-кинетической теории

P = (1/3)nm*<Vкв>

Где n – концентрация молекул, которая вычисляется делением их общего числа на объём.

Пример. 1.

Рассмотрим простейший случай, чтобы использование интегрирования не затруднило понимание сути явления и помогло лучше понять материал. Вычислим как меняется средняя скорость движения молекул в идеальном газе при линейном увеличении его давления. График следующий:

Где P — давление, ρ — плотность

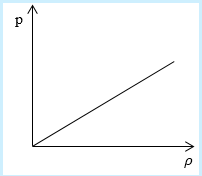
Напомним, что средняя скорость частиц:

[mathrm{Vcp}=sqrt{frac{8 R T}{pi m_{0}}}]

Если присмотреться к представленному графику, то можно заметить, что P приблизительно равно ρ‎. Эти две величины можно связать соотношением

P=C*ρ‎

Где С – некоторая постоянная величина, константа.

Далее считаем m0= ρ/n, p = n*k*T = C* ρ. Отсюда следует, что k*T = (C*ρ)/n.

Нужно лишь подставить эти значения в формулу для средней скорости:

[V c p=sqrt{8 mathrm{kT} / pi mathrm{m}}=sqrt{(8 mathrm{C} rho / pi mathrm{n})(mathrm{n} / rho)}=sqrt{8 mathrm{C} / pi}]

В полученном выражении нет ни одной переменной величины, т. е. при увеличении давления, вопреки ожиданиям, скорость оказалась неизменной.

Ответ: В процессе, который был дан нам на графике, при увеличении давления средняя скорость молекул никак не меняется.

Нет времени решать самому?

Наши эксперты помогут!

Пример. 2.

Определим среднюю квадратичную скорость молекул газа при условии, что нам известны его давление (P), молярная масса (M) и концентрация частиц (n).

Воспользуемся формулой:

[leftlanglemathrm{V}_{kappa в}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]

Также нам потребуется уравнение Менделеева-Клайперона

Здесь мы воспользовались тем, что:

m/μ = N/Na

PV = (m/μ)*RT = (N/Na)*RT

Если обе части этого уравнения поделить на V и принять во внимание, что

(N/V) = n, то можно получить

P = (n/Na)*RT. Отсюда находим, что RT = (p*N)/n

Если мы это подставим в выражение для среднеквадратичной скорости [leftlangle V_{K B}rightrangle=sqrt{3 mathrm{kT} / mathrm{m}_{0}}=sqrt{3 mathrm{RT} / mu}], получим, что средняя квадратичная скорость движения молекул газа: [leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]

Ответ: Формула средней квадратичной скорости молекул исходя из данный нам условий следующая:

[leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]

Источник

Определение средней квадратичной скорости молекул газа

Содержание:

  • Средняя квадратичная скорость молекул газа — что это за параметр
  • От каких величин зависит в идеальном газе
  • Формула средней квадратичной скорости молекул

    • Как посчитать в зависимости от природы газа и температуры?

Средняя квадратичная скорость молекул газа — что это за параметр

Молекулы любого газа пребывают в постоянном движении. Его можно охарактеризовать с точки зрения средней их скорости или средней квадратичной скорости. Первое понятие имеет специальный термин — скорость теплового движения. Второе — средняя квадратичная скорость — величина, для которой существует специальная формула.

Для того, чтобы полностью разобраться в понятии средней квадратичной скорости молекул газа, вводится условный участник процесса — идеальный газ.

Определение

Идеальный газ — это математическая модель, потенциальную энергию которой принимают за ноль, а кинетическую характеризуют в полном объеме. Идеальный газ подходит в качестве  модели окружающих нас газов, например, обычного воздуха.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Определение

Средняя квадратичная скорость — физическая величина, отличная от средней арифметической скорости молекул, определяемая по формуле: корень квадратный из средней арифметической квадратов скоростей различных молекул.

Кинетическая энергия определяется скоростью движения молекул, поэтому зависит от температуры. Скорости молекул одного газа не одинаковы. Часть молекул движутся очень быстро, часть — с незначительной скоростью. Однако для большинства существует некое среднее значение. Если изобразить это на графике в виде параболы, такие молекулы со средней скоростью будут составлять ее верхнюю часть.

В единице объема газа содержится огромное число молекул. Поэтому, например, его давление на стенки сосуда — величина постоянная. В ином случае, если бы в единицу времени о стенку ударялось различное количество молекул, давление бы «скакало».

Из изложенного можно сделать вывод: скорость — свойство отдельной молекулы газа, а давление — характеристика их совокупности.

От каких величин зависит в идеальном газе

Для идеального газа средняя квадратичная скорость прямо пропорциональна его температуре и обратно пропорциональна молярной массе газа.

В математическом выражении данная зависимость выражается через корень квадратный:

(V=surd(3RT/mu)
)

где R — универсальная постоянная величина, Т — температура газа, μ — молярная масса.

Из формулы видно, что искомая величина (средняя квадратичная скорость) зависит от природных свойств газа и его температуры.

Формула средней квадратичной скорости молекул

Математическое выражение формулы выглядит следующим образом:

(V_{ср;кв}=surd(V_{12}+V_{22}+V_{n2})/N)

В формуле присутствуют следующие условные обозначения: V1, V2, Vn — скорости молекул, а N — их количество.

Формула может иметь и другой вид:

(V_{ср;кв}=surd1/Nastsum V_2)

или

(V_{ср;кв}=int V_2F(V)dV)

Как посчитать в зависимости от природы газа и температуры?

Проведенное интегрирование формулы, цель которого определить зависимость искомой единицы от природных свойств иттемпературы газа, приводит расчеты к формуле:

(V_{ср;кв}=surd(3kT/mo))

или

(V_{ср;кв}=surd(3RT/mu))

При поступательном движении молекул газа Vср кв — составляющая уравнения для молекулярно-кинетической теории.

Если n=N/V, где N — число частиц, а V — объем, то концентрация частиц n получает следующее формульное выражение:

(p=1/3ast nmo(V_{ср;кв})^2)

Насколько полезной была для вас статья?

Рейтинг: 2.33 (Голосов: 3)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

Добавить комментарий