Средняя скорость
- Главная
- /
- Физика
- /
- Средняя скорость
Чтобы найти среднюю скорость воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Средняя скорость на протяжении всего пути
Расстояние (путь)
S =
Время
t =
Средняя скорость
Vср =
0
/
Округление ответа:
Средняя скорость через несколько скоростей
Средняя скорость
Vср =
0
Округление ответа:
Просто введите значения скоростей на разных участках пути и получите среднюю скорость. Для того чтобы добавить в ряд более двух чисел воспользуйтесь зелёной кнопкой “+”.
Теория
Как найти среднюю скорость зная расстояние (путь) и время
Чему равна средняя скорость Vср если известны путь S и время t за которое этот путь преодолён?
Формула
Vср = S⁄t
Пример
К примеру, поезд преодолел расстояние в 1000 км за 16 часов. Посчитаем с какой средней скоростью он двигался:
Vср = 1000/16 = 62.5 км/ч
Как найти среднюю скорость зная скорости на участках пути
Чтобы найти среднюю скорость Vср на протяжении всего пути, зная показатели скорости на его участках (V1 , V2 , … Vn), следует найти среднее гармоническое этих скоростей.
Формула
| Vср | = | n |
| 1⁄V1 + 1⁄V2 + … + 1⁄Vn |
Пример
Средняя скорость через две скорости
Автомобиль проехал некий путь, при этом первые полпути он ехал со скоростью 80 км/ч, а вторые полпути – со скоростью 20 км/ч. Определим среднюю скорость этого автомобиля:
| Vср | = | 2 | = | 2 | = 32 |
| 1⁄80 + 1⁄20 | 0.0125 + 0.05 |
Средняя скорость автомобиля равна 32 км/ч.
Содержание материала
- Основные характеристики и формулы
- Видео
- Угловая скорость
- Вращение Земли
- Период и частота
- Мгновенная и средняя скорости
- Центростремительное ускорение
- Период и частота вращения
- Примеры задач с решением
Основные характеристики и формулы
Так как за период  угловое перемещение
угловое перемещение  рад, угловая скорость связана с периодом и частотой вращения:
рад, угловая скорость связана с периодом и частотой вращения:



Рис.1. Линейное и угловое перемещение при равномерном движении точки по окружности
Наряду с понятием угловой скорости для характеристики равномерного движения по окружности сохраняет смысл привычное для нас понятие скорости движения точки вдоль траектории, которое в данном случае называется линейной скоростью.
Модуль линейной скорости равен отношению длины дуги окружности  к промежутку времени, за который эта дуга пройдена.
к промежутку времени, за который эта дуга пройдена.
Линейная скорость тела, которое движется по окружности, не изменяется по модулю, а все время изменяется по направлению, и в любой точке траектории направлена по касательной к дуге этой окружности (рис.1).
Угловая и линейная скорости связаны между собой соотношением:

где  радиус окружности.
радиус окружности.
Кинематическое уравнение или закон движения точки по окружности:

Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.



Видео
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Мгновенная и средняя скорости

Как найти линейную скорость? Формулу, согласно определению величины, можно записать следующую:
v¯ = dl¯/dt.
Где dl¯ — вектор перемещения тела за время dt. Эта скорость называется мгновенной, поскольку рассчитывается за чрезвычайно короткий промежуток времени dt. Мгновенная скорость в действительности является величиной не стабильной и постоянно меняющейся. Например, представим, что по дороге движется автомобиль. На первый взгляд можно полагать, что в любой момент времени его мгновенная скорость будет постоянной, однако, это не так. Мгновенная скорость испытывает колебания. Если спидометр автомобиля достаточно чувствителен, то он фиксирует эти колебания.
Формула линейной скорости средней ничем не отличается от таковой для мгновенной, однако, измеряется она за более длительный промежуток времени Δt:
v¯ = Δl¯/Δt, где Δt>>dt.
В примере с автомобилем выше, хотя мгновенная скорость испытывает колебания, средняя скорость остается постоянной с определенной точностью на всем участке пути Δl¯.
При решении задач, как правило, используют среднюю скорость. Мгновенная же величина имеет смысл только в случае движения с ускорением.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Период и частота вращения
Важными характеристиками любого вращательного движения являются частота и период:
Определение Период – время, за которое тело совершает полный оборот.
В нашем примере с мотоциклистом, период – это время, за которое мотоциклист проезжает один полный круг.
Из курса геометрии вспоминаем, что длину дуги окружности можно посчитать как (2*pi*R), где (R) – радиус окружности. Тогда в случае равномерного движения период можно посчитать по формуле, как расстояние деленое на скорость: $$T=frac{2*pi*R}{V};$$ Подставив сюда формулу ((1)) для линейной скорости через угловую: $$T=frac{2*pi}{omega};$$ Где (V) –линейная скорость вращения.
В системе СИ период измеряется в ([{cек}^{-1}]).
Определение Частота – количество оборотов за единицу времени.
В случае с мотоциклистом, частота – это сколько кругов он успевает проехать, например, за один час. Обычно частоту измеряют в оборотах в секунду.
Период и частота вращения связаны между собой выражением: $$T=frac{1}{nu};$$ Отсюда можно получить формулы для частоты, подставив период: $$nu=frac{V}{2*pi*R}=frac{omega}{2*pi};$$
Пример 1
Скорость точки, находящейся на краю вращающегося диска равна (V_A=15(м/с)), а точки, расположенной на 0,2 (м) ближе к центру вращения равна (V_B=10(м/с)). Найти частоту вращения и радиус диска.
Примеры задач с решением
Пример 1
Задание. Диск равномерно вращается вокруг оси (O), перпендикулярной его плоскости, проходящей через его центр (рис.3). Линейная скорость точки A равна $v_1$, Точка B находится на расстоянии $Delta l$ ближе к оси и имеет лилейную скорость $v_2$. Какова угловая скорость вращения диска ($omega $)?
Решение. Основой для решения задачи будет формула: [omega =frac{v}{R}left(1.1right).]
Угловые скорости движения точки A и B одинаковы (${omega }_A={omega }_B$), запишем выражение для каждой из этих скоростей используя (1.1): [{omega }_A=frac{v_1}{R_1};; {omega }_B=frac{v_2}{R_2}left(1.2right).]
$R_1$ — расстояние от точки O до точки A; $R_2=R_1-Delta l$ — расстояние от точки B до точки O. Приравняем правые части выражений (1.2), выразим расстояние $R_1$: [frac{v_1}{R_1}=frac{v_2}{R_1-Delta l}to R_1=frac{Delta lcdot v_1}{v_1-v_2}left(1.3right).]
Найдем угловую скорость точки A: [{omega }_A=v_1cdot frac{v_1-v_2}{Delta lcdot v_1}=frac{v_1-v_2}{Delta l}.]
Ответ. Угловая скорость всех точек диска равна $omega =frac{v_1-v_2}{Delta l}$
Пример 2
Задание. Колесо радиусом R=1 м вращается так, что угол поворота изменяется в соответствии с законом: $varphi left(tright)=2+5t^3(рад)$. Определите, какова линейная скорость точек обода колеса в момент времени, равный $t’=1 (с)$.
Решение. В качестве основы для решения задачи воспользуемся формулой: [v=Romega left(2.1right).]
Используя уравнение $varphi left(tright)$ и связь угла поворота и угловой скорости найдем $omega $: [omega =frac{dvarphi }{dt}=frac{d}{dt}left(A+Bt^3right)=3Bt^2(2.2).]
Подставим результат (2.2) в (2.1), имеем: [v=Rcdot 3Bt^2.]
Вычислим искомую скорость: [v=1cdot 3cdot 5cdot 1^2=15 left(frac{м}{с}right).]
Ответ. $vleft(t’right)=15frac{м}{с}$
Читать дальше: масса и плотность вещества.

Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут! Узнать стоимость
Теги
С точки зрения физики абсолютного покоя не существует. Каждое тело и частицы, которые его составляют, находятся в постоянном движении друг относительно друга. Важной кинематической величиной, характеризующей движение, является скорость. В данной статье приведем формулы линейной скорости для различных типов перемещения тел в пространстве.
Что такое линейная скорость?
Речь идет о физической величине, которая показывает, какое расстояние в пространстве проходит тело за единицу времени. Как правило, скорость обозначают буквой v¯, где символ черты говорит о том, что она является векторной величиной. Измеряется скорость в метрах в секунду (м/с), километрах в час (км/ч), милях в час (мил/ч) и других единицах, предполагающих отношение расстояния ко времени.
Вектор скорости v¯ показывает направление реального перемещения тела. Этим он отличается от вектора ускорения, который направлен в сторону действующей силы, но не в сторону движения тела, хотя они могут совпадать.
Мгновенная и средняя скорости

Как найти линейную скорость? Формулу, согласно определению величины, можно записать следующую:
v¯ = dl¯/dt.
Где dl¯ – вектор перемещения тела за время dt. Эта скорость называется мгновенной, поскольку рассчитывается за чрезвычайно короткий промежуток времени dt. Мгновенная скорость в действительности является величиной не стабильной и постоянно меняющейся. Например, представим, что по дороге движется автомобиль. На первый взгляд можно полагать, что в любой момент времени его мгновенная скорость будет постоянной, однако, это не так. Мгновенная скорость испытывает колебания. Если спидометр автомобиля достаточно чувствителен, то он фиксирует эти колебания.
Формула линейной скорости средней ничем не отличается от таковой для мгновенной, однако, измеряется она за более длительный промежуток времени Δt:
v¯ = Δl¯/Δt, где Δt>>dt.
В примере с автомобилем выше, хотя мгновенная скорость испытывает колебания, средняя скорость остается постоянной с определенной точностью на всем участке пути Δl¯.
При решении задач, как правило, используют среднюю скорость. Мгновенная же величина имеет смысл только в случае движения с ускорением.
Равномерное движение по прямой линии
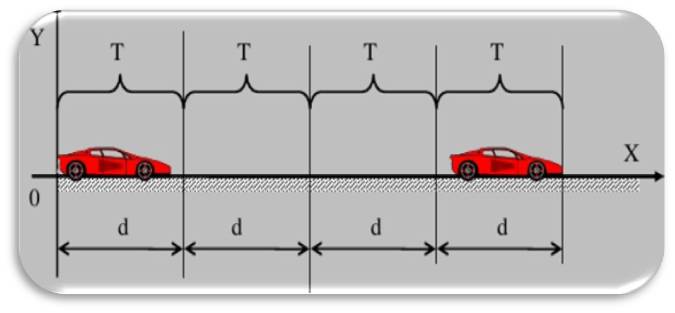
Это идеализированный тип движения, который предполагает, что тело в течение некоторого промежутка времени движется вдоль прямой в пространстве. При этом скорость тела не меняется. Обозначая пройденный путь символом l, получаем формулу:
l = v*t.
Здесь v = const.
Этот тип движения рассматривался еще философами Античной Греции. Они полагали, что для движения тел необходимо прикладывать некоторую силу, поэтому естественным состоянием всех окружающих объектов является покой. Только с приходом эпохи Возрождения благодаря работам Галилея и Ньютона было показано, что если на тело не воздействуют внешние силы, то равномерность и прямолинейность его движения не нарушается.
Скорость при движении по прямой с ускорением
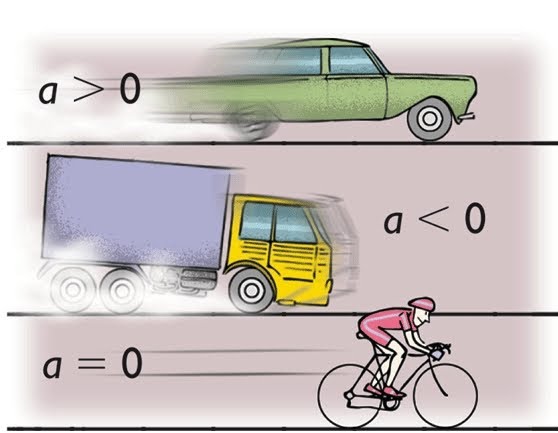
Когда появляется внешняя сила, то ее действие на тело приводит к изменению скорости тела. В динамике эта ситуация описывается вторым законом Ньютона:
F¯ = m*a¯.
Если действие силы F¯ происходит на покоящееся изначально тело массой m, то формула нахождения линейной скорости в любой момент времени t примет вид:
v¯ = a¯*t.
В данном случае обе векторные величины направлены в одну и ту же сторону. Эта формула может применяться для описания разгона какого-либо транспортного средства.
Теперь предположим, что автомобиль двигался с некоторой скоростью v0¯, а затем начал останавливаться. В этой случае соответствующее кинематическое уравнение примет вид:
v¯ = v0¯ + a¯*t.
Поскольку модуль скорости |v¯| авто будет уменьшаться со временем, в скалярной форме это равенство запишется так:
v = v0 – a*t.
В данном случае вектора скорости и ускорения направлены в противоположных направлениях.
Все формулы линейной скорости, приведенные в этом пункте, описывают прямолинейное движение с постоянным ускорением.
Вращение тел

Под вращением понимают тип движения, при котором траектория перемещающегося тела представляет собой окружность. Вращение может происходить вокруг оси или вокруг фиксированной точки. Вращение колеса, планет по своим орбитам, спортсменов во время соревнований по фигурному катанию – все это примеры указанного типа движения.
По аналогии с линейным перемещением, главной формулой динамики вращения является следующая:
M = I*α.
Здесь M и I – моменты силы и инерции, соответственно, α – ускорение угловое.
Для описания вращения удобно пользоваться не линейной, а угловой скоростью. Она определяется так:
ω = θ/t.
Где θ – угол, на который тело повернулось за время t. С записанным ускорением α скорость ω связана следующим равенством:
ω = α*t.
Для измерения всех угловых величин используются радианы.
Формула линейной скорости вращения
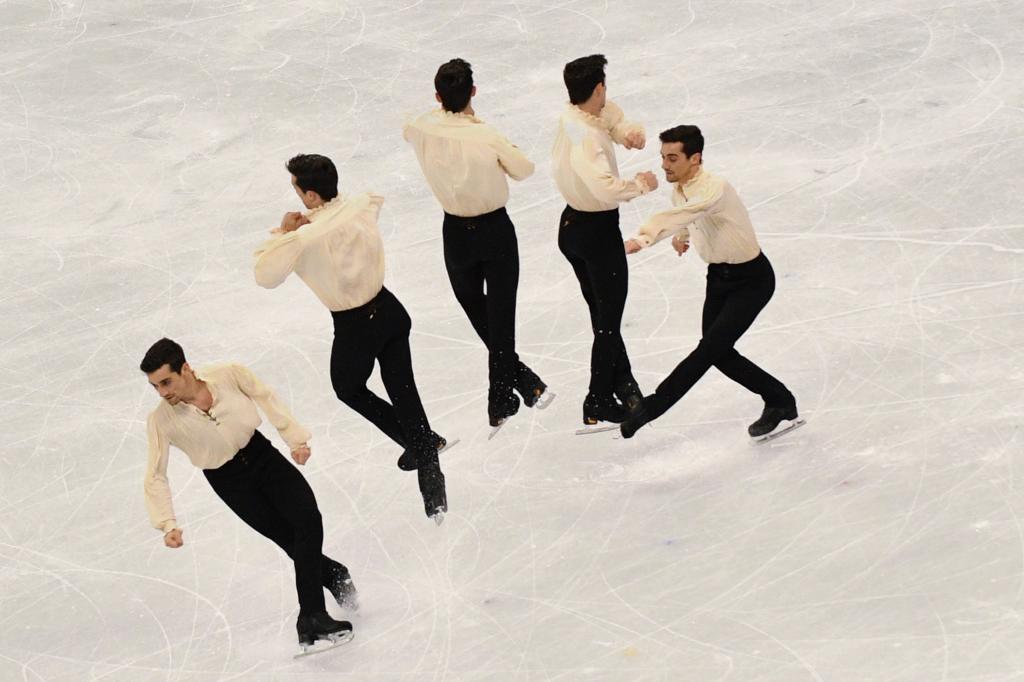
Выше отмечалось, что вращение удобно описывать в угловых характеристиках. Тем не менее в некоторых случаях важно знать, чему равна линейная скорость по окружности. Формула для этого случая приведена ниже:
v = ω*r.
Здесь r – радиус окружности, равный расстоянию от любой точки траектории тела до оси вращения. Связывающую линейную и угловую скорость формулу получить несложно самостоятельно. Для этого достаточно рассмотреть, какое расстояние по окружности преодолеет тело за известное время t.
Приведенное выражение можно использовать для вычисления линейных скоростей космических тел, например, нашей Земли, вращающейся вокруг Солнца.
Линейная скорость и центростремительное ускорение
Скорость является величиной векторной. Это означает, что тело получает ускорение не только при изменении модуля величины v, но и при изменении ее направления. Последняя ситуация реализуется во время вращения. Вектор мгновенной скорости тела всегда направлен по касательной к окружности. Если за равные промежутки времени тело описывает равные углы относительно центра вращения, то такое движение является равномерным с точки зрения модуля скорости.
Отклонение от прямолинейного движения во время вращения происходит за счет действия центростремительной силы, вызывающей центростремительное ускорение. Оно направлено всегда перпендикулярно скорости, поэтому изменить ее модуль не может. Ускорение центростремительное ac можно вычислить по формуле:
ac = v2/r.
Абсолютная величина ускорения ac показывает, насколько велики центробежные силы, связанные с инерцией вращающегося тела. Практическим примером является занос автомобиля во время крутого поворота. Заметим, что с уменьшением радиуса ac растет медленнее, чем с увеличением линейной скорости.
Задача на определения линейной скорости нашей планеты

Каждый человек понимает, что если автомобиль движется со скоростью 100 км/ч, то эта цифра является достаточно большой в сравнении со скоростями, с которыми люди сталкиваются в повседневной жизни. Любопытно сравнить указанную цифру со скоростью вращения Земли по своей орбите.
Для оценки этой скорости возьмем следующие данные:
- радиус орбиты – 150 млн км;
- период одного оборота – 365 земных дней.
Для определения требуемой величины воспользуемся формулой линейной и угловой скорости:
v = ω*r.
Значение ω через период T определяется так:
ω = 2*pi/T.
Тогда для v приходим к равенству:
v = 2*pi*r/T.
Подставляя данные из условия задачи, получим линейную скорость 107,5 тысяч км/ч! Эта цифра означает, что наша Земля перемещается в космическом пространстве в 1000 раз быстрее, чем автомобиль движется по дороге. Мы не чувствуем этой гигантскую скорости, поскольку силы гравитации Земли увлекают за собой атмосферу так, что она находится в покое относительно поверхности планеты.
Средняя скорость считается так: весь путь поделить на всё время движения. Формула одна и очень простая, но почему-то школьники часто путаются в задачах на среднюю скорость. Разберу три характерные задачи и основные ошибки. Возможно, статья будет полезна учителям и репетиторам, а также школьникам.
1. Половина пути
Первую половину пути поезд ехал со скоростью 60 км/ч, а вторую – 90 км/ч. С какой средней скоростью ехал поезд на всём пути?
Первым делом школьник захочет сложить эти две скорости и поделить пополам. Логично? Да. Но, к сожалению, неправильно.
Объясняю, почему. Поскольку первую половину пути поезд ехал с меньшей скоростью, то времени было затрачено больше, чем на вторую. А значит, вклад отдельных скоростей неравнозначен, и нельзя так просто делить пополам.
Тут школьник может впасть в панику. Что делать? Умножать? Делить? Непонятно. Воспользоваться напрямую формулой “расстояние поделить на время” не получится – ни расстояние, ни время нам неизвестно.
Для школьников, только начинающих изучать основы физики, бывает трудно оперировать с неизвестными величинами. Нам не дано ничего, кроме скоростей, как же быть? В качестве маленькой ступеньки к освоению неизвестности могу предложить следующий ход – сначала додумать неизвестные данные. Возьмём и сами решим, пусть поезд пройдет 180 километров, цифру возьмем так, чтобы легко делилась.
Тогда половина пути будет 90 километров. Поезд пройдет её за 1,5 часа. Вторую половину пути – за 1 час. Это легко посчитает любой школьник. Значит, общее время в пути будет 2,5 часа. Делим общее расстояние 180 километров на 2,5 часа, и получаем 72 км/ч.
Это просто и понятно, но учитель такую задачу не примет. Откуда мы взяли 180 километров, когда это неизвестно? Тем не менее, дав себе эти неизвестные данные, мы продумали алгоритм и довели задачу до ответа. Осталось формализовать это решение, так чтобы не использовать то, что не дано. Обозначим наши 180 километров за S, и опишем всё, что мы делали раньше, только вместо цифр используем буквы.
Получается, что зная ход решения “в цифрах”, мы переводим его в буквенные обозначения. И тут главное не остановиться на полдороги, не смущаться, что нам неизвестно расстояние. Ведь оно в конце сократилось, и средняя скорость оказалась независящей от расстояния (что вполне логично). И от школьника здесь требуются уже алгебраические умения – складывать дроби, переворачивать их.
Если подобная задача встретилась в тесте, где требуется только ответ, можно вообще не заморачиваться – так как средняя скорость в данной задаче не зависит от расстояния, можно посчитать при любом удобном расстоянии. По крайней мере, это лучше, чем сидеть и ломать голову, не зная, как подступиться к решению. Если же требуется оформление – тут числовое решение может помочь как переходный этап, чтобы понять, что именно делать с формулами, как их крутить-вертеть.
Школьникам часто бывает трудно переходить на новый уровень абстракции – от чисел к переменным, которые могут принимать разные числовые значения. В алгебре это тренируют, но там одна переменная икс, и иногда игреки встречаются. А в физике этих переменных пруд пруди, в каждой задаче они разные, и если ученик не освоил этот уровень, то физика кажется ему супер-трудной. Кроме того, в школе переход от чисел к переменным часто упускают, в программе отдельных навыков работы с формулами нет.
2. Средняя скорость по графику пути
Пусть нам дан график зависимости координаты от времени. Требуется определить среднюю скорость.
По графику видно, что движение состоит из четырех этапов:
- Тело стартует в нуле и через 2 секунды оказывается на координате 2 м.
- Тело останавливается, и в течение 4 секунд покоится в точке с координатой 2 м.
- Тело начинает движение, и через 2 секунды оказывается в точке 6 м.
- Тело движется в обратном направлении, и через 2 секунды оказывается в точке 5 м.
Проговорить, понять все эти этапы – важная часть решения. А дальше многие школьники начинают вычислять скорости движения на каждом этапе: На первом – 1 м/с, на втором – 0, на третьем – 2 м/с, на четвертом – 0,5 м/с. Вот это действие как раз лишнее. Для того, чтобы вычислить среднюю скорость, вовсе не обязательно знать скорости на каждом этапе!
Вспомним определение средней скорости – это весь путь, поделить на всё время. Поэтому просто по графику считаем весь путь – 6 метров “туда” и 1 метр “обратно”, в сумме 7 метров. Общее время движения – 10 секунд. Делим 7 метров на 10 секунд, получаем 0,7 м/с.
3. Средняя скорость по графику скорости
Бывает так, что нам дан график зависимости скорости от времени, и требуется определить среднюю скорость. Вот, к примеру, такой график.
Читаем график. Движение состоит из трёх этапов
- С начала движения до момента времени 2 с тело движется с постоянной скоростью 2 м/с
- От 2 до 6 с тело движется со скоростью 6 м/с
- В последние 4 секунды от 6 до 10 с тело замедляется, снижая свою скорость до нуля.
Попытки что-то сделать со значениями скорости самими по себе здесь обречены на провал. Опять надо найти весь путь и всё время движения. Путь по графику скорости определяется как площадь под графиком, причем если график идет ниже нуля, то соответствующие участки складываются.
Считаем площадь фигуры – два прямоугольника на первых двух этапах и треугольник на третьем. Первый этап – 4 м, второй этап – 24 м, третий этап – 12 м. Значит, весь путь будет 40 метров. Всё время 10 секунд, значит, средняя скорость 4 м/с.
Общие рекомендации для решения задач на среднюю скорость
1. Средняя скорость – это всегда весь путь делить на всё время. Данные об отдельных скоростях сами по себе не дадут полной информации о средней скорости. Используем только эту формулу.
2. Следует проанализировать конкретную ситуацию и понять, как можно применить формулу. Если кажется, что не хватает данных – не смущаться.
3. Данные по скоростям на отдельных этапах могут быть полезны для проверки готового ответа: средняя скорость должна лежать между минимальной и максимальной.
Спасибо, что прочитали до конца! Желаю школьникам хорошей учёбы, учителям – понятливых и любопытных учеников, родителям – чтобы дети радовали. Буду рада лайкам и новым подписчикам!
Средняя скорость – одна из основных функций, определяемых в движении. В этой статье мы узнаем, как найти среднюю скорость.
Основной метод определения средней скорости – это отношение суммы изменения положения объекта к общему времени, затраченному этим объектом на завершение своего движения. Поскольку это векторная физическая величина, направление объекта также имеет важное значение при вычислении средней скорости.
Далее мы изучим больше методов, как найти среднюю скорость, так как это основная цель поста.
Какая формула для средней скорости
Основная формула, используемая для расчета Vсредний включает как смещение во времени.
Общая используемая формула имеет следующий вид:
Он используется при решении основных задач, связанных со средней скоростью.
В = Сf – Si / т2 – т1
V = Δs / Δt
Где,
Δs = смещение
Δt = затраченное время
Теперь давайте посмотрим, как найти среднюю скорость с помощью расстояния и времени.
Как найти среднюю скорость в зависимости от расстояния и времени
Расстояние и время – основные термины, без которых невозможно определить среднюю скорость.
Прежде всего, мы должны рассчитать общую длину пути, по которому прошел объект, а затем мы должны проверить продолжительность времени, необходимого для достижения пункта назначения. Позже, чтобы найти среднюю скорость этого движения, нам нужно использовать ранее рассчитанные расстояние и время с помощью формулы.
Теперь давайте продолжим изучение, чтобы узнать больше подходов к нахождению средней скорости.
Как найти среднюю скорость за интервал
Увидев важность расстояния и времени при вычислении средней скорости. Теперь давайте, как рассчитать это за интервал.
- Если вы вычисляете среднюю скорость на графике, вам следует рассмотреть любые два интервала времени и расстояния, а затем найти значения расстояния и времени и подставить их в формулу средней скорости.
В = Сf – Si / т2 – т1
- В другом методе, если вы собираетесь напрямую использовать формулу, вы должны знать начальную и конечную точки, чтобы вам было легко вычислить Vсредний, вы даже можете рассмотреть некоторую часть интервала, чтобы найти Vсредний Это происходит путем деления общего расстояния на общее время.
V = общее расстояние / общее время или
В = (Вf + Vi) / 2
Теперь давайте посмотрим, как рассчитать Vсредний между двумя точками.
Средняя скорость между двумя точками
Среднюю скорость между двумя точками можно найти по простой формуле.
В общем, мы знаем, что Vavg тела равно среднему арифметическому начальных и конечных точек, приведенному ниже.
Vavg = [Начальная скорость (i) + Конечная скорость (v)] / 2
Пора узнать, как найти Vсредний на графике.
Как найти среднюю скорость на графике
Мы можем найти среднюю скорость с помощью графика смещения-времени.
- Здесь смещение будет по оси y, а время по оси x.
- Постройте точки в соответствии с осью и соедините их, чтобы создать область на графике.
- Затем найдите общую площадь на графике, взяв два интервала времени и расстояния.
- Измерьте его по линии графика и рассчитайте по формуле
Vсредний = (Vi+Vf) / 2.
Переменные, взятые на графике, имеют характерную природу, все факторы, такие как изменение положения (между начальной и конечной точками), характер графика, т. Е. Является ли он линейным или нет, имеет значение.
При таком подходе мы можем рассчитать среднюю скорость по графику.
Как найти среднюю скорость на линейном графике
Линейный график иногда называют прямолинейным графиком.
Если мы хотим узнать среднюю скорость на линейном графике, тогда мы должны взять как начальную, так и конечную скорости и разделить ее на число 2. Это похоже на среднее значение, которое мы используем в математике для решения определенных задач.
Теперь давайте узнаем условие вычисления средней скорости на нелинейном графике.
Как найти среднюю скорость на нелинейном графике
Нелинейный граф также можно рассматривать как искривленный граф.
В нелинейном графике, что мы можем сделать, чтобы вычислить Vсредний мы можем рассмотреть область под графиком, которая состоит из смещения (интегрировать его), а затем разделить на время.
Таким образом мы можем вычислить Vсредний в нелинейном графике.
Пример задачи средней скорости
Приведенное ниже – одна из основных проблем, которую можно решить, используя подходы к вычислению средней скорости.
Пример 1
Представьте, что человек едет на своей машине в какой-то пункт назначения, но в течение первых 15 секунд положение машины меняется с x1 = 80 м до x2= 100 м. Какова средняя скорость автомобиля?
Решение: учитывая исходное положение x1= 80m
Точно так же конечная позиция x2 = 100m
Изменение водоизмещения автомобиля рассчитывается следующим образом:
Δx = х2 – Икс1 = 100 м – 80 м = 20 м
Δt = 15 с
По формуле мы имеем
v = Δx / Δt
v = 20/15
v = 1.33 м / с
Таким образом, средняя скорость автомобиля составляет 1.33 м / с.
Из поставленной выше задачи мы узнали еще об одном подходе к нахождению средней скорости
Часто задаваемые вопросы | FAQs
Что такое средняя скорость?
Средняя скорость – заметное явление в физике.
Это векторная величина, определяемая как деление ∆x на ∆t. Где ∆x обозначает смещение, а ∆t обозначает общее время, затрачиваемое телом на завершение движения. Иногда может быть положительным или отрицательным, все зависит от направления смещения. Обозначается с помощью единицы СИ м / с.
Чем средняя скорость отличается от других скоростей?
Есть два основных типа скоростей, с которыми мы обычно сталкиваемся в физике.
Два основных типа скоростей – средние и мгновенные скорости. Как следует из их названия, среднее означает сумму скоростей каждого интервала, рассчитанную за общее время. Напротив, мгновенная скорость будет вычислением скорости в конкретный период движения.
Чем средняя скорость отличается от мгновенной скорости в конкретный интервал времени?
Если мы возьмем конкретный временной интервал, тогда будет разница в измерении средней и мгновенной скорости.
Основное различие заключается в том, что для определенного периода интервала мгновенная скорость измеряется смещением и временем в определенной точке (s, t), а средняя скорость считается общим изменением положения во времени в определенном временном интервале.
Сохраняется ли средняя скорость в движении?
Скорость не остается неизменной в конкретном движении, она продолжает изменяться.
Мы выяснили, что скорость является переменной, зависящей от многих факторов. Он не остается постоянным, но продолжает изменять свое значение с помощью перемещения и времени этого объекта. Исходя из этого, мы можем сказать, что средняя скорость движения не остается неизменной.
Каковы два основных способа вычисления средней скорости?
Есть много приложений, с помощью которых мы можем легко измерить среднюю скорость.
Первый метод – найти среднюю скорость, взяв первую и конечную точки движения, вычтя ее, а затем разделив весь член на 2.
Второй метод основан на использовании формулы, известной как уравнение средней скорости.
Уравнение средней скорости = В = (Вf + Vi) / 2
- V = средняя скорость.
- Vf = конечная скорость.
- Vi = начальная скорость
Это простое уравнение для измерения средней скорости.
Как найти смещение со средней скоростью?
Есть много способов найти смещение в кинематике.
Один из них – найти смещение с помощью формулы средней скорости, которая состоит из изменения положения / смещения. Меняя местами члены формулы, мы можем использовать ее для расчета смещения.
Почему различаются средняя скорость и средняя скорость?
Оба термина означают совершенно разные друг от друга, когда мы изучаем их в физике.
Здесь мы знаем, что скорость – это скаляр, а скорость – вектор, тогда основное различие заключается в физических величинах, которые измеряют важность того, как их можно измерить.
Разница между средней скоростью и средней скоростью
Основные различия между этими двумя величинами приведены ниже:
- Средняя скорость говорит только о положении движущегося тела, здесь мы должны заметить, что величина будет разной для каждого положения, и определение скорости на любом временном интервале на длине курса осуществляется с помощью средней скорости.
- Средняя скорость говорит о сохранении скорости на всем пути движения. Это общая скорость, рассчитанная с учетом общей длины пути и времени, и, поскольку это скаляр, мы не можем определить направление пути.
