Как найти среднюю линию описанной трапеции

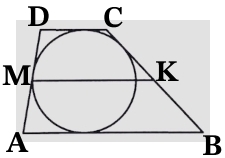
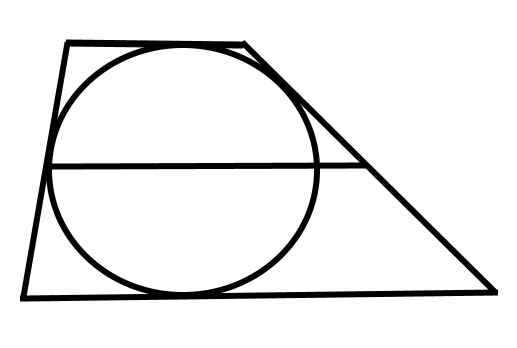
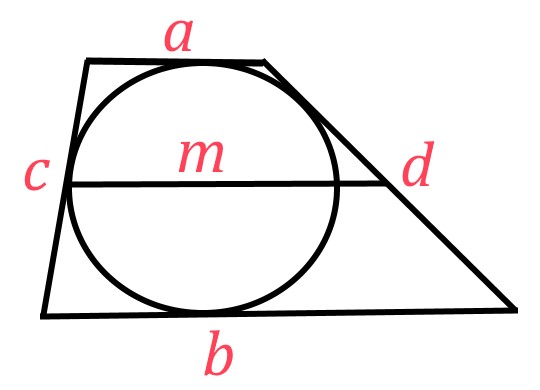
Решение №2018 Боковые стороны трапеции, описанной около окружности, равны 15 и 22.

Боковые стороны трапеции, описанной около окружности, равны 15 и 22. Найдите среднюю линию трапеции.

Суммы противоположных сторон описанного четырёхугольника равны. Суммы боковых сторон трапеции:

15 + 22 = 37

Тогда и сумма оснований равна 37. Средняя линяя равна половине суммы оснований:

37/2 = 18,5

Ответ: 18,5.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 5 / 5. Количество оценок: 2

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.

Трапеция. Формулы, признаки и свойства трапеции

Параллельные стороны называются основами трапеции, а две другие боковыми сторонами

Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.

• Основы трапеции – параллельные стороны
• Боковые стороны – две другие стороны
• Средняя линия – отрезок, соединяющий середины боковых сторон.

• Равнобедренная трапеция – трапеция, у которой боковые стороны равны
• Прямоугольная трапеция – трапеция, у которой одна из боковых сторон перпендикулярна основам

Основные свойства трапеции

AK = KB, AM = MC, BN = ND, CL = LD

3. Средняя линия трапеции параллельна основаниям и равна их полусумме:

BC : AD = OC : AO = OB : DO

d ₁ 2 + d ₂ 2 = 2 a b + c 2 + d 2

Сторона трапеции

Формулы определения длин сторон трапеции:

a = b + h · ( ctg α + ctg β )

b = a – h · ( ctg α + ctg β )

a = b + c· cos α + d· cos β

b = a – c· cos α – d· cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

Средняя линия трапеции

Формулы определения длины средней линии трапеции:

1. Формула определения длины средней линии через длины оснований:

2. Формула определения длины средней линии через площадь и высоту:

Высота трапеции

Формулы определения длины высоты трапеции:

h = c· sin α = d· sin β

2. Формула высоты через диагонали и углы между ними:

h =	sin γ ·	d 1 d 2	=	sin δ ·	d 1 d 2
a + b	a + b

3. Формула высоты через диагонали, углы между ними и среднюю линию:

h =	sin γ ·	d 1 d 2	=	sin δ ·	d 1 d 2
2 m	2 m

4. Формула высоты трапеции через площадь и длины оснований:

5. Формула высоты трапеции через площадь и длину средней линии:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

d ₁ = √ a 2 + d 2 – 2 ad· cos β

d ₂ = √ a 2 + c 2 – 2 ac· cos β

2. Формулы диагоналей через четыре стороны:

d 1 =	√	d 2 + ab –	a ( d 2 – c 2 )
a – b

d 2 =	√	c 2 + ab –	a ( c 2 – d 2 )
a – b

d ₁ = √ h 2 + ( a – h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2

d ₂ = √ h 2 + ( a – h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2

d ₁ = √ c 2 + d 2 + 2 ab – d ₂ 2

d ₂ = √ c 2 + d 2 + 2 ab – d ₁ 2

Площадь трапеции

Формулы определения площади трапеции:

1. Формула площади через основания и высоту:

3. Формула площади через диагонали и угол между ними:

S =	d 1 d 2	· sin γ	=	d 1 d 2	· sin δ
2	2

4. Формула площади через четыре стороны:

S =	a + b	√	c 2 –	(	( a – b ) 2 + c 2 – d 2	)	2
2	2( a – b )

5. Формула Герона для трапеции

S =	a + b	√ ( p – a )( p – b )( p – a – c )( p – a – d )
| a – b |

где

p =	a + b + c + d	– полупериметр трапеции.
2

Периметр трапеции

Формула определения периметра трапеции:

1. Формула периметра через основания:

Окружность описанная вокруг трапеции

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d 1
4√ p ( p – a )( p – c )( p – d 1)

где

a – большее основание

Окружность вписанная в трапецию

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
2	2	a + b

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Боковые стороны трапеции, описанной около

27936. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.

Средняя линия трапеции равна полусумме её оснований, значит:

Следовательно для нахождения средней линии трапеции необходимо найти сумму её оснований.

Воспользуемся свойством четырёхугольника описанного около окружности: известно, что суммы противолежащих сторон такого четырёхугольника равны.

Значит сумма боковых сторон трапеции равна сумме её оснований, то есть:

Таким образом, средняя линия трапеции равна

[spoiler title=”источники:”]

http://ru.onlinemschool.com/math/formula/trapezium/

http://matematikaege.ru/trapeciya/27936-bokovye-storony-trapecii-opisannoj-okolo.html

[/spoiler]

Сайты, меню, вход, новости

автор вопроса выбрал этот ответ лучшим

Перейти к содержанию