Как найти среднюю линию по координатам вершин

Как составить уравнение средней линии треугольника по координатам его вершин? Как записать уравнение средней линии трапеции?

Для решения этих задач используем свойства средней линии треугольника и средней линии трапеции.

1 способ

Найти координаты середин двух сторон и составить уравнение прямой, проходящей через две найденные точки.

Пример.

1) Написать уравнение прямой, содержащей среднюю линию треугольника с вершинами в точках A(-2;-4), B(1;6), C(7;0), пересекающей стороны AB и BC в точках M и N.

Решение:

М — середина отрезка AB, N — середина BC.

По формулам координат середины отрезка

   

   

   

   

Таким образом,

   

Составим уравнение прямой MN, например, в виде y=kx+b:

   

Отсюда

   

   

2 способ

Найти координату одной из точек средней линии и составить уравнение прямой, параллельной стороне треугольника.

Решение:

   

— середина отрезка AB. Составим уравнение прямой AC:

   

   

Составим уравнение прямой MN как уравнение прямой, проходящей через точку M и параллельной прямой AC.

Угловой коэффициент прямой MN равен угловому коэффициенту прямой AC:

   

то есть уравнение прямой MN ищем в виде

   

Поскольку точка M принадлежит прямой, её координаты удовлетворяют этому уравнению. Отсюда находим значение b:

   

Таким образом, уравнение прямой MN

   

или

   

Аналогичные рассуждения применимы и при составлении уравнения средней линии трапеции.

Написать уравнение прямой, содержащей среднюю линию трапеции с вершинами в точках A(-2;1), B(1;5), C(4;-1), D(0;-3).

Решение:

1 способ

Сначала следует определить основания данной трапеции.

Составим уравнения сторон AD и BC. Если эти прямые параллельны, то AD и BC — основания трапеции. Если эти прямые не параллельны, то основания трапеции — AB и CD.

A(-2;1), D(0;-3), отсюда

   

Значит, уравнение прямой AD:  y= -2k-3.
B(1;5), C(4;-1),

   

Уравнение прямой BC: y= -2k+7.

Поскольку угловые коэффициенты прямых равны:

   

то AD ∥BC, то есть AD и BC являются основаниями трапеции ABCD. Значит AB и CD — боковые стороны. Найдём координаты точек M и N — середины  AB и CD соответственно.

   

   

   

   

Составим уравнение прямой MN, M(-1/2;3), N(2;-2):

   

то есть y=-2k+2.

2 способ

Уравнение AD — y= -2k-3, середина AB — M(-1/2;3). Составляем уравнение прямой MN, параллельной прямой AD.

   

Значит уравнение MN ищем в виде y= -2x+b.

Так как прямая проходит через точку M, её координаты удовлетворяют уравнению прямой:

   

Следовательно, уравнение средней линии трапеции ABCD имеет вид y=-2x+2 или 2x+y-2=0.

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Средние линии

Средние линии треугольника

Определение . Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).

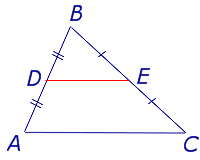
На рисунке 1 средней линией является отрезок DE .

Утверждение 1 . Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.

Доказательство . Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .

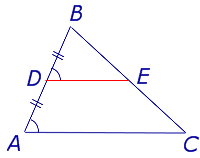
Поскольку AD = DB , а прямые AC и DE параллельны, то выполнены все условия теоремы Фалеса, и можно заключить, что выполнено равенство: CE = EB . Отсюда вытекает, что точка E является серединой стороны CB , а отрезок DE является средней линией треугольника.

Первую часть утверждения 1 мы доказали.

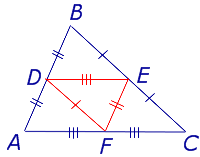
Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии – отрезки DE , EF и FD (рис.3).

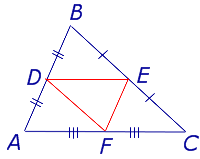
Но поскольку AF = FC , то отсюда вытекает равенство

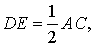
что и требуется доказать.

Доказательство утверждения 1 закончено.

• Три средних линии делят треугольник на 4 равных треугольника ADF , DBE , ECF , DEF (рис. 4).
• Каждый из четырёх треугольников ADF , DBE , ECF , DEF подобен треугольнику ABC с коэффициентом подобия 0,5 .

Средняя линия трапеции

Напомним, что трапецией трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.

Параллельные стороны трапеции называют основаниями , а непараллельные стороны – боковыми сторонами трапеции.

Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.

Определение . Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 5).

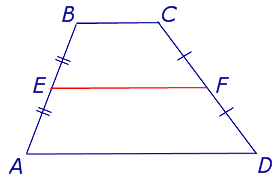
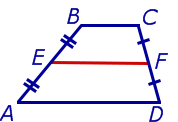
На рисунке 5 средней линией трапеции является отрезок EF .

Утверждение 2 . Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.

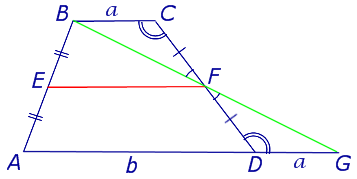
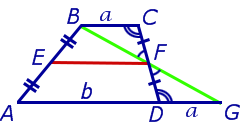
Доказательство . Проведем через вершину B и середину боковой стороны F трапеции прямую линию (рис. 6). Обозначим точку пересечения прямых BF и AD буквой G . Рассмотрим треугольники BCF и FDG . У этих треугольников стороны CF и FD равны, поскольку точка F – середина стороны CD . Углы BCF и FDG равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых BC и AD с секущей CD . Углы BFC и DFG равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники BCF и FDG равны. Из равенства треугольников BCF и FDG следует равенство отрезков BF и FG , откуда вытекает, что отрезок EF является средней линией треугольника ABG . Поэтому

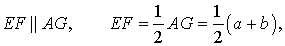
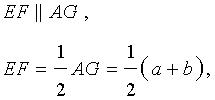
что и требовалось доказать.

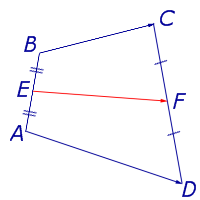
Задача 1 . Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.

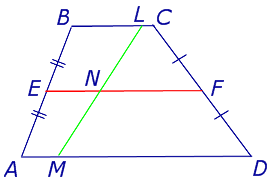
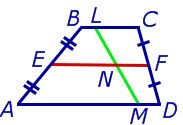
Решение . Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.7). Поскольку AE = EB , то, в силу теоремы Фалеса, выполнено равенство: LN = NM , что и требовалось доказать.

Задача 2 . Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.

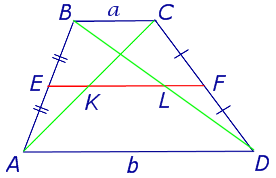
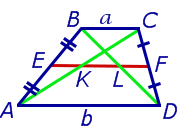
Решение . Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC , а точка L – середина отрезка BD . Поэтому отрезок EK – средняя линия треугольника BAC , а отрезок EL – средняя линия треугольника ABD . В силу утверждения 1 выполнены равенства:

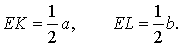
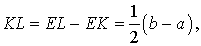
что и требовалось доказать.

Утверждение 3 . Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.

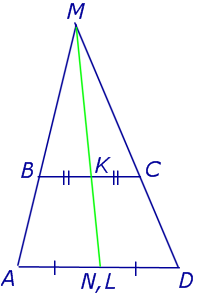
Доказательство . Пусть K и L – середины оснований BC и AD трапеции ABCD соответственно (рис.9). Обозначим буквой M точку пересечения боковых сторон AB и CD . Проведем через точки M и K прямую и обозначим точку пересечения этой прямой с основанием AD символом N . Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:

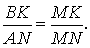
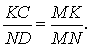
Из этих соотношений получаем:

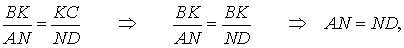
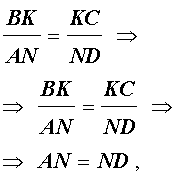
откуда вытекает, что точки N и L совпадают. Доказательство завершено.

Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.

Утверждение 4 . Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.

Следствие . Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.

Средние линии четырехугольника. Теорема Вариньона

Определение . Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.

Поскольку у каждого четырехугольника имеются две пары непересекающихся сторон, то у каждого четырехугольника имеются две средних линии (рис.10).

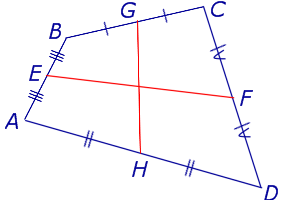
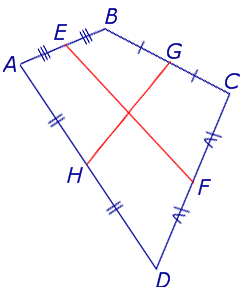
На рисунке 10 средние линии – это отрезки EF и GH .

Замечание 1 . Приведенное определение средней линии относится не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис.11). «Пространственным четырехугольником» мы называем замкнутую ломаную линию из 4 звеньев без самопересечений, не лежащую в одной плоскости.

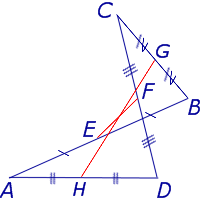
На рисунке 11 изображен «пространственный четырёхугольник» ABCD , средними линиями которого являются отрезки EF и GH .

Замечание 2 . Несмотря на то, что трапеция является четырехугольником, принято средней линией трапеции называть только отрезок, соединяющий середины её боковых сторон.

Замечание 3 . В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями.

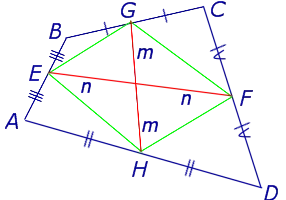
Теорема Вариньона . Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограмма параллелограмма .

Доказательство . Рассмотрим плоский четырёхугольник ABCD , изображенный на рисунке 12. Точки E, G, F, H – середины сторон, отрезок AC – диагональ четырёхугольника.

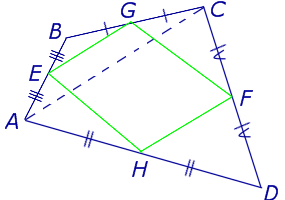
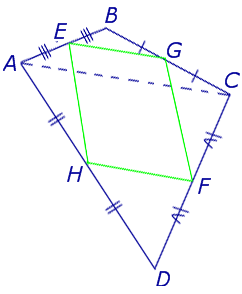
Поскольку отрезок EG – средняя линия треугольника ABC , то отрезок EG параллелен диагонали AC и равен её половине. Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине. Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограмма признака параллелограмма признака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать.

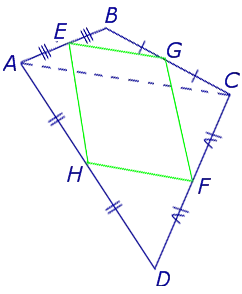
Замечание 4 . В случае «пространственного четырёхугольника» ABCD доказательство остаётся тем же (рис. 13).

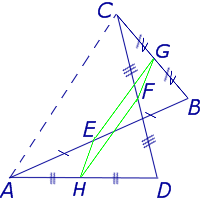
Утверждение 5 . Средние линии произвольного четырёхугольника пересекаются и в точке пересечения делятся пополам (рис. 14).

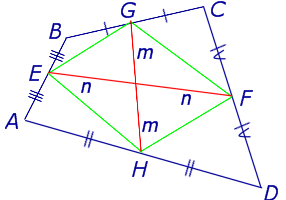
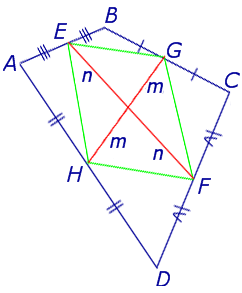
Утверждение 6 . Рассмотрим произвольный плоский или «пространственный» четырёхугольник ABCD , у которого отрезок EF является одной из средних линий (рис. 15). Тогда будет выполнено векторное равенство:

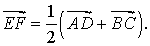
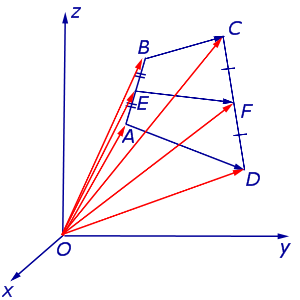
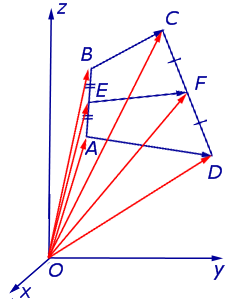
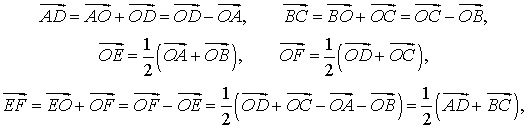
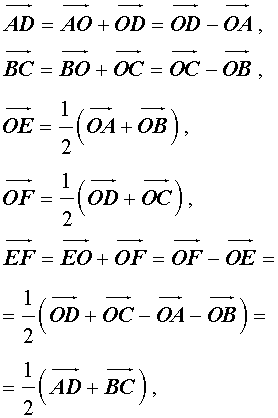
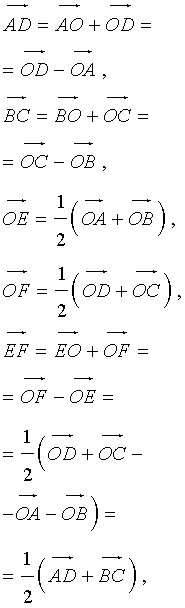
что и требовалось доказать.

Следствие . Средняя линия четырёхугольника меньше или равна половине суммы не пересекающих её сторон четырёхугольника, причём равенство достигается лишь в том случае, когда указанные стороны четырёхугольника параллельны.

Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапецией трапецией , а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.

Средние линии тетраэдра

Тетраэдром называют произвольную треугольную пирамиду (рис.17).

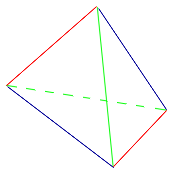
У каждого тетраэдра имеется 4 вершины, 4 грани и 6 рёбер, причем все рёбра делятся на 3 пары непересекающихся рёбер . На рисунке 17 каждая пара непересекающихся рёбер выделена отдельным цветом. Каждые два непересекающихся ребра тетраэдра лежат на скрещивающихся прямых скрещивающихся прямых .

Определение . Средней линией (бимедианой) тетраэдра называют отрезок, соединяющий середины двух непересекающихся рёбер тетраэдра.

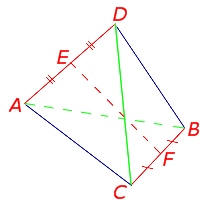
У каждого тетраэдра имеется 3 средних линии. Изображённый на рисунке 18 отрезок EF является одной из средних линий тетраэдра.

Утверждение 7 . Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.

Доказательство . Выберем какую-нибудь среднюю линию тетраэдра, например, EF и докажем, что любая другая средняя линия тетраэдра проходит через середину отрезка EF . Для этого рассмотрим, например, среднюю линию GH , соединяющую середины рёбер AC и BD , и соединим отрезками точки E, H, F, G (рис.19).

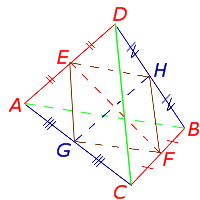
Заметим, что отрезок EH является средней линией треугольника ADB , поэтому

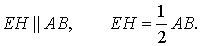
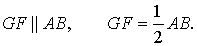
Определение . Точку пересечения средних линий тетраэдра называют центроидом тетраэдра .

Утверждение 8 . Рассмотрим в пространстве декартову систему координат с началом в точке O и произвольный тетраэдр ABCD . Если обозначить буквой M центроид этого тетраэдра (рис. 20), то будет выполнено векторное равенство:

[spoiler title=”источники:”]

http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik

http://www.resolventa.ru/spr/planimetry/mline.htm

[/spoiler]

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Уравнение средней линии

Как составить уравнение средней линии треугольника по координатам его вершин? Как записать уравнение средней линии трапеции?

Для решения этих задач используем свойства средней линии треугольника и средней линии трапеции.

Найти координаты середин двух сторон и составить уравнение прямой, проходящей через две найденные точки.

1) Написать уравнение прямой, содержащей среднюю линию треугольника с вершинами в точках A(-2;-4), B(1;6), C(7;0), пересекающей стороны AB и BC в точках M и N.

М — середина отрезка AB, N — середина BC.

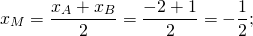
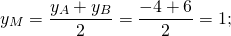
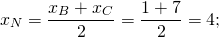
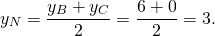
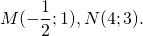
Составим уравнение прямой MN, например, в виде y=kx+b:

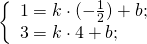
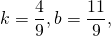
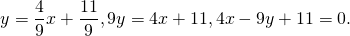
Найти координату одной из точек средней линии и составить уравнение прямой, параллельной стороне треугольника.

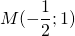
— середина отрезка AB. Составим уравнение прямой AC:

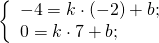
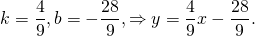
Составим уравнение прямой MN как уравнение прямой, проходящей через точку M и параллельной прямой AC.

Угловой коэффициент прямой MN равен угловому коэффициенту прямой AC:

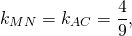
то есть уравнение прямой MN ищем в виде

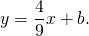
Поскольку точка M принадлежит прямой, её координаты удовлетворяют этому уравнению. Отсюда находим значение b:

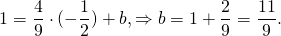
Таким образом, уравнение прямой MN

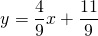
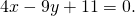
Аналогичные рассуждения применимы и при составлении уравнения средней линии трапеции.

Написать уравнение прямой, содержащей среднюю линию трапеции с вершинами в точках A(-2;1), B(1;5), C(4;-1), D(0;-3).

Сначала следует определить основания данной трапеции.

Составим уравнения сторон AD и BC. Если эти прямые параллельны, то AD и BC — основания трапеции. Если эти прямые не параллельны, то основания трапеции — AB и CD.

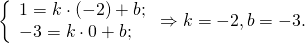
Значит, уравнение прямой AD: y= -2k-3.
B(1;5), C(4;-1),

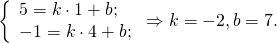
Уравнение прямой BC: y= -2k+7.

Поскольку угловые коэффициенты прямых равны:

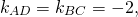
то AD ∥BC, то есть AD и BC являются основаниями трапеции ABCD. Значит AB и CD — боковые стороны. Найдём координаты точек M и N — середины AB и CD соответственно.

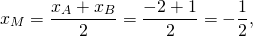
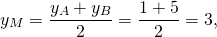
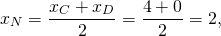
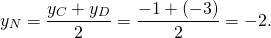
Составим уравнение прямой MN, M(-1/2;3), N(2;-2):

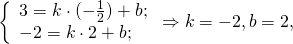
Уравнение AD — y= -2k-3, середина AB — M(-1/2;3). Составляем уравнение прямой MN, параллельной прямой AD.

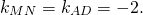
Значит уравнение MN ищем в виде y= -2x+b.

Так как прямая проходит через точку M, её координаты удовлетворяют уравнению прямой:

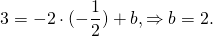
Следовательно, уравнение средней линии трапеции ABCD имеет вид y=-2x+2 или 2x+y-2=0.

Как найти среднюю линию треугольника?

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

• Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
• Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
• Тупоугольный. Один угол тупой, два других — острые.

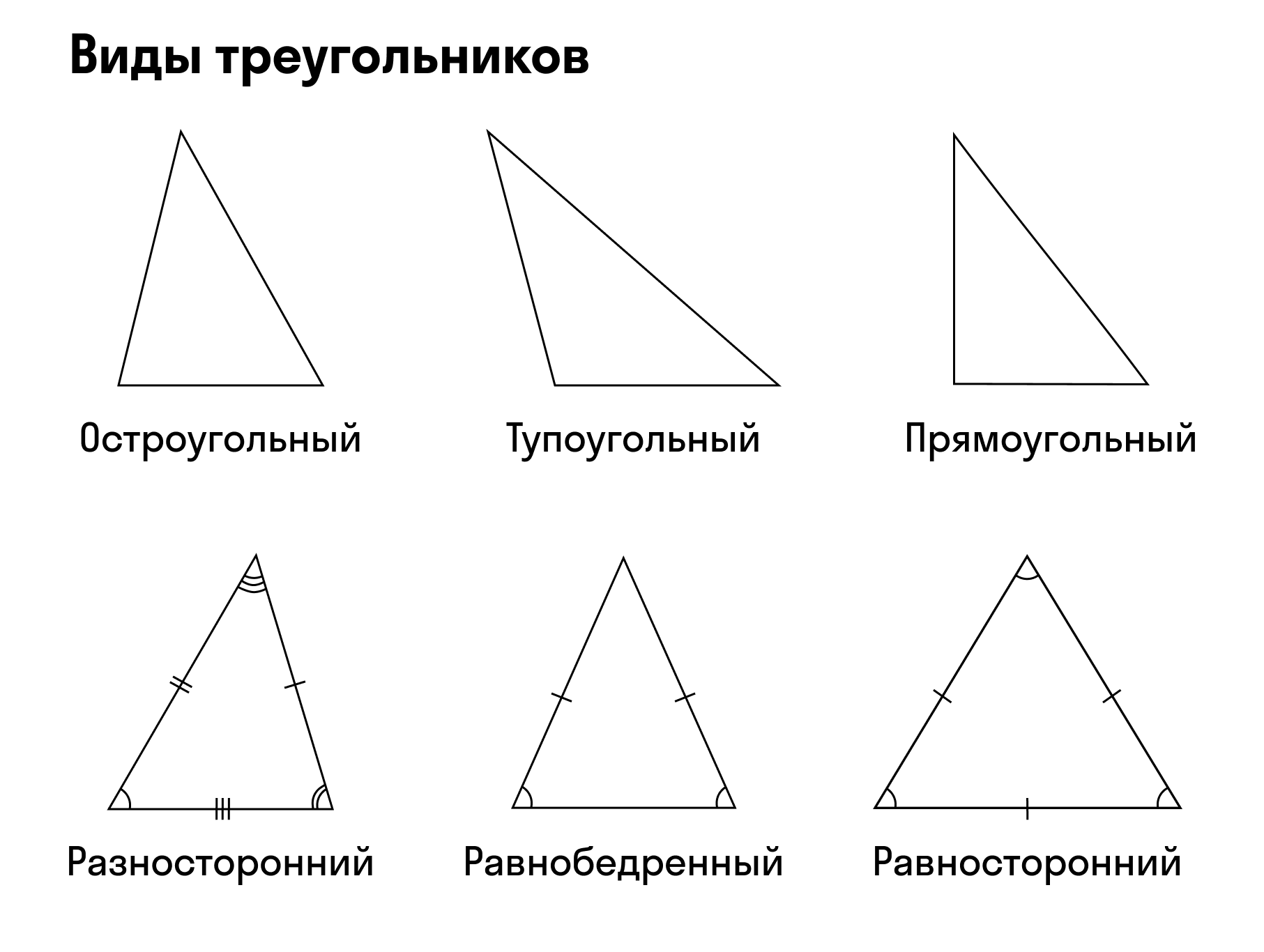
Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства треугольников:

• В треугольнике против большего угла лежит большая сторона — и наоборот.
• Сумма углов треугольника равна 180 градусов.
• Все углы равностороннего треугольника равны 60 градусам.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

​Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.

​Основанием считается сторона, которой параллельна средняя линия.

Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.

Понятие средней линии прямоугольного треугольника

Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

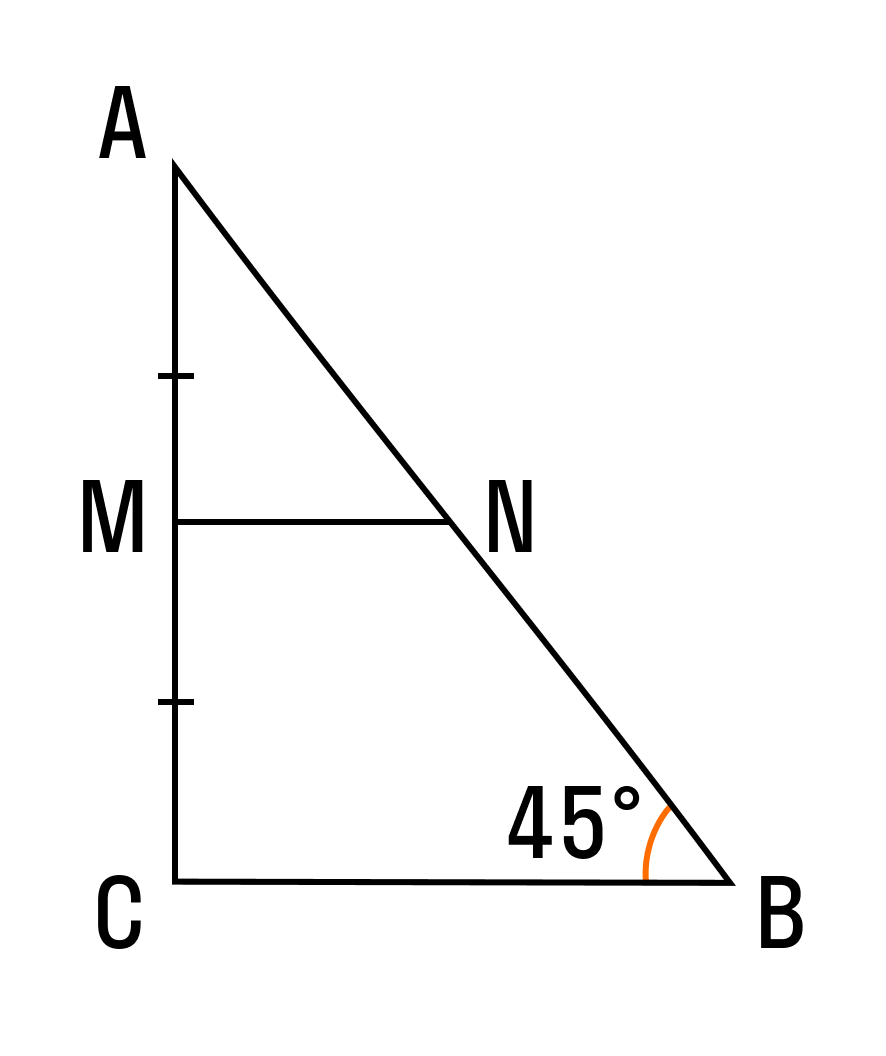
Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Свойства средней линии треугольника

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

Свойства:

1. Средняя линия равна половине длины основания и параллельна ему.
2. Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
3. Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
4. Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Теорема о средней линии треугольника

Теорема о средней линии треугольника звучит так:

Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:

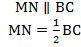
Докажем теорему:

По условию нам дано, что MA = MB, NA = NC

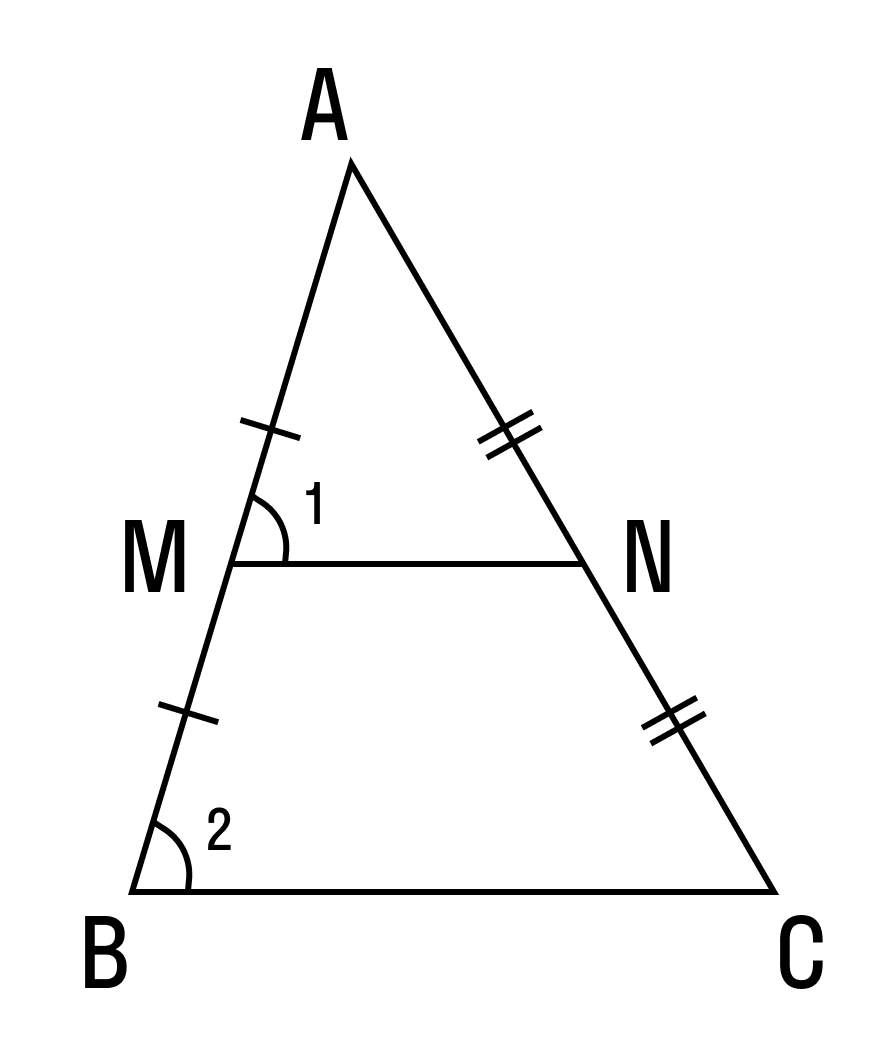
Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.

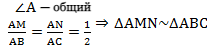(по второму признаку подобия треугольников).

△ABC, то 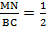Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.

△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.

Параллельность средней линии и соответствующего ей основания доказана.

Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

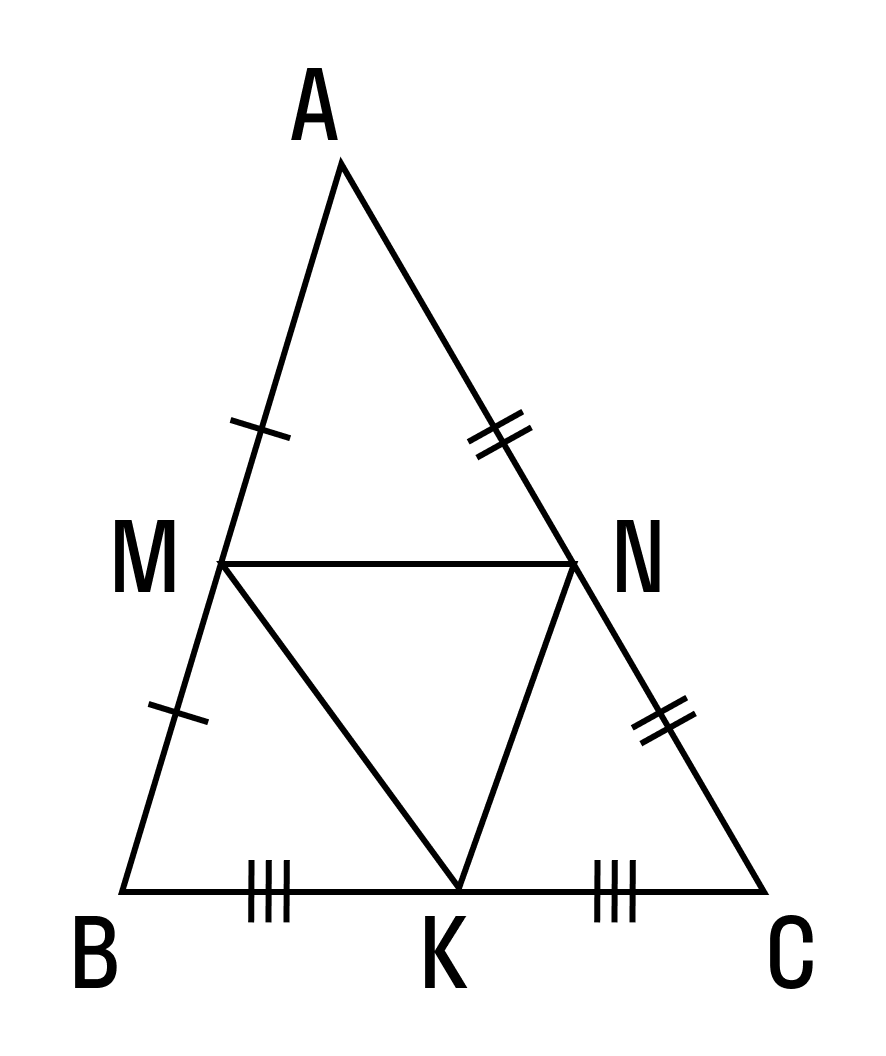
Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

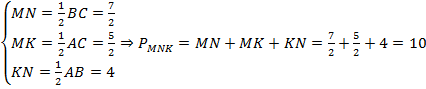
Ответ: периметр треугольника ΔMNK равен 10.

Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

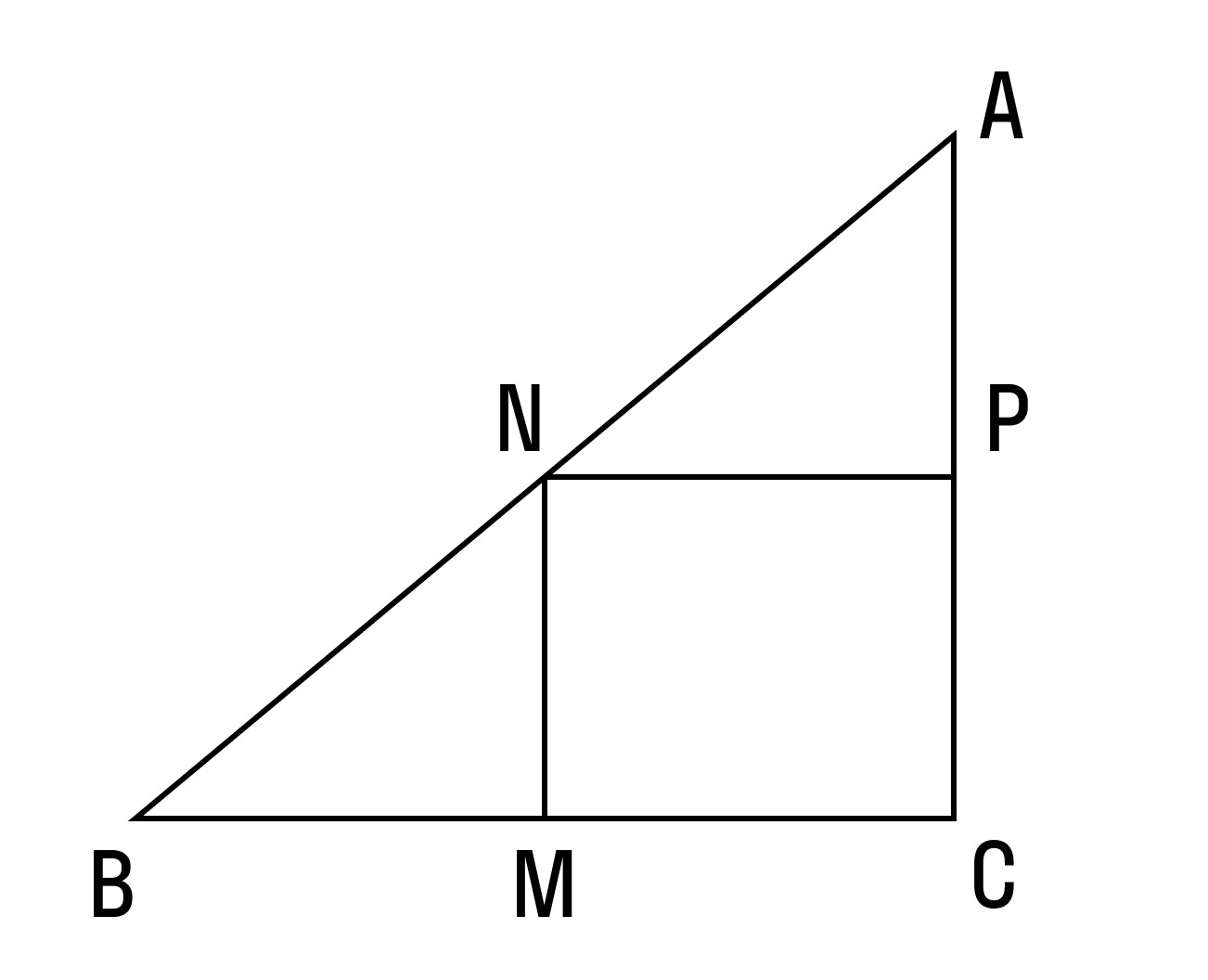
Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:

Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:

Значит, AC = 2MN = 2 × 3 = 6.

Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:

Значит, BC = 2NP = 2 × 4 = 8.

Тогда найдем площадь большого треугольника, используя формулу, указанную выше:

S = ½ × 6 × 8 = ½ × 48 = 24.

Ответ: площадь большого прямоугольного треугольника равна 24.

Решение. Пусть ABCD — таблица, а ее средняя линия, lm — определенное сечение (рис. 7). Поскольку AE = EB, по теории Талиса выполняется следующее равенство: ln= nm, что и требовалось доказать.

Понятие треугольника

Треугольники — это геометрические фигуры, возникающие из трех отрезков. Они соединены с тремя точками, которые не лежат на прямой линии. Отрезки называются сторонами, а точки — вершинами.

• Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
• Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
• Тупоугольный. Один угол тупой, два других — острые.

Треугольник является равнобедренным, если две его стороны равны. Эти стороны называются боковыми сторонами, а третья сторона называется основанием.

Треугольник, у которого все стороны равны, называется равносторонним или прямоугольным.

Треугольник называется прямоугольным, если он имеет прямой угол, т.е. угол, равный 90°. Сторона прямоугольного треугольника, противоположная прямому углу, является подчиненной; две другие стороны — катеты.

Прямоугольный (равносторонний или эквивалентный) треугольник — это прямоугольный многоугольник, у которого все стороны равны и все углы также равны 60°. В равносторонних треугольниках высота является одновременно биссектрисой и медианой.

Свойство треугольника:.

• В треугольнике против большего угла лежит большая сторона — и наоборот.
• Сумма углов треугольника равна 180 градусов.
• Все углы равностороннего треугольника равны 60 градусам.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Нужно быстро систематизировать свои знания перед экзаменом? Запишитесь на урок математики Use Maths на SkySmart!

Понятие средней линии треугольника

Определение средней линии треугольника подходит для каждого типа этой фигуры.

Средняя линия треугольника — это часть треугольника, которая соединяет центры двух сторон. Для каждого треугольника можно разработать три средние линии.

Основание — это сторона с параллельными средними линиями.

Как найти средние линии треугольника — мы объясним далее, но сначала давайте разберемся со всеми определениями немного подробнее.

Понятие средней линии прямоугольного треугольника

Математики говорят: в каждом треугольнике можно провести три средние линии. В прямоугольном треугольнике этот отрезок равен половине основания. Это тип средней линии для прямоугольных треугольников.

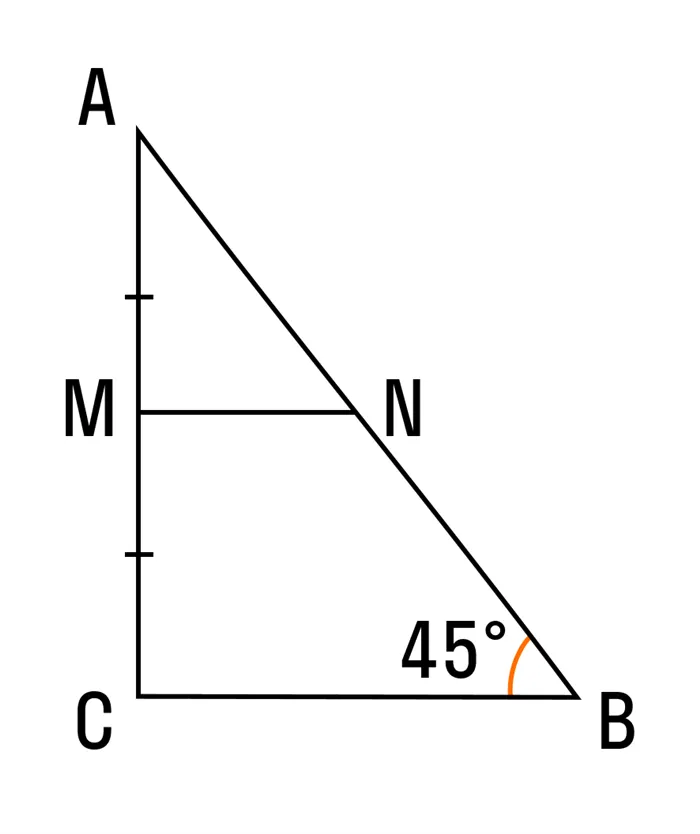
Прямые углы помогают применять другие точки равенства и подобия. Геометрическое тождество можно использовать для углов прямоугольного треугольника без дополнительной структуры, а по теореме Пифагора можно найти любую сторону.

В прямоугольном треугольнике две средние линии перпендикулярны перпендикуляру, а третья равна медиане, призванной быть подчиненной. Средние линии кислотных и неправильных треугольников не обладают аналогичными свойствами.

Выделяя срединные линии, мы говорили о вторичных свойствах отрезков. Мы привели свойства центральной линии и рассказали об особенностях формулировки этих свойств. Мы обсудили, как типы проявляются в длине центральной линии треугольника и как средняя линия делит треугольник. Все эти свойства используются при разрешении треугольника.

Видео

Математики говорят: в каждом треугольнике можно провести три средние линии. В прямоугольном треугольнике этот отрезок равен половине основания. Это тип средней линии для прямоугольных треугольников.

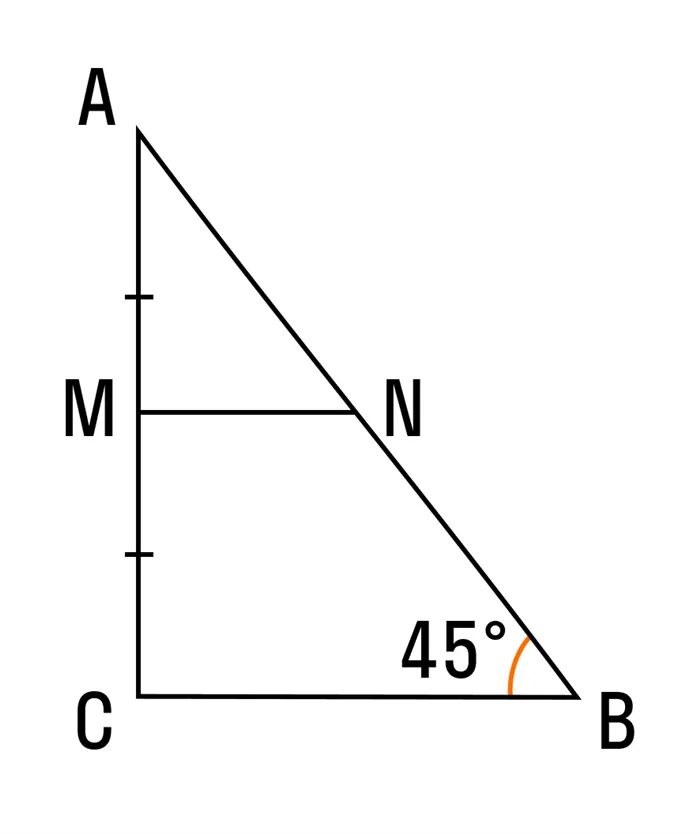
Прямые углы помогают применять другие точки равенства и подобия. Геометрическое тождество можно использовать для углов прямоугольного треугольника без дополнительной структуры, а по теореме Пифагора можно найти любую сторону.

В прямоугольном треугольнике две средние линии перпендикулярны перпендикуляру, а третья равна медиане, призванной быть подчиненной. Средние линии кислотных и неправильных треугольников не обладают аналогичными свойствами.

Средняя линия прямоугольного треугольника делит его на четыре прямоугольных треугольника.

Средняя линия

Чтобы понять, как найти центр треугольника, можно воспользоваться простой линейкой. Для этого выделите две любые стороны фигуры. Затем отметьте каждую точку, равноудаленную от каждой из вершин, примыкающих к этой стороне. Чтобы спроектировать центральную часть, эти две точки необходимо соединить. Их названия интуитивно понятны всем, поскольку они соединяют носителей информации с обеих сторон.

Важные свойства

Этот компонент имеет три основных свойства Предположим, у нас есть произвольный треугольник типа ABC, с P и Q в серединах AB и AC соответственно. Учитывая эту запись, PQ является средней линией ABC. Применяются следующие геометрические свойства.

1. Полученный треугольник APQ является подобным исходной фигуре ABC. Доказать это утверждение несложно, если обратить внимание на два факта: во-первых, угол A у обеих фигур является общим, во-вторых, отношение AB/AP равно величине AC/AQ и составляет 2 согласно выполненным геометрическим построениям. Таким образом, выполняется один из признаков подобия.
2. Длина средней линии PQ оказывается в два раза меньше, чем сторона BC. Кроме того, оба отрезка параллельны друг другу. Утверждение о равенстве PQ = ½*BC следует из факта подобия треугольников APQ и ABC, коэффициент которых составляет 2. Это равенство также можно доказать, если воспользоваться координатным методом.
3. Треугольник APQ имеет в 4 раза меньшую площадь, чем исходная фигура ABC.

Пункт №3 списка применим к любому треугольнику. Для доказательства используйте формулу Герона. В соответствии с этим, площадь этой фигуры можно рассчитать следующим образом:.

где p = (a + b + c)/2 — полуокружность диаграммы. Пусть α, β и γ — длины его сторон. Символизируйте стороны ABC таким же образом. Тогда длины отрезка APQ равны a / 2, b / 2 и c / 2. Полупериметр APQ равен p1 = (a + b + c)/4 = ½*p. Подставив все известные величины в формулу Герона, получим площадь S1.

Другими словами, площадь треугольника APQ составляет одну четверть от данной величины ABC.

Решение задачи

PQ — середина треугольника ABC, граничные точки P и Q которого лежат в точках AB и AC соответственно. Используя метод координат, докажите, что эта линия равна половине длины стороны BC.

Прежде чем найти решение этой проблемы, необходимо определить координаты вершин исходной фигуры. Они следующие.

Точка P делит ребро AB ровно пополам, поэтому для нахождения ее координат необходимо выполнить следующее вычисление

Координаты точки Q вычисляются аналогичным образом.

Вспоминая формулу длины вектора, когда известны координаты начала и конца, можно выполнить следующий расчет для средней линии PQ

PQ = ((x1 + x3)/ 2-(x1 + x2)/ 2)^ 2 + ((y1 + y3)/ 2-(y1 + y2)/ 2)^ 2)^ 2)^ 0,5 =½*((x3-x2)^ 2 + (y3-y2)^ 2)^ 0,5.

Тогда длина стороны BC становится равной

Из цитаты этих двух уравнений следует, что уравнение, которое необходимо доказать, следующее

Поскольку в доказательстве использовались произвольные координаты вершин треугольника, полученные выводы являются общими и универсальными для каждого типа рассматриваемой фигуры.

Формула для расчета

Центральная линия треугольника параллельна основанию и равна его половине.

ЭВИДЕНЦИЯ.

Рассмотрим dž (dž треугольник BA_1C_1 ) и dž (dž треугольник BAC ).

Мы видим, что треугольники похожи по двум соответствующим сторонам и углу между ними.

Следовательно, ἀ (ἀ угол BA_1C_1 = ἀ угол BAC ) является соответствующим элементом подобного треугольника. Поэтому, согласно принципу параллелизма (A_1C_1 параллельно AC ).

Подобие также показывает, что ǁ(ǁ frac = frac12 )

Это уравнение работает для любого треугольника, включая изоклетки, изоклетки и правильные треугольники.

Проведите центральные линии см, см и см на заданном треугольнике. Найдите периметр треугольника. Решение Средняя линия равна половине параллельных сторон, поэтому можно найти длины всех сторон треугольника. см см см см см см см Теперь можно найти периметр треугольника как сумму всех длин. Его стороны: см см Ответ: см см см.

Средние линии четырехугольника. Теорема Вариньона

Значение. Средняя линия четырехугольника соединяет середины непересекающихся сторон четырехугольника.

Поскольку каждый четырехугольник имеет две пары непересекающихся сторон, каждый четырехугольник имеет две средние линии (рис. 10).

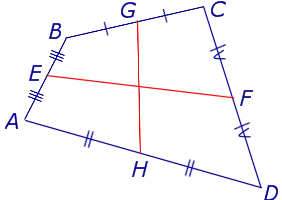
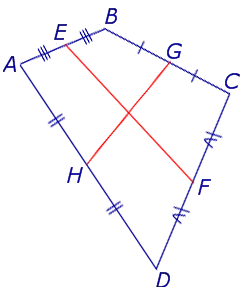
Средние линии на рисунке 10 — это отрезки EF и GH.

Примечание 1: Приведенное выше определение средней линии применимо не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис. 11). Пространственный четырехугольник» — это замкнутая четырехсвязная линия, не имеющая самопересечений и не находящаяся на одном уровне.

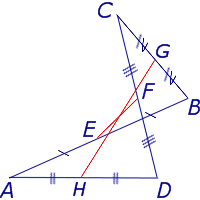
На рис. 11 показан «пространственный четырехугольник» ABCD. Его середины — отрезки EF и GH.

Замечание 2. Хотя таблица является четырехугольником, принято называть среднюю линию банкира единственной частью, соединяющей середины ее сторон.

Замечание 3. В этом разделе книги невыпуклые четырехугольники и четырехугольники с независимыми сечениями не рассматриваются.

Теорема Валлиньона. Середины сторон любого плоского или «пространственного» четырехугольника являются вершинами прямоугольника.

Доказательство Рассмотрим плоский четырехугольник ABCD, изображенный на рисунке 12. Точки E, G, F и H являются средними точками, а отрезок AC — диагональю четырехугольника.

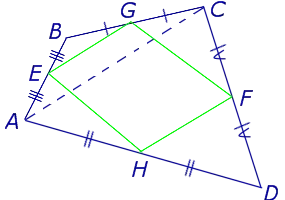
Отрезок EG — перпендикулярная биссектриса треугольника ABC, поэтому отрезок EG параллелен и равен половине диагонали AC. Отрезок FH — перпендикулярная биссектриса треугольника CDA, поэтому отрезок FH параллелен диагонали AC и составляет ее половину. Таким образом, в четырехугольнике EGFH противоположные стороны EG и FH одинаково параллельны. Знак прямоугольника указывает на то, что четырехугольник EGFH является прямоугольным, что и требуется доказать.

Замечание 4. Для «пространственного четырехугольника» ABCD доказательство остается прежним (рис. 13).

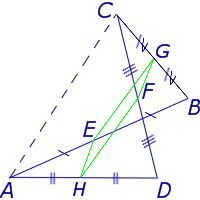
Пункт 5. Средние линии любого четырехугольника пересекаются и делятся пополам в точке пересечения (рис. 14).

Средние линии тетраэдра

Тетраэдры представляют собой произвольные треугольники (рис. 17).

Каждый тетраэдр имеет четыре вершины, четыре поверхности и шесть ребер, разделенных на три пары непересекающихся ребер. На рисунке 17 каждая пара непересекающихся ребер показана другим цветом. Все две непересекающиеся грани тетраэдра располагаются на пересекающихся линиях пересечения.

Значение. Центральная линия тетраэдра (с обеих сторон) — это часть, соединяющая середины двух непересекающихся граней тетраэдра.

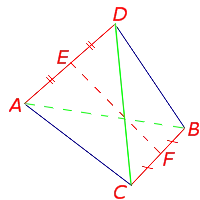
Каждый тетраэдр имеет три центральные линии. Часть EF на рис. 18 является одной из центральных линий тетраэдра.

Утверждение 7. Все центральные линии тетраэдра пересекаются в одной точке и делятся посередине этой точкой.

ДОКАЗАТЕЛЬСТВА Выберите среднюю линию тетраэдра. Например, EF и докажите, что остальные средние линии тетраэдра проходят через центр отрезка EF. Для этого рассмотрим, например, медиану GH, соединяющую средние точки AC и BD и соединяющую точки E, H, F и G с отрезком (рис. 19).

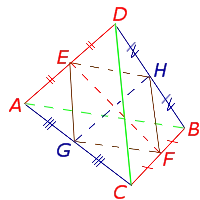
Так как отрезок EH является средней линией треугольника ADB, он является

Значение. Точка пересечения средних точек тетраэдра называется центростремительной силой тетраэдра.

Пункт 8. Рассмотрим декартову систему координат с началом в точке O и произвольный тетраэдр ABCD. Если центр этого тетраэдра обозначить буквой М (рис. 20), то векторное равенство выполняется.

Прямые углы помогают применять другие точки равенства и подобия. Геометрическое тождество можно использовать для углов прямоугольного треугольника без дополнительной структуры, а по теореме Пифагора можно найти любую сторону.

Что такое средняя линия треугольника

В данной публикации рассматриваются определения, качества и признаки треугольников. Вы также получите примеры решений для лучшего понимания теоретического материала.

Часть треугольника, соединяющая центры двух сторон треугольника, называется средней линией.

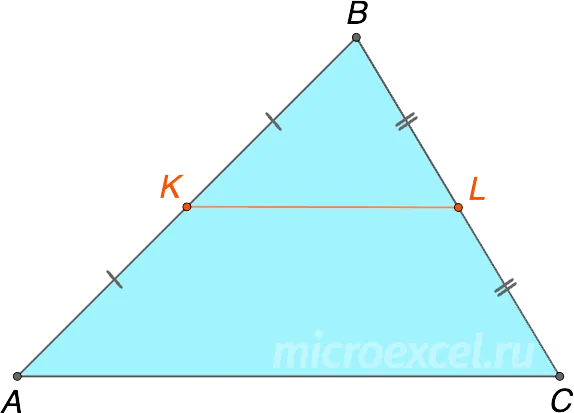
• KL – средняя линия треугольника ABC
• K – середина стороны AB: AK = KB
• L – середина стороны BC: BL = LC

Свойства средней линии треугольника

Свойство 1

Средняя линия треугольника параллельна одной из его сторон (не пересекается) и вдвое меньше этой стороны.

Свойство 2

Средняя линия треугольника разрезает аналогичный треугольник (1:2), который в четыре раза меньше исходного треугольника.

• △KBL ∼ △ABC (подобие по пропорциональности всех сторон)
• Стороны △KBL в два раза меньше соответствующих сторон △ABC: AB = 2KB, BC = 2BL, AC = 2KL .
• S_abc. =4⋅s_△KBL

Свойство 3

Для каждого треугольника можно разработать три средние линии.

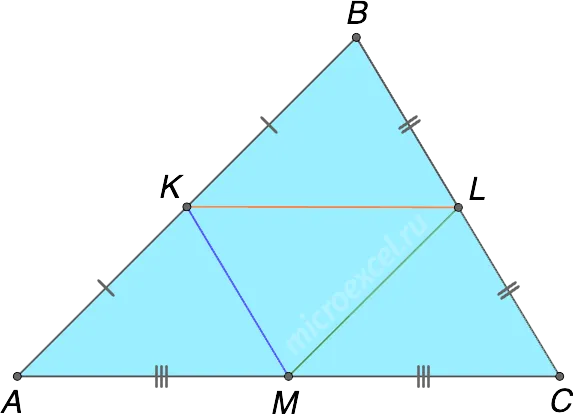
KL, KM и ML — средние линии треугольника ABC.

Свойство 4

Три центральные линии треугольника делят его на четыре треугольника равной площади.

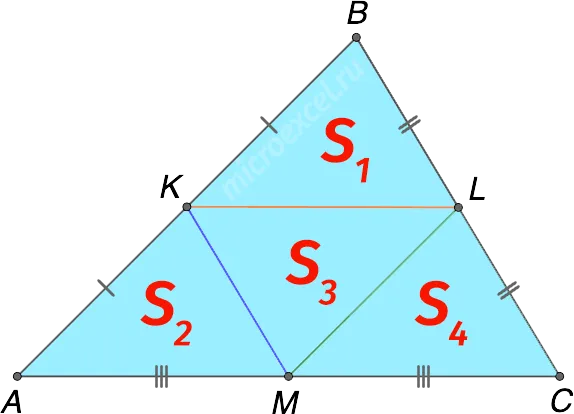
Признак средней линии треугольника

Отрезок, проходящий через середину одной стороны треугольника, пересекает вторую и параллелен третьей — это центральный класс треугольника.

Дан треугольник, стороны которого равны 6 см и 8 см. Найдите длину средней линии, соединяющей эти стороны.

Треугольник с заданными сторонами является прямоугольным, а известные величины — длинами перпендикуляров. Средняя линия, соединяющая катетеры, параллельна нижней и равна половине ее длины.

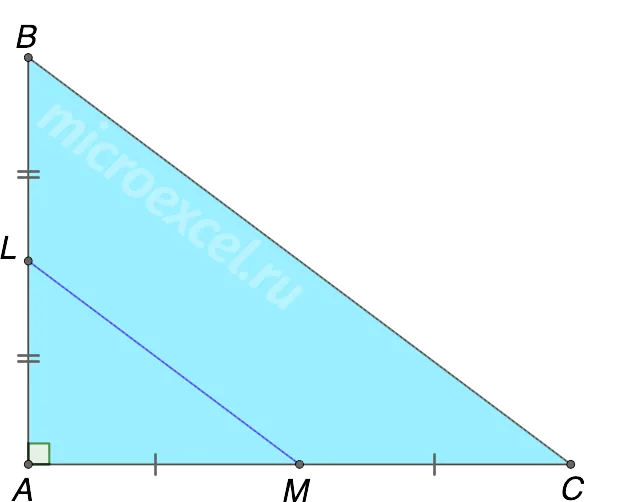
Для нахождения подчиненных можно использовать теорему Пифагора.

BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100. bc = 10.

Поэтому центральная линия lm = 1 /₂ de bc = 1 /₂ ⋅ 10 = 5.

Теорема Валлиньона. Середины сторон любого плоского или «пространственного» четырехугольника являются вершинами прямоугольника.

Длина средней линии треугольника

Средняя линия треугольника — интересный классификационный отрезок, так как он обладает рядом свойств, позволяющих находить простые решения, казалось бы, сложных задач. Давайте рассмотрим основные свойства средней линии и поговорим о том, как длину этого отрезка можно найти в треугольнике.

Треугольник и его характеризующие отрезки

Треугольник — это фигура, состоящая из трех сторон и трех углов. В зависимости от величины углов треугольник делится на

Основные характеристики треугольника следующие

• Медиана – отрезок, соединяющий вершину с серединой противоположной стороны.
• Биссектриса – отрезок, проведенный из вершины угла к противоположной стороне и делящий угол пополам
• Высота – перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону.

Рисунок 2.Высота, межстрочный и биссектрисальный треугольники

За каждый раздел характеристики начисляется балл. Когда три центральных пересечения класса, бисквит и возвышение, соединяются, возникает золотое пересечение треугольников.

Однако существует несколько дополнительных классифицированных разделов.

• Серединный перпендикуляр – перпендикуляр восстановленный из середины стороны. Как правило серединный перпендикуляр продлевается до пересечения с другой стороной.
• Средняя линия – отрезок, соединяющий середины смежных сторон.
• Радиус вписанной окружности. Вписанная окружность – окружность, которая касается каждой из сторон треугольника. Центр вписанной окружности – точка пересечения биссектрис треугольника
• Радиус описанной окружности. Описанная окружность – окружность, содержащая в себе все вершины треугольника. Центр описанной окружности – точка пересечения серединных перпендикуляров треугольника.

Смежные стороны треугольника — это стороны с общей вершиной. В геометрии существует понятие противоположных сторон, то есть сторон, противоположных друг другу и не имеющих общей вершины. Однако это понятие не применимо к треугольникам — все стороны треугольника смежные.

Свойства средней линии

Средняя линия не обладает многими свойствами, все из которых важны для решения задачи. Дело в том, что лишь немногие задачи связаны с нахождением длины средней линии, некоторые из них, несмотря на свою простоту, могут привести учащихся в апатию.

Давайте теперь приведем и обсудим все свойства средней линии треугольника.

• Средняя линия треугольника равна половине основания. Вообще правильнее сказать не половине основания, а половине противолежащей стороны. Так как сторон в треугольнике 3, а основание всего одно. Но в общем случае, основанием можно считать любую из сторон треугольника, так что подобная формулировка считается допустимой. К тому же ее проще выучить. В общем случае по этому свойству и определяется длина средней линии треугольника.
• Средняя линия параллельна основанию. С понятием основания здесь та же ситуация, что и в предыдущем свойстве.
• Средняя линия отсекает от треугольника малый подобный треугольник с коэффициентом подобия, равным 0,5
• Три средние линии делят треугольник на 4 равных треугольника, подобных большому треугольнику с коэффициентом подобия 0,5

Фактический вид длины срединной линии вытекает из второго свойства.

$ m = 1 над * a $-, где m — средняя линия, а a — сторона, противоположная средней линии.