Около окружности описана трапеция, периметр которой равен 30. Найдите длину её средней линии.
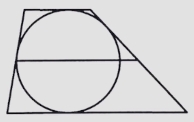
Источник: Ященко ЕГЭ 2023 (36 вар)
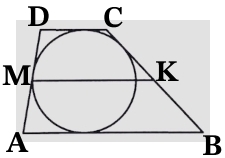
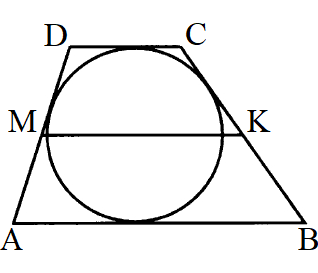
Дано:
ABCD – трапеция, описанная около окружности;
PABCD = 30;
MK – средняя линия;
Найти: MK.
Решение:
Длина средней линии трапеции равна полусумме её оснований.
MK = frac{DC + AB}{2}
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы противоположных сторон равны.
DC + AB = DA + CB
То, зная PABCD, найдём сумму оснований DC и АВ:
PABCD = DC + AB + DA + CB = DC + AB + DC + AB = 2·(DC + AB) = 30
DC + AB = frac{30}{2} = 15
Средняя линия MK равна:
MK = frac{DC + AB}{2}=frac{15}{2}=7,5
Ответ: 7,5.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.8 / 5. Количество оценок: 62
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Перейти к содержанию
На чтение 2 мин. Просмотров 456
Простая задача по геометрии из сборника типовых заданий ЕГЭ. Простая – если знать свойство четырехугольника, в который вписана окружность. А если не знать – практически нерешаемая.
Около окружности описана трапеция, периметр которой равен 30. Найдите длину ее средней линии.
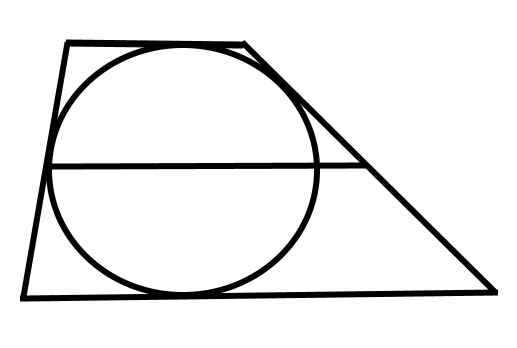
Решение: Не в каждую трапецию можно вписать окружность. Если это возможно, то стороны такой трапеции обладают следующим свойством:
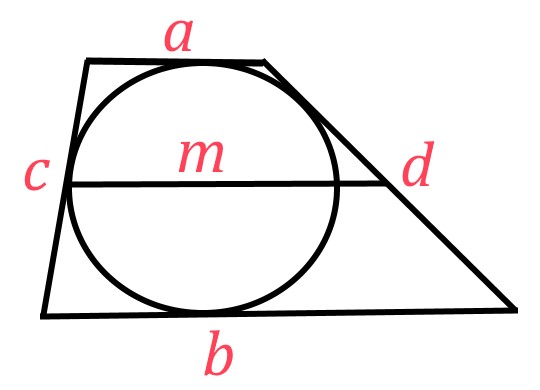
Таким образом, сумма длин сторон трапеции равна половине ее периметра. Так как ![]() , и
, и ![]() . Заменим
. Заменим ![]() на
на ![]() , получим:
, получим:
![]()
или
![]()
или ![]() .
.
Отсюда:
![]() .
.
Так как средняя линия трапеции равна половине суммы ее оснований, то находим:
![]() .
.
Ответ: 7,5
( 1 оценка, среднее 5 из 5 )
Решение №281 Около окружности описана трапеция, периметр которой равен 28. Найдите длину её средней линии.
Около окружности описана трапеция, периметр которой равен 28. Найдите длину её средней линии.

Дано:
P ABCD = 28 ;
MK – средняя линия;
Найти: MK .
Решение:
Длина средней линии трапеции равна полусумме её оснований.
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы противоположных сторон равны.
То, зная P ABCD , найдём сумму оснований DC и АВ:
P ABCD = DC + AB + DA + CB ;
P ABCD = 2•(DC + AB) = 28 ;
DC + AB = 28 / 2 = 14 ;
Средняя линия равна:
MK = (DC + AB) / 2 = 14 / 2 = 7 ;
Ответ: 7.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
Как найти периметр трапеции со вписанной окружностью
Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a — h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a — c· cos α — d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 — 2 ad· cos β
d 2 = √ a 2 + c 2 — 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab — | a ( d 2 — c 2 ) |
| a — b |
| d 2 = | √ | c 2 + ab — | a ( c 2 — d 2 ) |
| a — b |
d 1 = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab — d 2 2
d 2 = √ c 2 + d 2 + 2 ab — d 1 2
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 — | ( | ( a — b ) 2 + c 2 — d 2 | ) | 2 |
| 2 | 2( a — b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p — a )( p — b )( p — a — c )( p — a — d ) |
| | a — b | |
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
a — большее основание
Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Трапеция. Свойства трапеции
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то
Площадь
или где – средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Периметр трапеции
Периметр трапеции часто нужно определить в задачах по геометрии. Периметр трапеции определяется также как и периметр любой другой фигуры на плоскости:
Периметр плоской фигуры — есть сумма всех сторон фигуры.
Чему равен периметр равнобедренной трапеции — то же самое — сумме всех ее сторон.
Найти периметр трапеции в задачах ЕГЭ
В задачах ЕГЭ вы найдете периметр трапеции. Например,
Задача 1
Около окружности описана трапеция, периметр которой равен 60. Найдите длину ее средней линии.
Решение:
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы противолежащих сторон равны:
Где PABCD — периметр трапеции. В самом деле PABCD =AD+CB+DC+AB=2(DC+AB), а значит, DC+AB=PABCD /2
Средняя линия трапеции — это полусумма ее оснований, то есть MN=(DC+AB)/2=(PABCD /2)/2=PABCD /4 = 60/4=15 .
Ответ: 15.
Задача 2
Около окружности описана трапеция, периметр которой равен 44. Найдите длину ее средней линии.
Решение. Рассуждаем аналогично и получаем MN=(DC+AB)/2=(PABCD /2)/2=PABCD /4 = 44/4=11.
Ответ: 11.
То есть мы сами с вами вывели лайфхак для решения этой задачи:
И обратный лайфхак:
Применим наш лайфхак 1 к решению следующей задачи?
Задача 3
Около окружности описана трапеция, периметр которой равен 30. Найдите длину ее средней линии.
Ответ: 7,5.
Задача 4
Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 37, найдите радиус окружности.
Решение. Периметр трапеции равен: АD+DC+CB+AB=PABCD (1)
В трапецию можно вписать окружность, если суммы длин противоположных сторон равны. То есть, имеем: AD+CB=DC+AB (2)
С учетом (2) равенство (1) можно записать в виде: 2(АD+CB)=PABCD (3)
Теперь давайте посмотрим на вот такой рисунок:
Видно, что сторона AD=2R, где R — радиус окружности.
Тогда, AD+CB=2R+37, тогда равенство (3): 2(2R+37)=100.
Решаем уравнение, относительно R:
Ответ: 6,5
Задача 5
Из сборника ЕГЭ по математике профильный уровень 2020 год вариант 19 задание 6.
Около окружности описана трапеция, периметр которой равен 28. Найдите длину ее средней линии.
Решение: пользуясь лайфхаком, который мы вывели выше, вычисляем длину средней линии трепеции: делим периметр трапеции на 4.
Получаем 28:4=7
Ответ: 7.
Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции – параллельные стороны
- Боковые стороны – две другие стороны
- Средняя линия – отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция – трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a – h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a – c· cos α – d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 – 2 ad· cos β
d 2 = √ a 2 + c 2 – 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab – | a ( d 2 – c 2 ) |
| a – b |
| d 2 = | √ | c 2 + ab – | a ( c 2 – d 2 ) |
| a – b |
d 1 = √ h 2 + ( a – h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a – h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab – d 2 2
d 2 = √ c 2 + d 2 + 2 ab – d 1 2
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 – | ( | ( a – b ) 2 + c 2 – d 2 | ) | 2 |
| 2 | 2( a – b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p – a )( p – b )( p – a – c )( p – a – d ) |
| | a – b | |
где
| p = | a + b + c + d | – полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p – a )( p – c )( p – d 1) |
где
a – большее основание
Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/kak-nayti-perimetr-trapetsii-so-vpisannoy-okruzhnostyu
http://ru.onlinemschool.com/math/formula/trapezium/
[/spoiler]
выар ыаро
Ученик
(95),
на голосовании
10 лет назад
Дополнен 10 лет назад
У трапеции вроде основания не могут быть одинаковыми, это уже не трапеция, а фиг знает что. Если БОКОВЫЕ! стороны 13 и 15 см, а основания по 10 см – это уже четырёхугольник, т. к основания у трапеции не будут параллельны.
Дополнен 10 лет назад
Блин, я сам что-то напутал, простите.
Голосование за лучший ответ
Периметр трапеции часто нужно определить в задачах по геометрии. Периметр трапеции определяется также как и периметр любой другой фигуры на плоскости:
Периметр плоской фигуры – есть сумма всех сторон фигуры.
Периметр трапеции
Периметр трапеции – есть сумма всех сторон трапеции.
Чему равен периметр равнобедренной трапеции – то же самое – сумме всех ее сторон.
Найти периметр трапеции в задачах ЕГЭ
В задачах ЕГЭ вы найдете периметр трапеции. Например,
Задача 1
Около окружности описана трапеция, периметр которой равен 60. Найдите длину ее средней линии.
Решение:
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы противолежащих сторон равны:

АD+CD=DC+AB=PABCD /2,
Где PABCD – периметр трапеции. В самом деле PABCD =AD+CB+DC+AB=2(DC+AB), а значит, DC+AB=PABCD /2
Средняя линия трапеции – это полусумма ее оснований, то есть MN=(DC+AB)/2=(PABCD /2)/2=PABCD /4 = 60/4=15 .
Ответ: 15.
Задача 2
Около окружности описана трапеция, периметр которой равен 44. Найдите длину ее средней линии.
Решение. Рассуждаем аналогично и получаем MN=(DC+AB)/2=(PABCD /2)/2=PABCD /4 = 44/4=11.
Ответ: 11.
То есть мы сами с вами вывели лайфхак для решения этой задачи:
Лайфхак 1
Если в трапецию вписана окружность, и дан периметр трапеции, то для того чтобы найти среднюю линию трапеции, нужно периметр разделить на 4.
И обратный лайфхак:
Лайфхак 2
Если в трапецию можно вписать окружность, и дана средняя линия трапеции (l), то формула периметра трапеции P:
P=4l
Применим наш лайфхак 1 к решению следующей задачи?
Задача 3
Около окружности описана трапеция, периметр которой равен 30. Найдите длину ее средней линии.
Вычисление
Делим периметр на 4 и получаем среднюю линию трапеции: 30/4=7,5.
Ответ: 7,5.
Задача 4
Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 37, найдите радиус окружности.

Решение. Периметр трапеции равен: АD+DC+CB+AB=PABCD (1)
В трапецию можно вписать окружность, если суммы длин противоположных сторон равны. То есть, имеем: AD+CB=DC+AB (2)
С учетом (2) равенство (1) можно записать в виде: 2(АD+CB)=PABCD (3)
Теперь давайте посмотрим на вот такой рисунок:

Видно, что сторона AD=2R, где R – радиус окружности.
Тогда, AD+CB=2R+37, тогда равенство (3): 2(2R+37)=100.
Решаем уравнение, относительно R:
4R+74=100
4R=100-74
4R=26
R=26/4
R= 6,5
Ответ: 6,5
Задача 5
Из сборника ЕГЭ по математике профильный уровень 2020 год вариант 19 задание 6.
Около окружности описана трапеция, периметр которой равен 28. Найдите длину ее средней линии.
Решение: пользуясь лайфхаком, который мы вывели выше, вычисляем длину средней линии трепеции: делим периметр трапеции на 4.
Получаем 28:4=7
Ответ: 7.
