![]()
В этой статье для вас сделана очередная подборка задач с трапецией. Условия так или иначе связаны с её средней линией. Типы заданий взяты из открытого банка типовых задач. Если есть желание, то можете освежить свои теоретические знания связанные с трапецией. На блоге уже рассмотрены задачи условия которых связаны с площадью трапеции, а также с углами. Кратко о средней линии:
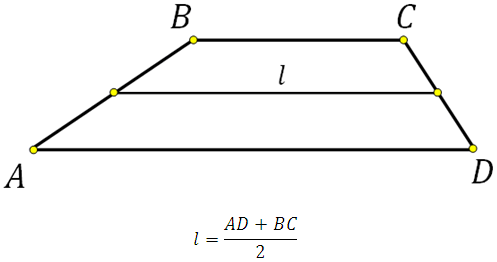
Средняя линия трапеции соединяет середины боковых сторон. Она параллельна основаниям и равна их полусумме.
Перед решением задач давайте рассмотрим теоретический пример.
Дана трапеция ABCD. Диагональ АС пересекаясь со средней линией образует точку К, диагональ BD точку L. Доказать, что отрезок KL равен половине разности оснований.
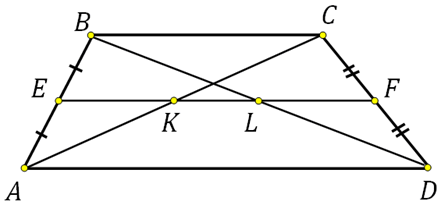
Давайте сначала отметим тот факт, что средняя линия трапеции делит пополам любой отрезок концы которого лежат на её основаниях. Этот вывод напрашивается сам собой. Представьте отрезок соединяющий две точки оснований, он разобьёт данную трапецию на две других. Получится, что отрезок параллельный основаниям трапеции и проходящий через середину боковой стороны на другой боковой стороне пройдёт через её середину.
Так же это основывается на теореме Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
То есть в данном случае К середина АС и L середина BD. Следовательно EK есть средняя линия треугольника АВС, LF есть средняя линия треугольника DCB. По свойству средней линии треугольника:
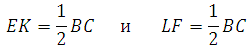
Можем теперь выразить отрезок KL через основания:
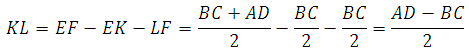
Доказано!
Данный пример приведён не просто так. В задачах для самостоятельного решения имеется именно такая задача. Только в ней не сказано, что отрезок соединяющий середины диагоналей лежит на средней линии. Рассмотрим задачи:

27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.
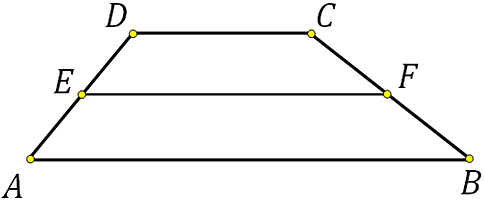
Вычисляем по формуле:
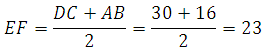
Ответ: 23

27820. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.
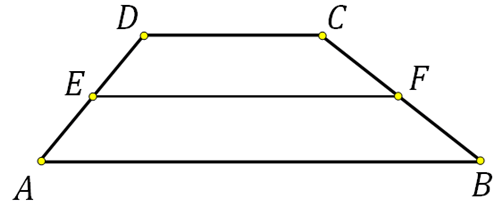
Выразим большее основание:
![]()
Таким образом:
![]()
Ответ: 38

27836. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
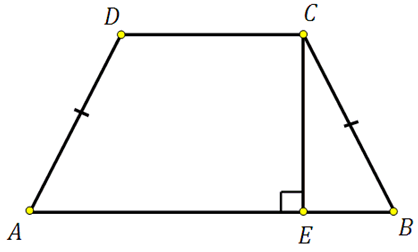
Для того, чтобы найти среднюю линию необходимо знать основания. Основание АВ найти просто: 10+4=14. Найдём DC.
Построим второй перпендикуляр DF:
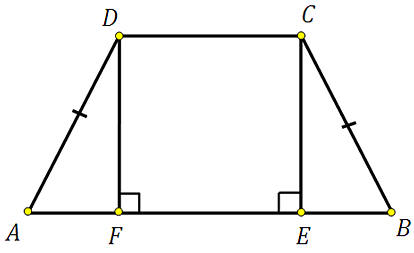
Отрезки AF, FE и EB будут равны соответственно 4, 6 и 4. Почему?
В равнобедренной трапеции перпендикуляры опущенные к большему основанию разбивают его на три отрезка. Два из них, являющиеся катетами отсекаемых прямоугольных треугольников, равны друг другу. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а в прямоугольнике противолежащие стороны равны. В данной задаче:
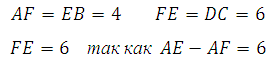
Таким образом DC=6. Вычисляем:
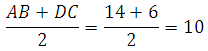
Ответ: 10

27839. Основания трапеции относятся 2:3, а средняя линия равна 5. Найдите меньшее основание.
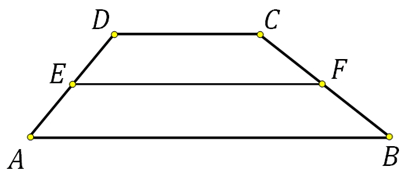
Введём коэффициент пропорциональности х. Тогда АВ=3х, DC=2х. Можем записать:
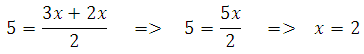
Следовательно меньшее основание равно 2∙2=4.
Ответ: 4

27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции.
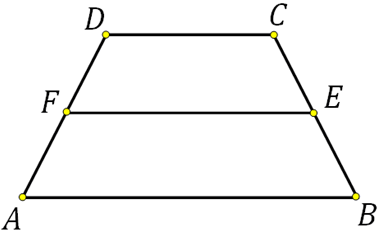
Исходя из условия можем записать:
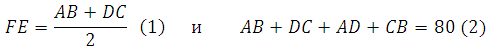
Если обозначить среднюю линию через величину х, то получится:
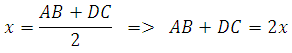
Второе уравнение уже можно записать в виде:
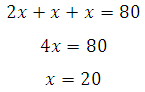
Ответ: 20

27841. Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.

Обозначим меньшее основание (DC) как х, тогда большее (AB) будет равно х+4. Можем записать
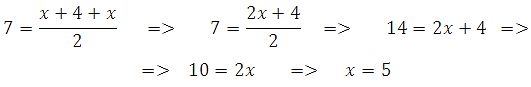
Получили, что меньшее основание рано пяти, значит большее равно 9.
Ответ: 9

27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции.
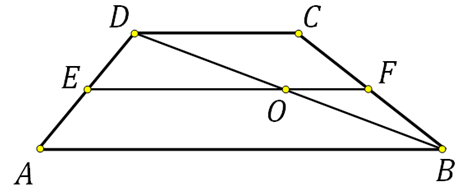
Большее основание трапеции мы без труда найдём если вычислим отрезок ЕО. Он является средней линией в треугольнике ADB, и АВ=2∙ЕО.
Что имеем? Сказано что средняя линия равна 12 и разность отрезков ЕО и ОF равна 2. Можем записать два уравнения и решить систему:
![]()
Понятно, что в данном случае подобрать пару чисел можно без вычислений, это 5 и 7. Но, всё-таки, решим систему:
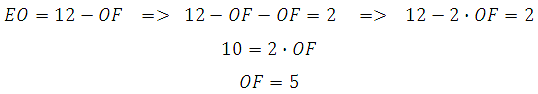
Значит ЕО=12–5=7. Таким образом, большее основание равно АВ=2∙ЕО=14.
Ответ: 14

27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
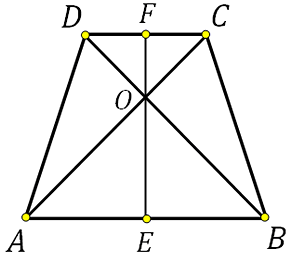
Сразу отметим, что высота проведённая через точку пересечения диагоналей в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
Казалось бы, для вычисления средней линии мы должны найти основания. Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество. Как быть?
Посмотрите на формулу средней линии трапеции. Ведь нам необязательно знать сами основания, достаточно узнать их сумму (или полусумму). Это мы сделать можем.
Так как диагонали пересекаются под прямым углом, то высотой EF образуются равнобедренные прямоугольные треугольники:
![]()
При чём:
![]()
Из выше сказанного следует, что FO=DF=FC, а OE=AE=EB. Теперь запишем чему равна высота выраженная через отрезки DF и AE:
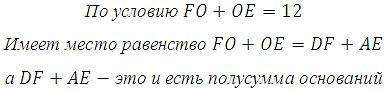
Таким образом, средняя линия равна 12.
*Вообще это задачка, как вы поняли, для устного счёта. Но, уверен, представленное подробное объяснение необходимо. А так… Если взглянуть на рисунок (при условии, что при построении соблюдён угол между диагоналями), сразу в глаза бросается равенство FO=DF=FC, а OE=AE=EB.
Ответ: 12
В составе прототипов имеется ещё типы заданий с трапециями. Построена она на листе в клетку и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть другая величина.

27848. Найдите среднюю линию трапеции ABCD, если стороны квадратных клеток равны 1.
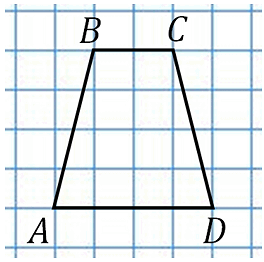
Всё просто, вычисляем основания по клеткам и используем формулу: (2+4)/2=3
Ответ: 3
Если же основания построены под углом к клеточной сетке, то есть два способа. Например!

28854.Найдите среднюю линию трапеции ABCD, если стороны квадратных клеток равны √2.
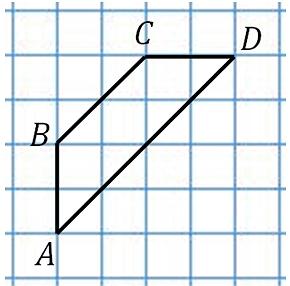
В данном случае видно, что средняя линия трапеции равна трём диагоналям клетки. Диагональ одной клетки по теореме Пифагора будет равна:
![]()
Значит средняя линия равна 2∙3=6.
Конечно, есть и другой путь решения.
Если допустить мысль, что основания трапеции могут лежать по отношению к сетке под углом не 45 градусов, а например 30, или другим, то вполне применим следующий метод (таких задач на ЕГЭ не предвидится):
Вычисляем основания используя теорему Пифагора, а далее используем формулу средней линии.
Основание AD при данных условиях это диагональ в прямоугольном треугольнике с катетами равными 4 сторонам клетки, вычисляем:
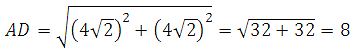
Основание BC это диагональ в прямоугольном треугольнике катетами равными 2 сторонам клетки, вычисляем:
![]()
Средняя линия будет равна (8+4)/2=6.
*То есть при данном подходе, как бы ни была построена трапеция всегда можно вычислить основания.
Ответ: 6

27853. Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны √2.

Высота трапеции равна диагонали клетки. Вычисляем по теореме Пифагора:
![]()
Ответ: 2
![]()
27821. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
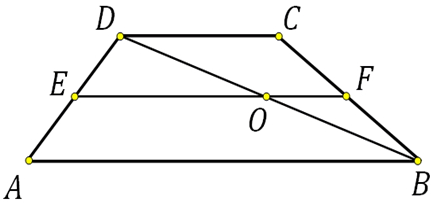
Посмотреть решение
27838.Периметр трапеции равен 50, а сумма непараллельных сторон равна 20. Найдите среднюю линию трапеции.
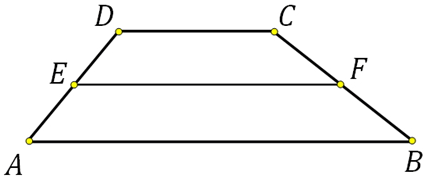
Посмотреть решение
27843. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
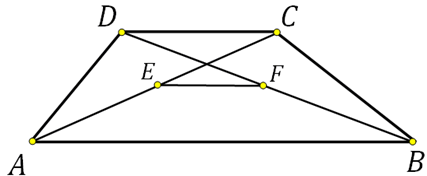
Посмотреть решение
На этом всё, успеха вам!
С уважением, Александр Крутицких.
P,S: Расскажите о сайте в социальных сетях.
В данной публикации мы рассмотрим определение, свойства и признак средней линии трапеции, а также разберем пример решения задачи для лучшего понимания изложенного материала.
- Определение средней линии трапеции
-
Свойства средней линии трапеции
- Свойство 1
-
Свойство 2
- Свойство 3
- Признак средней линии трапеции
- Вторая средняя линия
- Пример задачи
Определение средней линии трапеции
Отрезок, соединяющий середины боковых сторон трапеции, называется ее средней линией.

- LM – средняя линия трапеции ABCD
- L – середина стороны AB, т.е. AL = LB
- M – середина стороны CD, т.е. CM = MD
Свойства средней линии трапеции
Свойство 1
Средняя линия трапеции параллельна ее основаниям и равняется их полусумме.
Для рисунка выше:
![]()
Свойство 2
Средняя линия трапеции делит пополам любой отрезок, концы которого лежат на основаниях данной трапеции.

Свойство 3
Средняя линия трапеции делит ее на две другие трапеции, площади которых соотносятся следующим образом (см. первый чертеж публикации):
![]()
![]()
![]()
Признак средней линии трапеции
Если отрезок, выходящий из середины боковой стороны трапеции, пересекает ее вторую боковую сторону и, при этом, параллелен основаниям фигуры, то он является средней линией этой трапеции.
Вторая средняя линия
Иногда дополнительно выделяют вторую среднюю линию трапеции – отрезок, соединяющий середины ее оснований. При этом следует помнить, что к ней не применимы Свойства 1-3 и Признак, рассмотренные выше.

Вторая средняя линия равнобедренной трапеции одновременно является ее высотой.

Пример задачи
Средняя линия трапеции равняется 25 см, а ее высота – 7 см. Найдите площадь фигуры.
Решение
Как мы знаем, площадь трапеции равняется полусумме оснований, умноженной на высоту h: S = (a+b)/2 ⋅ h
В данном случае полусумма оснований – это и есть средняя линия. Обозначим ее буквой m. То есть m = (a+b)/2.
Таким образом, S = m ⋅ h = 25 см ⋅ 7 см = 175 см2.
Средняя линия трапеции
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Мы снова затронем тему трапеций (что это?).
И расскажем о том, что такое средняя линия этой геометрической фигуры.
Средняя линия – это…
Вообще, этот термин в геометрии весьма распространен.
Средняя линия – это отрезок, проходящий через противоположные стороны, и который делит их ровно на две одинаковых части.
Средняя линия есть практически у каждой геометрической фигуры. Например, у четырехугольников она выглядит вот так:
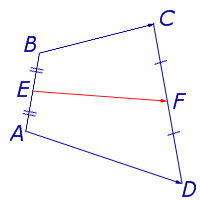
А вот так у треугольников:
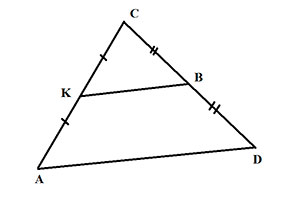
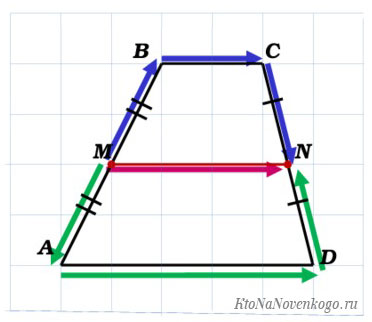
И наконец, в случае трапеции изображение средней линии будет вот таким:
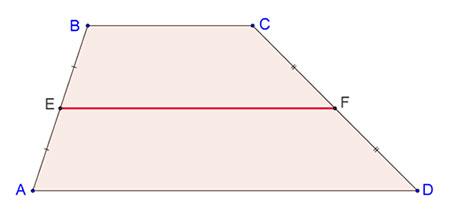
На данном рисунке показана трапеция ABCD. Если кто забыл, то у такой фигуры две противоположные грани расположены на параллельных прямых.
Они называются основаниями. А оставшиеся стороны, которые соответственно не параллельны друг другу, это боковые.
Так вот в нашем случае мы имеем среднюю линию EF, которая делит боковые стороны АВ и СD на две половинки. То есть:
AE = EB и СF = FD
Как найти среднюю линию трапеции (формула)
Есть одна главная формула, позволяющая рассчитать значение нашего отрезка.
Так, длина средней линии будет равна сумме оснований фигуры, поделенной на два. Или, другими словами, половине суммы оснований.
Возьмем для примера трапецию:
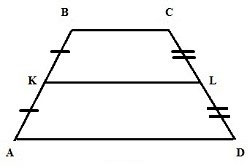
И тогда формула расчета будет выглядеть так:
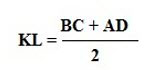
Если есть желание доказать правдивость этой формулы, нужно несколько дорисовать нашу изначальную фигуру. А именно провести линию через В и L, а также продлить сторону АD. И сделать так, чтобы эти две линии пересеклись.
В итоге получится вот что:
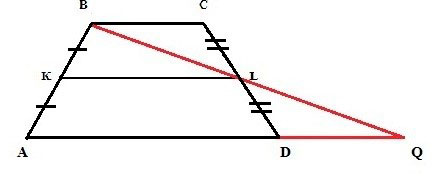
Далее нас будут интересовать оба треугольника, которые получились. Это BLC и DLQ. Необходимо доказать, что они имеют равные размеры.
И это просто, так как у них одинаковы углы:
- BLC и QLD – как вертикальные;
- BCL и QDL – как лежащие накрест при имеющихся параллельных прямых и секущей.
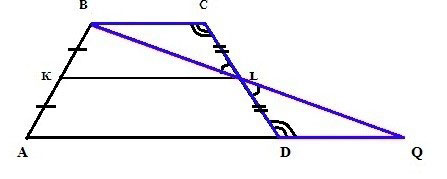
Соответственно, если равны в треугольниках углы и стороны между ними, то и сами фигуры одинаковы.
DLQ = BLC
А уже из этого следует, что ВL и LQ равны. А значит, КL является не только средней линией трапеции, но также и аналогичной линией для треугольника ABQ.
А дальше уже совсем просто, так как есть специальная формула для расчета средней линии треугольника. Она равна одной второй (половине) длины параллельной стороны:
KL = 1/2AQ
Длина стороны AQ у нас равна AD + DQ (или ВС). И таким образом мы и получаем ту самую формулу расчета средней линии трапеции:
KL = ½ AQ = ½ (AD + DQ) = ½ (AD + ВС)
Как принято говорить в таких случаях – что и требовалось доказать.
Свойства средней линии трапеции
У средней линии трапеции есть три главных свойства:
- Она параллельна основаниям трапеции;
- Она равна полусумме оснований (та самая формула, о которой мы только что рассказывали);
- Она разбивает исходную трапецию на две более маленькие по площади. Причем их площади имеют вполне конкретное соотношение друг к другу. А именно:
S1/S2 = (3BC + AD) / (BC + 3AD)
Эту формулу мы не будем доказывать. Просто поверьте, что так и есть на самом деле.
Вторая средняя линия
Внимательный читатель мог бы заметить, что мы рассказывали до этого только про одну среднюю линию. Ту, что лежит параллельно основаниям. Но ведь у этой геометрической фигуры, как и любого четырехугольника, таких отрезков должно быть два.
И действительно, у трапеции имеется вторая такая линия. И она уже делит на две равные части оба основания:
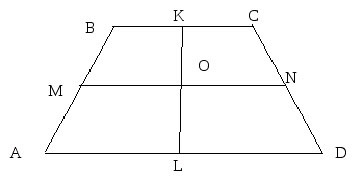
В нашем случае, это отрезок KL.
Интересно, что эту среднюю линию крайне мало изучают во время школьного обучения. И на экзаменах нет задач, с ней связанных. Хотя у нее есть несколько интересных свойств:
- Диагонали трапеции и эта средняя линия пересекаются в одной точке;
- Та прямая, частью которой эта линия является, пересекается в единой точке с теми прямыми, которые совпадают с боковыми сторонами;
- В равнобокой трапеции (у которой боковые стороны идут под одним углом) средняя линия пересекает основания под углом в 90 градусов;
- В точке, в которой пересекаются две средние линии, они делятся пополам…
Вот и все, что мы хотели рассказать о средних линиях в трапеции.
Александр Мельник
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Понятие средней линии трапеции
Для начала вспомним, какую фигуру называют трапецией.
Определение 1
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами трапеции.
Определение 2
Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем её векторным методом.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство.
Пусть нам дана трапеция $ABCD$ с основаниями $AD и BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).
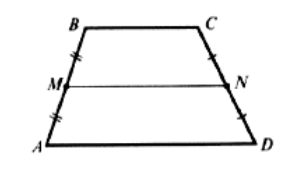
Рисунок 1. Средняя линия трапеции
Докажем, что $MN||AD и MN=frac{AD+BC}{2}$.
Рассмотрим вектор $overrightarrow{MN}$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что
С другой стороны
Сложим два последних равенства, получим
Так как $M$ и $N$ – середины боковых сторон трапеции, то будем иметь
Получаем:
Следовательно
Из этого же равенства (так как $overrightarrow{BC}$ и $overrightarrow{AD}$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.
Теорема доказана.
Примеры задач на понятие средней линии трапеции
Пример 1
Боковые стороны трапеции равны $15 см$ и $17 см$ соответственно. Периметр трапеции равен $52 см$. Найти длину средней линии трапеции.
Решение.
Обозначим среднюю линию трапеции через $n$.
Сумма боковых сторон равна
[15 см+17 см=32 см]
Следовательно, так как периметр равен $52 см$, сумма оснований равна
[52 см-32 см=20 см]
Значит, по теореме 1, получаем
[n=frac{20 см}{2}=10 см]
Ответ: $10 см$.
«Средняя линия трапеции» 👇
Пример 2
Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см. Найти диаметр этой окружности.
Решение.
Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9 см$ и $BC=5 см$. Проведем радиус $OH$ (рис. 2).
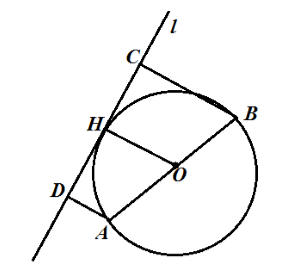
Рисунок 2.
Так как $AD$ и $BC$ – расстояния до касательной, то $ADbot l$ и $BCbot l$ и так как $OH$ — радиус, то $OHbot l$, следовательно, $OH|left|ADright||BC$. Из этого всего получаем, что $ABCD$ – трапеция, а $OH$ – ее средняя линия. По теореме 1, получаем
[OH=frac{AD+BC}{2}=frac{9 см+5 см}{2}=7 см.]
Значит
[d=2OH=2cdot 7 см=14 см.]
Ответ: $14$ см.
Пример 3
Доказать, что средняя линия трапеции проходит через середину произвольной диагонали данной трапеции.
Доказательство.
Пусть нам дана трапеция $ADCD$ со средней линией $MN$. Рассмотрим диагональ $AC$. Обозначим точкой $K$ – точку пересечения средней линии с этой диагональю (Рис. 3).
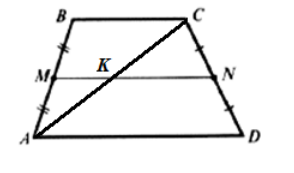
Рисунок 3.
Докажем, что $AK=KC$.
Так как $MN$ – средняя линия трапеции, то по теореме 1 $MN||BC$. Следовательно, $AM=NB$ и $MK||BC$. Тогда, по теореме о средней линии треугольника, получим что $MK$ – средняя линия треугольника $ABC$. Значит $AK=KC$.
ч. т. д.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Как найти среднюю линию трапеции
Содержание:
- Средняя линия трапеции – что это?
- Свойства
-
Как вычислить, основные формулы
- Через основания
- Через основание, высоту и углы при нижнем основании
- Через диагонали, высоту и угол между диагоналями
- Через площадь и высоту
- Примеры задач
Средняя линия трапеции – что это?
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон трапеции.
Свойства
- Параллельна обоим основаниям трапеции.
- Вычисляется как половина суммы оснований.
- Разбивает трапецию на две, площади которых соотносятся как (frac{S_1}{S_2}=frac{3,BC+AD}{BC+3,AD})
Как вычислить, основные формулы
Через основания
(m=frac{a+b}2)
Где (a) – нижнее основание, (b) – верхнее, (m) – средняя линия.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Через основание, высоту и углы при нижнем основании
(m=a-htimesfrac{ctgalpha+ctgbeta}2)
(m=b+htimesfrac{ctgalpha+ctgbeta}2)
Где (a) – нижнее основание, (b) – верхнее, (m) – средняя линия, (h) – высота, (alpha,beta) – углы при нижнем основании.
Через диагонали, высоту и угол между диагоналями
(m=frac{d_1d_2}{2h}timessinalpha=frac{d_1d_2}{2h}timessinbeta)
Где (a) – нижнее основание, (b) – верхнее, (m) – средняя линия, (h) – высота, (alpha,beta) – углы между диагоналями, (d_1), (d_2) – диагонали трапеции.
Через площадь и высоту
(m=frac{{}_S}h)
Где (h) – высота трапеции, (m) – средняя линия, (S) – площадь.
Примеры задач
Задача 1
Найдите площадь трапеции, если большее основание равно 18, меньшее 6, боковая сторона равна 7. Угол между боковой стороной и одним из оснований 150 градусов.
(angle ABC) и (angle BAH) односторонние (Rightarrow angle ABC+angle BAH;=;180^circ Rightarrow angle BAH;=;30^circ)
Рассмотрим (angle ABH)
(BH=frac12AB=3,5)
(S_{ABCD}=frac{AD+BC}2times BH=frac{6+18}2times3,5=42)
Ответ: 42
Задача 2
Основания трапеции равны 4 и 10. Чему равен больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей?
Средняя линия трапеции ABCD так же является средней линией треугольников ABC и ACD т.к. проходит через середину одной стороны и параллельна основанию. Значит, из треугольника ACD x = 5.
Ответ: 5
Задача 3
ABCD – трапеция, BC = 2, AD = 3, PQ – средняя линия, BD и AC – диагонали. Найти MN.
(PQ=frac{BC+AD}2=2,5)
Отрезок MN лежит на средней линии трапеции. Докажем: PM и NQ средние линии треугольников ABC и BCD, значит M и N середины соответственно AC и BD. Из треугольника ABC находим длину PM = 1, из треугольника BCD находим NQ = 1, следовательно MN = 2,5 – 1 – 1 = 0,5
Ответ: 0,5
