Треугольник — геометрическая фигура, составленная из трёх отрезков. Они объединены тремя точками, не
лежащие в единственной прямой. Такие отрезки обычно именуют сторонами, а заданные точки — вершинами.
Средняя линия такого многоугольника — отрезок, объединяющий средины двух сторон.
Во всяком
треугольнике можно проложить три средних линии. В прямоугольном многоугольнике такой отрезок
равняется половине основания. Средняя линия прямоугольного треугольника разделяет его на четыре
прямоугольных треугольника. Существует и признак срединного отрезка треугольника: если отрезок в
многоугольнике пролегает через средину одной из его сторон, пересекает вторую и параллелен ей, тогда
такой отрезок называется средней линией.
Выделяют свойства срединного отрезка:
- Средняя линия равняется половине длины основания и параллельна ему;
- Этот отрезок отделяет треугольник, подобный заданному с коэффициентом 0.5, а его площадь
равняется четверти площади заданной фигуры; - Три средние линии дробят заданный многоугольник на четыре других, эквивалентных друг другу.
Находящуюся по центру фигуру именуют дополнительной.
- Средняя линия треугольника через сторону
- Средняя линия равностороннего треугольника через высоту
- Средняя линия равностороннего треугольника через радиус
вписанной окружности - Средняя линия равностороннего треугольника через радиус
описанной окружности - Средняя линия треугольника через площадь и высоту
- Средняя линия равнобедренного треугольника через боковую
сторону и высоту - Средняя линия равностороннего треугольника через
площадь
Через сторону
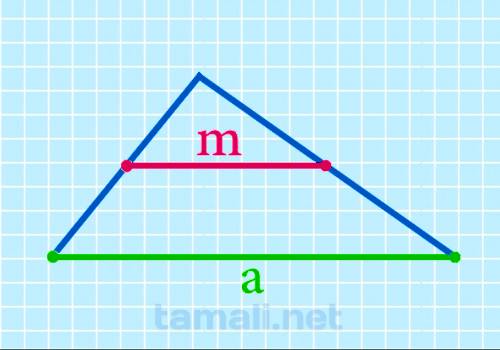
Срединный отрезок равняется половине противолежащей стороны. Следовательно, формула выглядит так:
m = a/2
где a — противолежащая сторона.
Цифр после
запятой:
Результат в:
Следовательно, если такая сторона будет равна 50, то срединный отрезок будет равен m = 50/2 = 25. Если же сторона будет равна 20, тогда срединный отрезок
будет рассчитываться так: m = 20/2 = 10.
Средняя линия равностороннего треугольника через радиус вписанной окружности
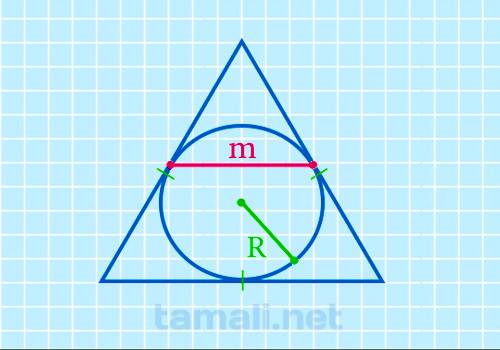
Срединный отрезок равностороннего многоугольника через радиус вписанной окружности высчитывается
так:
m = r√3
где r — радиус вписанной окружности.
Цифр после
запятой:
Результат в:
Таким образом, если радиус такой окружности равняется 5, тогда m= 5√3 ≈ 8,66. Если же радиус будет равен, допустим, 9, в таком случае
m = 9√3 ≈ 15,59.
Средняя линия треугольника через площадь и высоту
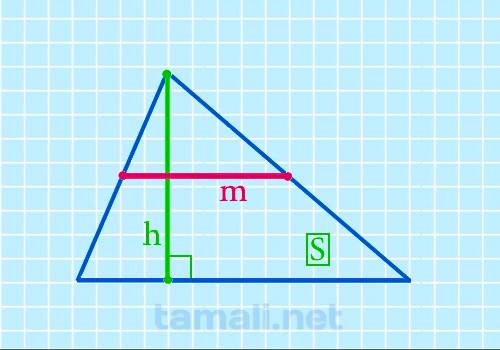
Срединный отрезок многоугольника равен частному площади и высоты, перпендикулярной этой средней
линии. Таким образом, тождество имеет такой вид:
m = S/h
где S — это площадь, а h — перпендикуляр, ортогональный срединному отрезку.
Цифр после
запятой:
Результат в:
Если площадь некоторого многоугольника будет равна 25, а перпендикуляр — 5, тогда m = 25/5 = 5. Если
же в качестве площади взять число 60, а в качестве перпендикуляра — 3, получится следующий срединный
отрезок: m = 60/3 = 20.
Средняя линия равностороннего треугольника через высоту
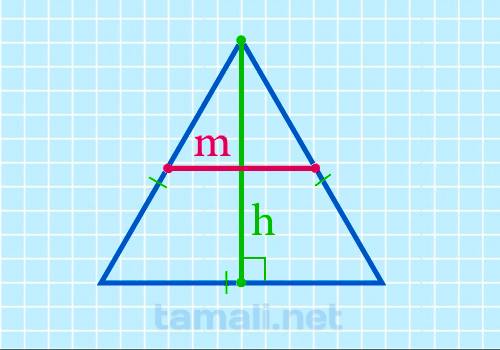
Срединный отрезок равностороннего многоугольника через перпендикуляр высчитывается следующим
образом:
m = h/√3
где h — перпендикуляр равностороннего многоугольника.
Цифр после
запятой:
Результат в:
К примеру, если перпендикуляр равностороннего многоугольника равен 5, тогда срединный отрезок будет
такой: m = 5/√3 ≈ 2,89.
Если же перпендикуляр будет равен 10, тогда
срединный отрезок будет около m = 10/√3 ≈ 5,77.
Средняя линия равнобедренного треугольника через боковую сторону и высоту
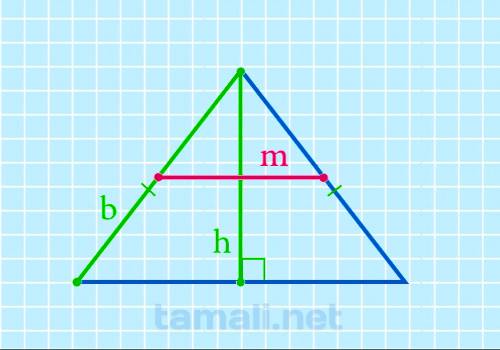
Срединный отрезок равнобедренного многоугольника через боковую сторону и высоту вычисляется следующим
образом:
m = a2 – h2
где a — боковая сторона, а h — перпендикуляр.
Цифр после
запятой:
Результат в:
Допустим, если боковая сторона многоугольника равна 5, а перпендикуляр — 3, тогда m = 25 – 9 = 16.
Если же в качестве боковой стороны взять число 8, а в качестве перпендикуляра равнобедренного
многоугольника — 2, в таком случае m = 64 – 4 = 60.
Средняя линия равностороннего треугольника через площадь
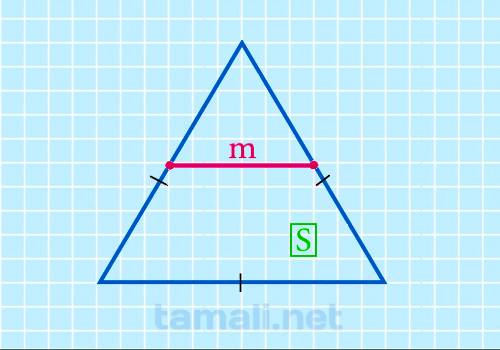
Срединный отрезок равнобедренного многоугольника через площадь находится по следующей формуле:
m = 1/4 √(√3/S)
где S — это площадь равностороннего многоугольника.
Цифр после
запятой:
Результат в:
Допустим, если площадь равностороннего многоугольника будет равна 5, тогда m = 1/4 √(√3/5) ≈ 0,15.
Если выбрать равносторонний многоугольник побольше, к примеру, с площадью 25, в таком случае m = 1/4 √(√3/25) ≈ 0,065.
Средняя линия равностороннего треугольника через радиус описанной окружности
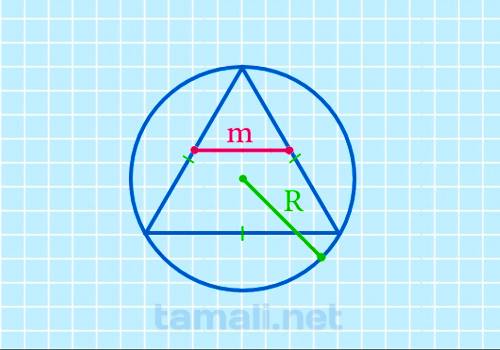
Срединный отрезок равностороннего многоугольника через радиус описанной окружности высчитывается
так:
m = R√3/2
где R — радиус описанной окружности.
Цифр после
запятой:
Результат в:
Следовательно, если радиус такой окружности будет равен 15, тогда m = 15√3/2 =12,99. Если в качестве
радиуса взять число 24, в таком случае m = 24√3/2 = 20,78.
Средняя линия фигур в планиметрии — отрезок, который объединяет средины двух сторон представленной
фигуры. Такой термин используется при описании треугольников, четырёхугольников и трапеций. В
некоторых случаях рассматривается вырожденный треугольник, три вершины которого пролегают на
единственной прямой. Треугольник считается одной из основных геометрических фигур, повсюду
применяемых в науке и технике, потому изучение его качеств велось с давних времён.
Что такое средняя линия треугольника
В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.
Определение средней линии треугольника
Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.

- KL – средняя линия треугольника ABC
- K – середина стороны AB: AK = KB
- L – середина стороны BC: BL = LC
Свойства средней линии треугольника
Свойство 1
Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.
На рисунке выше:
Свойство 2
Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.
На рисунке выше:
- △KBL ∼ △ABC (подобие по пропорциональности всех сторон)
- Стороны △KBL в два раза меньше соответствующих сторон △ABC:
AB = 2KB, BC = 2BL, AC = 2KL. - S△ABC = 4 ⋅ S△KBL
Свойство 3
В любом треугольнике можно провести три средние линии.

KL, KM и ML – средние линии треугольника ABC.
Свойство 4
Три средние линии треугольника делят его на 4 равных по площади треугольника.

Признак средней линии треугольника
Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.
Пример задачи
Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.
Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.

Мы можем найти гипотенузу, воспользовавшись теоремой Пифагора.
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
BC = 10.
Таким образом, средняя линия LM = 1 /2 ⋅ BC = 1 /2 ⋅ 10 = 5.
Как найти среднюю линию треугольника?

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие треугольника
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
- Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
- Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
- Тупоугольный. Один угол тупой, два других — острые.
Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.
Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Свойства треугольников:
- В треугольнике против большего угла лежит большая сторона — и наоборот.
- Сумма углов треугольника равна 180 градусов.
- Все углы равностороннего треугольника равны 60 градусам.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Понятие средней линии треугольника
Определение средней линии треугольника подходит для любого вида этой фигуры.
Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.
Основанием считается сторона, которой параллельна средняя линия.
Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.
Понятие средней линии прямоугольного треугольника
Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.
Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.
В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.
Свойства средней линии треугольника
Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.
Свойства:
- Средняя линия равна половине длины основания и параллельна ему.
- Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
- Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
- Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.
Теорема о средней линии треугольника
Теорема о средней линии треугольника звучит так:
Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:
Докажем теорему:
По условию нам дано, что MA = MB, NA = NC
Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.
(по второму признаку подобия треугольников).
△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.
△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.
Параллельность средней линии и соответствующего ей основания доказана.
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.
Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:
Ответ: периметр треугольника ΔMNK равен 10.
Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.
Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:
Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:
Значит, AC = 2MN = 2 × 3 = 6.
Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:
Значит, BC = 2NP = 2 × 4 = 8.
Тогда найдем площадь большого треугольника, используя формулу, указанную выше:
S = ½ × 6 × 8 = ½ × 48 = 24.
Ответ: площадь большого прямоугольного треугольника равна 24.
Средняя линия треугольника – свойства, признаки и формулы
Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.
Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.
Определение и признаки средней линии треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.
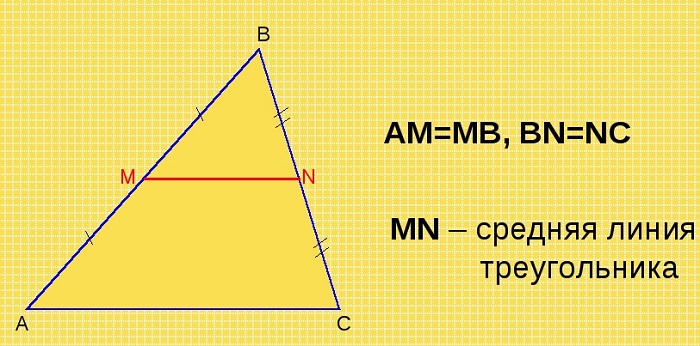
Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.
Доказательство следует из теоремы Фалеса.

Теорема о средней линии треугольника
Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.
Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.
Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.
По определению, MN – средняя линия ΔABC.
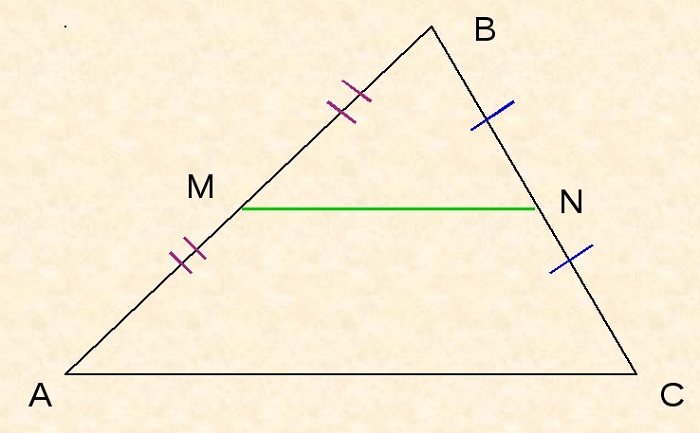
Необходимо доказать, что MN II AC, MN = ½AC.
Доказательства
Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.
Следовательно, MN II AC.
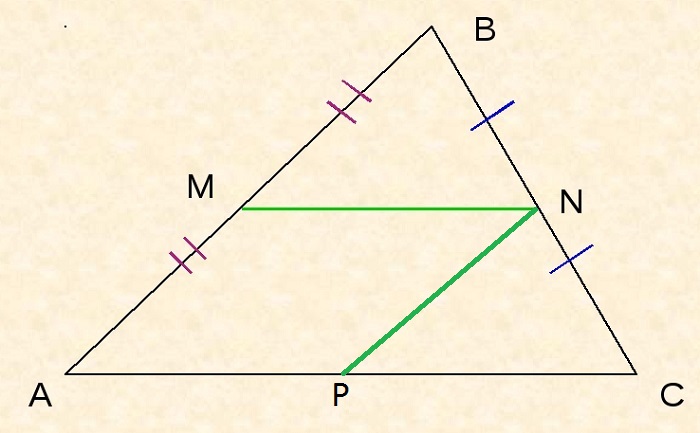
Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.
Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.
Рассматриваются треугольники MBN и ABC. В них угол B является общим,
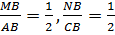
По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.
Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.
Формула MN = ½AC следует из условий
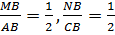
поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.
Рассматривается сумма векторов
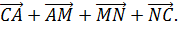
Поскольку в результате образуется замкнутая ломаная, то
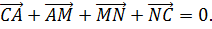
Отсюда следует, что
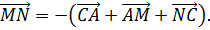
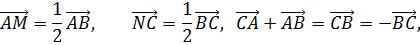
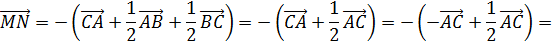
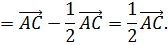
Из последнего равенства следуют условия теоремы.
Следствия из теоремы с доказательствами
Следствие №1
Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.

По определению стороны AB и BC делятся пополам, поэтому
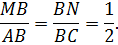
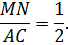
Из третьего признака подобия вытекает рассматриваемое свойство.
Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как
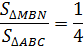
Следствие №2
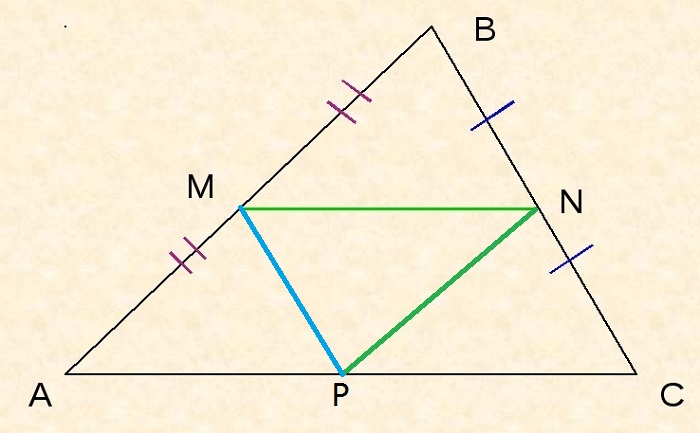
Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.
Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.
Таким образом: ∠BNM = ∠BCA = ∠MPA.
Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.
Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.
Равенство остальных пар треугольников доказывается аналогично.
По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.
Свойства средней линии треугольника
Теорема и следствия из неё составляют основные свойства средней линии треугольника.
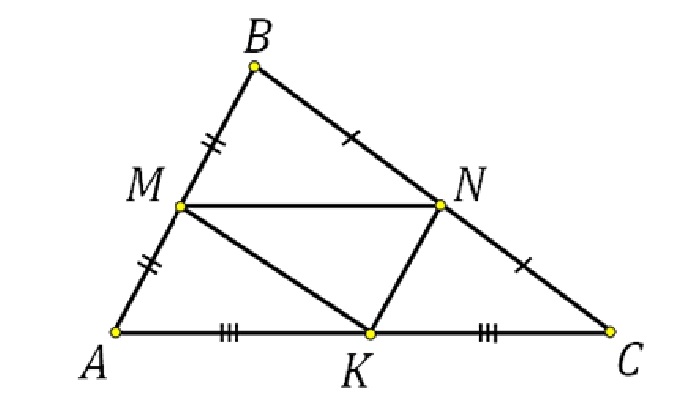
Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.
Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.
Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.
Средняя линия прямоугольного треугольника
Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.
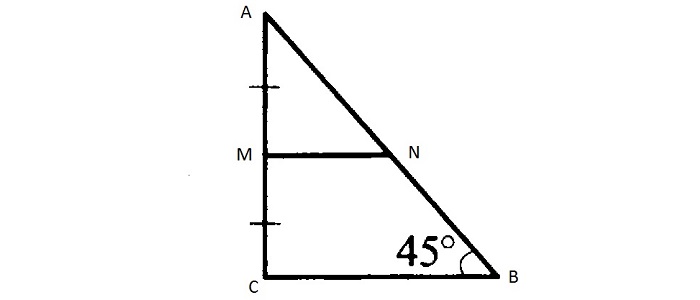
Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.
Пример решения задачи
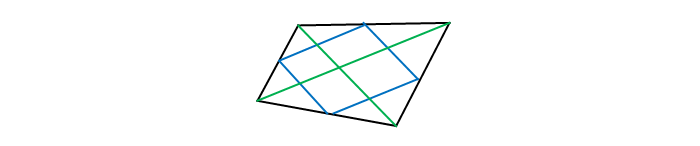
Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.
Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.
Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.
Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/kak-najti-srednyuyu-liniyu-treugolnika
http://nauka.club/matematika/geometriya/srednyaya-liniya-treugolnika.html
[/spoiler]
Содержание материала
- Средняя линия треугольника + Задачи по теме
- ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ
- Видео
- Понятие средней линии прямоугольного треугольника
- Средняя линия
- Важные свойства
- Решение задачи
- Формула для расчета
- Примеры решения задач
Средняя линия треугольника + Задачи по теме

Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника: 1. Средняя линия параллельна третьей стороне и равна ее половине. 2. Средняя линия трeугольника отсекает от него треугольник, подобный данному (с коэффициентом подобия 1/2 ). 3. Три средние линии треугольника делят его на 4 равных треугольника, подобных данному, с коэффициентом подобия 1/2.
Свойство средней линии треугольника является следствием теоремы Фалеса.
ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ
Задача № 1. Дано: ΔABC; AB = 8 см; BC = 10 см; AC = 12 см; M — середина AB; N — середина BC; L — середина AC. Найти: MN, NL, ML.

Задача № 2.

Задача № 3. ΔABC; K — середина AB; O — середина BC; P — середина AC; PABC = 52 см. Найти: PКOР

Задача № 4.

Это конспект по теме «Средняя линия треугольника + Задачи по теме». Выберите дальнейшие действия:
- Перейти к следующему конспекту:
- Вернуться к Списку конспектов по геометрии
Видео
Понятие средней линии прямоугольного треугольника
Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.
В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.
Важное свойство
Средняя линия прямоугольного треугольника делит его на четыре прямоугольных треугольника.
Средняя линия
Чтобы понять, как найти середину треугольника, можно воспользоваться обычной линейкой. Для этого необходимо выбрать произвольные две стороны фигуры. Затем отметить на каждой из них точки, отстоящие на одинаковом расстоянии от соответствующих вершин, которые ограничивают данную сторону. Полученные две точки следует соединить, чтобы начертить средний отрезок. Его название является интуитивно понятным каждому, поскольку он соединяет середины двух сторон.
Важные свойства
Существует три основных свойства, которыми обладает рассматриваемый отрезок. Пусть имеется треугольник произвольного типа ABC, в котором точки P и Q лежат на серединах сторон AB и AC соответственно. При таком обозначении отрезок PQ будет средней линией треугольника ABC. Справедливы следующие геометрические свойства:
- Полученный треугольник APQ является подобным исходной фигуре ABC. Доказать это утверждение несложно, если обратить внимание на два факта: во-первых, угол A у обеих фигур является общим, во-вторых, отношение AB/AP равно величине AC/AQ и составляет 2 согласно выполненным геометрическим построениям. Таким образом, выполняется один из признаков подобия.
- Длина средней линии PQ оказывается в два раза меньше, чем сторона BC. Кроме того, оба отрезка параллельны друг другу. Утверждение о равенстве PQ = ½*BC следует из факта подобия треугольников APQ и ABC, коэффициент которых составляет 2. Это равенство также можно доказать, если воспользоваться координатным методом.
- Треугольник APQ имеет в 4 раза меньшую площадь, чем исходная фигура ABC.
Утверждение № 3 из списка справедливо для произвольного треугольника. Для его доказательства следует воспользоваться формулой Герона. Согласно ей, площадь рассматриваемой фигуры может быть вычислена следующим образом:
S = (p*(p-a)*(p-b)*(p-c))^0,5.
Здесь p = (a+b+c)/2 — полупериметр фигуры. Буквами a, b и c обозначены длины ее сторон. Пусть таким же образом обозначаются стороны для треугольника ABC. Тогда для фигуры APQ они будут иметь длины a/2, b/2 и c/2. Полупериметр для APQ составит величину p1 = (a+b+c)/4 = ½*p. Теперь необходимо подставить все известные величины в формулу Герона, получается площадь S1:
S1 = (p1*(p1-a/2)*(p1-b/2)*(p1-c/2))^0,5 = (½*p*(½*p-a/2)*(½*p-b/2)*(½*p-c/2))^0,5 = ¼*S.
Иными словами, площадь треугольника APQ составляет четвертую часть от этой величины для ABC.
Решение задачи
В треугольнике ABC проведен средний отрезок PQ, граничные точки которой P и Q находятся на сторонах AB и AC соответственно. Необходимо с использованием метода координат доказать, что эта линия имеет в два раза меньшую длину, чем сторона BC.
Прежде чем находить решение этой задачи, следует обозначить координаты вершин исходной фигуры. Они будут следующие:
- A (x1, y1);
- B (x2, y2);
- C (x3, y3).
Поскольку точка P делит ровно пополам сторону AB, то для нахождения ее координат необходимо провести следующие вычисления:
P = ((x1+x2)/2, (y1+y2)/2).
Аналогичным образом рассчитываются координаты точки Q:
Q = ((x1+x3)/2, (y1+y3)/2).
Вспоминая формулу для длины вектора, координаты конца и начала которого известны, для средней линии PQ можно произвести следующие вычисления:
PQ = (((x1+x3)/2 — (x1+x2)/2)^2 + ((y1+y3)/2 — (y1+y2)/2)^2)^0,5 = ½*((x3-x2)^2 + (y3-y2)^2)^0,5.
В свою очередь, длина стороны BC равна:
BC = ((x3-x2)^2 + (y3-y2)^2)^0,5.
Из сопоставления этих двух равенств следует искомая формула, которую требовалось доказать:
PQ = ½*BC.
Поскольку в процессе доказательства были использованы произвольные координаты для вершин треугольника, полученный вывод является общим и универсальным для любого типа рассматриваемых фигур.
Формула для расчета
Теорема
Средняя линия треугольника параллельна основанию и равна её половине.
(A_1C_1=frac12AC)
Доказательство
Дано:
(triangle ABC)
(A_1C_1)— средняя линия
Доказать:
(A_1C_1parallel AC)
(A_1C_1=frac12AC)
Рассмотрим (triangle BA_1C_1) и (triangle BAC):
(left{begin{array}{l}angle B;-;общий\frac{BA_1}{BA}=frac{BC_1}{BC}=frac12end{array}right.)
Из этого следует, что треугольники подобны по двум пропорциональным сторонам и углу между ними.
Следовательно, (angle BA_1C_1=angle BAC) , как соответственные элементы подобных треугольников. Следовательно (A_1C_1parallel AC) по признаку параллельности.
Кроме того, из подобия следует, что (frac{A_1C_1}{AC}=frac12)
Следовательно, (A_1C_1=frac12AC)
Утверждение доказано.
Примечание
Данная формула одинаково работает для любого треугольника: равнобедренного, равностороннего (правильного).
Примеры решения задач
ПРИМЕР 1
Задание В треугольнике провели среднюю линию , параллельную. Найти площадь треугольника , если известно, что см, а высота , опущенная на сторону , равна 5 см. Решение В треугольнике (см. рис. 1) средняя линия равна половине стороны , поэтому
Найдем площадь треугольника :
Так как средняя линия отсекает треугольник , площадь которого равна одной четвёртой площади исходного треугольника , то площадь треугольника равна:
Ответ см.
ПРИМЕР 2
Задание В треугольнике провели средние линии см, см и см. Найти периметр треугольника . Решение Так как средняя линия равна половине стороны, которой она параллельна, то можем найти длины всех сторон треугольника :
см см см
Теперь можно найти периметр треугольника как сумму длин всех его сторон:
см Ответ см.
Теги
Длина средней линии треугольника – формула
4.3
Средняя оценка: 4.3
Всего получено оценок: 150.
Обновлено 11 Января, 2021
4.3
Средняя оценка: 4.3
Всего получено оценок: 150.
Обновлено 11 Января, 2021
Средняя линия треугольника интересный характеризующий отрезок, так как обладает несколькими свойствами, позволяющими найти простое решение для, казалось бы, сложной задачи. Поэтому рассмотрим основные свойства средней линии и поговорим о том, как найти длину этого отрезка в треугольнике.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Треугольник и его характеризующие отрезки
Треугольник это фигура, состоящая из трех сторон и трех углов. В зависимости от величин углов, треугольники делятся на:
- Остроугольные
- Тупоугольные
- Прямоугольные
Рис. 1. Виды треугольников
Основными характеризующими отрезками треугольника являются:
-
Медиана – отрезок, соединяющий вершину с серединой противоположной стороны.
- Биссектриса – отрезок, проведенный из вершины угла к противоположной стороне и делящий угол пополам
- Высота – перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону.
Рис. 2. Высота, медиана и биссектриса в треугольнике
Для каждого из характеризующих отрезков существует своя точка пересечения. При соединении трех точек пересечения медиан, биссектрис и высот получается золотое сечение треугольника.
Однако существует и ряд дополнительных характеризующих отрезков:
- Серединный перпендикуляр – перпендикуляр восстановленный из середины стороны. Как правило серединный перпендикуляр продлевается до пересечения с другой стороной.
- Средняя линия – отрезок, соединяющий середины смежных сторон.
- Радиус вписанной окружности
. Вписанная окружность – окружность, которая касается каждой из сторон треугольника. Центр вписанной окружности – точка пересечения биссектрис треугольника - Радиус описанной окружности.
 Описанная окружность – окружность, содержащая в себе все вершины треугольника. Центр описанной окружности – точка пересечения серединных перпендикуляров треугольника.
Описанная окружность – окружность, содержащая в себе все вершины треугольника. Центр описанной окружности – точка пересечения серединных перпендикуляров треугольника.
Смежными сторонами треугольников называют стороны, которые имеют общую вершину. В геометрии существует понятие противоположных сторон, т.е. сторон, которые лежат друг напротив друга и не имеют общих вершин. Но это понятие для треугольников не применимо – любая пара сторон в треугольнике является смежной.
Свойства средней линии
Свойств средней линии не так много, но все они имеют значение при решении задач. Дело в том, что задач на нахождение длины средней линии мало, а потому некоторые из них способны построить ученика в ступор при всей своей простоте.
Поэтому приведем и обсудим все свойства средней линии треугольника:
- Средняя линия треугольника равна половине основания. Вообще правильнее сказать не половине основания, а половине противолежащей стороны. Так как сторон в треугольнике 3, а основание всего одно.
 Но в общем случае, основанием можно считать любую из сторон треугольника, так что подобная формулировка считается допустимой. К тому же ее проще выучить. В общем случае по этому свойству и определяется длина средней линии треугольника.
Но в общем случае, основанием можно считать любую из сторон треугольника, так что подобная формулировка считается допустимой. К тому же ее проще выучить. В общем случае по этому свойству и определяется длина средней линии треугольника. - Средняя линия параллельна основанию. С понятием основания здесь та же ситуация, что и в предыдущем свойстве.
- Средняя линия отсекает от треугольника малый подобный треугольник с коэффициентом подобия, равным 0,5
- Три средние линии делят треугольник на 4 равных треугольника, подобных большому треугольнику с коэффициентом подобия 0,5
Рис. 3. Средние линии треугольника
Собственно формула длины средней линии вытекает из второго свойства:
$m=1over{2}*a$- где m – средняя линия, а – сторона противоположная средней линии.
Что мы узнали?
Мы поговорили о второстепенных характеризующих отрезках, выделив среднюю линию. Привели свойства средних линий и поговорили об особенностях формулировки этих свойств. Рассказали, как выводится формула длины средней линии треугольника и как средняя линия разбивает треугольник. Все эти свойства используются при решении треугольников.
Все эти свойства используются при решении треугольников.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.3
Средняя оценка: 4.3
Всего получено оценок: 150.
А какая ваша оценка?
Средняя ⚠️ линия треугольника: определение, признаки, теорема, формулы
Содержание:
- Свойства и признаки
- Формула для расчета
- Задачи на использование теоремы
Содержание
- Свойства и признаки
- Формула для расчета
- Задачи на использование теоремы
Средняя линия треугольника — отрезок, соединяющий середины двух его сторон.
Свойства и признаки
Признак средней линии: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок называется средней линией данного треугольника.
Свойства:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- Равна половине длины основания и параллельна ему.
- Отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
- Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным треугольником.
- Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.
Формула для расчета
Теорема
Средняя линия треугольника параллельна основанию и равна её половине.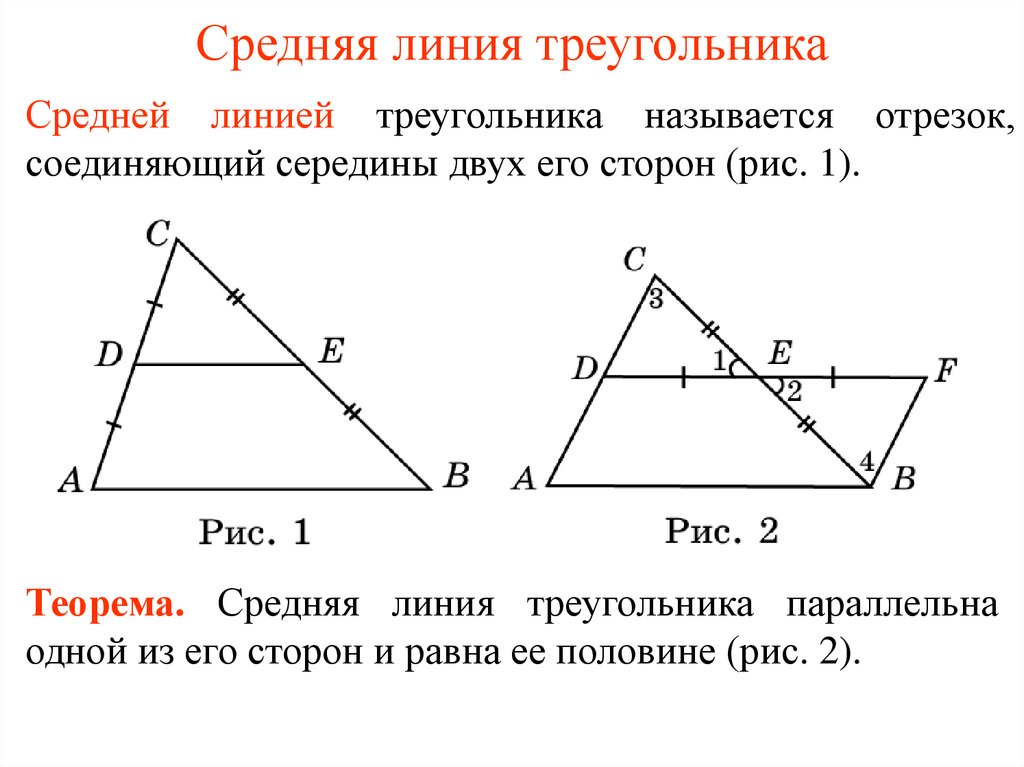
(A_1C_1=frac12AC)
Доказательство
Дано:
(triangle ABC)
(A_1C_1)- средняя линия
Доказать:
(A_1C_1parallel AC)
(A_1C_1=frac12AC)
Рассмотрим (triangle BA_1C_1) и (triangle BAC):
(left{begin{array}{l}angle B;-;общий\frac{BA_1}{BA}=frac{BC_1}{BC}=frac12end{array}right.)
Из этого следует, что треугольники подобны по двум пропорциональным сторонам и углу между ними.
Следовательно, (angle BA_1C_1=angle BAC) , как соответственные элементы подобных треугольников. Следовательно (A_1C_1parallel AC) по признаку параллельности.
Кроме того, из подобия следует, что (frac{A_1C_1}{AC}=frac12)
Следовательно, (A_1C_1=frac12AC)
Утверждение доказано.
Примечание
Данная формула одинаково работает для любого треугольника: равнобедренного, равностороннего (правильного).
Задачи на использование теоремы
Задача 1
В прямоугольном треугольнике ABC проведены средние линии: MN; NP; MP.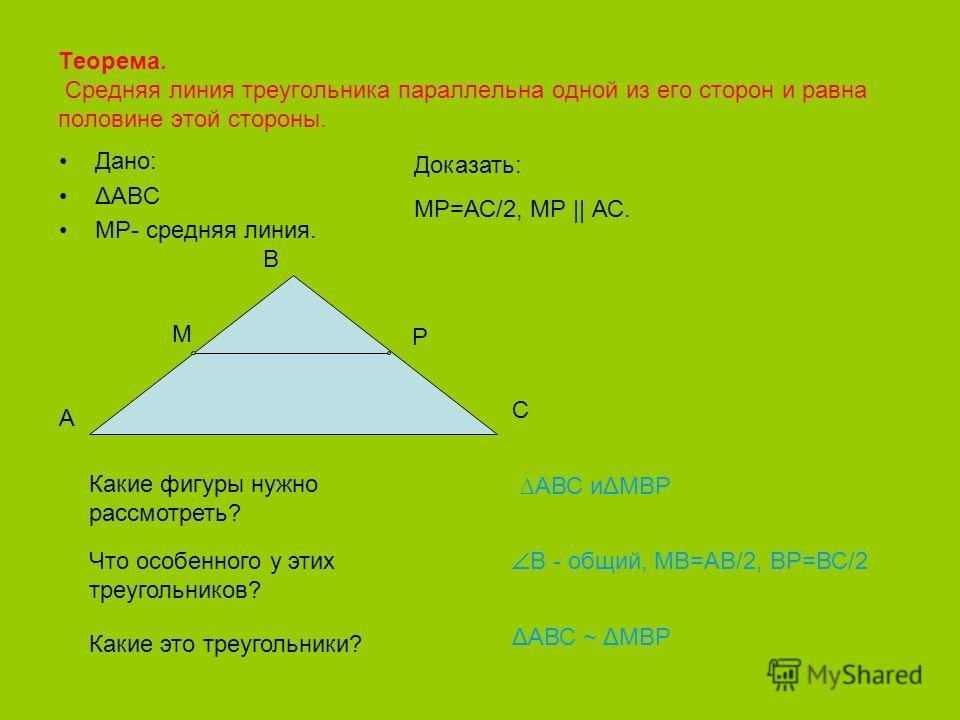 При этом MN=NP=2. Найти площадь треугольника ABC.
При этом MN=NP=2. Найти площадь треугольника ABC.
Рассмотрим прямоугольный треугольник NMP:
(S_{triangle NMP}=frac12times MNtimes NP=frac12times2times2=2)
Все маленькие треугольники равны, следовательно (S_{triangle ABC}=2times4=8)
Ответ: 8
Задача 2
Площадь треугольника ABC равна 8. MN — средняя линия. Необходимо вычислить площадь треугольника BMN.
(S_{triangle BMN}=frac14S_{triangle ABC}=frac14times8=2)
Ответ: 2
Задача 3
В треугольнике ABC точки M, N, K – середины сторон AB, BC, AC соответственно, MN=12, MK=10, KN=8. Необходимо узнать периметр треугольника ABC.
Средняя линия равна половине основания, следовательно находим:
MN = 12 ⇒ AC = 24
MK = 10 ⇒ BC = 20
KN = 8 ⇒ BA = 16
Значит, (P_{triangle ABC}=24+20+16=60)
Ответ: 60
Насколько полезной была для вас статья?
Рейтинг: 3. 67 (Голосов: 3)
67 (Голосов: 3)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Калькулятор формул для уравнений равностороннего треугольника
Изменить уравнение
Выберите, чтобы найти другое неизвестное
Разносторонний треугольник:
Стороны не имеют одинаковой длины
Нет равных углов
Уравнения разностороннего треугольника
Эти уравнения применимы к любому типу треугольника. Сокращенные
уравнений для равностороннего, прямого и равнобедренного треугольников приведены ниже.
| Периметр | |
| Semiperimeter | |
| Area | |
| Area | |
| Base | |
| Height | |
| Angle Bisector of side a | |
| Angle Bisector of сторона b | |
| Биссектриса угла стороны c | |
| Медиана стороны a | |
| Медиана стороны b0018 | |
| Median of side c | |
| Altitude of side a | |
| Altitude of side b | |
| Altitude of side c | |
| Circumscribed Circle Radius | |
| Радиус вписанной окружности |
Закон косинусов
60017 Угол
Эквиласторный треугольник:
Все три стороны имеют равную длину
. Площадь Высота Медиана Угол0018 Circumscribed Circle Radius Inscribed Circle Radius
Площадь Высота Медиана Угол0018 Circumscribed Circle Radius Inscribed Circle Radius
Right Triangle:
One angle is equal to 90 degrees
Right Triangle Equations
9 9
| Pythagorean Theorem | |||||
| Периметр | |||||
| Полупериметр | |||||
| Площадь | |||||
| Altitude of a | |||||
| Altitude of b | |||||
| Altitude of c | |||||
| Angle Bisector of a | |||||
| Angle Bisector of b | |||||
| Angle Бискектор C | |||||
| Медиана A | |||||
| Медиана B | |||||
| Медиана из C | |||||
| из C | |||||
| из C | |||||
| C | |||||
. 0018 0018 |
Inscribed Circle Radius | ||||
| Circumscribed Circle Radius |
Isosceles Triangle:
Two sides have equal length
Two angles are equal
Isosceles Triangle Equations
| Perimeter | |
| Полупериметр | |
| Площадь | |
| Высота сторон а и с | |
| Altitude of side b | |
| Median of sides a and c | |
| Median of side b | |
| Angle Bisector of sides a and c | |
| Angle Bisector стороны b | |
| Радиус описанной окружности | |
| Радиус вписанной окружности |
9017 P 9
6
= Perimeter s = Semiperimeter a = Length of side a b = Length of side b c = Length of side c h = Altitude m = Median A = Angle A B = Angle B C = Angle C t = Angle bisector R = Circumscribed Радиус окружности r = Радиус вписанной окружности
Справочник — Книги: 1) Макс А. Собель и Норберт Лернер. 1991. Предварительная математика. Прентис Холл. 4-е изд.
Собель и Норберт Лернер. 1991. Предварительная математика. Прентис Холл. 4-е изд.
теорема о средней линии Архивы — Математика и мультимедиа
19 марта 2010 г. ГБ
Учебники по программному обеспечению, Технология Web 2.0, Wingeom
Введение
Wingeom — это программное обеспечение для динамической геометрии, созданное Университетом Филипа Эксетера. Он способен к 2-мерному и 3-мерному геометрическому рисунку и построению.
Это первое руководство из серии учебных пособий Wingeom. Большая часть построения в этой серии руководств будет иметь дело с 2-мерными объектами.
Окружающая среда Wingeom
Когда вы откроете Wingeom, появится окно, показанное ниже. Вы должны щелкнуть меню Window , а затем выбрать среду, которую вы хотите отобразить. Wingeom может строить фигуры в евклидовой, гиперобличной и сферической плоскостях.
Рисунок 1 – Окно Wingeom.
Он также способен строить диаграммы Вороного и мозаики.
Использование Wingeom при изучении теоремы о средней линии
В этой конструкции мы исследуем отношения треугольника и его средней линии (или средней линии), отрезка, соединяющего середины двух его сторон, как показано на рисунке 2.
Рисунок 2 – Треугольник ABC со средней линией DE.
В приведенной ниже конструкции мы построим 3 точки A, B и C и соединим их инструментом отрезок . Нарисовав треугольник, мы получим середины AB и AC и исследуем длину и внутренние углы двух образованных треугольников.
Чтобы выполнить сборку, следуйте приведенным ниже инструкциям и ответьте на вопросы.
Этапы построения
1.) Чтобы открыть окно построения, показанное на рис. 2, щелкните меню Window , а затем выберите параметр 2-dim .
2.) Далее мы покажем панель инструментов Wingeom. На панели инструментов отображается инструмент, который мы можем использовать для рисования геометрических фигур и управления ими. Чтобы отобразить панель инструментов, щелкните меню Btns , а затем щелкните Панель инструментов .
На панели инструментов отображается инструмент, который мы можем использовать для рисования геометрических фигур и управления ими. Чтобы отобразить панель инструментов, щелкните меню Btns , а затем щелкните Панель инструментов .
Рисунок 3 – Окно Wingeom и его панель инструментов.
3.) Первый шаг в нашей конструкции, мы нарисуем вершины нашего треугольника. Для этого щелкните правой кнопкой мыши три разных места на панели для рисования. Обратите внимание, что Wingeom автоматически называет точки в алфавитном порядке.
4.) Далее, чтобы построить стороны треугольника, выберите кнопку выбора сегментов на панели инструментов, затем перетащите точку A в точку B для построения сегмента AB .
5.) Используя шаги из 4, нарисуйте сегменты AC и BC .
6. ) Далее мы проведем середину AB . Для этого щелкните меню Point , а затем щелкните Segment… , чтобы отобразить диалоговое окно новой точки.
) Далее мы проведем середину AB . Для этого щелкните меню Point , а затем щелкните Segment… , чтобы отобразить диалоговое окно новой точки.
Рисунок 4 – Диалоговое окно новой точки.
7.) В относительно сегмента , введите AB , оставьте координату 1/2 и нажмите кнопку , отметьте . Обратите внимание, что точка теперь лежит на AB . Это означает, что Wingeom должен построить сегмент на полпути A B .
8.) Чтобы создать среднюю точку AC , удалите текст в текстовом поле относительно сегмента и введите AC . Затем нажмите отметка кнопка. Обратите внимание, что точка E теперь лежит на AC . Нажмите кнопку закрытия в диалоговом окне новая точка для завершения.
9.) Вытяжной сегмент DE . Обратитесь к шагу 4.
10.) Давайте посмотрим, что произойдет, если мы перетащим вершины треугольника. Чтобы перетащить вершины треугольника, нажмите кнопку выбора перетаскивания вершин на панели инструментов, затем перетащите вершины треугольника.
11.) Теперь мы отобразим длину DE и BC . Для отображения длины DE. Для этого щелкните меню Meas для отображения диалогового окна измерений . Введите DE в текстовом поле диалогового окна измерений , а затем нажмите клавишу ENTER .
Рисунок 5 – Диалоговое окно измерений.
12.) Далее введите BC в текстовое поле и нажмите клавишу ENTER . Что можно сказать о длинах отрезков BC и DE ?
13. ) Выберите кнопку опции drag vertices на панели инструментов и перетащите вершины треугольника. Ваше наблюдение осталось прежним?
) Выберите кнопку опции drag vertices на панели инструментов и перетащите вершины треугольника. Ваше наблюдение осталось прежним?
14.) Далее попробуем проследить соотношение между внутренними углами двух треугольников – треугольник ABC и треугольник ADE . Сначала мы отобразим меру угла ABC . Для этого введите в текстовое поле диалогового окна измерений и нажмите клавишу ENTER.
15.) Отобразите размеры следующих углов, используя шаг 14: ADE , AED и ACB .
16.) Что вы заметили относительно внутренних углов треугольника 9?0483 Азбука ?
17.) Закройте диалоговое окно измерений и перетащите вершины треугольника (см. шаг 13). Ваши наблюдения остались прежними?
18.) На основании своих наблюдений сделайте предположение о соотношении треугольника ABC и его средней линии DE .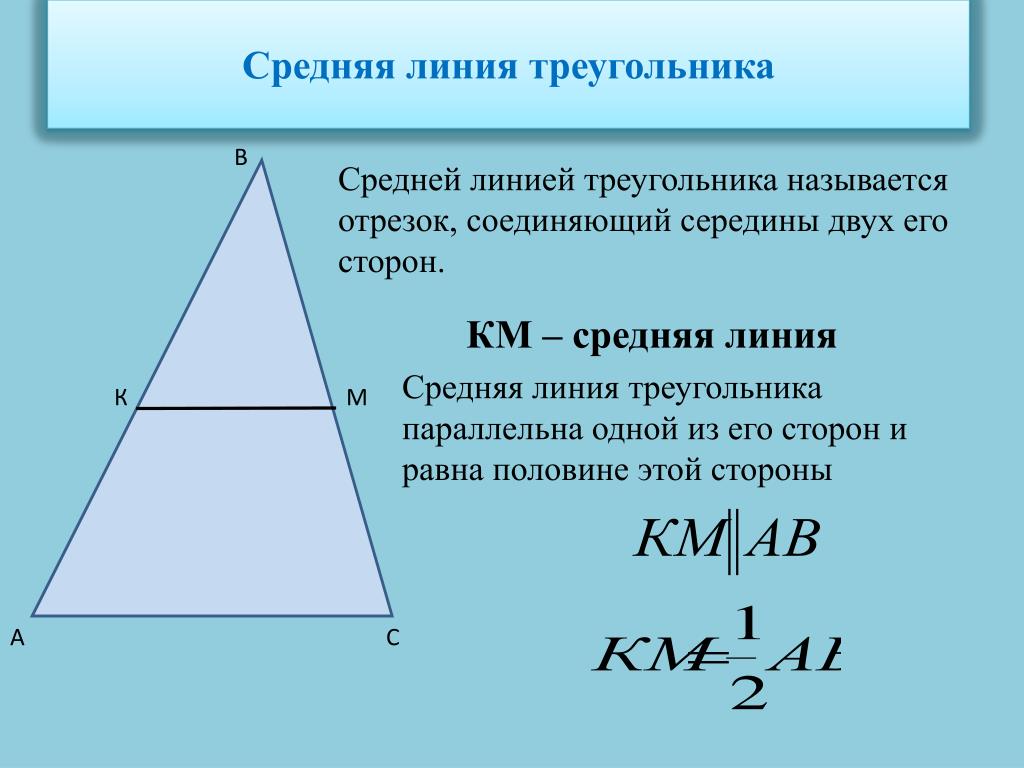
19.) Докажите свои предположения.
4 комментария
Трехмерное геометрическое рисование, программное обеспечение для динамической геометрии, бесплатное программное обеспечение для геометрии, теорема о средней линии, теорема о среднем отрезке, университет Филиппа Экстера, Рик Пэррис, учебник 9 wingeom0006
3 марта 2010 г. ГБ
Компас и линейка, геометрия для средней школы, учебные пособия по программному обеспечению
В предыдущем уроке CaR мы построили равнобедренный треугольник. В этом уроке мы собираемся изучить свойства отрезка, соединяющего середины двух его сторон. В этом уроке мы изучим следующее:
- использовать инструмент перемещения, инструмент треугольника и инструмент сегмента
- найти середину двух отрезков
- измерение углов с помощью углового инструмента
- редактировать свойства и показывать размеры углов и сегментов
Строительные ступени
1.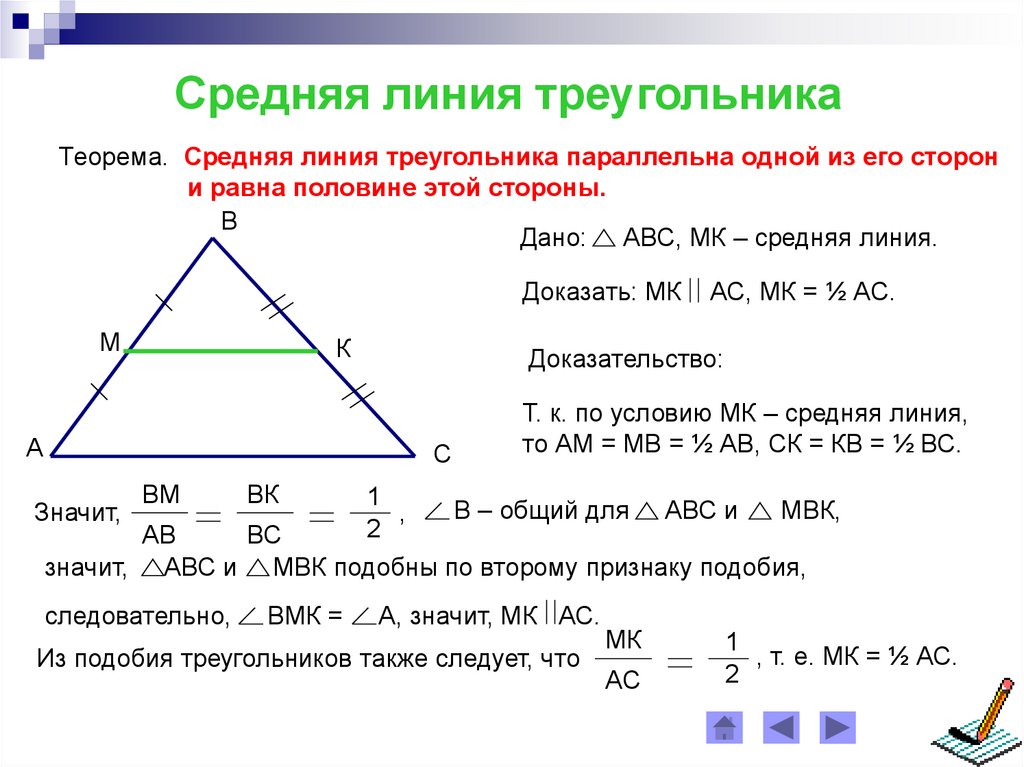 ) Открыть CaR . Нам не понадобится Оси координат , поэтому нажимайте значок Показать сетку , пока не появится значок Показать сетку , пока сетка или оси не будут отображаться. ) Открыть CaR . Нам не понадобится Оси координат , поэтому нажимайте значок Показать сетку , пока не появится значок Показать сетку , пока сетка или оси не будут отображаться. |
|
| 2.) Щелкните инструмент «Треугольник» 9.0512 и щелкните три разных точки на панели для рисования. | |
| 3.) Щелкните инструмент Move и щелкните правой кнопкой мыши одну из точек, чтобы отобразить диалоговое окно Edit Point . В текстовом поле Имя измените имя на A , затем нажмите кнопку Показать имена объектов (обведена красным эллипсом на рис. 1).
Рис. 1. Диалоговое окно «Редактировать точку». |
|
4.) Измените название двух других точек на 9.0483 В и С .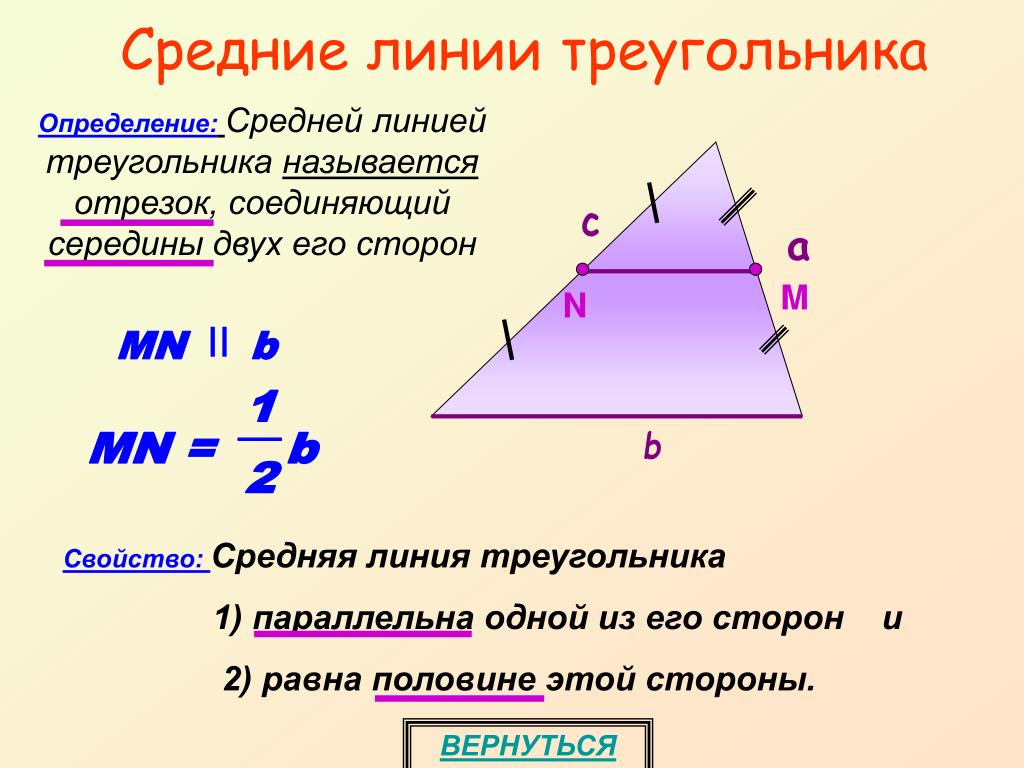 |
|
| 5.) Щелкните инструмент средней точки , щелкните точку A и щелкните точку B , чтобы получить среднюю точку AB . Теперь найдите середину BC . Переименуйте среднюю точку AB в E и среднюю точку AC в F (см. шаг 3). Ваш рисунок должен выглядеть как на рисунке 2.
Рисунок 2 – Треугольник ABC с серединами D и E. |
|
| 6.) Щелкните правой кнопкой мыши и перетащите метки, чтобы отрегулировать их положение. С помощью инструмента Перемещение переместите вершины треугольника. Что вы наблюдаете? | |
7.) Мы увидим соотношение углов и отрезков в треугольнике ABC. Сначала измерим угол.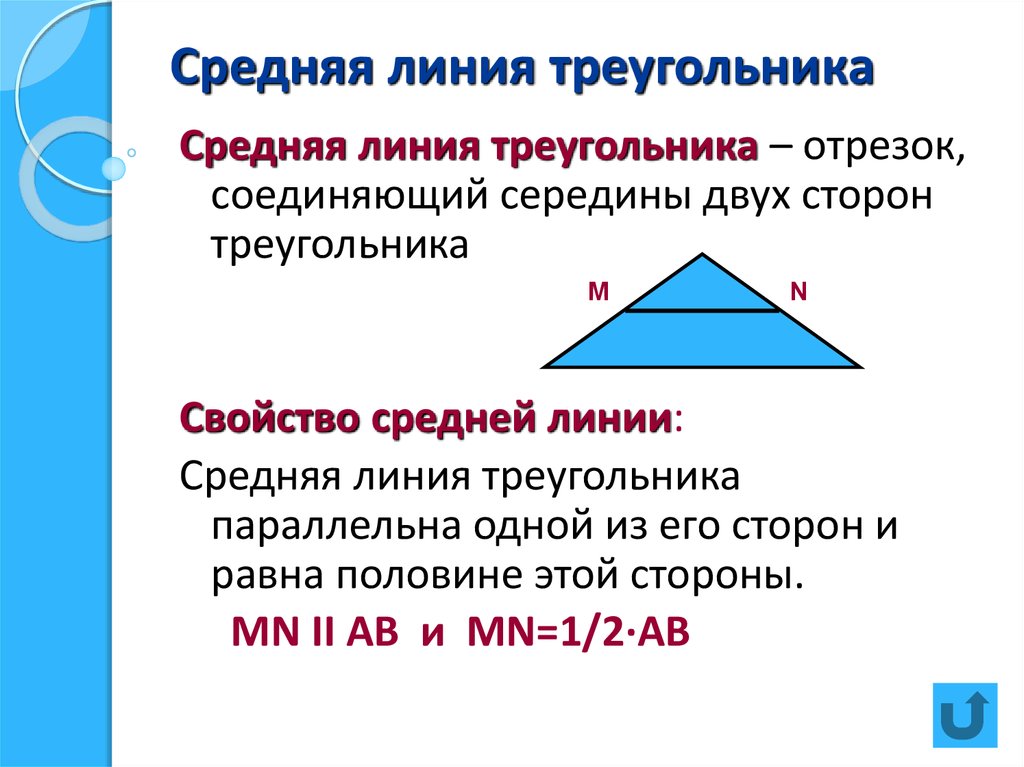 Чтобы измерить угол ADE, щелкните точки в следующем порядке: точка A , точка B и точка C . После этого шага вы увидите символ угла под углом ADE . Чтобы измерить угол ADE, щелкните точки в следующем порядке: точка A , точка B и точка C . После этого шага вы увидите символ угла под углом ADE . |
|
| 8.) Чтобы отобразить величину угла, щелкните инструмент Перемещение и щелкните правой кнопкой мыши символ угла. Отобразится диалоговое окно Edit Angle , показанное на рис. 2. | |
| 9.) Чтобы отобразить величину угла, щелкните значок Показать значения объекта значок. Затем щелкните наименьший размер символа угла, чтобы уменьшить размер угла. Теперь нажмите кнопку OK , чтобы применить изменения.
Рис. 3. Диалоговое окно «Редактировать угол». |
|
10.) Используя шаги 8–9, измерьте углы ABC , ACB и AED .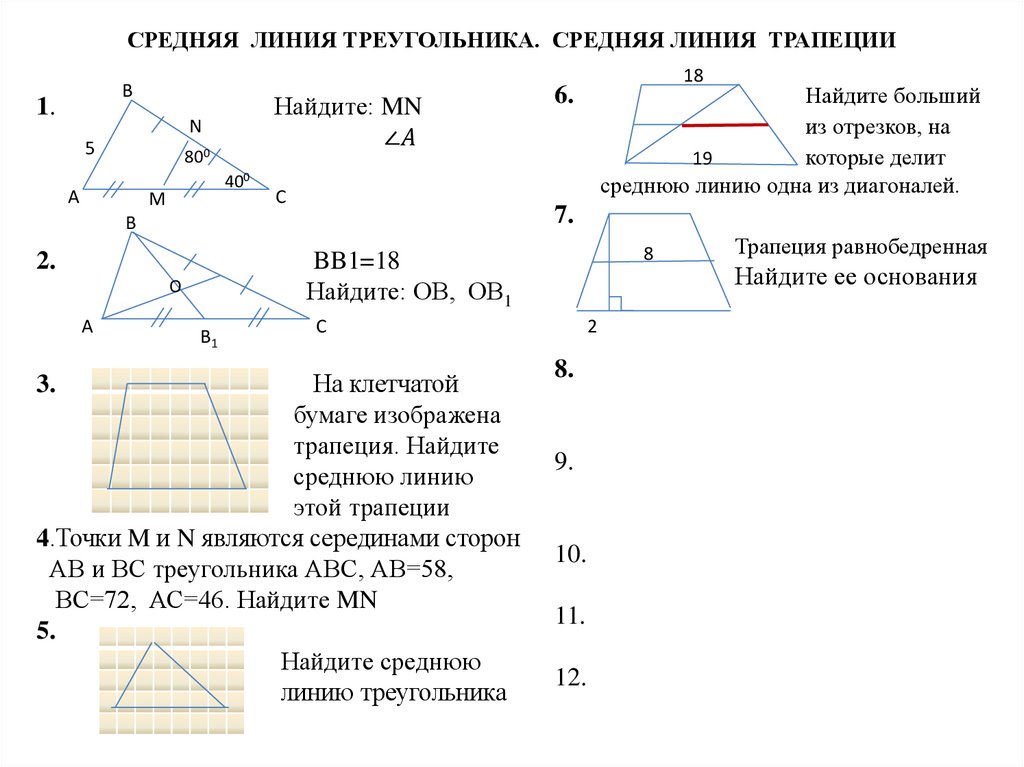 После измерения ваш рисунок должен выглядеть так, как показано на рисунке ниже. После измерения ваш рисунок должен выглядеть так, как показано на рисунке ниже.
|
|
| 11.) С помощью инструмента «Перемещение» перетащите вершины треугольника. Что вы наблюдаете? | |
| 12.) Основываясь на размерах углов, показанных на вашем рисунке, что вы можете сказать об сегменте DE и сегменте BC ? | |
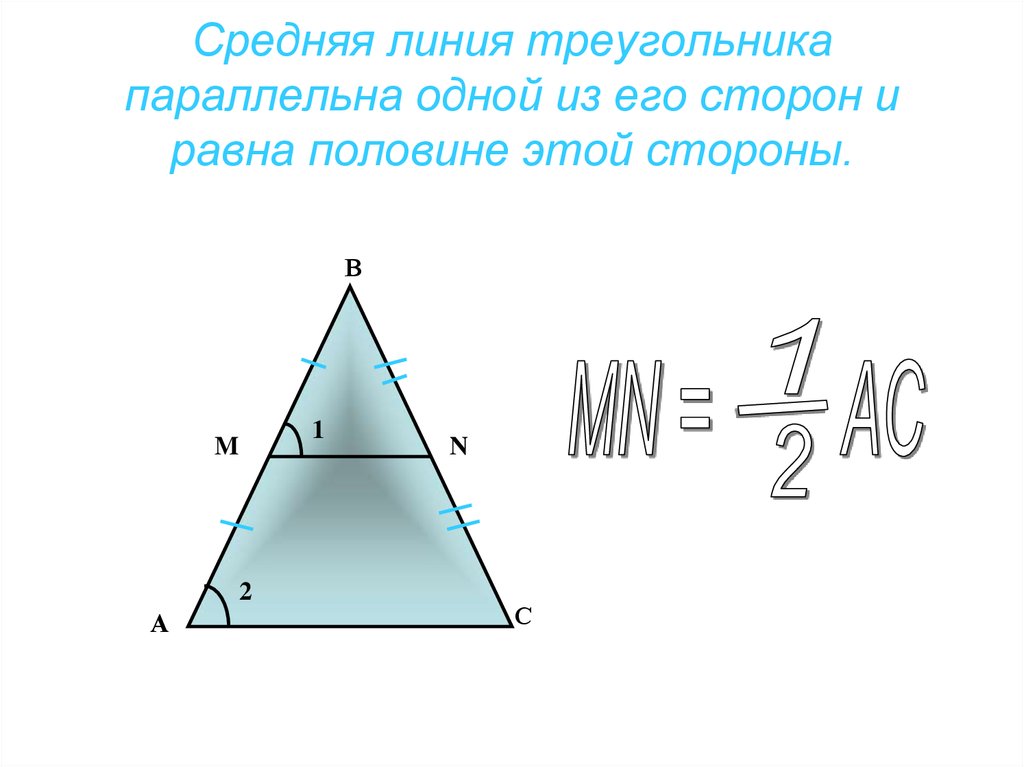
| 13. ) Теперь посмотрим, есть ли связь между длинами отрезков в треугольнике ABC . Чтобы раскрыть меру DE , используйте инструмент Перемещение и щелкните правой кнопкой мыши сегмент. Откроется диалоговое окно Edit Line, Ray, Segment , как показано на рисунке 3.
Рис. 5. Диалоговое окно «Редактировать линию, луч, сегмент». |
|
14.
No related posts. |
Что нужно знать о средней линии треугольника — основные сведения
Содержание:
- Определение средней линии треугольника
- Средняя линия треугольника — свойства, признаки и формулы
- Теорема о средней линии треугольника
- Задачи на использование теоремы
Использование понятия «средняя линия треугольника» помогает решить многие задачи по геометрии. Ее можно провести в любом треугольнике, независимо от соотношения длин его сторон и видов имеющихся углов.
Определение средней линии треугольника
Средней линией треугольника называется отрезок, который располагается внутри него таким образом, что соединяет точки, являющиеся серединами двух сторон, лежащих противоположно.
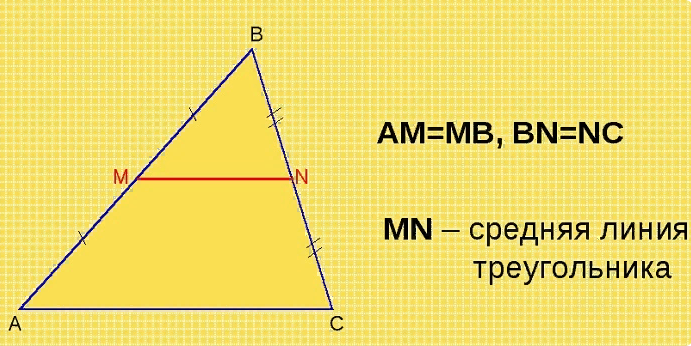
Такое определение не является единственным. Исходя из доказательства теоремы Фалеса:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если отрезок, начинающийся на середине одной из сторон треугольника, заканчивается на другой стороне и параллелен третьей, то это средняя линия этого треугольника.
В любом треугольнике можно провести три срединные линии, поскольку он имеет три стороны, в т.ч. две — лежащие друг против друга.
Доказательством этого утверждения является теорема Фалеса:

Средняя линия треугольника — свойства, признаки и формулы
Cвойства средних линий могут различаться. Так, в прямоугольном треугольнике две из трех средних линии перпендикулярны катетам. В то же время третья — по длине аналогична медиане, которую провели к гипотенузе.
Для треугольника, имеющего острые углы и стороны различной длины, средние линии таким свойством не обладают.
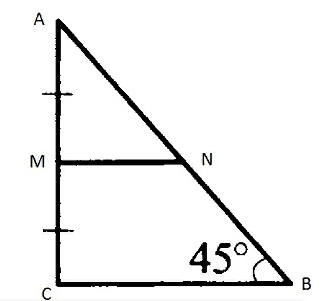
Для прямоугольного треугольника является справедливым утверждение, что его средняя линия делит площадь на 4 треугольника, имеющие прямые углы.
В геометрии к свойствам средней линии относят:
- Найти длину средней линии можно разделив длину основания пополам. При этом основание треугольника и его средняя линия являются параллельными.
- Проведя в треугольнике среднюю линию, можно смело утверждать, что он отсек еще один треугольник, который с коэффициентом ½ подобен основному — большому. Вычислить его площадь можно, разделив площадь основного треугольника на 4.
- Проведя в треугольнике все три средние линии, получают четыре треугольника равной площади. При этой центральный из них получил название дополнительного.
- Три средние линии, проведенные в прямоугольном треугольнике, также делят его на 4 меньших треугольника. При этом все они имеют прямые углы.
свойство 1
Из приведенного списка позволяет находить длину средней линии через длину стороны, которая ей параллельна.
Рассмотрим треугольник: Формулу для такого действия, исходя из ниже приведенной схемы, можно выразить так:
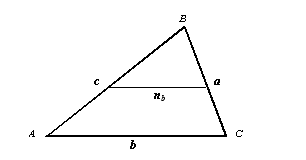
Формулу для такого действия, исходя из выше приведенной схемы, можно выразить так:
nb=1/2b
Свойство
Это же свойство № 1 лежит в основе следующей формулы — для нахождения площади треугольника, который образуется в результате отсекания части основного средней линией (S1) нужно площадь основного треугольника (S) разделить на 4:
S1=S/4
Теорема о средней линии треугольника
Утверждение, что средняя линия треугольника параллельна его основанию (либо третьей стороне) и по длине составляет половину этого основания, носит название теоремы о средней линии. Доказать ее можно с помощью трех способов:
- Рассмотрим треугольник.
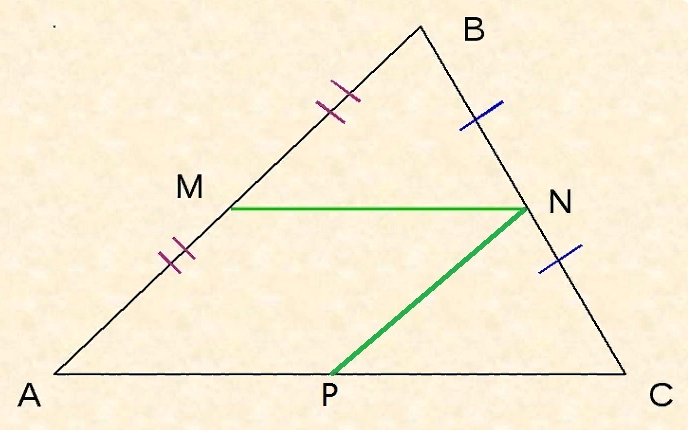
Из рисунка видно, что прямая MK параллельна AC. Исходя из теоремы Фалеса понятно, что точкой пересечения стороны BC является ее половина. Так как MN∈MK, значит MN параллельна AC.
Это доказательство первой части теоремы.
Приступаем к доказательству второй части: длина средней линии равна половине длины основания треугольника.
Предположим, что NP параллельна AB. По этому признаку она является средней линией треугольника (согласно теореме Фалеса). Если это так, то AP=PC.
Из рисунка видно, что фигура AMNP является параллелограммом, поэтому AP=MN. Из приведенных фактов следует, что MN=1/2AC
Второй способ основывается на том, что угол B — общий для треугольников MBN и ABC.
По известному признаку, лежащему в основе подобия треугольников, можно утверждать, что ΔMBN∼ΔABC.
Отсюда следует равенство углов BMN и BAC. Данные углы соответственные, поэтому прямые MN и AC являются параллельными.
Поскольку MN является средней линией треугольника, ее длина — равная половине AC.
Правильным является утверждение, что пропорциональность двух пар сторон обуславливает аналогичное отношение, касающееся третьей пары сторон.
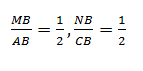
Третий вариант доказательства теоремы средней линии использует такое понятие, как сумма векторов: CA, AM, MN, NC. Из вышеприведенного рисунка можно узнать, что последовательно сменяющие друг друга обозначенные векторы образуют замкнутую линию. Поэтому их сумма равна нулю.
Проведя простые математические действия, получаем формулу:
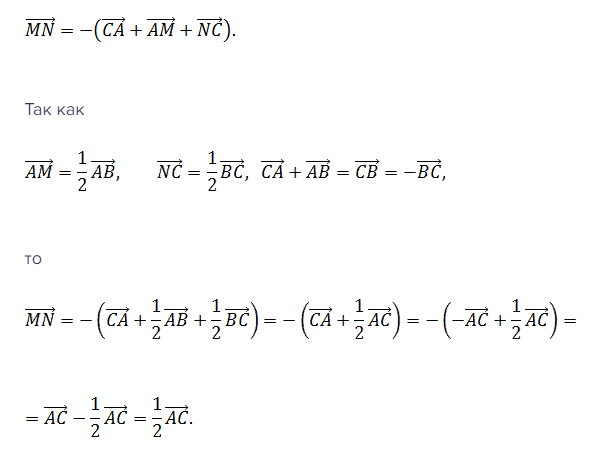
Для решения задач по нахождению параметров равнобедренных, равносторонних, прямоугольных треугольников важно знать следствия из теоремы средней линии. К ним относятся:
- С помощью средней линии можно отсечь в основном треугольнике второй, меньший по размеру, но подобный треугольник. Его площадь составляет четверть основного, а коэффициент подобия равен ½.
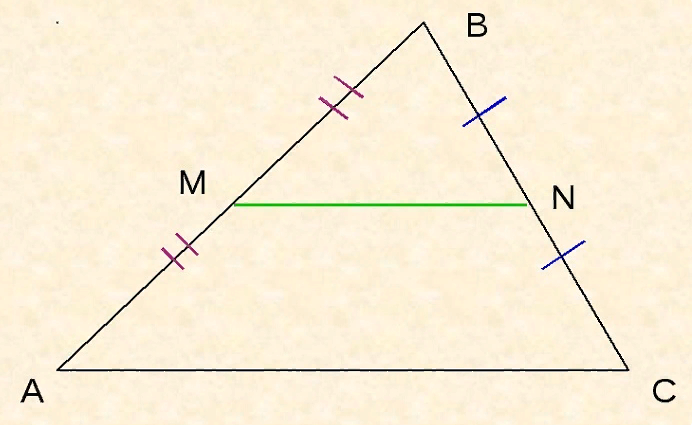
Данное утверждение может быть доказано исходя из следующего:
Согласно своим особенностям средняя линия треугольника пересекается с двумя его сторонами в их серединах. Следовательно, она делит стороны AB и BC пополам. Можно записать, что MB/AB=BN/BC=1/2
В то же время сама теорема средней линии утверждает, что ее длина составляет половину основания (третьей стороны треугольника). Значит MN/AC=1/2
Искать продолжение доказательства следствия теоремы следует в третьем признаке подобия. Установлено, что площади фигур, являющихся подобными, относятся друг к другу как коэффициента подобия в квадрате. То есть приходим ко второй части свойства: площадь меньшего треугольника находится по отношению к площади большего как дробь ¼.
Поэтому записываем:
SΔMBN/SΔABC=1/4
Это результат, какой и следовало доказать.
Существует еще одно следствие из теоремы средней линии. Оно звучит следующим образом:
Если в треугольнике провести три средние линии, то они разделят его на четыре одинаковых по площади треугольника, которые будут подобными исходному с коэффициентом подобия 0,5.
Для доказательства рассмотрим рисунок.
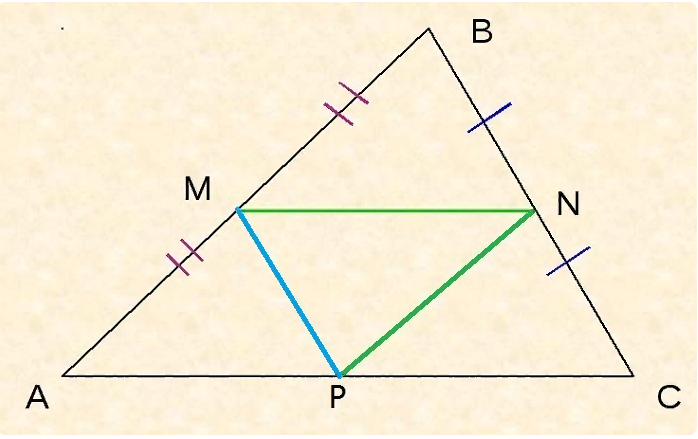
На рисунке отрезок MN является средней линией треугольника. Поэтому по одному из своих свойств он параллелен AC. Вытекающий признак: угол BMN равен углу BAP, а угол BNM равен углу BCA, поскольку они прилегают к параллельным прямым и линиям, которые являются секущими (AB и BC).
Аналогичная ситуация по линии MP. Она параллельна BC, откуда следует, что угол MPA равен углу BCA. Это углы соответственные с учетом параллельности прямых и секущей AC.
Из вышеприведенного следует, что углы BNM, BCA, MPA равны.
MN — средняя линия треугольника, поэтому ее длина составляет половину AC и равна AP.
Поэтому треугольники AMP и MBN равны (согласно второму признаку равенства).
Факт, что остальные пары треугольников равны, можно доказать аналогичным образом.
Треугольники MBN и ABС подобны с коэффициентом 0,5. Поскольку все образовавшиеся треугольники равны, то любой из них является подобным основному (большому) с одним и тем же коэффициентом.
Задачи на использование теоремы
Задача 1
Дан рисунок. Необходимо доказать, что в произвольном выпуклом четырехугольнике середины сторон — вершины параллелограмма.
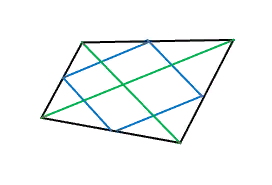
При проведении диагонали в четырехугольнике образуется два треугольника. В обоих необходимо построить средние линии, которые по определению будут параллельными диагонали (являющейся основанием).
Существует правило: если две прямые параллельны третьей, то они параллельны между собой. В тот же время стороны, которые лежат противоположно и образованы средними линиями в 4-х угольнике, также параллельны.
Это и есть запрашиваемое по условию задачи доказательство.
Касательно параллельности двух других сторон вновь образованного 4-х угольника, то ее можно доказать аналогичным путем. Четырехугольник, который образовался в результате соединения середин сторон первоначально данного четырехугольника, называется параллелограммом.
Задача 2
На рисунке изображен треугольник. Его сторона имеют длины 6 и 8 см. В треугольнике провели среднюю линию, соединив две стороны. Какой размер она имеет?
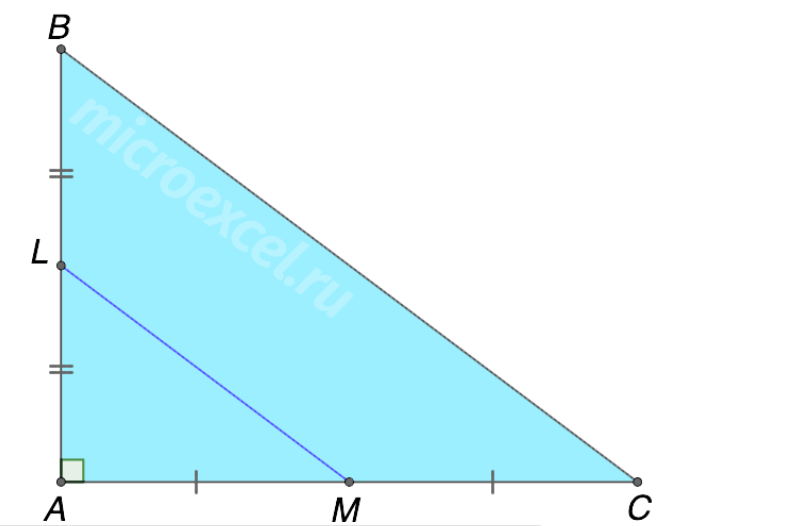
Изобразив схематически треугольник с заданными сторонами (катетами), видим, что он прямоугольный. По своему определению средняя линия, соединяющая эти катеты, параллельна основанию (гипотенузе) и составляет половину ее длины.
Для дальнейшего решения обратимся к теореме Пифагора, которая говорит: «для прямоугольного треугольника справедливо выражение: квадрат гипотенузы равняется сумме квадратов катетов».
Записываем данное утверждение математически применительно для имеющегося треугольника:
BC2=AB2+AC2=62+82=100
Проведя несложные вычисления, получаем ответ задачи:
BC=√100=10
Отсюда длина средней линии LM составляет половину длины BC и равна 10/2=5 см
