Как найти массу одной молекулы вещества
Молекула вещества является одновременно минимально возможной его порцией, а потому именно ее свойства являются определяющими для вещества в целом. Эта частица принадлежит микромиру, поэтому рассмотреть, а тем более взвесить ее, не представляется возможным. Но массу одной молекулы можно рассчитать.
Вам понадобится
- – периодическая таблица химических элементов;
- – понятие о строении молекулы и атома;
- – калькулятор.
Инструкция
Если известна химическая формула вещества, определите его молярную массу. Для этого определите атомы, из которых состоит молекула, и найдите их относительные атомные массы в периодической системе химических элементов. Если один атом встречается в молекуле n раз, умножьте его массу на это число. Затем сложите найденные значения и получите молекулярную массу данного вещества, которая равна его молярной массе в г/моль. Найдите массу одной молекулы, поделив молярную массу вещества M на постоянную Авогадро NА=6,022∙10^23 1/моль, m0=M/ NА.
Пример Найдите массу одной молекулы воды. Молекула воды (Н2О) состоит из двух атомов водорода и одного атома кислорода. Относительная атомная масса водорода равна 1, для двух атомов получим число 2, а относительная атомная масса кислорода равна 16. Тогда молярная масса воды будет равна 2+16=18 г/моль. Определите массу одной молекулы: m0=18/(6,022^23)≈3∙10^(-23) г.
Массу молекулы можно рассчитать, если известно количество молекул в данном веществе. Для этого поделите общую массу вещества m на количество частиц N (m0=m/N). Например, если известно, что в 240 г вещества содержится 6∙10^24 молекул, то масса одной молекулы составит m0=240/(6∙10^24)=4∙10^(-23) г.
Определите массу одной молекулы вещества с достаточной точностью, узнав количество протонов и нейтронов, которые входят в состав ее ядер атомов, из которых она состоит. Массой электронной оболочки и дефектом масс в данном случае следует пренебречь. Массу протона и нейтрона берите равной 1,67∙10^(-24) г. Например, если известно, если молекула состоит из двух атомов кислорода, какова ее масса? Ядро атома кислорода имеет в своем составе 8 протонов и 8 нейтронов. Общее количество нуклонов 8+8=16. Тогда масса атома равна 16∙1,67∙10^(-24)=2,672∙10^(-23) г. Поскольку молекула состоит из двух атомов, то ее масса равна 2∙2,672∙10^(-23)=5,344∙10^(-23) г.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Каждому человеку известно, что окружающие нас тела состоят из атомов и молекул. Они имеют разную форму и структуру. При решении задач по химии и физике часто требуется найти массу молекулы. Рассмотрим в данной статье несколько теоретических методов решения данной задачи.
Общие сведения
Прежде чем рассматривать, как найти массу молекулы, следует познакомиться с самим понятием. Далее приведем несколько примеров.
Молекулой принято называть совокупность атомов, которые объединены друг с другом тем или иным видом химической связи. Также они должны и могут рассматриваться, как единое целое в различных физико-химических процессах. Эти связи могут носить ионный, ковалентный, металлический или вандерваальсовский характер.
Всем известная молекула воды имеет химическую формулу H2O. Атом кислорода в ней соединен с помощью полярных ковалентных связей с двумя атомами водорода. Такое строение обуславливает многие физические и химические свойства жидкой воды, льда и пара.
Природный газ метан – это еще один яркий представитель молекулярного вещества. Его частицы образованы атомом углерода и четырьмя атомами водорода (CH4). В пространстве молекулы имеют форму тетраэдра с углеродом в центре.

Воздух – сложная смесь газов, которая главным образом состоит из молекул кислорода O2 и азота N2. Оба типа соединены прочными двойными и тройными ковалентными неполярными связями, что обуславливает их высокую химическую инертность.
Определение массы молекулы через ее молярную массу
В периодической таблице химических элементов содержится большое количество информации, среди которой имеются атомные единицы массы (а.е.м.). Например, атом водорода имеет а.е.м., равную 1, а атом кислорода – 16. Каждая из этих цифр показывает массу в граммах, которую будет иметь система, содержащая 1 моль атомов соответствующего элемента. Напомним, что единица измерения количества вещества 1 моль представляет собой количество частиц в системе, соответствующее числу Авогадро NA, оно равно 6,02*1023.
Когда рассматривают молекулу, то пользуются понятием не а.е.м., а молекулярной массой. Последняя представляет собой простую сумму а.е.м. для атомов, входящих в состав молекулы. Например, молярная масса для H2O будет равна 18 г/моль, а для O2 – 32 г/моль. Имея общее понятие, далее можно перейти к расчетам.
Молярную массу M просто использовать для вычисления массы молекулы m1. Для этого следует воспользоваться простой формулой:
m1 = M/NA.
В некоторых задачах может быть дана масса системы m и количество вещества в ней n. В таком случае масса одной молекулы вычисляется так:
m1 = m/(n*NA).
Идеальный газ

Этим понятием называется такой газ, молекулы которого хаотично движутся в разных направлениях с большими скоростями, друг с другом не взаимодействуют. Расстояния между ними намного превышают их собственные размеры. Для такой модели оказывается справедливым следующее выражение:
P*V = n*R*T.
Оно носит название закона Менделеева-Клапейрона. Как видно, уравнение связывает между собой давление P, объем V, абсолютную температуру T и количество вещества n. В формуле R – газовая константа, численно равная 8,314. Записанный закон называется универсальным, потому что он не зависит от химического состава системы.
Если известны три термодинамических параметра – T, P, V и значение m системы, то масса молекулы идеального газа m1 не сложно определить по следующей формуле:
m1 = m*R*T/(NA*P*V).
Это выражение также можно записать через плотность ρ газа и постоянную Больцмана kB:
m1 = ρ*kB*T/P.
Пример задачи
Известно, что плотность некоторого газа составляет 1,225 кг/м3 при атмосферном давлении 101325 Па и температуре 15 oC. Чему равна масса молекулы? О каком газе идет речь?
Поскольку нам даны давление, плотность и температура системы, то можно воспользоваться полученной в предыдущем пункте формулой, чтобы определить массу одной молекулы. Имеем:
m1 = ρ*kB*T/P;
m1 = 1,225*1,38*10-23*288,15/101325 = 4,807*10-26 кг.
Чтобы ответить на второй вопрос задачи, найдем молярную массу M газа:
M = m1*NA;
M = 4,807*10-26*6,02*1023 = 0,029 кг/моль.

Полученное значение молярной массы соответствует газу воздуху.
From Wikipedia, the free encyclopedia
The molecular mass (m) is the mass of a given molecule: it is measured in daltons or atomic mass (Da or u).[1][2] Different molecules of the same compound may have different molecular masses because they contain different isotopes of an element. The related quantity relative molecular mass, as defined by IUPAC, is the ratio of the mass of a molecule to the unified atomic mass unit (also known as the dalton) and is unitless. The molecular mass and relative molecular mass are distinct from but related to the molar mass. The molar mass is defined as the mass of a given substance divided by the amount of a substance and is expressed in g/mol. That makes the molar mass an average of many particles or molecules, and the molecular mass the mass of one specific particle or molecule. The molar mass is usually the more appropriate figure when dealing with macroscopic (weigh-able) quantities of a substance.
The definition of molecular weight is most authoritatively synonymous with relative molecular mass; however, in common practice, it is highly variable. When the molecular weight is used with the units Da or u, it is frequently as a weighted average similar to the molar mass but with different units. In molecular biology, the mass of macromolecules is referred to as their molecular weight and is expressed in kDa, although the numerical value is often approximate and representative of an average.
The terms molecular mass, molecular weight, and molar mass are often used interchangeably in areas of science where distinguishing between them is unhelpful. In other areas of science, the distinction is crucial. The molecular mass is more commonly used when referring to the mass of a single or specific well-defined molecule and less commonly than molecular weight when referring to a weighted average of a sample. Prior to the 2019 redefinition of SI base units quantities expressed in daltons (Da or u) were by definition numerically equivalent to otherwise identical quantities expressed in the units g/mol and were thus strictly numerically interchangeable. After the 20 May 2019 redefinition of units, this relationship is only nearly equivalent.
The molecular mass of small to medium size molecules, measured by mass spectrometry, can be used to determine the composition of elements in the molecule. The molecular masses of macromolecules, such as proteins, can also be determined by mass spectrometry; however, methods based on viscosity and light-scattering are also used to determine molecular mass when crystallographic or mass spectrometric data are not available.
Calculation[edit]
Molecular masses are calculated from the atomic masses of each nuclide present in the molecule, while relative molecular masses are calculated from the standard atomic weights[3] of each element. The standard atomic weight takes into account the isotopic distribution of the element in a given sample (usually assumed to be “normal”). For example, water has a relative molecular mass of 18.0153(3), but individual water molecules have molecular masses which range between 18.010 564 6863(15) Da (1H
216O) and 22.027 7364(9) Da (2H
218O).
Atomic and molecular masses are usually reported in daltons which is defined relative to the mass of the isotope 12C (carbon 12). Relative atomic and molecular mass values as defined are dimensionless. However, the “unit” Dalton is still used in common practice. For example, the relative molecular mass and molecular mass of methane, whose molecular formula is CH4, are calculated respectively as follows:
The uncertainty in molecular mass reflects variance (error) in measurement not the natural variance in isotopic abundances across the globe. In high-resolution mass spectrometry the mass isotopomers 12C1H4 and 13C1H4 are observed as distinct molecules, with molecular masses of approximately 16.031 Da and 17.035 Da, respectively. The intensity of the mass-spectrometry peaks is proportional to the isotopic abundances in the molecular species. 12C 2H 1H3 can also be observed with molecular mass of 17 Da.
Determination[edit]
Mass spectrometry[edit]
In mass spectrometry, the molecular mass of a small molecule is usually reported as the monoisotopic mass, that is, the mass of the molecule containing only the most common isotope of each element. Note that this also differs subtly from the molecular mass in that the choice of isotopes is defined and thus is a single specific molecular mass of the many possibilities. The masses used to compute the monoisotopic molecular mass are found on a table of isotopic masses and are not found on a typical periodic table. The average molecular mass is often used for larger molecules since molecules with many atoms are unlikely to be composed exclusively of the most abundant isotope of each element. A theoretical average molecular mass can be calculated using the standard atomic weights found on a typical periodic table, since there is likely to be a statistical distribution of atoms representing the isotopes throughout the molecule. The average molecular mass of a sample, however, usually differs substantially from this since a single sample average is not the same as the average of many geographically distributed samples.
Mass photometry[edit]
Mass photometry (MP) is a rapid, in-solution, label-free method of obtaining the molecular mass of proteins, lipids, sugars & nucleic acids at the single-molecule level. The technique is based on interferometric scattered light microscopy.[4] Contrast from scattered light by a single binding event at the interface between the protein solution and glass slide is detected and is linearly proportional to the mass of the molecule. This technique is also capable of measuring sample homogeneity,[5] detecting protein oligomerisation state, characterisation of complex macromolecular assemblies (ribosomes, GroEL, AAV) and protein interactions such as protein-protein interactions.[6] Mass photometry can measure molecular mass to an accurate degree over a wide range of molecular masses (40kDa – 5MDa).
Hydrodynamic methods[edit]
To a first approximation, the basis for determination of molecular mass according to Mark–Houwink relations[7] is the fact that the intrinsic viscosity of solutions (or suspensions) of macromolecules depends on volumetric proportion of the dispersed particles in a particular solvent. Specifically, the hydrodynamic size as related to molecular mass depends on a conversion factor, describing the shape of a particular molecule. This allows the apparent molecular mass to be described from a range of techniques sensitive to hydrodynamic effects, including DLS, SEC (also known as GPC when the eluent is an organic solvent), viscometry, and diffusion ordered nuclear magnetic resonance spectroscopy (DOSY).[8] The apparent hydrodynamic size can then be used to approximate molecular mass using a series of macromolecule-specific standards.[9] As this requires calibration, it’s frequently described as a “relative” molecular mass determination method.
Static light scattering[edit]
It is also possible to determine absolute molecular mass directly from light scattering, traditionally using the Zimm method. This can be accomplished either via classical static light scattering or via multi-angle light scattering detectors. Molecular masses determined by this method do not require calibration, hence the term “absolute”. The only external measurement required is refractive index increment, which describes the change in refractive index with concentration.
See also[edit]
- Cryoscopy and cryoscopic constant
- Ebullioscopy and ebullioscopic constant
- Dumas method of molecular weight determination
- François-Marie Raoult
- Standard atomic weight
- Mass number
- Absolute molar mass
- Molar mass distribution
- Dalton (unit)
- SDS-PAGE
References[edit]
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), p. 126, ISBN 92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16
- ^ Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2011). “CODATA Recommended Values of the Fundamental Physical Constants: 2010”. Database developed by J. Baker, M. Douma, and S. Kotochigova. National Institute of Standards and Technology, Gaithersburg, MD 20899.
- ^ “Atomic Weights and Isotopic Compositions for All Elements”. NIST. Retrieved 2007-10-14.
- ^ Young et al. (2018). Quantitative imaging of single biological macromolecules. Science 360, 423-427. DOI: https://doi.org/10.1126/science.aar5839
- ^ Sonn-Segev, A., Belacic, K., Bodrug, T. et al. Quantifying the heterogeneity of macromolecular machines by mass photometry. Nat Commun 11, 1772 (2020). https://doi.org/10.1038/s41467-020-15642-w
- ^ Soltermman et al. Quantifying protein-protein interactions by molecular counting using mass photometry. Angew. Chem Int Ed, 2020, 59(27), 10774-10779
- ^ Paul, Hiemenz C., and Lodge P. Timothy. Polymer Chemistry. Second ed. Boca Raton: CRC P, 2007. 336, 338–339.
- ^ Johnson Jr., C. S. (1999). “Diffusion ordered nuclear magnetic resonance spectroscopy: principles and applications”. Progress in Nuclear Magnetic Resonance Spectroscopy. 34 (3–4): 203–256. doi:10.1016/S0079-6565(99)00003-5.
- ^ Neufeld, R.; Stalke, D. (2015). “Accurate Molecular Weight Determination of Small Molecules via DOSY-NMR by Using External Calibration Curves with Normalized Diffusion Coefficients” (PDF). Chem. Sci. 6 (6): 3354–3364. doi:10.1039/C5SC00670H. PMC 5656982. PMID 29142693.
External links[edit]
- A Free Android application for molecular and reciprocal weight calculation of any chemical formula
- Stoichiometry Add-In for Microsoft Excel for calculation of molecular weights, reaction coefficients and stoichiometry.
Формулы молекулярной физики
Формула концентрации молекул
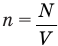
Здесь n — концентрация  , N — количество молекул (безразмерное), V — объем
, N — количество молекул (безразмерное), V — объем  .
.
Формула плотности
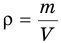
Здесь  — плотность вещества
— плотность вещества  , m — масса вещества (кг), V — объем
, m — масса вещества (кг), V — объем  .
.
Формула относительной молекулярной массы
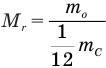
Здесь 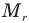 — относительная молекулярная масса (безразмерная),
— относительная молекулярная масса (безразмерная),  — масса одной молекулы (кг),
— масса одной молекулы (кг), 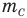 — масса атома углерода (кг).
— масса атома углерода (кг).
Формула количества вещества (количества молей)
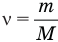
Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).
Формулы массы одной молекулы
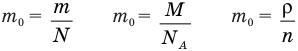
Здесь 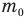 — масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль),
— масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль), 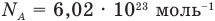 — число Авогадро,
— число Авогадро,  — плотность вещества
— плотность вещества  , n — концентрация молекул
, n — концентрация молекул  .
.
Формулы количества молекул
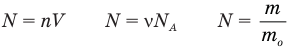
Здесь A — количество молекул (безразмерное), п — концентрация молекул  , V— объем
, V— объем  , v — количество вещества (количество молей) (моль),
, v — количество вещества (количество молей) (моль), 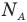 — число Авогадро
— число Авогадро 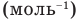 , m — масса вещества (кг),
, m — масса вещества (кг),  — масса одной молекулы.
— масса одной молекулы.
Формулы средней квадратичной скорости молекул
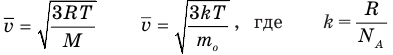
Здесь 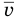 — средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль),
— средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль), 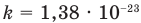 Дж/К — постоянная Больцмана,
Дж/К — постоянная Больцмана,  — масса одной молекулы (кг).
— масса одной молекулы (кг).
Основное уравнение кинетической теории идеального газа

Здесь р — давление газа (Па),  — масса одной молекулы (кг), n — концентрация молекул
— масса одной молекулы (кг), n — концентрация молекул  ,
, 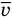 — средняя квадратичная скорость молекул (м/с),
— средняя квадратичная скорость молекул (м/с),  — средняя кинетическая энергия молекул (Дж).
— средняя кинетическая энергия молекул (Дж).
Формула средней кинетической энергии молекул
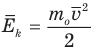
Здесь 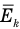 — средняя кинетическая энергия молекул (Дж),
— средняя кинетическая энергия молекул (Дж), 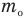 — масса одной молекулы (кг),
— масса одной молекулы (кг), 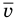 — средняя квадратичная скорость молекул (м/с).
— средняя квадратичная скорость молекул (м/с).
Связь шкал Цельсия и Кельвина
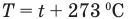
Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.
Связь средней кинетической энергии молекул идеального газа с абсолютной температурой
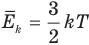
Здесь  — средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
— средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
У равнение состояния идеального газа — уравнение Клапейрона — Менделеева
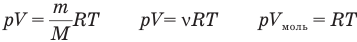
Здесь р — давление газа (Па), V — объем  , т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль),
, т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль), 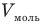 — объем моля
— объем моля 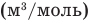 .
.
Объединенный газовый закон — уравнение Клапейрона
при 
Здесь 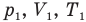 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 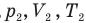 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Бойля — Мариотта (изотермический процесс)
при 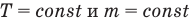
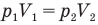
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), 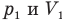 — давление (Па) и объем газа
— давление (Па) и объем газа  в первом состоянии,
в первом состоянии, 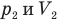 — давление (Па) и объем
— давление (Па) и объем  газа во втором состоянии.
газа во втором состоянии.
Закон Гей-Люссака (изобарный процесс)
при 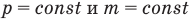
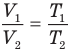
Здесь р — давление газа (Па), m — масса газа (кг), 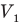 и
и 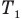 — объем
— объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 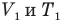 — объем
— объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Шарля
при 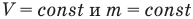
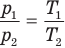
Здесь V — объем газа  , m — масса газа (кг),
, m — масса газа (кг), 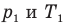 — давление (Па) и абсолютная температура (К) газа в первом состоянии,
— давление (Па) и абсолютная температура (К) газа в первом состоянии, 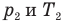 — давление (Па) и абсолютная температура (К) газа во втором состоянии.
— давление (Па) и абсолютная температура (К) газа во втором состоянии.
Связь давления идеального газа с концентрацией его молекул и температурой
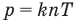
Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа  , абсолютная температура Т (К).
, абсолютная температура Т (К).
Формулы относительной влажности
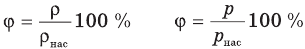
Здесь 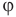 — относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре
— относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре 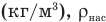 — плотность насыщенного водяного пара при той же температуре
— плотность насыщенного водяного пара при той же температуре 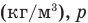 — давление водяного пара в воздухе при данной температуре (Па),
— давление водяного пара в воздухе при данной температуре (Па), 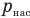 — давление насыщенного водяного пара в воздухе при той же температуре (Па).
— давление насыщенного водяного пара в воздухе при той же температуре (Па).
Работа при изобарном изменении объема газа
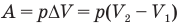
Здесь А — работа (Дж), р — давление газа (Па), 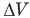 — изменение объема газа
— изменение объема газа 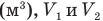 — соответственно начальный и конечный объемы газа
— соответственно начальный и конечный объемы газа  .
.
Внутренняя энергия идеального одноатомного газа
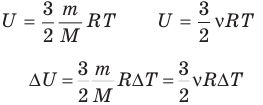
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), 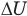 — изменение внутренней энергии (Дж),
— изменение внутренней энергии (Дж), 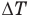 — изменение температуры (К).
— изменение температуры (К).
Первый закон термодинамики
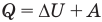
Здесь Q — количество теплоты, переданное термодинамической системе (Дж),  — изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
— изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
Применение первого закона термодинамики к термодинамическим процессам
к изотермическому: при 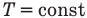
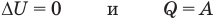
к изохорному: при V = const
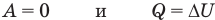
к изобарному: при р = const
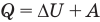
к адиабатному: при Q = 0

Здесь Т — абсолютная температура (К),  — изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем
— изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем 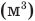 , р — давление (Па).
, р — давление (Па).
Формулы количества теплоты при нагревании или охлаждении тел
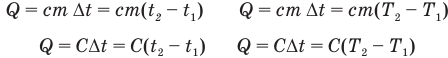
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), 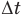 — изменение температуры тела по шкале Цельсия,
— изменение температуры тела по шкале Цельсия, 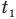 и
и 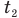 — температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия,
— температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия, 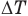 — изменение абсолютной температуры тела (К),
— изменение абсолютной температуры тела (К), 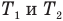 — абсолютные температуры тела в начале и в конце процесса передачи теплоты (К),
— абсолютные температуры тела в начале и в конце процесса передачи теплоты (К), 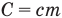 — теплоемкость тела (Дж/К).
— теплоемкость тела (Дж/К).
Формула количества теплоты при плавлении или кристаллизации
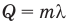
Здесь Q — количество теплоты (Дж), т — масса тела (кг), 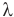 — удельная теплота плавления вещества (Дж/кг).
— удельная теплота плавления вещества (Дж/кг).
Формула количества теплоты при парообразовании или конденсации
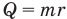
Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).
Формула количества теплоты при сгорании топлива
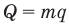
Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).
Коэффициент полезного действия теплового двигателя
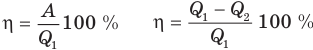
Здесь  — коэффициент полезного действия (безразмерный или в %),
— коэффициент полезного действия (безразмерный или в %), 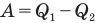 — работа, совершенная двигателем (Дж),
— работа, совершенная двигателем (Дж), 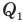 — количество теплоты, полученное рабочим веществом от нагревателя (Дж),
— количество теплоты, полученное рабочим веществом от нагревателя (Дж), 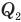 — количество теплоты, отданное рабочим веществом холодильнику (Дж).
— количество теплоты, отданное рабочим веществом холодильнику (Дж).
Коэффициент полезного действия идеального теплового двигателя
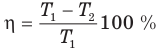
Здесь  — коэффициент полезного действия идеального теплового двигателя (безразмерный или в %),
— коэффициент полезного действия идеального теплового двигателя (безразмерный или в %), 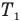 — абсолютная температура нагревателя (К),
— абсолютная температура нагревателя (К), 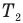 — абсолютная температура холодильника(К).
— абсолютная температура холодильника(К).
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:

Многие опыты показывают, что размер молекулы очень мал. Линейный размер молекулы или атома можно найти различными способами. Например, с помощью электронного микроскопа, получены фотографии некоторых крупных молекул, а с помощью ионного проектора (ионного микроскопа) можно не только изучить строение кристаллов, но определить расстояние между отдельными атомами в молекуле.
Используя достижения современной экспериментальной техники, удалось определить линейные размеры простых атомов и молекул, которые составляют около 10-8 см. Линейные размеры сложных атомов и молекул намного больше. Например, размер молекулы белка составляет 43*10-8 см.
Для характеристики атомов используют представление об атомных радиусах, которые дают возможность приближённо оценить межатомные расстояния в молекулах, жидкостях или твёрдых телах, так как атомы по своим размерам не имеют чётких границ. То есть атомный радиус – это сфера, в которой заключена основная часть электронной плотности атома (не менее 90…95%).
Размер молекулы настолько мал, что представить его можно только с помощью сравнений. Например, молекула воды во столько раз меньше крупного яблока, во сколько раз яблоко меньше земного шара.
Моль вещества
Массы отдельных молекул и атомов очень малы, поэтому в расчётах удобнее использовать не абсолютные значения масс, а относительные.
Относительная молекулярная масса (или относительная атомная масса) вещества Мr – это отношение массы молекулы (или атома) данного вещества к 1/12 массы атома углерода.
Мr = (m0) : (m0C / 12)
где m0 – масса молекулы (или атома) данного вещества, m0C – масса атома углерода.
Относительная молекулярная (или атомная) масса вещества показывает, во сколько раз масса молекулы вещества больше 1/12 массы изотопа углерода С12. Относительная молекулярная (атомная) масса выражается в атомных единицах массы.
Атомная единица массы – это 1/12 массы изотопа углерода С12. Точные измерения показали, что атомная единица массы составляет 1,660*10-27 кг, то есть
1 а.е.м. = 1,660 * 10-27 кг
Относительная молекулярная масса вещества может быть вычислена путём сложения относительных атомных масс элементов, входящих в состав молекулы вещества. Относительная атомная масса химических элементов указана в периодической системе химических элементов Д.И. Менделеева.
В периодической системе Д.И. Менделеева для каждого элемента указана атомная масса, которая измеряется в атомных единицах массы (а.е.м.). Например, атомная масса магния равна 24,305 а.е.м., то есть магний в два раза тяжелее углерода, так как атомная масса углерода равна 12 а.е.м. (это следует из того, что 1 а.е.м. = 1/12 массы изотопа углерода, который составляет большую часть атома углерода).
Зачем измерять массу молекул и атомов в а.е.м., если есть граммы и килограммы? Конечно, можно использовать и эти единицы измерения, но это будет очень неудобно для записи (слишком много чисел придётся использовать для того, чтобы записать массу). Чтобы найти массу элемента в килограммах, нужно атомную массу элемента умножить на 1 а.е.м. Атомная масса находится по таблице Менделеева (записана справа от буквенного обозначения элемента). Например, вес атома магния в килограммах будет:
m0Mg = 24,305 * 1 a.e.м. = 24,305 * 1,660 * 10-27 = 40,3463 * 10-27 кг
Массу молекулы можно вычислить путём сложения масс элементов, которые входят в состав молекулы. Например, масса молекулы воды (Н2О) будет равна:
m0Н2О = 2 * m0H + m0O = 2 * 1,00794 + 15,9994 = 18,0153 a.e.м. = 29,905 * 10-27 кг
Количество вещества принято считать пропорциональным числу частиц. Количество вещества – это физическая величина, характеризующая относительное число молекул и атомов в теле. Единица количества вещества называется молем (моль).
Моль равен количеству вещества системы, в которой содержится столько же молекул, сколько содержится атомов в 0,012 кг углерода С12. То есть, если у нас есть система с каким-либо веществом, и в этой системе столько же молекул этого вещества, сколько атомов в 0,012 кг углерода, то мы можем сказать, что в этой системе у нас 1 моль вещества.
Постоянная Авогадро
Количество вещества ν равно отношению числа молекул в данном теле к числу атомов в 0,012 кг углерода, то есть количеству молекул в 1 моле вещества.
ν = N / NA
где N – количество молекул в данном теле, NA – количество молекул в 1 моле вещества, из которого состоит тело.
NA – это постоянная Авогадро. Количество вещества измеряется в молях.
Постоянная Авогадро – это количество молекул или атомов в 1 моле вещества. Эта постоянная получила своё название в честь итальянского химика и физика Амедео Авогадро (1776 – 1856).
В 1 моле любого вещества содержится одинаковое количество частиц.
NA = 6,02 * 1023 моль-1
Молярная масса – это масса вещества, взятого в количестве одного моля:
μ = m0 * NA
где m0 – масса молекулы.
Молярная масса выражается в килограммах на моль (кг/моль = кг*моль-1).
Молярная масса связана с относительной молекулярной массой соотношением:
μ = 10-3 * Mr [кг*моль-1]
Масса любого количества вещества m равна произведению массы одной молекулы m0 на количество молекул:
m = m0N = m0NAν = μν
Количество вещества равно отношению массы вещества к его молярной массе:
ν = m / μ
Массу одной молекулы вещества можно найти, если известны молярная масса и постоянная Авогадро:
m0 = m / N = m / νNA = μ / NA
Более точное определение массы атомов и молекул достигается при использовании масс-спректрометра – прибора, в котором происходит разделение пучком заряженных частиц в пространстве в зависимости от их массы заряда при помощи электрических и магнитных полей.
Для примера найдём молярную массу атома магния. Как мы выяснили выше, масса атома магния равна m0Mg = 40,3463 * 10-27кг. Тогда молярная масса будет:
μ = m0Mg * NA = 40,3463 * 10-27 * 6,02 * 1023 = 2,4288 * 10-2 кг/моль
То есть в одном моле «помещается» 2,4288 * 10-2 кг магния. Ну или примерно 24,28 грамм.
Как видим, молярная масса (в граммах) практически равна атомной массе, указанной для элемента в таблице Менделеева. Поэтому когда указывают атомную массу, то обычно делают так:
Атомная масса магния равна 24,305 а.е.м. (г/моль).
Можете посчитать молярную массу для различных элементов и убедиться в правоте этого утверждения. Для расчёта молярной массы можно использовать простой калькулятор, который находится внизу страницы:
