Мощность, формула
Мощностью P называется отношение произвольной работы W к времени t, в течение которого совершается работа.
[
textit{Мощность} = frac{textit{Работа}}{textit{Время}}
]
Единица СИ мощности
[
[P] = text{Ватт} enspace text{(Вт)} = frac{text{Джоуль}}{text{секунда}} = text{кг} frac{м^2}{с^3}
]
Средняя мощность, формула
Если:
P — Средняя мощность (Ватт),
W — Работа (Джоуль),
t — Время затраченное на совершение работы (секунд),
то
[
average{P} = frac{W}{t}
]
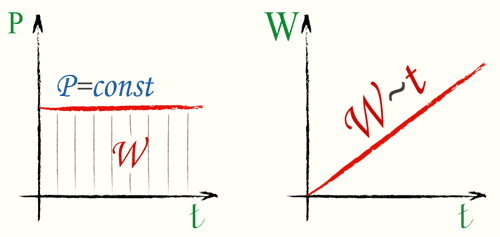
Вычислить, найти среднюю мощность по формуле (3)
Мгновенная мощность, формула
В большинстве случаев мощность зависит от времени, P=P(t).
Мгновенная мощность есть производная работы по времени:
[
P = frac{dW}{dt} = dot{W}
]
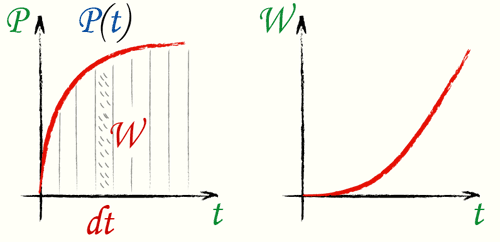
Поскольку см. (Работа)
[
dW = Fds
]
то отсюда следует см. (Мгновенная скорость)
[
P = F frac{ds}{dt} = Fu
]
Здесь:
F — Мгновенная сила (Ньютон),
u — мгновенная скорость (метр/секунда),
Мгновенная мощность равна произведению мгновенной силы на мгновенную скорость
При равномерно ускоренном движении F=const
[
P_{max} = F u_{max} ; average{P} = F average{u}
]
Вычислить, найти мгновенную мощность, по формуле (6)
Мощность |
стр. 471 |
|---|
Single Phase System
Instantaneous Power
The instantaneous power in an AC circuit is defined as the product of instantaneous voltage (v) across the element and instantaneous current (i) through the element and is denoted by lower case letter p.
Instantaneous Power, $mathrm{p=vtimes:i}$
Since, the values of instantaneous voltage and instantaneous current changes from instant to instant, thus the instantaneous power changes with time. The instantaneous power (p) is measured in watts. The instantaneous power may be positive or negative. A positive instantaneous power means power flows from source to load whereas negative instantaneous power means power flows from load to source.
Instantaneous Power Formula
Case 1 – Pure Resistive Circuit
In case of pure resistive circuit, the instantaneous value current and voltage being,
$$mathrm{v=V_{m}sinomega:t}$$
$$mathrm{i=I_{m}sinomega:t}$$
Therefore, the instantaneous power will be,
$$mathrm{p=vtimes:i=(v_{m}sinomega:t)times:(I_{m}sinomega:t)}$$
$$mathrm{Rightarrow:p=frac{V_{m}I_{m}}{2}-frac{V_{m}I_{m}}{2}cos2omega:t:::…(1)}$$
Case 2 – Pure Inductive Circuit
For pure inductive circuit, the equation of instantaneous voltage and current is given by,
$$mathrm{v=V_{m}sinomega:t}$$
$$mathrm{i=I_{m}sin(omega:t-90)}$$
Hence, the instantaneous power will be,
$$mathrm{p=vtimes:i=(V_{m}sinomega:t)times:(I_{m}sin(omega:t-90))}$$
$$mathrm{Rightarrow:p=-frac{V_{m}I_{m}}{2}sin2omega:t:::…(2)}$$
Case 3 – Pure Capacitive Circuit
The equation of instantaneous voltage and current for a pure capacitive circuit is given by,
$$mathrm{v=V_{m}sinomega:t}$$
$$mathrm{i=I_{m}sin(omega:t+90)}$$
Therefore, the instantaneous power will be,
$$mathrm{p=vtimes:i=(V_{m}sinomega:t)times:(I_{m}sin(omega:t+90))}$$
$$mathrm{Rightarrow:p=frac{V_{m}I_{m}}{2}sin2omega:t:::…(3)}$$
From the equations (1), (2) and (3) it can be noted that the instantaneous power in a single phase system varies from zero to maximum values at twice the supply frequency and also it may be positive or negative.
Average Power
The average power is defined as the average of instantaneous power over one cycle and is denoted by upper case letter P. It is also measured in watts.
Avergae Power, p = Avg. of p over one cycle
$$mathrm{p=frac{1}{2pi}int_{0}^{2pi}p:domega:t::::…(4)}$$
Average Power Formula
Case 1 – Pure Resistive Circuit
$$mathrm{mathrm{p=frac{1}{2pi}int_{0}^{2pi}p:domega:t=frac{1}{2pi}int_{0}^{2pi}frac{V_{m}I_{m}}{2}-frac{V_{m}I_{m}}{2}cos2omega:t:domega:t}}$$
$$mathrm{Rightarrow:p=frac{V_{m}I_{m}}{2}=frac{V_{m}}{sqrt{2}}times:frac{I_{m}}{sqrt{2}}=VI:::…(5)}$$
Where, V and I are the RMS values of voltage and current respectively.
Case 2 – Pure Inductive Circuit
$$mathrm{p=frac{1}{2pi}int_{0}^{2pi}p:domega:t=frac{1}{2pi}int_{0}^{2pi}-frac{V_{m}I_{m}}{2}cos2omega:t:domega:t=0:::…(6)}$$
Hence, average power absorbed by a pure inductor is zero.
Case 3 – Pure Capacitive Circuit
$$mathrm{p=frac{1}{2pi}int_{0}^{2pi}p:domega:t=frac{1}{2pi}int_{0}^{2pi}frac{V_{m}I_{m}}{2}cos2omega:t:domega:t=0:::…(7)}$$
Hence, average power absorbed by a pure capacitor is also zero.
Three Phase System
Instantaneous Power
As we know, the single phase instantaneous power (for lagging power factor load) is given by,
$$mathrm{p=frac{V_{m}I_{m}}{2}cosvarphi-frac{V_{m}I_{m}}{2}cos(2omega:t-varphi)}$$
In terms of RMS values, it becomes,
$$mathrm{p=VIcosvarphi-VIcos(2omega:t-varphi)}$$
Now, the instantaneous power in three phases (RYB –phase sequence) can be written as,
$$mathrm{p_{R}=V_{ph}I_{ph}cosvarphi-V_{ph}I_{ph}cos(2omega:t-varphi)}$$
$$mathrm{p_{Y}=V_{ph}I_{ph}cosvarphi-V_{ph}I_{ph}cos(2omega:t-varphi-120^{circ})}$$
$$mathrm{p_{H}=V_{ph}I_{ph}cosvarphi-V_{ph}I_{ph}cos(2omega:t-varphi+120^{circ})}$$
Therefore, total instantaneous power in three phase system is given by,
$$mathrm{p=P_{R}+P_{Y}+P_{H}}$$
$$mathrm{p=3V_{ph}I_{ph}cosvarphi-V_{ph}I_{ph}begin{bmatrix}cos(2omega:t-varphi)+cos(2omega:t-varphi-120^{circ}) +cos(2omega:t-varphi+120^{circ})end{bmatrix}}$$
$$mathrm{becausebegin{bmatrix}cos(2omega:t-varphi)+cos(2omega:t-varphi-120^{circ}) +cos(2omega:t-varphi+120^{circ})end{bmatrix}=0}$$
Thus,
$$mathrm{p=3V_{ph}I_{ph}cosvarphi:::…(8)}$$
$$mathrm{Rightarrow:p=sqrt{3}V_{L}I_{L}cosvarphi:::…(9)}$$
The eqns. (8) & (9) shows that the 3 phase instantaneous power is constant and is not the function of supply frequency.
Average Power
By the definition of average power, we obtain,
$$mathrm{P=frac{1}{2pi}int_{0}^{2pi}3V_{ph}I_{ph}cosvarphi:domega=3V_{ph}I_{ph}cosvarphi}$$
$$mathrm{Rightarrow:P=3V_{ph}I_{ph}cosvarphi=sqrt{3}V_{L}I_{L}cosvarphi:::…(10)}$$
Therefore, in case of a three system, the average power and instantaneous power are same.
Мощность
Различные машины и механизмы, выполняющие одинаковую работу, могут отличаться мощностью. Мощность характеризует быстроту совершения работы. Очевидно, что чем меньшее время требуется для выполнения данной работы, тем эффективнее работает машина, механизм и др.
При движении любого тела на него в общем случае действует несколько сил. Каждая сила совершает работу, и, следовательно, для каждой силы мы можем вычислить мощность.
Средняя мощность силы — скалярная физическая величина Ν, равная отношению работы А, совершаемой силой, к промежутку времени Δt, в течение которого она совершается:
(~N = frac{A}{Delta t}.)
В СИ единицей мощности является ватт (Вт).
Если тело движется прямолинейно и на него действует постоянная сила, то она совершает работу (~A = F Delta r cos alpha). Поэтому мощность этой силы
(~N = frac{F Delta r cos alpha}{Delta t} = F upsilon cos alpha = F_{upsilon} cdot upsilon.)
где Fυ — проекция силы на направление движения.
По этой формуле можно рассчитывать и среднюю, и мгновенную мощности, подставляя значения средней (~mathcal h upsilon mathcal i) или мгновенной υ скорости.
Мгновенная мощность — это мощность силы в данный момент времени.
(~N_m = lim_{Delta t to 0} frac{A}{Delta t} = A’ .)
Любой двигатель или механизм предназначены для выполнения определенной механической работы, которую называют полезной работой Ap. Но любой машине приходится совершать большую работу, так как вследствие действия сил трения часть подводимой к машине энергии не может быть преобразована в механическую работу. Поэтому эффективность работы машины характеризуют коэффициентом полезного действия η (КПД).
Коэффициент полезного действия η — это отношение полезной работы Ap, совершенной машиной, ко всей затраченной работе Az (подведенной энергии W):
(~eta = frac{A_p}{A_z} = frac{A_p}{W} = frac{N_p}{N_z},)
где Np, Nz — полезная и затраченная мощности соответственно. КПД обычно выражают в процентах.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 63-64.
Алексей Алексеевич Ивахно
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Под мощностью подразумевают работу, выполненную за единицу времени, однако этот подход в большинстве случаев требует уточнений, поскольку интенсивность выполнения работы может многократно измениться за рассматриваемое время. Например, при движении автомобиля водитель увеличивает и уменьшает поступление топливно-воздушной смеси в зону сгорания, переключает передачи трансмиссии, притормаживает. Всё это влияет на текущую мощность двигателя. Поэтому в физике различают мгновенную мощность – мощность, измеренную за промежуток времени достаточно малый, чтобы считать ее величину постоянной:
$P = limlimits_{t to 0}frac{Delta A}{Delta t}$,
где $Delta t$ – промежуток времени, $Delta A$ – проделанная за это время работа.
Поскольку мгновенные величины мощности могут меняться без какой-либо четко выраженной закономерности, подсчитать их среднее значение бывает затруднительно. Поэтому среднюю мощность находят просто как

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
${langle}Prangle = frac{Delta A}{Delta t}$.
Следует различать мощность, связанную с общими затратами на движение и ту, что развивается для выполнения полезной работы. Так, один и тот же груз с одной и той же скоростью на одно и то же расстояние можно перевезти разными способами, например, на старинном паровозе и современном электровозе. Полезная работа будет выполнена одинаковая, но интенсивность затрат энергии – различная. Поэтому существует понятие средней полезной мощности, расчет которой зависит от многих факторов, связанных с особенностями движителей и сред, в которых выполняется работа.
Пример 1
Автомобиль массой 2 т поднимается в гору с постоянным ускорением по участку дороги с уклоном 30°. Движение длится 10 с. Скорость транспортного средства в начале подъема 20 км/ч, в конце 40 км/ч. Общая сила сопротивления (трение, вязкость воздуха и т.д.), постоянна и равна 600 Н. Определить среднюю полезную мощность двигателя.
Двигатель должен развить следующие силы:
- преодолевающую силу сопротивления;
- преодолевающую гравитацию, поскольку транспорт движется в гору;
- обеспечивающую ускорение.
Найдем их последовательно.
На преодоление силы сопротивления необходимо развить те же 600 ньютонов, но в направлении, совпадающем с вектором скорости.
Сила, преодолевающая силу тяжести, поскольку ее вектор находится под углом к вектору скорости, будет исчисляться по формуле:
$F_g = m cdot g cdot sin(alpha)$,
где $g$ – ускорение свободного падения, $m$ – масса. $alpha$ – угол наклона.
Приращение скорости:
$Delta v = v_1 – v_0 = frac{40000 – 20000}{3600} approx 5,56 frac{м}{с}$
Ускорение:
$a = frac{Delta v}{t} approx 0,556 frac{м}{с^2}$.
Просуммируем силы:
$F = 600 + 2000 cdot 9,8 cdot 0,5 + 2000 cdot 0.556 approx 600 + 9800 + 1112 = 11512 Н$
Работа равна произведению силы и пути, который можно выразить через время, начальную скорость и ускорение:
$A = F cdot (v_0 cdot t + frac{a cdot t^2}{2}) approx 11512 cdot (55,6 + 0,556 cdot 100) approx 11512 cdot 111,11 approx 1279111 Дж$
Разделив работу на время, получим среднюю полезную мощность:
$P = frac{1279111}{10} approx 127911 Вт$
Ответ: $approx 127911$ Вт. Примечание: полную мощность двигателя можно найти разделив это значение на КПД.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Это величина, отображающая как быстро выполняется работа или как быстро энергия передается из одного места в другое или преображается из одного типа в другой.
В разных областях физики мощность принято обозначать разными символами, например в механике — NN, в электротехнике — PP, а также иногда WW.
Для нахождения величины мощности используют разные формулы:
P = △E△tP;=;frac{triangle E}{triangle t},
где PP мощность, ΔEΔE – изменение энергии, ΔtΔt – изменение времени. Или другая интерпретация:
P = FvcosαP;=;Fvcosalpha,
в случае, если на тело, движущееся со скоростью vv, действует определенная сила FF, то она совершает работу. Мощность будет равна скалярному произведению силы на скорость, на косинус угла между ними.
Стандартная единица мощности – это ватт, обозначенный Вт (или WW). Получила название в честь шотландского инженера-механика Джеймса Уатта.
Выходная мощность электрического оборудования, тостера или микроволновой печи, указывается в ваттах. Исходя из понятия мощности один ватт соответсвует одному джоулю работы, выполняемой за одну единицу времени.
Еще одна единица мощности, которая часто используется, особенно, в автомобильной индустрии: лошадиная сила.
Она обозначается сокращением л.с. и берет свое начало в XVII веке. С тех пор метрическая мощность была определена как мощность, необходимая для подъема массы 75 кг на расстояние 1 метр за 1 секунду.
Как измерить переменную мощность?
Использование электричества – один из примеров применения мощности, которая изменяется со временем.
Минимальные потребности электрической энергии наблюдаются в течение дня, но сопровождаются пиковыми скачками в вечернее время при приготовлении пищи, освещения и обогрева.
Существует три способа выражения мощности, которые здесь важны:
- мгновенная мощность PмгP_{мг};
- средняя мощность PсрP_{ср};
- пиковая PпикP_{пик}.
Это мощность сейчас, в данный момент времени.
Если мы рассмотрим уравнение для мощности P = △E△tP;=;frac{triangle E}{triangle t}, то это измерение, получается, когда ΔtΔt очень мало.
Это мощность, которую считают за очень длительное время, то есть, когда ΔtΔt в уравнении для мощности очень велико.
Это максимальное значение, которое мгновенная мощность может иметь в конкретной системе в течение длительного периода.
Автомобильные двигатели и стереосистемы являются примером систем, способные выдавать пиковую мощность, которая намного выше их номинальной средней мощности. Тем не менее, как правило, это возможно только в течение короткого времени, чтобы избежать повреждений устройств.
