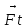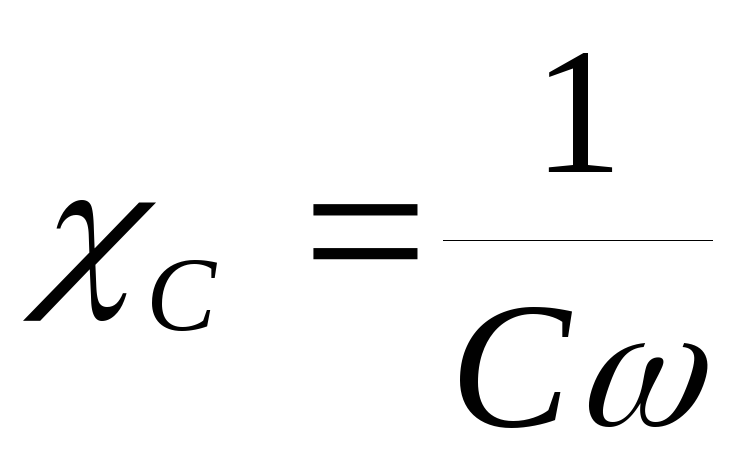Как найти среднюю мощность сил сопротивления

Мощность в механике: мгновенная и средняя

(методика решения задач на расчет мощности постоянной силы)

Решение задач механики такого типа основано на применении формул:

N_min=F_t*υ N_ср=F_t*υ_ср

где N_{min –} минимальная (мгновенная) мощность

F_t – сила тяги, строго определенная сила, направленная в сторону перемещения рассматриваемого тела и обросшего согласно уравнения II Закона Ньютона

υ – модуль мгновенной скорости тела в конце перемещения

N_{ср –} средняя мощность

υ_ср – модуль средней скорости на заданном участке пути

Рационально применить примерный алгоритм решения:

1. Установить, какую мощность требуется определить мгновенную или среднюю

2. Записать кратко условие задачи в СИ

3. Сделать чертеж, указав на нем все силы, приложенные к телу и заданные кинематические характеристики движения.

4. Составить основное уравнение динамики материальной точки и найти из него модуль силы тяги

5. Если значения υ и υ_ср не заданы, то определить их из формул кинематики

6. Подставить в формулу мощности υ и Ft их выражения и провести окончательный расчет

Пример №1

Самолет АН-24 массой 21т для взлета должен иметь скорость υ = 216 км/ч и длину разбега S=850 м Какова должна быть минимальная мощность двигателей, необходимая для взлета самолета?

(Силу сопротивления движению считать пропорциональной силе нормального давления, средний коэффициент сопротивления принять равным 0,2 Движение при разгоне самолета считать равноускоренным)

Анализ и решение

Дано:

1

Самолет АН-24 N_min=F_t*υ

РУД, υ₀ = 0

m = 21000 кг При разгоне самолета на него действует со стороны воздуха сила тяги

υ = 216 км/ч = 60 м/с

S=850 м

M = 0,2 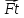, кроме того к самолету приложены следующие силы:

Сила тяжести, равная m*g, нормальная реакция опоры Q и сила

Сопротивления равная по модулю M* m*g

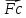
Найти N_min = ? Применяя II Закон Ньютона учитывая условие задачи можно

записать

F_t – M* m*g = m*a →

2

F_t = m*a + M* m*g

Ускорение самолета 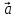находим из формулы кинематики

Ответ: Nmin = 5,1 МВт

Пример №2

Поезд массой m = 800 т начинает двигаться под уклон и за t = 50 c развивает скорость

υ = 36 км/ч Коэффициент сопротивления равен M = 0,005 φ =0,005

Определить среднюю мощность локомотива, считая силу сопротивления пропорциональной силе нормального давления.

Анализ и решение

1

Дано N_cр = F_t * υ_ср

Поезд РУД

m = 800т = 8*10⁵ кг

t = 50 c υ_ср является средней скоростью на заданном участке пути

υ=36 км/ч=10м/c F_t сила тяги локомотива

М = 0,005 Силу тяги F_t действующую со стороны рельсов находим из

φ_уклон =0,005 II закона Ньютона. Здесь силой тяги является сила трения сцепления

g = 10м/с² колес с рельсами.

Для составления уравнения, II закон Ньютона на чертеже

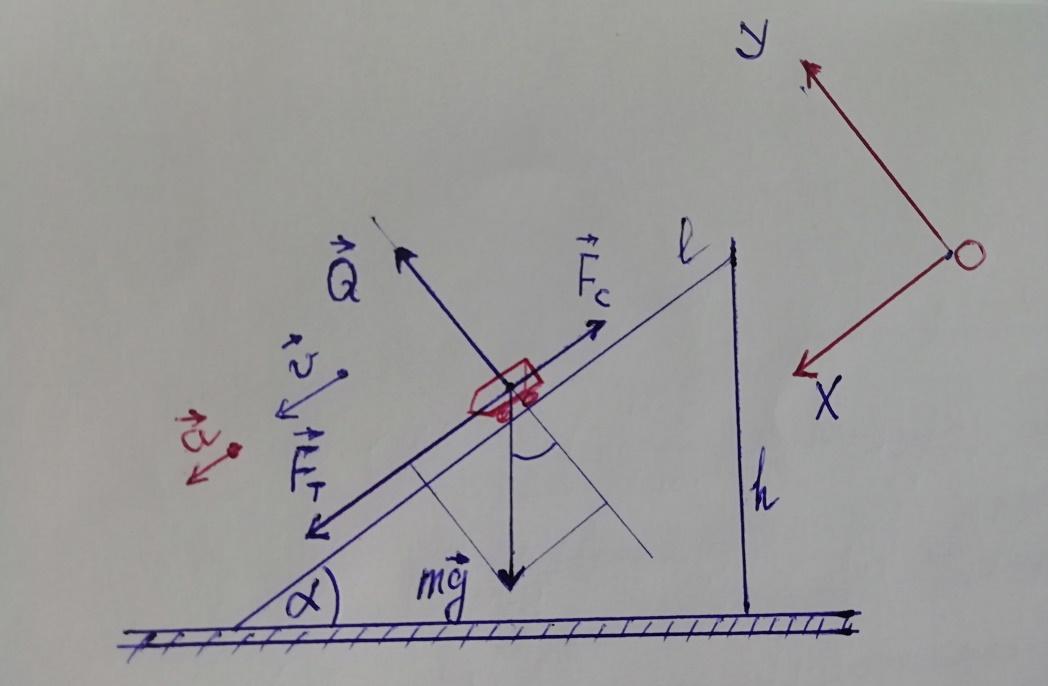
Найти: расставляем силы, приложенные к поезду:

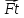
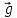
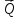
N_ср = ? , m, ,

Спроецировав силы на оси составляем уравнение Динамики в проекциях:

OX : Ft + m*g*sinα – F*c = m*a

OY: Q = m*g*cosα

А так как по условию

Fc = M*Q=M*m*g*cosα, то

Ft+m*g*sinα- M*m*g*cosα = m*a,

Ft = m*a+ M*m*g*cosα-m*g*sinα

2

Ft = m(a+M*g*cosα – g*sinα)

Подставляя выражение в получим

1

2

Nср=Ft*υ_ср = m(a+M*g*cosα – g*sinα) * υ_ср

Из кинематики:

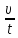
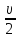
a = υ_ср = тогда

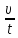
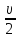
N_ср= m*(+M*g* cosα- g*sinα)*

Учитывая условие φ_уклон = 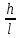= sinα

Получаем формулу для расчета средней мощности локомотива

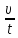
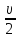
Nср= m*(+M*g- g*φ)*

4

N_ср = 8*10⁵ кг *(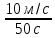 +0,005*10м/с²– 10м/с²*0,005)*5м/с= 8*10⁵ Вт = 800кВт=0,8МВт

Ответ: N_ср = 0,8 МВт

Под мощностью подразумевают работу, выполненную за единицу времени, однако этот подход в большинстве случаев требует уточнений, поскольку интенсивность выполнения работы может многократно измениться за рассматриваемое время. Например, при движении автомобиля водитель увеличивает и уменьшает поступление топливно-воздушной смеси в зону сгорания, переключает передачи трансмиссии, притормаживает. Всё это влияет на текущую мощность двигателя. Поэтому в физике различают мгновенную мощность – мощность, измеренную за промежуток времени достаточно малый, чтобы считать ее величину постоянной:

$P = limlimits_{t to 0}frac{Delta A}{Delta t}$,

где $Delta t$ – промежуток времени, $Delta A$ – проделанная за это время работа.

Поскольку мгновенные величины мощности могут меняться без какой-либо четко выраженной закономерности, подсчитать их среднее значение бывает затруднительно. Поэтому среднюю мощность находят просто как

${langle}Prangle = frac{Delta A}{Delta t}$.

Следует различать мощность, связанную с общими затратами на движение и ту, что развивается для выполнения полезной работы. Так, один и тот же груз с одной и той же скоростью на одно и то же расстояние можно перевезти разными способами, например, на старинном паровозе и современном электровозе. Полезная работа будет выполнена одинаковая, но интенсивность затрат энергии – различная. Поэтому существует понятие средней полезной мощности, расчет которой зависит от многих факторов, связанных с особенностями движителей и сред, в которых выполняется работа.

Мощность на резисторе в цепи переменного тока

По закону Джоуля-Ленца, мгновенное значение тепловой мощности на участке цепи определяется как произведение силы тока на напряжение:

Эта величина непрерывно изменяется. В промышленной сети частота изменения равна 50 Гц, то есть 50 раз в секунду изменяется значение тепловой мощности. Поэтому практического значения знание мгновенной мощности не имеет.

Вычислим среднее значение мощности за период колебаний:

Введем определение:

Действующим значением силы тока (или напряжения) называется сила такого постоянного тока (или напряжения), который, протекая по данной цепи, выделяет в ней мощность, равную средней мощности в цепи переменного тока за период

Средняя мощность, выделяющаяся на резисторе в цепи переменного тока за период, равна произведению действующего значения силы тока на действующее значение напряжения.

Домашнее задание Повторить: конденсатор, емкость конденсатора, единицы измерения электроемкости, энергия заряженного конденсатора, последовательное и параллельное соединение конденсаторов, энергия электрического поля заряженного конденсатора, закон Ома для участка цепи.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

11 класс

§ 34. Резистор в цепи переменного тока. Действующие значения силы тока и напряжения

Резистор в цепи переменного тока.

Пусть электрическая цепь состоит из проводников (резисторов) с малой индуктивностью и большим сопротивлением R. Например, такой цепью может быть нить накаливания электрической лампы и подводящие к ней провода. Величину R, которую мы до сих пор называли сопротивлением, теперь будем называть активным сопротивлением. Итак, в цепи имеется резистор, активное сопротивление которого R, а катушка индуктивности и конденсатор отсутствуют (рис. 6.17).

Напряжение на концах цени меняется но гармоническому закону:

Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому можно считать, что мгновенное значение силы тока определяется законом Ома:

Следовательно, в проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения (рис. 6.18), а амплитуда колебаний силы тока:

При небольших значениях частоты переменного тока активное сопротивление проводника не зависит от частоты. Можно считать, что оно практически совпадает с сопротивлением в цепи постоянного тока.

Действующие значения силы тока и напряжения.

При совпадении фазы колебаний силы тока и напряжения мгновенная мощность переменного тока равна р = i 2 R.

C учётом формулы (1) можно записать:

Понятно, что мгновенная мощность с течением времени непрерывно изменяется. Определим среднюю мощность переменного тока, выделяемую на резисторе за период:

Среднее значение функции sin 2 ωt за период равно 1/2, поэтому

Данная формула позволяет ввести физические величины, характеризующие переменный ток с точки зрения мощности.

Действующим значением I силы переменного тока называют квадратный корень из среднего квадрата силы тока:

Действующее значение переменного напряжения определяется подобным образом:

В формулах (2) и (3) I_m и U_m — амплитудные значения силы переменного тока и переменного напряжения.

Средняя мощность переменного тока при совпадении фаз колебаний силы тока и напряжения равна произведению действующих значений силы тока и напряжения:

Формулы (4), полученные через действующие значения, полностью аналогичны формулам для мощности постоянного тока (см. § 5 «Работа и мощность электрического тока. Закон Джоуля — Ленца»).

Отметим, что амперметр может измерять силу тока только в цепях постоянного тока. При включении его в цепь переменного тока он покажет нуль. «Это связано с тем, что стрелка обладает инертностью и не успевает отклоняться в такт с изменением силы тока. Поэтому амперметры и вольтметры градуируют таким образом, чтобы они показывали действующее значение силы тока и напряжения. Конечно, можно было бы охарактеризовать силу тока и напряжение амплитудами, а не действующими значениями. Но действующие значения непосредственно определяют мощность переменного тока в цепи.

Действующее значение силы переменного тока равно силе постоянного тока, выделяющего в цепи такое же количество теплоты, что и переменный ток за то же время.

Вопросы:

1. Какое сопротивление называют активным?

2. Как соотносятся между собой фазы колебаний силы переменного тока в резисторе и переменного напряжения между его выводами?

3. Чем определяется мощность в цепи переменного тока?

4. Что называют действующим значением:

а) силы переменного тока;

б) переменного напряжения?

5. Почему амперметры и вольтметры градуируют в действующих значениях силы тока и напряжения?

Вопросы для обсуждения:

1. Что покажет вольтметр при его включении в цепь переменного тока?

2. В чём состоит отличие амперметров и вольтметров для переменного и постоянного токов?

Пример решения задачи

Сила переменного тока в электрической цепи изменяется по закону i(t) = 0,564sin 4πt (А). Какое количество теплоты выделится в проводнике с активным сопротивлением 15 Ом за время, равное 10 периодам колебаний тока?

Таким образом, нас интересует количество теплоты, выделившееся в проводнике за Δt = 10T = 5 с.

В проводнике выделится такое же количество теплоты, как если бы по нему протекал не переменный, а постоянный ток, такой что

По закону Джоуля — Ленца:

Подставляя числовые данные, получим:

Ответ: Q = 12 Дж.

Упражнения:

1. В цепь переменного тока стандартной частоты с действующим значением напряжения 220 В включено активное сопротивление, равное 50 Ом. Найдите действующее и амплитудное значения силы тока. Запишите уравнения зависимости напряжения и силы тока от времени.

2. На участке цепи с активным сопротивлением 4 Ом сила тока изменяется по закону i(t) = 6,4sin10πt (А). Определите действующее значение силы тока и мощность, выделяющуюся на этом участке. Запишите уравнение зависимости u = u(t).

3. Напряжение в сети изменяется по закону u(t) = 310sin10πt (В). Какое количество теплоты отдаёт за 1 мин электрическая плитка с активным сопротивлением 60 Ом, включённая в эту сеть?

Источник

Мощность резистора

Как рассчитать мощность резистора?

У резистора есть довольно важный параметр, который целиком и полностью влияет на надёжность его работы. Этот параметр называется мощностью рассеивания. Он уже упоминался в статье о параметрах резистора.

Сама по себе мощность постоянного тока рассчитывается по простой формуле:

Как видим, мощность зависит от напряжения и тока. В реальной цепи через резистор протекает определённый ток. Поскольку резистор обладает сопротивлением, то под действием протекающего тока резистор нагревается. На нём выделяется какое-то количество тепла. Это и есть та мощность, которая рассеивается на резисторе.

Если в схему установить резистор меньшей мощности рассеивания, чем требуется, то резистор будет нагреваться и в результате сгорит. Поэтому, если в схеме нужно заменить резистор мощностью 0,5 Ватт, то ставим на 0,5 Ватт и более. Но никак не меньше !

Каждый резистор рассчитан на свою мощность. Стандартный ряд мощностей рассеивания резисторов состоит из значений:

Чем больше резистор по размерам, тем, как правило, на большую мощность рассеивания он рассчитан.

Допустим, у нас есть резистор с номинальным сопротивлением 100 Ом. Через него течёт ток 0,1 Ампер. На какую мощность должен быть рассчитан этот резистор?

Тут нам потребуется формула. Выглядит она так:

R_(Ом) – сопротивление цепи (в данном случае резистора);

I_(А) – ток, протекающий через резистор.

Все расчёты следует производить, строго соблюдая размерность. Так, если сопротивление резистора не 100 Ом, а 1 кОм, то в формулу нужно подставить значение в Омах, т.е. 1000 Ом (1 кОм = 1000 Ом). Тоже правило касается и других величин (тока, напряжения).

Рассчитаем мощность для нашего резистора:

Мы получили мощность 1 Ватт. Теперь небольшое отступление.

В реальную схему необходимо устанавливать резистор с мощностью в полтора – два раза выше рассчитанной.

Поэтому нам подойдёт резистор мощностью 2 Вт (см. стандартный ряд мощностей резисторов).

Также есть и другая формула для расчёта мощности. Она применяется в том случае, если неизвестен ток, который протекает через резистор.

Всё бы хорошо, но в жизни бывают случаи, когда применяется последовательное или параллельное соединение резисторов. Как рассчитать мощность рассеивания для каждого из резисторов в последовательной или параллельной цепи?

Допустим, нам требуется заменить резистор сопротивлением 100 Ом. Протекающий через него ток равен 0,1 Ампер. Следовательно, мощность этого резистора 1 Ватт.

Для его замены можно применить два соединённых последовательно резистора сопротивлением 20 Ом и 80 Ом. На какую мощность должны быть рассчитаны эти резисторы?

Для последовательной цепи действует одно правило. Через последовательно соединённые резисторы течёт один и тот же ток. Теперь применим формулу для расчёта мощности и получим, что мощность рассеивания резистора на 20 Ом должна быть равна 0,2 Вт, а резистора на 80 Ом — 0,8 Вт. Выбираем резисторы согласно стандартному ряду мощностей:

Как видим, если сопротивления резисторов будут разные, то и мощность на них будет выделяться разная.

Мощность, рассеивающаяся на резисторе, зависит в первую очередь от тока, который течёт через данный резистор. А ток зависит от сопротивления резистора. Поэтому, если вы соединяете последовательно резисторы разных номиналов, то и рассеивающаяся мощность распределиться между ними.

Это обстоятельство необходимо учитывать при самостоятельном конструировании электронных самоделок иначе при неправильном подборе резисторов может получиться так, что на одном резисторе выделиться больше мощности, чем на другом, и он будет работать в тяжёлом температурном режиме.

Чтобы не ломать голову и не рассчитывать мощность каждого в отдельности резистора, можно поступать так:

Мощность каждого резистора, входящего в составляемую нами цепь (параллельную или последовательную) должна быть равна мощности заменяемого резистора. Иными словами, если нам надо заменить резистор, мощностью 1 Вт, то каждый из резисторов для его замены должен иметь мощность не менее 1 Ватта. На практике это самое быстрое и эффективное решение.

Для параллельного соединения резисторов нужно учитывать, что через резистор с меньшим сопротивлением протекает больший ток. Следовательно, и мощности на нём будет рассеиваться больше.

Источник

Мощность на резисторе в цепи переменного тока

По закону Джоуля-Ленца, мгновенное значение тепловой мощности на участке цепи определяется как произведение силы тока на напряжение:

Эта величина непрерывно изменяется. В промышленной сети частота изменения равна 50 Гц, то есть 50 раз в секунду изменяется значение тепловой мощности. Поэтому практического значения знание мгновенной мощности не имеет.

Вычислим среднее значение мощности за период колебаний:

Действующим значением силы тока (или напряжения) называется сила такого постоянного тока (или напряжения), который, протекая по данной цепи, выделяет в ней мощность, равную средней мощности в цепи переменного тока за период

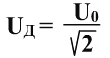
Средняя мощность, выделяющаяся на резисторе в цепи переменного тока за период, равна произведению действующего значения силы тока на действующее значение напряжения.

Домашнее задание Повторить: конденсатор, емкость конденсатора, единицы измерения электроемкости, энергия заряженного конденсатора, последовательное и параллельное соединение конденсаторов, энергия электрического поля заряженного конденсатора, закон Ома для участка цепи.

Лекция 6 Конденсатор в цепи переменного тока

Включим конденсатор в цепь постоянного тока. Некоторый заряд перетечет от источника тока на обкладки конденсатора. В цепи возникает кратковременный импульс зарядного тока. Конденсатор заряжается до напряжения источника, после чего ток прекращается. Через конденсатор постоянный ток течь не может!

Р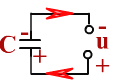ассмотрим процессы, происходящие при включении конденсатора в цепь переменного тока

Через диэлектрик, разделяющий обкладки конденсатора, электрический ток протекать, как и прежде, не может. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора в цепи появится переменный ток.

Если напряжение в цепи изменяется по гармоническому закону,

то заряд на обкладках конденсатора изменяется

также по гармоническому закону

и силу тока в цепи можно найти как производную заряда

Из полученной формулы видно, что в любой момент времени

фаза тока больше фазы напряжения на π/2.

В цепи переменного напряжение на конденсаторе тока отстает по фазе от тока на π/2, или на четверть периода.

Емкостное сопротивление

Величину

называют емкостным сопротивлением.

Связь между амплитудными значениями силы тока и напряжения формально совпадает с законом Ома для участка цепи

Такое же соотношение выполняется для действующих значений силы тока и напряжения.

Емкостное сопротивление конденсатора зависит от частоты переменного напряжения. С увеличением частоты колебаний напряжения емкостное сопротивление уменьшается, поэтому амплитуда силы тока увеличивается прямо пропорционально частоте I₀ = CU₀ω.

При уменьшении частоты амплитуда силы тока уменьшается и при ω=0 обращается в 0. Отметим, что нулевая частота колебаний означает, что в цепи протекает постоянный ток.

Источник

• ГДЗ

• 10 класс

• Физика

• Рымкевич 10-11

• 379

Подробное решение задание 379 по физике задачник для учащихся 10 класса, авторов А.П. Рымкевич 2016

показать содержание

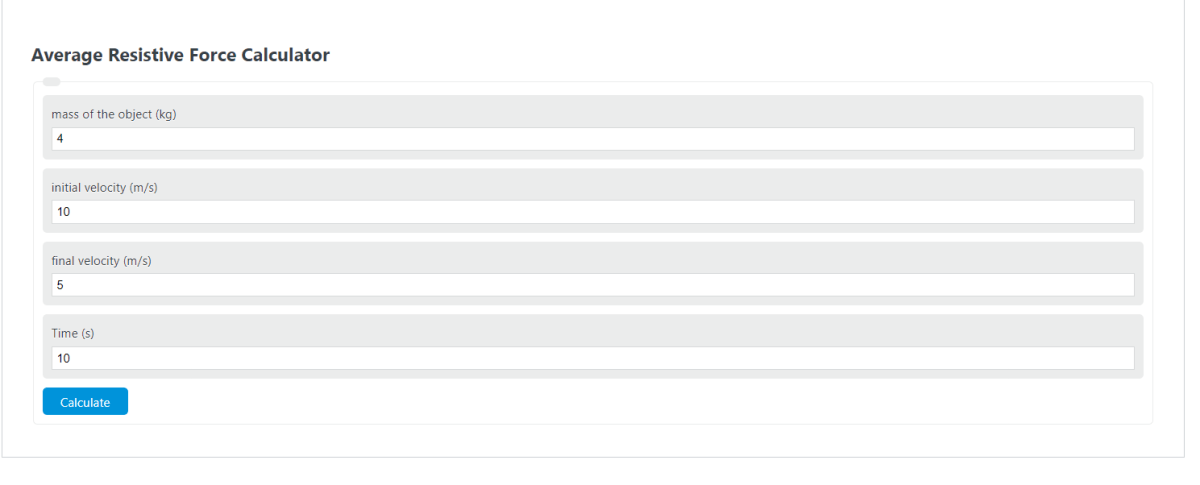
Unit Converter