Как найти среднюю мощность силы трения

Условие задачи:

Шайба массы 0,1 кг, пущенная по льду с начальной скоростью 0,5 м/с, остановилась через 5 с. Чему равна средняя мощность силы трения за время движения шайбы?

Задача №2.7.51 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(m=0,1) кг, (upsilon_0=0,5) м/с, (t=5) с, (N_ср-?)

Решение задачи:

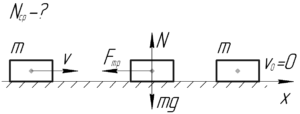Среднюю мощность силы трения (N_{ср}) можно определить как отношение работы (A), совершенной силой трения, ко времени движения (t).

[{N_{ср}} = frac{A}{t};;;;(1)]

Работу силы трения (A) определим по теореме об изменении кинетической энергии тела. Согласно этой теореме работа этой силы равна изменению кинетической энергии шайбы.

[A = 0 – frac{{m{upsilon ^2}}}{2} =  – frac{{m{upsilon ^2}}}{2}]

Понятно, что работа силы трения отрицательна, так как вектор силы трения (overrightarrow {{F_{тр}}}) направлен противоположно вектору перемещения (overrightarrow {S}). В формулу (1) мы подставим абсолютное значение работы.

[{N_{ср}} = frac{{m{upsilon ^2}}}{{2t}}]

Задача решена в общем виде. Посчитаем ответ:

[{N_{ср}} = frac{{0,1 cdot {{0,5}^2}}}{{2 cdot 5}} = 2,5 cdot {10^{ – 3}};Вт = 2,5;мВт]

Ответ: 2,5 мВт.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.7.50 Для растяжения недеформированной пружины на 1 см требуется сила, равная 30 Н
2.7.52 На тело массы 5 кг действует постоянная сила 10 Н. Чему будет равна кинетическая
2.7.53 Какой кинетической энергией обладает свободно падающее тело массой 0,1 кг

Лабораторная работа №1

Исследование зависимости силы трения скольжения от веса тела

   Цель работы: 1. выяснить, зависит ли сила трения скольжения от силы нормального давления, если зависит, то как.

                           2. Определить коэффициент трения дерева по дереву.

   Приборы и материалы: динамометр, деревянный брусок, деревянная линейка или деревянная плоскость, набор грузов по 100 г.

 Выполнение работы.

1. Определили цену деления шкалы динамометра.

Цена деления динамометра: 

(2H-1H)/10 дел = 0,1Н/дел

2. Определили массу бруска. Сначала подвесив брусок к динамометру нашли вес бруска   Pбруска=0,7Н

Зная, что  P=mg  и   g=10м/с²   получим m_бруска=P/g 

m_бруска=0,7Н/10м/с²=0,07кг

Определяем общий вес тела (силу нормального давления по формуле:

Р=N=(m1+m2)∙g

1.Р=N=(0,07кг+0,1кг)∙10м/с2=1,7Н

2.Р=N=(0,07кг+0,2кг)∙10м/с2=2,7Н

3.Р=N=(0,07кг+0,3кг)∙10м/с2=3,7Н

4.Р=N=(0,07кг+0,4кг)∙10м/с2=4,7Н

5.Р=N=(0,07кг+0,5кг)∙10м/с2=5,7Н

Провели измерения силы трения.

5. Подготовили таблицу для записи результатов измерений и вычислений:

№ опыта	Масса бруска, m1 , кг	Масса груза, m2 , кг	Общий вес тела  (сила нормального давления), Р=N=(m1+m2)g, Н	Сила трения, Fтр, Н	Коэффициент трения, μ	Среднее значение коэффициента трения, μср
1	0,07	0,1	1,7	0,4
2	0,2	2,7	0,6
3	0,3	3,7	0,8
4	0,4	4,7	1
5	0,5	5,7	1,2

6. Из опыта видим, что сила трения зависит от силы нормального давления прямо пропорционально(т.е. чем больше сила нормального давления, тем больше сила трения)

7. В каждом опыте рассчитали коэффициент трения по формуле: . 

μ=0,4Н/1,7Н=0,235

μ=0,6Н/2,7Н=0,222

μ=0,8Н/3,7Н=0,216

μ=1,0Н/4,7Н=0,213

μ=1,2Н/5,7Н=0,211

Результаты расчётов занесли в таблицу.

8. По результатам измерений построили график зависимости силы трения от силы нормального давления: 

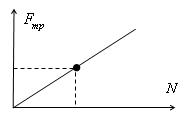
Определили по графику средние значения силы трения и силы нормального давления:

N=3Н

Fтр=0,68Н

Вычислили среднее значение коэффициент трения:

μ_ср=0,68Н/3Н=0,227

Вывод: мы определили, что сила трения зависит от силы нормального давления прямо пропорционально(т.е. чем больше сила нормального давления, тем больше сила трения). Коэффициент трения дерева по дереву получился равен 0,227

Ответы на контрольные вопросы.

1. Что называется силой трения?

Сила трения – это сила, которая возникает в том месте, где тела соприкасаются друг с другом, и препятствует перемещению тел.

2. Какова природа сил трения?

Сила трения – это сила электромагнитной природы.

3. Назовите основные причины, от которых зависит сила трения?

Возникновение силы трения объясняется двумя причинами:

   1) Шероховатостью поверхностей
   2) Проявлением сил молекулярного взаимодействия.

4. Перечислите виды трения.

Силы трения подразделяются на силы трения покоя, скольжения, качения.

5. Можно ли считать явление трения вредным? Почему?

Лист 2.

Расскажите о силовом расчете механизма (задача силового расчета, использованный метод и основные уравнения).

Ответ:основной задачей силового расчета является определение реакций в кинематических парах. Для решения этой задачи была численно решена система уравнений, составленная из уравнений движения звеньев и замыкающих уравнений. Для одного положения была сделана проверка с использованием графических методов.

2. Как вы определяли главные векторы и главные моменты инерции для каждого из звеньев рычажного механизма?

Ответ:аналитически – по рассчитанным кинематическим функциям, графически – по векторным уравнениям скоростей и ускорений.

3. В какой последовательности выполнен силовой расчет механизма? Как использовалось условие статической определимости группы звеньев?

Ответ:силовой расчет в графике сделан, начиная с последней группы Ассура.

4. Проанализируйте векторные уравнения сил, использованные при силовом расчете. В чем состояла цель силового анализа и как она была достигнута?

Ответ:Насчет уравнений – см. силовые многоугольники на чертеже. Цель состояла в определении реакций. Они были определены путем решения векторных уравнений.

5. Была ли проведена вами оценка погрешностей вычислений при силовом расчете относительно расчетов, выполненных при определении закона движения механизма под действием заданных сил? Каковы результаты этой оценки.

Ответ:проверка было проведена, погрешность составила 3,2%.

6. В какой последовательности выполнен силовой расчет с учетом сил трения в кинематических парах? От каких параметров зависят силы трения в кинематических парах?

Ответ:сила трения в данном механизме возникает только в поступательной паре. Она зависит от нормальной силы реакции. Эта сила, как и сила трения, определяется заранее из кинематических функций, а затем вводится в матрицу как внешний фактор.

7. Как определить механический коэффициент полезного действия? Как определить среднюю мощность сил трения в механизме?

Ответ:КПД определяем как отношение выходной мощности ко входной. Мощность сил трения определяем как среднюю за период разность между входной и выходной мощностью.

Поясните, как влияет угловое ускорение звеньев первой группы на реакции в кинематических парах входного звена.

Ответ:при одинаковом движущем моменте составляем уравнения моментов относительно центров кинематических пар. В результате имеем зависимости между угловым ускорением и реакциями.

Дата добавления: 2015-01-05 ; просмотров: 14 | Нарушение авторских прав

iSopromat.ru

Силовой расчет механизмов относится к решению первой задачи динамики. Как видно из содержания задач динамики, приведенного выше, первая задача включает в себя две части: изучение сил, действующих на звенья механизма; определение неизвестных сил при заданном законе движения на входе (эта вторая часть и есть задача силового расчета).

В целях дальнейшего понимания терминологии и систематизации материала целесообразно повторить известные из физики и теоретической механики сведения о силах, а также ввести некоторые новые (применяемые в теории механизмов и машин) понятия. С точки зрения решения задач динамики силы (в данном случае под силой понимается обобщенное понятие силового фактора – собственно сила или момент) можно классифицировать следующим образом:

а) по взаимодействию звена механизма с другими объектами. По этому признаку силы подразделяются на внешние и внутренние:

• внешние силы – это силы взаимодействия звена механизма с какими-то телами или полями, не входящими в состав механизма;
• внутренние силы – это силы взаимодействия между звеньями механизма (реакции в кинематических парах);

б) по мощности, развиваемой силой. По этому признаку силы делятся на силы движущие и силы сопротивления (рисунок 16):

• движущая сила – это сила, которая помогает движению звена и развивает положительную мощность;
• сила сопротивления препятствует движению звена и развивает отрицательную мощность.

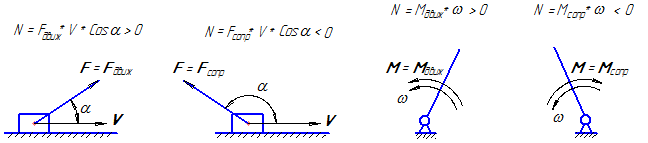
В свою очередь силы сопротивления можно разделить на силы полезного сопротивления и силы вредного сопротивления:

• силы полезного сопротивления – это силы, для преодоления которых и создан механизм. Преодолевая силы полезного сопротивления, механизм создает полезную работу (например, преодолевая сопротивления резанию на станке, добиваются необходимого изменения формы детали; или, преодолевая сопротивление воздуха в компрессоре, сжимают его до требуемого давления и т.д.);
• силы вредного сопротивления – это силы, на преодоление которых затрачивается мощность и эта мощность теряется безвозвратно. Обычно в качестве вредных сил сопротивления выступают силы трения, гидравлического и аэродинамического сопротивлений.

Работа по преодолению этих сил переводится в тепло и рассеивается в пространство, поэтому коэффициент полезного действия любого механизма всегда меньше единицы;

в) силы веса – это силы взаимодействия звеньев механизма с гравитационным полем земли;

г) силы трения – силы, сопротивляющиеся относительному перемещению соприкасающихся поверхностей;

д) силы инерции – силы, возникающие при неравномерном движении звена и сопротивляющиеся его ускорению (замедлению). Сила инерции действует на то тело, которое заставляет ускоряться (замедляться) данное звено. В общем случае при неравномерном движении возникает сила инерции и момент сил инерции:

где
F_ин – главный вектор сил инерции, приложенный в центре масс звена;
M_ин – главный момент сил инерции;
m – масса звена;
I_s – момент инерции звена относительно центра масс;
a_s – ускорение центра масс звена;
e – угловое ускорение звена.

Знак минус в формулах показывает, что сила инерции направлена противоположно ускорению центра масс звена, а момент сил инерции направлен противоположно угловому ускорению звена. Знак силы или момента учитывается только при установлении истинного направления силы или момента на расчетной схеме, а в аналитических вычислениях используется абсолютные их значения.

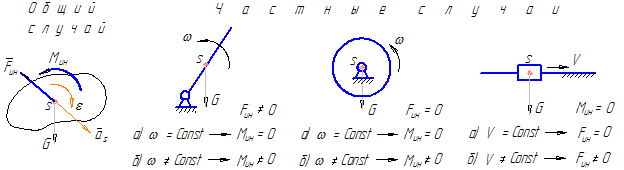
При силовом анализе механизмов могут встретиться различные случаи, когда один или оба силовых инерционных фактора могут иметь нулевое значение. На рисунке 17, приведенном выше, показаны некоторые случаи возникновения сил и моментов сил инерции при движении звеньев механизма.

Непосредственно силовой расчет сводится к определению неизвестных сил, действующих на звенья механизма. Как известно из теоретической механики для определения неизвестных сил используются уравнения статики.

Механизм же является неравновесной системой, т.к. большинство его звеньев имеет неравномерное движение, а точки, принадлежащие этим звеньям, движутся по сложным криволинейным траекториям (напомним: состояние равновесия – это состояние покоя или прямолинейного равномерного движения).

Поэтому для решения поставленной задачи применяется метод кинетостатики.

Метод кинетостатики основан на принципе Даламбера: если ко всем внешним силам, действующим на звенья механизма, добавить силы инерции и моменты сил инерции, то данный механизм будет находиться в состоянии статического равновесия. То есть это искусственный прием, приводящий неравновесную систему в состояние равновесия.

Искусственность приема заключается в том, что силы инерции прикладываются не к тем телам, которые заставляют двигаться звенья ускоренно (замедленно), а к самим звеньям.

Применив этот прием, в дальнейшем можно производить силовой расчет с использованием уравнений статики. Однако, чтобы решить задачу с помощью только уравнений равновесия, система должна быть статически определимой.

Условие статической определимости плоской кинематической цепи:

Для каждого звена, расположенного в плоскости, можно составить три независимых уравнения статики. Если в кинематической цепи имеется «n» подвижных звеньев, то в совокупности для этой цепи можно записать 3n независимых уравнений статики (равновесия). Эти уравнения используются для определения реакций в кинематических парах и неизвестных внешних сил.

На плоскости существуют кинематические пары только пятого и четвертого классов. Пары пятого класса представлены вращательной кинематической парой (шарниром) и поступательной парой (соединение ползуна с направляющей). В шарнире усилие между звеньями может передаваться в любом направлении, поэтому у реакции в шарнире неизвестными являются величина и направление (два компонента), т.е. для определения полной реакции во вращательной паре надо затратить два уравнения статики.

В первом приближении расчет ведется без учета сил трения. В этом случае перемещению ползуна вдоль направляющей ничто не препятствует. Перемещаться же поперек направляющей и поворачиваться ползун не может, поэтому в поступательной паре реакция направлена перпендикулярно направляющей и возникает реактивный момент, препятствующий повороту ползуна.

При силовом расчете обычно реактивный момент не определяют, а находят условную точку приложения реакции (произведение реакции на расстояние до ее условной точки приложения и есть реактивный момент). На определение реакции в поступательной паре также надо затратить два уравнения статики (определить два компонента – величину и точку приложения). Таким образом, на определение полной реакции в кинематической паре пятого класса необходимо затратить два уравнения статики.

Пары четвертого класса (высшие пары) на плоскости представляют соприкасающиеся между собой профили. В высшей паре усилие между звеньями передается по общей нормали к касающимся профилям (без учета сил трения). Поэтому в высшей паре четвертого класса реакция неизвестна только по величине (точка приложения реакции в точке контакта профилей, направление вдоль общей нормали к этим профилям).

Таким образом, для определения реакции в паре четвертого класса надо затратить одно уравнение статики (определить один компонент – величину реакции).

Если в кинематической цепи количество пар пятого класса равно Р₅, то на определение реакций во всех этих парах надо затратить 2Р₅ уравнений статики. На определение реакций во всех парах четвертого класса используется число уравнений, равное количеству этих пар Р₄.

Таким образом, из 3n независимых уравнений статики 2Р₅ уравнений используются для определения реакций в парах пятого класса и Р₄ – для определения реакций в парах четвертого класса. Оставшиеся уравнения используются для определения неизвестных внешних сил, действующих на звенья механизма.

Пусть X – число уравнений, оставшихся для определения неизвестных внешних сил, тогда

но эта формула совпадает с формулой Чебышева для определения числа степеней свободы плоской кинематической цепи. В результате можно сформулировать условие статической определимости кинематической цепи следующим образом: кинематическая цепь статически определима в том случае, когда число неизвестных внешних сил, действующих на ее звенья, не превышает числа степеней свободы этой цепи.

Так как методы решения разработаны для групп Ассура, то необходимо сформулировать условие статической определимости группы Ассура. Группа Ассура – это кинематическая цепь, имеющая собственную степень свободы, равную нулю. Поэтому группа Ассура статически определима, если на ее звенья не действуют неизвестные внешние силы.

Уравнений в группе Ассура достаточно лишь для определения реакций в кинематических парах. Это обстоятельство предопределяет порядок силового расчета механизма:

1. разбивают механизм на группы Ассура, взяв в качестве начального то звено, на которое действует неизвестная внешняя сила;
2. решение начинают с последней присоединенной группы и заканчивают начальным звеном.

При таком подходе на группы Ассура всегда будут действовать только известные внешние силы и из рассмотрения их равновесия будут определены реакции в кинематических парах, а из рассмотрения условий равновесия начальных звеньев будут определены оставшиеся реакции и неизвестные внешние силы.

Поскольку решение ведется по группам Ассура, то ниже рассматривается принцип силового расчета групп на примере групп второго класса.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Задача силового расчета используемый метод и основные уравнения

Лекция 4. Силовой ( кинетостатический ) анализ механизмов.

Общие сведения и определения

Проектирование нового механизма всегда включает его силовое исследование, так как по найденным силам производится последующий расчет на прочность элементов кинематических пар и звеньев механизма.

При проведении силового анализа решаются основные задачи:

1. Определение реакций в кинематических парах механизмов, находящихся под действием заданных внешних сил. Эти реакции затем используются для расчёта звеньев и элементов кинематических пар (например, подшипников) на прочность, жёсткость, долговечность и т.д.

2. Определение уравновешивающей силы или уравновешивающего момента , приложенных к ведущему звену. Они уравновешивают внешние силы, приложенные к механизму. Эти величины нужны, например, для выбора двигателя, приводящего в движение данный механизм.

3. Дополнительно выясняют вопросы об уравновешенности механизма, износе его звеньев, о потерях на трение в отдельных кинематических парах, о коэффициенте полезного действия механизма в целом и др.

При силовом анализе, кроме основной (полезной) нагрузки на рабочий орган, необходимо учитывать силы тяжести звеньев, их силы инерции, силы трения в кинематических парах.

Силовой расчет ведется методом кинетостатики. В отличие от статического , кинетостатический расчет механизмов наряду с внешними силами (движущими силами, силами полезных и вредных сопротивлений, силами тяжести) учитывает и силы инерции масс звеньев.

Метод кинетостатики основан на принципе Даламбера, который применительно к механизмам можно сформулировать так: если ко всем внешним силам, действующим на систему звеньев, добавить силы инерции, тогда под действием всех этих сил система звеньев может условно считаться находящейся в равновесии.

При кинетостатическом расчете кинематическая цепь механизма разбивается на группы Ассура , которые являются статически определимыми. Расчет ведется путем последовательного рассмотрения условий равновесия отдельно каждой группы, начиная с наиболее удаленной от исходного механизма (ведущего звена), последним рас c читывается ведущее звено.

При рассмотрении условий равновесия группы без учета силы трения составляющие реакции во внешней вращательной паре представляются направленными по звену (нормальная реакция) и перпендикулярно звену (тангенциальная реакция) и приложены они в центре шарнира, во вращательной паре подлежат определению величины и направления нормальной и тангенциальной реакций.

В поступательной паре, в общем случае, подлежат определению величина и точка приложения реакции, так как известно только то, что направление реакций всегда перпендикулярно оси направляющих пары.

Анализ свойств механизма можно получить путем исследования каждой группы Ассура через 10 градусов (20 градусов или 30 градусов) угла поворота кривошипа. В этом случае выявляется полная картина силового нагружения всех подвижных соединений механизма и звеньев за цикл движения машины.

Цикл – промежуток времени, по истечении которого все кинематические параметры принимают первоначальное значение, а технологический процесс, происходящий в рабочей машине, начинает повторяться вновь.

Классическая задача силового анализа механизма обычно решается при таких исходных данных:

1) Кинематическая схема механизма.

2) Размеры и иные геометрические параметры звеньев.

3) Законы движения входных звеньев.

4) Массы и моменты инерции звеньев.

5) Силы и моменты полезных сопротивлений.

В дальнейшем будем считать, что к моменту начала силового расчета механизма выполнен его полный кинематический анализ и рассчитаны веса звеньев, их инерционные силы и моменты, а силы и моменты полезных сопротивлений заданы.

Этапы кинетостатического расчёта

Различают два этапа кинетостатического расчёта:

– Расчёт механизма без учёта потерь на трение в кинематических парах.

– После конкретного конструирования узлов производится дополнительный расчёт потерь мощности в кинематических парах на преодоление трения.

Итогом кинетостатического расчёта является определение движущей силы на ведущем звене, которая даёт возможность определить крутящий момент по формуле и мощность, по формуле: .

Полная мощность определяется по формуле: . По значению полной мощности выбирается мощность двигателя.

Порядок проведения кинетостатического расчёта:

1. Определение степени подвижности механизма.

2. Для каждого отдельного положения механизма внутри цикла его работы строятся планы скоростей и планы ускорений. С помощью планов ускорений определяются ускорения центров масс.

3. Механизм раскладывается на структурные группы Ассура .

4. Производится кинетостатический расчёт отдельных структурный групп начиная с последней , постепенно приближаясь к ведущему звену.

5. Кинетостатический расчёт ведущего звена.

6. Определение крутящего момента или движущей силы на ведущем звене.

7. Определение мощности двигателя.

8. Пункты 4-7 повторяются для множества положений механизма за полный цикл его работы.

9. Выбираются наибольшие значения мощности и усилий, действующие в кинематических парах.

10. На основании полученных данных составляется задание на проектирование.

Силы, действующие в механизмах

Различают две группы внешних сил.

Движущие силы Р_дв или моменты движущих сил М_дв , которые:

– совершают положительную работу;

– направлены в сторону скорости точки приложения силы или под острым углом к ней;

– задаются посредством механической характеристики двигателя.

Пример: силы давления газа на поршень в двигателе внутреннего сгорания, силы веса при опускании груза и т.д.

Силы сопротивления Р_С и их моменты М_С, которые:

– совершают отрицательную работу;

– направлены противоположно скорости.

В свою очередь силы сопротивления делятся на силы:

– полезного сопротивления Р_{п .с} и моменты М_п.с (силы тяжести при подъеме груза);

– вредного сопротивления: трение в кинематических парах, сопротивление среды, внутреннее сопротивление (например, силы упругости звеньев).

Кроме этого существуют:

– силы веса (тяжести) , где – масса звена в кг; м/с 2 – ускорение свободного падения. При кинематическом исследовании считают, что сила тяжести приложена в центре тяжести звена. Если звено выполнено в виде стержня, то его ц.т . расположен в центре симметрии звена, а если в виде ползуна, то в центре шарнира. Силы тяжести в течени и расчётного цикла могут быть как движущими, так и силами полезного сопротивления, поэтому работа этих сил за цикл равна нулю. Эти силы считаются внешними силами.

– силы инерции ;

– моменты сил инерции , где m , J_S – масса и массовый момент инерции звена; и – линейное и угловое ускорения;

– силы реакций в кинематических парах , возникающие в опорах звеньев и являющиеся внутренними силами для механизма в целом и внешними для каждого отдельного звена.

Необходимо отметить, что под силами понимаются равнодействующие соответствующих распределенных в месте контакта кинематической пары нагрузок. Все вышесказанное относительно сил распространяется и на моменты сил.

Силы инерции звеньев и моменты сил инерции. Так как звенья механизма находятся в движении, и имеют свои массы, то, особенно в быстродействующих механизмах рычажного типа, обязательно имеет место неравномерность движения звеньев. Это означает, что ускорения этих звеньев не равны нулю, что приводит к возникновению дополнительных сил динамического характера в виде сил инерции и моментов инерции . Из теоретической механики известно, что все силы инерции звена, совершающего плоскопараллельное движение и имеющего плоскость симметрии, параллельную плоскости движения, могут быть сведены к силе инерции , приложенной в центре масс S звена, и паре сил инерции, момент которых обозначим (рис. 4.1).

Рис. 4.1. Сила инерции звена и момента сил инерции

– главный вектор сил инерции, или сила инерции;

– главный момент сил инерции, или момент сил инерции; m – масса звена;

– массовый момент инерции относительно центра масс;

– ускорение центра масс;

– угловое ускорение звена.

и направлены в стороны, противоположные ускорениям и .

Для дальнейших расчётов удобно заменить и одной силой, использовав для этого 3 метода:

Перенос силы на плечо : момент сил инерции заменяется парой сил с плечом h_u (рис. 4.2), причём одна сила приложена к центру масс звена S и направлена противоположно преобразуемой силе , а другая смещена на плечо h_u и приложена к точке К – центру качания звена.

Рис. 4.2. Перенос силы на плечо при замене силы и момента одной силой

Определение центра качания звена через мгновенный центр ускорений (МЦУ). При этом сила инерции переносится параллельно самой себе на расстояние (рис. 4.3), вычисленное по формуле

, мм ,

где – мгновенный центр ускорений звена; откладывается в сторону, являющуюся продолжением отрезка .

Рис. 4.3. Определение центра качания звена

Метод замещающих точек. Подробно рассмотрен в литературе.

Рассмотрим определение сил и моментов в различных случаях.

;

; ;

; .

;

; ;

; .

;

; ;

; .

;

; ;

; .

;

; ;

; .

;

; ;

; .

Статическая определимость кинематической цепи

При силовом анализе механизмов (определении неизвестных сил, действующих на движущиеся звенья) можно использовать уравнения (законы) статики. Докажем это положение, проанализировав реакции в кинематических парах (табл.).

[spoiler title=”источники:”]

http://www.teormach.ru/lect4.htm

[/spoiler]