Допустим, что все значения
количественного признака X
совокупности,
безразлично-генеральной или выборочной,
разбиты на несколько групп. Рассматривая
каждую группу как самостоятельную
совокупность, можно найти ее среднюю
арифметическую.
Групповой средней называют среднее
арифметическое значений признака,
принадлежащих группе.
Теперь целесообразно ввести специальный
термин для средней всей совокупности.
Общей средней
называют среднее
арифметическое значений признака,
принадлежащих всей совокупности.
Зная групповые средние и
объемы групп, можно найти общую среднюю:
общая средняя равна
средней арифметической групповых
средних, взвешенной по объемам групп,
Опуская доказательство, приведем
иллюстрирующий пример.
Пример.
Найти
общую среднюю совокупности, состоящей
из
следующих
двух групп:
|
Группа………………………. |
первая |
вторая |
||
|
Значение |
1 |
6 |
1 |
5 |
|
Частота……………………… |
10 |
15 |
20 |
30 |
|
Объем………………………. |
10+15 = 25 |
20 + 30 = 50 |
Решение.
Найдем групповые средние:
=(10*1+15*6)/25=4;
=
(20*1+30*5)/50
= 3,4.
Найдем общую
среднюю по групповым средним:
=(25*
4 + 50*3,4)/(25 + 50) = 3,6.
Замечание.
Для упрощения расчета общей средней
совокупности большого объема целесообразно
разбить ее на несколько групп, найти
групповые
средние и по ним общую среднюю.
§ 7. Отклонение от общей средней и его свойство
Рассмотрим совокупность,
безразлично-генеральную или выборочную,
значений количественного признака X
объема n:
значения признака .…… x1
x2
…
xk
частоты………………………
n1
n2
… nk
При
этом
.
Далее
для удобства записи знак суммы
заменен знаком
.
Найдем общую среднюю:
.
Отсюда
.
(*)
Заметим, что поскольку x
– постоянная величина,
то
.
(**)
Отклонением называют
разность
между значением
признака и общей средней.
Теорема. Сумма
произведений отклонений на соответствующие
частоты равна нулю:
.
Доказательство. Учитывая (*) и (**), получим
.
Следствие. Среднее
значение отклонения равно нулю.
Пример.
Дано
распределение количественного признака
X:
xi
1
2 3
ni
10
4 6
Убедиться,
что сумма произведений отклонений на
соответствующие
частоты равна нулю.
Решение.
Найдем общую среднюю:
=
(10*1+4*2+6*3)/20
=1,8
Найдем
сумму произведений отклонений на
соответствующие
частоты:
.
§ 8. Генеральная дисперсия
Для того чтобы охарактеризовать
рассеяние значений количественного
признака X
генеральной совокупности
вокруг своего среднего значения, вводят
сводную характеристику – генеральную
дисперсию.
Генеральной дисперсией
Dг
называют среднее арифметическое
квадратов отклонений значений признака
генеральной совокупности от их среднего
значения .
Если все значения x1,
х2,
…, xN
признака генеральной
совокупности объема N
различны, то

Если же значения признака
x1,
х2,
…, xk
имеют соответственно
частоты N1,
N2,…,
Nk,
причем N1
+N2+…+Nk=N,
то

т.е. генеральная дисперсия есть средняя
взвешенная квадратов отклонений с
весами, равными соответствующим частотам.
Пример.
Генеральная
совокупность задана таблицей распределения
xi
2
4
5 6
Ni
8
9 10 3
Найти генеральную
дисперсию.
Решение.
Найдем генеральную среднюю (см. § 3):
.
Найдем генеральную
дисперсию;
.
Кроме дисперсии для характеристики
рассеяния значений признака генеральной
совокупности вокруг своего среднего
значения пользуются сводной характеристикой
– средним квадратическим отклонением.
Генеральным средним
квадратическим отклонением (стандартом)
называют квадратный
корень из
генеральной дисперсии:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Генеральная средняя
Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 1
Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.
Определение 2
Генеральная средняя — среднее арифметическое значений вариант генеральной совокупности.
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная средняя вычисляется по формуле:
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная средняя вычисляется по формуле:
Выборочная средняя
Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 3
Выборочная совокупность — часть отобранных объектов из генеральной совокупности.
Определение 4
Выборочная средняя — среднее арифметическое значений вариант выборочной совокупности.
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная средняя вычисляется по формуле:
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная средняя вычисляется по формуле:
«Средняя выборки: генеральная, выборочная» 👇
!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной средних значений за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$
Примеры задач на нахождение средней выборки
Пример 1
В магазин завезли 10 видов шоколадных конфет. По ним проведена следующая выборка по цене за килограмм: 70, 65, 97, 83, 120, 107, 77, 88, 100, 86. Построить ряд распределения данной генеральной совокупности и найти её генеральное среднее.
Решение.
Видим, что все значения вариант различны, поэтому частоты равны единице. Ряд распределения можно записать следующим образом, перечислив значения вариант в порядке возрастания:
Рисунок 1.
Так как наша совокупность является генеральной и все варианты различны, то мы будем пользоваться следующей формулой:
[overline{x_г}=frac{sumlimits^k_{i=1}{x_i}}{n}]
Получим:
[overline{x_г}=frac{65+70+77+83+86+88+97+100+107+120}{10}=89,3]
Ответ: 89,3.
Пример 2
Выборочная совокупность задана следующей таблицей распределения:
Рисунок 2.
Найти среднее выборочное данной совокупности.
Решение.
Для нахождения значения выборочной средней будем пользоваться следующей формулой:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]
Обычно, для наглядности и удобности вычислений составляется расчетная таблица, в которую входят необходимые промежуточные вычисления. В нашем случае составим таблицу со следующей «шапкой»:
Рисунок 3.
Внизу таблицы также добавляется строка «итог», в которой подсчитывается сумма по всем значениям столбцов. Проведя необходимые вычисления, получим следующую расчетную таблицу:
Рисунок 4.
Используя формулу, получим:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{305}{20}=15,25]
Ответ: 15,25.
Пример 3
Проводится социальный опрос среди 100 пенсионеров об уровне их пенсии. Получена следующая таблица распределения результатов опроса (размер пенсии указан в тысячах рублей):
Рисунок 5.
Найти среднее выборочное данной совокупности.
Данная совокупность является выборочной, поэтому будем пользоваться следующей формулой:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]
Составим, для начала, расчетную таблицу.
Рисунок 6.
Получаем:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{964}{100}=9,64]
Ответ: 9,64.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Статистические оценки параметров генеральной совокупности
Определение статистической оценки. Точечные статистические оценки: смещенные и несмещенные, эффективные и состоятельные. Интервальные статистические оценки. Точность и надежность оценки; определение доверительного интервала; построение доверительных интервалов для средней при известном и неизвестном среднеквадратическом отклонении.
Определение статистической оценки
Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Возникает задача оценки параметров, которыми определяется это распределение. Например, если известно, что изучаемый признак распределен в генеральной совокупности по нормальному закону, то необходимо оценить математическое ожидание и среднеквадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение. Если имеются основания считать, что признак имеет распределение Пуассона, то необходимо оценить параметр , которым это распределение определяется. Обычно имеются лишь данные выборки, полученные в результате
наблюдений:
. Через эти данные и выражают оцениваемый параметр. Рассматривая
как значения независимых случайных величин
можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения означает найти функцию от наблюдаемых случайных величин, которая и дает приближенное значение оцениваемого параметра.
Точечные статистические оценки
Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Статистическая оценка неизвестного параметра генеральной совокупности одним числом называется точечной. Рассмотрим следующие точечные оценки: смещенные и несмещенные, эффективные и состоятельные.
Для того чтобы статистические оценки давали хорошие приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Укажем эти требования. Пусть есть статистическая оценка неизвестного параметра
теоретического распределения. Допустим, что по выборке объема
найдена оценка
. Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку
и т. д. Получим числа
, которые будут различаться. Таким образом, оценку
можно рассматривать как случайную величину, а числа
— как возможные ее значения.
Если оценка дает приближенное значение
с избытком, то найденное по данным выборок число
будет больше истинного значения
. Следовательно, и математическое ожидание (среднее значение) случайной величины
будет превышать
, то есть
. Если
дает приближенное значение
с недостатком, то
.
Использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, приводит к систематическим ошибкам. Поэтому нужно потребовать, чтобы математическое ожидание оценки было равно оцениваемому параметру. Соблюдение требования
устраняет систематические ошибки.
Несмещенной называют статистическую оценку , математическое ожидание которой равно оцениваемому параметру
, то есть
.
Смещенной называют статистическую оценку , математическое ожидание которой не равно оцениваемому параметру.
Однако ошибочно считать, что несмещенная оценка всегда дает хорошее приближение оцениваемого параметра. Действительно, возможные значения могут быть сильно рассеяны вокруг своего среднего значения, т. е. дисперсия величины
может быть значительной. В этом случае найденная по данным одной выборки оценка, например
, может оказаться удаленной от своего среднего значения
, а значит, и от самого оцениваемого параметра
. Приняв
в качестве приближенного значения
, мы допустили бы ошибку. Если потребовать, чтобы дисперсия величины
была малой, то возможность допустить ошибку будет исключена. Поэтому к статистической оценке предъявляются требования эффективности.
Эффективной называют статистическую оценку, которая (при заданном объеме выборки ) имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности.
Состоятельной называют статистическую оценку, которая при стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при
стремится к нулю, то такая оценка оказывается также состоятельной.
Рассмотрим вопрос о том, какие выборочные характеристики лучше всего в смысле несмещённости, эффективности и состоятельности оценивают генеральную среднюю и дисперсию.
Пусть изучается дискретная генеральная совокупность относительно количественного признака. Генеральной средней называется среднее арифметическое значений признака генеральной совокупности. Она вычисляется по формуле
или
где — значения признака генеральной совокупности объема
;
— соответствующие частоты, причем
Пусть из генеральной совокупности в результате независимых наблюдений над количественным признаком извлечена выборка объема со значениями признака
. Выборочной средней называется среднее арифметическое значений признака выборочной совокупности и вычисляется по формуле
или
где — значения, признака в выборочной совокупности объема
;
— соответствующие частоты, причем
Если генеральная средняя неизвестна и требуется оценить ее по данным выборки, то в качестве оценки генеральной средней принимают выборочную среднюю, которая является несмещенной и состоятельной оценкой. Отсюда следует, что если по нескольким выборкам достаточно большого объема из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой. В этом состоит свойство устойчивости выборочных средних.
Если дисперсии двух совокупностей одинаковы, то близость выборочных средних к генеральным не зависит от отношения объема выборки к объему генеральной совокупности. Она зависит- от объема выборки: чем больше объем выборки, тем меньше выборочная средняя отличается от генеральной.
Для того чтобы охарактеризовать рассеяние значений количественного признака генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию. Генеральной дисперсией
называется среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения
, которое вычисляется по формуле
или
Для того чтобы охарактеризовать рассеяние наблюденных значений количественного признака выборки вокруг своего среднего значения хв, вводят сводную характеристику — выборочную дисперсию. Выборочной дисперсией называется среднее арифметическое квадратов отклонений наблюденных значений признака от их среднего значения
, которое вычисляется по формуле
или
Кроме дисперсии для характеристики рассеяния значений признака генеральной (выборочной) совокупности вокруг своего среднего значения используют сводную характеристику — среднее квадратическое отклонение. Генеральным средним квадратическим отклонением называют квадратный корень из генеральной дисперсии: . Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии:
.
Пусть из генеральной совокупности в результате независимых наблюдений над количественным признаком
извлечена выборка объема
. Требуется по данным выборки оценить неизвестную генеральную дисперсию
. Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка приведет к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что выборочная дисперсия является смещенной оценкой
. Другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно
.
Легко исправить выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Для этого нужно умножить на дробь
. В результате получим исправленную дисперсию
, которая будет несмещенной оценкой генеральной дисперсии:
Интервальные оценки
Наряду с точечным оцениванием, статистическая теория оценивания параметров занимается вопросами интервального оценивания. Задачу интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал, относительно которого с заранее выбранной вероятностью можно сказать, что внутри него находится оцениваемый параметр. Интервальное оценивание особенно необходимо при малом количестве наблюдений, когда точечная оценка малонадежна.
Доверительным интервалом для параметра
называется такой интервал, относительно которого с заранее выбранной вероятностью
, близкой к единице, можно утверждать, что он содержит неизвестное значение параметра
, то есть
. Чем меньше для выбранной вероятности число
, тем точнее оценка неизвестного параметра
. И, наоборот, если это число велико, то оценка, проведенная с помощью данного интервала, малопригодна для практики. Так как концы доверительного интервала зависят от элементов выборки, то значения
и
могут изменяться от выборки к выборке. Вероятность
принято называть доверительной (надежностью). Обычно надежность оценки задается наперед, причем в качестве
берут число, близкое к единице. Выбор доверительной вероятности не является математической задачей, а определяется конкретной решаемой проблемой. Наиболее часто задают надежность, равную 0,95; 0,99; 0,999.
Доверительный интервал для генеральной средней при известном значении среднего квадратического отклонения и при условии, что случайная величина (количественный признак ) распределена нормально, задается выражением
где — наперед заданное число, близкое к единице, а значения функции
приведены в таблице прил. 2.
Смысл этого соотношения заключается в следующем: с надежностью можно утверждать, что доверительный интервал
покрывает неизвестный параметр
, точность оценки
. Число
определяется из равенства
, или
. По прил. 2 находят аргумент
, которому соответствует значение функции Лапласа, равное
.
Пример 1. Случайная величина имеет нормальное распределение с известным средним квадратическим отклонением
. Найти доверительные интервалы для оценки неизвестной генеральной средней по выборочным средним, если объем выборок
и надежность оценки
.
Решение. Найдем . Из соотношения
получим, что
. По прил. 2 находим
. Найдем точность оценки
. Доверительные интервалы будут таковы:
. Например, если
, то доверительный интервал имеет следующие доверительные границы:
. Таким образом, значения неизвестного параметра
, согласующиеся с данными выборки, удовлетворяют неравенству
.
Доверительный интервал для генеральной средней нормального распределения признака при неизвестном значении среднего квадратического отклонения задается выражением
Отсюда следует, что с надежностью можно утверждать, что доверительный интервал
покрывает неизвестный параметр
.
Существуют таблицы (прил. 4), пользуясь которыми, по заданным и
находят вероятность
и, наоборот, по заданным
и
находят
.
Пример 2. Количественный признак генеральной совокупности распределен нормально. По выборке объема
найдены выборочная средняя
и исправленное среднеквадратическое отклонение
. Оценить неизвестную генеральную среднюю с помощью доверительного интервала с надежностью
.
Решение. Найдем . Пользуясь прил. 4 по
и
находим
. Найдем доверительные границы:
Итак, с надежностью неизвестный параметр
заключен в доверительном интервале
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
3.1. Показатели центральной тенденции
Простейший пример такого показателя нам уже встречался – это среднее арифметическое значение. Но средней
дело не ограничивается, впрочем, обо всём по порядку:
3.1.1. Генеральная и выборочная средняя
Пусть исследуется некоторая генеральная совокупность объёма , а именно её числовая характеристика
, не важно, дискретная или непрерывная.
Генеральной средней называют среднее арифметическое всех значений этой совокупности:
Если среди чисел есть одинаковые (что
характерно для дискретного ряда), то формулу можно записать в более компактном
виде:
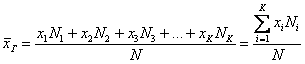
варианта повторяется
раз;
варианта –
раз;
варианта –
раз;
…
варианта –
раз.
Живой пример вычисления генеральной средней встретился в Примере 2, но чтобы не занудничать, я даже не буду
напоминать его содержание. Далее.
Как мы помним, обработка всей генеральной совокупности часто затруднена либо невозможна, и поэтому из неё организуют представительную выборку объема , и на основании исследования этой выборки делают вывод обо всей совокупности.
Выборочной средней называется среднее арифметическое всех значений выборки:
и при наличии одинаковых вариант формула запишется компактнее:
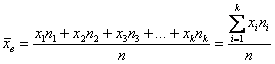
на соответствующие частоты
, делённая на объём совокупности
.
Выборочная средняя позволяет достаточно
точно оценить истинное значение , при этом, чем
больше выборка, тем точнее будет эта оценка.
Практику начнём с дискретного вариационного ряда и знакомого условия:
Пример 8
По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4,
4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3.
Это числа из Примера 4, но теперь нам требуется: вычислить выборочную среднюю, и, не отходя от станка, найти моду
и медиану.
Как решать задачу? Если нам даны первичные данные (конкретные варианты ), то их можно тупо просуммировать и разделить результат на объём
выборки:
– средний квалификационный разряд рабочих
цеха.
Но здесь удобнее составить вариационный ряд:
и использовать «цивилизованную» формулу:


| Оглавление |
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).
Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.
- Например, курс акций корпорации в основном определяется финансовыми результатами ее деятельности. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу.
Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:
- средняя арифметическая;
- средняя гармоническая;
- средняя геометрическая;
- средняя квадратическая.
Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
- Средняя арифметическая простая (невзвешенная) – вычисляется когда каждый вариант совокупности встречается только один раз.
- Средняя арифметическая (взвешенная) – варианты повторяются различное число раз, при этом число повторений вариантов называется частотой, или статистическим весом.
ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН
- Средняя арифметическая простая – самый распространенный вид средней величины, рассчитывается по формуле (8.8):
(8.8 -формула средней арифметической простой)
- где хi – вариант, а n – количество единиц совокупности.
- Пример вычисления средней арифметической простой. Провели опрос о желаемом размере заработной платы у пяти сотрудников офиса. По результатам опроса выяснили, что желаемый размер заработной платы составляет соответственно для каждого сотрудника: 50000, 100000, 200000, 350000, 500000 рублей человек. Рассчитаем среднюю арифметическую простую по формуле (8.8):
Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
- Средняя арифметическая взвешенная формула 8.9.
(8.9 -формула средней арифметической взвешенной)
- где хi – вариант, а fi – частота или статистический вес.
- Пример вычисления средней арифметической взвешенной. Результаты опроса всех работников офиса приведены в табл. 8.2.
Таблица 8.2 – Результаты опроса работников офиса
|
Желаемый размер заработной платы, тыс.руб хi |
Количество работников fi | хifi |
| 1 | 2 | 3 |
|
50 100 200 350 500 |
6
10 20 9 5 |
300
1000 4000 3150 2500 |
| Итого | 50 | 10950 |
Пример. Вычислим (ориентируясь на итоговые строки таблицы) желаемый размер заработной платы, 50 сотрудников офиса (используем формулу 8.9):
Пример вычисления средней арифметической взвешенной
Вывод: в среднем желаемый размер заработной платы по результатам опроса 50 человек составил 219 тысяч рублей.
Среднеарифметическая – всегда обобщающая количественная характеристика варьирующего признака совокупности.
- Средняя гармоническая вычисляется в тех случаях, когда приходится суммировать не сами варианты, а обратные им величины.
- Средняя гармоническая простая представлена ниже:
(8.10 – формула средней гармонической простой)
Средняя гармоническая взвешенная определяется по формуле
(8.11- формула средней гармонической взвешенной)
где xi – вариант, n – количество вариантов, Vi – веса для обратных значений xi.
Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, чем взвешенная. Для иллюстрации области ее применения воспользуемся упрощенным условным примером.
- Пример (вычисление средней гармонической простой (невзвешенной)).
Предположим, в фирме, специализирующейся на торговле по почте на основе предварительных заказов, упаковкой и отправкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 5 мин., второй – 15 мин.
- Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна?
На первый взгляд, ответ на этот вопрос заключается в осреднении индивидуальных значений затрат времени на 1 заказ, т.е. если используем среднюю арифметическую простую получим: (5+15):2=10, мин.
- Проверим обоснованность такого подхода на примере одного часа (60 минут) работы. За этот час первый работник обрабатывает 12 заказов (60:5), второй – 4 заказа (60:15), что в сумме составляет 16 заказов.
Если же заменить индивидуальные значения их предполагаемым средним значением, то общее число обработанных обоими работниками заказов в данном случае уменьшится: (60/10) + (60/10) = 12 заказов (что не соответствует истине).
- Подойдем к решению через исходное соотношение средней. Для определения средних затрат времени необходимо общие затраты времени за любой интервал (например, за час) разделить на общее число обработанных за этот интервал двумя работниками заказов, т.е. используем среднюю гармоническую:
Пример вычисления средней гармонической простой (невзвешенной)
Если теперь мы заменим индивидуальные значения их средней величиной, то общее количество обработанных за час заказов не изменится: (60/7,5) + (60/7,5) = 16 заказов
- Подведем итог: средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения Wj для единиц совокупности равны (в рассмотренном примере рабочий день у сотрудников одинаковый).
Пример (вычисление средней гармонической взвешенной) В ходе торгов на валютной бирже за первый час работы заключено пять сделок. Данные о сумме продажи рублей и курсе рубля по отношению к доллару США приведены в табл.8.3.
Таблица 8.3 – Данные о ходе торгов на валютной бирже (цифры условные)
Номер сделки Сумма продажи V, млн руб. Курс рубля x, руб. за 1 дол. V/x 1 2 3 4 1
2
3
4
5
455,00
327,50
528,00
266,00
332,50
65,00 65,50
66,00
66,50
66,50
7,00
5,00
8,00
4,00
5,00
итого 1909,00 – 29,00 Для того чтобы определить средний курс рубля по отношению к доллару, нужно найти соотношение между суммой продажи рублей, которые затрачены на покупку долларов в ходе всех сделок, и суммой приобретенных в результате этих сделок долларов.
- Вывод: средний курс за один доллар составил 65,83 руб.;
- Если бы для расчета среднего курса была использована средняя арифметическая простая:
то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака обычно представляют собой относительные показатели динамики, построенные в виде цепных величин как отношение каждого уровня ряда к предыдущему уровню.
- Средняя геометрическая простая рассчитывается по формуле 8.12
(8.12)
- Если использовать частоты m, получим формулу средней геометрической взвешенной
- Средняя геометрическая взвешенная рассчитывается по формуле 8.13
(8.13)
Средняя квадратическая применяется, когда изучается вариация признака. В качестве вариантов используются отклонения фактических значений признака либо от средней арифметической, либо от заданной нормы.
Для несгруппированных данных используют формулу средней квадратической простой
Средняя квадратическая простая (формула 8.14)
8.14
Для сгруппированных данных используют формулу средней квадратической взвешенной
Средняя квадратическая взвешенная (формула 8.15)
(8.15) – Формула -средняя квадратическая взвешенная
Средние арифметическая, гармоническая, геометрическая и квадратическая, рассчитанные для одного и того же ряда вариантов, отличаются друг от друга. Их численное значение возрастает с ростом показателя степени в формуле степенной средней правило мажорантности средних А.Я. Боярского, т.е.
Мода и Медиана (структурные средние) формулы и примеры вычисления см. по ссылке

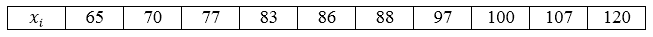

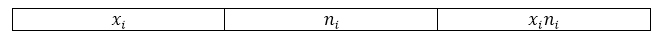


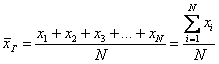
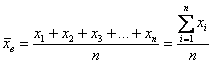
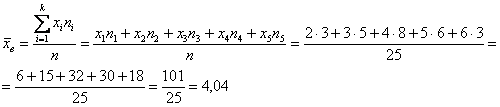


 Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.





 то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.




