1. Формула площади параллелограмма через стороны и углы

a, b – стороны параллелограмма
α, β – углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):

Калькулятор – вычислить, найти площадь параллелограмма:
a(сторона)=
b(сторона)=
α или β (угол в градусах)= ( sin α=sin β )
S=
2. Формула площади параллелограмма через сторону и высоту

a, b – стороны параллелограмма
Hb – высота на сторону b
Ha – высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):

3. Формула площади параллелограмма через диагонали и угол между ними

D – большая диагональ
d –меньшая диагональ
α, β – углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):

Калькулятор – вычислить, найти площадь параллелограмма:
D (большая диагональ)=
d (меньшая диагональ )=
α или β (угол в градусах)= ( sin α=sin β )
S=
Формулы для параллелограмма:
Как найти стороны параллелограмма
Как найти диагонали параллелограмма
Острый угол и тупой угол параллелограмма
Углы между диагоналями параллелограмма
Формула суммы квадратов диагоналей параллелограмма
Высота параллелограмма и угол пересечения высот
Свойства и длина биссектрисы параллелограмма
Периметр параллелограмма
Все формулы по геометрии
Как найти площадь параллелограмма — три основных формулы
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Эта статья на еще одну математическую тему. Мы расскажем, как правильно посчитать площадь параллелограмма. Эту тему подробно изучают только в 8-м классе. И это говорит, что она не такая простая.

Но для начала давайте все-таки напомним, какая фигура называется параллелограммом.
Параллелограмм – это разновидность четырехугольников, у которого противоположные стороны параллельны друг другу.
Классический параллелограмм выглядит вот так:

Впервые об этой фигуре подробно написал древнегреческий математик Евклид в своем известном произведении «Начала». Он же рассказал и о двух частных случаях параллелограмма, которые нам сегодня хорошо известны.
Это и прямоугольник, у которого противоположные стороны не только параллельны друг другу, но и пересекаются под прямым углом. И квадрат, у которого помимо параллельности противоположных сторон, все стороны еще и равны между собой.

И наконец, не лишним будет вспомнить, что подразумевается под термином «площадь».
Площадь геометрической фигуры – это размер плоскости, которая находится внутри сторон фигуры.
Ну а теперь объединим эти два понятия и расскажем, как надо считать площадь параллелограмма.
Формулы для расчета площади параллелограмма
Есть три основных формулы для вычисления площади параллелограмма:
- если известна длина стороны и высота, проведенная к ней;
- если известны длины сторон и углы между ними;
- если известны длины диагоналей и угол между ними.
Теперь о каждом из этих способов подробнее.
Как найти площадь параллелограмма, если известны сторона и высота
Возьмем для примера такой параллелограмм:
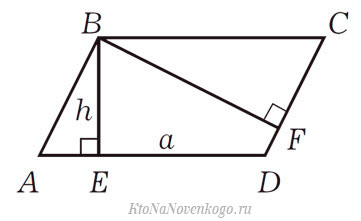
В нем указаны две высоты – BE и BF. Напомню, что высота — это отрезок, который опускается из вершины на противоположную сторону под прямым углом.
В данном случае площадь считается весьма просто. Надо всего лишь перемножить длину высоты и длину стороны, к которой она проведена.
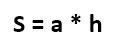
И то же самое касается, если знать длины стороны DC и высоты BF. Тогда для вычисления площади достаточно их перемножить.
Кстати, у этой формулы есть весьма интересное доказательство. Так как у параллелограмма противоположные стороны параллельны и равны, то можно взять треугольник ABE и переставить его к стороне CD. Вот так это будет выглядеть:
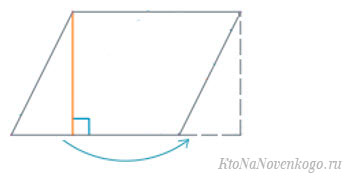
В результате мы получим прямоугольник, у которого нам известны длины обеих сторон (высота параллелограмма превратилась в одну из сторон). А как известно, площадь прямоугольника равна произведению его сторон.
Формула площади параллелограмма, если известны стороны и угол
Площадь параллелограмма можно посчитать, если известны длины обеих его сторон и величина острого угла между ними.
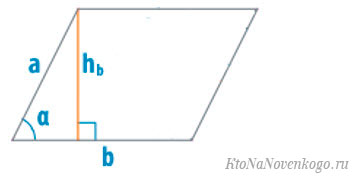
Собственно, этот способ вытекает из предыдущего, Просто по исходным данным нужно вычислить высоту параллелограмма, а уже потом по ней посчитать площадь.
Согласно тригонометрии, синус острого угла в прямоугольнике равен отношению противоположного катета к гипотенузе. В нашем примере таким катетом является высота, а гипотенузой сторона «а». И получается:
![]()
Соответственно, чтобы посчитать значение высоты надо:
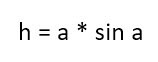
И наша конечная формула для расчета площади будет выглядеть следующим образом:
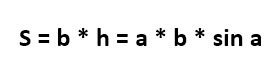
Как найти площадь параллелограмма через диагонали
Этот способ используется крайне редко, но знать его все равно нужно. Во всяком случае, на экзаменах у школьников такие примеры вполне могут встретиться.
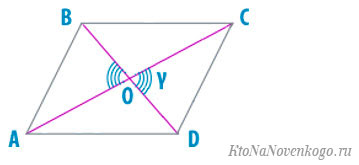
В данном случае для вывода формулы используются весьма непростые математические вычисления. И мы не будем ими вас загружать. А просто покажем конечный результат:
![]()
Соответственно, здесь d1 и d2 – длины диагоналей, а y – острый угол между ними.
Вот и все, что мы хотели рассказать о вычислении площади параллелограмма.
Параллелограмм — это четырехугольник, в котором противоположные стороны равны и параллельны.
Онлайн-калькулятор площади параллелограмма
Параллелограмм обладает некоторыми полезными свойствами, которые упрощают решение задач, связанных с этой фигурой. Например, одно из свойств заключается в том, что противоположные углы параллелограмма равны.
Рассмотрим несколько способов и формул с последующим решением простых примеров.
Формула площади параллелограмма по основанию и высоте
Данный способ нахождения площади является, наверно, одним из основных и простых, так как он практически идентичен формуле по нахождению площади треугольника за небольшим исключением. Для начала разберем обобщенный случай без использования чисел.
Пусть дан произвольный параллелограмм с основанием aa, боковой стороной bb и высотой hh, проведенной к нашему основанию. Тогда формула для площади этого параллелограмма:
S=a⋅hS=acdot h
aa — основание;
hh — высота.
Разберем одну легкую задачу, чтобы потренироваться в решении типовых задач.
Найти площадь параллелограмма, в котором известно основание, равное 10 (см.) и высота, равная 5 (см.).
Решение
a=10a=10
h=5h=5
Подставляем в нашу формулу. Получаем:
S=10⋅5=50S=10cdot 5=50 (см. кв.)
Ответ: 50 (см. кв)
Формула площади параллелограмма по двум сторонам и углу между ними
В этом случае искомая величина находится так:
S=a⋅b⋅sin(α)S=acdot bcdotsin(alpha)
a,ba, b — стороны параллелограмма;
αalpha — угол между сторонами aa и bb.
Теперь решим другой пример и воспользуемся вышеописанной формулой.
Найти площадь параллелограмма если известна сторона aa, являющаяся основанием и с длиной 20 (см.) и периметр pp, численно равный 100 (см.), угол между смежными сторонами (aa и bb) равен 30 градусам.
Решение
a=20a=20
p=100p=100
α=30∘alpha=30^{circ}
Для нахождения ответа нам неизвестна лишь вторая сторона данного четырехугольника. Найдем ее. Периметр параллелограмма дается формулой:
p=a+a+b+bp=a+a+b+b
100=20+20+b+b100=20+20+b+b
100=40+2b100=40+2b
60=2b60=2b
b=30b=30
Самое сложное позади, осталось только подставить наши значения для сторон и угла между ними:
S=20⋅30⋅sin(30∘)=300S=20cdot 30cdotsin(30^{circ})=300 (см. кв.)
Ответ: 300 (см. кв.)
Формула площади параллелограмма по диагоналям и углу между ними
S=12⋅D⋅d⋅sin(α)S=frac{1}{2}cdot Dcdot dcdotsin(alpha)
DD — большая диагональ;
dd — малая диагональ;
αalpha — острый угол между диагоналями.
Даны диагонали параллелограмма, равные 10 (см.) и 5 (см.). Угол между ними 30 градусов. Вычислить его площадь.
Решение
D=10D=10
d=5d=5
α=30∘alpha=30^{circ}
S=12⋅10⋅5⋅sin(30∘)=12.5S=frac{1}{2}cdot 10 cdot 5 cdotsin(30^{circ})=12.5 (см. кв.)
Ответ: 12.5 (см. кв.)
Решение контрольной работы по геометрии онлайн – от профильных экспертов Студворк!
Тест по теме «Площадь параллелограмма»
Задачи на нахождение площади параллелограмма довольно часто встречаются в геометрии при выполнении контрольных работ, написании зачетов и решении практических заданий экзаменационных билетов. Для получения отличных оценок необходимо знать доказательства теорем, основные соотношения и методику их нахождения, а также уметь применять знания, полученные в процессе обучения, на практике.

Содержание
- Общие сведения
- Признаки параллелограмма
- Свойства фигуры
- Теоремы о площади
- Сторона и высота
- Стороны и острый угол
- Величины диагоналей
- Информация о периметре
- Другие параметры
- Пример решения
Общие сведения
Перед обучением решению задач специалисты рекомендуют изучить теорию и разобраться в ней. Параллелограмм — геометрическая фигура, состоящая из четырех вершин и взаимно-параллельными, а также равными между собой противоположными сторонами. Высота — часть прямой (отрезок), исходящая из вершины на противоположную сторону и образующая с последней прямой угол.
Диагонали не равны между собой. Для удобства их обозначают литерами F и f (большая и малая соответственно). Однако у квадрата и прямоугольника они эквивалентны. Специалисты рекомендуют на начальных этапах обучения правильно определять геометрическую фигуру. Для этой цели существуют признаки параллелограмма.
Признаки параллелограмма
Признаки — набор критериев и правил, при помощи которых определяется тип геометрического тела. В некоторых задачах с повышенной сложностью дается четырехугольник с определенными исходными данными. Далее необходимо найти один из его параметров по формуле. Для этого следует правильно идентифицировать фигуру, чтобы воспользоваться необходимым соотношением.
Вот на этом этапе будут полезны признаки, позволяющие отнести геометрическое тело к классу параллелограммов. К ним относятся следующие:

Следует отметить, что при выполнении одного условия фигура принадлежит к классу параллелограммов.
Свойства фигуры
Свойства — утверждения, доказанные математиками. Они применяются для доказательств теорем, решения диофантовых (линейных) систем уравнений на нахождение двух неизвестных величин, вычисления параметров фигуры, а также для проектирования деталей. Для этих целей можно применять такие утверждения:
После свойств математики рекомендуют ознакомиться с некоторыми теоремами, позволяющими выводить формулу площади параллелограмма.
Теоремы о площади
Формулы площади — базовые соотношения, позволяющие найти другие параметры параллелограмма. Однако начинающему математику рекомендуется посмотреть, каким образом они доказываются. В отличие от прямоугольника величина рассчитывается немного иначе. Формулы — математическая запись определенной теоремы про площадь. Их всего три:

Однако для удобства доказательства утверждений следует ввести обозначения основных параметров фигуры:
Следует отметить, что специалисты при решении любой задачи или доказательстве геометрических тождеств рекомендуют использовать сокращенные записи. Этот подход является признаком мастерства и правилом хорошего тона в точных науках.
Сторона и высота
Первую теорему можно сформулировать следующим образом: площадь параллелограмма равна произведению большей стороны на значение высоты. Доказывается утверждение довольно просто по такому алгоритму:

Следует отметить, что высоты, проведенные из вершин тупого и острого углов (h1 и h2), равны между собой. Их можно обозначить для удобства одной литерой H.
Стороны и острый угол
Следующая теорема имеет такую формулировку: при известных сторонах параллелограмма и размерности угла между ними его площадь эквивалентна произведению первых двух на синус третьего, то есть S=k*l*sin (∠v). Доказывается утверждение по такой методике:
Утверждение доказано. Следует отметить, что в геометрии очень часто одна теорема используется для доказательства другой.
Величины диагоналей
Третья теорема определения величины площади параллелограмма через диагонали имеет следующую формулировку: размерность эквивалентна произведению диагоналей на острый угол между ними (S=F*f*sin (∠z)). Доказывается утверждение по такому алгоритму:

Следует отметить, что результирующая формула с подстановкой всех величин имеет следующий вид: S=[(Ff/2)]*sin (∠z). Однако для решения задач возможно использовать еще один параметр, который называется периметром.
Информация о периметре
Периметр или поверхность плоского геометрического тела — алгебраическая сумма сторон параллелограмма. Он обозначается литерой «Р». Базовое соотношение имеет следующий вид: S=MN+NO+OP+MP=2 (k+l). Кроме того, существуют другие соотношения для определения Р:
Следует отметить, что из этих соотношений можно найти стороны, высоту и углы. Кроме того, последнее соотношение можно записать в другом виде: P=2[k+H/sin (z)]=2[l+H/cos (v)]. Эти формулы строятся на основании теорем о площади параллелограмма, в которых стороны и другие параметры выражаются через S треугольников. Специалисты рекомендуют после изученного материала переходить к рассмотрению других соотношений.
Другие параметры
Определение сторон и диагоналей осуществляется посредством следствий из теорем. Математики рекомендуют воспользоваться готовыми формулами, но не стоит забывать и о тренировках. Последние реализуются при помощи самостоятельного выражения одной величины через другую. Стороны можно найти, когда известны следующие параметры:

Для нахождения диагонали специалисты рекомендуют также воспользоваться следствием из последней теоремы. Кроме того, возможности расчетов расширяются при использовании и других соотношений:
Для практического применения знаний специалисты рекомендуют переходить к заданиям по геометрии.
Пример решения
Для закрепления теоретических знаний рекомендуется постоянно решать задачи. Условие одной из них имеет следующий вид:
Необходимо найти площадь (S), высоту (H). Вычисляются необходимые параметры по следующему алгоритму:

Задачу можно решать при помощи других соотношений. Однако это приведет к увеличению количества вычислений, в результате которых могут возникнуть ошибки.
Таким образом, для нахождения площади параллелограмма нужно знать признаки фигуры, свойства, теоремы, формулы и соотношения, а также чаще решать различные задачи.
Предыдущая
ГеометрияПравильный треугольник – свойства, признаки и формулы
Следующая
ГеометрияУглы при параллельных прямых и секущей – виды и свойства

{S = a cdot h}
Найти площадь параллелограмма
На этой странице вы можете рассчитать площадь параллелограмма с помощью калькулятора по трем формулам. Просто введите известные вам данные – основание, высоту, стороны, диагонали и углы между ними и получите ответ.
Параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
Содержание:
- калькулятор площади параллелограмма
- формула площади параллелограмма через сторону и высоту
- формула площади параллелограмма через две стороны и угол между ними
- формула площади параллелограмма через диагонали и угол между ними
- примеры задач
Формула площади параллелограмма через сторону и высоту
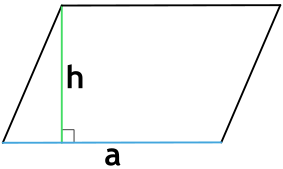
{S = a cdot h}
a – сторона параллелограмма
h – высота параллелограмма
Формула площади параллелограмма через две стороны и угол между ними

{S=a cdot b cdot sin(alpha)}
a, b – стороны параллелограмма
α – угол между сторонами a и b
Формула площади параллелограмма через диагонали и угол между ними
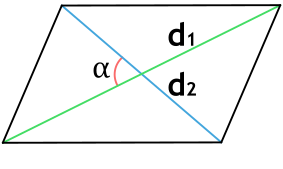
{S = dfrac{1}{2} cdot d_1 cdot d_2 cdot sin(alpha)}
d1, d2 – диагонали параллелограмма
α – угол между диагоналями
Примеры задач на нахождение площади параллелограмма
Задача 1
Найдите площадь параллелограмма, стороны которого равны 9 см и 12 см, а угол между ними 60 градусов.
Решение
Для решения задачи нам подойдет вторая формула, так как из условия нам известны стороны параллелограмма и угол между ними. Подставим значения в формулу и произведем расчет.
S = a cdot b cdot sin(alpha) = 9 cdot 12 cdot sin(60) = 108 cdot sin(60) = 108 cdot 0.866 approx 93.53074 : см^2
Ответ: 108 cdot 0.866 approx 93.53074 : см^2
Мы можем проверить ответ с помощью калькулятора .
Задача 2
Найдите площадь параллелограмма, если две его стороны равны 8 см и 12 см, а угол между ними равен 30 градусов.
Решение
Задача похожа на предыдущую, поэтому ее решение будет выглядеть аналогично.
S = a cdot b cdot sin(alpha) = 8 cdot 12 cdot sin(30) = 96 cdot sin(30) = 96 cdot 0.5 = 48 : см^2
Ответ: 48 см²
И снова проверить ответ нам поможет калькулятор .
Задача 3
Найдите площадь параллелограмма, сторона которого равна 12 см, а высота проведенная к ней 8 см.
Решение
В этом случае нам известны сторона параллелограмма и высота, поэтому воспользуемся первой формулой.
S = a cdot h = 12 cdot 8 = 96 : см^2
Ответ: 96 см²
И снова проверить ответ нам поможет калькулятор .
