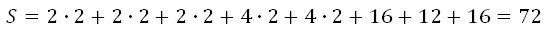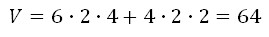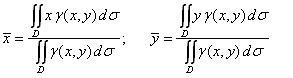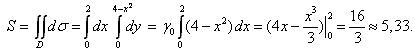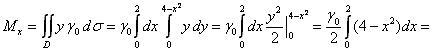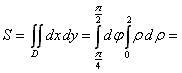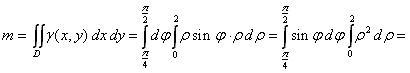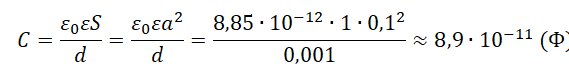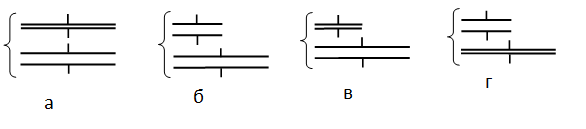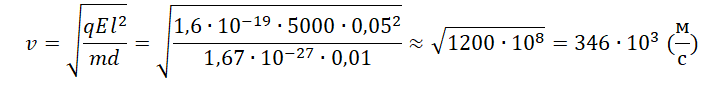Как найти площадь поверхности детали
Площадь поверхности многогранника. В данной рубрике в опубликованных статьях ” Общий обзор. Формулы стереометрии ” и ” Что ещё необходимо знать для решения по стереометрии ” мы уже рассмотрели теоретические моменты, которые необходимы для решения.
В составе ЕГЭ по математике имеется целый ряд задач на определение площади поверхности и объема составных многогранников. Это, наверное, одни из самых простых задач по стереометрии. НО! Имеется нюанс. Не смотря на то, что сами вычисления просты, ошибку при решении такой задачи допустить очень легко.
В чём же дело? Далеко не все обладают хорошим пространственным мышлением, чтобы сразу увидеть все грани и параллелепипеды из которых «состоят» многогранники. Даже если вы умеете делать это очень хорошо, можете мысленно сделать такую разбивку, всё-таки следует не торопиться и воспользоваться рекомендациями из этой статьи.
Кстати, пока работал над данным материалом, нашёл ошибку в одной из задач на сайте. Нужна внимательность и ещё раз внимательность, вот так.
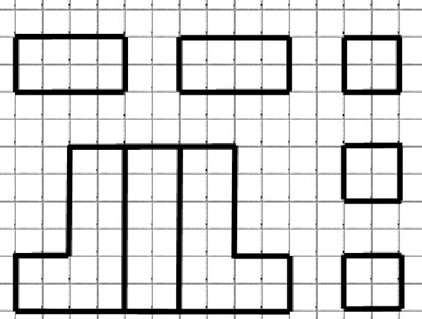
Итак, если стоит вопрос о площади поверхности, то на листе в клетку постройте все грани многогранника, обозначьте размеры. Далее внимательно вычисляйте сумму площадей всех полученных граней. Если будете предельно внимательны при построении и вычислении, то ошибка будет исключена.
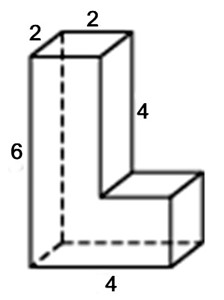
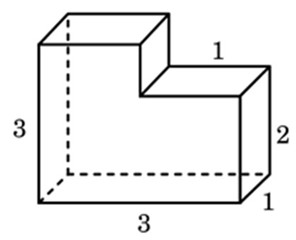
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Используем оговоренный способ. Он нагляден. На листе в клетку строим все элементы (грани) в масштабе. Если длины рёбер будут большими, то просто подпишите их.
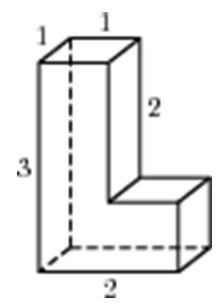
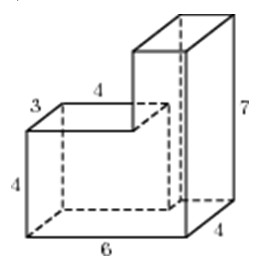
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
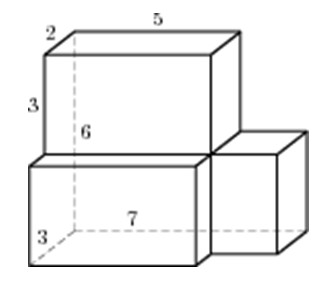
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ещё задачи 25881 , 77155 , 77156 . В них приведены решения другим способом (без построения), постарайтесь разобраться — что откуда взялось. Также решите уже представленным способом.
Если требуется найти объём составного многогранника. Разбиваем многогранник на составляющие его параллелепипеды, записываем внимательно длины их рёбер и вычисляем.
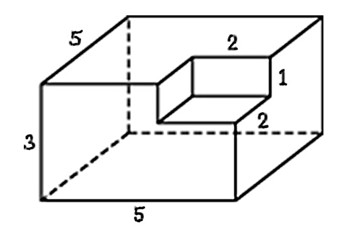
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Объем многогранника, изображенного на рисунке равен сумме объёмов двух многогранников с рёбрами 6,2,4 и 4,2,2
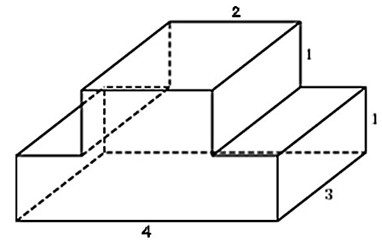
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
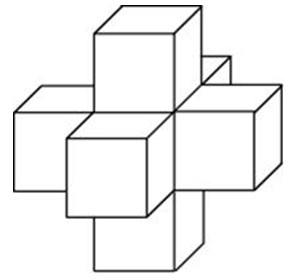
Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
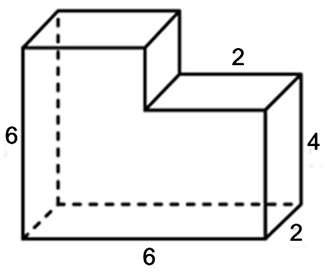
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Казалось бы, данные задачи можно вообще не рассматривать, они же просты и понятны. Но в их решении важна практика. Повторюсь, что ошибиться очень легко, попрактикуйтесь с подобными задачами и вы убедитесь.
В отк рытом банке задач много примеров аналогичных задач (смотрите здесь и здесь ). Договоритесь с одноклассниками решить одни и те же задачи, затем сверьтесь.
Мы продолжим рассматривать задачи данной части, не пропустите! Успехов вам.
Задание 8 (№ 25641) из Открытого банка заданий для подготовки к ЕГЭ по математике.
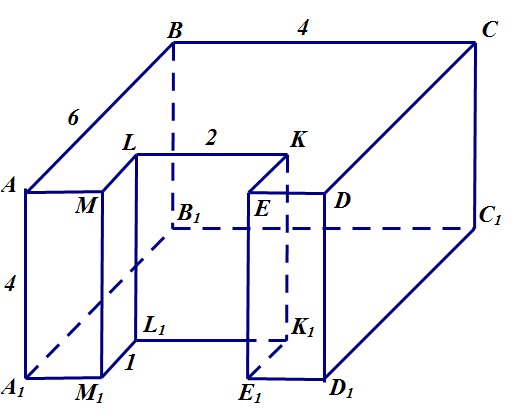
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые)
Решение. Площадь поверхности многогранника равна сумме площадей всех его граней. Так как все грани этого многогранника — прямоугольники, то для нахождения площади каждой грани мы используем формулу площади прямоугольника:
S=ab, где a и b — длины двух смежных сторон прямоугольника.
Обозначим вершины многогранника:
1.Найдем сначала площадь боковой поверхности. Для этого, чтобы не пропустить ни одной грани, обойдем наш многогранник по часовой стрелке, и запишем площадь каждой грани:
2. Найдем площадь верхней грани. Для этого из площади прямоугольника ABCD вычтем площадь прямоугольника MLKE:
3. Площадь нижней грани равна площади верхней грани и равна 22.
4. Сложим получившиеся площади: 88+22+22=132.
Задание 8_1. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности многогранника можно вычислить как сумму площадей всех его граней. Причем площади передней и задней граней, равны
и вся площадь поверхности равна
Задание 8_2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Найдем площадь поверхности как площадь поверхности прямоугольного параллелепипеда со сторонами 3, 3, 5 и вычтем площади двух граней 1х1 прямоугольного параллелепипеда со сторонами 1, 1 и 3 (см. рисунок).
Площадь поверхности большого параллелепипеда, равна
Площади двух граней 1х1 малого параллелепипеда, равны:
и площадь поверхности фигуры
Задание 8_3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Из рисунка видно, что площадь поверхности фигуры будет меньше площади прямоугольного параллелепипеда со сторонами 3, 4 и 5 на площади двух квадратов, размером 1х1, имеем:
Задание 8_4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Можно заметить, что площадь поверхности данной фигуры будет в точности совпадать с площадью поверхности прямоугольного параллелепипеда со сторонами 5, 3 и 5 и равна
Замечание. Не путайте вычисление объема фигуры и площади его поверхности!
Задание 8_5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности данной фигуры равна площади поверхности прямоугольного параллелепипеда со сторонами 3, 5 и 4, и равна
Замечание. Не путайте вычисление объема фигуры и площади его поверхности!
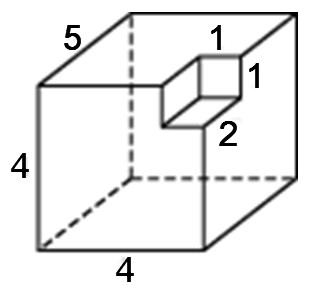
Задание 8_6. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности данной фигуры можно вычислить как площадь поверхности прямоугольного параллелепипеда со сторонами 4, 4 и 6 плюс две грани 1х4 площадью 4 (см. рисунок) и минус две грани площадью 2х1 (они вычитаются из оснований). Таким образом, площадь фигуры равна
Задание 8_7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площади нижней и верхней граней равны , площади боковых граней можно вычислить как , площади передней и задней граней соответственно и еще нужно учесть две площади внутренней нижней и верхней граней . Таким образом, вся площадь поверхности фигуры равна
Задание 8_8. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности фигуры можно вычислить как площадь поверхности прямоугольного параллелепипеда со сторонами 4, 3 и 2, минус четыре площади боковых квадратов, размером 1х1. Имеем:
Задание 8_9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
На рисунке изображен прямоугольный параллелепипед с вырезом. Площадь поверхности такой фигуры будет равна площади поверхности всего параллелепипеда со сторонами 5, 7 и 1 минус две площади фронтального выреза площадью 2х1=2 и плюс четыре площади внутренних сторон выреза размерами 1х1 и 2х1. Таким образом, вся площадь поверхности многогранника равна
Задание 8_10. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности многогранника можно найти как сумму площадей двух прямоугольных параллелепипедов со сторонами 5, 4, 3 и 3, 2, 3 минус две площади основания нижнего параллелепипеда площадью 2х3 (две площади, т.к. она будет дважды учтена в большом и малом параллелепипедах). Таким образом, получаем:
Задание 8_11. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Найдем площадь поверхности фигуры как площадь прямоугольного параллелепипеда со сторонами 2, 2, 1 и вычтем две площади граней 1х1 во фронтальных плоскостях (передней и задней), получим:
Задание 8_12. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Площадь поверхности данной фигуры можно найти как сумму площадей поверхности 6 кубов минус площадь поверхности одного куба (тот что внутри и эти грани не входят в площадь поверхности), получаем:
Задание 8_13. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдем площадь поверхности этого многогранника как сумму площадей поверхности большого (6х6х2) и малого (3х3х4) прямоугольных параллелепипедов и вычтем дважды площадь поверхности соприкосновения граней этих параллелепипедов, которая имеет размер 3х4, получим:
Задание 8_14. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности этого многогранника можно найти как сумму площадей поверхности каждого из трех параллелепипедов размерами 2х5х6, 2х5х3 и 2х3х2 минус удвоенные площади соприкосновения этих параллелепипедов, то есть минус удвоенные площади двух граней размерами 3х5 и 2х3 соответственно. В результате получаем площадь поверхности фигуры:
Задание 8_15. Через среднюю линию основания треугольной призмы, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности призмы, если площадь боковой поверхности отсеченной треугольной призмы равна 37.
Так как плоскость сечения проведена через среднюю линию, то она делит боковую плоскость пополам. Следовательно, площадь боковой поверхности большей призмы в 2 раза больше площадь боковой поверхности малой призмы и равна 74.
Определить площадь пластин плоского воздушного конденсатора электроемкостью 1 мкФ
Определить площадь пластин плоского воздушного конденсатора электроемкостью 1 мкФ, если расстояние между пластинами 1 мм.
Задача №6.4.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
Электроемкость плоского конденсатора определяется по следующей известной формуле:
Выразим из этой формулы искомую площадь пластин конденсатора (S):
Задача решена в общем виде, остается только произвести расчет. Напомним, что электрическая постоянная (varepsilon _0) равна 8,85·10 -12 Ф/м, диэлектрическая проницаемость воздуха (varepsilon) равна 1. Не забывайте переводить численные значения величин в систему СИ.
Мы получили какое-то огромное число, тем не менее в ответах в конце сборника указан такой же ответ.
Ответ: 113 м 2 .
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Масса пластины
Масса тела — это его объем 






2. Масса треугольной пластины



3. Масса круглой пластины


Тогда масса:
4. Масса эллиптической пластины



Масса пластины более сложной формы может быть вычислена как сумма (или разность) масс пластин простой формы. Примеры:
5. Масса овальной пластины


Перейти к контенту
Условие задачи:
Определить площадь пластин плоского воздушного конденсатора электроемкостью 1 мкФ, если расстояние между пластинами 1 мм.
Задача №6.4.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(C=1) мкФ, (d=1) мм, (S-?)
Решение задачи:
Электроемкость плоского конденсатора определяется по следующей известной формуле:
[C = frac{{varepsilon {varepsilon _0}S}}{d}]
Выразим из этой формулы искомую площадь пластин конденсатора (S):
[S = frac{{Cd}}{{varepsilon {varepsilon _0}}}]
Задача решена в общем виде, остается только произвести расчет. Напомним, что электрическая постоянная (varepsilon _0) равна 8,85·10-12 Ф/м, диэлектрическая проницаемость воздуха (varepsilon) равна 1. Не забывайте переводить численные значения величин в систему СИ.
[S = frac{{{{10}^{ – 6}} cdot {{10}^{ – 3}}}}{{1 cdot 8,85 cdot {{10}^{ – 12}}}} = 113;м^2]
Мы получили какое-то огромное число, тем не менее в ответах в конце сборника указан такой же ответ.
Ответ: 113 м2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.4.9 Плоский воздушный конденсатор состоит из двух пластин площадью 100 см2 каждая
6.4.11 Плоский конденсатор составлен из двух круглых пластин диаметром 0,54 м каждая
6.4.12 Плоский воздушный конденсатор погрузили в керосин. Во сколько раз изменилась
( 9 оценок, среднее 4.56 из 5 )
3 Приложения
двойных интегралов
3.1 Теоретическое
введение
Рассмотрим приложения двойного интеграла
к решению ряда геометрических задач и
задач механики.
3.1.1 Вычисление площади и массы плоской
пластины
Рассмотрим тонкую материальную
пластину D,
расположенную в плоскости Оху.
Площадь
S
этой пластины может быть найдена с
помощью двойного интеграла по формуле:
|
|
(1) |
Пусть в каждой точке пластины
задана ее поверхностная плотность γ
= γ (x,
y) ≥ 0. Будем считать,
что функция γ = γ (x,
y) непрерывна в области
D.
Тогда масса
m
этой пластины равна двойному интегралу
от функции плотности γ (x,
y) по области D:
|
|
(2) |
3.1.2
Статические моменты. Центр масс плоской
пластины
Статическим моментом
Mx
относительно оси Ox
материальной точки P(x;y),
лежащей в плоскости Oxy
и имеющей массу m,
называется произведение массы точки
на ее ординату, т.е. Mx=
my. Аналогично
определяется статический момент My
относительно оси Oy:
My
= mx.
Статические
моменты плоской
пластины с поверхностной плотностью γ
= γ (x,
y) вычисляются по
формулам:
|
|
(3) |
|
|
(4) |
Как известно из механики,
координаты xc
, yc
центра масс плоской материальной системы
определяются равенствами:
|
|
(5) |
где m
– масса системы, а Mx
и My
– статические моменты системы. Масса
плоской пластины m
определяется формулой (1), статические
моменты плоской пластины можно вычислить
по формулам (3) и (4). Тогда, согласно
формулам (5), получаем выражение для
координат центра масс плоской пластины:
|
|
(6) |
3.2 Содержание
типового расчета
Типовой расчет содержит
две задачи. В каждой задаче задана
плоская пластина D,
ограниченная линиями, указанными в
условии задачи. Г(x,y)
– поверхностная плотность пластины D.
Для этой пластины найти:
1. S
– площадь;
2. m
– массу;
3. My
, Mx
– статические моменты относительно
осей Оy
и Ох
соответственно;
4.
,
–
координаты центра масс.
3.3 Порядок
выполнения типового расчета
При решении каждой задачи
необходимо:
1. Выполнить чертеж заданной
области. Выбрать систему координат, в
которой будут вычисляться двойные
интегралы.
2. Записать область в виде
системы неравенств в выбранной системе
координат.
3. Вычислить площадь S
и массу m
пластины по формулам (1) и (2).
4. Вычислить
статические моменты My
, Mx
по формулам (3) и (4).
5. Вычислить
координаты центра масс
,
по
формулам (6). Нанести центр масс на чертеж.
При этом возникает визуальный
(качественный) контроль полученных
результатов.
Численные ответы должны
быть получены с тремя значащими цифрами.
3.4 Примеры
выполнения типового расчета
Задача 1.
Пластина D
ограничена линиями: y
= 4 – x2;
х =
0; y
= 0 (x
≥ 0; y
≥ 0) Поверхностная плотность γ0
= 3.
Решение.
Область, заданная в задаче, ограничена
параболой y
= 4 – x2,
осями координат и лежит в первой четверти
(рис. 1). Задачу будем решать в декартовой
системе координат. Эта область может
быть описана системой неравенств:
Рис.
1
Площадь S
пластины равна (1):
Так
как пластина однородная, ее масса m
= γ0S
= 3·
= 16.
По формулам (3), (4) найдем статические
моменты пластины:
Координаты
центра масс находятся по формуле (6):
Ответ:
S ≈
5,33; m
= 16; Mx
= 25,6; My
= 12;
=
0,75;
=
1,6.
Задача 2.
Пластина D
ограничена линиями: х2
+ у2
= 4; х
= 0, у
= х
( х
≥ 0, у
≥ 0). Поверхностная плотность γ(x,y)
= у.
Решение.
Пластина ограничена окружностью и
прямыми, проходящими через начало
координат (рис. 2). Поэтому для решения
задачи удобно использовать полярную
систему координат. Полярный угол φ
меняется от π/4 до π/2. Луч, проведенный
из полюса через пластину, «входит» в
неё при ρ = 0 и «выходит» на окружность,
уравнение которой: х2
+ у2
= 4 <=> ρ = 2.
Рис.
2
Следовательно, заданную
область можно записать системой
неравенств:
Площадь
пластины найдем по формуле (1):
Массу
пластины найдем по формуле (2), подставив
γ(x,y)
= у = ρ
sinφ:
Для
вычисления статических моментов пластины
используем формулы (3) и (4):
Координаты
центра масс получим по формулам (6):
Ответ:
S ≈
1,57; m
≈ 1,886; Mx
= 2,57; My
= 1;
=
0,53;
=
1,36.
3.5 Оформление
отчета
В отчете должны быть представлены все
выполненные расчеты, аккуратно выполненные
чертежи. Численные ответы должны быть
получены с тремя значащими цифрами.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Конденсаторы
- теория по физике 🧲 электростатика
- Электроемкость конденсатора
- Энергия конденсатора
- Подсказки к задачам
- Соединения конденсаторов
- Подсказки к задачам
- Разбор задач на тему «Заряженная частица в поле конденсатора»
Конденсаторы
теория по физике 🧲 электростатика
Конденсатор служит для накопления электрического заряда. Он представляет собой два проводника, разделенных слоем диэлектрика.
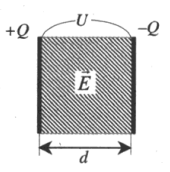
Плоский конденсатор — система двух разноименно заряженных пластин.
Разность потенциалов U (В) между обкладками конденсатора (напряжение между пластинами), определяется произведением напряженности создаваемого ими электрического поля на расстояние между ними:
Электроемкость конденсатора
Электрическая емкость — характеристика проводника, мера его способности накапливать электрический заряд.
Электроемкость обозначается как C. Единица измерения электрической емкости — Фарад (Ф).
Электроемкость конденсатора определяется формулой:
- ε 0 — диэлектрическая постоянная, равная 8,85∙10 –12 Кл 2 /(Н∙м 2 );
- ε — диэлектрическая проницаемость среды;
- S (м 2 ) — площадь каждой пластины.
Внимание! У воздушного конденсатора диэлектрическая проницаемость среды равна 1.
Связь между электроемкостью конденсатора, зарядом и напряжением определяется формулами:
Важно! Электроемкость конденсатора зависит только от площади его пластин, расстояния между ними и диэлектрической проницаемости среды. От заряда и напряжения эта величина не зависит.
Энергия конденсатора
Энергия конденсатора связана с его электроемкостью и вычисляется по следующим формулам:
W э = q 2 2 C . . = C U 2 2 .
Подсказки к задачам
| Конденсатор отключен от источника | q = q′ |
| Конденсатор подключен к источнику | U = U′ |
| Количество теплоты и энергия конденсатора | Q = ∆Wэ |
Пример №1. Вычислить электроемкость плоского воздушного конденсатора с квадратными пластинами со стороной 10 см, расположенными на расстоянии 1 мм друг от друга. Ответ округлить до десятых.
Так как между обкладками конденсатора находится воздух, примем диэлектрическую проницаемость среды за единицу.
Площадь квадратной пластины равна квадрату ее стороны:
Соединения конденсаторов
1 C . . = 1 C 1 . . + 1 C 2 . .
Подсказки к задачам
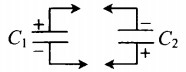
| Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов одноименными полюсами. | Схема соединения конденсаторов одноименными полюсами: 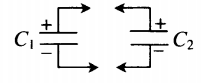 Заряд системы после соединения: Заряд системы после соединения: |
q′ = C 1 U 1 + C 2 U 2
Электрическая емкость системы:
U′ = q ′ C ′ . . = C 1 U 1 + C 2 U 2 C 1 + C 2 . .
Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов разноименными полюсами.
Схема соединения конденсаторов разноименными полюсами:
Заряд системы после соединения:
q′ = C 1 U 1 − C 2 U 2
Электрическая емкость системы:
U′ = q ′ C ′ . . = C 1 U 1 − C 2 U 2 C 1 + C 2 . .
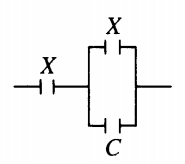
Пример №2. К конденсатору, электрическая емкость которого C = 16 пФ, подключают два одинаковых конденсатора емкостью X: один параллельно, а второй — последовательно (см. рисунок). Емкость образовавшейся батареи конденсаторов равна емкости C. Какова емкость X? Ответ округлите до десятых.
Электрическая емкость параллельного соединения равна:
C п а р а л = X + C
Электроемкость последовательного соединения:
1 C п о с л е д . . = 1 C п а р а л . . + 1 X . . = 1 X + C . . + 1 X . .
Учтем, что суммарная электроемкость равна C:
1 C . . = 1 X + C . . + 1 X . .
Преобразуем, умножим выражение на CX(X+C):
X ( X + C ) = C X + C ( X + C )
X 2 + X C = C X + C X + C 2
X 2 − C X − C 2 = 0
Решив уравнение, получим: X = 25,9 пФ.
Разбор задач на тему «Заряженная частица в поле конденсатора»
| Шарик, находящийся в масле плотностью ρ, «висит» в поле плоского конденсатора. Плотность вещества шарика ρш > ρ, его радиус r, расстояние между обкладками конденсатора d. Каков заряд шарика, если электрическое поле направлено вверх, а разность потенциалов между обкладками U? | Условие равновесия исходит из второго закона Ньютона: |
− F т я ж + − F K + − F A = 0
ρш > ρ, поэтому − F т я ж > − F A . В этом случае сила Кулона направлена вверх, а заряд шарика положительный. Схематически это можно отобразить так:
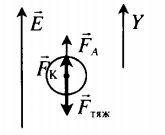
F K + F A = F т я ж
Сила тяжести равна произведению объема на плотность шарика и на ускорение свободного падения:
F т я ж = ρ ш 4 3 . . π r 3 g
Архимедова сила равна произведению объема шарика на плотность масла и на ускорение свободного падения:
F А = ρ 4 3 . . π r 3 g
q U d . . + ρ 4 3 . . π r 3 g = ρ ш 4 3 . . π r 3 g
q = ( ρ ш 4 3 . . π r 3 g − ρ 4 3 . . π r 3 g ) d U . . = 4 π r 3 g d ( ρ ш − ρ ) 3 U . .
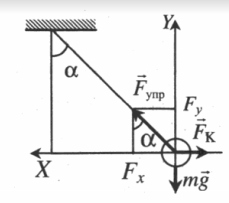
Маленький шарик с зарядом q и массой m, подвешенный на невесомой нити с коэффициентом упругости k, находится между вертикальными пластинами воздушного конденсатора. Расстояние между обкладками конденсатора d. Какова разность потенциалов между обкладками конденсатора U, если удлинение нити ∆l?
Условие равновесия исходит из второго закона Ньютона:
− F т я ж + − F K + − F у п р = 0
Проекции на оси ОХ и ОУ соответственно:
F у п р sin . α − F K = 0
F у п р cos . α − m g = 0
k Δ l sin . α = q U d . .
k Δ l cos . α = m g
Чтобы избавиться от угла α, возведем уравнения в квадрат и сложим их:
( k Δ l ) 2 sin 2 . α + ( k Δ l ) 2 cos 2 . α = ( q U d . . ) 2 + ( m g ) 2
( k Δ l ) 2 ( sin 2 . α + cos 2 . α ) = ( q U d . . ) 2 + ( m g ) 2
sin 2 . α + cos 2 . α = 1
( k Δ l ) 2 = ( q U d . . ) 2 + ( m g ) 2
U = d q . . √ ( k Δ l ) 2 − ( m g ) 2
Пластины плоского конденсатора расположены горизонтально на расстоянии d друг от друга. Напряжение на пластинах конденсатора U. В пространстве между пластинами падает капля жидкости. Масса капли m, ее заряд q. Определите расстояние между пластинами. Влиянием воздуха на движение капли пренебречь. Второй закон Ньютона в векторной форме:
− F т я ж + − F K = 0
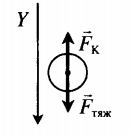
F т я ж − F K = 0
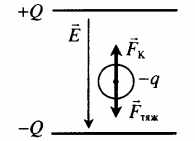
Между двумя параллельными горизонтально расположенными диэлектрическими пластинами создано однородное электрическое поле с напряженностью − E , направленное вертикально вниз. Между пластинами помещен шарик на расстоянии d от верхней пластины и b от нижней. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Через какой промежуток времени t шарик ударится об одну из пластин, если система находится в поле силы тяжести Земли? Второй закон Ньютона в векторной форме:
− F т я ж + − F K = m − a
Согласно условию данной задачи, сила тяжести противоположно направлена силе Кулона. Построим рисунок:
Если Fтяж > FK, то шарик движется с ускорением вниз. Ускорение и перемещение в этом случае равны:
Если Fтяж a = q E − m g m . .
Начальная скорость шарика равна нулю. Поэтому перемещение также равно:
m g − q E m . . t 2 2 . . = b
t = √ 2 b m m g − q E . .
Выполняя вычисления для случая Сделаем вычисления для случая Fтяж t = √ 2 b m q E − m g . .
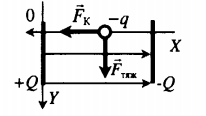
Между двумя параллельными, вертикально расположенными диэлектрическими пластинами создано однородное электрическое поле, напряженность которого − E и направлена слева направо. Между пластинами помещен шарик на расстоянии b от левой пластины и d от правой. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Найдите смещение шарика по вертикали ∆h до удара об одну из пластин. Пластины имеют достаточно большой размер. Второй закон Ньютона в векторной форме:
− F т я ж + − F K = m − a
Если сила Кулона направлена вправо, то sx = d.
Если сила Кулона направлена вправо, то sx = b.
Учитывая, что заряд меньше нуля, а вектор напряженности направлен вправо, делаем вывод, что кулоновская сила направлена влево.
Из проекций второго закона Ньютона выразим проекции ускорения на оси ОХ и ОУ соответственно:
Проекции перемещений на эти же оси:
s x = Δ h = g t 2 2 . .
q E m . . t 2 2 . . = b
Так как время движения шарика по вертикали и горизонтали одинаково:
t 2 = 2 Δ h g . . = 2 m b q E . .
Введите ответ в поле ввода Плоский конденсатор подключён к гальваническому элементу. Как изменятся при уменьшении зазора между обкладками конденсатора три величины: ёмкость конденсатора, величина заряда на его обкладках, разность потенциалов между ними?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Емкость конденсатора определяется формулой:
Следовательно, емкость имеет обратно пропорциональную зависимость от расстояния между обкладками. Если расстояние уменьшить, то емкость увеличится.
Вот как взаимосвязана электроемкость и заряд конденсатора:
Мы выяснили, что электроемкость увеличивается. Следовательно, увеличится и заряд, так как они имеют прямо пропорциональную зависимость.
С учетом того, что плоский конденсатор подключен к гальваническому элементу, разность потенциалов никак не зависит от расстояния между обкладками. Поэтому величина U остается неизменной.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Воспользовавшись оборудованием, представленным на рис. 1, учитель собрал модель плоского конденсатора (рис. 2), зарядил нижнюю пластину положительным зарядом, а корпус электрометра заземлил. Соединённая с корпусом электрометра верхняя пластина конденсатора приобрела отрицательный заряд, равный по модулю заряду нижней пластины. После этого учитель сместил одну пластину относительно другой не изменяя расстояния между ними (рис. 3). Как изменились при этом показания электрометра (увеличились, уменьшились, остались прежними)? Ответ поясните, указав, какие явления и закономерности Вы использовали для объяснения. Показания электрометра в данном опыте прямо пропорциональны разности потенциалов между пластинами конденсатора.
Алгоритм решения
Решение
На первом рисунке стрелка и стержень электрометра, соединённые с нижней пластиной, но изолированные от корпуса, заряжаются положительно. Поэтому стрелка отклоняется на некоторый угол. В верхней пластине и металлическом корпусе электрометра происходит перераспределение свободных электронов таким образом, что верхняя пластина заряжается отрицательно.
На втором рисунке заряды пластин одинаковы по модулю и противоположны по знаку, пластины образуют конденсатор с ёмкостью:
S — площадь перекрытия пластин, d — расстояние между ними, ε — диэлектрическая проницаемость диэлектрика между пластинами.
Характер изменения угла отклонения стрелки совпадает с изменением разности потенциалов между пластинами: при увеличении разности потенциалов увеличивается угол отклонения, при уменьшении разности потенциалов угол уменьшается.
На рисунке 3 площадь перекрытия пластин уменьшилась. Следовательно, уменьшилась электроемкость, которая имеет обратно пропорциональную зависимость от разности потенциалов:
Заряд остается постоянным, поскольку система изолированная — заряду просто некуда деться. Поэтому с уменьшением электроемкость растет разность потенциалов. Поэтому показания электрометра увеличатся.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Ученик изучает свойства плоского конденсатора. Какую пару конденсаторов (см. рисунок) он должен выбрать, чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками?
Алгоритм решения
- Установить, какие величины в данном эксперименте должны быть переменными, а какие — постоянными.
- Найти рисунок с парой конденсаторов, удовлетворяющий требованиям, выявленным в шаге 1.
Решение
Чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками, нужно сохранить все величины постоянными, кроме самого расстояния. Поэтому площади обкладок должны быть одинаковыми, но расстояние между ними разными, как на рисунке 1.
pазбирался: Алиса Никитина | обсудить разбор | оценить
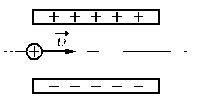
Ответ записать в км/с, округлив до десятков.
Алгоритм решения
Решение
Запишем исходные данные:
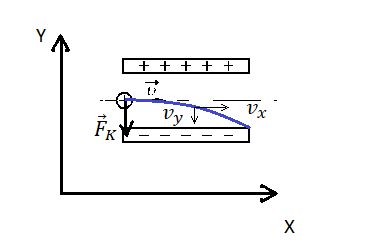
Изначально протон обладает только горизонтальной скоростью v, равной vx. Влетев в однородное электростатическое поле внутри конденсатора, протон обретает вертикальную компоненту скорости, которая растет за счет ускорения, придаваемого кулоновскими силами. Положительно заряженный протон притягивается нижней отрицательно зараженной пластиной конденсатора.
Чтобы протон вылетел из конденсатора, его горизонтальная компонента скорости должна быть достаточной для того, чтобы частица не притянулась к нижней пластине раньше. Время, которое понадобится протону для преодоления длины пластин конденсатора со скоростью vx:
t = l v x . . = l v . .
Протон влетел в пространство между обкладками конденсатора на одинаковом расстоянии от них. Следовательно, прежде чем он упадет на нижнюю пластину, по оси OY он переместится на расстояние, равное 0,5d. Так как начальная компонента скорости равна нулю (мы пренебрегаем силой тяжести):
0 , 5 d = a t 2 2 . .
Протон вылетит из конденсатора, а не упадет на его пластину, если время горизонтального перемещения до конца пластин будет как минимум равно времени падения. Выразим время падения:
Приравняем правые части уравнений времени и получим:
Отсюда скорость равна:
Ускорение выразим из второго закона Ньютона:
F K = m a = q U d . .
Но известно, что:
a = q E d m d . . = q E m . .
Минимальная скорость, с которой протон должен влететь в конденсатор, составляет 346∙10 3 м/с. Округлим до десятков и переведем в км/с. Получим 350 км/с.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Источник
Число Маха при заданной газовой постоянной
Идти
Число Маха = sqrt(2*Динамическое давление/(Плотность окружающего воздуха*Удельная теплоемкость воздуха*Газовая постоянная*Температура))
Удельная теплоемкость воздуха с учетом газовой постоянной новой
Идти
Удельная теплоемкость воздуха = 2*Динамическое давление/(Плотность окружающего воздуха*Число Маха^2*Газовая постоянная*Температура)
Плотность окружающего воздуха с учетом газовой постоянной
Идти
Плотность окружающего воздуха = 2*Динамическое давление/(Число Маха^2*Удельная теплоемкость воздуха*Газовая постоянная*Температура)
Газовая постоянная при динамическом давлении
Идти
Газовая постоянная = 2*Динамическое давление/(Плотность окружающего воздуха*Число Маха^2*Удельная теплоемкость воздуха*Температура)
Температурная заданная газовая постоянная
Идти
Температура = 2*Динамическое давление/(Плотность окружающего воздуха*Число Маха^2*Удельная теплоемкость воздуха*Газовая постоянная)
Пролет в боковой плоскости с учетом индуктивного сопротивления
Идти
Пролет в боковой плоскости = sqrt((Подъемная сила^2)/(3.14*Индуцированное сопротивление*Динамическое давление))
Индуктивное сопротивление с учетом коэффициента полезного действия пролета
Идти
Индуцированное сопротивление = Коэффициент сопротивления*Плотность материала*Скорость^2*Справочная область/2
Индуцированное сопротивление
Идти
Индуцированное сопротивление = (Подъемная сила^2)/(3.14*Динамическое давление*Пролет в боковой плоскости^2)
Смоченная площадь при заданной площади плоской пластины
Идти
Зона смачивания самолета = (Площадь плоской пластины)/(Форм-фактор сопротивления*Коэффициент трения кожи)
Форм-фактор с учетом площади плоской пластины
Идти
Форм-фактор сопротивления = (Площадь плоской пластины)/(Коэффициент трения кожи*Зона смачивания самолета)
Коэффициент трения кожи с учетом площади плоской пластины
Идти
Коэффициент трения кожи = Площадь плоской пластины/(Форм-фактор сопротивления*Зона смачивания самолета)
Пролет в боковой плоскости с заданным удлинением
Идти
Пролет в боковой плоскости = sqrt(Соотношение сторон в боковых плоскостях*Зона смачивания самолета)
Плотность окружающего воздуха с учетом числа Маха
Идти
Плотность окружающего воздуха = 2*Динамическое давление/(Число Маха*Звуковая скорость)^2
Площадь плоской пластины
Идти
Площадь плоской пластины = Фактор формы*Коэффициент трения кожи*Зона смачивания самолета
Удельная теплоемкость воздуха при нормальном давлении
Идти
Удельная теплоемкость воздуха = 2*Динамическое давление/(Давление*Число Маха^2)
Нормальное давление при динамическом давлении
Идти
Давление = 2*Динамическое давление/(Удельная теплоемкость воздуха*Число Маха^2)
Полная масса с учетом сопротивления
Идти
Общий вес = Сила сопротивления*(Коэффициент подъема/Коэффициент сопротивления)
Смоченная площадь с заданным соотношением сторон
Идти
Зона смачивания самолета = (Пролет в боковой плоскости)^2/Соотношение сторон в боковых плоскостях
Соотношение сторон в боковой плоскости
Идти
Соотношение сторон в боковых плоскостях = (Пролет в боковой плоскости)^2/Зона смачивания самолета
Плотность окружающего воздуха при динамическом давлении
Идти
Плотность окружающего воздуха = 2*Динамическое давление/(Скорость полета^2)
Скорость полета с учетом динамического давления
Идти
Скорость полета = 2*Динамическое давление/(Плотность окружающего воздуха)
Аэродинамическая сила
Идти
Аэродинамическая сила = Сила сопротивления+Подъемная сила