Как найти среднюю плотность планеты в астрономии

Как найти среднюю плотность в астрономии

Астрономия – одна из самых увлекательных наук, которая помогает человечеству лучше понимать небесные явления. Одним из главных понятий в астрономии является плотность, которая позволяет узнать, насколько компактна и массивна планета, звезда или галактика. В данной статье мы рассмотрим, как найти среднюю плотность в астрономии и какие формулы использовать для этого.

Понятие плотности в астрономии

Плотность – это физическая характеристика вещества, которая определяет, насколько компактно расположены молекулы или атомы этого вещества. В астрономии плотность позволяет определить массу объекта небесной механики и насколько он компактен.

Плотность вычисляется как отношение массы объекта к его объему:

Плотность = масса / объем

Единицей измерения плотности в СИ является килограмм на кубический метр (кг/м³).

Средняя плотность планеты

Давайте рассмотрим, как вычислить среднюю плотность планеты. Для этого необходимо знать ее массу и объем. Например, массу Земли можно найти, используя законы Кеплера и формулу Ньютона. Результаты показывают, что Земля имеет массу приблизительно в 5,97 x 10^24 кг.
Для нахождения объема Земли можно использовать формулу для объема шара:

Объем = 4/3πR³

Где R – радиус планеты. Радиус Земли составляет примерно 6 371 км. Подставив значения, мы получаем, что объем Земли равен 1,083 x 10^12 кубических километров (или 1.083 x 10^21 кубических метров).

Теперь, когда у нас есть масса и объем Земли, мы можем вычислить среднюю плотность:

Плотность Земли = 5,97 x 10^24 кг / (1,083 x 10^21 м³) = 5 515 кг/м³

Средняя плотность звезды

Среднюю плотность звезды также можно вычислить, зная ее массу и радиус. Плотность звезды влияет на ее процессы сжатия и нагревания и, следовательно, на ее жизненный цикл.

Предположим, что у нас есть Бетельгейзе – красный сверхгигант, расположенный в созвездии Ориона, который обладает массой примерно в 20 раз больше массы Солнца и радиусом примерно в 1 000 раз больше радиуса Солнца. Можно использовать формулу для объема сферы, чтобы найти объем Бетельгейзе:

Объем = 4/3πR³

Радиус Бетельгейзе составляет 1,08 млрд км, или 7,6 астрономических единиц. Подставив значение в формулу, мы получим, что объем Бетельгейзе составляет примерно 3,65 x 10^12 кубических километров (или 3,65 x 10^27 кубических метров).

Массу Бетельгейзе можно найти, измерив ее гравитационное воздействие на окружающие звезды. Измерения показывают, что масса Бетельгейзе составляет примерно 3,4 x 10^31 кг.

Теперь мы можем вычислить среднюю плотность Бетельгейзе:

Плотность Бетельгейзе = 3,4 x 10^31 кг / (3,65 x 10^27 м³) = 0,93 кг/м³

Средняя плотность галактики

Вычисление средней плотности галактики – это гораздо более сложная задача, чем вычисление плотности планеты или звезды. Это связано с тем, что галактики имеют очень сложную структуру и содержат множество различных компонентов – звезды, пыль, газ и темную материю.

Некоторые ученые используют космологические симуляции для вычисления средней плотности галактики. Другие используют спектроскопию для измерения плотности газа и других компонентов галактики в разных участках.

Средняя плотность Млечного Пути, нашей галактики, составляет примерно 0,1 массы Солнца на кубический парсек (1 солярная масса / кубический парсек), что соответствует примерно 0,0002 кг/м³.

Итог

Средняя плотность в астрономии является важной характеристикой, которая помогает ученым лучше понять небесные объекты и их структуру. Вычисление средней плотности планет, звезд и галактик может осуществляться различными способами, но как правило, определяется отношением массы объекта к его объему.

Кроме того, плотность играет важную роль в космических исследованиях, так как она влияет на гравитационное и электромагнитное взаимодействие между небесными объектами и управляет их движением и эволюцией.

Изучение плотности помогает нам лучше понимать вселенную и расширять наши знания о ее устройстве. Таким образом, средняя плотность небесных объектов является ключевым показателем в астрономии, который может помочь в решении многих важных вопросов.

Как найти среднюю плотность в астрономии

Плотность – важный параметр, который помогает понять, как устроен объект небесной механики. Знание плотности позволяет определить массу космических тел и их размеры, понять, как такие объекты формировались и на какой стадии развития они находятся.

Что такое средняя плотность

Средняя плотность – это количество массы, которая содержится в единице объема. Она применяется для описания космических объектов, которые не имеют однородной структуры. Например, планеты, которые состоят из коры, мантии и ядра, имеют разную плотность в разных частях своей структуры. Средняя плотность – это среднее значение плотности по всему объему планеты.

Как вычислить среднюю плотность

Средняя плотность вычисляется по формуле:

ρ = m/V

где ρ – средняя плотность, m – масса объекта, V – его объем.

Для вычисления средней плотности планеты или другого космического объекта, необходимо знать ее массу и объем. Масса планеты может быть вычислена по скорости ее спутника, а также по влиянию планеты на соседние объекты одной звездной системы. Объем можно найти, используя радиус планеты и предполагаемую форму ее поверхности.

Примеры вычисления средней плотности

Например, средняя плотность Земли равна 5,52 г/см³. Масса Земли составляет 5,97·10²⁴ кг, а ее объем равен 1083,21·10⁹ км³. Расчет sредней плотности выглядит так:

ρ = 5,97·10²⁴ кг : 1083,21·10⁹ км³ = 5,52 г/см³

Другой пример – плутон. Его средняя плотность составляет 1,85 г/см³. Масса Плутона – 1,31·10²² кг, и его объем – 7,19·10³ км³. Вычисляем:

ρ = 1,31·10²² кг : 7,19·10³ км³ = 1,85 г/см³

Что могут дать знания о средней плотности

Знание средней плотности космических объектов – это ключевой момент в изучении Вселенной. Например, при изучении космических тел с помощью радарной астрономии можно получить около-поверхностный обзор их структуры, что позволит определить материал, из которого они состоят и, соответственно, их плотность.

Знание плотности также полезно для изучения процессов, протекающих во Вселенной. Например, для понимания процессов формирования звезд, галактик и космических туманностей.

Общий итог

Средняя плотность является важным параметром для изучения космических объектов. Она позволяет определить их массу и размеры, понять, как они формировались и на какой стадии развития находятся. Расчет средней плотности может быть произведен по массе и объему космического объекта. Знание средней плотности помогает изучать процессы, протекающие во Вселенной, и определять материал, из которого состоят космические тела.

• Средняя плотность выражает количество массы в единице объема.
• Вычисляется по формуле ρ = m/V.
• Для определения средней плотности необходимо знать массу и объем объекта.
• Средняя плотность важна для определения массы, размеров и стадии развития космических объектов.
• Знание средней плотности позволяет изучать процессы, протекающие во Вселенной.

Как найти среднюю плотность в астрономии?

Астрономия — это великая наука об устройстве вселенной, её свойствах и эволюции. Изучение астрономии помогает понять, откуда мы пришли и куда идём, что такое гравитация и как она влияет на нашу жизнь, а также многое другое. Среднюю плотность в астрономии можно найти из расчётов, основанных на изучении различных объектов, таких как звёзды, планеты, галактики и тёмная материя.

Что такое плотность?

Плотность — это физическая величина, которая определяет отношение массы к объёму, т.е. плотность = масса / объём. В астрономии плотность является важной характеристикой для изучения объектов. Например, знание плотности звёзд помогает ученым определить стадию жизненного цикла звезды.

Как найти плотность звёзды?

Плотность звёзды можно определить, зная её массу и радиус. Для того, чтобы найти массу звезды, учёные измеряют её орбитальную скорость вокруг общего центра масс, в то время как радиус звезды измеряют при помощи метода эффективной температуры и светимости. Используя эти данные, можно найти плотность звезды.

Как найти плотность планеты?

Плотность планеты также может быть найдена из её массы и радиуса, что помогает ученым определить её химический состав и стадию развития. Например, плотность Земли является фактором, который указывает на присутствие жидкого железа в её ядре.

Как найти плотность галактики?

Галактики — это огромные скопления звезд, газа и пыли, которые вращаются вокруг центра массы. Для того, чтобы найти плотность галактики, учёные измеряют её массу и размеры. Измерения массы галактик могут быть выполнены при помощи астрономических наблюдений, например, измерения скорости звёзд и газа, которые находятся внутри галактики. Используя эти данные, можно найти плотность галактики.

Что такое тёмная материя и как найти её плотность?

Тёмная материя — это загадочная форма материи, которая является наиболее распространённой формой материи во вселенной. Она взаимодействует со светом и гравитационными полями, но в остальном она не взаимодействует с «обычной» материей, из-за чего её не удаётся прямо наблюдать. Тем не менее, учёные могут определить наличие тёмной материи и её плотность при астрономических наблюдениях гравитационных линз и формирований космических структур.

Итак, средняя плотность в астрономии — это физическая величина, которая может быть определена при помощи измерения массы и размеров объектов. Зная плотность звезд, планет, галактик и тёмной материи, учёные могут более глубоко понимать свойства Вселенной и её эволюцию.

• плотность — физическая величина, которая определяет отношение массы к объёму;
• плотность звёзды можно определить, зная её массу и радиус;
• плотность планеты может быть найдена, исходя из её массы и радиуса;
• плотность галактики можно измерить, зная её массу и размеры;
• тёмная материя — это загадочная форма материи, плотность которой может быть определена при помощи астрономических наблюдений.

1. Плотность планеты

Рассмотрим, как выразить ускорение свободного падения на поверхности планеты и первую космическую скорость для этой планеты через ее радиус R и среднюю плотность ρ. (Средняя плотность планеты равна отношению массы планеты к ее объему.)

? 1. Выразите массу планеты M через ее радиус R и среднюю плотность ρ.

? 2. Чему равно ускорение свободного падения g на поверхности планеты радиусом R, имеющей среднюю плотность ρ?

Подсказка. Воспользуйтесь формулой (8) из в § 14, заменив массу и радиус Земли на массу и радиус данной планеты.

? 3. Вблизи поверхности планеты-гиганта Юпитер (на рисунке 18.1 Юпитер изображен в одном масштабе с Землей) ускорение свободного падения в 2,6 раза больше, чем вблизи поверхности Земли. Радиус Юпитера примерно в 11 раз больше радиуса Земли. Какова средняя плотность Юпитера?

? 4. На планете радиусом 3400 км камень падает с обрыва высотой 200 м в течение 10 с. Чему равна средняя плотность планеты? Считайте, что сопротивлением атмосферы планеты можно пренебречь.

? 5. Чему равна первая космическая скорость для планеты радиусом R со средней плотностью ρ?

Подсказка. Воспользуйтесь формулой (10) из § 14, заменив радиус Земли и ускорение свободного падения на поверхности Земли на массу данной планеты и ускорение свободного падения на ее поверхности.

А сейчас мы получим несколько неожиданный результат.

? 6. Чему равен период T обращения спутника по низкой круговой орбите вокруг планеты радиусом R со средней плотностью ρ? (В таком случае радиус орбиты можно считать равным радиусу планеты.)

Итак, период обращения спутника на низкой круговой орбите зависит только от средней плотности планеты!

? 7. Астронавты облетели три планеты А, Б и В на низких круговых орбитах с выключенным двигателем. Время облета каждой из планет составило: T_А = 55 мин, T_Б = 106 мин, T_В = 72 мин. У какой из этих планет наибольшая средняя плотность? У каких из этих планет средняя плотность больше средней плотности Земли? Напомним, что период обращения искусственного спутника Земли на низкой орбите 85 мин.

2. Учет вращения планеты вокруг своей оси

Геостационарная орбита

Телевизионные программы передают в разные точки Земли с помощью спутников связи (рис. 18.2), которые движутся по круговым орбитам.

Сигнал со спутника принимает укрепленная на стене или крыше дома спутниковая антенна. Она направлена постоянно на одну и ту же точку небосвода, поэтому спутник связи должен постоянно «висеть» над одной и той же точкой поверхности Земли.

? 8. Чему равен период одного оборота спутника связи?

Орбиту, по которой движется спутник, находящийся постоянно над одной и той же точкой поверхности Земли, называют геостационарной. Она лежит в экваториальной плоскости Земли (так называют плоскость, в которой лежит экватор).

? 9. Выразите радиус rгс геостационарной орбиты через ускорение свободного падения g вблизи поверхности Земли, радиус Земли и продолжительность суток T.

Подсказка. Запишите уравнение второго закона Ньютона для спутника связи, выразив в нем гравитационную постоянную G через g, MЗем, Rзем.

? 10. Чему равен радиус геостационарной орбиты? На какой высоте над поверхностью Земли находится эта орбита?

Выполнив это задание, вы оцените уровень современной техники: спутниковая антенна устойчиво принимает сигнал с расстояния в десятки тысяч километров!

Вес тела на полюсе и на экваторе

Вследствие вращения планеты вокруг своей оси (его называют суточным) вес одного и того же тела на экваторе планеты меньше, чем на ее полюсе. Выясним, от чего зависит разность значений веса на экваторе и на полюсе.

Пусть тело покоится на поверхности шарообразной планеты вблизи ее полюса. В этом случае вес тела

P_П = mg,     (1)

где g – ускорение свободного падения.

Чтобы найти вес тела на поверхности планеты вблизи экватора, надо учесть суточное вращение планеты.

Вследствие этого вращения находящееся на экваторе тело равномерно движется по окружности относительно инерциальной системы отсчета, связанной с удаленными звездами (рис. 18.3). Радиус окружности равен радиусу планеты R, а период обращения T равен продолжительности суток.

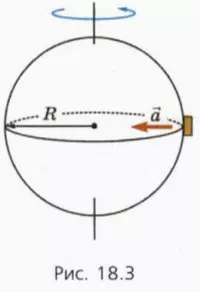
Вследствие суточного вращения планеты находящееся на ее экваторе тело движется относительно инерциальная центростремительным ускорением

Это ускорение направлено к центру планеты, то есть вниз. А если тело движется с ускорением , направленным вниз, вес этого тела выражается формулой (см. § 16):

P_Э = m(g – a).

? 11. Чему равно уменьшение веса тела массой m на экваторе шарообразной планеты радиусом R по сравнению с его весом на полюсе, если период обращения планеты равен T?

? 12. С помощью каких весов можно обнаружить уменьшение веса тела на экваторе – рычажных, в которых используются гири, или пружинных, когда вес тела измеряют по удлинению пружины?

? 13. Каково обусловленное суточным вращением Земли уменьшение веса корабля массой 40000 т при переходе его из приполярной области в экваториальные воды? Уменьшается ли при этом масса корабля?

? 14. На сколько процентов уменьшается вес тела вследствие суточного вращения Земли при перемещении его с полюса Земли на экватор?

Существует еще одна причина уменьшения веса тела на экваторе Земли по сравнению с весом на полюсе.

Дело в том, что Земля немного сплюснута у полюсов – расстояние между Северным и Южным полюсами (по прямой сквозь Землю) примерно на 43 км меньше, чем расстояние между диаметрально противоположными точками экватора Земли. Вследствие этого на полюсе находящаяся на уровне моря точка расположена примерно на 21,5 км ближе к центру Земли, чем точка на экваторе.

Общее уменьшение веса, обусловленное суточным вращением и сплюснутостью Земли, составляет примерно 0,5 %.

? 15. Каким должен быть период обращения шарообразной планеты массой M и радиусом r вокруг своей оси, чтобы находящиеся на ее экваторе тела находились в состоянии невесомости?

? 16. При какой продолжительности земных суток тела на земном экваторе были бы в состоянии невесомости?

Дополнительные вопросы и задания

17. Сорвавшийся с обрыва на некоторой планете камень падал с высоты h в течение времени t. Радиус планеты равен R. Чему равна масса планеты M?

18. Высадившийся на планету радиусом R астронавт бросает камешки с начальной скоростью v₀ под разными углами к горизонту. Чему равна средняя плотность планеты, если все камешки упали на расстоянии от космонавта, не превышающем l?

19. Космонавты высадились на экваторе шарообразной малой планеты. Средняя плотность планеты ρ, радиус R, продолжительность суток T.
а) Чему равна скорость точек поверхности планеты на экваторе?
б) Чему равна первая космическая скорость для этой планеты?
в) С какой скоростью космонавты могут ехать на гусеничном вездеходе вдоль экватора по направлению суточного вращения планеты, не отрываясь от ее поверхности?

20. Над находящейся на экваторе Земли африканской деревней 2 раза в сутки – в полдень и в полночь – пролетают одновременно два искусственных спутника, А и Б. Орбиты спутников лежат в экваториальной плоскости, спутник А движется на восток, а Б – на запад.
а) Какой спутник движется в направлении суточного вращения Земли, а какой – в противоположном?
б) Чему равен период обращения каждого спутника?
в) Каковы радиусы орбит спутников?

21. Космический корабль массой 10 т должен постоянно находиться в точке, где силы притяжения со стороны Земли и Луны уравновешивают друг друга. Примите, что Землю можно считать неподвижной, а расстояние от Земли до Луны постоянным.
а) Как направлена сила тяги двигателя корабля?
б) Выразите расстояние r от Земли до корабля через массу Земли M_Зем массу Луны M_Л и расстояние R_ЗЛ от Земли до Луны.
в) Чему равна сила тяги двигателя корабля?

Решебник по астрономии 11 класс на урок №13 (рабочая тетрадь) – Планеты земной группы

1. Пользуясь справочными данными учебника, заполните таблицу с основными физическими характеристиками планет земной группы.

Физические характеристики планет	Меркурий	Венера	Земля	Марс
Масса (в массах Земли)	0.055	0.815	1	0.107
Диаметр (в диаметрах Земли)	0.382	0.949	1	0.533
Плотность, кг/м^3	5440	5240	5520	3940
Период вращения	58.6 сут	243 сут	23 ч 56 мин	24 ч 37 мин
Атмосфера: давление, химический состав	Практически нет	95 атм, 96.5% CO(2), 3.5% N(2) и др.	1 атм, 78% N(2), 21% O(2) и др.	1/150 атм, 95% CO(2), 2.5% N(2) и др.
Температура поверхности, °C	+430 днём; -170 ночью	+480	От +60 до +17 днём; -80 ночью	От +15 до -60 днём; -120 ночью
Число спутников	—	—	1	2
Названия спутников	—	—	Луна	Фобос и Деймос

Заполните таблицу, сделайте выводы и укажите сходства и различия между планетами земной группы.

Выводы: Планеты земной группы практически все имеют одинаковые плоскости близких массы. Планеты земной группы, кроме Меркурия, имеют атмосферу.

2. На графиках показаны зависимости давления и температуры в атмосфере Венеры. На основе анализа графиков ответьте на вопросы.

На какой высоте давление атмосферы Венеры равно атмосферному давлению у поверхности Земли? (Примерно 50 км.)

Чему равна температура атмосферы Венеры на данной высоте? (Около 330К, или +50 °C.)

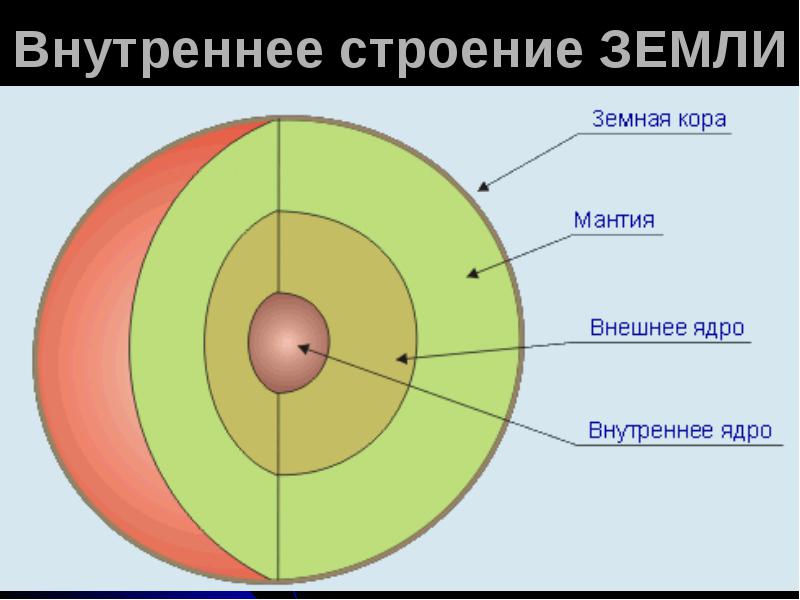
3. С помощью рисунка опишите внутреннее строение Земли.

4. Закончите предложения.

Вариант 1.
Самый большой перепад дневной и ночной температур поверхности у планеты Меркурий.
Высокая температуры поверхности Венеры обусловлена парниковым эффектом.
Планета земной группы, средняя температура поверхности которой ниже 0 °C, — это Марс.
Большая часть поверхности покрыта водой у планеты Земля.
В состав облаков входят капельки серной кислоты у планеты Венера.

Вариант 2.
Планета, суточный перепад температур поверхности которой составляет около 100 °C, — это Марс.
Планеты, температуры поверхности которых бывает выше +400 °C, — это Меркурий и Венера.
Планета, в атмосфере которой часто происходят глобальные пылевые бури, — это Марс.
Практически не имеют атмосферы планета Меркурий.
Планета, обладающая биосферой, — это Земля.

5. Какие физические характеристики планеты необходимо знать, чтобы вычислить её среднюю плотность?

Необходимо знать массу планеты и её средний радиус. Средняя плотность определяется делением массы на объём планеты.

Астрономия — один из разделов физики. Она изучает космические тела и объекты: планеты, звезды, астероиды. В школе эту тему практически не рассматривают, хотя в ЕГЭ она встречается. Формулы по астрономии — это задание 24 из итоговой аттестации. Для его выполнения нужно анализировать таблицы с информацией о небесных телах, а также проводить некоторые расчеты. Если вам интересна эта тема, и вы хотите подготовиться к экзамену лучше, подумайте о посещении курсов. На них, помимо других разделов, разбираются небесные тела. А в статье мы дадим краткую теорию, перечислим формулы по астрономии для физики. 

Теория

Теоретические вопросы и формулы по астрономии для ЕГЭ можно разделить на 4 группы: 

• звезды;
• планеты Солнечной системы;
• спутники;
• остальные тела: кометы, астероиды.

Формул по теме «Звезды» нет. Для решения заданий нужно уметь пользоваться диаграммой Герцшпрунга-Расселла, показывающей классификацию небесных тел. Для этого разберитесь в светимости, температуре, спектральных классах. 

Планеты и спутники

Планеты и спутники Солнечной системы представляют собой шарообразные тела. К ним применимы многие формулы из геометрии. Одно из таких выражений — объем V = 4/3 • πR³ = πd³ / 6. Зная среднюю плотность небесного тела, можно вычислить ее массу m = 4/3 • ρπR³ = ρπd³ / 6. Еще одно важное определение — первая космическая скорость. При ее достижении небесное тело приобретает круговую орбиту и становится спутником. Если тело приобретет вторую космическую скорость, оно победит силу гравитационного притяжения, сможет покинуть свою орбиту и улететь в пространство на бесконечность. Важная характеристика — период вращения, показывающий отношение радиуса планеты к ее скорости. Период вращения определяет длительность суток или года.

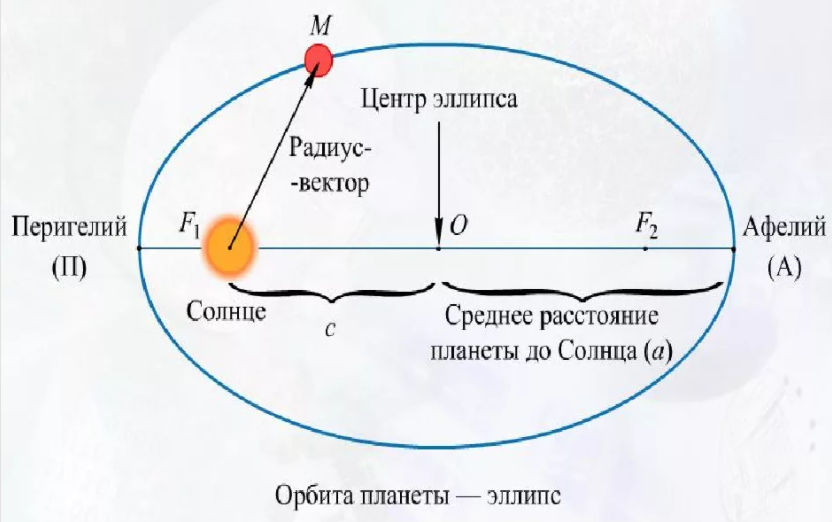
Астероиды и другие тела

Астероиды движутся по эллиптическим орбитам. Из-за вытянутости траектории они то приближаются к Солнцу, то удаляются от него. В астрономии и математике «вытянутость» называется эксцентриситетом. Для расчета этой величины нужно знать размеры полуосей. Большая — расстояние от центра до самой дальней точки. Малая — до самой ближней. Эксцентриситет рассчитывается в астрономии формулой Кеплера: .

Формулы

В этом разделе рассмотрим астрономические формулы с объяснениями: 

Мы разобрали основные формулы для 24 задания ЕГЭ по физике, немного коснулись теоретического материала. Обязательно выучите уравнения из статьи — они пригодятся при решении задач. Чтобы выполнять номер без ошибок, не забывайте практиковаться. Примеры заданий можно найти на ФИПИ и Решу.ЕГЭ. Если решать задачи самостоятельно не получается, запишитесь на курсы подготовки к ЕГЭ. Там с вами разберут все сложные моменты. Мы уверены — вы справитесь и наберете высокие баллы на экзамене!