Как найти среднюю плотность вещества в физике

Как найти среднюю плотность

Большинство тел имеет сложную структуру, ведь они состоят из различных веществ. Поэтому найти их плотность при помощи таблиц практически невозможно. Чтобы получить представление об их структуре, используют такое понятие, как средняя плотность, которая рассчитывается после измерения массы и объема тела.

Вам понадобится

• – весы;
• – мерный цилиндр;
• – таблица плотностей различных веществ.

Инструкция

Если тело состоит не из однородного вещества, найдите с помощью весов его массу, а затем измерьте объем. Если это жидкость, произведите измерение при помощи мерного цилиндра. Если же это твердое тело правильной формы (куб, призма, многогранник, шар, цилиндр и т.д.), найдите его объем геометрическими методами. Если тело неправильной формы, погрузите его в воду, которая залита в мерный цилиндр, и по ее подъему определите объем тела. Поделите измеренную массу тела на его объем, в результате получите среднюю плотность тела ρ=m/V. Если масса измерялась в килограммах, объем выразите в м³, если же в граммах – в см³. Соответственно плотность получится в кг/м³ или г/ см³.

Если же взвесить тело не представляется возможным, узнайте плотность материалов, из которых оно состоит, затем измерьте объем каждой составной части тела. Затем найдите массы материалов, из которых состоит тело, перемножив их плотности на объемы и общий объем тела, сложив объемы его составных частей, в том числе пустот. Поделите общую массу тела на его объем, и получите среднюю плотность тела ρ= (ρ1•V1+ ρ2•V2+…)/(V1+V2+…).

Если тело можно погрузить в воду, найдите его вес в воде с помощью динамометра. Определите объем вытолкнутой воды, который будет равен объему погруженного в нее тела. При расчетах учитывайте, что плотность воды составляет 1000 кг/м³. Чтобы найти среднюю плотность тела, погруженного в воду, к его весу в Ньютонах, прибавьте произведение числа 1000 (плотность воды) на ускорение свободного падения 9,81 м/с² и объем тела в м³. Получившееся число поделите на произведение объема тела и 9,81 ρ=(Р+ ρв•V•9,81)/(9,81• V).

Когда тело плавает в воде, найдите объем вытолкнутой жидкости, объем тела. Тогда средняя плотность тела будет равна отношению произведения плотности воды на ее вытолкнутый телом объем и объема самого тела ρ= ρв•Vв/Vт.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Плотность
Размерность	L−3 M
Единицы измерения
СИ	кг/м³
СГС	г/см³
Примечания
скалярная величина

Пло́тность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму или как производная массы по объёму:

.

Данные выражения не эквивалентны, и выбор зависит от того, какая именно плотность рассматривается. Различаются:

Для точечной массы плотность является бесконечной. Математически её можно определить или как меру, или как производную Радона — Никодима по отношению к некоторой опорной мере.

Для обозначения плотности обычно используется греческая буква (ро) (происхождение обозначения подлежит уточнению), иногда используются латинские буквы D и d (от лат. densitas «плотность»). Исходя из определения плотности, её размерность представляет собой кг/м³ в СИ и г/см³ в системе СГС.

Понятие «плотность» в физике может иметь более широкую трактовку. Существуют поверхностная плотность (отношение массы к площади) и линейная плотность (отношение массы к длине), применяемые соответственно к плоским (двумерным) и вытянутым (одномерным) объектам. Кроме того, говорят не только о плотности массы, но и о плотности других величин, например энергии, электрического заряда. В таких случаях к термину «плотность» добавляются конкретизирующие слова, скажем «линейная плотность заряда». «По умолчанию» под плотностью понимается вышеуказанная (трёхмерная, кг/м³) плотность массы.

Формула нахождения плотности[править | править код]

Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:

где M — масса тела, V — его объём;
формула является просто математической записью определения термина «плотность», данного выше.

При вычислении плотности газов при стандартных условиях эта формула может быть записана и в виде:

где  — молярная масса газа,  — молярный объём (при стандартных условиях приближённо равен 22,4 л/моль).

Плотность тела в точке записывается как

тогда масса неоднородного тела (тела с плотностью, зависящей от координат) рассчитывается как

Случай сыпучих и пористых тел[править | править код]

В случае сыпучих и пористых тел различают

• истинную плотность, определяемую без учёта пустот;
• насыпную плотность, рассчитываемую как отношение массы вещества ко всему занимаемому им объёму.

Истинную плотность из насыпной (кажущейся) получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме.

Зависимость плотности от температуры[править | править код]

Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность в определённом диапазоне температур ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого значения.

При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Вода, кремний, висмут и некоторые другие вещества являются исключениями из данного правила, так как их плотность при затвердевании уменьшается.

Диапазон плотностей в природе[править | править код]

Для различных природных объектов плотность меняется в очень широком диапазоне.

• Самую низкую плотность имеет межгалактическая среда (2·10⁻³¹—5·10⁻³¹ кг/м³, без учёта тёмной материи)^[2].
• Плотность межзвёздной среды приблизительно равна 10⁻²³—10⁻²¹ кг/м³.
• Средняя плотность красных гигантов в пределах их фотосфер много меньше, чем у Солнца — из-за того, что их радиус в сотни раз больше при сравнимой массе.
• Плотность газообразного водорода (самого лёгкого газа) при стандартных условиях равна 0,0899 кг/м³.
• Плотность сухого воздуха при стандартных условиях составляет 1,293 кг/м³.
• Один из самых тяжёлых газов, гексафторид вольфрама, примерно в 10 раз тяжелее воздуха (12,9 кг/м³ при +20 °C)
• Жидкий водород при атмосферном давлении и температуре −253 °C имеет плотность 70 кг/м³.
• Плотность жидкого гелия при атмосферном давлении равна 130 кг/м³.
• Усреднённая плотность тела человека от 940—990 кг/м³ при полном вдохе, до 1010—1070 кг/м³ при полном выдохе.
• Плотность пресной воды при 4 °C 1000 кг/м³.
• Средняя плотность Солнца в пределах фотосферы около 1410 кг/м³, примерно в 1,4 раза выше плотности воды.
• Гранит имеет плотность 2600 кг/м³.
• Средняя плотность Земли равна 5520 кг/м³.
• Плотность железа равна 7874 кг/м³.
• Плотность металлического урана 19100 кг/м³.
• Плотность золота 19320 кг/м³.
• Плотность нептуния — самого плотного актиноида — 20200 кг/м³.
• Самые плотные вещества при стандартных условиях — металлы платиновой группы шестого периода (осмий, иридий, платина), а также рений. Имеют плотность 21000—22700 кг/м³.
• Плотность атомных ядер приблизительно 2·10¹⁷ кг/м³.
• Теоретически верхняя граница плотности по современным^{[когда?]} физическим представлениям — это планковская плотность 5,1⋅10⁹⁶ кг/м³.

Плотности астрономических объектов[править | править код]

• Средние плотности небесных тел Солнечной системы см. на врезке.
• Межпланетная среда в Солнечной системе достаточно неоднородна и может меняться во времени, её плотность в окрестностях Земли ~10⁻²¹÷10⁻²⁰ кг/м³.
• Плотность межзвёздной среды ~10⁻²³÷10⁻²¹ кг/м³.
• Плотность межгалактической среды 2×10⁻³⁴÷5×10⁻³⁴ кг/м³.
• Средняя плотность красных гигантов на много порядков меньше чем у Солнца из-за того, что их радиус в сотни раз больше.
• Плотность белых карликов 10⁸÷10¹² кг/м³
• Плотность нейтронных звёзд имеет порядок 10¹⁷÷10¹⁸ кг/м³.
• Средняя (по объёму под горизонтом событий) плотность чёрной дыры зависит от её массы и выражается формулой:

Средняя плотность падает обратно пропорционально квадрату массы чёрной дыры (ρ~M⁻²). Так, если чёрная дыра с массой порядка солнечной обладает плотностью около 10¹⁹ кг/м³, превышающей ядерную плотность (2×10¹⁷ кг/м³), то сверхмассивная чёрная дыра с массой в 10⁹ солнечных масс (существование таких чёрных дыр предполагается в квазарах) обладает средней плотностью около 20 кг/м³, что существенно меньше плотности воды (1000 кг/м³).

Плотности некоторых газов[править | править код]

Плотность газов, кг/м³ при НУ.

Азот	1,250	Кислород	1,429
Аммиак	0,771	Криптон	3,743
Аргон	1,784	Ксенон	5,851
Водород	0,090	Метан	0,717
Водяной пар (100 °C)	0,598	Неон	0,900
Воздух	1,293	Радон	9,81
Гексафторид вольфрама	12,9	Углекислый газ	1,977
Гелий	0,178	Хлор	3,164
Дициан	2,38	Этилен	1,260

Для вычисления плотности произвольного идеального газа, находящегося в произвольных условиях, можно использовать формулу, выводящуюся из уравнения состояния идеального газа:^[6]

,

где:

Плотности некоторых жидкостей[править | править код]

Плотность жидкостей, кг/м³

Бензин	710	Молоко	1040
Вода (4 °C)	1000	Ртуть (0 °C)	13600
Керосин	820	Диэтиловый эфир	714
Глицерин	1260	Этанол	789
Морская вода	1030	Скипидар	860
Масло оливковое	920	Ацетон	792
Масло моторное	910	Серная кислота	1835
Нефть	550—1050	Жидкий водород (−253 °C)	70

Плотность некоторых пород древесины[править | править код]

Плотность древесины, г/см³

Бальса	0,15	Пихта сибирская	0,39
Секвойя вечнозелёная	0,41	Ель	0,45
Ива	0,46	Ольха	0,49
Осина	0,51	Сосна	0,52
Липа	0,53	Конский каштан	0,56
Каштан съедобный	0,59	Кипарис	0,60
Черёмуха	0,61	Лещина	0,63
Грецкий орех	0,64	Берёза	0,65
Вишня	0,66	Вяз гладкий	0,66
Лиственница	0,66	Клён полевой	0,67
Тиковое дерево	0,67	Бук	0,68
Груша	0,69	Дуб	0,69
Свитения (Махагони)	0,70	Платан	0,70
Жостер (крушина)	0,71	Тис	0,75
Ясень	0,75	Слива	0,80
Сирень	0,80	Боярышник	0,80
Пекан (кария)	0,83	Сандаловое дерево	0,90
Самшит	0,96	Эбеновое дерево	1,08
Квебрахо	1,21	Бакаут	1,28
Пробка	0,20

Плотность некоторых металлов[править | править код]

Значения плотности металлов могут изменяться в весьма широких пределах: от наименьшего значения у лития, который легче воды, до наибольшего значения у осмия, который тяжелее золота и платины.

Плотность металлов, кг/м³

Осмий	22610[7]	Родий	12410[8]	Хром	7190[9]
Иридий	22560[10]	Палладий	12020[11]	Германий	5320[12]
Плутоний	19840[13]	Свинец	11350[14]	Алюминий	2700[15]
Платина	19590[16]	Серебро	10500[17]	Бериллий	1850[18]
Золото	19300[14]	Никель	8910[19]	Рубидий	1530[20]
Уран	19050[21]	Кобальт	8860[22]	Натрий	970[23]
Тантал	16650[24]	Медь	8940[25]	Цезий	1840[26]
Ртуть	13530[27]	Железо	7870[28]	Калий	860[29]
Рутений	12450[30]	Марганец	7440[31]	Литий	530[32]

Измерение плотности[править | править код]

Для измерений плотности используются:

• Пикнометр — прибор для измерения истинной плотности
• Различные виды ареометров — измерители плотности жидкостей.
• Бурик Качинского и бур Зайдельмана — приборы для измерения плотности почвы.
• Вибрационный плотномер — прибор для измерения плотности жидкости и газа под давлением.
• Метод гидростатического взвешивания.

Остеоденситометрия — процедура измерения плотности костной ткани человека.

См. также[править | править код]

• Список химических элементов с указанием их плотности
• Удельный вес
• Удельная плотность
• Относительная плотность
• Объёмная плотность
• Конденсация
• Консистенция (лат. consistere — состоять) — состояние вещества, степень мягкости или плотности (твёрдости) чего-либо — полутвердых-полумягких веществ (масел, мыла, красок, строительных растворов и т. д.); наприм., глицерин имеет сиропообразную консистенцию.
• Консистометр — прибор для измерения в условных физических единицах консистенции различных коллоидных и желеобразных веществ, а также суспензий и грубодисперсных сред, к примеру, паст, линиментов, гелей, кремов, мазей.
• Концентрация частиц
• Концентрация растворов
• Плотность заряда
• Уравнение неразрывности

Примечания[править | править код]

Литература[править | править код]

• Плотность — статья из Большой советской энциклопедии.  — М.: «Советская Энциклопедия», 1975. — Т. 20. — С. 49.
• Плотность — статья из Физической энциклопедии. Т. 3, С. 637.
• Krebs R. E. . The History and Use of Our Earth’s Chemical Elements: A Reference Guide. 2nd edition. — Westport: Greenwood Publishing Group, 2006. — xxv + 422 p. — ISBN 0-313-33438-2.

Ссылки[править | править код]

• Онлайн интерактивная таблица плотности веществ Архивная копия от 29 апреля 2011 на Wayback Machine (рус.)
• Подробная таблица значений плотности распространенных жидкостей Архивная копия от 5 октября 2016 на Wayback Machine (рус.)
• Урок по теме “Плотность вещества” Архивная копия от 30 января 2022 на Wayback Machine

В курсе физики 7 класса мы при прохождении темы
“ Механическое движение” вводим понятие
средней скорости, и при определенном полученном
навыке решения задач большинство учащихся с
расчетами средней скорости справляются. (Только
жаль, что часто при решении ребята сталкиваются с
громоздким математическим решением, а они пока к
этому не готовы)

Через несколько уроков мы приступаем к
введению понятий массы и плотности.

На начальном уровне все основное по данному
вопросу в любом учебнике-7 ,в принципе, сказано, но
почему мы не оговариваем сразу такой важный
закон, как закон сохранения массы? Он нам
пригодится для введения понятия средней
плотности!

Если растворить сахар в воде, то масса раствора
строго равна массе сахара и воды.

При любом дроблении и при растворении масса
остается одной и той же.

Формулировка закона: При любых
изменениях изолированной системы тел или частиц
масса этой системы остается неизменной и равна
сумме масс составляющих ее частей.

Так как понятие изолированной системы мы пока
не вводим, то можно закон сформулировать проще;

Масса тел до взаимодействия равна массе тел
после взаимодействия,т. е. остается неизменной

Математическое выражение закона: m₁ + m₂
+ … + m_N =m ^/₁ + m ^/₂ + … + m ^/_N

Границы и условия применимости закона можно
пока не вводить

Приоритет в открытии закона сохранения массы
вещества принадлежит российскому ученому
Михаилу Васильевичу Ломоносову и французу
Антуану Лавуазье (Antoine Laurent Lavoisier).

Закон был открыт и сформулирован ими
независимо друг от друга на основе анализа
многочисленных опытных данных.

В 1756 г. М.В.Ломоносов самостоятельно
сформулировал философский принцип сохранения
материи и движения: “…все перемены, в натуре
случающиеся, такого суть состояния, что сколько
чего у одного тела отнимется, столько
присовокупится к другому…”.

Он считал этот закон одним из основных законов
природы!

Примеры проявления закона в природе

1. Явления диффузии
2. Процессы растворения веществ.
3. Дробление и разрушение тел.
4. Глобальный круговорот вещества в биосфере,
   перенос твердых, жидких и газообразных тел при
   различных давлениях и температурах, в течение
   веков и тысячелетий происходит в полном
   соответствии с законом сохранения массы. Эти же
   самые слова можно сказать об одном из самых
   грандиозных процессов – круговороте воды на
   поверхности земного шара.

Пример:

1) Если взять 1 кг манки, 2 кг гречки, 3 кг пшена и
все крупы смешать, то получим массу строго 6 кг

m_см = m_манки + m_гречки + m_пшена
= 1 кг + 2 кг +3 кг = 6 кг

2) В пассажирский самолет перед началом рейса
погрузили 300 кг продуктов. Изменилась ли масса
авиалайнера после того, как в полете все продукты
были съедены?

Так как заданий на закон сохранения массы в
задачниках нет, то можно предложить ребятам дома
самим поработать над их составлением. А из лучших
работ составить сборник и вклеить в задачник,
которым пользуемся на уроке. Я думаю, что многие
ребята захотят в этом поучаствовать.

А теперь о понятии плотность.

При введении этой величины в учебниках
почему-то не оговаривается, что речь идет о
сплошных телах! И хотя в олимпиадных задачах и
в некоторых сборниках предлагаются задачи на
нахождение средней плотности (или задачи,
связанные с этой величиной) на уроках мы о ней не
говорим. А ведь несколько уроков назад было
введено понятие средней скорости, так почему по
аналогии не ввести понятие средней плотности?

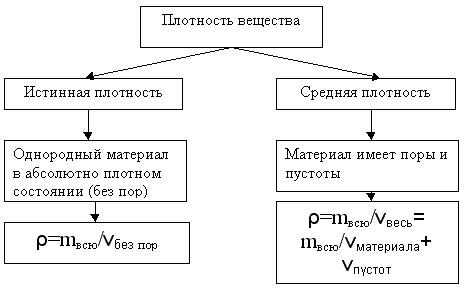
Истинная плотность – отношение массы к
объему в абсолютно плотном состоянии (без пор и
пустот)

Средняя плотность – физическая величина,
определяемая отношением массы материала ко
всему занимаемому им объему, включая поры и
пустоты.

Средняя плотность не является величиной
постоянной и изменяется в зависимости от
пористости материала.

Интересно, что средняя плотность играет очень
важное значение для человека. Его плавучесть
зависит от средней плотности тканей его тела,
плотности воды, вдоха и выдоха. Чем меньше
средняя плотность тканей тела, тем лучше его
плавучесть. При глубоком вдохе пловец, как
правило, обладает положительной плавучестью, при
полном выдохе – отрицательной, он тонет. Человек
способен изменять свою среднюю плотность,
регулируя количество воздуха в легких! При
полном вдохе средняя плотность человеческого
тела становится меньше плотности воды. При
выдохе, когда тело теряет плавучесть, человеку
приходится создавать подъемную силу движением
рук. Получается, что умение плавать – это умение
правильно дышать!

Когда вводится понятие выталкивающей силы,
может ребятам будет понятнее, почему такие
огромные, тяжелые корабли плавают, если
поговорить опять о средней плотности корабля и
воды! Или привести такой пример: Плотность
стекла, из которого сделана бутылка, равна 2200 кг/
м³; плотность воды – 1000 кг/ м³.
Следовательно, стекло пойдет ко дну. Но если
стеклянная бутылка, наполненная воздухом, плотно
закрыта пробкой, она будет плавать на
поверхности воды. Масса стеклянной литровой
бутылки примерно равна 0,5 кг; масса воздуха,
заключенного в ней, – около 0,001 кг, а средняя
плотность закупоренной бутылки с воздухом – 501 кг/
м³ (0,5001 кг / 0,001 м³), т.е. вдвое меньше
плотности воды!

На уроке можно решить следующие задачи:

Какова плотность смеси глицерина и спирта, если
объем спирта составляет половину объема смеси?

Как изменится ответ, если масса спирта
составляет половину массы смеси?

Ответ: (900 кг/ м³)

Сплав золота и серебра массой 400г имеет
плотность 1,4 · 10⁴ кг/ м³. Полагая объем
сплава равным сумме объемов его составных
частей, определите массу золота в сплаве.

Ответ: (0,2 кг)

(Примеры данных задач взяты из сборника
“Решение ключевых задач по физике для основной
школы. 7-9 классы. Гейндешптейн Л.Э., Кирик Л.А.,
Гельфгат И.М, там же представлены их подробные
решения)

Использованная литература:

1. Гейндешптейн Л.Э., Кирик Л.А., Гельфгат И.М.
   “Решение ключевых задач по физике для основной
   школы. 7-9 классы. – М.: Илекса, 2006.
2. Детская энциклопедия, том 3 , издательство
   “Просвещение”, 1966
3. С.Е.Каменецкий, В.П.Орехов “Методика решения
   задач по физике в средней школе” издательство
   “Просвещение”, 1986
4. Г.С.Ландсберг “Элементарный учебник физики”,
   том 3, издательство “Физматлит”, 2000

Целью данной работы
является проверка навыков по определению объёма тела с помощью измерительного
цилиндра (мензурки).

Для выполнения этой работы нам предлагают использовать
комплект оборудования № 1 в составе: мензурка, цилиндр, номер которого будет
указан в работе, стакан с водой и весы (это могут быть как электронные весы,
так и рычажные весы с разновесом).

Теперь давайте с вами вспомним, что же такое плотность
вещества. Плотность вещества — это масса вещества, содержащаяся в
единице его объёма:

Единицей измерения плотности в СИ:

Хотя при выполнении этой работы допускается
использование внесистемной единицы измерения плотности.

Анализ формулы плотности и оборудования, которое нам
предоставлено, показывает, что массу цилиндра мы можем найти прямыми
измерениями. А вот его объём придётся находить косвенными измерениями.

Для начала определим с вами массу предложенного
цилиндра. Если в комплекте оборудования идут электронные весы, то мы просто
ставим тело на весы и снимаем показания электронного циферблата. При этом не
забываем, что результаты мы должны записать с учётом погрешности измерения (её
значение дано в задании):

Если же в комплекте будут идти рычажные весы, то перед
взвешиванием необходимо убедиться, что весы уравновешены. При необходимости для
установления равновесия на более лёгкую чашку нужно положить полоски бумаги,
картона и тому подобного. Затем нужно на левую чашу весов аккуратно поставить
взвешиваемое тело, а на правую — гири. Масса гирь подбирается таким образом,
чтобы плечи весов находились в равновесии.

Теперь определим объём цилиндра. Для этого мы должны
взять мензурку и определить её цену деления.

Затем в мензурку необходимо налить столько воды, чтобы
тело могло полностью погрузиться в воду, и измерить начальный объём воды
(обозначим его через V₁).

После этого мы аккуратно на нитке опускаем цилиндр в
мензурку так, чтобы он смог полностью погрузиться в воду. И вновь измеряем
объём воды в мензурке (его мы обозначим V₂).

Теперь, чтобы определить объём цилиндра, мы должны
найти разницу объёмов воды после погружения цилиндра и до него (эту формулу мы
записываем рядом с формулой плотности):

Подставив в формулу числа найдём, что объём данного
нам цилиндра, с учётом погрешности измерений, равен (26 ± 2) см³.

Вернёмся к пункту «один» и схематически изобразим нашу
экспериментальную установку для определения объёма цилиндра.

Наконец можно найти числовое значение плотности
материала цилиндра, подставив в формулу значения массы и объёма цилиндра. После
несложных вычислений получаем 7,5 см³.

В конце работы можно написать вывод: плотность вещества, из которого изготовлен цилиндр, равна семи с
половиной граммам на кубический сантиметр.

Средняя плотность

Плотность вещества характеризует именно вещество, а не тело, которое из него состоит. Если мы, например, разрежем шарики пополам, то массы и объёмы их половинок будут меньше изначальных, но плотности стали и пенопласта останутся неизменными

На практике тела чаще состоят не из одного вещества, а из нескольких. Поэтому, помимо плотности вещества, существует понятие средней плотности тела. Средняя плотность тела – это отношение массы тела к его объёму.



В качестве примера вновь обратимся к шарикам из стали и пенопласта. Возьмём коробку и наполним её разными шариками – и из стали, и из пенопласта

Измерив её массу и объём, мы сможем найти среднюю плотность такой коробки.

Она будет отличаться и от плотности стали, и от плотности пенопласта и примет некоторое среднее значение.

Задача

• Медный цилиндр объёмом   имеет массу 890 г. Сплошной этот цилиндр или полый? Если полый, найдите объём полости.
• Давайте порассуждаем:
• – в условии нам даны масса и объём цилиндра, значит, мы можем найти его плотность.
• – в случае если цилиндр полый, найденная плотность будет его средней плотностью – ведь внутри полости будет некоторый объём воздуха.
• Рассчитаем плотность цилиндра: .
• Полученное значение меньше плотности меди, которое равно .

• Значит, цилиндр полый. Масса воздуха внутри полости пренебрежимо мала по сравнению с массой меди, поэтому мы можем считать, что масса цилиндра – это и есть масса меди.
• А значит, зная плотность меди, мы найдём объём, который она занимает: .

Разница между объёмом всего цилиндра и объёмом, который занимает только медь, это и есть объём полости. Он будет равен:  .

Подставим числа и рассчитаем ответ: 

Правильный ответ: цилиндр полый, объём полости равен 30 см 3 .

• Список рекомендованной литературы:
• Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
• Перышкин А.В. Физика: Учебник 7 класс. – Издательство: М.: Дрофа, 2013. – 224 с.
•  
• Дополнительные рекомендованные ссылки на ресурсы сети Интернет
• Интернет-портал Yaklass.ru ( Источник ).
• Интернет-портал School.xvatit.com ( Источник ).