Как найти среднюю полезную мощность - Сайт, где вы сможете решить свои вопросы

Алексей Алексеевич Ивахно

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Под мощностью подразумевают работу, выполненную за единицу времени, однако этот подход в большинстве случаев требует уточнений, поскольку интенсивность выполнения работы может многократно измениться за рассматриваемое время. Например, при движении автомобиля водитель увеличивает и уменьшает поступление топливно-воздушной смеси в зону сгорания, переключает передачи трансмиссии, притормаживает. Всё это влияет на текущую мощность двигателя. Поэтому в физике различают мгновенную мощность – мощность, измеренную за промежуток времени достаточно малый, чтобы считать ее величину постоянной:

$P = limlimits_{t to 0}frac{Delta A}{Delta t}$,

где $Delta t$ – промежуток времени, $Delta A$ – проделанная за это время работа.

Поскольку мгновенные величины мощности могут меняться без какой-либо четко выраженной закономерности, подсчитать их среднее значение бывает затруднительно. Поэтому среднюю мощность находят просто как

${langle}Prangle = frac{Delta A}{Delta t}$.

Следует различать мощность, связанную с общими затратами на движение и ту, что развивается для выполнения полезной работы. Так, один и тот же груз с одной и той же скоростью на одно и то же расстояние можно перевезти разными способами, например, на старинном паровозе и современном электровозе. Полезная работа будет выполнена одинаковая, но интенсивность затрат энергии – различная. Поэтому существует понятие средней полезной мощности, расчет которой зависит от многих факторов, связанных с особенностями движителей и сред, в которых выполняется работа.

Пример 1

Автомобиль массой 2 т поднимается в гору с постоянным ускорением по участку дороги с уклоном 30°. Движение длится 10 с. Скорость транспортного средства в начале подъема 20 км/ч, в конце 40 км/ч. Общая сила сопротивления (трение, вязкость воздуха и т.д.), постоянна и равна 600 Н. Определить среднюю полезную мощность двигателя.

Двигатель должен развить следующие силы:

преодолевающую силу сопротивления;
преодолевающую гравитацию, поскольку транспорт движется в гору;
обеспечивающую ускорение.

Найдем их последовательно.

На преодоление силы сопротивления необходимо развить те же 600 ньютонов, но в направлении, совпадающем с вектором скорости.

Сила, преодолевающая силу тяжести, поскольку ее вектор находится под углом к вектору скорости, будет исчисляться по формуле:

$F_g = m cdot g cdot sin(alpha)$,

где $g$ – ускорение свободного падения, $m$ – масса. $alpha$ – угол наклона.

Приращение скорости:

$Delta v = v_1 – v_0 = frac{40000 – 20000}{3600} approx 5,56 frac{м}{с}$

Ускорение:

$a = frac{Delta v}{t} approx 0,556 frac{м}{с^2}$.

Просуммируем силы:

$F = 600 + 2000 cdot 9,8 cdot 0,5 + 2000 cdot 0.556 approx 600 + 9800 + 1112 = 11512 Н$

Работа равна произведению силы и пути, который можно выразить через время, начальную скорость и ускорение:

$A = F cdot (v_0 cdot t + frac{a cdot t^2}{2}) approx 11512 cdot (55,6 + 0,556 cdot 100) approx 11512 cdot 111,11 approx 1279111 Дж$

Разделив работу на время, получим среднюю полезную мощность:

$P = frac{1279111}{10} approx 127911 Вт$

Ответ: $approx 127911$ Вт. Примечание: полную мощность двигателя можно найти разделив это значение на КПД.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Автор: .

Издательство:

Дрофа 2016

Тип: Задачник

Подробный решебник (ГДЗ) по Физике за 10‐11 (десятый‐одиннадцатый) класс задачник – готовый ответ номер – 398. Авторы учебника: Рымкевич. Издательство: Дрофа 2016.

Условие /
номер / 398

398. Найти среднюю полезную мощность при разбеге самолёта, предназначенного для работ в сельском и лесном хозяйстве. Масса самолёта 1 т, длина разбега 300 м, взлётная скорость 30 м/с, коэффициент сопротивления 0,03.

Решебник №1 / номер / 398

Видеорешение / номер / 398

Решебник №2 / номер / 398

Оцените решебник:

4.4/5

387

Источник

Под мощностью подразумевают работу, выполненную за единицу времени, однако этот подход в большинстве случаев требует уточнений, поскольку интенсивность выполнения работы может многократно измениться за рассматриваемое время. Например, при движении автомобиля водитель увеличивает и уменьшает поступление топливно-воздушной смеси в зону сгорания, переключает передачи трансмиссии, притормаживает. Всё это влияет на текущую мощность двигателя. Поэтому в физике различают мгновенную мощность — мощность, измеренную за промежуток времени достаточно малый, чтобы считать ее величину постоянной:

где $Delta t$ — промежуток времени, $Delta A$ — проделанная за это время работа.

Следует различать мощность, связанную с общими затратами на движение и ту, что развивается для выполнения полезной работы. Так, один и тот же груз с одной и той же скоростью на одно и то же расстояние можно перевезти разными способами, например, на старинном паровозе и современном электровозе. Полезная работа будет выполнена одинаковая, но интенсивность затрат энергии — различная. Поэтому существует понятие средней полезной мощности, расчет которой зависит от многих факторов, связанных с особенностями движителей и сред, в которых выполняется работа.

Найдем их последовательно.

где $g$ — ускорение свободного падения, $m$ — масса. $alpha$ — угол наклона.

$F = 600 + 2000 cdot 9,8 cdot 0,5 + 2000 cdot 0.556 approx 600 + 9800 + 1112 = 11512 Н$

Работа равна произведению силы и пути, который можно выразить через время, начальную скорость и ускорение:

Разделив работу на время, получим среднюю полезную мощность:

$P = frac<1279111> <10>approx 127911 Вт$

Ответ: $approx 127911$ Вт. Примечание: полную мощность двигателя можно найти разделив это значение на КПД.

Как найти среднюю мощность по графику

Если ток и напряжение синусоидальны, то их мгновенные значения могут быть представлены в виде:

так что мгновенная мощность

Но с другой стороны, по известной формуле

Подставляя выражения и произведения синусов в формулу () получим:

Таким образом, мгновенная мощность переменного тока может быть представлена в виде суммы постоянной величины и синусоидальной величины изменяющейся с двойной (по сравнению с током и напряжением) частотой.

Средняя (за период) мощность P может быть определена по формуле

и так как среднее значение второго члена равно 0, то

Это основная формула средней мощности переменного тока. Так как вывод ее не связан с какими-либо особенностями рассматриваемой цепи, то она может быть применена к любой цепи синусоидального переменного тока или к любому участку такой цепи.

Средняя мощность называется также активной мощностью в отличие от реактивной и кажущейся мощностей.

Найденное значение средней мощности отличается от выражения мощности постоянного тока наличием множителя , называемого коэффициентом мощности. Чем меньше коэффициент мощности, то есть чем больше сдвиг фаз между напряжением и током, тем меньше средняя мощность при тех же значениях тока и напряжения или тем больше ток при заданных значениях напряжения и мощности.

Низкий коэффициент мощности имеет следствием неполное использование оборудования электрической установки и уменьшение ее КПД. Если, например, генератор теплоэлектрической станции, работающей при напряжении 6000В, или 6кВ, рассчитан на наибольший ток 200А, то при =0,9 он может давать среднюю мощность

на которую будут рассчитаны и вращающая этот генератор паровая турбина и соответствующие паровые котлы. Но если окажется, что приемник, получающий энергию от этого генератора, имеет в действительности =0,45, т.е. вдвое меньше, то вдвое уменьшится и средняя мощность, которую можно получить от генератора, а следовательно, генератор, турбина и котлы будут использованы на половину своей мощности. Вместе с тем, так как тепловые потери в генераторе и соединительных проводах при неизменном токе также останутся неизменными, то в процентах от средней мощности они окажутся уже вдвое большими, т.е. КПД генератора и соединительных проводов заметно снизится. Отсюда понятна важность поддержания на достаточно высоком уровне.

Чтобы стимулировать работу при высоком , применяется дифференциальный тариф на электрическую энергию, при котором стоимость единицы энергии () зависит от среднего (за месяц), уменьшаясь по мере его увеличения. Низкий чаще всего бывает обусловлен недогрузкой электродвигателей; поэтому правильный выбор мощности электродвигателей является основным средством для получения высокого . На уже существующих установках недостаточно высокий может быть увеличен путем применения конденсаторов.

представляющей собой наибольшее значение активной мощности при заданных действующих значениях напряжения и тока. Хотя единицей кажущейся мощности является тот же ватт (или киловатт), который служит для измерения любой мощности, однако в применении кажущейся мощности ей дается измененное название вольт-ампер (или киловольт-ампер). Благодаря этому можно вместо кажущаяся мощность генератора можно говорить просто мощность генератора, не рискуя быть неправильно понятым. Так, в выражении “генератор мощностью 20 000 ква” имеется в виду кажущаяся мощность этого генератора.

Кажущаяся мощность связана с активной мощностью очевидным соотношением

позволяющим найти активную мощность генератора в определенных условиях нагрузки или подобрать необходимую кажущуюся мощность генератора, способного принять заданную нагрузку.

Пользуясь величинами P и S, можно представить выражение мгновенной мощности в более компактной форме:

представляет собой переменную составляющую мгновенной мощности. Последнее выражение показывает, что кажущаяся мощность является амплитудой этой переменной составляющей.

Если в цепи находится два или более последовательно соединенных приемника с разными , то есть с разными отношениями активной мощности к кажущейся, то кажущаяся мощность всей цепи (или равная ей необходимая кажущаяся мощность генератора) не может быть получена простым сложением кажущихся мощностей отдельных приемников. Действительно, кажущаяся мощность всей цепи

Где I-ток в любом из приемников, а U— общее напряжение в цепи, которое является, как уже известно, векторной, а не арифметической суммой напряжения отдельных приемников. Его абсолютная величина может быть определена по формуле:

A. Мощность

Кадровое агентство «Staff-Up» найдет нужного сотрудника!

Мощность

Различные машины и механизмы, выполняющие одинаковую работу, могут отличаться мощностью. Мощность характеризует быстроту совершения работы. Очевидно, что чем меньшее время требуется для выполнения данной работы, тем эффективнее работает машина, механизм и др.

При движении любого тела на него в общем случае действует несколько сил. Каждая сила совершает работу, и, следовательно, для каждой силы мы можем вычислить мощность.

Средняя мощность силы — скалярная физическая величина Ν, равная отношению работы А, совершаемой силой, к промежутку времени Δt, в течение которого она совершается:

В СИ единицей мощности является ватт (Вт).

Если тело движется прямолинейно и на него действует постоянная сила, то она совершает работу (

A = F Delta r cos alpha). Поэтому мощность этой силы

где F_υ — проекция силы на направление движения.

По этой формуле можно рассчитывать и среднюю, и мгновенную мощности, подставляя значения средней (

mathcal h upsilon mathcal i) или мгновенной υ скорости.

Мгновенная мощность — это мощность силы в данный момент времени.

Любой двигатель или механизм предназначены для выполнения определенной механической работы, которую называют полезной работой A_p. Но любой машине приходится совершать большую работу, так как вследствие действия сил трения часть подводимой к машине энергии не может быть преобразована в механическую работу. Поэтому эффективность работы машины характеризуют коэффициентом полезного действия η (КПД).

Коэффициент полезного действия η — это отношение полезной работы A_p, совершенной машиной, ко всей затраченной работе A_z (подведенной энергии W):

где N_p, N_z — полезная и затраченная мощности соответственно. КПД обычно выражают в процентах.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 63-64.

Мощность: средняя и мгновенная

Автор: – Логика наших рассуждений будет та же, что и при изучении средней и мгновенной скорости. Рассмотрим работу как функцию времени. Пусть А(t) – работа, совершенная за время t. А(t+Δt) – работа, совершенная за время (t+Δt). Тогда [А(t+Δt) – А(t)]/Δt – средняя мощность за промежуток времени от t до (t+Δt). Предел последовательностей значений таких средних мощностей при Δt→0 есть мгновенная мощность, т. е. мощность в момент времени t есть производная от работы по времени.

N(t)=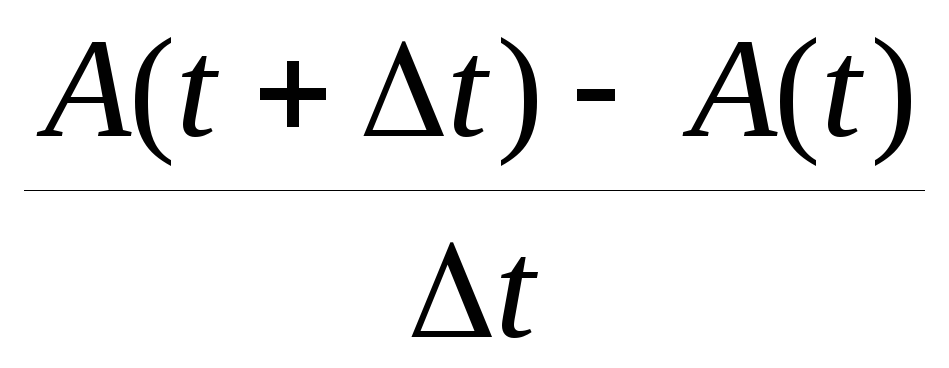=А’(t) (2.10.1)

Выведите частный случай, когда мощность не зависит от времени.

Студент: – N=A/t.

Автор: – Приведите пример, когда мощность постоянна.

Студент: – Это бывает, когда постоянна сила, действующая на тело.

Автор: – Неверно! Смотрите сами. Предположим, что сила, ускоряющая тело, постоянна со временем. Тогда из (2.10.1) следует, что

N(t)= [FS(t+Δt)– FS(t)]/Δt=F[S(t+Δt)–S(t)]/Δt=FV.

Или, используя правила вычисления производных:

Видим, что мощность зависит не только от силы, но и от скорости, которая при равноускоренном движении является функцией времени.

Заметим, что выражение для мгновенной мощности N(t)=F(t)·V(t) является справедливым для любого механического движения. Доказательство опирается на знания интегрального исчисления, и мы его пропускаем.

Для тренировки разберем одну интересную и практическую задачу 2.5.

Автомобиль массой m трогается с места. Коэффициент трения колес о дорогу k. Обе оси автомобиля ведущие. Найдите зависимость скорости автомобиля от времени. Мощность двигателя N.

Студент: – Я не понимаю, зачем в условии сказано про ведущие оси. Мы никогда с этим не сталкивались.

Автор: – Это связано с расчетом силы трения. Можно с хорошей точностью принять, что масса автомобиля равномерно распределена на обе оси. Раз обе оси ведущие, значит, сила трения скольжения равна произведению всей массы автомобиля на коэффициент трения. В случае если ведущей является только одна ось, то на нее приходилась половина массы автомобиля и сила трения, толкающая автомобиль вперед вычислялась бы так: kmg/2. Отметим, что здесь принята максимально возможная сила трения скольжения, т. е. считаем, что колеса автомобиля пробуксовывают на дороге. Правда, на собственных автомобилях водители так не стартуют.

Студент: – Тогда по условию нашей задачи получается, что ускоряет автомобиль только сила трения, которая равна kmg. Отсюда легко получатся ответ: автомобиль двигается равноускоренно и скорость зависит от времени так: V(t)=at=kgt.

Автор: – Это справедливо только отчасти. Вспомните выражения для мощности (2.10.2). При ограниченной мощности скорость не может неограниченно возрастать. Поэтому должен Вам дать две подсказки: 1) найдите предельное время, до которого Ваш ответ будет справедлив; 2) затем воспользуйтесь энергетическими соображениями.

Студент: – Раз предельная мощность N, то из (2.10.2) получим:

N=FV(t)=kmg kgt.

Отсюда предельное время t₀=N/(mk 2 g 2 ).

Автор: – Дальше мощности не хватает, чтобы поддерживать равноускоренное движение. Как поступим?

Студент: – В дальнейшем за какой-то промежуток времени Δt=t–t₀ двигатель совершит работу А=NΔt, которая пойдет на увеличение кинетической энергии. Сначала найдем кинетическую энергию автомобиля в момент времени t₀ :

mV₀ 2 /2=m[kgN/(mk 2 g 2 )] 2 /2=.

Изменение кинетической энергии равно

V 2 =(t – ),

V=.

Автор: – Это правильный ответ. Как видим, сначала зависимость скорости от времени линейная, затем корневая. Комбинируя обе эти ситуации, представим ответ в окончательном варианте:

◄V(t)=kgt при t≤ t₀=N/(mk 2 g 2 ),

V(t)= при t> t₀►.

Эразм Дарвин считал, что время от времени следует производить самые дикие эксперименты. Из них почти никогда ничего не выходит, но если они удаются, то результат бывает потрясающим. Дарвин играл на трубе перед своими тюльпанами. Никаких результатов.

Вопросы и задания

1. Колесо толкнули с одинаковой скоростью по двум разным дорогам: а) по ровной горизонтальной, б) по дороге, имеющей неглубокие ямки, такие, что на всем пути колесо не оторвется от земли. В каком случае а) или б) колесо быстрее доедет до конечного пункта, находящегося на одинаковом расстоянии от места старта?

Указание. Нарисуйте векторы всех сил, действующих на колесо в обоих случаях, и сравните характер движения тела.

2. На Бердском шоссе есть достаточно крутой подъем. Можно заметить, что перегруженный автомобиль медленно поднимается по нему, даже если на дороге нет пробок. Почему?

3. Предположим, что Вы поднимаете чемодан с пола на стол. Зависит ли работа, совершаемая вами над чемоданом: а) от того, поднимаете ли Вы его вертикально вверх, или по более сложному пути; б) от времени, которое Вы на это затрачиваете; в) от высоты стола; г) от массы чемодана?

4. Почему легче подниматься в гору по зигзагообразному пути, а не по прямой?

Источник

Найти среднюю полезную мощность при разбеге самолета, предназначенного для работ в сельском и лесном хозяйстве. Масса самолета 1 т, длина

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Полезная мощность

Мощность (физика) — это… Что такое Мощность (физика)?

— физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

Читайте также: Выпрямители напряжения: основные понятия

, мощность двигателя, отдаваемая рабочей машине непосредственно или через силовую передачу. Различают полезную, полную и номинальную Э. м. двигателя. Полезной называют Э. м.

двигателя за вычетом затрат мощности на приведение в действие вспомогательных агрегатов или механизмов, необходимых для его работы, но имеющих отдельный привод (не от двигателя непосредственно). Полная Э. м. — мощность двигателя без вычета указанных затрат. Номинальная Э. м., или просто номинальная мощность, — Э. м.

, гарантированная заводом-изготовителем для определённых условий работы. В зависимости от типа и назначения двигателя устанавливаются Э. м.

, регламентируемые стандартами или техническими условиями (например, наибольшая мощность судового реверсивного двигателя при определённой частоте вращения коленчатого вала в случае заднего хода судна — так называемая мощность заднего хода, наибольшая мощность авиационного двигателя при минимальном удельном расходе топлива — так называемая крейсерская мощность и т. п.). Э. м. зависит от форсирования (интенсификации) рабочего процесса, размеров и механического кпд двигателя.[1]

Так как работа является мерой изменения энергии, мощность можно определить также как скорость изменения энергии системы.

Единицы измерения

В системе СИ единицей измерения мощности является ватт, равный одному джоулю, делённому на секунду.

Другой распространённой единицей измерения мощности является лошадиная сила.

Соотношения между единицами мощности Единицы Вт кВт МВт кгс·м/с эрг/с л. с.

1 ватт	1	10-3	10-6	0,102	107	1,36·10-3
1 киловатт	103	1	10-3	102	1010	1,36
1 мегаватт	106	103	1	102·103	1013	1,36·103
1 килограмм-сила-метр в секунду	9,81	9,81·10-3	9,81·10-6	1	9,81·107	1,33·10-2
1 эрг в секунду	10-7	10-10	10-13	1,02·10-8	1	1,36·10-10
1 лошадиная сила[2]	735,5	735,5·10-3	735,5·10-6	75	7,355·109	1

Виды мощности постоянного тока

Любая мощностная величина определяется работой, которая совершается за определенную единицу времени. Чаще всего ею становится секунда. Она означает величину, характеризующую, насколько быстро совершается работа. Касаемо электрической мощности это расход электроэнергии за одну секунду.

Мощностная характеристика тока соответствует отношению его работы ко времени

Работой тока называется процесс превращения электроэнергии в какую-либо другую энергию (механическую, тепловую или световую). Именно по мощности, которая обозначается буквой «P» или «W», и оценивается работоспособность электротока.

К сведению! Вообще у тока постоянного значения нет активной и реактивной P. Для этого вида сети характерна только мгновенная характеристика.

Мгновенная мощность

Если говорить о сетях переменного электротока, то рассматриваемая величина в них, как и электроток или напряжение, регулярно меняет свои значения. Это напрямую влияет на другие параметры. При константном течении зарядов все остается неизменным. Именно поэтому и возникает термин «мгновенная мощность».

Силы в сети регулярного тока остаются неизменными и равняются мгновенным их значениям, взятым в произвольный момент времени. Такую характеристику можно высчитать по мгновенным значениям. Для этого подходит формула мощности постоянного тока в цепи: P = I * U.

Рассматриваемая величина может быть найдена из произведения силы электротока и напряжения

Если сеть пассивна и в ней соблюдается закон Ома, то справедливо равенство. В случае подключения источника ЭДС нужна другая формула: P = I * E, где E — это электродвижущая сила.

Активная мощность

Активная мощность — это среднее за период значение мгновенной P. При активной P происходит конвертация мощности тока в энергию любого вида (механическую, световую или тепловую). Подобный перевод электротока нельзя выполнить в обратном направлении. Активный тип также измеряется в ваттах. 1 Ватт равен 1 вольту умноженному на 1 ампер.

Работа неразрывно связана с определением мощностных характеристик

К сведению! В бытовых и уж тем более промышленных масштабах единицу измерения ватт никогда не используют. Для этих целей задействуют показатели на порядок выше: мегаватты в киловатты.

Реактивная мощность

Реактивная мощностная характеристика определяет нагрузку, которая создается электрическими устройствами определенными колебаниями энергии электромагнитного поля в сетях синусоидального тока переменной частоты. Она равна произведению среднеквадратичных значений напряжения и силы тока, умноженных на синус угла, на который сдвигается фаза между ними. Реактивный параметр неразрывно связан с полной P и активным параметром.

Все основные величины могут быть найдены с использованием закона Ома

Если говорить про физический смыл реактивности, то он представляет собой некую энергию, которая перекачивается из источника к реактивным элементам приемника (конденсатор, обмотка генератора, катушка индуктивности и т. д.), а потом возвращается обратно в источник за время одного периода колебаний.

Полная мощность

Полная P электротока представляет собой значение, соответствующее произведению силы электротока и напряжения в цепи. Она неразрывно связана с активной и реактивной величинами и определяется следующим уравнением: , где Sos = полная мощность, а P и Q — ее активная и реактивная характеристики соответственно.

Общая мощность, которую можно представить в виде кружки пива

Если говорить проще, то активная P есть везде, где присутствует нагрузка активного плана. Например, в спиральных нагревателях, сопротивлении проводов и т. д. Реактивный параметр характерен для реактивной нагрузки, которая имеется в элементах индуктивности или емкости.

Определение и формула полезной мощности

Стоит рассмотреть понятие полезной мощности и формулу на примере электрической цепи. Та мощность, которую источник питания (ИП), в частности, тока, развивает в замкнутой цепи, будет полной мощностью.

Цепь включает в себя: источник тока, имеющий ЭДС (E), внешнюю цепь с нагрузкой R и внутреннюю цепь ИП, сопротивление которого R0. Формула полной (общей) мощности равна:

Здесь I – это значение тока, проходящего по цепи (А), а E – величина ЭДС (В).

Внимание! Падение напряжения на каждом из участков будет равно U и U0, соответственно.

Значит, формула примет вид:

Pобщ = E*I = (U + U0) *I = U*I + U0*I.

Видно, что значение произведения U*I равняется мощности, отдаваемой источником на нагрузке, и соответствует полезной мощности Pпол.

Величина, равная произведению U0*I, соответствует мощности, которая теряется внутри ИП на нагрев и преодоление внутреннего сопротивления R0. Это мощность потерь P0.

Подставляемые в формулу значения показывают, что сумма полезной и потерянной мощностей составляют общую мощность ИП:

Важно! При работе любого аппарата (механического или электрического) полезной мощностью будет та, которая останется для совершения нужной работы после преодоления факторов, вызывающих потери (нагрев, трение, противодействующие силы).

Полная, полезная мощности и КПД цепи постоянного тока

Рассмотрим замкнутую неразветвленную цепь, состоящую из источника тока и резистора.
Применим закон сохранения энергии ко всей цепи:

Так как , а для замкнутой цепи точки 1 и 2 совпадают, мощность электрических сил в замкнутой цепи равна нулю. Это равносильно утверждению о потенциальности электрического поля постоянного тока, о которой уже упоминалось ранее.

Итак, в замкнутой цепи всё тепло выделяется за счет работы сторонних сил: , или , и мы снова приходим к закону Ома, теперь для замкнутой цепи: .

Полной мощностью цепи называют мощность сторонних сил, она же равна полной тепловой мощности:

Полезнойназывают тепловую мощность, выделяемую во внешней цепи (независимо от того, полезна она или вредна в данном конкретном случае):

Роль электрических сил в цепи. Во внешней цепи, на нагрузке R

, электрические силы совершают положительную работу, а при перемещении заряда внутри источника тока – такую же по величине отрицательную. Во внешней цепи теплота выделяется за счет работы электрического поля. Работу, отданную во внешней цепи, электрическое поле «возвращает» себе внутри источника тока. В итоге вся теплота в цепи «оплачена» работой сторонних сил: источник тока постепенно теряет запасенную в нем химическую (или какую-то другую) энергию. Электрическое же поле играет роль «курьера», доставляющего энергию во внешнюю цепь.
Зависимость полной, полезной мощностей и КПД от сопротивления нагрузки R.
Эти зависимости получаем из формул (1 – 2) и закона Ома для полной цепи:

Графики этих зависимостей вы видите на рисунке.

Полная мощность монотонно убывает с ростом , т.к. убывает сила тока в цепи. Максимальная полная мощность выделяется при , т.е. при коротком замыкании

Формула мощности тока. Фактическая и номинальная мощность. КПД электрического прибора :

Действие всех известных электрических приборов происходит за счет электрической энергии. В результате этого мы получаем свет, тепло, звук, механическое движение, то есть разные виды энергии. В этой статье мы рассмотрим и изучим такое физическое понятия, как мощность электрического тока.

Под мощностью тока так же, как и в механике, понимают работу, которая выполняется за единицу времени. Рассчитать мощность, зная работу, которую выполняет электрический ток за некоторый промежуток времени, поможет физическая формула.

Ток, напряжение, мощность в электростатике связаны равенством, которое можно вывести из формулы A = UIt. По ней определяют работу, которую выполняет электрический ток:
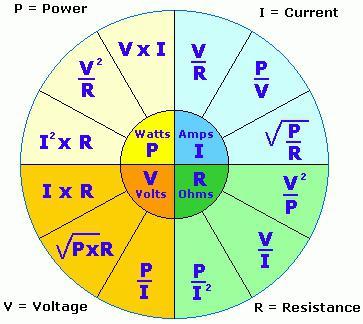
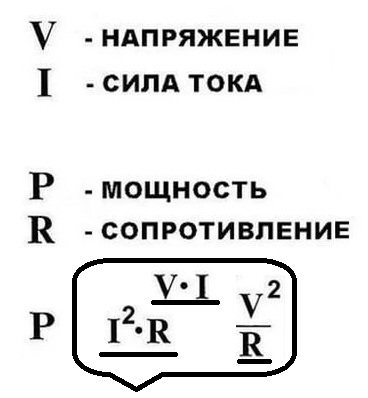
P = A/t = UIt/t = UI Таким образом, формула мощности постоянного тока на любом участке цепи выражается как произведение силы тока на напряжение между концами участка.

Используя закон Ома, формула мощности тока P = UI записывается в таком виде:

P = UI = U2/R = I2/R Итак, мощность, выделяемая на проводниках, прямо пропорциональна силе тока, протекающей через проводник, и напряжению на его концах.

Как известно, идеальных машин и механизмов не существует (то есть таких, которые бы полностью превращали один вид энергии в другой или генерировали бы энергию).

Во время работы устройства обязательно часть затраченной энергии уходит на преодоление нежелательных сил сопротивления или просто «рассеивается» в окружающую среду.

Таким образом, только часть затраченной нами энергии уходит на выполнение полезной работы, для выполнения которой и было создано устройство.

Физическая величина, которая показывает, какая часть полезной работы в затраченной, называется коэффициентом полезного действия (далее КПД).

Другими словами, КПД показывает, насколько эффективно используется затраченная работа при ее выполнении, например, электрическим прибором.
КПД (обозначается греческой буквой η («эта»)) — физическая величина, которая характеризует эффективность электрического прибора и показывает, какая часть полезной работы в затраченной.
КПД определяется (как и в механике) по формуле:
η = AП/AЗ·100%
Если известна мощность электрического тока, формулы для определения ККД будут выглядеть так:
η = PП/PЗ·100%
Прежде чем определять КПД некоторого устройства, необходимо определить, что является полезной работой (для чего создано устройство), и что является затраченной работой (работа выполняется или какая энергия затрачивается для выполнения полезной работы).

Формула полезной мощности источника тока

Пусть электрическая цепь состоит из источника тока, имеющего сопротивление $r$ и нагрузки (сопротивление $R$). Мощность источника найдем как:

где $?$ – ЭДС источника тока; $I$ – сила тока. При этом $P$ – полная мощность цепи.

Обозначим $U$ – напряжение на внешнем участке цепи, тогда формулу (7) представим в виде:

где $P_p=UI=I^2R=frac(9)$ – полезная мощность; $P_0=I^2r$ – мощность потерь. При этом КПД источника определяют как:

Максимальную полезную мощность (мощность на нагрузке) электрический ток дает, если внешнее сопротивление цепи будет равно внутреннему сопротивлению источника тока. При этом условии полезная мощность равна 50% общей мощности.

При коротком замыкании (когда $Rto 0;;Uto 0$) или в режиме холостого хода $(Rto infty ;;Ito 0$) полезная мощность равна нулю.

Взаимосвязь полезной мощности и КПД

Коэффициент полезного действия (КПД) – величина безразмерная, численно выражается в процентах. КПД обозначают буквой η.

Формула имеет вид:

А – полезная работа (энергия);
Q – затраченная энергия.

По мере увеличения КПД в различных двигателях допустимо выстроить следующую линейку:

электродвигатель – до 98%;
ДВС – до 40%;
паровая турбина – до 30%.

Что касается мощности, КПД равен отношению полезной мощности к полной мощности, которую выдает источник. В любом случае η ≤ 1.

Важно! КПД и Pпол не одно и то же. В разных рабочих процессах добиваются максимума или одного, или другого.

Получение максимальной энергии на выходе ИП

К сведению. Чтобы увеличить КПД подъёмных кранов, нагнетательных насосов или двигателей самолётов, нужно уменьшить силы трения механизмов или сопротивления воздуха. Этого достигают применением разнообразных смазок, установкой подшипников повышенного класса (заменив скольжение качением), изменением геометрии крыла и т.д.

Максимальная энергия или мощность на выходе ИП может быть достигнута при согласовании сопротивления нагрузки Rн и внутреннего сопротивления R0 ИП. Это значит, что Rн = R0. В этом случае КПД равен 50%. Это вполне приемлемо для малоточных цепей и радиотехнических устройств.

Однако этот вариант не подходит для электрических установок. Чтобы впустую не тратились большие мощности, режим эксплуатации генераторов, выпрямителей, трансформировав и электродвигателей таков, что к.п.д. приближается к 95% и выше.

Достижение максимального КПД

Формула КПД источника тока имеет вид:

η = Pн/Pобщ = R/Rн+r,

Pн – мощность нагрузки;
Pобщ – общая мощность;
R – полное сопротивление цепи;
Rн – сопротивление нагрузки;
r – внутреннее сопротивление ИТ.

Как видно из графика, изображённого на рис. выше, мощность Pн с уменьшением тока в цепи стремится к нулю. КПД, в свою очередь, достигнет максимального значения, когда цепь будет разомкнута, и ток равен нулю, при коротком замыкании в цепи станет равным нулю.

Если обратиться к элементарному тепловому двигателю, состоящему из поршня и цилиндра, то у него степень сжатия равна степени расширения. Повышение КПД такого мотора возможно в случае:

изначально высоких параметров: давления и температуры рабочего тела перед началом расширения;
приближения их значений к параметрам окружающей среды по окончании расширения.

Достижение ηmax доступно лишь при наиболее эффективном изменении давления рабочего компонента во вращательное движение вала.

К сведению. Термический коэффициент полезного действия повышается с повышением доли теплоты, подаваемой к рабочему телу, которая преобразуется в работу. Подаваемая теплота делится на два вида энергии: внутренняя в виде температуры и энергия давления.

Механическую работу, по сути, совершает только второй вид энергии. Это порождает целый ряд минусов тормозящих процесс повышения КПД:

некоторая часть давления уходит на внешнюю среду;
достижение максимального коэффициента полезного действия невозможно без увеличения процента использования энергии давления для преобразования в работу;
нельзя поднять КПД тепловых двигателей, не изменяя S поверхности приложения давления, и без удаления этой поверхности от точки вращения;
использование только газообразного рабочего тела не способствует повышению η тепловых двигателей.

Для достижения высокого коэффициента полезного действия теплового двигателя нужно определяться с рядом решений. Этому способствуют следующие модели устройства:

ввести в цикл расширения ещё одно рабочее тело с другими физическими свойствами;
наиболее полно перед расширением использовать оба вида энергии рабочего тела;
осуществлять генерацию добавочного рабочего тела прямо при расширении газообразного.

Информация. Все доработки двигателей внутреннего сгорания в виде: нагнетателя турбонадува, организации многократного или распределённого впрыска, а также повышения влажности воздуха, доведения топлива при впрыске до состояния пара, не дали ощутимых результатов резкого повышения КПД.

Реактивный коэффициент

По-другому он называется коэффициентом мощности и является безразмерной величиной, вводимой для вычисления реактивной составляющей. Говоря научным языком, он показывает, насколько сдвигается фаза переменного тока, протекающего через нагрузку, от возникшего на ней напряжения. Численно он принимается равным косинусу сдвига. Математически это сдвиг интерпретируется как косинус угла между векторными значениями тока и напряжения.

Простыми же словами, коэффициент мощности, обозначаемый φ, указывает на ту часть расходуемой электроэнергии, которая преобразуется в полезную работу. Например, при cos φ = 0,9 девяносто процентов от полной энергии уйдёт на совершение полезного действия, а остальные десять будут считаться потерями. Поэтому если в паспорте на какой-либо прибор указано, что мощность изделия составляет 500 Вт, а cos φ = 0,5, то полный расход его энергии будет составлять 500/0,5 = 250 ВА.

То есть коэффициент φ находится из отношения потребляемой устройством энергии к значению полной мощности. Нередко в паспорте оборудования указывается и составляющая φ (характер нагрузки). Она может быть резистивно-ёмкостной или резистивно-индуктивной. При этом сам коэффициент соответственно является опережающим или отстающим.

Если же напряжение в цепи изменяется по синусоидальному закону, а ток по несинусоидальному, то нагрузка никакой реактивной составляющей иметь не будет, а коэффициент принимается равным главной волне (первой гармонике). Под несинусоидальными понимаются искажения электрического сигнала, связанные с гармониками, преобладающими над основной частотой.

В математике формулой для нахождения коэффициента мощности является выражение: cos φ= P/S. Поэтому чем больше его значение, тем меньше потребляет устройство энергию из сети. Существуют различные способы поднятия значения cos φ, даже до максимального значения, равного единице, называемые коррекцией. Наиболее эффективным является добавление в схему сложного электронного узла, размещаемого на входе устройства.

Определение и формула полезной мощности

Здесь I – это значение тока, проходящего по цепи (А), а E – величина ЭДС (В).

Внимание! Падение напряжения на каждом из участков будет равно U и U0, соответственно.

Значит, формула примет вид:

Pобщ = E*I = (U + U0) *I = U*I + U0*I.

Параметры источника питания

На практике часто приходится думать, какой должна быть мощность источника тока, сколько нужно ватт (вт) или киловатт (квт) для обеспечения бесперебойной работы устройства. Для понимания сути нужно иметь представления о таких понятиях, применяемых в физике, как:

полная энергия цепи;
ЭДС и напряжение;
внутреннее сопротивление источника питания;
потери внутри ИП;
полезная мощность.

Независимо от того, какую энергию выдаёт источник (механическую, электрическую, тепловую), мощность его должна подбираться с небольшим запасом (5-10%).

При включении в цепь нагрузки, которая будет потреблять энергию от источника тока (ИТ), ток будет совершать работу. Энергия, выделяемая на всех включенных в цепь потребителях и элементах цепи (провода, электронные компоненты т.д.), носит название полной. Источник энергии может быть любой: генератор, аккумулятор, тепловой котёл. Цифра значения полной энергии будет складываться из энергии, затрачиваемой источником на потери, и количества, затрачиваемого на выполнение конкретной работы.

В чём разница между этими двумя понятиями?

ЭДС – электродвижущая сила, это напряжение, которое сторонние силы (химическая реакция, электромагнитная индукция) создают внутри источника тока (ИТ). ЭДС – это сила перемещения электрических зарядов в ИТ.

К сведению. Измерить значение E (ЭДС) представляется возможным только в режиме холостого хода (х.х.). Подключение любой нагрузки вызывает потерю напряжения внутри ИП.

Напряжение (U) – физическая величина, представляющая собой разность потенциалов ϕ1 и ϕ2 на выходе источника напряжения (ИН).

Определение понятия полной мощности применяют не только в отношении электрических цепей. Оно применимо и по отношению к электродвигателям, трансформаторам и прочим устройствам, способным потреблять, как активную, так и реактивную составляющую энергии.

Подобные потери происходят на внутреннем сопротивлении двухполюсника. У аккумулятора это сопротивление электролита, у генератора – обмоточное сопротивление, провода выводов которого выходят из корпуса.

Взять и просто измерить R0 тестером не получится, узнать его обязательно нужно для вычисления потерь Р0. Поэтому применяют косвенные методы.

Косвенный метод определения R0 заключается в следующем:

в режиме х.х. замеряют E (В);
при включенной нагрузке Rн (Ом) измеряют Uвых (В) и ток I (А);
падение напряжения внутри источника считают по формуле:

На последнем этапе находят R0=U0/I.

Схема для измерения R0

Зависимость мощности от силы тока, формула мощности, физический смысл

Первое упоминание об электричестве встречается в опытах древнегреческого философа Фалеса. Именно он первым обнаружил, что предметы при трении притягиваются. Одноименный термин был введен в начале 17-го века английским физиком Гилбертом, после опытов, проведенных с магнитами. Отцом же науки об электричестве считается французский ученый Кулон – именно после открытия закона, получившего его имя, электротехника начала свою победную поступь, которая продолжается до сих пор. Этот закон утверждает, что два точечных заряда в безвоздушной среде взаимодействуют с силой, прямо пропорциональной их модулям и обратно – расстоянию между ними, возведенному в квадрат.
Выясним, что же представляет собой понятие электричество?

Если коротко, то это – направленное движение потока заряженных частиц. Тела, через которые они проходят, называются проводниками. Каждый проводник имеет определенное сопротивление электрическому току, которое раз

И, перед тем, как перейти к основным законам, несколько слов о заряженных частицах: они бывают, условно говоря, положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные – притягиваются.

А теперь, перейдем к главному

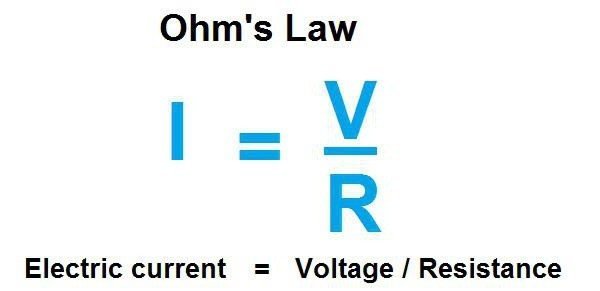
Основа-основ науки об электричестве – закон Ома.

Эксперимент, который провел этот немецкий физик, привел его к следующему убеждению: сила тока I, проходящего через металлический проводник, пропорциональна напряжению на его концах, или I = U/R

Здесь напряжением называется разность, образно говоря, «давлений», созданных двумя точками электрической цепи. Измеряют его в вольтах.

Электрический ток представляет собой число электронов, которые пропускает участок электрической цепи и измеряется в амперах. Сопротивлением считается свойство цепи помешать этому движению. В честь упомянутого физика, его измеряют в омах.

Иначе говоря, проводник, через который проходит ток в 1 ампер при напряжении в 1 вольт, обладает сопротивлением в 1 ом.

Вся остальная электротехника «пляшет» от этого.

О мощности электрического тока

В физике мощностью считают скорость выполнения работы. Неважно, какой. Чем эта операция проводится быстрее, тем большей считается мощность того, кто ее исполняет, будь то человек, механическое устройство или что-то еще.

Так же и в случае с электрическим током: ее мощность представляет собой отношение работы, произведенной движущимися электрическими зарядами к промежутку времени, которое для этого понадобилось.

Проще говоря, для того, чтобы получить электрическую мощность в 1 ватт, когда источник тока имеет напряжение 1 вольт, необходимо пропустить через проводник ток в 1 ампер. Другими словами, мощность (P) можно посчитать, перемножив друг на друга электрическое напряжение и ток:

Запомнив эту нехитрую формулу, на практике можно рассчитать мощность. Например, если известны значения тока и сопротивления, а о напряжении сведений нет, можем воспользоваться законом Ома, подставив в формулу вместо него I*R. Получится, что мощность равна квадрату электрического тока, помноженному на сопротивление.

Этот закон точно так же придет на помощь, если известны величины напряжения и сопротивления. В этом случае подставив вместо значения тока I = U/R, получим значение мощности, равное квадрату напряжения, поделенному на сопротивление.

Закон Ома и мощность

Используя закон Ома, формула мощности тока P = UI записывается в таком виде:

Коэффициент полезного действия электрического прибора

Другими словами, КПД показывает, насколько эффективно используется затраченная работа при ее выполнении, например, электрическим прибором.
КПД (обозначается греческой буквой η («эта»)) — физическая величина, которая характеризует эффективность электрического прибора и показывает, какая часть полезной работы в затраченной.
КПД определяется (как и в механике) по формуле:
η = AП/AЗ·100%
Если известна мощность электрического тока, формулы для определения ККД будут выглядеть так:
η = PП/PЗ·100%
Прежде чем определять КПД некоторого устройства, необходимо определить, что является полезной работой (для чего создано устройство), и что является затраченной работой (работа выполняется или какая энергия затрачивается для выполнения полезной работы).

Активная, реактивная и полная (кажущаяся) мощности

Простое объяснение с формулами

Активная мощность (P)

Другими словами активную мощность можно назвать: фактическая, настоящая, полезная, реальная мощность. В цепи постоянного тока мощность, питающая нагрузку постоянного тока, определяется как простое произведение напряжения на нагрузке и протекающего тока, то есть

потому что в цепи постоянного тока нет понятия фазового угла между током и напряжением. Другими словами, в цепи постоянного тока нет никакого коэффициента мощности.

Но при синусоидальных сигналах, то есть в цепях переменного тока, ситуация сложнее из-за наличия разности фаз между током и напряжением. Поэтому среднее значение мощности (активная мощность), которая в действительности питает нагрузку, определяется как:

В цепи переменного тока, если она чисто активная (резистивная), формула для мощности та же самая, что и для постоянного тока: P = V I.

Формулы для активной мощности

P = V I – в цепях постоянного тока

P = V I cosθ – в однофазных цепях переменного тока

P = √3 VL IL cosθ – в трёхфазных цепях переменного тока

P = 3 VPh IPh cosθ

P =√ (ВА2 – вар2) или

Активная мощность = √ (Полная мощность2 – Реактивная мощность2) или

кВт = √ (кВА2 – квар2)

Реактивная мощность (Q)

Также её мощно было бы назвать бесполезной или безваттной мощностью.

Мощность, которая постоянно перетекает туда и обратно между источником и нагрузкой, известна как реактивная (Q).

Реактивной называется мощность, которая потребляется и затем возвращается нагрузкой из-за её реактивных свойств. Единицей измерения активной мощности является ватт, 1 Вт = 1 В х 1 А. Энергия реактивной мощности сначала накапливается, а затем высвобождается в виде магнитного поля или электрического поля в случае, соответственно, индуктивности или конденсатора.

Реактивная мощность определяется, как

и может быть положительной (+Ve) для индуктивной нагрузки и отрицательной (-Ve) для емкостной нагрузки.

Единицей измерения реактивной мощности является вольт-ампер реактивный (вар): 1 вар = 1 В х 1 А. Проще говоря, единица реактивной мощности определяет величину магнитного или электрического поля, произведённого 1 В х 1 А.

Формулы для реактивной мощности

Реактивная мощность = √ (Полная мощность2 – Активная мощность2)

квар = √ (кВА2 – кВт2)

Полная мощность (S)

Полная мощность – это произведение напряжения и тока при игнорировании фазового угла между ними. Вся мощность в сети переменного тока (рассеиваемая и поглощаемая/возвращаемая) является полной.

Комбинация реактивной и активной мощностей называется полной мощностью. Произведение действующего значения напряжения на действующее значение тока в цепи переменного тока называется полной мощностью.

Она является произведением значений напряжения и тока без учёта фазового угла. Единицей измерения полной мощности (S) является ВА, 1 ВА = 1 В х 1 А. Если цепь чисто активная, полная мощность равна активной мощности, а в индуктивной или ёмкостной схеме (при наличии реактивного сопротивления) полная мощность больше активной мощности.

Формула для полной мощности

Полная мощность = √ (Активная мощность2 + Реактивная мощность2)

kVA = √(kW2 + kVAR2)

Следует заметить, что:

резистор потребляет активную мощность и отдаёт её в форме тепла и света.
индуктивность потребляет реактивную мощность и отдаёт её в форме магнитного поля.
конденсатор потребляет реактивную мощность и отдаёт её в форме электрического поля.

Все эти величины тригонометрически соотносятся друг с другом, как показано на рисунке:

Источник

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

Все категории
экономические
43,660
гуманитарные
33,654
юридические
17,917
школьный раздел
611,971
разное
16,905

Популярное на сайте:

Источник

Оцените решебник:

Как найти среднюю мощность по графику

A. Мощность

Мощность

Литература

Мощность: средняя и мгновенная

Найти среднюю полезную мощность при разбеге самолета, предназначенного для работ в сельском и лесном хозяйстве. Масса самолета 1 т, длина

Полезная мощность

Мощность (физика) — это… Что такое Мощность (физика)?

Единицы измерения

Виды мощности постоянного тока

Мгновенная мощность

Активная мощность

Реактивная мощность

Полная мощность

Определение и формула полезной мощности

Полная, полезная мощности и КПД цепи постоянного тока

Формула мощности тока. Фактическая и номинальная мощность. КПД электрического прибора :

Формула полезной мощности источника тока

Взаимосвязь полезной мощности и КПД

Получение максимальной энергии на выходе ИП

Достижение максимального КПД

Реактивный коэффициент

Определение и формула полезной мощности

Параметры источника питания

Зависимость мощности от силы тока, формула мощности, физический смысл

А теперь, перейдем к главному

О мощности электрического тока

Закон Ома и мощность

Коэффициент полезного действия электрического прибора

Активная, реактивная и полная (кажущаяся) мощности

Вам также может понравиться

Виндовс 10 диск 100 загрузка как исправить

Как найти нового абонента в ватсапе

Как составить формулу зависимости скорости от времени

Добавить комментарий Отменить ответ