Имеются следующие данные о возрастных коэффициентах смертности:
для детей, в возрасте до одного года – 26,2‰ (К0),
для детей, достигших возраста один год – 6,5‰ (К1),
для детей, достигших возраста два года – 4,0‰ (К2),
для детей, достигших возраста три года – 2,5‰ (К3),
для детей, достигших возраста четыре года – 0,6‰ (К4).
Сумма предстоящих человеко-лет жизни для совокупности родившихся (10 тыс. чел.) составляет 636 600.
Составьте таблицу смертности для данных возрастных групп и определите среднюю ожидаемую продолжительность предстоящей жизни для возраста 0, 1, 2, 3 и 4 года.
Решение:
Таблицы смертности и средней продолжительности жизни, таблицы дожития – система взаимосвязанных упорядоченных по возрасту рядов чисел, организованных как описание процесса уменьшения с возрастом под действием смертности некоторого абстрактного поколения с фиксированной начальной численностью, именуемой корнем таблицы.
Макет таблицы смертности имеет вид:
| Возраст, лет | Число доживших до возраста х, лет | Вероятность дожить до следующего возраста | Вероятность смерти в течение года | Число живущих в возрасте х | Предстоящее число чел.-лет жизни | Средняя продолжительность предстоящей жизни | Коэффициент дожития |
|---|---|---|---|---|---|---|---|
| х | lx | px | qx | Lx | Tx | ex0 | Px |
В нашей задаче численность поколения условно равна 10 000 чел.
На основе возрастных коэффициентов смертности можно определить вероятность смерти в течение года для каждого года жизни (qх):
q0 = 0,0262
q1 = 0,0065
q2 = 0,0040
q3 = 0,0025
q4 = 0,0006
Затем определим вероятность дожития от возраста х до возраста х + 1 (рх):
p0 = 1 – q0 = 1 – 0,0262 = 0,9738
p1 = 1 – q1 = 1 – 0,0065 = 0,9935
p2 = 1 – q2 = 1 – 0,0040 = 0,9960
p3 = 1 – q3 = 1 – 0,0025 = 0,9975
p4 = 1 – q4 = 1 – 0,0006 = 0,9994
Теперь рассчитаем число доживающих до возраста х (lx) :
l0 = 10 000 (по условию)
l1 = l0 × p0 = 10 000 × 0,9738 = 9 738
l2 = l1 × p1 = 9 738 × 0,9935 = 9 675
l3 = l2 × p2 = 9 675 × 0,9960 = 9 636
l4 = l3 × p3 = 9 636 × 0,9975 = 9 612
l5 = l4 × p4 = 9 612 × 0,9994 = 9 606
Найдём число живущих в возрасте х лет (Lх), представляющее собой среднюю арифметическую из числа доживающих до возраста х и до возраста х + 1:
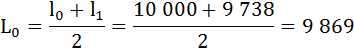
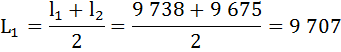
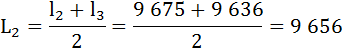
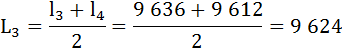
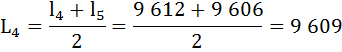
Определим число предстоящих человеко-лет жизни (Тх) для разных возрастов.
По условию задания
Т0 = 636 600
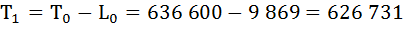
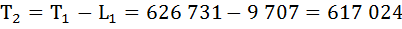
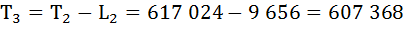
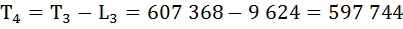
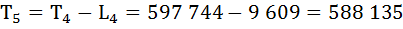
Рассчитаем среднюю продолжительность предстоящей жизни населения по формуле:
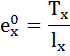
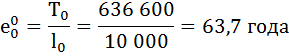
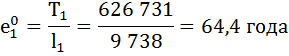
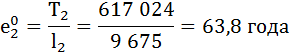
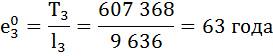
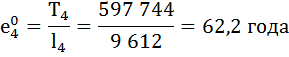
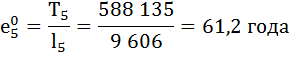
Коэффициент передвижки Px – вероятность для индивидуума в интервале возраста от х до х+1 прожить 1 год и попасть в интервал от х+1 до х+2 – определяется по формуле:
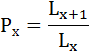
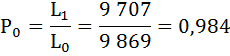
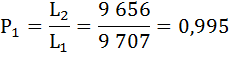
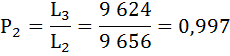
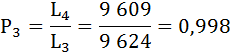
Полученные результаты занесём в таблицу:
| х | lx | px | qx | Lx | Tx | e0x | Px |
|---|---|---|---|---|---|---|---|
| 0 | 10 000 | 0,9738 | 0,0262 | 9 869 | 636 600 | 63,7 | 0,984 |
| 1 | 9 738 | 0,9935 | 0,0065 | 9 707 | 626 731 | 64,4 | 0,995 |
| 2 | 9 675 | 0,9960 | 0,0040 | 9 656 | 617 024 | 63,8 | 0,997 |
| 3 | 9 636 | 0,9975 | 0,0025 | 9 624 | 607 368 | 63 | 0,998 |
| 4 | 9 612 | 0,9994 | 0,0006 | 9 609 | 597 744 | 62,2 | – |
| 5 | – | – | – | – | 588 135 | 61,2 | – |
| – | – | – | – | – | – | – | – |
| 100 | – | – | – | – | – | – | – |
| 636 600 |
Условие задачи взято из: Социально-экономическая статистика: Практикум/Под ред. В. Н. Салина, Е. П. Шпаковской: Учеб. пособие. – М.:Финансы и статистика, 2003. – 192 с.
6.9. Продолжительность жизни.
1. Способы вычисления. Продолжительность
жизни, ее исследование является одной
из самых важных задач демографии.
Изучением ее занимаются в ряде других
научных дисциплин — в геронтологии,
биологии человека [7] и др. Этот показатель
широко используется в гуманитарных
науках, научных направлениях управленческого
типа как критерий успешности последнего,
критерий социального благополучия
жизни населения региона, страны. Именно
поэтому показательсредней
продолжительности илиожидаемой
продолжительности предстоящей жизни
в таблицах смертности приводится для
каждого возраста (см. табл. 16.3).
Первый способ вычисления ожидаемой
продолжительности жизни или средней
продолжительности предстоящей при
рождении![]() ,
,
приближенно можно вычислить по формуле:
 (17.1)
(17.1)
где dx— числа умерших в возрасте х, х — возраст
в годах;![]() — численность новорожденных, по таблице
— численность новорожденных, по таблице
дожития.
Второй способ более точен, в нем
используется показательTx,
размерность которого выражается в
человеко-летах. Он определяется по
формуле
![]() (17.2)
(17.2)
где 1 (1 год) — величина межгруппового
интервала.
По этой формуле значение ожидаемой
продолжительности жизни при рождении
равно «накопленным суммам» T0человеко-лет, деленным на численность
исследуемой когорты при рождении, наL0:
![]() (17.3)
(17.3)
Величина
![]() естьмедиана продолжительности
естьмедиана продолжительности
предстоящей жизни. Привесок в полгода
демографы включают в формулу на том
основании, что «человек редко умирает
в свой день рождения, обычно живет
некоторое время в год своей смерти, в
среднем не менее 6 месяцев до дня смерти»
[1,c. 184].
Приведем пример вычисления показателя
средней продолжительности
![]() предстоящей жизни небольшой когорты
предстоящей жизни небольшой когорты
мужчин, состоящей из 10 человек, достигших
70-летнего возраста. Требуется определить![]() на основании указанного в таблице 17.1
на основании указанного в таблице 17.1
порядка вымирания — значенийdx.
Таблица 17.1
Пример вычисления продолжительности
предстоящей жизни
|
Возраст (годы) х |
70 |
71 |
72 |
73 |
74 |
75 |
76 |
77 |
78 |
79 |
80 |
|
Численность когорты, |
10 |
9 |
8 |
8 |
8 |
6 |
6 |
5 |
4 |
1 |
0 |
|
Число умерших dx(человек) |
0 |
1 |
1 |
0 |
0 |
2 |
0 |
1 |
1 |
3 |
1 |
|
Средняя величина |
10,0 |
9,5 |
8,5 |
8,0 |
8,0 |
7,0 |
6,0 |
5,5 |
4,5 |
2,5 |
0,5 |
Приведенный пример вычислений показывает
как определяется величина
![]() ,
,![]() с использованием формул (17.2) и (17.3):
с использованием формул (17.2) и (17.3):![]() =(10
=(10
+ 9,5 + 8,5 + … + 0,5) : 10 = 7,0 лет.
На этом же примере показано как вычисляется
средняя продолжительность жизни . Этот
показатель равен сумме х прожитых
лет и![]() и применяется в отношении когорт
и применяется в отношении когорт
реального населения. Тогда как показатель![]() (иногда он обозначается той же буквой
(иногда он обозначается той же буквой
с двумя нулями![]() )
)
рассчитывается для условного поколения.
6.10 Динамика показателя .
Основная закономерность динамики
средней продолжительности предстоящей
жизни такова: с увеличением возраста х
средняя продолжительность жизни![]() убывает. В этом можно убедиться проследив
убывает. В этом можно убедиться проследив
значения следующих величин![]() ,
,
взятых из таблицы дожития населения
одной из областей СССР (использованы
данные [1,c. 189]).
Возраст мужчины женщины
0 62,41 71,39
1 64,66 73,42
2 64,13 72,96
3 63,30 72,15
4 62,44 71,32
5 61,55 70,44
Из приведенных данных видно, что мальчиков
до 5-летнего возраста, у девочек до
возраста в 4 года
![]() растет и лишь позже начинает выполняться
растет и лишь позже начинает выполняться
сформулированное выше правило об
убывающей с возрастом средней
продолжительности предстоящей жизни.
Динамика чисел умирающих dxснижается с первых дней жизни до возраста
12-13 лет, а затем растет, достигая максимума
в точке, принятой в статистике населения
за моду, модальную продолжительность
предстоящей жизни. После пика, максимумаdxнепрерывно уменьшается. В регионе России
по статистическим материалам которого
получены кривая рис. 16.2 и 16.3, модальная
продолжительность жизни мужчин пришлась
на возраст 67 лет, а женщин на 81 год.
Эволюция продолжительности жизни мужчин
и женщин в мире во второй половине XXв. (по данным работ [1, 17]) характеризовалась
следующими значениями:
мужчины женщины
1960-1964 50,9 53,4
1970-1974 54,6 57,1
1980-1984 57,9 60,5
1994 61,8 64,6
Изменения ожидаемой продолжительности
жизни в нашей стране показаны в таблице
17.2
Таблица 17.2
Средняя продолжительность предстоящей
жизни населения СССР (РФ) с 1926 по 1994 (по
данным 1, с. 187, 49]).
|
Годы |
Все население |
Городское население |
Сельское население |
|
|
1926-1927 |
Европейская часть |
44,0 |
46,0 |
44,0 |
|
1938-1939 |
СССР в границах 1922 |
47,0 |
45,0 |
48,0 |
|
1958-1959 |
СССР в границах 1945 |
69,0 |
68,0 |
69,0 |
|
1971-1972 |
-‘- |
70,0 |
70,0 |
69,0 |
|
1978-1979 |
-“- |
68,0 |
68,0 |
67,0 |
|
1984-1985 |
-“- |
68,0 |
69,0 |
66,0 |
|
1986-1987 |
-”- |
70,0 |
70,0 |
68,0 |
|
1994 |
Российская Федерация |
64,01* |
– |
– |
3. Средний возраст умерших. Средняя
продолжительность прожитой человеком
жизни или средний возраст умерших по
сути должна равняться средней
продолжительности предстоящей жизни,
вычисленной первым способом, по формуле
(17.1). Потому что![]() возраст умерших равенсумме произведений
возраст умерших равенсумме произведений
Мiчисла
умершихi-й возрастной
группы на среднее значение возраста
ее, разделенной на общую численность
умерших.
Величина
![]() может служить ориентировочной оценкой
может служить ориентировочной оценкой![]() ,
,
рассчитанного по таблицам дожития, в
особенности, когда таблицы эти устарели,
как в РФ, в связи с длительной задержкой
переписи. Ниже приводятся сопоставления
величины![]() ,
,
сообщенной СПб-госкомитетом [28] для
мужского населения Петербурга и
вычисленной нами оценки![]() среднего возраста умерших, для 1987 и
среднего возраста умерших, для 1987 и
1994 гг.
![]()
![]()
1987 65,7 лет 62,8 лет
1994 58,1 лет 55,2 лет
Есть основание полагать, что представленные
официальные сведения на 2-3 года завышены.
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Средняя продолжительность жизни в стране высчитывается только среди живых людей ,начиная с момента рождения, и до самого большего достигшего возраста.Смертность и продолжительность жизни , это разные понятия. Для расчета средней продолжительности жизни берутся группы жителей по годам, от момента рождения, и до групп с самой высокой продолжительностью жизни. Этот показатель складывается и делится на количество жителей. Чем больше групп с большой продолжительностью жизни, тем выше средний показатель средней продолжительности жизни..
пример расчета среднего возраста
1 группа – 1 год -5 чел.
2 группа – 2 года – 10 чел.
3 группа – 20 лет -2 человека
всего 17 человек
Их общий возраст составляет 5 +20 + 40 =65 . В группах 17 человек. Общий возраст делиться на количество человек.И получаем среднюю продолжительность жизни этой группы на данный момент.
Эта цифра постоянно меняется.И она зависит от рождаемости и смертности.

Пример решения задачи. Статистика предприятия.
Условие задачи
В годовом отчете КСП имеются такие данные об
использовании рабочего времени за 2003 год (человеко-дней): отработано – 159520; количество неявок на
работу – 99120, в том числе за счет очередных отпусков – 12800, отпусков на
обучение – 460, отпусков в связи с родами – 700, болезнью -8340, неявок по
закону -950, неявок с разрешения администрации -850, прогулов – 80, праздничных и выходных дней -75790;
количество отработанных человеко-часов – всего 1256200, в том числе в
сверхнормированное время -9610.
Определите:
- календарный, табельный и максимально возможный фонды рабочего времени и их
относительные показатели; - среднесписочную, среднюю явочную и среднюю фактическую численность рабочих;
- среднюю фактическую длительность рабочего периода;
- среднюю фактическую длительность рабочего дня.
Сделайте выводы.
Решение задачи
Фонды рабочего времени и их относительные показатели
Календарный фонд рабочего времени
соответствует сумме человеко-дней явок и неявок на работу:
-человеко-дни
явок на работу
-человеко-дни
неявок на работу
Табельный фонд рабочего времени
меньше календарного на число человеко-дней неявок в праздничные и в выходные
дни:
-человеко-дни
неявок на работу в праздничные и выходные дни
Максимально возможный фонд рабочего
времени меньше табельного на число человеко-дней очередных отпусков:
-человеко-дни
неявок на работу в отпусках
Относительные
показатели рассчитываются путем отношения фактически отработанного времени к
соответствующему фонду времени:
Коэффициент
использования календарного времени:
Коэффициент
использования табельного времени:
Коэффициент
использования максимально-возможного фонда:
Показатели численности работников
Среднесписочная численность
рабочих:
-число календарных
дней в периоде (в нашем случае в 2003 году 365 дней)
Среднеявочная численность:
-количество
рабочих дней в периоде (в 2003 году было 250 рабочих дней)
Средняя численность фактически
работающих:
-целодневные
простои
Продолжительность рабочего периода
Среднюю фактическая длительность
рабочего периода вычислим как отношение количества отработанных человеко-дней
на среднесписочную численность работников:
Продолжительность рабочего дня
Среднюю фактическую
продолжительность рабочего дня вычислим как отношение отработанных
человеко-часов за вычетом сверхнормированного времени к количеству отработанных
человеко-дней:
Таким
образом, коэффициент использования максимально-возможного фонда составил 0,938
при средней фактической длительности рабочего периода 225 дней и фактической
продолжительности рабочего дня 7,8 ч.
При среднесписочной численности рабочих 709 чел. среднеявочная
численность составила 638 чел.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).
Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.
- Например, курс акций корпорации в основном определяется финансовыми результатами ее деятельности. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу.
Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:
- средняя арифметическая;
- средняя гармоническая;
- средняя геометрическая;
- средняя квадратическая.
Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
- Средняя арифметическая простая (невзвешенная) – вычисляется когда каждый вариант совокупности встречается только один раз.
- Средняя арифметическая (взвешенная) – варианты повторяются различное число раз, при этом число повторений вариантов называется частотой, или статистическим весом.
ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН
- Средняя арифметическая простая – самый распространенный вид средней величины, рассчитывается по формуле (8.8):

(8.8 -формула средней арифметической простой)
- где хi – вариант, а n – количество единиц совокупности.
- Пример вычисления средней арифметической простой. Провели опрос о желаемом размере заработной платы у пяти сотрудников офиса. По результатам опроса выяснили, что желаемый размер заработной платы составляет соответственно для каждого сотрудника: 50000, 100000, 200000, 350000, 500000 рублей человек. Рассчитаем среднюю арифметическую простую по формуле (8.8):
 Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
- Средняя арифметическая взвешенная формула 8.9.

(8.9 -формула средней арифметической взвешенной)
- где хi – вариант, а fi – частота или статистический вес.
- Пример вычисления средней арифметической взвешенной. Результаты опроса всех работников офиса приведены в табл. 8.2.
Таблица 8.2 – Результаты опроса работников офиса
|
Желаемый размер заработной платы, тыс.руб хi |
Количество работников fi | хifi |
| 1 | 2 | 3 |
|
50 100 200 350 500 |
6
10 20 9 5 |
300
1000 4000 3150 2500 |
| Итого | 50 | 10950 |
Пример. Вычислим (ориентируясь на итоговые строки таблицы) желаемый размер заработной платы, 50 сотрудников офиса (используем формулу 8.9):

Пример вычисления средней арифметической взвешенной
Вывод: в среднем желаемый размер заработной платы по результатам опроса 50 человек составил 219 тысяч рублей.
Среднеарифметическая – всегда обобщающая количественная характеристика варьирующего признака совокупности.
- Средняя гармоническая вычисляется в тех случаях, когда приходится суммировать не сами варианты, а обратные им величины.
- Средняя гармоническая простая представлена ниже:

(8.10 – формула средней гармонической простой)
Средняя гармоническая взвешенная определяется по формуле

(8.11- формула средней гармонической взвешенной)
где xi – вариант, n – количество вариантов, Vi – веса для обратных значений xi.
Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, чем взвешенная. Для иллюстрации области ее применения воспользуемся упрощенным условным примером.
- Пример (вычисление средней гармонической простой (невзвешенной)).
Предположим, в фирме, специализирующейся на торговле по почте на основе предварительных заказов, упаковкой и отправкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 5 мин., второй – 15 мин.
- Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна?
На первый взгляд, ответ на этот вопрос заключается в осреднении индивидуальных значений затрат времени на 1 заказ, т.е. если используем среднюю арифметическую простую получим: (5+15):2=10, мин.
- Проверим обоснованность такого подхода на примере одного часа (60 минут) работы. За этот час первый работник обрабатывает 12 заказов (60:5), второй – 4 заказа (60:15), что в сумме составляет 16 заказов.
Если же заменить индивидуальные значения их предполагаемым средним значением, то общее число обработанных обоими работниками заказов в данном случае уменьшится: (60/10) + (60/10) = 12 заказов (что не соответствует истине).
- Подойдем к решению через исходное соотношение средней. Для определения средних затрат времени необходимо общие затраты времени за любой интервал (например, за час) разделить на общее число обработанных за этот интервал двумя работниками заказов, т.е. используем среднюю гармоническую:

Пример вычисления средней гармонической простой (невзвешенной)
Если теперь мы заменим индивидуальные значения их средней величиной, то общее количество обработанных за час заказов не изменится: (60/7,5) + (60/7,5) = 16 заказов
- Подведем итог: средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения Wj для единиц совокупности равны (в рассмотренном примере рабочий день у сотрудников одинаковый).
Пример (вычисление средней гармонической взвешенной) В ходе торгов на валютной бирже за первый час работы заключено пять сделок. Данные о сумме продажи рублей и курсе рубля по отношению к доллару США приведены в табл.8.3.
Таблица 8.3 – Данные о ходе торгов на валютной бирже (цифры условные)
Номер сделки Сумма продажи V, млн руб. Курс рубля x, руб. за 1 дол. V/x 1 2 3 4 1
2
3
4
5
455,00
327,50
528,00
266,00
332,50
65,00 65,50
66,00
66,50
66,50
7,00
5,00
8,00
4,00
5,00
итого 1909,00 – 29,00 Для того чтобы определить средний курс рубля по отношению к доллару, нужно найти соотношение между суммой продажи рублей, которые затрачены на покупку долларов в ходе всех сделок, и суммой приобретенных в результате этих сделок долларов.

- Вывод: средний курс за один доллар составил 65,83 руб.;
- Если бы для расчета среднего курса была использована средняя арифметическая простая:
 то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака обычно представляют собой относительные показатели динамики, построенные в виде цепных величин как отношение каждого уровня ряда к предыдущему уровню.
- Средняя геометрическая простая рассчитывается по формуле 8.12

(8.12)
- Если использовать частоты m, получим формулу средней геометрической взвешенной
- Средняя геометрическая взвешенная рассчитывается по формуле 8.13

(8.13)
Средняя квадратическая применяется, когда изучается вариация признака. В качестве вариантов используются отклонения фактических значений признака либо от средней арифметической, либо от заданной нормы.
Для несгруппированных данных используют формулу средней квадратической простой
Средняя квадратическая простая (формула 8.14)

8.14
Для сгруппированных данных используют формулу средней квадратической взвешенной
Средняя квадратическая взвешенная (формула 8.15)

(8.15) – Формула -средняя квадратическая взвешенная
Средние арифметическая, гармоническая, геометрическая и квадратическая, рассчитанные для одного и того же ряда вариантов, отличаются друг от друга. Их численное значение возрастает с ростом показателя степени в формуле степенной средней правило мажорантности средних А.Я. Боярского, т.е.

Мода и Медиана (структурные средние) формулы и примеры вычисления см. по ссылке

