Сегодня разберем с вами очередной сложный момент, который ломает мозг не только ученикам 9-11 класса, но и студентам, которые запустили тему кинематики и подзабыли основные определения…
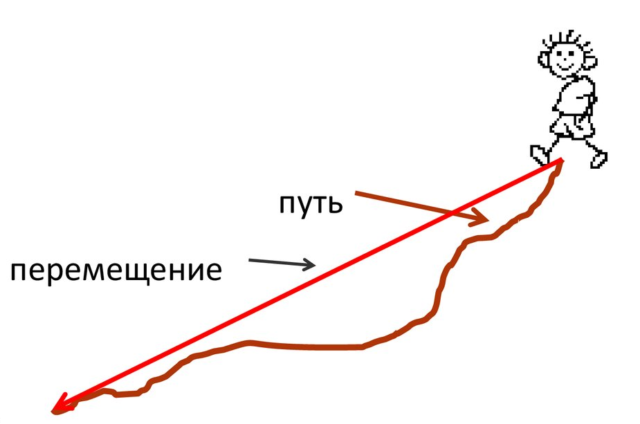
Средняя скорость в физике — один из подвохов, на котором попадаются учащиеся. По аналогии со средним арифметическим школьники и студенты частенько просто берут, складывают, делят пополам. Но в задачах по физике и математике на среднюю скорость так работает далеко не всегда. Предлагаю вам подумать над тем, почему не всегда работает среднее арифметическое двух скоростей, если у нас есть первая половина пути, где тело двигалось с постоянной скоростью v₁ и есть вторая половина пути, на которой тело двигалось с постоянной скоростью v₂. Почему средняя скорость на всём пути не равна среднему арифметическому ? Свой ответ напишите в комментариях. А сегодня мы рассматрим более интересную и редко встречающуюся задачку.
А пока прошу вас подписаться на мой канал в telegram IT mentor. Там я делюсь более короткими постами, рассказываю некоторые интересные случаи из жизни, непосредственно связанные с физикой, математий и IT.
Задача
Двигаясь равноускорено по прямой из состояния покоя, тело проходит некоторый путь. Чему равно отношение средней скорости тела на второй половине пути к средней скорости на первой половине пути?
Попробуйте на этом этапе остановиться, взять черновик с карандашом и решить задачку самостоятельно. Ваши ответы, комментарии, идеи и мнение о задаче обязательно напишите в комментариях. Так я лучше понимаю что интересно моим дорогим читателям 🤗
Решение:
Сделаем небольшой рисунок, уточняющий что происходит в задаче:
Для начала определим средние скорости на каждой части. Уже в этой части задачи нужно кое-что понимать. Обычно, под средней скоростью подразумевают именно среднюю путевую скорость. В то же время есть и просто средняя скорость. И две эти величины, в общем случае, отличаются. Давайте вспоминать определения.
Средняя путевая скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.
Средняя скорость — это скорость, определяемая отношением перемещения (S) при неравномерном движении к промежутку времени, за который это перемещение произошло.
Чувствуете подвох? Просто средняя скорость вполне может обнулиться, если вы попадете в момент, когда перемещение становится нулевым. В круговом движении или периодических колебаниях это реализуемо. А вот средняя путевая скорость всегда величина ненулевая, если тело прошло хоть какое-то расстояние. В нашей задаче будем иметь в виду именно среднюю путевую скорость.
1 способ
Средняя скорость на первой половине пути:
Здесь учитывается, что тело стартует с нулевой начальной скоростью.
Средняя скорость на второй половине пути:
Здесь уже учитывается, что начальная скорость для этого участка ненулевая. И находится она из времени разгона на предыдущем участке. Конечная скорость первого участка есть начальная скорость для второго участка. В полученном квадратном уравнении относительно нужного нам момента времени, корень будем выбирать заведомо положительный, т.к. нелогично предполагать, что время получится отрицательной величиной):
Отсюда средняя скорость на данном участке получается:
А теперь мы можем посчитать конечное отношение средней скорости на второй части пути к средней скорости на первой части пути:
Итак, у нас появился первый ответ на задачу. Логичный ли он? Похож ли на правду? А может нам второй способ бахнуть? 😎
2 способ
Хотите второй способ решения задачи? Для любителей хардкорных формул математического анализа я приведу альтернативное решение.
Мы помним общую формулу скорости для движения с постоянным ускорением:
Интегральное обобщенное определение средней скорости можно записать в виде:
Определим моменты времени t₁ и t₂ :
Получили точно такой же ответ, какой был в первом способе решения задачи. Задача решена. И похоже, что решена верно 😊
Краткое решение двумя способами
Какой способ решение вам больше понравился? Напишите в комментариях!
Понравилась статья? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в telegram
Неравномерное прямолинейное движение. Средняя скорость
- График скорости при неравномерном прямолинейном движении
- Как найти путь и перемещение по графику скорости?
- Средняя скорость и средняя путевая скорость
- Задачи
- Лабораторная работа №3. Определение средней скорости движения тела
п.1. График скорости при неравномерном прямолинейном движении
Прямолинейное и равномерное движение возможно лишь на участке пути.
Любое тело со временем меняет свою скорость, как по величине, так и по направлению.
Движение с переменной скоростью называют неравномерным.
Для описания неравномерного движения его можно разбить на участки, на которых скорость постоянна, и свести задачу к уже известному нам равномерному прямолинейному движению.
Например, пусть велосипедист добрался из города A в город B за 1 час. Первые полчаса он ехал со скоростью 9 км/ч, а потом проколол шину, и вторые полчаса шел пешком со скоростью 3 км/ч.
Направим ось ОХ также от A к B и получим значения проекций скоростей: $$ v_{x1}=9 text{км/ч}, v_{x2}=3 text{км/ч} $$ Построим график скорости для этого случая:
Графиком скорости (v_x=v_x(t)) при неравномерном прямолинейном движении, которое можно разбить на участки с постоянной скоростью, является ломаная линия.
п.2. Как найти путь и перемещение по графику скорости?
Мы уже знаем, что путь равен площади прямоугольника, который образуется между отрезком графика скорости и отрезком (triangle t) на оси (t) (см. §8 данного справочника).
В таком случае, путь велосипедиста в нашем примере:
Общий путь велосипедиста равен 6 км. Расстояние между городами 6 км.
Если принять город A за начало отсчета с (x_0=0), то координата велосипедиста в конце пути: $$ x_{к}=x_0+s=0+6=6 text{(км)} $$ Перемещение по оси ОХ: (triangle x=x_{к}-x_0=6 text{(км)}).
Теперь рассмотрим другую ситуацию. Пусть велосипедист выехал из A в B и двигался со скоростью 9 км/ч в течение получаса. Но, после того как проколол шину, он развернулся и пошел пешком назад в A. Где будет находиться велосипедист через полчаса после разворота?
Снова направим ось ОХ от A к B и получим значения проекций скоростей: $$ v_{x1}=9 text{км/ч}, v_{x2}=-3 text{км/ч} $$ Построим график скорости для этого случая:
Путь велосипедиста по-прежнему будет равен сумме площадей прямоугольников, которые образует ломаная (v_x(t)) с осью (t): begin{gather*} x=v_{x1}cdot triangle t_1+|v_{x2}|cdottriangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text{(км)} end{gather*}
Если мы учтем знак (v_{x2}) и уберем модуль, то получим величину перемещения по оси ОХ: begin{gather*} triangle x=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2\ triangle x=9cdot 0,5-3cdot 0,5=4,5-1,5=3 text{(км)} end{gather*} Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км в обратном направлении.
Конечная координата: $$ x_{к}=x_0+triangle x=0+3=3 text{(км)} $$
Ответ на вопрос задачи найден. Через полчаса после разворота велосипедист будет находиться в точке D в 3 км от города A.
Пусть неравномерное прямолинейное движение разбито на (n) участков с постоянными скоростями. Каждому такому участку соответствует промежуток времени (triangle t_i) и постоянная скорость (v_{xi}, i=overline{1,n}).
Тогда:
Весь пройденный путь равен сумме площадей прямоугольников на графике скорости: $$ s=|v_{x1}|cdottriangle t_1+|v_{x2}|cdottriangle t_2+…+|v_{xn}|cdottriangle t_n $$ Величина перемещения по оси ОХ равна сумме площадей прямоугольников с учетом знака: $$ triangle x=v_{x1}cdottriangle t_1+v_{x2}cdottriangle t_2+…+v_{xn}cdottriangle t_n $$ Конечная координата равна: (x_{к}=x_0+triangle x).
п.3. Средняя скорость и средняя путевая скорость
Средняя скорость на нескольких участках движения равна отношению общего перемещения к общему времени, затраченному на это перемещение: $$ overrightarrow{v_{cp}}=frac{overrightarrow{r_1}+overrightarrow{r_2}+…+overrightarrow{r_n}}{t_1+t_2+…+t_n}=frac{overrightarrow{r}}{t} $$
Средняя путевая скорость на нескольких участках движения равна отношению общего пути к общему времени, затраченному на этот путь: $$ v_{cp.п}=frac{s_1+s_2+…+s_n}{t_1+t_2+…+t_n}=frac{s}{t} $$
Если тело все время движется в одном направлении, величина средней скорости равна средней путевой скорости, т.к. на каждом участке путь совпадает с модулем перемещения.
Если тело меняет направление движения, величина средней скорости меньше средней путевой скорости.
В нашем примере с велосипедистом, который все время двигался в одну сторону и дошел до города B, получаем: begin{gather*} |overrightarrow{v_{cp}}|=frac{|overrightarrow{r}|}{t}=frac{triangle x}{t}=frac 61=6 text{(км/ч)}\ v_{cp.п}=frac st=frac 61=6 text{(км/ч)} end{gather*} Величина средней скорости равна средней путевой скорости.
А вот для случая, когда велосипедист развернулся и пошел обратно: begin{gather*} |overrightarrow{v_{cp}}|=frac{|overrightarrow{r}|}{t}=frac{triangle x}{t}=frac 31=3 text{(км/ч)}\ v_{cp.п}=frac st=frac 61=6 text{(км/ч)} end{gather*} Величина средней скорости меньше средней путевой скорости.
п.4. Задачи
Задача 1. По графику скоростей найдите среднюю скорость и среднюю путевую скорость движения.
a)
Все движение можно разделить на три участка с постоянной скоростью:
begin{gather*} triangle t_1=3-0=3 c, v_{x1}=5 text{м/с}\ triangle t_2=5-3=2 c, v_{x2}=1 text{м/с}\ triangle t_3=7-5=2 c, v_{x3}=2 text{м/с}\ end{gather*} Общий путь: begin{gather*} s=|v_{x1}|cdot triangle t_1+|v_{x2}|cdot triangle t_2+|v_{x3}|cdot triangle t_3\ s=5cdot 3+1cdot 2+2cdot 2=21 text{(м)} end{gather*} Все проекции скоростей положительны, тело двигалось в одном направлении, общее перемещение равно общему пути: (triangle x=s=21) (м)
Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (с)
Величина средней скорости равна средней путевой скорости: $$ |overrightarrow{v_{cp}}|=v_{cp.п}=frac st=frac{21}{7}=3 text{(м/с)} $$ Ответ: (|overrightarrow{v_{cp}}|=v_{cp.п}=3 text{(м/с)})
б)
Все движение можно разделить на три участка с постоянной скоростью:
begin{gather*} triangle t_1=3-0=3 c, v_{x1}=5 text{м/с}\ triangle t_2=5-3=2 c, v_{x2}=-2 text{м/с}\ triangle t_3=7-5=2 c, v_{x3}=1 text{м/с}\ end{gather*} Общий путь: begin{gather*} s=|v_{x1}|cdot triangle t_1+|v_{x2}|cdot triangle t_2+|v_{x3}|cdot triangle t_3\ s=5cdot 3+2cdot 2+1cdot 2=21 text{(м)} end{gather*} Проекции скоростей имеют разные знаки, тело двигалось вперед и назад.
Общее перемещение будет меньше общего пути: begin{gather*} triangle x=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2+v_{x3}cdot triangle t_3\ triangle x=5cdot 3-2cdot 2+1cdot 2=13 text{(м)} end{gather*} Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (c)
Величина средней скорости: $$ |overrightarrow{v_{cp}}|=frac{triangle x}{t}=frac{13}{7}approx 1,86 text{(м/с)} $$ Средняя путевая скорость: $$ v_{cp.п}=frac st=frac{21}{7}=3 text{(м/с)} $$ Ответ: (|overrightarrow{v_{cp}}|approx 1,86 text{(м/с)}; v_{cp.п}=3 text{(м/с)})
Задача 2. Мотоциклист проехал расстояние между двумя пунктами со скоростью 40 км/ч. Потом увеличил скорость до 80 км/ч и проехал расстояние в два раза меньше. Найдите среднюю скорость мотоциклиста за все время движения.
Мотоциклист двигался все время в одном направлении, величина средней скорости равна средней путевой скорости: (v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 40 | (frac{2d}{40}=frac{d}{20}) | (2d) |
| 2й участок | 80 | (frac{d}{80}) | (d) |
| Сумма | – | (t=frac{d}{20}+frac{d}{80}) | (s=2d+d=3d) |
Упростим сумму дробей: $$ t=frac{d}{20}+frac{d}{80}=frac{4d+d}{80}=frac{5d}{80}=frac{d}{16} $$ Получаем: $$ v_{cp}=frac st=frac{3d}{d/16}=3cdot 16=48 text{(км/ч)} $$
Ответ: 48 км/ч
Задача 3. Автомобиль проехал первую половину пути по шоссе со скоростью 90 км/ч, а вторую половину – по грунтовой дороге со скоростью 30 км/ч. Найдите среднюю скорость автомобиля.
Величина средней скорости равна средней путевой скорости:
(v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 90 | (frac{s}{2cdot 90}=frac{s}{180}) | (frac s2) |
| 2й участок | 30 | (frac{s}{2cdot 30}=frac{s}{60}) | (frac s2) |
| Сумма | – | (t=frac{s}{180}+frac{s}{60}) | (s) |
Упростим сумму дробей: $$ t=frac{s}{180}+frac{s}{60}=frac{s+3s}{180}=frac{4s}{180}=frac{s}{45} $$ Получаем: $$ v_{cp}=frac st=frac{s}{s/45}=45 text{(км/ч)} $$
Ответ: 45 км/ч
Задача 4*. Туристы прошли по маршруту со средней скоростью 32 км/ч. Маршрут был разделен на три участка, первый участок преодолевался пешком, второй – на автобусе, третий – на катере. Найдите скорость на каждом участке, если длины этих участков относятся как 1:4:45, а соответствующие интервалы времени как 4:1:20.
Величина средней скорости равна средней путевой скорости:
(v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | (frac{d}{4t}) | (4t) | (d) |
| 2й участок | (frac{4d}{t}) | (t) | (4d) |
| 3й участок | (frac{45d}{20t}) | (20t) | (45d) |
| Сумма | – | (25t) | (50d) |
По условию средняя скорость: $$ v_{cp}=frac st=frac{50d}{25t}=2cdot frac dt=32Rightarrow frac dt=16 $$ Получаем: begin{gather*} v_1=frac{d}{4t}=frac{16}{4}=4 text{(км/ч)}\ v_2=frac{4d}{t}=4cdot 16=64 text{(км/ч)}\ v_3=frac{9d}{4t}=frac{9}{4}cdot 16=36 text{(км/ч)} end{gather*}
Ответ: 4 км/ч, 64 км/ч и 36 км/ч
Задача 5*. Первую половину маршрута турист проехал на попутном автомобиле в 10 раз быстрее по сравнению с ходьбой пешком, а вторую половину – на попутном возу в 2 раза медленней. Сэкономил ли турист время на всем маршруте по сравнению с ходьбой пешком?
Пусть (v) – скорость туриста при ходьбе пешком.
Найдем среднюю путевую скорость (v_{cp}) и сравним ее со скоростью (v).
Если (v_{cp}gt v), то турист выиграл время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | (10v) | (frac{s}{2cdot 10v}=frac{s}{20v}) | (frac s2) |
| 2й участок | (frac{v}{2}) | (frac{s}{2cdot v/2}=frac sv) | (frac s2) |
| Сумма | – | (t=frac{s}{20v}+frac sv) | (s) |
Упростим сумму дробей: $$ t=frac{s}{20v}+frac sv=frac svleft(frac{1}{20}+1right)=frac{21}{20}cdot frac sv $$ Средняя скорость: $$ v_{cp}=frac{s}{frac{21}{20}cdotfrac sv}=frac{20}{21}vgt v $$Средняя скорость поездки оказалась меньше пешей скорости туриста.
Значит, он не выиграл по времени.
Ответ: нет
п.5. Лабораторная работа №3. Определение средней скорости движения тела
Цель работы
Научиться определять среднюю скорость движения тела по данным измерений на разных участках. Научиться вычислять абсолютные и относительные погрешности при подстановке данных измерений в формулы.
Теоретические сведения
В лабораторной работе изучается движение тела (шарика) по двум участкам (желобам) с различной скоростью.
Величина средней скорости при движении на двух участках определяется как средняя путевая скорость: $$ v_{cp}=frac{s_1+s_2}{t_1+t_2} $$ где (s_1) и (s_2) – длина первого и второго участка; (t_1) и (t_2) – время движения по каждому из участков.
Длина участков измеряется с помощью мерной ленты с ценой деления (triangle=1) см,
инструментальная погрешность равна: (d=frac{triangle}{2}=0,5) см
Абсолютная погрешность измерений при работе с мерной лентой равна инструментальной погрешности, поэтому: (triangle s_1=triangle s_2=d=0,5) см
Погрешность суммы двух длин: (triangle(s_1+s_2)= triangle s_1+triangle s_2=2d=1) см
Измерение времени на каждом участке проводится в сериях их 5 измерений по методике, описанной в Лабораторной работе №2 (см. §4 данного справочника).
Погрешность суммы двух измерений: (triangle(t_1+t_2)=triangle t_1+triangle t_2)
Относительная погрешность частного равна сумме относительных погрешностей делимого и делителя: $$ delta_{v_{cp}}=delta_{s_1+s_2}+delta_{t_1+t_2} $$ Абсолютная погрешность определения средней скорости: $$ triangle v_{cp}=v_{cp}cdot delta_{v_{cp}} $$
Приборы и материалы
Два желоба (не менее 1 м каждый), шарик, мерная лента, секундомер.
Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Соберите установку, как показано на рисунке. Установите один желоб под углом, другой – горизонтально, закрепите, поставьте в конце горизонтального участка упор. Подберите длину желобов и наклон так, чтобы движение по каждому участку было не менее 1 с. 
3. Измерьте фактическую длину каждого участка движения в готовой установке с помощью мерной ленты.
4. Найдите относительную погрешность суммы двух длин (delta_{s_1+s_2}=frac{triangle(s_1+s_2)}{s_1+s_2})
5. Проведите серии по 5 экспериментов для определения (t_1) и (t_2) с помощью секундомера.
6. Найдите (triangle t_1, triangle t_2, triangle(t_1+t_2), delta_{t_1+t_2})
7. По результатам измерений и вычислений найдите (v_{cp}, delta_{v_{cp}}) и (triangle v_{cp}).
8. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
1) Измерение длин
Цена деления мерной ленты (triangle =1) см
Инструментальная погрешность мерной ленты (d=frac{triangle}{2}=0,5) см
Результаты измерений:
(s_1=112) cм
(s_2=208) cм
Сумма длин участков: (s_1+s_2=112+208=320) (см)
Абсолютная погрешность суммы: (triangle (s_1+s_2)=triangle s_1+triangle s_2=2d=1) см
Относительная погрешность суммы: $$ delta_{s_1+s_2}=frac{triangle (s_1+s_2)}{s_1+s_2}=frac{1}{320}=0,3125% $$
2) Измерение времени
Цена деления секундомера (triangle =0,2) с
Инструментальная погрешность секундомера (d=frac{triangle}{2}=0,1) с
Время движения по наклонному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t_1) c | 1,5 | 1,6 | 1,5 | 1,4 | 1,4 | 7,4 |
| (triangle) c | 0,02 | 0,12 | 0,02 | 0,08 | 0,08 | 0,32 |
Найдем среднее время спуска с наклонного желоба: $$ t_1=frac{1,5+1,6+1,5+1,4+1,4}{5}=frac{7,4}{5}=1,48 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_1): $$ triangle_1=|1,5-1,48|=0,02; triangle_2=|1,6-1,48|=1,02 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0,02+0,12+0,02+0,08+0,08}{5}=frac{0,32}{5}=0,064 text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_1=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,064right}=0,1 text{c} $$ Округляем полученное значение времени до десятых. begin{gather*} t_1=(1,5pm 0,1) text{c}\ delta_{t_1}=frac{0,1}{1,5}=frac{1}{15}approx 6,7text{%} end{gather*} Время движения по горизонтальному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t_2) c | 2,3 | 2,4 | 2,2 | 2,2 | 2,4 | 11,5 |
| (triangle) c | 0 | 0,1 | 0,1 | 0,1 | 0,1 | 0,4 |
Найдем среднее время движения по горизонтали: $$ t_2=frac{2,3+2,4+2,2+2,2+2,4}{5}=frac{11,5}{5}=2,3 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_2): $$ triangle_1=|2,3-2,3|=0; triangle_2=|2,4-2,3|=0,1 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0+0,1+0,1+0,1+0,1}{5}=frac{0,4}{5}=0,08 text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_2=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,08right}=0,1 text{c} $$ Получаем: begin{gather*} t_2=(2,3pm 0,1) text{c}\ delta_{t_2}=frac{0,1}{2,3}=frac{1}{23}approx 4,4text{%} end{gather*}
3) Расчет погрешности суммы интервалов времени
Сумма интервалов времени: $$ t_1+t_2=1,5+2,3=3,8 text{(c)} $$ Абсолютная погрешность суммы: $$ triangle(t_1+t_2)=triangle t_1+triangle t_2=0,1+0,1=0,2 text{(c)} $$ Относительная погрешность суммы: $$ delta_{t_1+t_2}=frac{triangle (t_1+t_2)}{t_1+t_2}=frac{0,2}{3,8}=frac{1}{19}approx 5,3text{%} $$
4) Расчет средней скорости $$ v_{cp}=frac{s_1+s_2}{t_1+t_2}=frac{320}{3,8}approx 84,2 left(frac{text{см}}{text{c}}right) $$ Относительная ошибка частного: $$ delta_{v_{cp}}=delta_{s_1+s_2}+delta_{t_1+t_2}=frac{1}{320}+frac{1}{19}approx 0,003125+0,0526approx 0,0557approx 0,056=5,6text{%} $$ (оставляем две значащие цифры).
Абсолютная ошибка: $$ v_{cp}=v_{cp}cdotdelta_{v_{cp}}=84,2cdot 0,056approx 4,7 left(frac{text{см}}{text{c}}right) $$ Получаем: begin{gather*} v_{cp}=(84,2pm 4,7) text{см/с}\ delta_{v_{cp}}=5,6text{%} end{gather*}
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения длин проводились с помощью мерной ленты. Ошибка измерений равна инструментальной ошибке 0,5 см.
Измерения времени проводились с помощью секундомера. По результатам серий экспериментов ошибка была принята равной инструментальной 0,1 с.
Получена величина средней скорости: begin{gather*} v_{cp}=(84,2pm 4,7) text{см/с}\ delta_{v_{cp}}=5,6text{%} end{gather*}
Средняя путевая скорость

4.6
Средняя оценка: 4.6
Всего получено оценок: 166.
Обновлено 30 Июля, 2021
4.6
Средняя оценка: 4.6
Всего получено оценок: 166.
Обновлено 30 Июля, 2021
Из курса физики в 10 классе известно, что быстрота движения характеризуется такой величиной, как скорость. При этом скорость может быть мгновенной, а может быть средней. Средняя скорость, в свою очередь, может рассчитываться по перемещению, а может по пройденному пути. Рассмотрим понятие средней скорости, получим формулу средней путевой скорости.
Мгновенная и средняя скорость
Скорость движения материальной точки — это физическая величина, характеризующая быстроту движения и равная отношению пройденной длины ко времени, за которое эта длина была пройдена:
$$v={Δl over Δt}$$
Поскольку длина в системе СИ измеряется в метрах, а время — в секундах, то скорость измеряется в метрах в секунду.
Наиболее точной является мгновенная скорость, то есть такая скорость, при которой величина $Δt$ стремится к нулю. При этом получающееся значение скорости $v$ может быть постоянным, а может меняться в каждой точке пройденного пути.
Вычисление мгновенной скорости позволяет моделировать движение материальной точки наиболее детально. Однако в реальных условиях настолько большая точность чаще всего не требуется. Как правило, важно, чтобы движение было совершено к определённому моменту времени, а как именно это произошло — не имеет значения.
В этом случае используется понятие средней скорости. Средняя скорость отличается от мгновенной тем, что для вычисления используется сразу весь отрезок времени. Величина $Δt$ в приведённой формуле равна общему времени движения:
$$v_{ср}={l_{общ} over t_{общ}}$$
Средняя путевая скорость
В приведённой формуле числитель (величина $l_{общ}$) может быть рассчитан по-разному.
Во-первых, эта величина может быть равна разности координат в начале и в конце пути. В этом случае мы получаем вектор перемещения $overrightarrow {Δx}$, полученное значение средней скорости также будет вектором $overrightarrow {v_{ср}}$, направленным в ту же сторону.
Во-вторых, эта величина может быть равна длине траектории движения. В этом случае мы получаем пройденный путь $S$. Это скалярная величина, и значение средней скорости $v_{ср}$ также получается скаляром.
Как правило, в физике, когда говорят о средней скорости, имеют в виду первый случай — среднюю скорость по перемещению. В бытовом же обиходе чаще используется длина пройденного пути, и говорят о средней путевой скорости.
Использование средней путевой скорости удобно потому, что затраты на движение (и материальные, и временные), как правило, зависят именно от длины пройденного пути, а не от перемещения. Расстояние между начальным и конечным пунктом по прямой (это и есть перемещение) может быть значительно меньше пути между этими пунктами. Но если нам задана средняя скорость движения транспортного средства, то для нахождения времени прибытия мы должны исходить именно из путевой средней скорости, поскольку при движении будет пройдена вся траектория пути.
Отсюда можно сделать важный вывод — средняя путевая скорость, как правило, больше средней скорости по перемещению (при одинаковом времени). Эти две скорости могут быть равны, только если траектория пути представляет собой прямую.
Ещё одно важное отличие — скалярный характер средней путевой скорости. Зная координаты начального пункта, время пути и вектор средней скорости по перемещению, мы можем найти координаты конечного пункта. Если же известна средняя путевая скорость, то мы можем указать лишь круг (или сферу в трёхмерном пространстве), в пределах которого находится конечный пункт: точные его координаты по средней путевой скорости установить невозможно.
Что мы узнали?
Средняя путевая скорость — это величина, равная отношению пути, пройденного материальной точкой, ко время его прохождения. В формуле средней путевой скорости в качестве расстояния используется длина траектории. Средняя путевая скорость удобна для определения затрат, материальных и временных, на движение.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 166.
А какая ваша оценка?
Физическое понятие «скорость» является неоднозначным термином: зависимость от расстояния и времени позволяет ввести два понятия скорости, так как в физике используются векторные (перемещение) и скалярные (модуль перемещения, пройденный путь, время) величины.
1. Отношение вектора перемещения (vec{S}) к интервалу времени (Delta{t}) определяет среднюю (по времени) скорость:
(vec{v}_{ср}=frac{vec{S}}{Delta{t}}) ((1)).
-
Направление вектора средней (по времени) скорости определяется согласно математической формуле ((1)) определения данной физической величины (сравни математическое выражение (vec{a}) (=) (frac{vec{b}}{2}) и формулу ((1))):
Длина вектора (vec{v}_{ср}) не связана с длиной вектора (vec{S}), так как данные физические величины имеют разные размерности (единицы измерения).
-
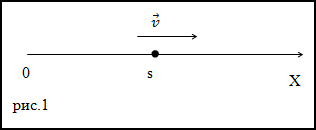
Числовое значение данной физической величины в случае равномерного прямолинейного движения является постоянным (рис. (1)):
υx=const
.
Примечание: «const» — «постоянный» (сокращение от латинского).
Рис. (1). Изменение координаты точки при равномерном движении
2. При движении тела с постоянной скоростью и его возврате в исходное положение с той же скоростью значение средней (по времени) скорости будет равно нулю.
Отношение пути (l) (длины траектории) к интервалу времени (Delta{t}) определяет средний модуль скорости (среднюю путевую скорость):
(overline{v}=frac{l}{Delta{t}}) ((2)).
Обозначение: черта над символом ((overline{v})) обозначает среднее значение этой величины.
Именно физическое понятие «средняя путевая скорость» используется при описании движения в ситуациях следующего типа: «спортсмен/турист… пробежал/прошёл… дистанцию/расстояние… со средней скоростью <…> м/с».
Источники:
Рис. 1. Изменение координаты точки при равномерном движении. © ЯКласс.
Содержание:
- Определение и формула средней скорости
- Вектор средней скорости
- Единицы измерения
- Примеры решения задач
Определение и формула средней скорости
Определение
Средней путевой скоростью материальной точки на отрезке времени
$Delta t$называется скалярная физическая величина, равная отношению
длины пути, пройденного точкой к промежутку времени, в течение которого данный путь пройден. Среднюю скорость обозначают:
$$langle vrangle, bar{v}, v_{s r}$$
Математически определение средней скорости можно записать в следующем виде:
$$langle vrangle(t+Delta t)=frac{Delta s}{Delta t}=frac{s(t+Delta t)-s(t)}{Delta t}(1)$$
где $Delta s=s(t+Delta t)-s(t)$ – длина пути, которую прошла точка за время
$Delta t$.
Если перейти к пределу при $Delta t rightarrow 0$ , получим:
$$lim _{Delta t rightarrow 0}langle vrangle=lim _{Delta t rightarrow 0} frac{Delta s}{Delta t}=frac{d s}{d t}=v(t)(2)$$
средняя путевая скорость в пределе совпадает с величиной (модулем) мгновенной скорости точки в момент времени t.
При равномерном движении:
$$langle vrangle=v(3)$$
Вектор средней скорости
Определение
Вектором средней скорости $langlevec{v}rangle$ материальной точки на
отрезке времени $Delta t$называют величину, равную приращению радиус-вектора,
который определяет положение данной точки к промежутку времени $Delta t$:
$$langlebar{v}rangle(t+Delta t)=frac{Delta bar{r}}{Delta t}=frac{bar{r}(t+Delta t)-bar{r}(t)}{Delta t}(4)$$
где $Delta bar{r}$ – приращение радиус-вектора материальной точки.
Вектор средней скорости в пределе при $Delta t rightarrow 0$ совпадает с вектором скорости в момент времени t:
$$lim _{Delta t rightarrow 0}langlebar{v}rangle=lim _{Delta t rightarrow 0} frac{Delta bar{r}}{Delta t}=frac{d bar{r}}{d t}=bar{v}(t)(5)$$
где $bar{v}(t)$ – вектор мгновенной скорости токи.
Если точка совершает равномерное и прямолинейное движение, то выполняется равенство:
$$langlebar{v}rangle=bar{v}(6)$$
Средняя путевая скорость и модуль вектора средней скорости равны
$(langle vrangle=|langlebar{v}rangle|)$ только при прямолинейном движении.
При всех остальных видах движения выполняется неравенство:
$$langle vrangle>|langlebar{v}rangle|(7)$$
Единицы измерения
Основной единицей измерения средней скорости в системе СИ является: м/с
В СГС: см/с
Примеры решения задач
Пример
Задание. Какова средняя скорость материальной точки за время ее движения, если точка прошла первую половину
пути имея скорость v1, остальную часть пути данная точка 1/2 времени двигалась со скоростью v2, последний
участок пути точка двигалась со скоростью v3.
Решение. В качестве основы для решения задачи формулу:
$$langle vrangle=frac{s}{Delta t}(1.1)$$
где время потраченное на путь ($Delta t$) делится на три части:
$$Delta t=t_{1}+t_{2}+t_{3}(1.2)$$
При этом имеют место следующие соотношения между отрезками пути, скоростью их преодоления и временем:
$$left{begin{array}{c}frac{1}{2} s=v_{1} t_{1} rightarrow t_{1}=frac{s}{2 v_{1}} \ frac{1}{2} s=v_{2} t_{2}+v_{3} t_{3} rightarrow t_{3}=frac{s}{2left(v_{2}+v_{3}right)}(1.3) \ t_{2}=t_{3}=frac{1}{2} tend{array}right.$$
$$langle vrangle=frac{2 v_{1}left(v_{2}+v_{3}right)}{v_{2}+v_{3}+2 v_{1}}$$
Ответ. $langle vrangle=frac{2 v_{1}left(v_{2}+v_{3}right)}{v_{2}+v_{3}+2 v_{1}}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какова средняя скорость частицы, движущейся по оси Xза время в течение которого, она пройдет первые
s метров пути, если функция скорости задана уравнением: $v=A sqrt{x}$,
где A=const>0. Считать, что x=0 при t=0.
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для средней путевой скорости, так как движение прямолинейное,
то средняя путевая скорость равна модулю вектора средней скорости. По условию задачи точка движется по оси X, тогда:
$$langle vrangle(t+Delta t)=frac{Delta x}{Delta t}(2.1)$$
По условиям x(t=0)=0, среднюю скорость ищем, когда тело находится в точкеx=sследовательно, выражение (2.1) преобразуем к виду:
$$langle vrangle=frac{s}{t}(2.2)$$
Найдем зависимость скорости от времени, исходя из определения мгновенной скоростидля движения точки по оси X:
$$v=frac{d x}{d t}=A sqrt{x}(2.3)$$
Выразим из (2.2) x:
$$frac{d x}{sqrt{x}}=A d t rightarrow x=frac{A^{2} t^{2}}{4}(2.4)$$
Так как движение происходит по оси X, то $x=s=frac{A^{2} t^{2}}{4}$ . Выразим время, которое точка затратила на путьs :
$$t=frac{2 sqrt{s}}{A}(2.5)$$
Подставим время из (2.4) в формулу (2.2):
$$langle vrangle=frac{A}{2} sqrt{s}$$
Ответ. $langle vrangle=frac{A}{2} sqrt{s}$
Читать дальше: Формула угловой скорости.