поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,655 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,939 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Условие задачи:
Аквариум наполнен доверху водой. С какой средней силой давит вода на стенку аквариума длиной 50 см и высотой 30 см?
Задача №3.2.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(a=50) см, (h=30) см, (P_{ст}-?)
Решение задачи:
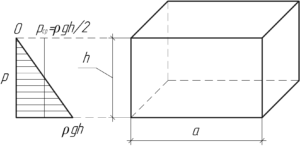 Так как давление – это сила, действующая на единицу площади, то искомую силу (P_{ст}) можно найти по формуле:
Так как давление – это сила, действующая на единицу площади, то искомую силу (P_{ст}) можно найти по формуле:
[{P_{ст}} = {p_{ст}}{S_{ст}};;;;(1)]
Давление воды линейно зависит от давления: на уровне поверхности оно равно нулю, на уровне дна аквариума – величине (rho gh). Поэтому среднее давление на стенку аквариума можно найти таким образом:
[{p_{ст}} = rho gfrac{h}{2};;;;(2)]
Так как аквариум заполнен доверху, то площадь боковой стенки, на которую давит вода, равна:
[{S_{ст}} = ah;;;;(3)]
Подставим (2) и (3) в (1), получим:
[{P_{ст}} = rho gfrac{h}{2}ah]
[{P_{ст}} = rho gfrac{{a{h^2}}}{2}]
Переведем геометрические размеры аквариума в систему СИ:
[50;см = frac{{50}}{{100}};м = 0,5;м]
[30;см = frac{{30}}{{100}};м = 0,3;м]
Численно сила давления на стенку аквариума равна:
[{P_{ст}} = 1000 cdot 10 cdot frac{{0,5 cdot {{0,3}^2}}}{2} = 225;Н]
Ответ: 225 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.2.4 Аквариум имеет форму куба со стороной 0,6 м. До какой высоты следует налить в него
3.2.6 В сосуд, имеющий форму прямоугольной призмы, шириной 15 см и длиной 35 см налита
3.2.7 На сколько отличается давление столбика ртути высотой 10 мм от давления столбика
Формула давления на дно и стенки сосуда
Давление жидкости обусловлено ее весом и, соответственно сила этого давления F равна весу жидкости P. Вес жидкости можно определить, зная ее массу m. А массу можно вычислить по формуле: m=ρV. Объем жидкости в прямоугольном сосуде легко рассчитать. Обозначим высоту сосуда h, а площадь дна буквой S. Тогда объем будет равен: V=Sh. Формула массы в таком случае принимает вид: m=ρV=ρSh . Вес жидкости будет равен: P=gm=gρSh. чтобы рассчитать давление, нам нужна сила этого давления. А мы уже говорили, что сила давления в данном случае равна весу жидкости, поэтому формула давления принимает следующий вид:
Формула для этого давления в атмосфере. Кроме того, поскольку давление представляет собой силу на единицу измерения площади, то. Чтобы рассчитать давление через инструмент барометра, можно было бы заменить объем ртути в барометре в уравнение. Это дало бы уравнение. Вероятно, метеоролог даст атмосферное давление или барометрическое давление в 30 дюймов. Он состоит из длинной трубки, закрытой на одном конце, заполненной ртутью и перевернутой в сосуде с ртутью. На уровне моря сила атмосферного давления будет поддерживать колонку с содержанием ртути 760 мм в высоту.
p=P/S=gρSh/S или p=gρh
То есть в итоге мы пришли к очень интересному моменту – давление не зависит от объема и формы сосуда. Оно зависит только от плотности и высоты столба конкретной жидкости в данном случае. Из чего следует, что, увеличив высоту сосуда, мы можем при небольшом объеме создать довольно высокое давление.
Для давления газа на дно и стенки сосуда формула будет иметь точно такой же вид.
Простые приложения, связанные с давлением
Фактически вес столба ртути равен силе атмосферного давления. Подобным же образом атмосферное давление заставляет воду в подобной колонне высотой до 34 футов! После запуска атмосферное давление на поверхность верхнего контейнера заставляет воду за короткую трубу заменить воду, вытекающую из длинной трубки.
- Фактически это приводит к снижению давления воздуха внутри соломы.
- Сифон можно запустить, заполнив трубку водой.
Наблюдения Бойля можно суммировать в утверждении: при постоянной температуре объем газа изменяется обратно пропорционально давлению, оказываемому на него.
Применение давления на дно и стенки сосуда
Еще один интересный момент заключается в том, что согласно закону Паскаля давление распределяется равномерно не только на дно и стенки, но и в направлении вверх. То есть, если мы погрузим какое-либо тело на определенную глубину, то на него снизу будет действовать сила, равная силе давления на данной глубине, как бы выталкивая тело на поверхность. Именно благодаря этому явлению возможно плавание кораблей. Несмотря на довольно внушительный вес, вода выталкивает судно вследствие эффекта давления воды на стенки сосуда, которыми в данном случае являются борта корабля. С понижением глубины давление увеличивается. Люди научились использовать это явление
, делая борта кораблей в форме сужающихся вниз конусов. Именно поэтому нас доступно покорение морей и океанов.
Кинетическая молекулярная теория Пояснение
Наблюдения за давлением можно объяснить, используя следующие идеи. Быстрое движение и столкновения молекул со стенками контейнера вызывает давление. Давление пропорционально числу молекулярных столкновений и силе столкновений в определенной области. Чем больше столкновений молекул газа со стенками, тем выше давление.
В 17 веке Роберт Бойл впервые сформулировал связь между давлением, объемом и температурой, поскольку они связаны с газом по формуле. Эта формула была результатом его экспериментов с газом, и, как он заметил, газ имел тенденцию к изменению давления, когда он занимал контейнеры различного размера.
А что по поводу давления газов?
Что касается газов, то для них расчет будет абсолютно таким же. Соответственно, наибольший вес окружающего нас газа – воздуха, будет у поверхности Земли. А с увеличением высоты будет уменьшаться как среднее давление, так и плотность окружающего газа. Поэтому воздух на высоте очень разреженный. Там очень трудно как дышать, так и летать, потому что крыльям самолетов не на что опираться. Именно поэтому набирать очень большую высоту летательные аппараты могут только на очень высокой скорости, увеличивая таким образом количество воздуха под крылом в единицу времени.
Эта связь часто упоминается как Закон Бойля. Кроме того, Бойл отметил, что газы имеют тенденцию «возвращаться» к его первоначальному давлению после удаления из контейнера, в котором он либо был сжат, либо расширен. Общая разница в высоте напрямую коррелировала с давлением атмосферы.
Бойл проиллюстрировал это через формула. Рон Куртус. Давление – это сила на объекте, который распространяется по поверхности. Уравнение для давления – это сила, деленная на область, где применяется сила. Хотя это измерение является простым, когда твердое тело надавливает на твердое тело, корпус твердого тела, нажимая на жидкость или газ, требует, чтобы жидкость была ограничена в контейнере.
Нужна помощь в учебе?
Предыдущая тема: Давление в жидкости и газе
Следующая тема: Сообщающиеся сосуды
В соответствии с законом Паскаля
гидростатическое давление на уровне
горизонтального дна сосуда при высоте
жидкости в сосуде, равной Н
,
Сила также может быть создана весом объекта. Вопросы, которые могут возникнуть, включают.
- Какое давление, когда твердое тело подталкивает другое твердое тело?
- Что происходит, когда твердое тело нажимает на ограниченную жидкость?
- Что происходит, когда сила исходит из гравитации?
Этот урок ответит на эти вопросы.
Когда вы применяете силу к твердому объекту, давление определяется как прилагаемое усилие, деленное на область применения. Вы можете видеть, что при заданной силе, если площадь поверхности меньше, давление будет больше. Если вы используете большую область, вы распространяете силу, и давление становится меньше.
Отсюда следует, что абсолютное давление
р
на горизонтальное дно не зависит
от формы сосуда и объема жидкости в нем.
При данной плотности жидкости оно
определяется лишь высотой столба
жидкостиН
и внешним давлениемр
0 .
Сила давления жидкости Р
ж на
дно сосуда зависит от его площадиF
:
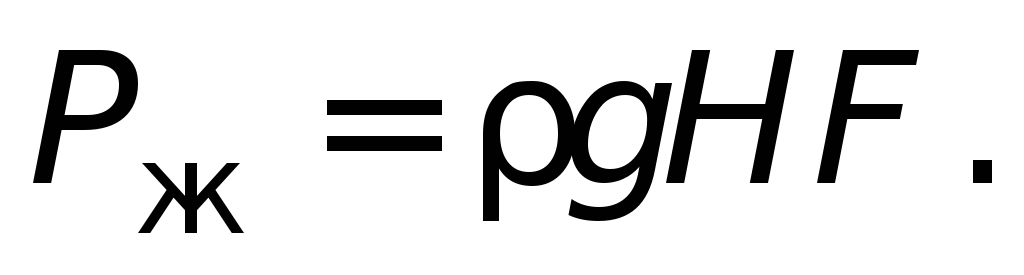 (1.8)
(1.8)
Твердое прессование на ограниченной жидкости
Когда жидкость или газ заключены в контейнер или цилиндр, вы можете создать давление, применяя усилие с помощью твердого поршня. В ограниченной жидкости – пренебрегая влиянием силы тяжести на жидкость – давление одинаково во всем контейнере, одинаково нажимая на все стенки. В случае велосипедного насоса давление, создаваемое внутри насоса, будет передаваться через шланг в велосипедную шину. Но воздух все еще ограничен.
Увеличение силы увеличит давление внутри цилиндра. Поскольку вес объекта является силой, вызванной гравитацией, мы можем заменить вес в уравнении давления. Таким образом, давление, вызванное весом объекта, – это вес, разделенный на область, где применяется вес.
Общая сила давления на дно сосуда
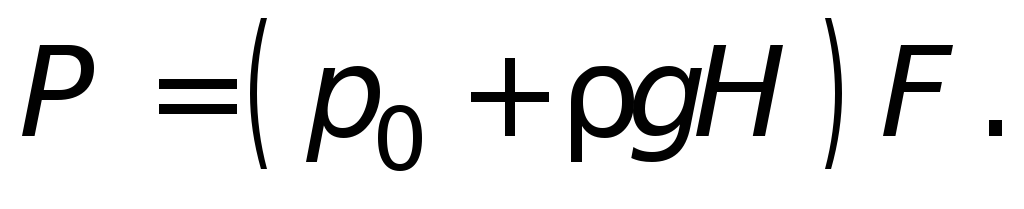 (1.9)
(1.9)
Внешнее давление р 0 передается
жидкостью каждому элементу поверхности
стенки одинаково, поэтому равнодействующая
внешнего давления приложена в точке
центра тяжести поверхности стенки.
Давление веса жидкости на стенку не
одинаково по высоте: чем глубже расположен
элемент стенки, тем большее давление
веса жидкости он испытывает. Поэтому
центр давления жидкости на вертикальную
стенку расположен всегда ниже центра
тяжести смоченной поверхности стенки.
Если вы помещаете твердый предмет на пол, давление на пол над областью контакта – это вес предмета, разделенного областью на полу. Хороший пример того, как сила на небольшой площади может привести к очень сильному давлению, наблюдается в обуви женщин с высокими шипами. Эти типы обуви могут нанести ущерб некоторым полам из-за очень высокого давления на пол на каблук.
Средний ботинок распределяет вес человека более 20 квадратных дюймов. В некоторых случаях этого достаточно, чтобы повредить пол. Если вы положите жидкость в контейнер, вес этой жидкости будет нажимать на дно контейнера, аналогичную весу твердого объекта. Давление на дно контейнера будет таким же, как если бы вес был из твердого вещества.
Сила полного гидростатического давления
на плоскую стенку равна произведению
гидростатического давления в центре
тяжести этой стенки и ее площади:
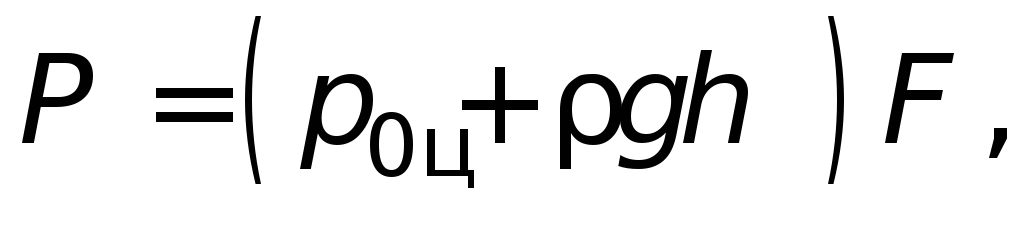 (1.10)
(1.10)
где
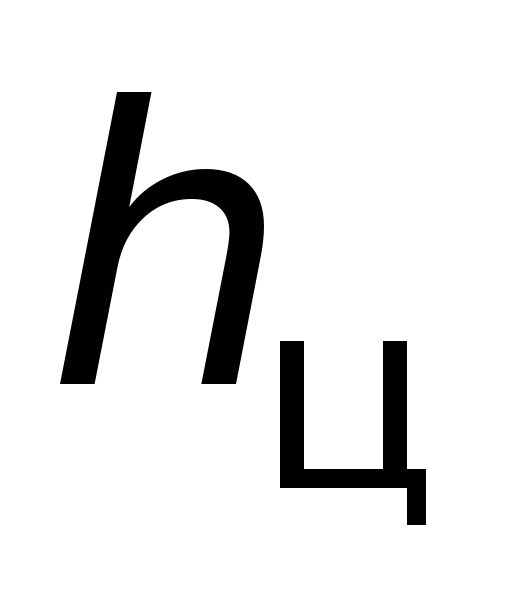 – расстояние от верхнего уровня жидкости
– расстояние от верхнего уровня жидкости
до центра тяжести смоченной поверхности
стенки; оно зависит от геометрической
формы стенки.
Единственное различие заключается в том, что давление в жидкости идет во все стороны. Таким образом, давление на сторонах внизу будет одинаковым. Газы и жидкости проявляют давление из-за их веса в каждой точке жидкости. Давление может быть измерено для твердого тела, нажимая на твердое тело, но в случае твердого тела, нажимающего на жидкость или газ, требуется, чтобы жидкость была ограничена в контейнере. Надавите на себя, чтобы преуспеть.
Самые популярные книги по физике силы. Если да, отправьте электронное письмо с отзывами. Пожалуйста, включите его в качестве ссылки на свой сайт или в качестве ссылки в своем отчете, документе или тезисе. Участники, подверженные воздействию осесимметричных нагрузок.
Точка приложения сил Р
иР
изб носит название центра давленияh
д и может быть определена в соответствии
с законами теоретической механики через
момент инерции смоченной поверхности
стенки
Тонкостенный цилиндр под давлением. Преамбула: сосуды высокого давления чрезвычайно важны в промышленности. Обычно в обычной практике используются два типа сосудов высокого давления, такие как цилиндрический сосуд высокого давления и сферический сосуд высокого давления.
При анализе этих стеновых цилиндров, подвергнутых внутренним давлениям, предполагается, что радиальные планы остаются радиальными, а доза толщины стенки не изменяется из-за внутреннего давления. Далее, при анализе их стеновых цилиндров, вес жидкости считается пренебрежимым.
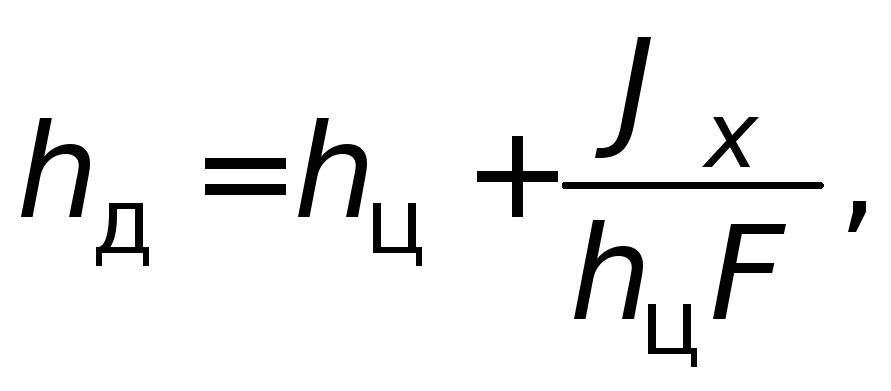 (1.11)
(1.11)
где J
x
– момент инерции
стенки относительно осиox
.
Для прямоугольной стенки при уровне
жидкости в сосуде, равном Н
, и ширине
стенкиВ
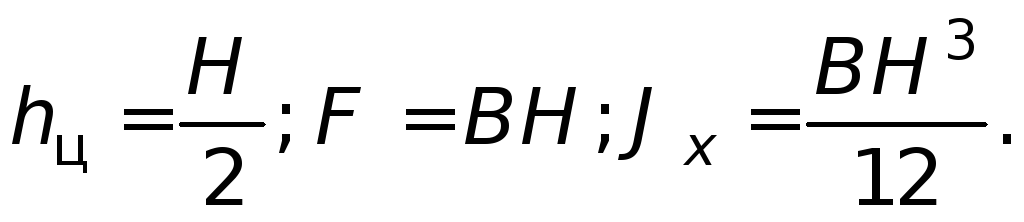
Следовательно,
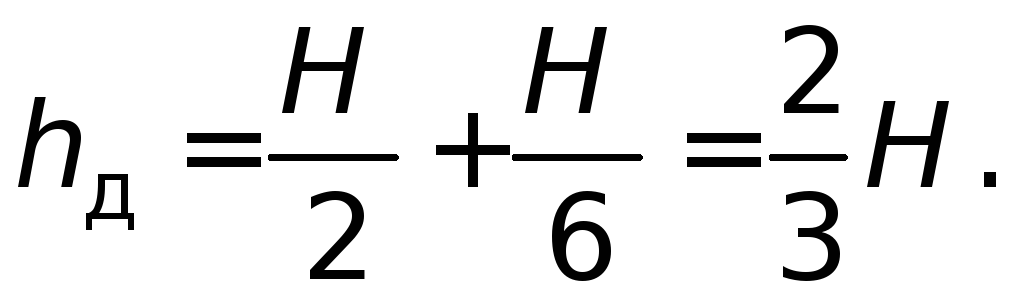
Этот цилиндр подвергается разности гидростатического давления р между его внутренней и внешней поверхностями. Во многих случаях р между давлением избыточного давления внутри цилиндра, заставляя внешнее давление быть окружающим. Небольшой кусок стенки цилиндра показан изолированно, а напряжения в соответствующем направлении также показаны.
Такой компонент не срабатывает, поскольку при чрезмерно высоком внутреннем давлении. Хотя это может потерпеть неудачу, разрываясь по пути, следующему окружности цилиндра. При нормальных обстоятельствах он терпит неудачу по обстоятельствам, которые он терпит неудачу, разрываясь вдоль пути, параллельного оси. Это говорит о том, что напряжение пялец значительно выше, чем осевое напряжение.
-
Практическое использование законов гидростатики
Применив закон Паскаля к сообщающимся
сосудам, можно прийти к следующим
выводам.
Если сосуды (рис. 1.4 а
) заполнены
однородной жидкостью (одинаковой
плотности), то при равновесии давление
в точке 0 может быть выражено:
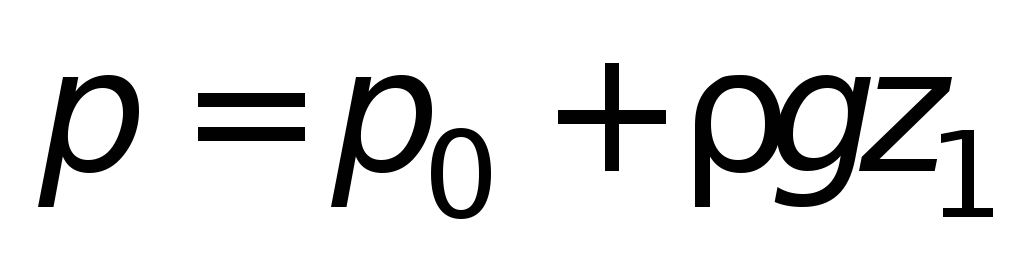 либо
либо
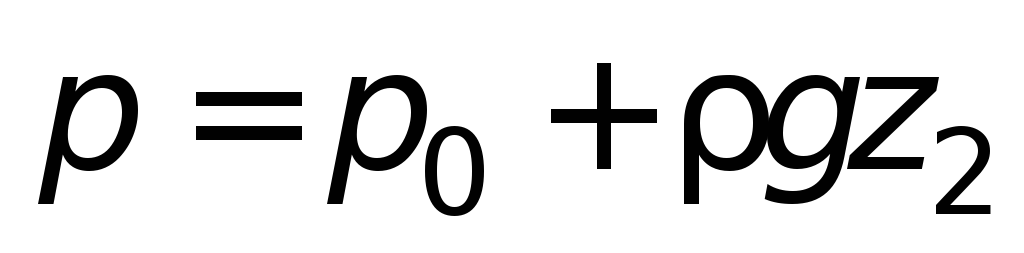 ,
,
Чтобы получить выражения для различных напряжений, сделаем следующее. Жидкие резервуары и емкости для хранения, водопроводные трубы, котлы, корпуса подводных лодок и некоторые компоненты воздушной плоскости являются общими примерами тонкостенных цилиндров и сфер, куполов крыши.
В стенке нет напряжений сдвига. Продольные и пястные напряжения не меняются через стену. Состояние выноса для элемента тонкостенного сосуда высокого давления считается двухосным, хотя внутреннее давление, действующее нормали к стене, вызывает локальное напряжение сжатия, равное внутреннему давлению. На самом деле состояние трехосевого напряжения существует на внутри судна. Однако для тогдашнего стенного сосуда давления третье напряжение намного меньше, чем два других напряжения, и по этой причине в этом можно пренебречь.
т.е. в сообщающихся сосудах заполняющая
их однородная жидкость располагается
на одинаковом уровне.
При заполнении сосудов жидкостями с
различной плотностью (рис 1.4 б
) в
условиях равновесия давление в точке
О будет
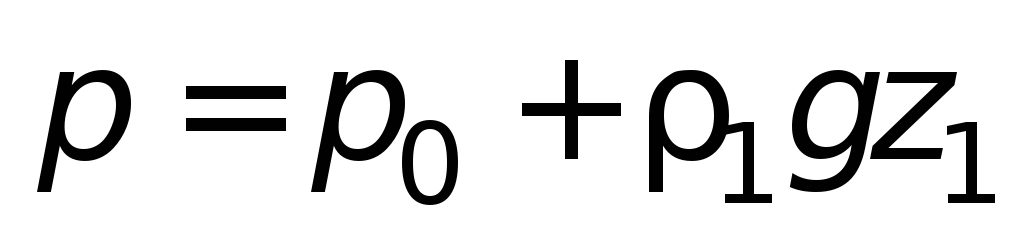 либо
либо
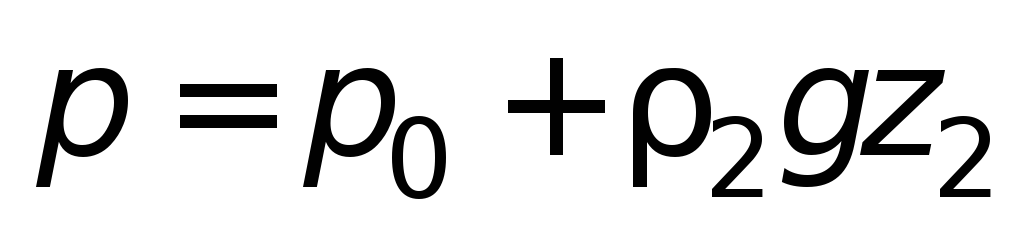 .
.
Тонкие цилиндры, подверженные внутреннему давлению. Когда тонкостенный цилиндр подвергается внутреннему давлению, в материалах цилиндра будут установлены три взаимно перпендикулярных главных напряжения, а именно. Окружность или шероховатость. Теперь определим эти напряжения и определим выражения для них.
Обруч или периферический стресс. Это напряжение, которое создается в противодействии разрушающему эффекту приложенного давления и может быть наиболее удобно обрабатываться с учетом равновесия цилиндра. На рисунке мы показали одну половину цилиндра. Общее усилие на одной половине цилиндра из-за внутреннего давления р.
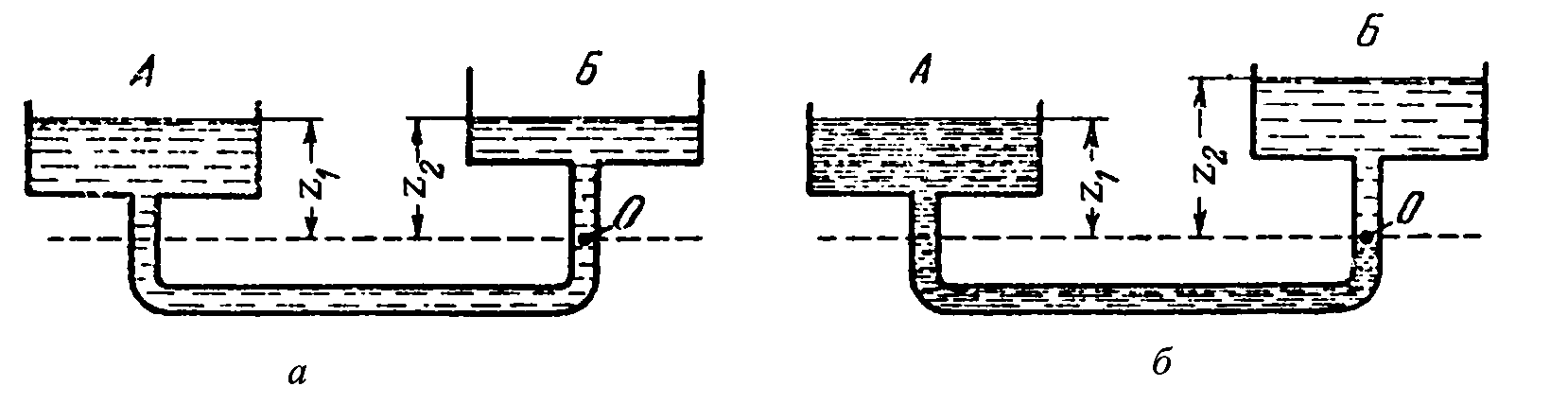
Рисунок 1.4
– Сообщающиеся сосуды, заполненные
жидкостью:
а
– одной плотности;б
– разной плотности
Следовательно
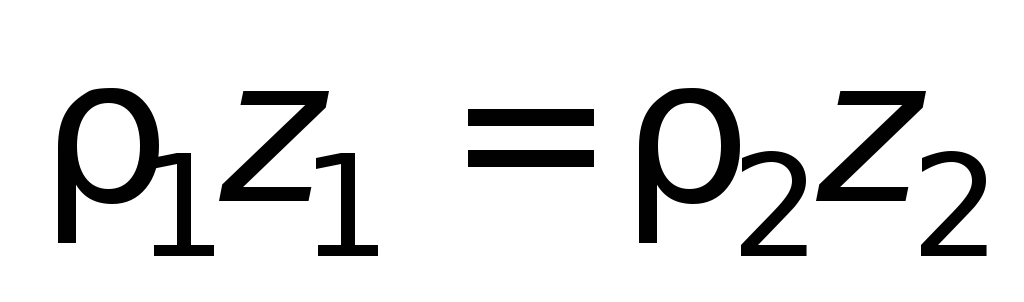 ,
,
т.е.
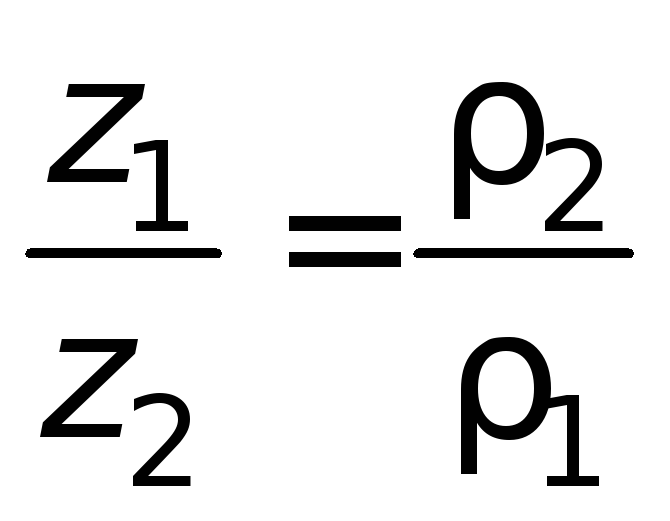 . (1.12)
. (1.12)
Т. – сила в одной стенке полуцилиндра. Требования к сложным системам автоматизированной обработки, потребность во все более жестком управлении технологическими процессами и все более строгая нормативная среда приводят к тому, что инженеры-разработчики стремятся получать более точные и надежные системы измерения уровня. Повышенная точность позволяет снизить изменчивость химического процесса, что приводит к повышению качества продукта, снижению затрат и меньшему количеству отходов. Правила, особенно касающиеся электронных документов, устанавливают жесткие требования к точности, надежности и электронной отчетности.
Соотношение (1.12) указывает на то, что
высоты уровней жидкости, отсчитываемые
от поверхности раздела, обратно
пропорциональны плотностям жидкостей.
Этот принцип используется для измерения
уровня жидкости в закрытых аппаратах
с помощью водомерных стёкол, в жидкостных
манометрах.
Если сообщающиеся сосуды заполнены
одной и той же жидкостью, но давление
над уровнем жидкости в них разное – р
1 ир
2 , то при равновесии
Технология измерения уровня в переходном периоде
Новые технологии измерения уровня помогают удовлетворить эти требования. Простейшим и самым старым промышленным устройством, конечно же, является смотровое стекло. Ручной подход к измерению, очки зрения всегда имели ряд ограничений. Уплотнения подвержены утечке, а наращивание, если оно присутствует, скрывает видимый уровень. Можно безоговорочно заявить, что обычные смотровые стекла являются самым слабым звеном любой установки. Поэтому их быстро заменяют более современные технологии.
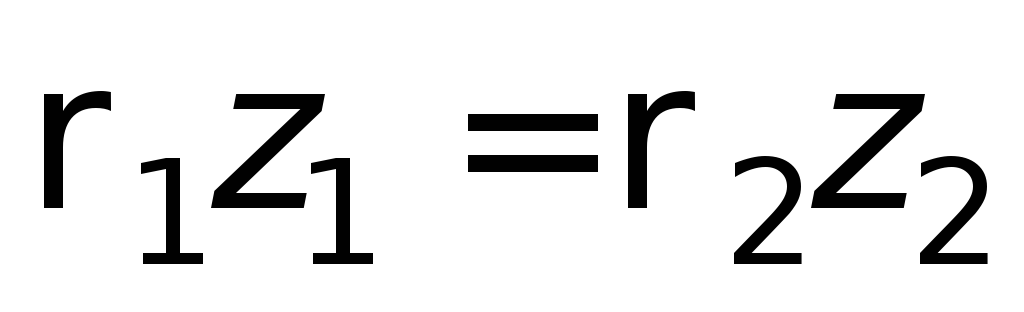 ,
,
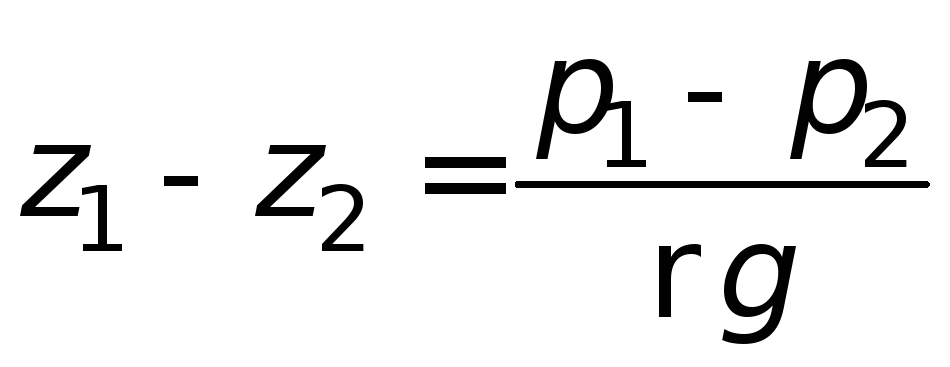 . (1.13)
. (1.13)
Последнее выражение используется при
измерении давления или разности давлений
между различными точками с помощью
дифференциальных U
-образных
манометров.
Другие устройства обнаружения уровня включают те, которые основаны на удельном весе, физическом свойстве, наиболее часто используемом для восприятия поверхности уровня. Простой поплавок, имеющий удельный вес между потоками технологической жидкости и паром свободного пространства, будет плавать на поверхности, точно после ее подъемов и падений. Измерения гидростатической головки также широко использовались для определения уровня.
Когда задействованы более сложные физические принципы, возникающие технологии часто используют компьютеры для выполнения вычислений. Это требует отправки данных в машиночитаемом формате от датчика к системе управления или мониторинга. Полезными форматами выходных сигналов преобразователя для компьютерной автоматизации являются токовые петли, аналоговые напряжения и цифровые сигналы. Аналоговые напряжения просты в настройке и работе, но могут иметь серьезные проблемы с помехами и помехами.
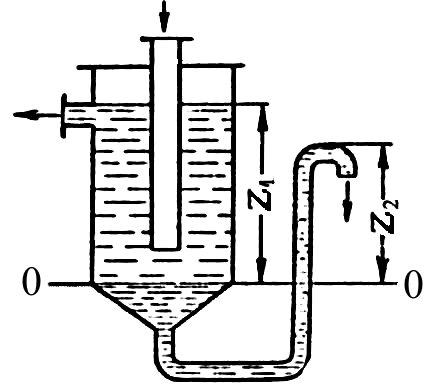
Рисунок 1.5.
– К определению высоты гидравлического
затвора
Этот же принцип используется для
определения высоты гидравлического
затвора в аппаратах, заполненных
жидкостью (рис. 1.5).
На рисунке представлен сосуд, заполненный
двумя жидкостями с плотностями 1 и 2 ; уровень
их раздела на глубинеz
1 необходимо поддерживать в процессе
работы постоянным с помощью гидрозатвора,
представляющего собойU
-образную
трубку, подсоединённую снизу (на выходе
жидкости из аппарата).
В соответствии с уравнением (1.12) высота
гидравлического затвора в случае
одинакового давления над жидкостью
внутри аппарата и на выходе из затвора
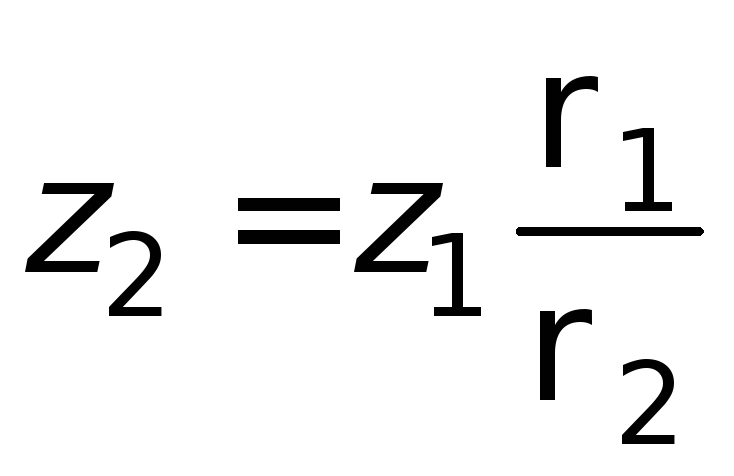 . (1.14)
. (1.14)
На использовании данного уравнения
гидростатики основана работа таких
простейших гидравлических машин, как
гидравлический пресс, мультипликатор
(для повышения давления), домкрат,
подъемник и др.
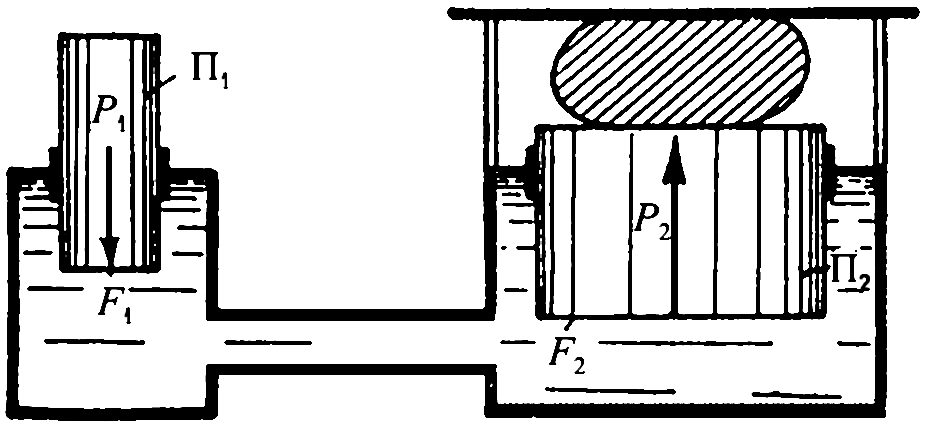
Рисунок 1.6
– Схема гидравлического пресса
На рис. 1.6 показана схема
гидравлического пресса. Если к поршню
П 1 , имеюшему площадьF
1 ,
приложена силаР
1 , то эта сила
будет передаваться на жидкость; жидкость
же будет давить на поршень П 2 ,
имеющий площадьF
2 , с силойР
2
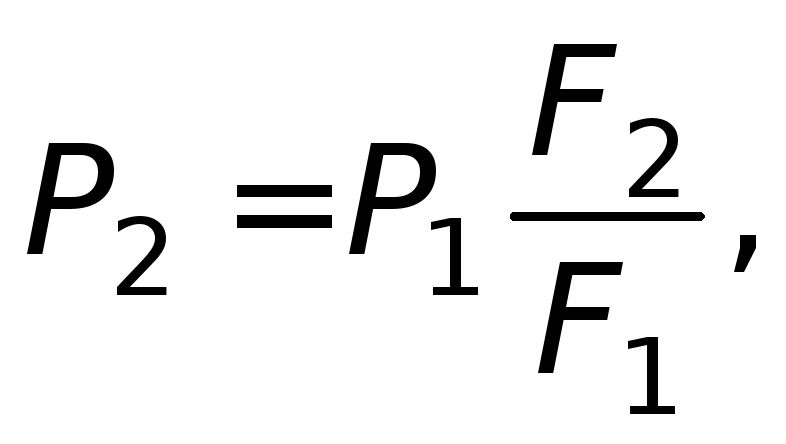 (1.15)
(1.15)
так как гидростатические давления в
точках площади F
1 и площадиF
2 практически равны между собой:
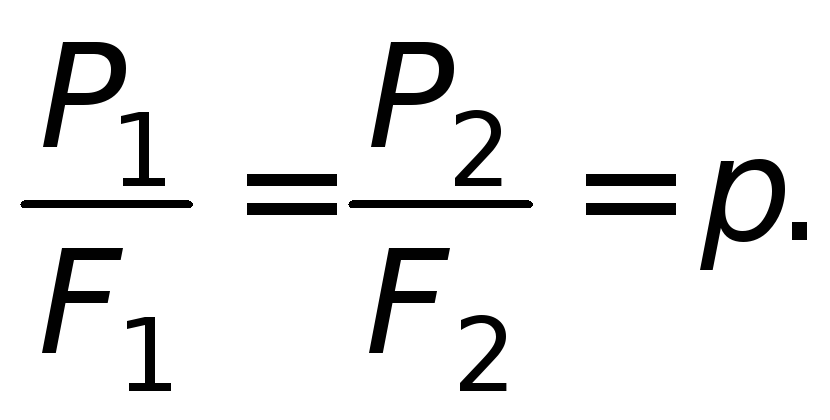 (1.16)
(1.16)
Из уравнения (1.16) следует, что при помощи
пресса сила Р
1 увеличивается
во столько раз, во сколько площадьF
2 больше площадиF
1 .
Сила давления жидкости на плоскую стенку
Рассмотрим вопрос
о силе давления жидкости на плоскую
стенку площадью
S, расположенную
под произвольным углом
к горизонту и ограниченную произвольным
контуром (Рис.13). Как известно, сила
характеризуется тремя параметрами:
– направлением:
– величиной;
– точкой приложения.
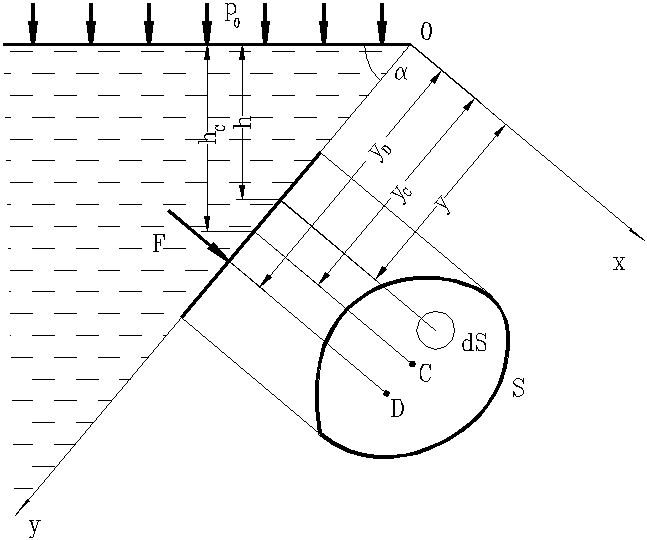
Рис. 13. Схема для
определения силы давления жидкости
на плоскую стенку
Давление в каждой
точке стенки направлено по нормали к
ней, следовательно, и равнодействующая
сила давления будет перпендикулярна
плоской стенке.
Ось 0x
направим по линии пересечения стенки
со свободной поверхностью жидкости, а
ось 0y
– перпендикулярно к этой линии в
плоскости стенки.
Вычислим элементарную
силу давления, приложенную к бесконечно
малой площадке dS:
![]() ,
,
где p0
– давление на свободную поверхность;
h
– глубина расположения площадки dS.
Для получения
полной силы давления F
проинтегрируем полученное выражение
по всей площади S:
![]() .
.
Полученный интеграл
представляет собой статический момент
площади S
относительно оси 0x
и равен произведению этой площади на
координату ее центра масс (точка С),
то есть
![]() .
.
Следовательно,
![]() ,
,
где hC,
pC
– глубина расположения центра масс
площадки и давление в этой точке.
Таким образом,
полная сила
давления жидкости на плоскую стенку
равна произведению площади стенки на
гидростатическое давление pC
в центре масс этой площади.
Силу давления F
можно представить как сумму двух сил:
F0
от внешнего давления p0
и силы Fж
от веса жидкости, то есть
F = F0
+ Fж
= (p0
+ pC)S.
Если давление p0
равно атмосферному и действует также
с обратной стороны стенки, то сила
избыточного давления жидкости на плоскую
стенку
Fизб
= Fж
= ghCS
= pC
изб
S.
Наиболее сложным
является вопрос о точке приложения силы
давления на плоскую стенку. Сила F0
будет приложена в центре масс плоской
стенки C,
так как давление p0
действует на все точки стенки одинаково.
Точка
приложения силы Fж
отыскивается путем составления уравнения
моментов равнодействующей и составляющих
сил относительно горизонтальной оси,
например, совпадающей с линией пересечения
стенки со свободной поверхностью:
![]() .
.
Выразим координату
точки приложения силы yD
и подставим
значения сил Fж
и dFж:
 ,
,
где
![]() – момент инерции площадиS
– момент инерции площадиS
относительно оси 0x.
Учитывая, что
![]()
где Jx0
– момент инерции площади S
относительно горизонтальной оси, лежащей
в плоскости стенки и проходящей через
ее центр масс.
Отсюда, точка
приложения силы Fж
имеет координату
![]()
Если давление p0
равно атмосферному, центр давления
будет находиться в точке D.
Как видно из формулы, yD
лежит ниже центра масс площади S.
Если внешнее давление p0
> pатм,
то равнодействующая будет приложена
выше т. D
и наоборот. Точное ее место приложения
вычисляют из уравнения моментов.
17.Сила давления жидкости на криволинейную (цилиндрическую) стенку. Закон Архимеда. Сила давления жидкости на криволинейные стенки. Плавание тел
Если поверхность
имеет произвольную форму, то требуется
находить 3 составляющих силы и 3 момента.
Чаще рассматривают цилиндрические и
сферические поверхности, имеющие
вертикальную плоскость симметрии.
Возьмем цилиндрическую поверхность
(Рис. 14) с образующей, перпендикулярной
плоскости рисунка и определим силу
давления на эту поверхность в двух
случаях:
– жидкость
расположена сверху;
– жидкость
расположена снизу.
На рисунке показана
реакция стенки на жидкость, которая,
как известно, равна силе давления
жидкости на стенку (по третьему закону
Ньютона). Рассмотрим условия равновесия
объема жидкости
ABDE, лежащей
строго над интересующей нас криволинейной
поверхностью. Условие равновесия в
вертикальном направлении
Fв
= p0Sг
+G,
где Sг
– горизонтальная проекция стенки;
G
– вес жидкости в объеме ABDE.
Условие равновесия
в горизонтальном направлении запишем
с учетом того, что силы давления на
площадки CD
и
AE равны:
![]()

Рис. 14. Схема для
определения силы давления жидкости
на цилиндрическую
поверхность
Fг
= (p0
+ ghC)Sв.
По вычисленным
составляющим Fг
и Fв
найдем величину силы давления жидкости
на стенку
![]()
Направление силы
давления на стенку определяет угол
![]()
Для нахождения
центра давления на цилиндрической
стенке необходимо дополнительно
определить положение центра масс объема
ABDE,
положение центра давления на вертикальную
проекцию стенки. Центр давления находится
из уравнения моментов. Если цилиндрическая
поверхность круговая, то задача
значительно упрощается, так как в этом
случае равнодействующая силы давления
жидкости на стенку проходит через ось
цилиндрической поверхности. Дело в том,
что в каждой точке поверхности давление
направлено по нормали к стенке, то есть
по радиусу и, таким образом, не создает
момента относительно оси, проходящей
через центр вращения. Тогда и
равнодействующая сила не должна создавать
момента относительно той же оси, то есть
должна проходить через центр вращения.
В случае, когда
жидкость находится ниже стенки, давления
в каждой точке будут иметь те же значения,
что и в первом случае, но направлены
противоположно. Следовательно, определять
силу давления на криволинейную стенку
можно точно так же, но направлена она
будет в противоположном направлении.
Следует обратить внимание на то, что
при определении вертикальной составляющей
силы все равно надо вычислять вес
жидкости в объеме ABDE,
хотя на самом деле жидкости там нет.
Примененный сейчас
прием определения вертикальной
составляющей силы давления применим и
для вывода закона Архимеда (Рис. 15).
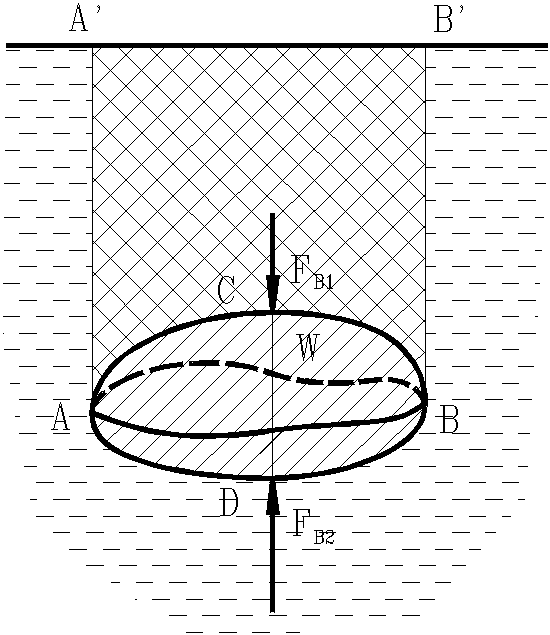
Рис. 15. Схема для
доказательства закона Архимеда
Пусть в жидкость
погружено тело произвольной формы
объемом W.
Возьмем проекцию этого тела на свободную
поверхность жидкости и проведем вдоль
полученной линии цилиндрическую
поверхность с вертикальной образующей.
Эта поверхность будет касаться тела по
замкнутой линии, делящей поверхность
тела на верхнюю и нижнюю части.
Найдем вертикальные
составляющие силы давления жидкости
на верхнюю и нижнюю части поверхности
тела. Они будут равны весам жидкости
соответственно в объемах ACBB’A’
и ADBB’A’.
Обозначим их Fв1
и Fв2.
Равнодействующая этих двух сил будет
равна их разности, то есть весу жидкости
в объеме тела, и направлена вверх.
Fa
= Fв2
– Fв1
= gW.
Равнодействующая
всех горизонтальных составляющих сил
давления всегда равна 0, так как
вертикальные проекции левой и правой,
передней и задней частей тела всегда
попарно равны, и противоположно
направленные горизонтальные составляющие
силы давления друг друга уравновешивают.
Этот вывод можно получить и, не анализируя
в тонкостях горизонтальные составляющие
силы давления. Ведь если бы горизонтальная
составляющая силы давления не была бы
равна 0, то тело под ее действием поплыло
бы в неподвижной жидкости, причем не
затрачивая энергии. Это означало бы
нарушение закона сохранения энергии.
Таким образом, мы
доказали закон Архимеда, который гласит:
на тело,
погруженное в жидкость, действует
выталкивающая сила, направленная
вертикально вверх, численно равная весу
жидкости, вытесненной телом, и приложенная
в центре масс объема погруженной части
тела (центре водоизмещения).
Следует отметить,
что центр масс тела и центр масс объема
тела в общем случае не совпадают. Они
совпадают только в случае, когда тело
имеет равномерную плотность.
Если сила поддержания
(архимедова) меньше веса тела, то оно
тонет. Если больше, то тело всплывает
на поверхность. Если равна, то тело
плавает в толще жидкости.
Для равновесия
плавающего тела необходимо, чтобы центр
масс и центр водоизмещения лежали на
одной вертикальной прямой. Если центр
масс лежит ниже центра водоизмещения,
то равновесие устойчивое, если выше, то
– неустойчивое.
-
Теорема
Коши-Гельмгольца.
-
Метод Лагранжа
и метод Эйлера изучения движения
жидкости. Траектория и линия тока.
Ускорение жидкой частицы в методе
Лагранжа и методе Эйлера.
Методы изучения
движения жидкости.
Жидкость представляет
собой физическое тело, состоящее из
бесконечно большого числа бесконечно
малых частиц. С большой степенью точности
мы можем рассматривать жидкое тело как
сплошную среду, эта модель позволяет
значительно упростить решение большинства
гидравлических задач. Тем не менее,
нередки случаи, когда уровень исследования
движения жидкого тела требует глубокого
знания физических процессов происходящих
в движущейся жидкости на молекулярном
уровне. В таких случаях вполне удобная
модель сплошной среды может оказаться
неприемлемой.
Исходя из практики
изучения гидравлики как прикладной
дисциплины, можно упомянуть два
метода изучения движения жидкости:
метод Лагранжа и метод Эйлера.
Описание
движения жидкости методом Лагранжа
сводится к рассмотрению положения
частиц жидкости (в полном смысле
слова) в любой момент времени. Так в
начальный момент времени частицы
находились в точках 1, 2, 3 и 4. По истечении
некоторого времени они переместились
в точки: Г, 2′,3’и4′, причём это перемещение
сопровождалось изменением объёмов
и форм частиц (упругой деформацией).
Тогда можно утверждать, что частицы
жидкости при
 своём движении участвуют в трёх видах
своём движении участвуют в трёх видах
движения (поступательном, вращательном
и деформации). Для описания такого
сложного движения жидкости необходимо,
таким образом, определить как траектории
частиц, так и гидравлические характеристики
частиц (плотностьр,
температуру
Т
и
скорость и)
в
функции времени и координат.

Переменные
а,
Ь, с, и
/ носят название переменных Лагранжа.
Задача сводится к решению систем
дифференциальных уравнений в частных
производных для каждой части-
цы жидкости. Метод
Лагранжа ввиду громоздкости и трудности
решения может использоваться в
случаях детального изучения поведения
лишь отдельных частиц жидкости.
Использование этого метода для
инженерных расчётов не рентабельно.
Суть другого
метода, метода Эйлера заключается в
том, что движение жидкости подменяется
изменением поля скоростей. Под полем
скоростей понимают некоторую достаточно
большую совокупность точек бесконечного
пространства занятого движущейся
жидкостью, когда в каждой точке
пространства в каждый момент времени
находится частица жидкости с
определённой скоростью (вектором
скорости). Припишем неподвижным точкам
пространства скорость частиц жидкости,
которые в данный момент времени находятся
в этих точках. Поскольку пространство
бесконечно и непрерывно, то мы имеем
массив данных о скоростях достаточно
полный, чтобы определить (задать) поле
в каждой его точке. Условно, нос достаточной
точностью такое поле можно считать
непрерывным.
Несмотря на то,
что исходные условия создания модели
движущийся жидкости довольно сложные,
тем не менее, метод Эйлера весьма удобен
для расчётов.
Построение поля
скоростей осуществляется следующим
образом:
На
некоторый момент времени (например, to)
произвольным
образом выберем необходимое число
точек, в которых находятся частицы
жидкости.
Приписав
их
скорости
![]() точкам неподвижного пространства
точкам неподвижного пространства
(1, 2, 3, 4, 5 и 6) мы сделаем «моментальную
фотографию» поля скоростей на выбранный
момент времени. В следующий момент
времени![]() в
в
тех же выбранных точках
неподвижного
пространства будут находиться другие
частицы жидкости, имеющие другие
скорости
![]() .
.
Выполнив уже
известную
процедуру второй раз, получим но вую «моментальную фотографию» поля
вую «моментальную фотографию» поля
скоростей на момент времени![]() .
.
Теперь вместо изучения траекторий
частиц жидкости
будем сравнивать
поля скоростей. Тогда система уравнений
примет вид:

Поле
скоростей движения жидкости иногда
называют гидродинамическим полем по
аналогии с электромагнитным, тепловым
и др. полями. Это определение не
противоречит физической стороне процесса
движения жидкости. Анализируя состояние
гидродинамического поля на разные
моменты времени![]() ,
,
можно отметить, что с течением времени
поле изменилось, несмотря на то, что в
отдельных точках 5 и 6 скорости остались
постоянными![]() Такое поле называют нестационарным
Такое поле называют нестационарным
гидродинамическим полем. В частном
случае, когда во всех точках неподвижного
пространства с течением времени
предыдущие частицы жидкости сменяются
другими с такими же скоростями, то
поле скоростей во времени не меняется.
Такое гидродинамическое поле называют
стационарным. В соответствии с этим
различают и два вида движения жидкости:
установившееся, когда поле скоростей
является стационарным и неустановившееся
при нестационарном гидродинамическом
поле.
-
Классификация
течений (потоков) жидкости. Принцип
обратимости движения.
Течение жидкости
может быть установившимся (стационарным)
и неустановившимся (нестационарным).
Установившимся
называется
течение, неизменное во времени, при
котором давление и скорость являются
только функциями координат, но не зависят
от времени. Давление и скорость могут
изменяться при перемещении частицы
жидкости, но в данной неподвижной
относительно русла точке давление и
скорость во времени не изменяются:

В частном случае
стационарное течение жидкости может
быть равномерным,
когда скорость каждой частицы не
изменяется при изменении ее координат,
и поле скоростей остается неизменным
вдоль потока.
Неустановившимся
называется
течение жидкости, все характеристики
которого (или некоторые из них) изменяются
во времени в точках рассматриваемого
пространства:
![]()
Исследовать
установившиеся течения значительно
проще, чем неустановившиеся. В дальнейшем
мы будем чаще всего вести речь об
установившихся течениях. Траектории
частиц при стационарном течении неизменны
во времени. При нестационарном течении
траектории частиц, проходящих через
данную точку пространства в различные
моменты времени, могут иметь различную
форму. Поэтому для рассмотрения картины
течения вводится понятие линии тока.
Установившимся
стационарным
движением
жидкости
называется такое движение, при котором
в каждой данной точке основные элементы
движения
жидкости – скорость движения и
и
гидродинамическое давление р
не
изменяются с течением времени,
т.е. зависят только от координат точки.
Аналитически
это условие запишется так:
![]() и
и
![]() .
.
Неустановившимся
(нестационарным) движением жидкости
называется такое
движение, при котором в каждой данной
точке основные элементы движения
жидкости –
скорость
движения и
и гидродинамическое давление р
– постоянно
изменяются, т.е. зависят не только от
положения точки в пространстве, но и от
времени
![]() .
.
Аналитически это условие запишется
так:
![]() и
и
![]() .
.
Примером
установившегося движения может быть:
движение жидкости в канале, в реке при
неизменных глубинах, истечение жидкости
из резервуара при постоянном уровне
жидкости в нем и др. Неустановившееся
движение – это движение жидкости в
канале или реке при переменном уровне
или при опорожнении резервуара, когда
уровень жидкости в нем непрерывно
изменяется.
В
дальнейшем будет изучаться главным
образом установившееся движение
жидкости и в отдельных случаях будут
разбираться примеры неустановившегося
движения.
Установившееся
движение в свою очередь
подразделяется на равномерное
и неравномерное.
Равномерным
называется
такое установившееся движение, при
котором живые
сечения вдоль потока не изменяются: в
этом случае
![]() ;
;
средниескорости
по длине потока также не изменяются,
т.е.
![]() .
.
Примером равномерного движения является:
движение жидкости в цилиндрической
трубе,
в канале постоянного сечения при
одинаковых глубинах.
Установившееся
движение называется неравномерным,
когда
распределение
скоростей в различных поперечных
сечениях неодинаково; при этом средняя
скорость
и площадь поперечного сечения потока
могут быть и
достоянными вдоль потока.
Примером неравномерного движения может
быть
движение жидкости в конической трубе
или в речном русле переменной ширины.
Напорным
называется
движение жидкости, при котором поток
полностью
заключен в твердые стенки и не имеет
свободной поверхности. Напорное движение
происходит вследствие разности давлений
и под действием
силы тяжести. Примером напорного движения
является движение жидкости
в замкнутых трубопроводах (например, в
водопроводных трубах).
Безнапорным
называется
движение жидкости, при котором поток
имеет свободную поверхность. Примером
безнапорного движения может быть:
движение
жидкости в реках, каналах, канализационных
и дренажных трубах. Безнапорное
движение происходит под действием силы
тяжести и за счет начальной
скорости. Обычно на поверхности
безнапорного потока давление атмосферное.
-
Векторная
линия (линия тока, вихревая линия) и ее
уравнение. Векторная трубка (трубка
тока, вихревая трубка). Поток вектора
через незамкнутую и замкнутую поверхность
(объемный расход, интенсивность вихревой
трубки). Дивергенция вектора а
(вектора
скорости v
и вектора вихря rot
v
).
Трубка тока.
Струйка тока. Поток жидкости, живое
сечение, поперечное сечение, смоченный
периметр. Гидравлический диаметр.
Поверхность,
образованная линиями тока и проходящая
ч/з точки замкнутого контура, называется
трубка тока. Линия тока – в каждой точке
вектор тока касательный. ( Если периметр
охватывает малую площадку, трубку
называют элементарной). Жидкость внутри
– элементарная струйка или струйка. В
пределах поперечного сечения элементарной
струйки скорость течения и др. параметры
принимаются постоянными. Поток жидкости
– совокупность элементарных струек.
Струйки в потоке плотно прилегают друг
к другу.
Живым сечением
называется сечение потока. Каждая
элементарная площадка которого нормальна
к соответствующему вектору скорости.
Если линии тока параллельны, то живое
сечение плоское.
Гидравлический
радиус
![]() ,-
,-
смоченный периметр, длина линии, по
которой живое сечение потока соприкасается
с огранич. поверхностями.
Гидравлический
диаметр
![]() .
.
Поперечным сечением
потока называется сечение площадью S,
перпендикулярное оси.
Объемным расходом
жидкости Q
называется объем жидкости, протекающий
через данную поверхность в секунду:
![]() .
.
Поток жидкости
– конечный движущийся объем жидкости,
состоящий из бесконечно большого числа
элементарных струек.

Рис. 16. Линия тока
Линия тока
(Рис. 16) –
это кривая,
в каждой точке которой вектор скорости
в данный момент времени направлен по
касательной.

Рис. 17. Трубка тока
Если в движущейся
жидкости взять бесконечно малый замкнутый
контур и через все его точки провести
линии тока, то образуется трубчатая
поверхность, называемая трубкой
тока (Рис.
17).
Часть потока, заключенная внутри трубки
тока, называется элементарной
струйкой.
В любой точке
трубки тока скорости частиц жидкости
направлены по касательной, нормальная
к этой поверхности составляющая скорости
отсутствует, следовательно, при
установившемся движении ни одна частица
жидкости ни в одной точке не может
проникнуть внутрь струйки или выйти
наружу. Таким образом, трубка тока
является как бы непроницаемой стенкой,
а элементарная струйка – это самостоятельный
элементарный поток.
Элементарная
струйка характеризует состояние движения
жидкости в данный момент
времени t.
При установившемся движении элементарная
струйка имеет
следующие свойства:
1.
форма и положение элементарной струйки
с течением времени остаются
неизменными, так как не изменяются линии
тока;
2.
приток жидкости в элементарную струйку
и отток из нее через боковую поверхность
невозможен, так как по контуру элементарной
струйки скорости
направлены по касательной;
3.
скорость
и гидродинамическое давление во всех
точках поперечного лечения
элементарной струйки можно считать
одинаковым ввиду малости
площади
![]() .
.
Поток.
Совокупность
элементарных струек движущейся жидкости,
проходящих
через площадку достаточно больших
размеров, называется потоком
жидкости.
Поток
ограничен твердыми поверхностями, по
которым происходит
движение жидкости (труба), и атмосферой
(река, лоток, канал и т.п.).
Смоченным
периметром живого сечения потока П
называется
часть контура живого сечения потока,
которая ограничена твёрдой средой. (На
рисунке смоченный периметр выделен
жирной линией).
Расходом
называется количество жидкости,
протекающее через живое сечение потока
(струйки) в единицу времени. Количество
жидкости можно задать объемом, массой
или весом. Соответственно и расходы
бывают объемный Q,
массовый Qm
и весовой
QG.
Для элементарной
струйки, имеющей бесконечно малые
площади живых сечений, можно считать
скорость жидкости в любой точке сечения
одинаковой. Тогда
dQ = V dS; dQm=
dQ = V
dS; dQG=
g dQm=
gV
dS,
где dS
– площадь живого сечения струйки.
Для потока конечных
размеров скорость в различных точках
сечения будет различной, поэтому расход
следует определять как сумму элементарных
расходов струек
![]()
Но это чисто
теоретическая формула, воспользоваться
ей для определения расхода проблематично.
Обычно вводят в рассмотрение среднюю
по сечению скорость потока, которую
можно найти по измерянному расходу
![]() ,
,
откуда Q
= VcpS.
Подскажите, пожалуйста, как высчитывается давление жидкости на стенки сосуда (например аквариума), если известно давлени
Ученик
(95),
закрыт
10 лет назад
Валентина ???
Гений
(71098)
12 лет назад
Понятно, что чем глубже, тем давление в жидкости больше. Поэтому давление на стенку аквариума находят на точки, лежащие на середине глубины, т. е.
p = (ро) gh/2
Площадь стенки здесь не нужна. Она была бы нужна, если бы требовалось найти силу давления на боковые стенки аквариума.
AlxKir
Профи
(811)
12 лет назад
на дно давление будет максимальным – у поверхности минимальным.. .
по стенке давление будет распределено не равномерно, но линейно, так ка давление будет зависеть только от высоты столба жидкости т. е. давление на всю стенку будет равно 1/2(давление у поверхности+давление у дна).. . если посчитать, что давление у поверхности = 0, тогда 1/2 давления у дна, соответственно / на площадь стенки
