Знаток
(304),
закрыт
14 лет назад
Александр Целиков
Просветленный
(39746)
14 лет назад
Сила может быть не постоянна в течении какого-либо процесса, поэтому среднюю силу можно определить как:
Fср=A/S
A-работа, совершенная силой F на пути S.
Или, если вы знаете изменение импульса ∆P за время t, то
Fср=∆P/t
Как определить среднюю силу
Средняя сила – это условная величина. В случаях, когда сила, действующая на тело, меняется со временем или действие силы очень мало, то определить величину силы в каждый момент времени не представляется возможным. Поэтому в данных случаях принимают допущение, что за определенное время на тело действовала постоянная сила равная средней и рассчитывают именно ее – Fср.

Вам понадобится
- умение интегрировать
Инструкция
Пусть тело под действием некой силы F изменило свою скорость с V1 до V2 за короткий промежуток времени Δt. Ускорение данного тела будет равно a=(V2-V1)/Δt, где а, V1 и V2 – являются векторными величинами.
Подставьте данное выражение в формулу второго закона Ньютона: F=ma=m(V2-V1)/Δt=(mV2-mV1)/Δt, не забывая, что сила F – тоже векторная величина.
Запишите полученную формулу в несколько ином виде: FΔt=mΔV =Δp. Векторную величину FΔt, равную произведению силы на время ее воздействия, называют импульсом силы и измеряют в ньютонах умноженных на секунду (Н•с). А произведение массы тела на его скорость p=mV – импульсом тела или количеством движения тела. Эту векторную величину измеряют в килограммах, умноженных на метр в секунду (кг•м/с).
Т.о. второй закон Ньютона можно сформулировать иначе: импульс силы, действующей на тело равен изменению импульса тела: FΔt=Δp.
Если время воздействия силы было очень мало, например, во время удара, то среднюю силу находят так: Fср=Δp/Δt=m(V2-V1)/Δt.Пример: Мяч массой 0,26кг летел со скоростью 10м/с. После удара волейболиста, мяч увеличил скорость до 20м/с. Время удара – 0,005с. Средняя сила воздействия руки волейболиста на мяч равна в данном случае Fср=0,26•(20-10)/0,005с=520Н.
Если сила, действующая на тело, не постоянна, а меняется со временем по закону F(t), то путем интегрирования функции F(t) по времени t на промежутке от 0 до T найдите изменение импульса тела: dр=F(t)dt.
И по формуле Fср=dp/dt определите значение средней силы.Пример: Сила меняется со временем по линейному закону F=30t+2. Найдите среднюю силу воздействия за 5с. Сначала вычисляем импульс тела p=∫(30t+2)dt=15t²+2t , а затем среднюю силу: Fср=(15t²+2t)/t=15t+2=15•5+2=77Н
Видео по теме
Обратите внимание
Сила является векторной величиной. Если в результате расчетов значение Fср получилось отрицательным, это значит, что вектор силы направлен в сторону, противоположную направлению координатной оси.
Полезный совет
Не забывайте при решении задач переводить все используемые в формулах величины в СИ. Т.е. массу – в килограммы, скорость – в метры, деленные на секунду, а силу – в ньютоны.
Источники:
- Физика для углубленного изучения, Е.И. Бутиков, А.С. Кондратьев
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Если на тело массой m за определенный промежуток времени Δt действует сила F→, тогда следует изменение скорости тела ∆v→=v2→-v1→. Получаем, что за время Δt тело продолжает движение с ускорением:
a→=∆v→∆t=v2→-v1→∆t.
Основываясь на основном законе динамики, то есть втором законе Ньютона, имеем:
F→=ma→=mv2→-v1→∆t или F→∆t=mv2→-mv1→=m∆v→=∆mv→.
Изменение импульса
Импульс тела, или количество движения – это физическая величина, равная произведению массы тела на скорость его движения.
Импульс тела считается векторной величиной, которая измеряется в килограмм-метр в секунду (кг м/с).
Импульс силы – это физическая величина, равняющаяся произведению силы на время ее действия.
Импульс относят к векторным величинам. Существует еще одна формулировка определения.
Изменение импульса тела равняется импульсу силы.
При обозначении импульса p→ второй закон Ньютона записывается как:
F→∆t=∆p→.
Данный вид позволяет формулировать второй закон Ньютона. Сила F→ является равнодействующей всех сил, действующих на тело. Равенство записывается как проекции на координатные оси вида:
FxΔt=Δpx; FyΔt=Δpy; FzΔt=Δpz.
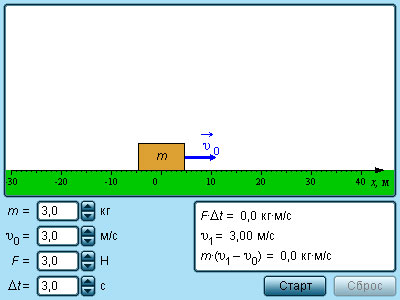
Рисунок 1.16.1. Модель импульса тела.
Изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось.
Одномерное движение – это движение тела по одной из координатный осей.
На примере рассмотрим свободное падение тела с начальной скоростью v0 под действием силы тяжести за промежуток времени t. При направлении оси OY вертикально вниз импульс силы тяжести Fт=mg, действующий за время t, равняется mgt. Такой импульс равняется изменению импульса тела:
Fтt=mgt=Δp=m(v–v0), откуда v=v0 + gt.
Запись совпадает с кинематической формулой определения скорости равноускоренного движения. По модулю сила не изменяется из всего интервала t. Когда она изменяема по величине, тогда формула импульса требует подстановки среднего значения силы Fср из временного промежутка t. Рисунок 1.16.2 показывает, каким образом определяется импульс силы, которая зависит от времени.
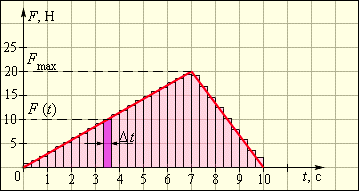
Рисунок 1.16.2. Вычисление импульса силы по графику зависимости F(t)
Необходимо выбрать на временной оси интервал Δt, видно, что сила F(t) практически неизменна. Импульс силы F(t)Δt за промежуток времени Δt будет равняться площади заштрихованной фигуры. При разделении временной оси на интервалы на Δti на промежутке от от 0 до t, сложить импульсы всех действующих сил из этих промежутков Δti, тогда суммарный импульс силы будет равняться площади образования при помощи ступенчатой и временной осей.
Применив предел (Δti→0), можно найти площадь, которая будет ограничиваться графиком F(t) и осью t. Использование определения импульса силы по графику применимо с любыми законами, где имеются изменяющиеся силы и время. Данное решение ведет к интегрированию функции F(t) из интервала [0; t].
Рисунок 1.16.2 показывает импульс силы, находящийся на интервале от t1=0 с до t2=10.
Из формулы получим, что Fср(t2-t1)=12Fmax(t2-t1)=100 Н·с=100 кг·м/с.
То есть, из примера видно Fср=12Fmax=10 Н.
Определение средней силы
Имеются случаи, когда определение средней силы Fср возможно при известных времени и данных о сообщенном импульсе. При сильной ударе по мячу с массой 0,415 кг можно сообщить скорость, равную v=30 м/с. Приблизительным временем удара является значение 8·10–3 с.
Тогда формула импульса приобретает вид:
p=mv=12,5 кг·м/с.
Чтобы определить среднюю силу Fср во время удара, необходимо Fср=p∆t=1,56·103 Н.
Получили очень большое значение, которое равняется телу массой 160 кг.
Когда движение происходит по криволинейной траектории, то начальное значение p1→ и конечное
p2→ могут быть различны по модулю и по направлению. Для определения импульса ∆p→ применяют диаграмму импульсов, где имеются векторы p1→ и p2→, а ∆p→=p2→-p1→ построен по правилу параллелограмма.
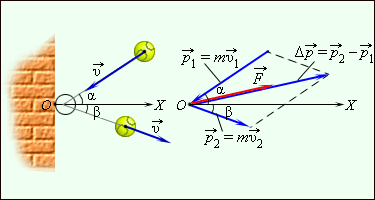
Для примера приводится рисунок 1.16.2, где нарисована схема импульсов мяча, отскакивающего от стены. При подаче мяч с массой m со скоростью v1→ налетает на поверхность под углом α к нормали и отскакивает со скоростью v2→ с углом β. При ударе в стену мяч подвергался действию силы F→, направленной также, как и вектор ∆p→.
Рисунок 1.16.3. Отскакивание мяча от шероховатой стенки и диаграмма импульсов.
Если происходит нормальное падение мяча с массой m на упругую поверхность со скоростью v1→=v→, тогда при отскоке она изменится на v2→=-v→. Значит, за определенный промежуток времени импульс изменится и будет равен ∆p→=-2mv→. Используя проекции на ОХ, результат запишется как Δpx=–2mvx. Из рисунка 1.16.3 видно, что ось ОХ направлена от стенки, тогда следует vx<0 и Δpx>0. Из формулы получим, что модуль Δp связан с модулем скорости, который принимает вид Δp=2mv.
Сила, второй закон Ньютона
Сила является мерой взаимодействия (взаимного действия). Если действие велико (мало), то говорят о большой (малой) силе. Сила обозначается буквой $$F$$ (первая буква слова force).
При взаимодействии чем больше сила, тем больше ускорение тела, на которое эта сила действует. Следовательно, ускорение прямо пропорционально действующей силе: a∼Fasim F.
Но уже говорилось о том, что ускорение зависит от массы тела: a∼1ma sim frac 1m
Обощая эти зависимости получим:
[a = frac{F}{m}, quad mathrm{или}quad F = ma.]
Теперь рассмотрим свойства силы, устанавливаемые опытным путём:
1) Результат действия (проявления) силы зависит от направления действующей силы, следовательно, сила – величина векторная.
2) Результат действия (проявления) силы зависит от величины приложенной силы .
3) Результат действия (проявления) силы зависит от точки приложения силы.
4) За единицу силы принято значение такой силы, которая вызывает ускорение 1 м/с21 mathrm{м}/mathrm{с}^2 у тела массой 1 кг1 mathrm{кг}. Единицу силы назвали в честь Исаака Ньютона 1 нью’тон. (Произносить фамилию считается правильным таким образом, как произносится фамилия в том государстве, где проживал или проживает учёный.)
[F→]=1 Н=1 кг·мс2 (ньютон).[overset{rightarrow}{F}] = 1 mathrm{Н} = 1 mathrm{кг}cdotfrac{mathrm{м}}{mathrm{с}^2}quad mathrm{(ньютон)}.
5) Если на тело одновременно действуют несколько сил, то каждая сила действует независимо от других. (Принцип суперпозиции сил). Тогда все силы необходимо сложить векторно и получить результирующую силу (рис. 4).
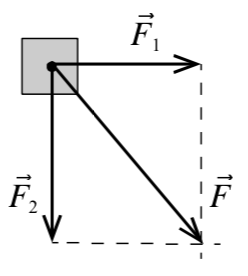 |
| Рис. 4 |
Из приведённых свойств силы следует, как обобщение опытных фактов, второй закон Ньютона:
Второй закон Ньютона: Сумма всех сил, действующих на тело, равна произведению массы тела на ускорение, сообщаемое этой суммой сил:
∑F→=ma→.boxed{sum vec{F} = mvec{a}}.
Данное выражение можно представить и в другой форме: так как a→=v→к-v→0tvec a = frac{vec v_mathrm{к} – vec v_0}{t}, то второй закон Ньютона примет вид: ∑F→=mv→к-v→0tsum vec F = mfrac{vec v_mathrm{к} – vec v_0}{t}.
Произведение массы тела и его скорости называют импульсом тела:
p→=mv→vec p = mvec v,
тогда получим новое выражение для второго закона Ньютона:
∑F→=mv→к-mv→0t=p→к-p→0t=Δp→tboxed{sum vec F = frac{mvec v_mathrm{к} – mvec v_0}{t}} = frac{vec p_mathrm{к} – vec p_0}{t} = frac{Delta vec p}{t}.
∑F→=p→к-p→0tboxed{sum vec F = frac{vec p_mathrm{к} – vec p_0}{t}} — второй закон Ньютона в импульсной форме для среднего значения силы. Здесь p→к-p→0=Δp→vec p_mathrm{к} – vec p_0 = Delta vec p — изменение импульса тела, t -t – время изменения импульса тела.
∑F→=dp→dt -boxed{sum vec F = frac{dvec p}{dt}} – второй закон Ньютона в импульсной форме для мгновенного значения силы.
Из второго закона в частности следует, что ускорение тела, подвергающегося действию нескольких сил, равно сумме ускорений, сообщаемых каждой силой:
a→=∑a→i=a→1+a→2+…+a→i=∑F→m=F→1+F→2+…+F→im=F→1m+F→2m+…+F→imboxed{vec a = sum vec a_i = vec a_1 + vec a_2 + dots + vec a_i = frac{sum vec F}{m} = frac{vec F_1 + vec F_2 + dots + vec F_i}{m} = frac{vec F_1}{m} + frac{vec F_2}{m} + dots + frac{vec F_i}{m}}.
Первая форма записи второго закона (∑F→=ma→)(sum vec F = mvec a) справедлива только при малых скоростях по сравнению со скоростью света. И, разумеется, выполняется второй закон Ньютона только в инерциальных системах отсчёта. Так же следует отметить, что второй закон Ньютона справедлив для тел неизменной массы, конечных размеров и движущихся поступательно.
Второе (импульсное) выражение имеет более общий характер и справедливо при любых скоростях.
Как правило, в школьном курсе физики сила со временем не меняется. Однако последняя импульсная форма записи позволяет учесть зависимость силы от времени, и тогда изменение импульса тела будет найдено с помощью определённого интеграла на исследуемом интервале времени. В более простых случаях (сила изменяется со временем по линейному закону) можно брать среднее значение силы.
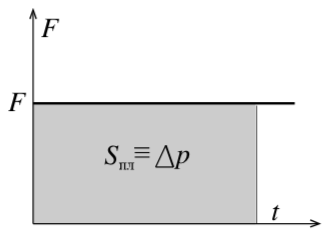 |
| Рис. 5 |
Иногда очень полезно знать, что произведение F→·tvec F cdot t называют импульсом силы, и его значение F→·t=Δp→vec F cdot t = Delta vec p равно изменению импульса тела.
Для постоянной силы на графике зависимости силы от времени можем получить, что площадь фигуры под графиком равна изменению импульса (рис. 5).
Но даже если сила будет изменяться со временем, то и в этом случае, разбивая время на малые интервалы ΔtDelta t такие, что величина силы на этом интервале остаётся неизменной (рис. 6), а потом, суммируя полученные «столбики», получим:
Площадь фигуры под графиком F(t)F(t) численно равна изменению импульса.
В наблюдаемых природных явлениях сила, как правило, меняется со временем. Мы же часто, применяя простые модели процессов, считаем силы постоянными. Сама же возможность использования простых моделей появляется из возможности подсчёта средней силы, т. е. такой постоянной силы, у которой площадь под графиком от времени будет равна площади под графиком реальной силы.
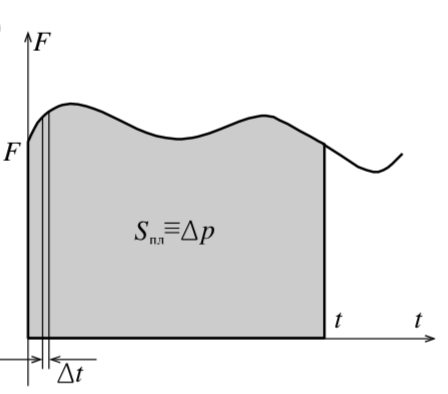 |
| Рис. 6 |
Следует добавить ещё одно очень важное следствие второго закона Ньютона, связанное с равенством инертной и гравитационной масс.
Неразличимость гравитационной и инертной масс означает, что и ускорения, вызванные гравитационным взаимодействием (законом всемирного тяготения) и любым другим тоже неразличимы.
Пример 2. Мяч массой 0,5 кг0,5 mathrm{кг} после удара, длящегося 0,02 с0,02 mathrm{с}, приобретает скорость 10 м/с10 mathrm{м}/mathrm{с}. Найти среднюю силу удара.
Решение. В данном случае рациональнее выбрать второй закон Ньютона в импульсной форме, т. к. известны начальная и конечная скорости, а не ускорение, и известно время действия силы. Также следует отметить, что сила, действующая на мяч, не остаётся постоянной. По какому закону меняется сила со временем, неизвестно. Для простоты мы будем пользоваться предположением, что сила постоянная, и её мы будем называть средней.
Тогда ∑F→=Δp→tsum vec F = frac{Delta vec p}{t}, т. е. F→ср·t=Δp→vec F_mathrm{ср}cdot t = Delta vec p. В проекции на ось, направленной вдоль линии действия силы, получим: Fср·t=pк-p0=mvкF_mathrm{ср}cdot t = p_mathrm{к}-p_0 = mv_mathrm{к}. Окончательно для искомой силы получим:
[F_mathrm{ср} = frac{mv_mathrm{к}}{t}.]
Количественно ответ будет таким: Fср=0,5 кг·10 мс0,02 с=250 НF_mathrm{ср} = frac{0,5 mathrm{кг}cdot 10 frac{mathrm{м}}{mathrm{с}}}{0,02 mathrm{с}} = 250 mathrm{Н}.
Unit Converter
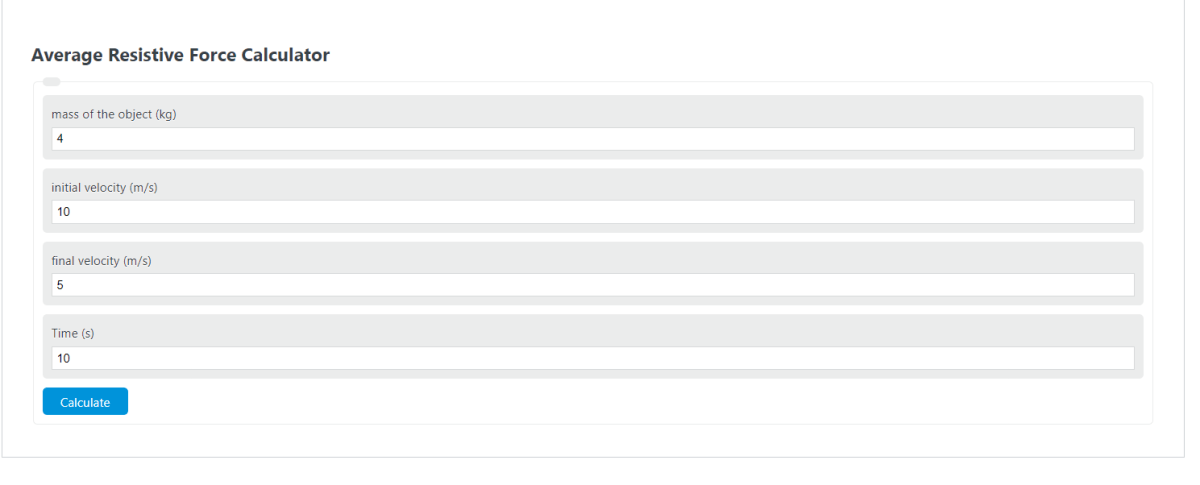
Enter the mass, initial velocity, final velocity, and time into the calculator to determine the average resistive force.
- All Force Calculators
- Resistance Force Calculator
- Momentum to Force Calculator
- Velocity to Force Calculator
The following equation is used to calculate the Average Resistive Force.
- Where ARF is the average resistive force (N)
- m is the mass of the object (kg)
- Vi is the initial velocity (m/s)
- Vf is the final velocity (m/s)
- t is the total time (s)
What is an Average Resistive Force?
Definition:
An average resistive force is the total force that has acted on an object over a given period of time which is caused the object to reduce its velocity.
How to Calculate Average Resistive Force?
Example Problem:
The following example outlines the steps and information needed to calculate Average Resistive Force.
First, determine the mass of the object. In this example, the mass of the object is found to be 4kg.
Next, determine the initial velocity. For this problem, the initial velocity is found to be 10m/s.
Next, determine the final velocity. In this case, the final velocity is measured to be 5m/s.
Next, determine the time. In this example, the time is 10s.
Finally, calculate the Average Resistive Force using the formula above:
ARF = m*(Vi-Vf)/t
ARF = 4*(10-5)/10
ARF = 2N