Как найти среднюю силу сопротивления в физике

Unit Converter

• ГДЗ

• 10 класс

• Физика

• Рымкевич 10-11

• 379

Подробное решение задание 379 по физике задачник для учащихся 10 класса, авторов А.П. Рымкевич 2016

показать содержание

Условие задачи:

Пуля массой 10 г, летевшая со скоростью 400 м/с, пробив доску толщиной 5 см, уменьшила скорость вдвое. Определить среднюю силу сопротивления доски движению пули.

Задача №2.1.27 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(m=10) г, (upsilon_0=400) м/с, (S=5) см, (upsilon=frac{upsilon_0}{2}), (F-?)

Решение задачи:

Задачу можно решить двумя способами, первый способ более сложный, чем второй, тем не менее они оба укладываются в рамки обычного курса физики.

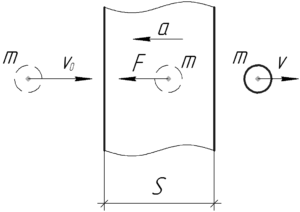
Первый способ – основан на применении второго закона Ньютона в, так называемом, общем виде.

[F = frac{{Delta p}}{{Delta t}};;;;(1)]

То есть сила сопротивления со стороны доски (F) равна отношению изменения импульса пули (Delta p) ко времени движения пули в доске (Delta t).

Импульс пули равен произведению массы пули на её скорость, тогда изменение импульса пули найти проще простого.

[Delta p = mupsilon  – m{upsilon _0} = mleft( {upsilon  – {upsilon _0}} right)]

Так как по условию скорость пули снизиться в 2 раза, то есть (upsilon=frac{upsilon_0}{2}), то:

[Delta p = mleft( {frac{{{upsilon _0}}}{2} – {upsilon _0}} right) =  – frac{{m{upsilon _0}}}{2}]

Знак “минус” показывает направление действия силы, при подстановке в выражение второго закона Ньютона (самая первая формула) его можно отбрасывать.

Осталось найти время движения пули в доске. Если на пулю действовала какая-то не изменяющаяся во времени (средняя) сила сопротивления (F), то она создала постоянное во времени ускорение (a). Воспользуемся известной формулой кинематики без времени:

[{upsilon ^2} – upsilon _0^2 =  – 2aS]

[frac{{upsilon _0^2}}{4} – upsilon _0^2 =  – 2aS Rightarrow frac{{3upsilon _0^2}}{4} = 2aS Rightarrow a = frac{{3upsilon _0^2}}{{8S}}]

Формула скорости для равнозамедленного движения применительно к этой задаче:

[upsilon {text{ }} = {upsilon _0} – aDelta t]

Так как по условию (upsilon=frac{upsilon_0}{2}), то:

[frac{{{upsilon _0}}}{2} = {upsilon _0} – aDelta t Rightarrow Delta t = frac{{{upsilon _0}}}{{2a}}]

Подставим в последнюю формулу полученное нами выражение для ускорения (a).

[Delta t = frac{{{upsilon _0} cdot 8S}}{{2 cdot 3upsilon _0^2}} = frac{{4S}}{{3{upsilon _0}}}]

В конце концов подставим выражения для изменения импульса и времени в формулу (1).

[F = frac{{m{upsilon _0} cdot 3{upsilon _0}}}{{2 cdot 4S}} = frac{{3mupsilon _0^2}}{{8S}}]

Посчитаем численный ответ, подставив данные задачи (переведя их в систему СИ) в формулу.

[F = frac{{3 cdot 0,01 cdot {{400}^2}}}{{8 cdot 0,05}} = 12000; Н = 12; кН]

Второй способ – для решения задачи применим закон сохранения энергии (или теорему об изменении кинетической энергии, как хотите). До попадания в доску у пули была одна кинетическая энергия, после вылета из доски – другая, но меньшая, вследствие того, что сила сопротивления совершила работу.

Напомним, что кинетическую энергию можно найти как половину произведения массы тела на квадрат скорости, работу силы – как скалярное произведение вектора силы на вектор перемещения.

[ – FS = frac{{m{upsilon ^2}}}{2} – frac{{mupsilon _0^2}}{2}]

[frac{{mupsilon _0^2}}{2} = FS + frac{{m{upsilon ^2}}}{2}]

Не забывайте, что работа силы сопротивления отрицательна, так как вектор силы и вектор перемещения противонаправлены. Так как (upsilon=frac{upsilon_0}{2}), то:

[frac{{mupsilon _0^2}}{2} = FS + frac{{mupsilon _0^2}}{8} Rightarrow F = frac{{3mupsilon _0^2}}{{8S}}]

Как видите, мы получили тот же ответ, но гораздо быстрее. Тем не менее оба способа интересны и достойны запоминания.

Ответ: 12 кН.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.1.26 Два автомобиля массами m и 2m движутся в одном направлении с одинаковыми
2.1.28 Пуля массой 9 г, летевшая со скоростью 600 м/с, попадает в деревянную стену
2.1.29 На тело, движущееся по горизонтальной поверхности, действуют следующие силы

• версия для печати