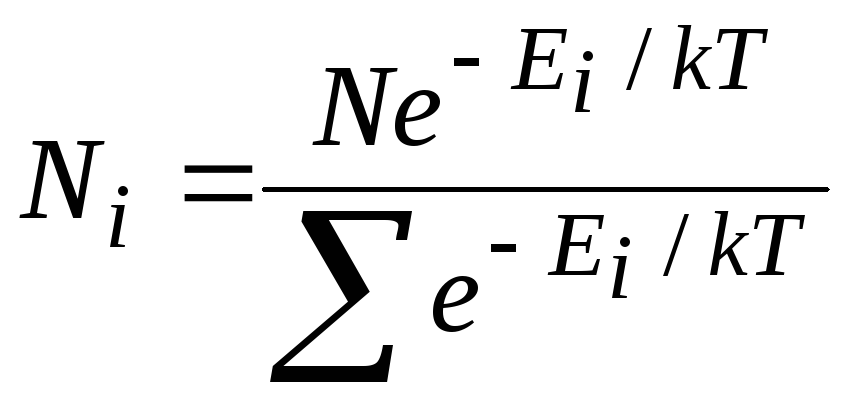Как найти среднюю квадратичную скорость?
Анонимный вопрос
1 февраля 2019 · 8,2 K
Engineer – programmer ⚡⚡ Разбираюсь в компьютерах, технике, электронике, интернете и… · 9 февр 2019 ·
Средняя квадратичная скорость теплового движения молекулы в газе находится по формуле:
v = √ ((3*k*T) / m0), где
v — средняя квадратичная скорость, м/с;
k — 1,38 * 10(−23) — постоянная Больцмана, Дж/К;
T — температура, К;
m0 — масса одной молекулы, кг.
8,5 K
это скорость идеального газа, для конкретного газа i не = 3
Комментировать ответ…Комментировать…
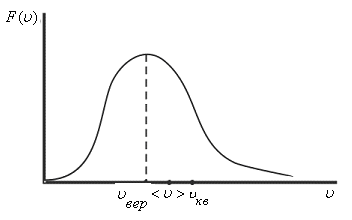
Для характеристики движения молекул в физике используют две скорости: среднюю и среднюю квадратичную скорость молекул.
Важно. Следует обязательно понимать, что в реальных условиях мы не можем точно знать ни конкретное число молекул в системе, ни тем более скорость каждой из них в конкретный момент времени. Это обусловлено неимоверно гигантским числом частиц в реальных и даже сколько-нибудь приближенных к ним системах. Например, в 1 см3 при давлении 200 мм. рт. ст. содержится 4,18*1018 молекул водорода. Говоря более понятными категориями, это более чем 4 миллиарда миллиардов. Заметим, что указанное давление меньше атмосферного почти в 4 раза. Последнее в среднем равняется 760 мм. рт. ст. Разрежённый водород по своим свойствам наиболее близок к идеальному газу. В данном случае физика вынуждена иметь дело с распределениями скоростей и энергий частиц.
Что такое средняя скорость движения молекул
Среднюю скорость движения молекул часто именуют скоростью их теплового движения.
Определение 1
Вид формулы средней относительной скорости молекул в физике можно представить выражением:
[text { Vотн }=sqrt{2} sqrt{frac{8 R T}{pi m_{0}}}]
Выражение под корнем – средняя скорость молекул идеального газа.
Как определить среднюю квадратичную скорость движения молекул
Определение 2
Средней квадратичной скоростью молекул идеального газа называют величину равную квадратному корню из среднего арифметического величины квадратов скоростей каждой из молекул.
Средняя скорость молекул равна:
[leftlanglemathrm{V}_{mathrm{KB}}rightrangle=sqrt{frac{1}{N} sum_{i=1}^{N} v_{i}^{2}}]
Если обе её части возвести в квадрат и проинтегрировать, то получим выражение:
[langlemathrm{VKB}rangle^{2}=int_{0}^{infty} v^{2} F(v) d v]
Ещё одно выражение для среднеквадратичной скорости:
[leftlangle V_{K B}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]
Именно она присутствует в уравнении, именуемом основным уравнением молекулярно-кинетической теории
P = (1/3)nm*<Vкв>
Где n – концентрация молекул, которая вычисляется делением их общего числа на объём.
Пример. 1.
Рассмотрим простейший случай, чтобы использование интегрирования не затруднило понимание сути явления и помогло лучше понять материал. Вычислим как меняется средняя скорость движения молекул в идеальном газе при линейном увеличении его давления. График следующий:
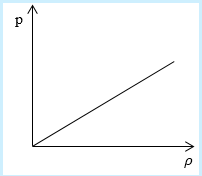
Напомним, что средняя скорость частиц:
[mathrm{Vcp}=sqrt{frac{8 R T}{pi m_{0}}}]
Если присмотреться к представленному графику, то можно заметить, что P приблизительно равно ρ. Эти две величины можно связать соотношением
P=C*ρ
Где С – некоторая постоянная величина, константа.
Далее считаем m0= ρ/n, p = n*k*T = C* ρ. Отсюда следует, что k*T = (C*ρ)/n.
Нужно лишь подставить эти значения в формулу для средней скорости:
[V c p=sqrt{8 mathrm{kT} / pi mathrm{m}}=sqrt{(8 mathrm{C} rho / pi mathrm{n})(mathrm{n} / rho)}=sqrt{8 mathrm{C} / pi}]
В полученном выражении нет ни одной переменной величины, т. е. при увеличении давления, вопреки ожиданиям, скорость оказалась неизменной.
Ответ: В процессе, который был дан нам на графике, при увеличении давления средняя скорость молекул никак не меняется.
Нет времени решать самому?
Наши эксперты помогут!
Пример. 2.
Определим среднюю квадратичную скорость молекул газа при условии, что нам известны его давление (P), молярная масса (M) и концентрация частиц (n).
Воспользуемся формулой:
[leftlanglemathrm{V}_{kappa в}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]
Также нам потребуется уравнение Менделеева-Клайперона
Здесь мы воспользовались тем, что:
m/μ = N/Na
PV = (m/μ)*RT = (N/Na)*RT
Если обе части этого уравнения поделить на V и принять во внимание, что
(N/V) = n, то можно получить
P = (n/Na)*RT. Отсюда находим, что RT = (p*N)/n
Если мы это подставим в выражение для среднеквадратичной скорости [leftlangle V_{K B}rightrangle=sqrt{3 mathrm{kT} / mathrm{m}_{0}}=sqrt{3 mathrm{RT} / mu}], получим, что средняя квадратичная скорость движения молекул газа: [leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]
Ответ: Формула средней квадратичной скорости молекул исходя из данный нам условий следующая:
[leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]
Екатерина Владимировна Мосина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Различают следующие скорости, характеризующие движение молекул.
Средняя скорость движения молекул
средняя скорость движения молекул $leftlangle vrightrangle $, которая определяется как:
где N — число молекул. Или, среднюю скорость можно найти как:
где $Fleft(vright)=4pi {left(frac{m_0}{2pi kT}right)}^{frac{3}{2}}expleft(-frac{m_0v^2}{2kT}right)v^2$ — функция распределения молекул по модулю скорости, указывающая долю молекул со скоростями, находящимися в единичном интервале $dv$ около величины скорости $v$, $m_0$- масса молекулы, $k$- постоянная Болцмана, T — термодинамическая температура. Для того, чтобы определить, как средняя скорость молекулы связана с макропараметрами газа, как системы частиц, найдем значение интеграла (2).
Произведем замену:
Следовательно:
Подставим (4) и (5) в (3), получим:
Проведем интегрирование по частям, получим:
где R — универсальная газовая постоянная, $mu $- молярная масса газа.
Среднюю скорость движения молекул называют также скоростью теплового движения молекул.
Средняя относительная скорость молекул:
[leftlangle v_{otn}rightrangle =sqrt{2}sqrt{frac{8kT}{pi m_0}}=sqrt{2}leftlangle vrightrangle left(7right).]
Средняя квадратичная скорость
Средней квадратичной скоростью движения молекул газа называют величину:
[leftlangle v_{kv}rightrangle =sqrt{frac{1}{N}sumlimits^N_{i=1}{{v_i}^2}}left(8right).]
Или
[{leftlangle v_{kv}rightrangle }^2=intnolimits^{infty }_0{v^2Fleft(vright)dv left(9right).}]
Проводя интегрирование, которое аналогично интегрированию при получении связи средней скорости с температурой газа, получим:
[leftlangle v_{kv}rightrangle =sqrt{frac{3kT}{m_0}}=sqrt{frac{3RT}{mu }}left(10right).]
Именно средняя квадратичная скорость поступательного движения молекул газа входит в основное уравнение молекулярно-кинетической теории:
[p=frac{1}{3}nm_0{leftlangle v_{kv}rightrangle }^2left(11right),]
где $n=frac{N}{V}$ — концентрация частиц вещества, $N$- число частиц вещества, V- объем.
«Средняя скорость молекул» 👇
Пример 1
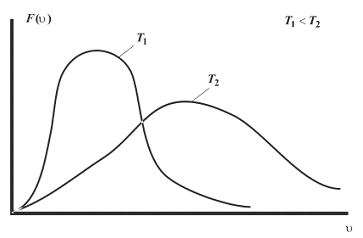
Задание: Определите, как изменяется средняя скорость движения молекул идеального газа при увеличении давления в процессе, представленном на графике (рис.1).
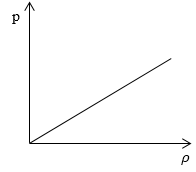
Рис. 1
Решение:
Запишем выражение для средней скорости движения молекул газа в виде:
[leftlangle vrightrangle =sqrt{frac{8kT}{pi m_0}} left(1.1right)]
По графику видим, что $psim rho или p=Crho , $ где C- некоторая константа.
[m_0=frac{rho }{n}, p=nkT=Crho to kT=frac{Crho }{n} left(1.2right).]
Подставим (1.2) в (1.1), получим:
[leftlangle vrightrangle =sqrt{frac{8kT}{pi m_0}}=sqrt{frac{8Crho }{pi n}frac{n}{rho }}=sqrt{frac{8C}{pi }}left(1.3right)]
Ответ: В процессе, изображенном на графике, с ростом давления средняя скорость движения молекул не изменяется.
Пример 2
Задание: Можно ли вычислить среднюю квадратичную скорость молекулы идеального газа, если известны: давление газа (p), молярная масса газа ($mu $) и концентрация молекул газа (n)?
Решение:
Используем выражение для $leftlangle v_{kv}rightrangle :$
[leftlangle v_{kv}rightrangle =sqrt{frac{3RT}{mu }}left(2.1right).]
Кроме того, из уравнения Менделеева — Клайперона и зная, что $frac{m}{mu }=frac{N}{N_A}$:
[pV=frac{m}{mu }RT=frac{N}{N_A}RTleft(2.2right).]
Разделим правую и левую части (2.2) на V, зная, что $frac{N}{V}=n$ получим:
[p=frac{n}{N_A}RTto RT=frac{pN_A}{n} left(2.3right).]
Подставим (2.3) в выражение для среднеквадратичной скорости (2.1), имеем:
[leftlangle v_{kv}rightrangle =sqrt{frac{3pN_A}{mu n}} left(2.4right).]
Ответ: По заданным в условии задачи параметрам среднеквадратичную скорость движения молекул газа вычислить можно с помощью формулы $leftlangle v_{kv}rightrangle =sqrt{frac{3pN_A}{mu n}}.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Средние скорости молекул
Найдём
наиболее
вероятную скорость,
соответствующую максимуму
функции
распределения.
Эта скорость определяется из условия
![]() ,
,
т.е.
![]()
Проведя
дифференцирование произведения функций,
получим
Средняя
скорость
молекул
![]() (имеется в видусредняя
(имеется в видусредняя
арифметическая скорость)
по определению из формулы статического
усреднения
Средняя
скорость входит в
коэффициенты диффузии, вязкости,
теплопроводности и, соответственно
используется в расчётах этих процессов.
Среднеквадратичная
скорость
![]() ;
;
![]() ,
,
откуда
Эта
скорость входит в основное уравнение
молекулярно-кинетической теории.
Качественно
положение характерных (средних) скоростей
показано на рис. 8.6
|
|
Проанализируем, |
|
Рис. 8.6 |
|
|
|
|
|
Рис. 8.7 |
3.
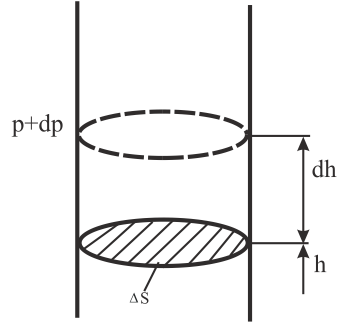
Барометрическая формула.
Атмосферное
давление на высоте h
обусловлено весом вышележащих слоёв
газа. Давление на высоте h+dh
будет P+dP
(dh>0,
dP<0,
т.к. вес и
давление с высотой убывают).
Разность
давлений
P
и P+dP
обусловлена
весом газа, заключённого в объёме
цилиндра, с площадью основания, равной
![]() и высотойdh
и высотойdh
(Рис. 8.8).
|
|
где
При
|
||
|
Рис. 8.8 |
М
– средняя масса моля воздуха. Плотность
![]() ,
,
подставим в (*), получим
![]() .
.
Поделим обе части на Р:
![]() .
.
Возьмём интеграл от левой и правой
частей:
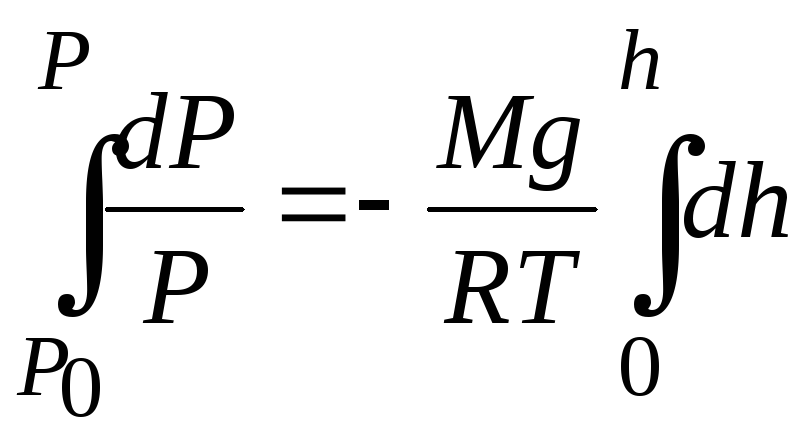 .
.
Предел
![]() давление на уровнеh=0.
давление на уровнеh=0.
Для случая, когда температура постоянная
(изотермическая атмосфера), интегрируя,
получим:
![]() ,
,
отсюда получаем барометрическую
формулу.
|
|
||
|
|
Графическая |
|
|
Рис. 8.9 |
Распределение Больцмана
В
барометрической формуле в отношении
M/R
разделим и
числитель и знаменатель на число Авогадро
![]() .
.
![]() ,
,
где
![]() масса
масса
одной молекулы,
![]() постоянная
постоянная
Больцмана.
Вместо
Р
и
![]() подставим соответственно.
подставим соответственно.![]()
![]() (см. лекцию №7), где
(см. лекцию №7), где![]() плотность
плотность
молекул на высотеh,
![]() плотность
плотность
молекул на высоте![]() .
.
Из барометрической
формулы в результате подстановок и
сокращений получим распределение
концентрации молекул по высоте в поле
силы тяжести Земли.
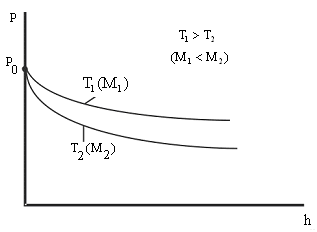
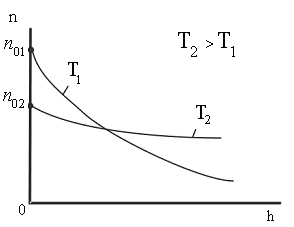
Из
этой формулы следует, что с понижением
температуры число частиц на высотах,
отличных от нуля, убывает (рис. 8.10),
обращаясь в 0 при Т=0 (при
абсолютном нуле все молекулы расположились
бы на поверхности Земли). При высоких
температурах n
слабо убывает с высотой, так
|
|
что |
|
Рис. 8.10 |
![]() .Следовательно,
.Следовательно,
распределение
молекул по высоте является и распределением
их по значениям потенциальной энергии.
-

(*)
где
![]() плотность молекул в том месте пространства,
плотность молекул в том месте пространства,
где потенциальная энергия молекулы
имеет значение![]() ;
;![]() плотность
плотность
молекул в том месте, где потенциальная
энергия равна 0.
Больцман
доказал, что распределение (*) справедливо
не только в случае потенциального поля
сил земного тяготения, но и в любом
потенциальном поле сил для совокупности
любых одинаковых частиц, находящихся
в состоянии хаотического теплового
движения.
Таким
образом, закон
Больцмана (*) даёт распределение частиц,
находящихся в состоянии хаотического
теплового движения, по значениям
потенциальной энергии.
(рис. 8.11)
|
|
|
|
Рис. 8.11 |
-
Распределение
Больцмана при дискретных уровнях
энергии.
Полученное
Больцманом распределение относится к
случаям, когда молекулы находятся во
внешнем поле и их потенциальная энергия
![]() может применяться непрерывно. Больцман
может применяться непрерывно. Больцман
обобщил полученный им закон на случай
распределения, зависящего от внутренней
энергии молекулы.
Известно,
что величина внутренней энергии молекулы
(или атома) Е
может принимать лишь дискретный ряд
дозволенных значений
![]() .
.
В этом случае распределение Больцмана
имеет вид:
![]() ,
,
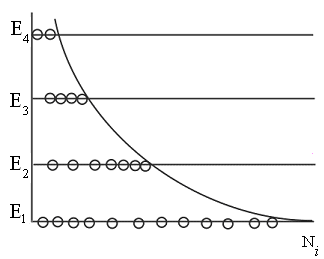
где
![]() число
число
частиц в состоянии с энергией![]() ;
;
![]() коэффициент
коэффициент
пропорциональности, который удовлетворяет
условию
![]() ,
,
где
N
– полное число частиц в рассматриваемой
системе.
Тогда
![]() и в результате для случая дискретных
и в результате для случая дискретных
значений энергии распределение Больцмана
|
|
Качественная
Заметим, |
|
Рис. 8.12 |
Но
состояние системы в этом случае
термодинамически неравновесное.
-
Статистика
Максвелла-Больцмана
Распределение
Максвелла и Больцмана можно объединить
в один закон Максвелла-Больцмана,
согласно которому число молекул,
компоненты скорости которых лежат в
пределах от
![]() до
до![]()
![]() ,
,
а координаты в пределах отx,
y,
z
до x+dx,
y+dy,
z+dz,
равно
где
![]() ,
,![]() плотность
плотность
молекул в том месте пространства, где![]() ;
;![]() ;
;![]() ;
;![]() полная
полная
механическая энергия частицы.
Распределение
Максвелла-Больцмана устанавливает
распределение молекул газа по координатам
и скоростям при наличии произвольного
потенциального силового поля.
Примечание:
распределение Максвелла и Больцмана
являются составными частями единого
распределения, называемого распределением
Гиббса (этот вопрос подробно рассматривается
в спецкурсах по статической физике, и
мы ограничимся только упоминанием этого
факта).
Вопросы для
самоконтроля.
-
Дайте определение
вероятности. -
Каков смысл функции
распределения? -
Каков смысл условия
нормировки? -
Запишите
формулу для определения среднего
значения результатов измерения величины
x
с помощью функции распределения. -
Что представляет
собой распределение Максвелла? -
Что
такое функция распределения Максвелла?
Каков ее физический смысл? -
Постройте
график функции распределения Максвелла
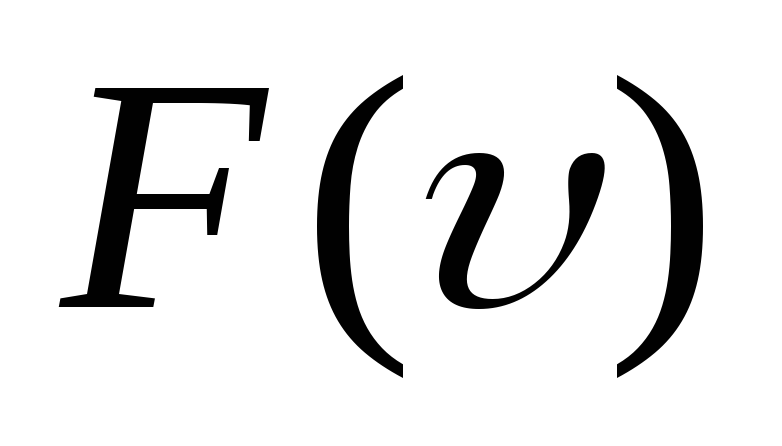 и укажите характерные особенности этой
и укажите характерные особенности этой
функции. -
Укажите
на графике
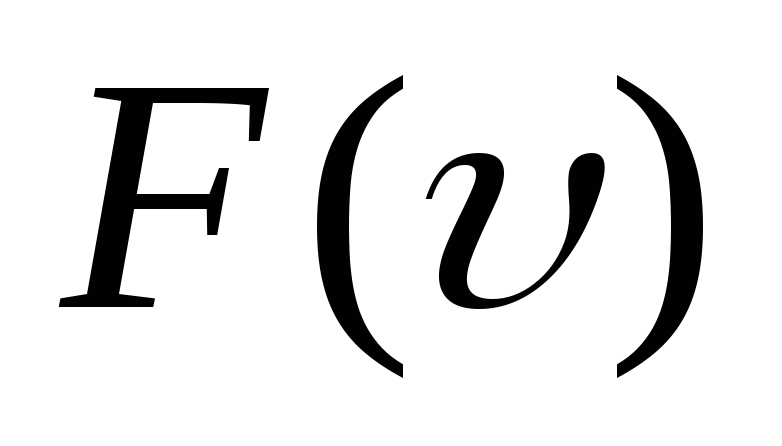 наиболее вероятную скорость
наиболее вероятную скорость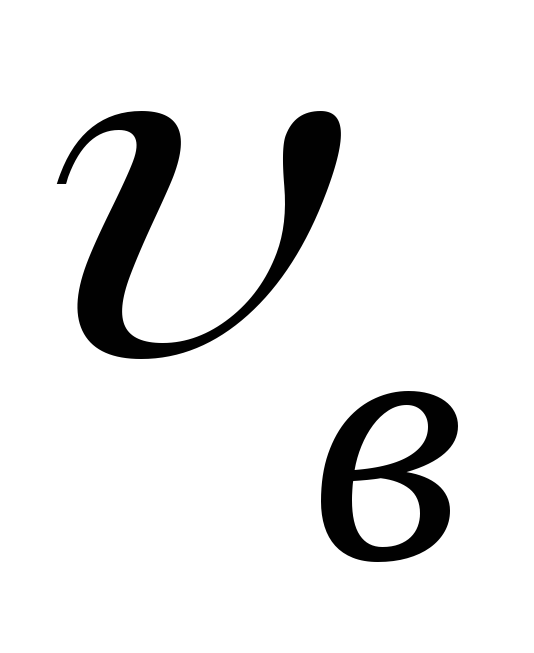 .
.
Получите выражение для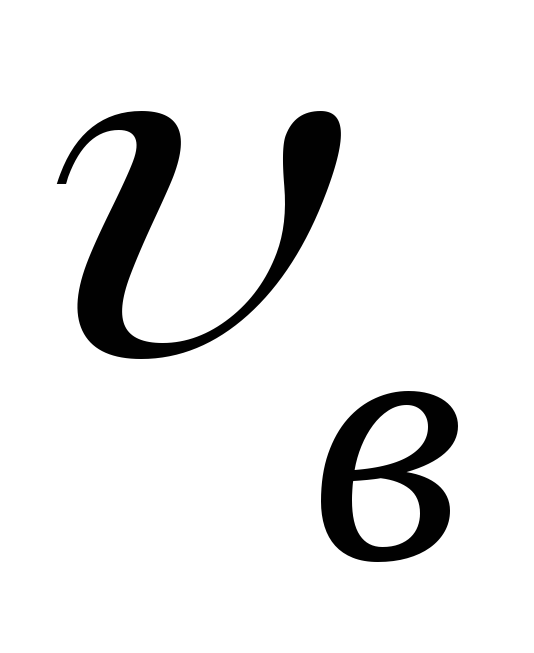 .
.
Как изменяется график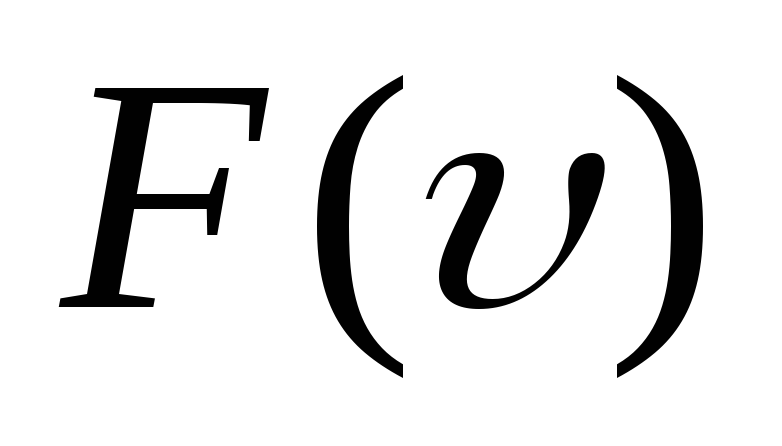 при повышении температуры?
при повышении температуры? -
Получите
барометрическую формулу. Что она
определяет? -
Получите
зависимость концентрации молекул газа
в поле силы тяжести от высоты. -
Запишите
закон распределения Больцмана а) для
молекул идеального газа в поле силы
тяжести; б) для частиц массой m,
находящихся в роторе центрифуги,
вращающейся с угловой скоростью
 .
. -
Объясните
физический смысл распределения
Максвелла-Больцмана.
Лекция №9
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение средней квадратичной скорости молекул газа
Содержание:
- Средняя квадратичная скорость молекул газа — что это за параметр
- От каких величин зависит в идеальном газе
-
Формула средней квадратичной скорости молекул
- Как посчитать в зависимости от природы газа и температуры?
Средняя квадратичная скорость молекул газа — что это за параметр
Молекулы любого газа пребывают в постоянном движении. Его можно охарактеризовать с точки зрения средней их скорости или средней квадратичной скорости. Первое понятие имеет специальный термин — скорость теплового движения. Второе — средняя квадратичная скорость — величина, для которой существует специальная формула.
Для того, чтобы полностью разобраться в понятии средней квадратичной скорости молекул газа, вводится условный участник процесса — идеальный газ.
Определение
Идеальный газ — это математическая модель, потенциальную энергию которой принимают за ноль, а кинетическую характеризуют в полном объеме. Идеальный газ подходит в качестве модели окружающих нас газов, например, обычного воздуха.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Средняя квадратичная скорость — физическая величина, отличная от средней арифметической скорости молекул, определяемая по формуле: корень квадратный из средней арифметической квадратов скоростей различных молекул.
Кинетическая энергия определяется скоростью движения молекул, поэтому зависит от температуры. Скорости молекул одного газа не одинаковы. Часть молекул движутся очень быстро, часть — с незначительной скоростью. Однако для большинства существует некое среднее значение. Если изобразить это на графике в виде параболы, такие молекулы со средней скоростью будут составлять ее верхнюю часть.
В единице объема газа содержится огромное число молекул. Поэтому, например, его давление на стенки сосуда — величина постоянная. В ином случае, если бы в единицу времени о стенку ударялось различное количество молекул, давление бы «скакало».
Из изложенного можно сделать вывод: скорость — свойство отдельной молекулы газа, а давление — характеристика их совокупности.
От каких величин зависит в идеальном газе
Для идеального газа средняя квадратичная скорость прямо пропорциональна его температуре и обратно пропорциональна молярной массе газа.
В математическом выражении данная зависимость выражается через корень квадратный:
(V=surd(3RT/mu)
)
где R — универсальная постоянная величина, Т — температура газа, μ — молярная масса.
Из формулы видно, что искомая величина (средняя квадратичная скорость) зависит от природных свойств газа и его температуры.
Формула средней квадратичной скорости молекул
Математическое выражение формулы выглядит следующим образом:
(V_{ср;кв}=surd(V_{12}+V_{22}+V_{n2})/N)
В формуле присутствуют следующие условные обозначения: V1, V2, Vn — скорости молекул, а N — их количество.
Формула может иметь и другой вид:
(V_{ср;кв}=surd1/Nastsum V_2)
или
(V_{ср;кв}=int V_2F(V)dV)
Как посчитать в зависимости от природы газа и температуры?
Проведенное интегрирование формулы, цель которого определить зависимость искомой единицы от природных свойств иттемпературы газа, приводит расчеты к формуле:
(V_{ср;кв}=surd(3kT/mo))
или
(V_{ср;кв}=surd(3RT/mu))
При поступательном движении молекул газа Vср кв — составляющая уравнения для молекулярно-кинетической теории.
Если n=N/V, где N — число частиц, а V — объем, то концентрация частиц n получает следующее формульное выражение:
(p=1/3ast nmo(V_{ср;кв})^2)
Насколько полезной была для вас статья?
Рейтинг: 2.33 (Голосов: 3)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так