Средняя скорость считается так: весь путь поделить на всё время движения. Формула одна и очень простая, но почему-то школьники часто путаются в задачах на среднюю скорость. Разберу три характерные задачи и основные ошибки. Возможно, статья будет полезна учителям и репетиторам, а также школьникам.
1. Половина пути
Первую половину пути поезд ехал со скоростью 60 км/ч, а вторую – 90 км/ч. С какой средней скоростью ехал поезд на всём пути?
Первым делом школьник захочет сложить эти две скорости и поделить пополам. Логично? Да. Но, к сожалению, неправильно.
Объясняю, почему. Поскольку первую половину пути поезд ехал с меньшей скоростью, то времени было затрачено больше, чем на вторую. А значит, вклад отдельных скоростей неравнозначен, и нельзя так просто делить пополам.
Тут школьник может впасть в панику. Что делать? Умножать? Делить? Непонятно. Воспользоваться напрямую формулой “расстояние поделить на время” не получится – ни расстояние, ни время нам неизвестно.
Для школьников, только начинающих изучать основы физики, бывает трудно оперировать с неизвестными величинами. Нам не дано ничего, кроме скоростей, как же быть? В качестве маленькой ступеньки к освоению неизвестности могу предложить следующий ход – сначала додумать неизвестные данные. Возьмём и сами решим, пусть поезд пройдет 180 километров, цифру возьмем так, чтобы легко делилась.
Тогда половина пути будет 90 километров. Поезд пройдет её за 1,5 часа. Вторую половину пути – за 1 час. Это легко посчитает любой школьник. Значит, общее время в пути будет 2,5 часа. Делим общее расстояние 180 километров на 2,5 часа, и получаем 72 км/ч.
Это просто и понятно, но учитель такую задачу не примет. Откуда мы взяли 180 километров, когда это неизвестно? Тем не менее, дав себе эти неизвестные данные, мы продумали алгоритм и довели задачу до ответа. Осталось формализовать это решение, так чтобы не использовать то, что не дано. Обозначим наши 180 километров за S, и опишем всё, что мы делали раньше, только вместо цифр используем буквы.
Получается, что зная ход решения “в цифрах”, мы переводим его в буквенные обозначения. И тут главное не остановиться на полдороги, не смущаться, что нам неизвестно расстояние. Ведь оно в конце сократилось, и средняя скорость оказалась независящей от расстояния (что вполне логично). И от школьника здесь требуются уже алгебраические умения – складывать дроби, переворачивать их.
Если подобная задача встретилась в тесте, где требуется только ответ, можно вообще не заморачиваться – так как средняя скорость в данной задаче не зависит от расстояния, можно посчитать при любом удобном расстоянии. По крайней мере, это лучше, чем сидеть и ломать голову, не зная, как подступиться к решению. Если же требуется оформление – тут числовое решение может помочь как переходный этап, чтобы понять, что именно делать с формулами, как их крутить-вертеть.
Школьникам часто бывает трудно переходить на новый уровень абстракции – от чисел к переменным, которые могут принимать разные числовые значения. В алгебре это тренируют, но там одна переменная икс, и иногда игреки встречаются. А в физике этих переменных пруд пруди, в каждой задаче они разные, и если ученик не освоил этот уровень, то физика кажется ему супер-трудной. Кроме того, в школе переход от чисел к переменным часто упускают, в программе отдельных навыков работы с формулами нет.
2. Средняя скорость по графику пути
Пусть нам дан график зависимости координаты от времени. Требуется определить среднюю скорость.
По графику видно, что движение состоит из четырех этапов:
- Тело стартует в нуле и через 2 секунды оказывается на координате 2 м.
- Тело останавливается, и в течение 4 секунд покоится в точке с координатой 2 м.
- Тело начинает движение, и через 2 секунды оказывается в точке 6 м.
- Тело движется в обратном направлении, и через 2 секунды оказывается в точке 5 м.
Проговорить, понять все эти этапы – важная часть решения. А дальше многие школьники начинают вычислять скорости движения на каждом этапе: На первом – 1 м/с, на втором – 0, на третьем – 2 м/с, на четвертом – 0,5 м/с. Вот это действие как раз лишнее. Для того, чтобы вычислить среднюю скорость, вовсе не обязательно знать скорости на каждом этапе!
Вспомним определение средней скорости – это весь путь, поделить на всё время. Поэтому просто по графику считаем весь путь – 6 метров “туда” и 1 метр “обратно”, в сумме 7 метров. Общее время движения – 10 секунд. Делим 7 метров на 10 секунд, получаем 0,7 м/с.
3. Средняя скорость по графику скорости
Бывает так, что нам дан график зависимости скорости от времени, и требуется определить среднюю скорость. Вот, к примеру, такой график.
Читаем график. Движение состоит из трёх этапов
- С начала движения до момента времени 2 с тело движется с постоянной скоростью 2 м/с
- От 2 до 6 с тело движется со скоростью 6 м/с
- В последние 4 секунды от 6 до 10 с тело замедляется, снижая свою скорость до нуля.
Попытки что-то сделать со значениями скорости самими по себе здесь обречены на провал. Опять надо найти весь путь и всё время движения. Путь по графику скорости определяется как площадь под графиком, причем если график идет ниже нуля, то соответствующие участки складываются.
Считаем площадь фигуры – два прямоугольника на первых двух этапах и треугольник на третьем. Первый этап – 4 м, второй этап – 24 м, третий этап – 12 м. Значит, весь путь будет 40 метров. Всё время 10 секунд, значит, средняя скорость 4 м/с.
Общие рекомендации для решения задач на среднюю скорость
1. Средняя скорость – это всегда весь путь делить на всё время. Данные об отдельных скоростях сами по себе не дадут полной информации о средней скорости. Используем только эту формулу.
2. Следует проанализировать конкретную ситуацию и понять, как можно применить формулу. Если кажется, что не хватает данных – не смущаться.
3. Данные по скоростям на отдельных этапах могут быть полезны для проверки готового ответа: средняя скорость должна лежать между минимальной и максимальной.
Спасибо, что прочитали до конца! Желаю школьникам хорошей учёбы, учителям – понятливых и любопытных учеников, родителям – чтобы дети радовали. Буду рада лайкам и новым подписчикам!
Неравномерное прямолинейное движение. Средняя скорость
- График скорости при неравномерном прямолинейном движении
- Как найти путь и перемещение по графику скорости?
- Средняя скорость и средняя путевая скорость
- Задачи
- Лабораторная работа №3. Определение средней скорости движения тела
п.1. График скорости при неравномерном прямолинейном движении
Прямолинейное и равномерное движение возможно лишь на участке пути.
Любое тело со временем меняет свою скорость, как по величине, так и по направлению.
Движение с переменной скоростью называют неравномерным.
Для описания неравномерного движения его можно разбить на участки, на которых скорость постоянна, и свести задачу к уже известному нам равномерному прямолинейному движению.
Например, пусть велосипедист добрался из города A в город B за 1 час. Первые полчаса он ехал со скоростью 9 км/ч, а потом проколол шину, и вторые полчаса шел пешком со скоростью 3 км/ч.
Направим ось ОХ также от A к B и получим значения проекций скоростей: $$ v_{x1}=9 text{км/ч}, v_{x2}=3 text{км/ч} $$ Построим график скорости для этого случая:
Графиком скорости (v_x=v_x(t)) при неравномерном прямолинейном движении, которое можно разбить на участки с постоянной скоростью, является ломаная линия.
п.2. Как найти путь и перемещение по графику скорости?
Мы уже знаем, что путь равен площади прямоугольника, который образуется между отрезком графика скорости и отрезком (triangle t) на оси (t) (см. §8 данного справочника).
В таком случае, путь велосипедиста в нашем примере:
begin{gather*} s=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text{(км)} end{gather*} Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км.
Общий путь велосипедиста равен 6 км. Расстояние между городами 6 км. 
Если принять город A за начало отсчета с (x_0=0), то координата велосипедиста в конце пути: $$ x_{к}=x_0+s=0+6=6 text{(км)} $$ Перемещение по оси ОХ: (triangle x=x_{к}-x_0=6 text{(км)}).
Теперь рассмотрим другую ситуацию. Пусть велосипедист выехал из A в B и двигался со скоростью 9 км/ч в течение получаса. Но, после того как проколол шину, он развернулся и пошел пешком назад в A. Где будет находиться велосипедист через полчаса после разворота?
Снова направим ось ОХ от A к B и получим значения проекций скоростей: $$ v_{x1}=9 text{км/ч}, v_{x2}=-3 text{км/ч} $$ Построим график скорости для этого случая:
Путь велосипедиста по-прежнему будет равен сумме площадей прямоугольников, которые образует ломаная (v_x(t)) с осью (t): begin{gather*} x=v_{x1}cdot triangle t_1+|v_{x2}|cdottriangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text{(км)} end{gather*} 
Если мы учтем знак (v_{x2}) и уберем модуль, то получим величину перемещения по оси ОХ: begin{gather*} triangle x=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2\ triangle x=9cdot 0,5-3cdot 0,5=4,5-1,5=3 text{(км)} end{gather*} Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км в обратном направлении.
Конечная координата: $$ x_{к}=x_0+triangle x=0+3=3 text{(км)} $$ 
Ответ на вопрос задачи найден. Через полчаса после разворота велосипедист будет находиться в точке D в 3 км от города A.
Пусть неравномерное прямолинейное движение разбито на (n) участков с постоянными скоростями. Каждому такому участку соответствует промежуток времени (triangle t_i) и постоянная скорость (v_{xi}, i=overline{1,n}).
Тогда:
Весь пройденный путь равен сумме площадей прямоугольников на графике скорости: $$ s=|v_{x1}|cdottriangle t_1+|v_{x2}|cdottriangle t_2+…+|v_{xn}|cdottriangle t_n $$ Величина перемещения по оси ОХ равна сумме площадей прямоугольников с учетом знака: $$ triangle x=v_{x1}cdottriangle t_1+v_{x2}cdottriangle t_2+…+v_{xn}cdottriangle t_n $$ Конечная координата равна: (x_{к}=x_0+triangle x).
п.3. Средняя скорость и средняя путевая скорость
Средняя скорость на нескольких участках движения равна отношению общего перемещения к общему времени, затраченному на это перемещение: $$ overrightarrow{v_{cp}}=frac{overrightarrow{r_1}+overrightarrow{r_2}+…+overrightarrow{r_n}}{t_1+t_2+…+t_n}=frac{overrightarrow{r}}{t} $$
Средняя путевая скорость на нескольких участках движения равна отношению общего пути к общему времени, затраченному на этот путь: $$ v_{cp.п}=frac{s_1+s_2+…+s_n}{t_1+t_2+…+t_n}=frac{s}{t} $$
Если тело все время движется в одном направлении, величина средней скорости равна средней путевой скорости, т.к. на каждом участке путь совпадает с модулем перемещения.
Если тело меняет направление движения, величина средней скорости меньше средней путевой скорости.
В нашем примере с велосипедистом, который все время двигался в одну сторону и дошел до города B, получаем: begin{gather*} |overrightarrow{v_{cp}}|=frac{|overrightarrow{r}|}{t}=frac{triangle x}{t}=frac 61=6 text{(км/ч)}\ v_{cp.п}=frac st=frac 61=6 text{(км/ч)} end{gather*} Величина средней скорости равна средней путевой скорости.
А вот для случая, когда велосипедист развернулся и пошел обратно: begin{gather*} |overrightarrow{v_{cp}}|=frac{|overrightarrow{r}|}{t}=frac{triangle x}{t}=frac 31=3 text{(км/ч)}\ v_{cp.п}=frac st=frac 61=6 text{(км/ч)} end{gather*} Величина средней скорости меньше средней путевой скорости.
п.4. Задачи
Задача 1. По графику скоростей найдите среднюю скорость и среднюю путевую скорость движения.
a)
Все движение можно разделить на три участка с постоянной скоростью:
begin{gather*} triangle t_1=3-0=3 c, v_{x1}=5 text{м/с}\ triangle t_2=5-3=2 c, v_{x2}=1 text{м/с}\ triangle t_3=7-5=2 c, v_{x3}=2 text{м/с}\ end{gather*} Общий путь: begin{gather*} s=|v_{x1}|cdot triangle t_1+|v_{x2}|cdot triangle t_2+|v_{x3}|cdot triangle t_3\ s=5cdot 3+1cdot 2+2cdot 2=21 text{(м)} end{gather*} Все проекции скоростей положительны, тело двигалось в одном направлении, общее перемещение равно общему пути: (triangle x=s=21) (м)
Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (с)
Величина средней скорости равна средней путевой скорости: $$ |overrightarrow{v_{cp}}|=v_{cp.п}=frac st=frac{21}{7}=3 text{(м/с)} $$ Ответ: (|overrightarrow{v_{cp}}|=v_{cp.п}=3 text{(м/с)})
б) 
Все движение можно разделить на три участка с постоянной скоростью:
begin{gather*} triangle t_1=3-0=3 c, v_{x1}=5 text{м/с}\ triangle t_2=5-3=2 c, v_{x2}=-2 text{м/с}\ triangle t_3=7-5=2 c, v_{x3}=1 text{м/с}\ end{gather*} Общий путь: begin{gather*} s=|v_{x1}|cdot triangle t_1+|v_{x2}|cdot triangle t_2+|v_{x3}|cdot triangle t_3\ s=5cdot 3+2cdot 2+1cdot 2=21 text{(м)} end{gather*} Проекции скоростей имеют разные знаки, тело двигалось вперед и назад.
Общее перемещение будет меньше общего пути: begin{gather*} triangle x=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2+v_{x3}cdot triangle t_3\ triangle x=5cdot 3-2cdot 2+1cdot 2=13 text{(м)} end{gather*} Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (c)
Величина средней скорости: $$ |overrightarrow{v_{cp}}|=frac{triangle x}{t}=frac{13}{7}approx 1,86 text{(м/с)} $$ Средняя путевая скорость: $$ v_{cp.п}=frac st=frac{21}{7}=3 text{(м/с)} $$ Ответ: (|overrightarrow{v_{cp}}|approx 1,86 text{(м/с)}; v_{cp.п}=3 text{(м/с)})
Задача 2. Мотоциклист проехал расстояние между двумя пунктами со скоростью 40 км/ч. Потом увеличил скорость до 80 км/ч и проехал расстояние в два раза меньше. Найдите среднюю скорость мотоциклиста за все время движения.
Мотоциклист двигался все время в одном направлении, величина средней скорости равна средней путевой скорости: (v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 40 | (frac{2d}{40}=frac{d}{20}) | (2d) |
| 2й участок | 80 | (frac{d}{80}) | (d) |
| Сумма | – | (t=frac{d}{20}+frac{d}{80}) | (s=2d+d=3d) |
Упростим сумму дробей: $$ t=frac{d}{20}+frac{d}{80}=frac{4d+d}{80}=frac{5d}{80}=frac{d}{16} $$ Получаем: $$ v_{cp}=frac st=frac{3d}{d/16}=3cdot 16=48 text{(км/ч)} $$
Ответ: 48 км/ч
Задача 3. Автомобиль проехал первую половину пути по шоссе со скоростью 90 км/ч, а вторую половину – по грунтовой дороге со скоростью 30 км/ч. Найдите среднюю скорость автомобиля.
Величина средней скорости равна средней путевой скорости:
(v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 90 | (frac{s}{2cdot 90}=frac{s}{180}) | (frac s2) |
| 2й участок | 30 | (frac{s}{2cdot 30}=frac{s}{60}) | (frac s2) |
| Сумма | – | (t=frac{s}{180}+frac{s}{60}) | (s) |
Упростим сумму дробей: $$ t=frac{s}{180}+frac{s}{60}=frac{s+3s}{180}=frac{4s}{180}=frac{s}{45} $$ Получаем: $$ v_{cp}=frac st=frac{s}{s/45}=45 text{(км/ч)} $$
Ответ: 45 км/ч
Задача 4*. Туристы прошли по маршруту со средней скоростью 32 км/ч. Маршрут был разделен на три участка, первый участок преодолевался пешком, второй – на автобусе, третий – на катере. Найдите скорость на каждом участке, если длины этих участков относятся как 1:4:45, а соответствующие интервалы времени как 4:1:20.
Величина средней скорости равна средней путевой скорости:
(v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | (frac{d}{4t}) | (4t) | (d) |
| 2й участок | (frac{4d}{t}) | (t) | (4d) |
| 3й участок | (frac{45d}{20t}) | (20t) | (45d) |
| Сумма | – | (25t) | (50d) |
По условию средняя скорость: $$ v_{cp}=frac st=frac{50d}{25t}=2cdot frac dt=32Rightarrow frac dt=16 $$ Получаем: begin{gather*} v_1=frac{d}{4t}=frac{16}{4}=4 text{(км/ч)}\ v_2=frac{4d}{t}=4cdot 16=64 text{(км/ч)}\ v_3=frac{9d}{4t}=frac{9}{4}cdot 16=36 text{(км/ч)} end{gather*}
Ответ: 4 км/ч, 64 км/ч и 36 км/ч
Задача 5*. Первую половину маршрута турист проехал на попутном автомобиле в 10 раз быстрее по сравнению с ходьбой пешком, а вторую половину – на попутном возу в 2 раза медленней. Сэкономил ли турист время на всем маршруте по сравнению с ходьбой пешком?
Пусть (v) – скорость туриста при ходьбе пешком.
Найдем среднюю путевую скорость (v_{cp}) и сравним ее со скоростью (v).
Если (v_{cp}gt v), то турист выиграл время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | (10v) | (frac{s}{2cdot 10v}=frac{s}{20v}) | (frac s2) |
| 2й участок | (frac{v}{2}) | (frac{s}{2cdot v/2}=frac sv) | (frac s2) |
| Сумма | – | (t=frac{s}{20v}+frac sv) | (s) |
Упростим сумму дробей: $$ t=frac{s}{20v}+frac sv=frac svleft(frac{1}{20}+1right)=frac{21}{20}cdot frac sv $$ Средняя скорость: $$ v_{cp}=frac{s}{frac{21}{20}cdotfrac sv}=frac{20}{21}vgt v $$Средняя скорость поездки оказалась меньше пешей скорости туриста.
Значит, он не выиграл по времени.
Ответ: нет
п.5. Лабораторная работа №3. Определение средней скорости движения тела
Цель работы
Научиться определять среднюю скорость движения тела по данным измерений на разных участках. Научиться вычислять абсолютные и относительные погрешности при подстановке данных измерений в формулы.
Теоретические сведения
В лабораторной работе изучается движение тела (шарика) по двум участкам (желобам) с различной скоростью.
Величина средней скорости при движении на двух участках определяется как средняя путевая скорость: $$ v_{cp}=frac{s_1+s_2}{t_1+t_2} $$ где (s_1) и (s_2) – длина первого и второго участка; (t_1) и (t_2) – время движения по каждому из участков.
Длина участков измеряется с помощью мерной ленты с ценой деления (triangle=1) см,
инструментальная погрешность равна: (d=frac{triangle}{2}=0,5) см
Абсолютная погрешность измерений при работе с мерной лентой равна инструментальной погрешности, поэтому: (triangle s_1=triangle s_2=d=0,5) см
Погрешность суммы двух длин: (triangle(s_1+s_2)= triangle s_1+triangle s_2=2d=1) см
Измерение времени на каждом участке проводится в сериях их 5 измерений по методике, описанной в Лабораторной работе №2 (см. §4 данного справочника).
Погрешность суммы двух измерений: (triangle(t_1+t_2)=triangle t_1+triangle t_2)
Относительная погрешность частного равна сумме относительных погрешностей делимого и делителя: $$ delta_{v_{cp}}=delta_{s_1+s_2}+delta_{t_1+t_2} $$ Абсолютная погрешность определения средней скорости: $$ triangle v_{cp}=v_{cp}cdot delta_{v_{cp}} $$
Приборы и материалы
Два желоба (не менее 1 м каждый), шарик, мерная лента, секундомер.
Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Соберите установку, как показано на рисунке. Установите один желоб под углом, другой – горизонтально, закрепите, поставьте в конце горизонтального участка упор. Подберите длину желобов и наклон так, чтобы движение по каждому участку было не менее 1 с. 
3. Измерьте фактическую длину каждого участка движения в готовой установке с помощью мерной ленты.
4. Найдите относительную погрешность суммы двух длин (delta_{s_1+s_2}=frac{triangle(s_1+s_2)}{s_1+s_2})
5. Проведите серии по 5 экспериментов для определения (t_1) и (t_2) с помощью секундомера.
6. Найдите (triangle t_1, triangle t_2, triangle(t_1+t_2), delta_{t_1+t_2})
7. По результатам измерений и вычислений найдите (v_{cp}, delta_{v_{cp}}) и (triangle v_{cp}).
8. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
1) Измерение длин
Цена деления мерной ленты (triangle =1) см
Инструментальная погрешность мерной ленты (d=frac{triangle}{2}=0,5) см
Результаты измерений:
(s_1=112) cм
(s_2=208) cм
Сумма длин участков: (s_1+s_2=112+208=320) (см)
Абсолютная погрешность суммы: (triangle (s_1+s_2)=triangle s_1+triangle s_2=2d=1) см
Относительная погрешность суммы: $$ delta_{s_1+s_2}=frac{triangle (s_1+s_2)}{s_1+s_2}=frac{1}{320}=0,3125% $$
2) Измерение времени
Цена деления секундомера (triangle =0,2) с
Инструментальная погрешность секундомера (d=frac{triangle}{2}=0,1) с
Время движения по наклонному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t_1) c | 1,5 | 1,6 | 1,5 | 1,4 | 1,4 | 7,4 |
| (triangle) c | 0,02 | 0,12 | 0,02 | 0,08 | 0,08 | 0,32 |
Найдем среднее время спуска с наклонного желоба: $$ t_1=frac{1,5+1,6+1,5+1,4+1,4}{5}=frac{7,4}{5}=1,48 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_1): $$ triangle_1=|1,5-1,48|=0,02; triangle_2=|1,6-1,48|=1,02 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0,02+0,12+0,02+0,08+0,08}{5}=frac{0,32}{5}=0,064 text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_1=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,064right}=0,1 text{c} $$ Округляем полученное значение времени до десятых. begin{gather*} t_1=(1,5pm 0,1) text{c}\ delta_{t_1}=frac{0,1}{1,5}=frac{1}{15}approx 6,7text{%} end{gather*} Время движения по горизонтальному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t_2) c | 2,3 | 2,4 | 2,2 | 2,2 | 2,4 | 11,5 |
| (triangle) c | 0 | 0,1 | 0,1 | 0,1 | 0,1 | 0,4 |
Найдем среднее время движения по горизонтали: $$ t_2=frac{2,3+2,4+2,2+2,2+2,4}{5}=frac{11,5}{5}=2,3 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_2): $$ triangle_1=|2,3-2,3|=0; triangle_2=|2,4-2,3|=0,1 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0+0,1+0,1+0,1+0,1}{5}=frac{0,4}{5}=0,08 text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_2=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,08right}=0,1 text{c} $$ Получаем: begin{gather*} t_2=(2,3pm 0,1) text{c}\ delta_{t_2}=frac{0,1}{2,3}=frac{1}{23}approx 4,4text{%} end{gather*}
3) Расчет погрешности суммы интервалов времени
Сумма интервалов времени: $$ t_1+t_2=1,5+2,3=3,8 text{(c)} $$ Абсолютная погрешность суммы: $$ triangle(t_1+t_2)=triangle t_1+triangle t_2=0,1+0,1=0,2 text{(c)} $$ Относительная погрешность суммы: $$ delta_{t_1+t_2}=frac{triangle (t_1+t_2)}{t_1+t_2}=frac{0,2}{3,8}=frac{1}{19}approx 5,3text{%} $$
4) Расчет средней скорости $$ v_{cp}=frac{s_1+s_2}{t_1+t_2}=frac{320}{3,8}approx 84,2 left(frac{text{см}}{text{c}}right) $$ Относительная ошибка частного: $$ delta_{v_{cp}}=delta_{s_1+s_2}+delta_{t_1+t_2}=frac{1}{320}+frac{1}{19}approx 0,003125+0,0526approx 0,0557approx 0,056=5,6text{%} $$ (оставляем две значащие цифры).
Абсолютная ошибка: $$ v_{cp}=v_{cp}cdotdelta_{v_{cp}}=84,2cdot 0,056approx 4,7 left(frac{text{см}}{text{c}}right) $$ Получаем: begin{gather*} v_{cp}=(84,2pm 4,7) text{см/с}\ delta_{v_{cp}}=5,6text{%} end{gather*}
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения длин проводились с помощью мерной ленты. Ошибка измерений равна инструментальной ошибке 0,5 см.
Измерения времени проводились с помощью секундомера. По результатам серий экспериментов ошибка была принята равной инструментальной 0,1 с.
Получена величина средней скорости: begin{gather*} v_{cp}=(84,2pm 4,7) text{см/с}\ delta_{v_{cp}}=5,6text{%} end{gather*}
Как найти среднюю скорость по графику
Движение различных тел в окружающей среде характеризуется рядом величин, одна из которых – средняя скорость. Этот обобщенный показатель определяет скорость тела на всем перемещении. Зная зависимость модуля мгновенной скорости от времени, среднюю скорость можно найти с помощью графического метода.
Инструкция
Постройте по данным задачи график зависимости скорости движения тела от времени v(t). Здесь горизонтальная координата представляет собой изменение времени (с), вертикальная – скорости (м/с). Как правило, в задачах рассматривается неравномерное перемещение тел в определенные промежутки времени. Любое изменение скорости на графике будет отображено возрастанием или убыванием. Например, при начале движения тела с постоянным ускорением в течение 20 с его скорость в итоге составила 15 м/с. Отложите на графике прямую, начинающуюся в начале координат (0, 0) и заканчивающуюся в точке (20, 15), где 20 с откладываются вправо по оси времени t, а 15 м/с – вверх по скорости. При наличии равномерного движения тела отобразите его прямой, параллельной горизонтальной оси.
Для нахождения средней скорости перемещения нужно знать путь и время, затраченное на движение. Вычислите площадь S под кривой v(t), которая является графическим представлением пройденного телом пути L. Часто график перемещения ограничивает фигуру трапецию. Ее площадь находится по формуле: S = ½*(t0 + t1)*vn, где t0 и t1 – основания трапеции – части графика скорости, vn – высота фигуры, здесь максимальная скорость в пути. Подставьте в формулу известные значения и вычислите результат. Если график v(t) представляет собой не трапецию, ее площадь вычисляется по иным формулам, в зависимости от полученной фигуры.
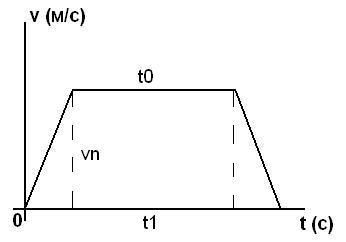
Найдите среднюю скорость движения тела по формуле Vср = L/t. Подставив заданное время перемещения и вычисленный путь, посчитайте числовое значение средней скорости.
Среднюю скорость можно вычислить и по графику зависимости пути от времени l(t). Для этого соедините прямой линией начальную и конечную точки рассматриваемого участка перемещения. Средняя скорость тела будет равна тангенсу угла наклона полученной прямой к оси времени.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Если движение связано с постоянным ускорением, в этой статье мы можем изучить простой метод определения средней скорости на графике времени ускорения.
Чтобы узнать, как найти среднюю скорость на графике времени ускорения, мы должны знать, что Vсредний объекта измеряется путем деления общего изменения положения, наблюдаемого в движении, на время, необходимое для завершения этого движения. Аналогично на графике АТ путем измерения наклона начальной и последней точек графика.
Теперь дайте нам знать, как найти среднюю скорость на графике времени разгона подробно.
Как найти среднюю скорость на графике положение-время
Чтобы найти среднюю скорость на графике PT, мы должны знать следующие основные идеи:
В общем, мы знаем, что Vсредний рассчитывается исходя из критериев положения и времени; эти два важны при измерении Vсредний, Итак, что мы можем сделать, так это присвоить значения и пометить ось, а затем построить ее. Нарисуйте наклон кривой, отметьте любые две точки и рассмотрите начальную и конечную точки. Значение этого наклона будет Vсредний.
Теперь дайте нам знать о графике времени разгона.
График ускорения-времени
В физике существует множество графиков отношений, позволяющих быстро находить значения конкретных величин.
Графики времени ускорения – один из тех важнейших графиков. Нам необходимо преобразовать график скорости-времени в график времени ускорения, чтобы узнать конкретные значения, т. Е. Путем нахождения производной определенных значений, таких как средняя скорость. Мы можем взять наклон касательной к кривой, проведенной на графике в любой точке.
Теперь, когда мы узнали о графике AT, расскажите нам о его особенностях.
Особенности графика времени разгона после средней скорости.
Существенные особенности графика времени ускорения в соответствии с расчетом средней скорости следующие:
- Чтобы найти Vсредний на графике AT, после выполнения всех маркировок, построения графиков и объединения значений.
- Нарисуйте уклон, и этот уклон называется рывком. Здесь значения наклона будут равны полной средней скорости.
- В случае постоянного ускорения s должен вычислить значение наклона для полученной горизонтальной линии, которая называется средней скоростью.
После всего этого пришло время увидеть различные аспекты этого подхода.
Аспекты графика времени ускорения и средней скорости
Ниже можно увидеть различные аспекты графика времени ускорения и средней скорости.
- График времени ускорения для всех объектов, движущихся с постоянной V, будет аналогичным.
- Объектом может быть большой самолет или маленький муравей, и график будет таким же, но с разными значениями.
- График будет коллинеарен по оси x (горизонтальная линия).
- Буква V будет одинаковой для всех этих объектов в их справочнике.
Как найти среднюю скорость на графике времени разгона?
Чтобы найти букву V на графике времени ускорения, необходимо выполнить определенные действия.
Прежде всего, мы должны отметить первоначальный скорость и постоянное ускорение тела в движении.
Затем используйте это ускорение и узнайте конечную скорость.
Найдя все значения, нанесите их на график AT.
- Рассмотрим любые две точки и нарисуем наклон.
- Затем измерьте площадь под этой кривой и используйте формулу
- Формула включает расстояние и время, используется формула средней скорости и выводится из термина, используемого для измерения средних значений.
- Позже проводятся касательная и наклон, чтобы получить значение требуемого V.
Таким образом, мы можем найти среднюю скорость на графике времени ускорения.
Связь между графиком времени ускорения и средней скоростью
Чтобы найти V., мы иногда используем график времени разгона. Есть два критических случая ускорения при измерении средней скорости.
- И средняя скорость величины, и ускорение не зависят друг от друга.
- Если ускорение больше, то изменение скорости будет максимальным, но это не говорит о скорости в конкретный момент времени. Здесь мы получаем общее значение скорости, называемое средней скоростью.
- Переходя к другому случаю, если ускорение постоянное, график AT будет линейным. Здесь средняя скорость будет одинаковой во всех точках.
Теперь давайте решим некоторые проблемы, чтобы лучше их понять.
Проблемы с нахождением средней скорости по графику времени разгона.
Вот несколько проблем, которые необходимо решить, чтобы лучше понять концепцию.
Проблема 1
The начальная скорость тела, движущегося в положительном направлении равен нулю, но при движении его ускорение равно 9 м/с; найти его скорость будет 8с?
Решение:
∆V = a∆t
∆V = (9.8 м / с) (1.0 с)
∆V = 9.8 м / с
Теперь нужно рассчитать окончательную скорость.
∆V = a∆t
∆V = (9 м / с) (8 с)
∆V = 72 м / с
Если мы найдем это на графике времени ускорения, мы найдем среднюю скорость, вычислив площадь под кривой.
Это одна из фундаментальных проблем, которые нужно решить на V на AT-графе.
Различные подходы к определению средней скорости
Среднюю скорость можно найти в основном двумя способами, которые показаны ниже:
- С помощью специальной формулы мы можем найти среднюю скорость разными способами, используя расстояние или изменение положения объекта на пути в определенное время.
- Мы даже можем использовать расчет, чтобы определить требуемую среднюю скорость.
- Еще один способ узнать Vсредний использует определенные графики, такие как график положения-времени, график скорости-времени и даже график ускорения-времени.
- Построив значения данных на графике, а затем выполнив определенные шаги, можно рассчитать среднюю скорость.
Упомянутые ранее подходы являются основными методами, используемыми для определения средней скорости.
Чтобы узнать о мгновенная скорость
Часто задаваемые вопросы | FAQs
Какая средняя скорость зависит от ускорения и времени?
На графике времени ускорения средняя скорость тела вычисляется с учетом двух точек на графике.
Если ускорение переменное, есть небольшие трудности с измерением средней скорости на графике времени ускорения. Тем не менее, если ускорение постоянное, Vavg можно найти, сложив скорость тела в начале и в конце по определенной формуле.
Как найти среднюю скорость по ускорению и времени?
Средняя скорость, которую обычно обозначают в Vсредний может быть дано следующим образом с использованием ускорения и времени.
Мы используем ускорение, обозначаемое как a, и время как t, с помощью расстояния и времени. Мы можем выполнить определенные шаги и вывести формулу с помощью, мы можем измерить Vсредний тела; формула приведена ниже.
S = vi + ½ в2
vсредний = s / t = vi + ½ в2
vсредний = Vi + ½ (вf – vi)
vсредний = (см.f – vi)
То есть ускорение, умноженное на время, равно общему изменению скорости.
Что такое график скорости-времени?
Даже график скорости-времени – один из важнейших графиков в физике.
Это реальное представление изменения скорости объекта во время движения в зависимости от затраченного времени. Графики могут быть любого типа в зависимости от постоянного и переменного аспектов. Если скорость быстрая, линия графика не будет горизонтальной по отношению к какой-либо оси, и наоборот, если есть какой-либо изменяемый член, тогда линия графика будет параллельна оси.
Что такое график ускорения-времени?
График времени ускорения включает ускорение и время соответственно по осям x и y.
График зависимости ускорения от времени строится в зависимости от времени, затраченного объектом на движение по линейной траектории. На этом графике можно найти среднюю скорость в зависимости от постоянного и переменного ускорения. Значение графика представлено в виде y = a (t). Уникальная особенность этого графика в том, что мы можем найти как положительные, так и отрицательные значения скорости и даже ускорения.
Средняя скорость неравномерного движения уравнение
Неравномерное движение — это движение, при котором за равные промежутки времени тело проходит разные пути.
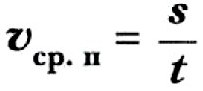Средняя путевая скорость — это физическая величина, равная отношению пути, пройденного телом за рассматриваемый промежуток времени, к длительности этого промежутка.
Средняя путевая скорость — скалярная неотрицательная величина.
Средняя скорость тела за промежуток времени t — это физическая величина, равная отношению перемещения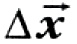 
, совершённого телом, к длительности этого промежутка времени.
Средняя скорость — вектор. Она направлена туда, куда направлено перемещение тела за рассматриваемый промежуток времени.
Если тело всё время движется в одном направлении, то модуль средней скорости равен средней путевой скорости. Если же в процессе своего движения тело меняет направление движения, то модуль средней скорости меньше средней путевой скорости.
Пример решения задач на среднюю скорость при неравномерном движении
Автомобиль проехал за первый час 50 км, а за следующие два часа он проехал 160 км. Какова его средняя скорость за все время движения?
Еще больше задач на движение (с решениями и ответами) в конспекте «Задачи на движение»
Это конспект по физике за 7 класс по теме «Неравномерное движение. Средняя скорость». Выберите дальнейшие действия:
Неравномерное прямолинейное движение. Средняя скорость
п.1. График скорости при неравномерном прямолинейном движении
Прямолинейное и равномерное движение возможно лишь на участке пути.
Любое тело со временем меняет свою скорость, как по величине, так и по направлению.
Для описания неравномерного движения его можно разбить на участки, на которых скорость постоянна, и свести задачу к уже известному нам равномерному прямолинейному движению.
Например, пусть велосипедист добрался из города A в город B за 1 час. Первые полчаса он ехал со скоростью 9 км/ч, а потом проколол шину, и вторые полчаса шел пешком со скоростью 3 км/ч.
Направим ось ОХ также от A к B и получим значения проекций скоростей: $$ v_=9 text<км/ч>, v_=3 text <км/ч>$$ Построим график скорости для этого случая:
п.2. Как найти путь и перемещение по графику скорости?
Мы уже знаем, что путь равен площади прямоугольника, который образуется между отрезком графика скорости и отрезком (triangle t) на оси (t) (см. §8 данного справочника).
В таком случае, путь велосипедиста в нашем примере:
begin s=v_cdot triangle t_1+v_cdot triangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text <(км)>end Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км.
Общий путь велосипедиста равен 6 км. Расстояние между городами 6 км.
Если принять город A за начало отсчета с (x_0=0), то координата велосипедиста в конце пути: $$ x_<к>=x_0+s=0+6=6 text <(км)>$$ Перемещение по оси ОХ: (triangle x=x_<к>-x_0=6 text<(км)>).
Теперь рассмотрим другую ситуацию. Пусть велосипедист выехал из A в B и двигался со скоростью 9 км/ч в течение получаса. Но, после того как проколол шину, он развернулся и пошел пешком назад в A. Где будет находиться велосипедист через полчаса после разворота?
Снова направим ось ОХ от A к B и получим значения проекций скоростей: $$ v_=9 text<км/ч>, v_=-3 text <км/ч>$$ Построим график скорости для этого случая:
Путь велосипедиста по-прежнему будет равен сумме площадей прямоугольников, которые образует ломаная (v_x(t)) с осью (t): begin x=v_cdot triangle t_1+|v_|cdottriangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text <(км)>end
Если мы учтем знак (v_) и уберем модуль, то получим величину перемещения по оси ОХ: begin triangle x=v_cdot triangle t_1+v_cdot triangle t_2\ triangle x=9cdot 0,5-3cdot 0,5=4,5-1,5=3 text <(км)>end Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км в обратном направлении.
Конечная координата: $$ x_<к>=x_0+triangle x=0+3=3 text <(км)>$$
Ответ на вопрос задачи найден. Через полчаса после разворота велосипедист будет находиться в точке D в 3 км от города A.
п.3. Средняя скорость и средняя путевая скорость
В нашем примере с велосипедистом, который все время двигался в одну сторону и дошел до города B, получаем: begin |overrightarrow>|=frac<|overrightarrow|>=frac<triangle x>=frac 61=6 text<(км/ч)>\ v_=frac st=frac 61=6 text <(км/ч)>end Величина средней скорости равна средней путевой скорости.
А вот для случая, когда велосипедист развернулся и пошел обратно: begin |overrightarrow>|=frac<|overrightarrow|>=frac<triangle x>=frac 31=3 text<(км/ч)>\ v_=frac st=frac 61=6 text <(км/ч)>end Величина средней скорости меньше средней путевой скорости.
п.4. Задачи
Задача 1. По графику скоростей найдите среднюю скорость и среднюю путевую скорость движения.
a)
Все движение можно разделить на три участка с постоянной скоростью:
begin triangle t_1=3-0=3 c, v_=5 text<м/с>\ triangle t_2=5-3=2 c, v_=1 text<м/с>\ triangle t_3=7-5=2 c, v_=2 text<м/с>\ end Общий путь: begin s=|v_|cdot triangle t_1+|v_|cdot triangle t_2+|v_|cdot triangle t_3\ s=5cdot 3+1cdot 2+2cdot 2=21 text <(м)>end Все проекции скоростей положительны, тело двигалось в одном направлении, общее перемещение равно общему пути: (triangle x=s=21) (м)
Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (с)
Величина средней скорости равна средней путевой скорости: $$ |overrightarrow>|=v_=frac st=frac<21><7>=3 text <(м/с)>$$ Ответ: (|overrightarrow>|=v_=3 text<(м/с)>)
б)
Все движение можно разделить на три участка с постоянной скоростью:
begin triangle t_1=3-0=3 c, v_=5 text<м/с>\ triangle t_2=5-3=2 c, v_=-2 text<м/с>\ triangle t_3=7-5=2 c, v_=1 text<м/с>\ end Общий путь: begin s=|v_|cdot triangle t_1+|v_|cdot triangle t_2+|v_|cdot triangle t_3\ s=5cdot 3+2cdot 2+1cdot 2=21 text <(м)>end Проекции скоростей имеют разные знаки, тело двигалось вперед и назад.
Общее перемещение будет меньше общего пути: begin triangle x=v_cdot triangle t_1+v_cdot triangle t_2+v_cdot triangle t_3\ triangle x=5cdot 3-2cdot 2+1cdot 2=13 text <(м)>end Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (c)
Величина средней скорости: $$ |overrightarrow>|=frac<triangle x>=frac<13><7>approx 1,86 text <(м/с)>$$ Средняя путевая скорость: $$ v_=frac st=frac<21><7>=3 text <(м/с)>$$ Ответ: (|overrightarrow>|approx 1,86 text<(м/с)>; v_=3 text<(м/с)>)
Задача 2. Мотоциклист проехал расстояние между двумя пунктами со скоростью 40 км/ч. Потом увеличил скорость до 80 км/ч и проехал расстояние в два раза меньше. Найдите среднюю скорость мотоциклиста за все время движения.
Мотоциклист двигался все время в одном направлении, величина средней скорости равна средней путевой скорости: (v_=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 40 | (frac<2d><40>=frac<20>) | (2d) |
| 2й участок | 80 | (frac<80>) | (d) |
| Сумма | – | (t=frac<20>+frac<80>) | (s=2d+d=3d) |
Упростим сумму дробей: $$ t=frac<20>+frac<80>=frac<4d+d><80>=frac<5d><80>=frac <16>$$ Получаем: $$ v_=frac st=frac<3d>=3cdot 16=48 text <(км/ч)>$$
Ответ: 48 км/ч
Задача 3. Автомобиль проехал первую половину пути по шоссе со скоростью 90 км/ч, а вторую половину – по грунтовой дороге со скоростью 30 км/ч. Найдите среднюю скорость автомобиля.
Величина средней скорости равна средней путевой скорости:
(v_=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 90 | (frac |
(frac s2) |
| 2й участок | 30 | (frac |
(frac s2) |
| Сумма | – | (t=frac |
(s) |
Задача 4*. Туристы прошли по маршруту со средней скоростью 32 км/ч. Маршрут был разделен на три участка, первый участок преодолевался пешком, второй – на автобусе, третий – на катере. Найдите скорость на каждом участке, если длины этих участков относятся как 1:4:45, а соответствующие интервалы времени как 4:1:20.
Величина средней скорости равна средней путевой скорости:
(v_=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | (frac<4t>) | (4t) | (d) |
| 2й участок | (frac<4d>) | (t) | (4d) |
| 3й участок | (frac<45d><20t>) | (20t) | (45d) |
| Сумма | – | (25t) | (50d) |
По условию средняя скорость: $$ v_=frac st=frac<50d><25t>=2cdot frac dt=32Rightarrow frac dt=16 $$ Получаем: begin v_1=frac<4t>=frac<16><4>=4 text<(км/ч)>\ v_2=frac<4d>=4cdot 16=64 text<(км/ч)>\ v_3=frac<9d><4t>=frac<9><4>cdot 16=36 text <(км/ч)>end
Ответ: 4 км/ч, 64 км/ч и 36 км/ч
Задача 5*. Первую половину маршрута турист проехал на попутном автомобиле в 10 раз быстрее по сравнению с ходьбой пешком, а вторую половину – на попутном возу в 2 раза медленней. Сэкономил ли турист время на всем маршруте по сравнению с ходьбой пешком?
Пусть (v) – скорость туриста при ходьбе пешком.
Найдем среднюю путевую скорость (v_) и сравним ее со скоростью (v).
Если (v_gt v), то турист выиграл время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | (10v) | (frac |
(frac s2) |
| 2й участок | (frac<2>) | (frac |
(frac s2) |
| Сумма | – | (t=frac |
(s) |
Упростим сумму дробей: $$ t=frac<20v>+frac sv=frac svleft(frac<1><20>+1right)=frac<21><20>cdot frac sv $$ Средняя скорость: $$ v_=frac<frac<21><20>cdotfrac sv>=frac<20><21>vgt v $$Средняя скорость поездки оказалась меньше пешей скорости туриста.
Значит, он не выиграл по времени.
Ответ: нет
п.5. Лабораторная работа №3. Определение средней скорости движения тела
Цель работы
Научиться определять среднюю скорость движения тела по данным измерений на разных участках. Научиться вычислять абсолютные и относительные погрешности при подстановке данных измерений в формулы.
Теоретические сведения
В лабораторной работе изучается движение тела (шарика) по двум участкам (желобам) с различной скоростью.
Длина участков измеряется с помощью мерной ленты с ценой деления (triangle=1) см,
инструментальная погрешность равна: (d=frac<triangle><2>=0,5) см
Абсолютная погрешность измерений при работе с мерной лентой равна инструментальной погрешности, поэтому: (triangle s_1=triangle s_2=d=0,5) см
Погрешность суммы двух длин: (triangle(s_1+s_2)= triangle s_1+triangle s_2=2d=1) см
Измерение времени на каждом участке проводится в сериях их 5 измерений по методике, описанной в Лабораторной работе №2 (см. §4 данного справочника).
Погрешность суммы двух измерений: (triangle(t_1+t_2)=triangle t_1+triangle t_2)
Относительная погрешность частного равна сумме относительных погрешностей делимого и делителя: $$ delta_>=delta_+delta_ $$ Абсолютная погрешность определения средней скорости: $$ triangle v_=v_cdot delta_> $$
Приборы и материалы
Два желоба (не менее 1 м каждый), шарик, мерная лента, секундомер.
Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Соберите установку, как показано на рисунке. Установите один желоб под углом, другой – горизонтально, закрепите, поставьте в конце горизонтального участка упор. Подберите длину желобов и наклон так, чтобы движение по каждому участку было не менее 1 с.
3. Измерьте фактическую длину каждого участка движения в готовой установке с помощью мерной ленты.
4. Найдите относительную погрешность суммы двух длин (delta_=frac<triangle(s_1+s_2)>)
5. Проведите серии по 5 экспериментов для определения (t_1) и (t_2) с помощью секундомера.
6. Найдите (triangle t_1, triangle t_2, triangle(t_1+t_2), delta_)
7. По результатам измерений и вычислений найдите (v_, delta_>) и (triangle v_).
8. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
1) Измерение длин
Цена деления мерной ленты (triangle =1) см
Инструментальная погрешность мерной ленты (d=frac<triangle><2>=0,5) см
Результаты измерений:
(s_1=112) cм
(s_2=208) cм
Сумма длин участков: (s_1+s_2=112+208=320) (см)
Абсолютная погрешность суммы: (triangle (s_1+s_2)=triangle s_1+triangle s_2=2d=1) см
Относительная погрешность суммы: $$ delta_=frac<triangle (s_1+s_2)>=frac<1><320>=0,3125% $$
2) Измерение времени
Цена деления секундомера (triangle =0,2) с
Инструментальная погрешность секундомера (d=frac<triangle><2>=0,1) с
Время движения по наклонному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t_1) c | 1,5 | 1,6 | 1,5 | 1,4 | 1,4 | 7,4 |
| (triangle) c | 0,02 | 0,12 | 0,02 | 0,08 | 0,08 | 0,32 |
Найдем среднее время спуска с наклонного желоба: $$ t_1=frac<1,5+1,6+1,5+1,4+1,4><5>=frac<7,4><5>=1,48 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_1): $$ triangle_1=|1,5-1,48|=0,02; triangle_2=|1,6-1,48|=1,02 text <и т.д.>$$ Среднее абсолютное отклонение: $$ triangle_=frac<0,02+0,12+0,02+0,08+0,08><5>=frac<0,32><5>=0,064 text $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_1=maxleft\right>=maxleft<0,1;0,064right>=0,1 text $$ Округляем полученное значение времени до десятых. begin t_1=(1,5pm 0,1) text\ delta_=frac<0,1><1,5>=frac<1><15>approx 6,7text <%>end Время движения по горизонтальному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t_2) c | 2,3 | 2,4 | 2,2 | 2,2 | 2,4 | 11,5 |
| (triangle) c | 0 | 0,1 | 0,1 | 0,1 | 0,1 | 0,4 |
Найдем среднее время движения по горизонтали: $$ t_2=frac<2,3+2,4+2,2+2,2+2,4><5>=frac<11,5><5>=2,3 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_2): $$ triangle_1=|2,3-2,3|=0; triangle_2=|2,4-2,3|=0,1 text <и т.д.>$$ Среднее абсолютное отклонение: $$ triangle_=frac<0+0,1+0,1+0,1+0,1><5>=frac<0,4><5>=0,08 text $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_2=maxleft\right>=maxleft<0,1;0,08right>=0,1 text $$ Получаем: begin t_2=(2,3pm 0,1) text\ delta_=frac<0,1><2,3>=frac<1><23>approx 4,4text <%>end
3) Расчет погрешности суммы интервалов времени
Сумма интервалов времени: $$ t_1+t_2=1,5+2,3=3,8 text <(c)>$$ Абсолютная погрешность суммы: $$ triangle(t_1+t_2)=triangle t_1+triangle t_2=0,1+0,1=0,2 text <(c)>$$ Относительная погрешность суммы: $$ delta_=frac<triangle (t_1+t_2)>=frac<0,2><3,8>=frac<1><19>approx 5,3text <%>$$
4) Расчет средней скорости $$ v_=frac=frac<320><3,8>approx 84,2 left(frac<text<см>><text>right) $$ Относительная ошибка частного: $$ delta_>=delta_+delta_=frac<1><320>+frac<1><19>approx 0,003125+0,0526approx 0,0557approx 0,056=5,6text <%>$$ (оставляем две значащие цифры).
Абсолютная ошибка: $$ v_=v_cdotdelta_>=84,2cdot 0,056approx 4,7 left(frac<text<см>><text>right) $$ Получаем: begin v_=(84,2pm 4,7) text<см/с>\ delta_>=5,6text <%>end
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения длин проводились с помощью мерной ленты. Ошибка измерений равна инструментальной ошибке 0,5 см.
Измерения времени проводились с помощью секундомера. По результатам серий экспериментов ошибка была принята равной инструментальной 0,1 с.
Получена величина средней скорости: begin v_=(84,2pm 4,7) text<см/с>\ delta_>=5,6text <%>end
Прямолинейное неравномерное движение в физике – формулы и определения с примерами
Содержание:
Прямолинейное неравномерное движение, ускорение:
На практике прямолинейное равномерное движение наблюдается очень редко. Скорость движущегося автомобиля, поезда, самолета, частей механизма и т.д. может изменяться и по величине, и по направлению.
Прямолинейное движение, при котором за равные промежутки времени материальная точка совершает разные перемещения, называют прямолинейным неравномерным движением.
При таком движении числовое значение скорости не остается неизменным, поэтому для описания неравномерного движения пользуются понятиями средней и мгновенной скорости.
Средняя скорость
Средняя скорость неравномерно движущейся материальной точки на данном участке траектории равна отношению ее перемещения на этом участке ко времени совершения этого перемещения:
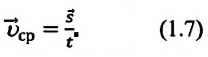
Средняя путевая скорость материальной точки при неравномерном движении равна отношению всего пройденного пути ко времени, затраченному на прохождение этого пути:
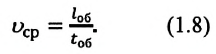
Средняя скорость материальной точки, движущейся со скоростями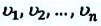 
на участках пути 
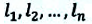промежутки времени 
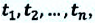соответственно, вычисляется так:
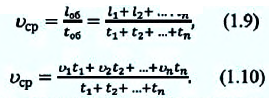
Если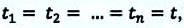 
то из уравнения (1.10) получается
Мгновенная скорость.
Скорость материальной точки в данный момент времени или в данной точке траектории называют мгновенной скоростью.
Мгновенная скорость в некоторой точке является векторной величиной и определяется как предел отношения достаточно малого перемещения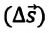 
на участке траектории, включающей эту точку, к малому промежутку времени 
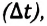затраченному на это перемещение (при условии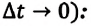 
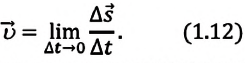
Где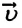 
– мгновенная скорость поступательного движения материальной точки.
С течением времени мгновенная скорость может увеличиваться, уменьшаться и изменять направление. Направление мгновенной скорости в данной точке траектории совпадает с направлением касательной к траектории в этой точке (b). Проекция вектора мгновенной скорости в прямоугольной системе координат равна первой производной координаты по времени:
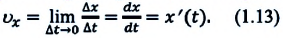
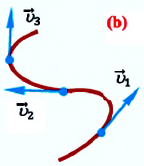
Ускорение
Быстрота изменения мгновенной скорости при неравномерном движении по величине и направлению характеризуется векторной физической величиной, называемой ускорением:
Ускорение – это физическая величина, равная отношению изменения скорости ко времени, за которое это изменение произошло:
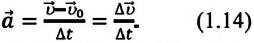
Если измерение времени начинается с нуля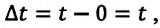 
то:
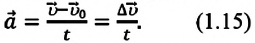
Направление ускорения совпадает с направлением вектора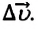 
Для простоты здесь и в последующем будет рассматриваться такое неравномерное прямолинейное движение материальной точки, при котором за любые равные промежутки времени происходит одинаковое изменение скорости. Такое движение называется равнопеременным движением.
Равнопеременное движение
Равнопеременное движение – это движение, при котором за любые равные промежутки времени происходит одинаковое изменение скорости. При равнопеременном движении значение и направление ускорения не меняются: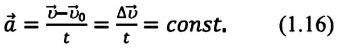 
При равнопеременном движении проекция ускорения на любую ось, например ось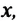 
также постоянная:
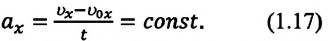
Это значит, что при равнопеременном движении график зависимости ускорения от времени представляет собой прямую линию, параллельную оси времени, – проекция ускорения на выбранную ось от времени не зависит (с).
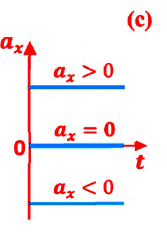
В СИ за единицу ускорения принят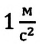 
– ускорение такого равнопеременного движения, при котором материальная точка за 1 секунду изменяет свою скорость на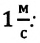 
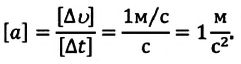
Знаете ли вы? Ускорение—одна из наиболее значимых величин, используемых в физике и технике. Известно, что при постепенном торможении автомобиля, автобуса и поезда пассажиры не чувствуют дискомфорта, однако при резком торможении для них возникает серьезная опасность. Значит, важно не просто изменение скорости, а быстрота изменения скорости. Для контроля за изменением скорости машин и механизмов используется прибор, измеряющий ускорение — акселерометр (лат.: accelero — “ускоряю ” и греч.: metreo – “измеряю “) (d).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Прямолинейное равноускоренное движение
- Сложение скоростей
- Ускорение в физике
- Скорость при равнопеременном движении
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось
- Путь и перемещение
- Равномерное прямолинейное движение
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
[spoiler title=”источники:”]
http://reshator.com/sprav/fizika/7-klass/neravnomernoe-pryamolinejnoe-dvizhenie-srednyaya-skorost/
http://www.evkova.org/pryamolinejnoe-neravnomernoe-dvizhenie-v-fizike
[/spoiler]
