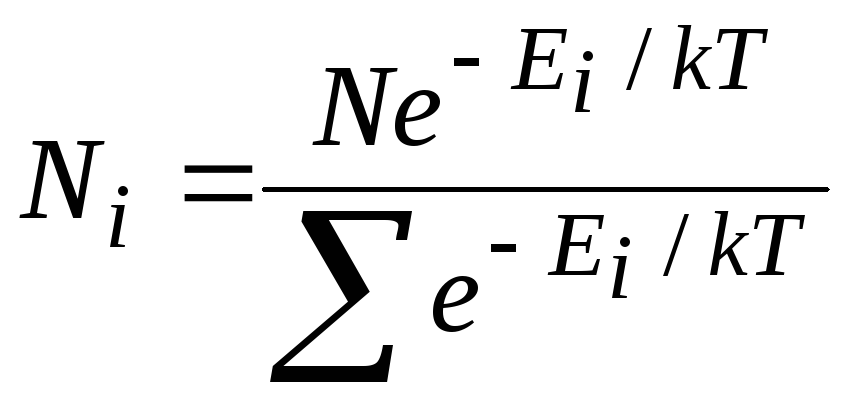Средняя скорость молекул
В физике выделяют 2 скорости, характеризующие движение молекул: средняя скорость движения молекул и средняя квадратичная скорость.
Средняя скорость движения молекул
Средняя скорость движения молекул называется также скоростью теплового движения молекул.
Формула средней относительной скорости молекул в физике представлена следующим выражением:
υotn=28kTπm0=2υ.
Средняя квадратичная скорость
Средняя квадратичная скорость движения молекул газа это следующая величина:
υkυ=1N∑i=1Nυi2
Формулу средней квадратичной скорости можно переписать так:
υkυ2=∫0∞υ2Fυdυ.
Проводя интегрирование, аналогичное интегрированию при получении связи средней скорости с температурой газа, получаем:
υkυ=3kTm0=3RTμ
Именно средняя квадратичная скорость поступательного движения молекул газа входит в состав основного уравнения молекулярно-кинетической теории:
p=13nm0υkυ,
где n=NV – это концентрация частиц вещества, N – это количество частиц вещества, V – это объем.
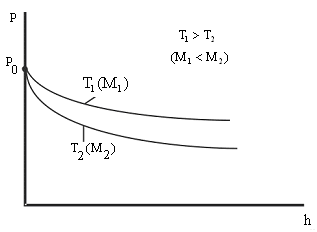
Необходимо определить, как изменяется средняя скорость движения молекул идеального газа с увеличением давления в процессе, изображенном на графике (рисунок 1).
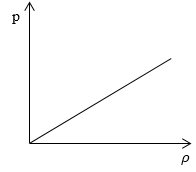
Рисунок 1
Решение
Запишем выражение для средней скорости движения молекул газа следующим образом:
υ=8kTπm0
Из графика видно, что p~ρ или p=Cρ, где C – это некоторая константа.
m0=ρn, p=nkT=Cρ→kT=Cρn
Подставив m0=ρn, p=nkT=Cρ→kT=Cρn в υ=8kTπm0, получаем:
υ=8kTπm0=8Cρπnnρ=8Cπ
Ответ: В процессе, представленном на графике, с увеличением давления средняя скорость движения молекул не меняется.
Можно ли найти среднюю квадратичную скорость молекулы идеального газа, если известно: давление газа (p), молярная масса газа (μ), а также концентрация молекул газа (n)?
Решение
Применим выражение для υkυ:
υkυ=3RTμ
Помимо этого, из уравнения Менделеева-Клайперона и зная, что mμ=NNA:
pV=mμRT=NNART.
Поделим правую и левую части pV=mμRT=NNART на V, и зная NV=n, получаем:
p=nNART→RT=pNAn
Подставляем p=nNART→RT=pNAn в выражение для среднеквадратичной скорости υkυ=3RTμ, получаем:
υkυ=3pNAμn
Ответ: По заданным в условии задачи параметрам среднеквадратичная скорость движения молекул газа вычисляется при помощи формулы υkυ=3pNAμn.
![]()
Для характеристики движения молекул в физике используют две скорости: среднюю и среднюю квадратичную скорость молекул.
Важно. Следует обязательно понимать, что в реальных условиях мы не можем точно знать ни конкретное число молекул в системе, ни тем более скорость каждой из них в конкретный момент времени. Это обусловлено неимоверно гигантским числом частиц в реальных и даже сколько-нибудь приближенных к ним системах. Например, в 1 см3 при давлении 200 мм. рт. ст. содержится 4,18*1018 молекул водорода. Говоря более понятными категориями, это более чем 4 миллиарда миллиардов. Заметим, что указанное давление меньше атмосферного почти в 4 раза. Последнее в среднем равняется 760 мм. рт. ст. Разрежённый водород по своим свойствам наиболее близок к идеальному газу. В данном случае физика вынуждена иметь дело с распределениями скоростей и энергий частиц.
Что такое средняя скорость движения молекул
Среднюю скорость движения молекул часто именуют скоростью их теплового движения.
Определение 1
Вид формулы средней относительной скорости молекул в физике можно представить выражением:
[text { Vотн }=sqrt{2} sqrt{frac{8 R T}{pi m_{0}}}]
Выражение под корнем – средняя скорость молекул идеального газа.
Как определить среднюю квадратичную скорость движения молекул
Определение 2
Средней квадратичной скоростью молекул идеального газа называют величину равную квадратному корню из среднего арифметического величины квадратов скоростей каждой из молекул.
Средняя скорость молекул равна:
[leftlanglemathrm{V}_{mathrm{KB}}rightrangle=sqrt{frac{1}{N} sum_{i=1}^{N} v_{i}^{2}}]
Если обе её части возвести в квадрат и проинтегрировать, то получим выражение:
[langlemathrm{VKB}rangle^{2}=int_{0}^{infty} v^{2} F(v) d v]
Ещё одно выражение для среднеквадратичной скорости:
[leftlangle V_{K B}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]
Именно она присутствует в уравнении, именуемом основным уравнением молекулярно-кинетической теории
P = (1/3)nm*<Vкв>
Где n – концентрация молекул, которая вычисляется делением их общего числа на объём.
Пример. 1.
Рассмотрим простейший случай, чтобы использование интегрирования не затруднило понимание сути явления и помогло лучше понять материал. Вычислим как меняется средняя скорость движения молекул в идеальном газе при линейном увеличении его давления. График следующий:
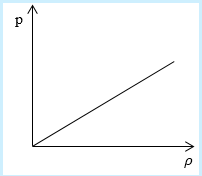
Напомним, что средняя скорость частиц:
[mathrm{Vcp}=sqrt{frac{8 R T}{pi m_{0}}}]
Если присмотреться к представленному графику, то можно заметить, что P приблизительно равно ρ. Эти две величины можно связать соотношением
P=C*ρ
Где С – некоторая постоянная величина, константа.
Далее считаем m0= ρ/n, p = n*k*T = C* ρ. Отсюда следует, что k*T = (C*ρ)/n.
Нужно лишь подставить эти значения в формулу для средней скорости:
[V c p=sqrt{8 mathrm{kT} / pi mathrm{m}}=sqrt{(8 mathrm{C} rho / pi mathrm{n})(mathrm{n} / rho)}=sqrt{8 mathrm{C} / pi}]
В полученном выражении нет ни одной переменной величины, т. е. при увеличении давления, вопреки ожиданиям, скорость оказалась неизменной.
Ответ: В процессе, который был дан нам на графике, при увеличении давления средняя скорость молекул никак не меняется.
Нет времени решать самому?
Наши эксперты помогут!
Пример. 2.
Определим среднюю квадратичную скорость молекул газа при условии, что нам известны его давление (P), молярная масса (M) и концентрация частиц (n).
Воспользуемся формулой:
[leftlanglemathrm{V}_{kappa в}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]
Также нам потребуется уравнение Менделеева-Клайперона
Здесь мы воспользовались тем, что:
m/μ = N/Na
PV = (m/μ)*RT = (N/Na)*RT
Если обе части этого уравнения поделить на V и принять во внимание, что
(N/V) = n, то можно получить
P = (n/Na)*RT. Отсюда находим, что RT = (p*N)/n
Если мы это подставим в выражение для среднеквадратичной скорости [leftlangle V_{K B}rightrangle=sqrt{3 mathrm{kT} / mathrm{m}_{0}}=sqrt{3 mathrm{RT} / mu}], получим, что средняя квадратичная скорость движения молекул газа: [leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]
Ответ: Формула средней квадратичной скорости молекул исходя из данный нам условий следующая:
[leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]
Средние скорости молекул
Найдём
наиболее
вероятную скорость,
соответствующую максимуму
функции
распределения.
Эта скорость определяется из условия
![]() ,
,
т.е.
![]()
Проведя
дифференцирование произведения функций,
получим
Средняя
скорость
молекул
![]() (имеется в видусредняя
(имеется в видусредняя
арифметическая скорость)
по определению из формулы статического
усреднения
Средняя
скорость входит в
коэффициенты диффузии, вязкости,
теплопроводности и, соответственно
используется в расчётах этих процессов.
Среднеквадратичная
скорость
![]() ;
;
![]() ,
,
откуда
Эта
скорость входит в основное уравнение
молекулярно-кинетической теории.
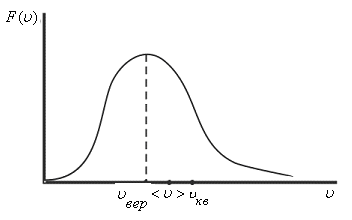
Качественно
положение характерных (средних) скоростей
показано на рис. 8.6
|
|
Проанализируем, |
|
Рис. 8.6 |
|
|
|
|
|
Рис. 8.7 |
3.
Барометрическая формула.
Атмосферное
давление на высоте h
обусловлено весом вышележащих слоёв
газа. Давление на высоте h+dh
будет P+dP
(dh>0,
dP<0,
т.к. вес и
давление с высотой убывают).
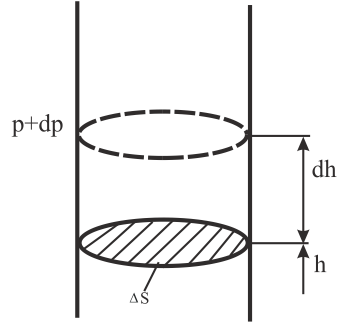
Разность
давлений
P
и P+dP
обусловлена
весом газа, заключённого в объёме
цилиндра, с площадью основания, равной
![]() и высотойdh
и высотойdh
(Рис. 8.8).
|
|
где
При
|
||
|
Рис. 8.8 |
М
– средняя масса моля воздуха. Плотность
![]() ,
,
подставим в (*), получим
![]() .
.
Поделим обе части на Р:
![]() .
.
Возьмём интеграл от левой и правой
частей:
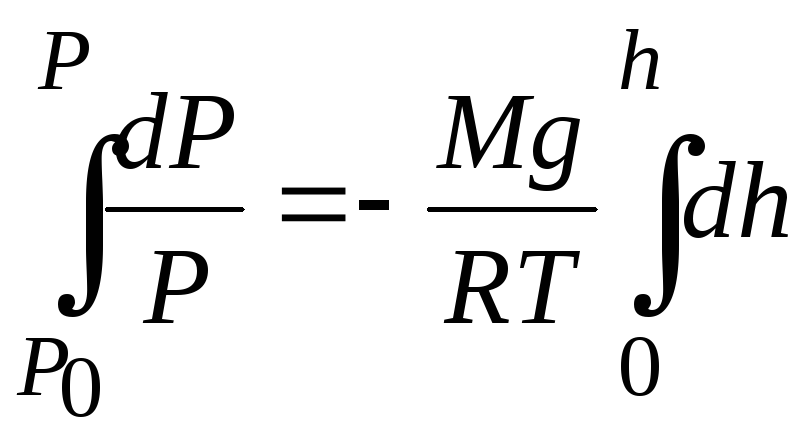 .
.
Предел
![]() давление на уровнеh=0.
давление на уровнеh=0.
Для случая, когда температура постоянная
(изотермическая атмосфера), интегрируя,
получим:
![]() ,
,
отсюда получаем барометрическую
формулу.
|
|
||
|
|
Графическая |
|
|
Рис. 8.9 |
Распределение Больцмана
В
барометрической формуле в отношении
M/R
разделим и
числитель и знаменатель на число Авогадро
![]() .
.
![]() ,
,
где
![]() масса
масса
одной молекулы,
![]() постоянная
постоянная
Больцмана.
Вместо
Р
и
![]() подставим соответственно.
подставим соответственно.![]()
![]() (см. лекцию №7), где
(см. лекцию №7), где![]() плотность
плотность
молекул на высотеh,
![]() плотность
плотность
молекул на высоте![]() .
.
Из барометрической
формулы в результате подстановок и
сокращений получим распределение
концентрации молекул по высоте в поле
силы тяжести Земли.
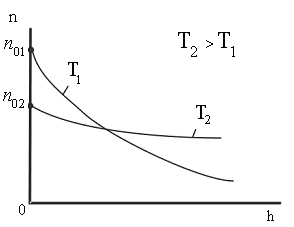
Из
этой формулы следует, что с понижением
температуры число частиц на высотах,
отличных от нуля, убывает (рис. 8.10),
обращаясь в 0 при Т=0 (при
абсолютном нуле все молекулы расположились
бы на поверхности Земли). При высоких
температурах n
слабо убывает с высотой, так
|
|
что |
|
Рис. 8.10 |
![]() .Следовательно,
.Следовательно,
распределение
молекул по высоте является и распределением
их по значениям потенциальной энергии.
-

(*)
где
![]() плотность молекул в том месте пространства,
плотность молекул в том месте пространства,
где потенциальная энергия молекулы
имеет значение![]() ;
;![]() плотность
плотность
молекул в том месте, где потенциальная
энергия равна 0.
Больцман
доказал, что распределение (*) справедливо
не только в случае потенциального поля
сил земного тяготения, но и в любом
потенциальном поле сил для совокупности
любых одинаковых частиц, находящихся
в состоянии хаотического теплового
движения.
Таким
образом, закон
Больцмана (*) даёт распределение частиц,
находящихся в состоянии хаотического
теплового движения, по значениям
потенциальной энергии.
(рис. 8.11)
|
|
|
|
Рис. 8.11 |
-
Распределение
Больцмана при дискретных уровнях
энергии.
Полученное
Больцманом распределение относится к
случаям, когда молекулы находятся во
внешнем поле и их потенциальная энергия
![]() может применяться непрерывно. Больцман
может применяться непрерывно. Больцман
обобщил полученный им закон на случай
распределения, зависящего от внутренней
энергии молекулы.
Известно,
что величина внутренней энергии молекулы
(или атома) Е
может принимать лишь дискретный ряд
дозволенных значений
![]() .
.
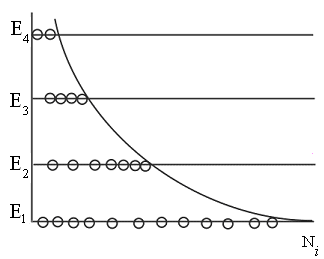
В этом случае распределение Больцмана
имеет вид:
![]() ,
,
где
![]() число
число
частиц в состоянии с энергией![]() ;
;
![]() коэффициент
коэффициент
пропорциональности, который удовлетворяет
условию
![]() ,
,
где
N
– полное число частиц в рассматриваемой
системе.
Тогда
![]() и в результате для случая дискретных
и в результате для случая дискретных
значений энергии распределение Больцмана
|
|
Качественная
Заметим, |
|
Рис. 8.12 |
Но
состояние системы в этом случае
термодинамически неравновесное.
-
Статистика
Максвелла-Больцмана
Распределение
Максвелла и Больцмана можно объединить
в один закон Максвелла-Больцмана,
согласно которому число молекул,
компоненты скорости которых лежат в
пределах от
![]() до
до![]()
![]() ,
,
а координаты в пределах отx,
y,
z
до x+dx,
y+dy,
z+dz,
равно
где
![]() ,
,![]() плотность
плотность
молекул в том месте пространства, где![]() ;
;![]() ;
;![]() ;
;![]() полная
полная
механическая энергия частицы.
Распределение
Максвелла-Больцмана устанавливает
распределение молекул газа по координатам
и скоростям при наличии произвольного
потенциального силового поля.
Примечание:
распределение Максвелла и Больцмана
являются составными частями единого
распределения, называемого распределением
Гиббса (этот вопрос подробно рассматривается
в спецкурсах по статической физике, и
мы ограничимся только упоминанием этого
факта).
Вопросы для
самоконтроля.
-
Дайте определение
вероятности. -
Каков смысл функции
распределения? -
Каков смысл условия
нормировки? -
Запишите
формулу для определения среднего
значения результатов измерения величины
x
с помощью функции распределения. -
Что представляет
собой распределение Максвелла? -
Что
такое функция распределения Максвелла?
Каков ее физический смысл? -
Постройте
график функции распределения Максвелла
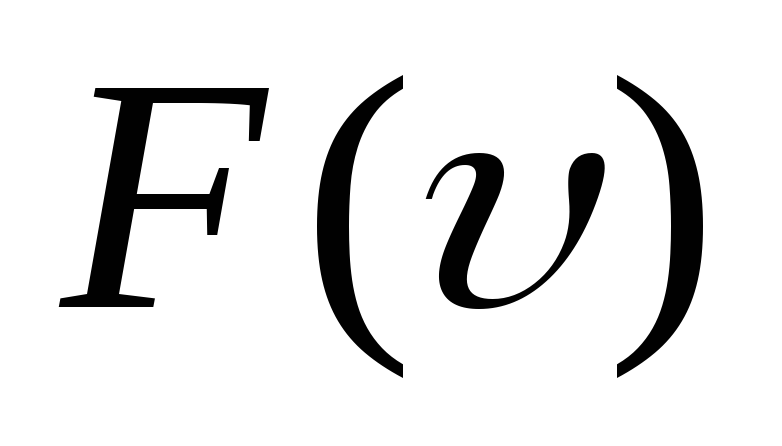 и укажите характерные особенности этой
и укажите характерные особенности этой
функции. -
Укажите
на графике
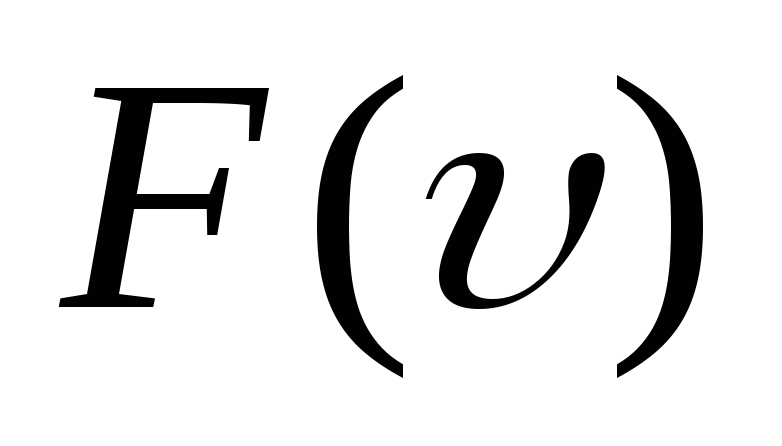 наиболее вероятную скорость
наиболее вероятную скорость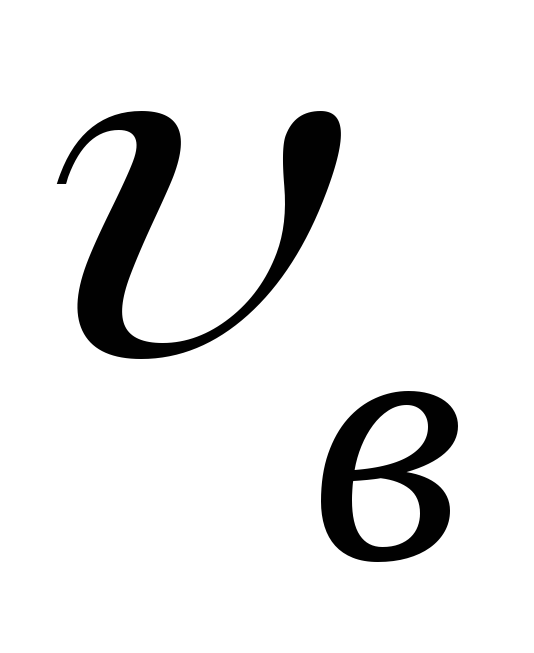 .
.
Получите выражение для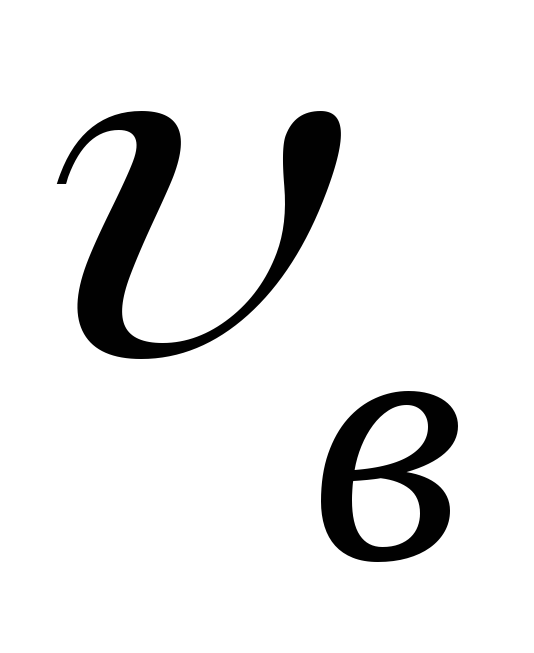 .
.
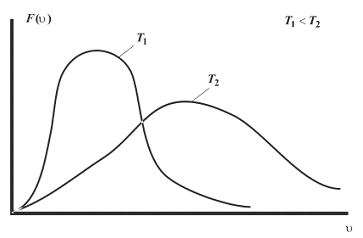
Как изменяется график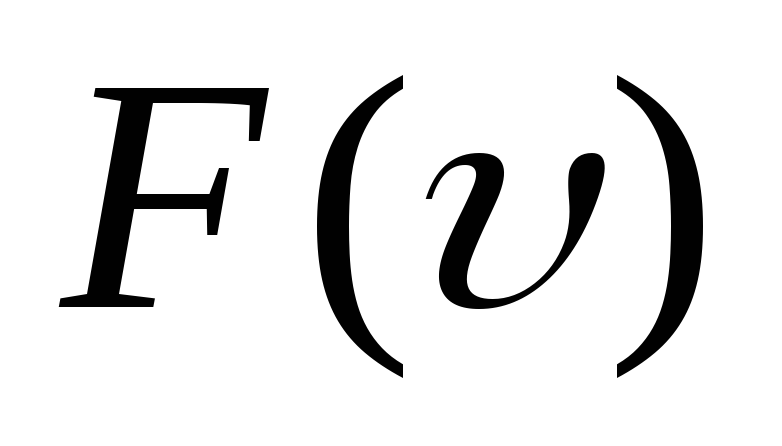 при повышении температуры?
при повышении температуры? -
Получите
барометрическую формулу. Что она
определяет? -
Получите
зависимость концентрации молекул газа
в поле силы тяжести от высоты. -
Запишите
закон распределения Больцмана а) для
молекул идеального газа в поле силы
тяжести; б) для частиц массой m,
находящихся в роторе центрифуги,
вращающейся с угловой скоростью
 .
. -
Объясните
физический смысл распределения
Максвелла-Больцмана.
Лекция №9
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обновлено: 19.05.2023
В физике выделяют 2 скорости, характеризующие движение молекул: средняя скорость движения молекул и средняя квадратичная скорость.
Средняя скорость движения молекул
Средняя скорость движения молекул называется также скоростью теплового движения молекул.
Формула средней относительной скорости молекул в физике представлена следующим выражением:
υ o t n = 2 8 k T πm 0 = 2 υ .
Средняя квадратичная скорость
Средняя квадратичная скорость движения молекул газа это следующая величина:
υ k υ = 1 N ∑ i = 1 N υ i 2
Формулу средней квадратичной скорости можно переписать так:
υ k υ 2 = ∫ 0 ∞ υ 2 F υ d υ .
Проводя интегрирование, аналогичное интегрированию при получении связи средней скорости с температурой газа, получаем:
υ k υ = 3 k T m 0 = 3 R T μ
Именно средняя квадратичная скорость поступательного движения молекул газа входит в состав основного уравнения молекулярно-кинетической теории:
p = 1 3 n m 0 υ k υ ,
где n = N V – это концентрация частиц вещества, N – это количество частиц вещества, V – это объем.
Необходимо определить, как изменяется средняя скорость движения молекул идеального газа с увеличением давления в процессе, изображенном на графике (рисунок 1 ).

Решение
Запишем выражение для средней скорости движения молекул газа следующим образом:
Из графика видно, что p ~ ρ или p = C ρ , где C – это некоторая константа.
m 0 = ρ n , p = n k T = C ρ → k T = C ρ n
Подставив m 0 = ρ n , p = n k T = C ρ → k T = C ρ n в υ = 8 k T πm 0 , получаем:
υ = 8 k T πm 0 = 8 C ρ π n n ρ = 8 C π
Ответ: В процессе, представленном на графике, с увеличением давления средняя скорость движения молекул не меняется.
Можно ли найти среднюю квадратичную скорость молекулы идеального газа, если известно: давление газа ( p ) , молярная масса газа ( μ ) , а также концентрация молекул газа ( n ) ?
Решение
Применим выражение для υ k υ :
Помимо этого, из уравнения Менделеева-Клайперона и зная, что m μ = N N A :
p V = m μ R T = N N A R T .
Поделим правую и левую части p V = m μ R T = N N A R T на V , и зная N V = n , получаем:
p = n N A R T → R T = p N A n
Подставляем p = n N A R T → R T = p N A n в выражение для среднеквадратичной скорости υ k υ = 3 R T μ , получаем:
υ k υ = 3 p N A μ n
Ответ: По заданным в условии задачи параметрам среднеквадратичная скорость движения молекул газа вычисляется при помощи формулы υ k υ = 3 p N A μ n .

Этот урок посвящен изучению того, каким способом можно измерить скорость молекул газа. Мы рассмотрим один из самых известных экспериментов в этой области – опыт Штерна.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока “Измерение скоростей молекул газа”
На прошлых уроках мы вывели уравнение, позволяющее связать среднюю кинетическую энергию молекул и температуру.
Как вы знаете, средняя кинетическая энергия молекул равна половине произведения массы молекулы и среднего значения квадрата скорости молекул:

Таким образом, зная температуру газа, мы можем найти среднее значение квадрата скорости его молекул:

Расчеты говорят о том, что при 0 о С, средняя скорость молекул азота достигает 500 м/с, а средняя скорость молекул водорода — 1800 м/с. Во второй половине 19 века это привело некоторых физиков в замешательство. Ведь всем хорошо известно, что запахи распространяются сравнительно медленно. Как же тогда получается, что молекулы газа двигаются с огромными скоростями, а само облако газа двигается в сотни раз медленнее?
Ответ на этот вопрос достаточно простой: молекулы двигаются беспорядочно, а потому их перемещения в сотни раз меньше пройденного пути. В качестве аналогии мы опять можем привести футбол. За один матч футболисты пробегают более десяти километров, однако, все это время они остаются в пределах футбольного поля, размеры которого равны 120 х 60 м.
Кроме расчетов скоростей молекул газа с помощью теории, существуют экспериментальные методы измерения скоростей. На сегодняшнем уроке, мы рассмотрим опыт Штерна, проведенный в 1920 году. Этот опыт был одним из первых экспериментальных подтверждений состоятельности молекулярно-кинетической теории.

Прибор Штерна представляет собой два коаксиальных цилиндра (то есть эти цилиндры обладают общей осью симметрии).
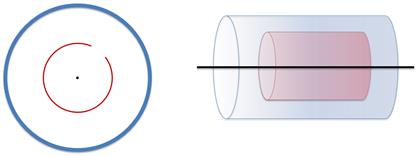
Из цилиндров откачан весь воздух. Вдоль оси малого цилиндра натянута тонкая платиновая проволока, покрытая серебром, а также в малом цилиндре имеется небольшая щель.
По проволочке пропускают электрический ток, с целью заставить серебро испаряться. В результате испарения, малый цилиндр заполняется газом из атомов серебра.
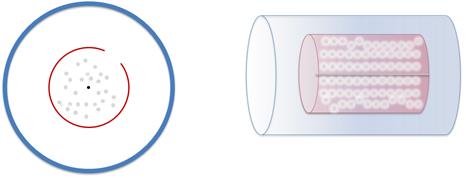
Разумеется, часть этих атомов пролетают через щель и оседают на внутренней стенке большого цилиндра. Этот слой серебра имеет определенное положение — прямо напротив щели в малом цилиндре.
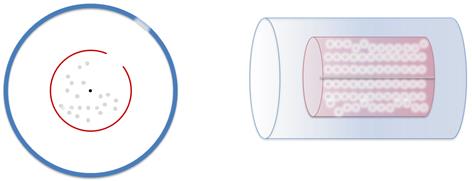
После этого, цилиндры приводят во вращение с одинаковой угловой скоростью и большой частотой (около 1500 об/с). Теперь атомы будут осаждаться не прямо напротив щели, поскольку за то время, пока они проходят расстояние от стенки малого цилиндра до стенки большого цилиндра, цилиндры поворачиваются на некоторый угол. Более того, слой серебра будет немного размытый из-за того, что не все атомы серебра двигаются с одинаковыми скоростями.
Обозначим за R радиус большого цилиндра, а радиус малого цилиндра — за r. Обозначим за d расстояние от конца радиуса, проходящего через центр щели до наибольшей концентрации атомов серебра после начала вращения. (Дело в том, что не все атомы имеют одинаковую скорость, поэтому, не все они попадают в одну и ту же точку). Поэтому, расстоянию d будет соответствовать средняя скорость атомов серебра:

Запишем теперь, что расстояние d равно:

Изучая криволинейное движение, мы убедились, что скорость вращения можно выразить через радиус вращения и частоту:

Из полученного выражения выразим время:

А теперь, это время подставим в формулу для средней скорости:

Таким образом, получили выражение, в котором средняя скорость задана через радиусы цилиндров, частоту вращения и расстояние d. Конечно же, радиусы цилиндров и расстояние d можно измерить. Частоту вращения задает сам экспериментатор, поэтому, она тоже известна. Модули скоростей, измеренные подобным способом, совпадают с теоретическим значением в пределах экспериментальной ошибки. Это говорит о том, что теоретическая формула, по которой мы вычисляли скорость, оказалась верна. Следовательно, верно и уравнение, связывающее среднюю кинетическую энергию молекул и температуру тела по абсолютной шкале Кельвина:
Квадратный корень из этой величины называется средней квадратичной скоростью:

Средняя квадратичная скорость мало отличается от наибо лее вероятной скорости, определяемой выражением (4.6.9). Так как постоянная Больцмана равна отношению универсальной газовой постоянной к постоянной Авогадро а массу молекулы можно выразить через ее молярную массу то из формулы (4.7.2) получается

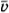
Вычисленные по этой формуле скорости для различных газов при t = 0 °С (Т = 273 К) приведены в таблице 1.
Таблица 1

Как видно из таблицы, скорости молекул очень велики — порядка скорости артиллерийских снарядов — и несколько больше скорости звука в соответствующем газе. На первых порах такой результат вызвал замешательство среди физиков. Ведь если скорости молекул столь велики, то как объяснить, например, что запах духов, пролитых в комнате, распространяется довольно медленно; должно пройти несколько секунд, чтобы запах распространился по всей комнате. Однако объяснить этот факт оказалось довольно просто.
Молекулы газа, несмотря на свои малые размеры, непрерывно сталкиваются друг с другом. Из-за большой скорости движения молекул число столкновений молекул воздуха в 1 с при нормальных атмосферных условиях достигает нескольких миллиардов. Средняя длина свободного пробега молекулы оказывается равной 10 -5 —10 -5 см. Поэтому траектория каждой молекулы представляет собой очень запутанную ломаную линию (рис. 4.14). Большие скорости молекула имеет на прямолинейных отрезках ломаной. Перемещение же молекулы в каком-либо направлении в среднем невелико даже за время порядка нескольких секунд. При перемещении молекулы из точки А в точку В пройденный ею путь оказывается гораздо больше расстояния АВ.

Экспериментальное определение скоростей молекул
Опыты по определению скорости молекул доказали справедливость формулы (4.7.3). Один из опытов был осуществлен немецким физиком О. Штерном в 1920 г.
Схема опыта показана на рисунке 4.15. Прибор состоит из сосуда 1, системы диафрагм 2, 3 и цилиндра 4, вращающегося с большой угловой скоростью ω.

В сосуде 1 натянута тонкая платиновая проволочка 5, покрытая слоем серебра. По проволочке пропускают электрический ток. При прохождении тока слой серебра испаряется и сосуд заполняется газом из атомов серебра. Газ находится в равновесном состоянии при температуре Т, которую можно измерить.
В стенке сосуда 1 имеется маленькое отверстие, через которое небольшое количество атомов серебра вылетает из сосуда в пространство, где создан высокий вакуум. Здесь атомы практически не сталкиваются друг с другом.
С помощью диафрагм 2, 3 выделяется пучок атомов, направленный вдоль диаметра вращающегося цилиндра. В цилиндре имеется узкая щель. В момент, когда щель оказывается на пути пучка, небольшая порция атомов попадает внутрь цилиндра и движется к его противоположной стенке. Расстояние, равное диаметру цилиндра D, эти атомы пролетают за время , где — среднее значение скорости. Зa это время цилиндр повернется на угол φ = ωτ = .

Если бы цилиндр был неподвижен, то атомы осаждались бы на его внутренней поверхности прямо против щели. Но при вращении цилиндра атомы попадают на участок цилиндра, смещенный на расстояние s = от точки, лежащей на одном диаметре со щелью 3 (см. рис. 4.15).
На внутренней поверхности цилиндра образуется след от осажденного серебра в виде темного пятна. Толщина пятна не везде одинакова. На определенном участке толщина слоя серебра максимальна. Измерив длину дуги s, соответствующую наибольшей толщине слоя серебра, и зная диаметр цилиндра и его угловую скорость, можно определить среднюю скорость молекул по формуле

Согласие со значением средней квадратичной скорости, вычисленной по формуле (4.7.3), оказывается вполне удовлетворительным. Это служит экспериментальным доказательством справедливости формулы (4.7.3), а значит, и выражения (4.5.5), из которого следует, что средняя кинетическая энергия прямо пропорциональна абсолютной температуре.
Измеряя толщину пятна серебра в разных местах, можно приблизительно подсчитать число атомов, скорости которых лежат в тех или иных интервалах. Таким образом осуществляется опытная проверка максвелловского распределения молекул по скоростям. Согласие с экспериментом для распределения Максвелла также оказывается удовлетворительным.
Средняя скорость броуновской частицы
Формула (4.7.2) позволяет понять, почему интенсивность броуновского движения возрастает с повышением температуры жидкости и уменьшается при увеличении массы частицы. Ведь броуновская частица участвует в тепловом движении молекул. Поэтому ее средняя кинетическая энергия также определяется формулой (4.5.5), а средняя квадратичная скорость — формулой

где mб — масса броуновской частицы. Если масса частицы велика, то средняя скорость ее движения настолько мала, что движение частицы практически обнаружить нельзя.
Скорость броуновской частицы в жидкости измерить непосредственно невозможно из-за крайней нерегулярности броуновского движения.
Средние скорости молекул превышают скорость звука и достигают сотен метров в 1 с. Эти скорости удалось измерить благодаря тому, что макроскопическому телу (цилиндру в опыте Штерна) можно сообщить столь большую угловую скорость, что за время пролета молекул внутри цилиндра он поворачивается на заметную величину.
Можно ли, зная температуру, вычислить среднюю кинетическую энергию молекул газа? среднюю скорость молекулы?
А можно ли эту скорость измерить?
Средняя скорость теплового движения молекул.

Уравнение (9.16) даёт возможность найти средний квадрат скорости движения молекулы. Подставив в это уравнение получим выражение для среднего значения квадрата скорости:

Средней квадратичной скоростью называется величина


Вычисляя по формуле (9.19) скорость молекул, например азота при t = 0 °С, получаем Молекулы водорода при той же температуре имеют среднюю квадратичную скорость Эти скорости велики, но так как молекулы газа движутся хаотично, непрерывно сталкиваясь друг с другом, и время между двумя столкновениями мало, то расстояние, которое пролетают молекулы также невелико. Из-за столкновения траектория каждой молекулы представляет собой запутанную ломаную линию (рис. 9.6). Большие скорости молекула имеет на прямолинейных отрезках ломаной. Как видно из рисунка, при перемещении молекулы из точки А в точку В пройденный ею путь оказывается гораздо больше расстояния АВ. При атмосферном давлении это расстояние порядка 10 -5 см.
Когда впервые были получены эти числа (вторая половина XIX в.), многие физики были ошеломлены. Скорости молекул газа по расчётам оказались больше, чем скорости артиллерийских снарядов! На этом основании высказывали даже сомнения в справедливости кинетической теории. Ведь известно, что запахи распространяются довольно медленно: нужно время порядка десятков секунд, чтобы запах духов, пролитых в одном углу комнаты, распространился до другого угла.
Экспериментальное определение скоростей молекул. Опыты по определению скоростей молекул доказали справедливость формулы (9.19). Один из опытов был предложен и осуществлён О. Штерном в 1920 г.
Что определяет среднюю кинетическую энергию теплового движения молекул и от чего зависит средняя квадратичная скорость этого движения.
Прибор Штерна состоит из двух коаксиальных цилиндров А и В, жёстко связанных друг с другом (рис. 9.7, а). Цилиндры могут вращаться с постоянной угловой скоростью. Вдоль оси малого цилиндра натянута тонкая платиновая проволочка С, покрытая слоем серебра.
Как вы думаете, почему проволочка сделана из платины?

По проволочке пропускают электрический ток. В стенке этого цилиндра имеется узкая щель О. Воздух из цилиндров откачан. Цилиндр В находится при комнатной температуре. Вначале прибор неподвижен. При прохождении тока по нити она нагревается и при температуре 1200 °С атомы серебра испаряются. Внутренний цилиндр заполняется газом из атомов серебра. Некоторые атомы пролетают через щель О и, достигнув внутренней поверхности цилиндра В, осаждаются на ней. В результате прямо против щели образуется узкая полоска D серебра (рис. 9.7, б).
Затем цилиндры приводят во вращение с большим числом оборотов n в секунду (до 1500 1/c).
Теперь за время t, необходимое атому для прохождения пути, равного разности радиусов цилиндров RB – RА, цилиндры повернутся на некоторый угол φ. В результате атомы, движущиеся с постоянной скоростью, попадают на внутреннюю поверхность большого цилиндра не прямо против щели О (рис. 9.7, в), а на некотором расстоянии s от конца радиуса, проходящего через середину щели (рис. 9.7, г): ведь атомы движутся прямолинейно.
Если через υB обозначить модуль скорости вращения точек поверхности внешнего цилиндра, то

В действительности атомы серебра имеют разные скорости. Поэтому расстояния s для различных атомов будут несколько различаться. Под s следует понимать расстояние между участками на полосках D и D’ с наибольшей толщиной слоя серебра. Этому расстоянию будет соответствовать средняя скорость атомов, которая равна
Подставляя в эту формулу значение времени t из выражения (9.20), получаем

Зная n, RA и RB и измеряя среднее смещение полоски серебра, вызванное вращением прибора, можно найти среднюю скорость атомов серебра.
Модули скоростей, определённые из опыта, совпадают с теоретическим значением средней квадратичной скорости. Это служит экспериментальным доказательством справедливости формулы (9.19), а следовательно, и формулы (9.16), согласно которой средняя кинетическая энергия молекулы прямо пропорциональна абсолютной температуре.
Основные положения МКТ. Тепловые явления – Физика, учебник для 10 класса – Класс!ная физика
Свидетельство и скидка на обучение каждому участнику
Зарегистрироваться 15–17 марта 2022 г.

Описание презентации по отдельным слайдам:

Измерение скоростей молекул газа
Федоров А.М. – учитель физики Кюкяйской СОШ Сунтарского улуса Республики Саха

Средняя скорость теплового движения молекул
Уравнение 𝑬 = 𝟑 𝟐 kT даёт возможность найти средний квадрат скорости движения молекулы. Подставив в это уравнение 𝑬 = 𝒎 𝟎 𝒗 𝟐 𝟐 , получим выражение для среднего значения квадрата скорости:
𝒗² = 3 kT 𝒎₀ .
Средней квадратичной скоростью называется величина

Вычисления по этой формуле…
Вычисляя по этой формуле скорость молекул, например азота при t=0°C получаем 𝒗 кв =500 м/с. Молекулы водорода при той же температуре имеют скорость 1800 м/с. Эти скорости велики, но так как молекулы газа движутся хаотично, непрерывно сталкиваясь друг с другом, и время между двумя столкновениями мало, то расстояние, которое пролетают молекулы также невелико.
Из-за столкновения траектория каждой молекулы представляет собой запутанную ломаную линию. Как видно из рисунка, при перемещении молекулы из точки А в В пройденный ею путь оказывается гораздо больше расстояния АВ. При атмосферном давлении это расстояние ~ 10⁻⁵ см.

Опыт Штерна
Опыт Штерна — физический эксперимент, впервые поставленный немецким физиком Отто Штерном в 1920 году, и ставший одним из первых практических доказательств состоятельности молекулярно-кинетической теории строения вещества. В нём были непосредственно измерены скорости теплового движения молекул и подтверждено наличие распределения молекул газов по скоростям.
Исследуемым газом в опыте служили разреженные пары серебра, которые получались при испарении слоя серебра, нанесённого на платиновую проволоку, нагревавшуюся электрическим током. Проволока располагалась в сосуде, из которого воздух был откачан, поэтому атомы серебра беспрепятственно разлетались во все стороны от проволоки.

Схема устройства
Исследуемым газом в опыте служили разреженные пары серебра, которые получались при испарении слоя серебра, нанесённого на платиновую проволоку, нагревавшуюся электрическим током. Проволока располагалась в сосуде, из которого воздух был откачан, поэтому атомы серебра беспрепятственно разлетались во все стороны от проволоки. Для получения узкого пучка летящих атомов на их пути была установлена преграда со щелью, через которую атомы попадали на латунную пластинку, имевшую комнатную температуру. Атомы серебра осаждались на ней в виде узкой полоски, образуя серебряное изображение щели.

Результаты опыта
Специальным устройством весь прибор приводился в быстрое вращение вокруг оси, параллельной плоскости пластинки. Вследствие вращения прибора атомы попадали в др. место пластинки: пока они пролетали расстояние l от щели до пластинки, пластинка смещалась. Наибольшая плотность соответствует наиболее вероятной скорости атомов. Полученные в Ш. о. значения наиболее вероятной скорости хорошо согласуются с теоретическим значением, полученным на основе Максвелла распределения молекул по скоростям.

Распределение Максвелла
Распределе́ние Ма́ксвелла — общее наименование нескольких распределений вероятности, которые описывают статистическое поведение параметров частиц идеального газа.


Упражнения
Найти среднюю квадратичную скорость молекул воздуха при температуре t = 17°C. Молярная масса воздуха м = 0,029 кг/моль.
Найти отношение средних квадратичных скоростей молекул гелия и азота при одинаковых температурах.

Упражнения
3. В момент взрыва атомной бомбы развивается температура Т ~10 в степени 7 К. Считая, что при такой температуре все молекулы полностью диссоциированы на атомы, а атомы ионизированы, найти среднюю квадратичную скорость иона водорода.
4. Плотность некоторого газа ρ = 0,06 кг, средняя квадратичная скорость его молекул = 500 м/с. Найти давление р, которое газ оказывает на стенки сосуда.(самостоятельно)

Домашнее задание
Вычислить среднюю квадратичную скорость молекул углекислого газа при температуре 223 К.
Вычислить среднюю квадратичную скорость молекул газа, если его масса m = 6 кг, объем V= 4,9 м3 и давление p = 200 кПа.
Чему равна средняя квадратичная скорость молекул газа, если его масса m = 6 кг, объем и давление р = 200 кПа?
Определить среднюю квадратичную скорость Vкв молекулы газа, заключенного в сосуд вместимостью V = 2 л под давлением P = 200 кПа. Масса газа m = 0,3 г.
Вычислить среднеквадратичную скорость молекул кислорода при 20°С.
Читайте также:
- Цитология и гистология кратко
- Противоречие интересов россии и стран запада кратко
- Пушкин выстрел мое впечатление кратко
- Кризис русского балета кратко
- Период судей в ветхом завете кратко
скоростей всех молекул, обладающих любыми скоростями, нужно эту функцию проинтегрировать по всем возможным скоростям от нуля до бесконечности. Следовательно, сумма всех скоростей равна

а средняя арифметическая скорость  равна
равна

Подставив сюда полученное раньше выражение (13.3) для  получим:
получим:

Чтобы вычислить входящий в это выражение интеграл, преобразуем подинтегральное выражение:

Так как  , то
, то

и

Введя новую переменную  получим:
получим:

Интегрирование по частям дает:

Таким образом, для интеграла в формуле (14.2) получаем выражение:

Подставляя его в (14.2), находим для  выражение:
выражение:

Подобным же образом можно вычислить и среднее арифметическое значение составляющей скорости по какой-либо координатной оси.
Собственно говоря, среднее значение любой компоненты скорости равно нулю, так как она с равной вероятностью может быть и положительной, и отрицательной. Но этого нельзя сказать о среднем значении модуля такой компоненты. Найдем, например, среднее арифметическое значение модуля х-компоненты скорости, т. е. величину  Для него можно написать уравнение, аналогичное (14.1):
Для него можно написать уравнение, аналогичное (14.1):

Здесь  это функция распределения молекул по составляющей
это функция распределения молекул по составляющей  найденная нами раньше:
найденная нами раньше:

Подставив это выражение в (14.4), получим:

Интеграл, входящий в эту формулу, берется с помощью замены переменной  Тогда для
Тогда для  получается выражение:
получается выражение:

Сравнивая выражения (14.3) и (14.5), мы видим, что среднее значение модуля  -компоненты
-компоненты  вдвое меньше среднего значения скорости
вдвое меньше среднего значения скорости 

Это выражение позволяет решить интересную задачу о среднем числе ударов молекул о единицу площади стенки сосуда в единицу времени.
В § 2 (стр. 21) мы видели, что число молекул, пересекающих за время  площадку площадью
площадку площадью  равно
равно  Отсюда следует, что на единицу площади в единицу времени падает
Отсюда следует, что на единицу площади в единицу времени падает 
молекул. Заменив здесь  ее средним значением
ее средним значением  мы получим, что среднее число ударов
мы получим, что среднее число ударов  молекул о единицу площади в единицу времени равно:
молекул о единицу площади в единицу времени равно:

Средняя квадратичная скорость молекул. Чтобы найти среднюю квадратичную скорость молекул  нужно вычислить отношение суммы квадратов скоростей молекул единицы объема к числу молекул в этом объеме. Повторяя предыдущие рассуждения, получаем:
нужно вычислить отношение суммы квадратов скоростей молекул единицы объема к числу молекул в этом объеме. Повторяя предыдущие рассуждения, получаем:

Поставив сюда выражение (13.3) для  получим:
получим:

Интеграл, входящий сюда, находим интегрированием по частям и получаем:

Отсюда

Такое выражение мы получили и раньше.