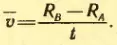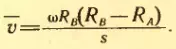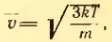Скорости молекул
Скорости молекул
Теория указывает, что при одной температуре средние кинетические энергии молекул mvср2/2 одинаковы. При нашем определении температуры эта средняя кинетическая энергия поступательного движения молекул газа пропорциональна абсолютной температуре. В виде равенства этот важнейший закон записывается так:
где энергия измеряется в эргах.
Мы уже поняли ранее, что температура является какой-то мерой интенсивности теплового движения. Теперь же мы видим, что измерение температуры термометром, заполненным идеальным газом, придает этой мере на редкость простой смысл. Температура пропорциональна среднему значению энергии поступательного движения молекул.
Определим среднюю скорость молекул кислорода при комнатной температуре, которую мы для круглого счета примем в 27 °C = 300 K. Молекулярный вес кислорода 32, так что вес одной молекулы равен 32/6·1023. Простое вычисление даст vср = 4,8·104 см/с, т.е. около 500 м/с. Существенно быстрее движутся молекулы водорода. Их массы в 16 раз меньше и скорости в sqrt(16) = 4 раза больше, т.е. при комнатной температуре составляют около 2 км/с. Прикинем, с какой тепловой скоростью движется маленькая, видимая в микроскоп частичка. Обычный микроскоп позволяет увидеть пылинку диаметром в 1 микрон (10?4 см), Масса такой частицы при плотности, близкой к единице, будет что-нибудь около 5·10?13 г. Для ее скорости получим около 0,5 см/с. Неудивительно, что такое движение вполне заметно.
Скорость броуновского движения горошины с массой в 0,1 г будет уже всего только 10?6 см/с. Немудрено, что мы не видим броуновского движения таких частиц.
Мы говорили о средних скоростях молекулы. Но ведь не все молекулы движутся с одинаковыми скоростями, какая-то доля молекул движется быстрее, а какая-то медленнее. Все это, оказывается, можно рассчитать. Приведем только результаты.
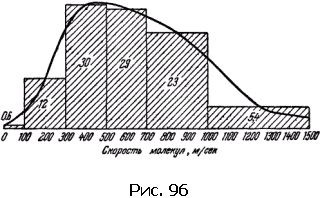
При температуре около 15 °C, например, средняя скорость молекул азота равна 500 м/с; со скоростями от 300 до 700 м/с движется 59 % молекул. С малыми скоростями – от 0 до 100 м/с – движется всего лишь 0,6 % молекул, Быстрых молекул со скоростями свыше 1000 м/с в газе всего лишь 5,4 % (рис. 96).
Можно рассчитать и распределение молекул по разным значениям энергии поступательного движения.
Число молекул, энергия которых более чем в два раза превосходит среднюю, уже меньше 10 %. Доля еще более «энергичных» молекул тает по мере увеличения энергии во все возрастающей степени. Так, молекул, энергия которых в 4 раза больше средней, – всего 0,7 %, в 8 раз больше средней – 0,06·10?4 %, в 16 раз больше средней – 2·10?8 %.
Энергия молекулы кислорода, движущейся со скоростью 11 км/с, равна 32·10?12 эрг. Средняя энергия молекулы при комнатной температуре равна всего 6·10?14 эрг.
Таким образом, энергия «одиннадцатикилометровой молекулы» по крайней мере в 500 раз больше энергии молекулы со средней скоростью. Неудивительно, что доля молекул со скоростями выше 11 км/с равна невообразимо малому числу – порядка 10?300.
Но почему нас заинтересовала скорость 11 км/с? На стр. 161 мы говорили о том, что оторваться от Земли могут лишь тела, имеющие эту скорость. Значит, забравшиеся на большую высоту молекулы могут потерять связь с Землей и отправиться в далекое межпланетное путешествие, но для этого надо иметь скорость 11 км/с. Доля таких быстрых молекул, как мы видим, настолько ничтожна, что опасность потери атмосферы Земле не грозит даже через миллиарды лет.
Скорость ухода атмосферы необычайно сильно зависит от гравитационной энергии ?(Mm/r).Если средняя кинетическая энергия молекулы во много раз меньше гравитационной энергии, то отрыв молекул практически невозможен. На поверхности Луны гравитационная энергия в 20 раз меньше, что дает для энергии «убегания» молекулы кислорода значение 1,5·10?12 эрг. Это значение превышает величину средней кинетической энергии молекулы всего лишь в 20–25 раз. Доля молекул, способных оторваться от Луны, равна 10?17. Это уже совсем не то, что 10?300, и подсчет показывает, что воздух будет довольно быстро уходить с Луны в межпланетное пространство. Неудивительно, что на Луне нет атмосферы.
Читайте также
Скорости капризничают
Скорости капризничают
Какую скорость имеет пассажир относительно полотна железной дороги, если он идет к голове поезда со скоростью 5 километров в час, а поезд движется со скоростью 50 километров в час? Ясно, что скорость человека относительно полотна дороги равна 50 + 5 = 55
Вычисление скорости
Вычисление скорости
Вычисление начальной скорости ядра, которое никогда не должно упасть на Землю.
Чтобы найти искомую скорость, спросим себя сначала: почему всякое ядро, выброшенное пушкой горизонтально, в конце концов, падает на Землю? Потому что земное притяжение
9. Упаковка молекул
9. Упаковка молекул
Характерная особенность описанных выше кристаллов – это отсутствие молекулы в кристалле. Кристалл построен из атомов или ионов, и выделить молекулу в кристалле нельзя. Действительно, вернёмся, например к рисунку 24, а, изображающему строение кристалла
5. Распределение Максвелла (распределение газовых молекул по скоростям) и Больцмана
5. Распределение Максвелла (распределение газовых молекул по скоростям) и Больцмана
Распределение Максвелла – в равновесном состоянии параметры газа (давление, объем и температура) остаются неизменными, однако микросостояния – взаимное расположение молекул, их
31. Разновидность пассивного переноса молекул и ионов через биологические мембраны
31. Разновидность пассивного переноса молекул и ионов через биологические мембраны
Простая диффузия через липидный слой в живой клетке обеспечивает прохождение кислорода и углекислого газа. Ряд лекарственных веществ и ядов также проникает через липидный слой. Однако
2. Вычисление скорости света
2. Вычисление скорости света
Впервые идея о способе измерения скорости света была высказана Г. Галилеем в 1607 г. в следующем виде. Два наблюдателя с фонарями находятся на известном друг от друга расстоянии в прямой видимости. Первый из них открывает свой фонарь и, отмечая
4.7. Измерение скорости света Солнца
4.7. Измерение скорости света Солнца
В конце 40-х гг. ХХ века, во время подготовки в СССР дискуссии о сущности теории относительности, С. И. Вавиловым, президентом АН СССР, было решено поставить лабораторный опыт по проверке достоверности постулата с = const. В качестве
6.3. Рост массы в зависимости от скорости
6.3. Рост массы в зависимости от скорости
Представление зависимости массы от скорости занимает особое положение в современной физике. История формирования соотношения между массой и энергией изложена В. В. Чешевым в работе [1], где, в частности, сказано: «Представление о
Глава 1 Ограничение скорости
Глава 1
Ограничение скорости
В тот день все банки были закрыты — выходной, и мистер Томпкинс, скромный служащий солидного городского банка, встал позже обычного и не спеша позавтракал. Пора было позаботиться о досуге, и мистер Томпкинс решил, что было бы неплохо сходить
Как складывать скорости
Как складывать скорости
Если я ждал полчаса и еще час, то всего я потерял времени полтора часа. Если мне дали рубль, а затем еще два, то я всего получил три рубля. Если я купил 200 г винограда, а затем еще 400 г, то у меня будет 600 г винограда. Про время, массу и другие подобные
Взаимодействие молекул
Взаимодействие молекул
Молекулы взаимно притягиваются, в этом невозможно сомневаться. Если бы в какое-то мгновение молекулы перестали притягиваться друг к другу, все жидкие и твердые тела распались бы на молекулы.Молекулы взаимно отталкиваются, и это несомненно, так как
Средняя скорость теплового движения молекул. Уравнение (2.9) дает возможность найти среднюю скорость теплового движения молекул. Подставляя в это уравнение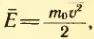 
получим выражение для среднего квадрата скорости:
(2.11)
Отсюда средняя скорость молекулы (точнее, средняя квадратическая скорость) равна:
(2.12)
Вычисляя по формуле (2.12) скорость молекул, например азота, при t = 0°C, получим: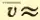 
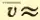
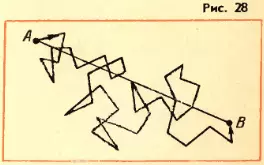
500 м/с. Молекулы водорода при той же температуре имеют скорость 1800 м/с.
Когда впервые были получены эти числа (вторая половина XIX в.), многие физики были ошеломлены. Скорости молекул газа по расчетам оказались большими, чем скорости артиллерийских снарядов! Высказывали на этом основании даже сомнения в справедливости кинетической теории. Ведь известно, что запахи распространяются довольно медленно: нужно время порядка десятков секунд, чтобы запах духов, пролитых в одном углу комнаты, распространился до другого угла. Это нетрудно объяснить. Из-за столкновений молекул траектория каждой молекулы представляет собой запутанную ломаную линию (рис. 28). Большие скорости молекула имеет на прямолинейных отрезках ломаной. Перемещение же молекулы в каком либо направлении в среднем невелико даже за время нарядна нескольких минут. При перемещении молекулы из точки A в точку B пройденный ею путь оказывается гораздо больше расстояния |AB|.
Экспериментальное определение скоростей молекул. Опыты по определению скоростей молекул доказали справедливость формулы (2.12). Один из опытов был предложен Штерном в 1920 г.
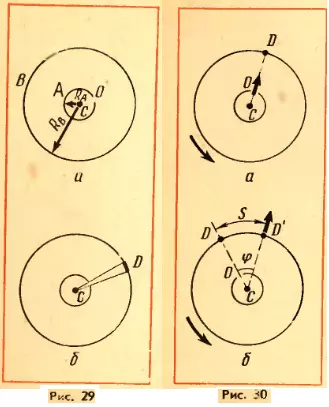
Прибор Штерна состоит из двух коаксиальных цилиндров А и В, жестко связанных друг с другом (рис. 29, а). Цилиндры могут вращаться с постоянной угловой скоростью. Вдоль оси малого цилиндра натянута тонкая платиновая проволочка C, покрытая слоем серебра. По проволочке пропускают электрический ток. В стенке этого цилиндра имеется узкая щель O. Воздух из цилиндров откачан. Цилиндр B находится при комнатной температуре.
Вначале прибор неподвижен. При прохождении тока по нити слой серебра испаряется и внутренний цилиндр заполняется газом из атомов серебра. Некоторые атомы пролетают через щель O и, достигнув внутренней поверхности цилиндра B, осаждаются на ней. В результате прямо против щели образуется узкая полоска серебра D (рис. 29, б).
Затем цилиндры приводит во вращение с угловой скоростью ω. Теперь за время t, необходимое атому для прохождения пути, равного разности радиусов цилиндров RB – RA, цилиндры повернутся на некоторый угол φ. В результате атомы, движущиеся с постоянной скоростью, попадут на внутреннюю поверхность большого цилиндра не прямо против щели O (рис. 30, а), а на некотором расстоянии s от конца радиуса, проходящего через середину щели (рис. 30, б). Ведь атомы движутся прямолинейно. Расстояние s равно:
s = φ RB = ωtRB (2.13)
В действительности не все атомы серебра имеют одну и ту же скорость. Поэтому расстояния s для различных атомов будут несколько различаться. Под s следует понимать расстояние между участками на полоскал D и D’ с наибольшей концентрацией атомов серебра. Этому расстоянию будет соответствовать средняя скорость атомов.
Средняя скорость атома равна:
Подставляя в эту формулу значение t из выражения (2.13), получим:
Зная ω, RA и RB и измеряя среднее смещение s полоски серебра, вызванное вращением прибора, находим среднюю скорость атомов серебра.
Модули скоростей, определенные из опыта, совпадают с теоретическим значением средней квадратической скорости. Это служит экспериментальным доказательством справедливости формулы (2.12), а следовательно и (2.9), согласно которой средняя кинетическая энергия молекулы прямо пропорциональна абсолютной температуре.
Средняя скорость броуновской частицы. Формула (2.12) позволяет понять почему интенсивность броуновского движения возрастает с повышением температуры жидкости и уменьшается при увеличении массы частицы. Ведь броуновская частица, участвует в тепловом движении молекул. Поэтому ее средняя кинетическая энергия также определяется формулой (2.9), а средняя квадратическая скорость – формулой
где m – масса броуновской частицы. Если масса частицы велике, то средняя скорость ее движения настолько мала, что движение частицы практически нельзя обнаружить.
1. Как изменится средняя квадратическая скорость движения молекул при увеличении температуры в 4 раза? 2. Какие молекулы в атмосфере движутся быстрее: молекулы азота или молекулы кислорода? 3. Почему толщина слоя полоски серебра на поверхности внешнего вращающегося цилиндра в опыте Штерна неодинакова по ширине полоски?
Средняя скорость молекул
В физике выделяют 2 скорости, характеризующие движение молекул: средняя скорость движения молекул и средняя квадратичная скорость.
Средняя скорость движения молекул
Средняя скорость движения молекул называется также скоростью теплового движения молекул.
Формула средней относительной скорости молекул в физике представлена следующим выражением:
υotn=28kTπm0=2υ.
Средняя квадратичная скорость
Средняя квадратичная скорость движения молекул газа это следующая величина:
υkυ=1N∑i=1Nυi2
Формулу средней квадратичной скорости можно переписать так:
υkυ2=∫0∞υ2Fυdυ.
Проводя интегрирование, аналогичное интегрированию при получении связи средней скорости с температурой газа, получаем:
υkυ=3kTm0=3RTμ
Именно средняя квадратичная скорость поступательного движения молекул газа входит в состав основного уравнения молекулярно-кинетической теории:
p=13nm0υkυ,
где n=NV – это концентрация частиц вещества, N – это количество частиц вещества, V – это объем.
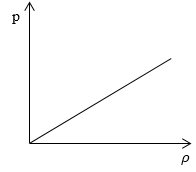
Необходимо определить, как изменяется средняя скорость движения молекул идеального газа с увеличением давления в процессе, изображенном на графике (рисунок 1).
Рисунок 1
Решение
Запишем выражение для средней скорости движения молекул газа следующим образом:
υ=8kTπm0
Из графика видно, что p~ρ или p=Cρ, где C – это некоторая константа.
m0=ρn, p=nkT=Cρ→kT=Cρn
Подставив m0=ρn, p=nkT=Cρ→kT=Cρn в υ=8kTπm0, получаем:
υ=8kTπm0=8Cρπnnρ=8Cπ
Ответ: В процессе, представленном на графике, с увеличением давления средняя скорость движения молекул не меняется.
Можно ли найти среднюю квадратичную скорость молекулы идеального газа, если известно: давление газа (p), молярная масса газа (μ), а также концентрация молекул газа (n)?
Решение
Применим выражение для υkυ:
υkυ=3RTμ
Помимо этого, из уравнения Менделеева-Клайперона и зная, что mμ=NNA:
pV=mμRT=NNART.
Поделим правую и левую части pV=mμRT=NNART на V, и зная NV=n, получаем:
p=nNART→RT=pNAn
Подставляем p=nNART→RT=pNAn в выражение для среднеквадратичной скорости υkυ=3RTμ, получаем:
υkυ=3pNAμn
Ответ: По заданным в условии задачи параметрам среднеквадратичная скорость движения молекул газа вычисляется при помощи формулы υkυ=3pNAμn.
Измерение скоростей молекул газа
Оценка 4.8
Зная температуру, нетрудно вычислить среднюю кинетическую энергию молекул газа. После этого легко вычислить и среднюю скорость молекулы. А можно ли эту скорость измерить? С помощью уравнения Е равно три вторых Ка Т можно найти средний квадрат скорости движения молекулы, подставив значение кинетической энергии в это уравнение.
Средняя кинетическая энергия молекул равна произведению массы молекулы эМ нулевое на среднюю скорость Вэ в квадрате деленное на 2.
В результате получим, что средний квадрат скорости Вэ в квадрате равно 3 умножить на Ка на Т и разделить на эМ нулевое.
Квадратный корень из этой величины называется средней квадратичной скоростью: средняя квадратичная скорость Вэ равна корню квадратному из дроби в числителе 3 КаТ, в знаменателе эМ нулевое.
Используя данную формулу, можно вычислить скорость молекул Например, скорость Вэ азота при t=0°С равна 500 метров в секунду.
Молекулы водорода при той же температуре имеют среднюю скорость Вэ равную 1800 метров в секунду.Рассмотрим пример решения задачи на определение средней квадратичной скорости.
Определите среднюю квадратичную скорость молекулы газа при 00С. Молярная масса газа М-0,019 кг/моль.
Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
Перейти к контенту
Условие задачи:
Определить среднюю квадратичную скорость молекул азота при температуре 27° C?
Задача №4.1.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(t=27^circ) C, (upsilon_{кв}-?)
Решение задачи:
Среднюю квадратичную скорость молекул идеального газа (upsilon_{кв}) определяют по такой формуле:
[{upsilon _{кв}} = sqrt {frac{{3RT}}{M}} ]
В этой формуле (R) – универсальная газовая постоянная, равная 8,31 Дж/(моль·К), (M) – молярная масса газа, равная у азота 0,028 кг/моль.
Переведем данную в условии температуру из шкалы Цельсия в шкалу Кельвина:
[27^circ;C = 300;К]
Посчитаем ответ:
[{upsilon _{кв}} = sqrt {frac{{3 cdot 8,31 cdot 300}}{{0,028}}} = 516,8;м/с approx 0,5;км/с]
Ответ: 0,5 км/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
4.1.25 Какова плотность сжатого воздуха при 0 C в камере шины автомобиля “Волга”? Давление
4.1.27 Определить плотность воздуха при нормальных условиях. Молярную массу принять
4.1.28 Каково давление азота, если его плотность равна 1,35 кг/м^3, а средняя квадратичная
( 16 оценок, среднее 3 из 5 )
