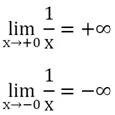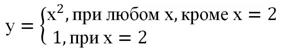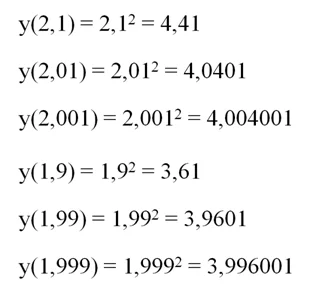Как найти среднюю скорость на графике функции

Как найти среднюю скорость по графику

Движение различных тел в окружающей среде характеризуется рядом величин, одна из которых – средняя скорость. Этот обобщенный показатель определяет скорость тела на всем перемещении. Зная зависимость модуля мгновенной скорости от времени, среднюю скорость можно найти с помощью графического метода.

Инструкция

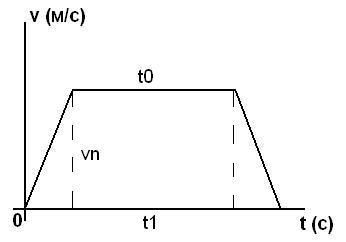
Постройте по данным задачи график зависимости скорости движения тела от времени v(t). Здесь горизонтальная координата представляет собой изменение времени (с), вертикальная – скорости (м/с). Как правило, в задачах рассматривается неравномерное перемещение тел в определенные промежутки времени. Любое изменение скорости на графике будет отображено возрастанием или убыванием. Например, при начале движения тела с постоянным ускорением в течение 20 с его скорость в итоге составила 15 м/с. Отложите на графике прямую, начинающуюся в начале координат (0, 0) и заканчивающуюся в точке (20, 15), где 20 с откладываются вправо по оси времени t, а 15 м/с – вверх по скорости. При наличии равномерного движения тела отобразите его прямой, параллельной горизонтальной оси.

Для нахождения средней скорости перемещения нужно знать путь и время, затраченное на движение. Вычислите площадь S под кривой v(t), которая является графическим представлением пройденного телом пути L. Часто график перемещения ограничивает фигуру трапецию. Ее площадь находится по формуле: S = ½*(t0 + t1)*vn, где t0 и t1 – основания трапеции – части графика скорости, vn – высота фигуры, здесь максимальная скорость в пути. Подставьте в формулу известные значения и вычислите результат. Если график v(t) представляет собой не трапецию, ее площадь вычисляется по иным формулам, в зависимости от полученной фигуры.

Найдите среднюю скорость движения тела по формуле Vср = L/t. Подставив заданное время перемещения и вычисленный путь, посчитайте числовое значение средней скорости.

Среднюю скорость можно вычислить и по графику зависимости пути от времени l(t). Для этого соедините прямой линией начальную и конечную точки рассматриваемого участка перемещения. Средняя скорость тела будет равна тангенсу угла наклона полученной прямой к оси времени.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Средняя скорость считается так: весь путь поделить на всё время движения. Формула одна и очень простая, но почему-то школьники часто путаются в задачах на среднюю скорость. Разберу три характерные задачи и основные ошибки. Возможно, статья будет полезна учителям и репетиторам, а также школьникам.

1. Половина пути

Первую половину пути поезд ехал со скоростью 60 км/ч, а вторую – 90 км/ч. С какой средней скоростью ехал поезд на всём пути?

Первым делом школьник захочет сложить эти две скорости и поделить пополам. Логично? Да. Но, к сожалению, неправильно.

Объясняю, почему. Поскольку первую половину пути поезд ехал с меньшей скоростью, то времени было затрачено больше, чем на вторую. А значит, вклад отдельных скоростей неравнозначен, и нельзя так просто делить пополам.

Тут школьник может впасть в панику. Что делать? Умножать? Делить? Непонятно. Воспользоваться напрямую формулой “расстояние поделить на время” не получится – ни расстояние, ни время нам неизвестно.

Для школьников, только начинающих изучать основы физики, бывает трудно оперировать с неизвестными величинами. Нам не дано ничего, кроме скоростей, как же быть? В качестве маленькой ступеньки к освоению неизвестности могу предложить следующий ход – сначала додумать неизвестные данные. Возьмём и сами решим, пусть поезд пройдет 180 километров, цифру возьмем так, чтобы легко делилась.

Тогда половина пути будет 90 километров. Поезд пройдет её за 1,5 часа. Вторую половину пути – за 1 час. Это легко посчитает любой школьник. Значит, общее время в пути будет 2,5 часа. Делим общее расстояние 180 километров на 2,5 часа, и получаем 72 км/ч.

Это просто и понятно, но учитель такую задачу не примет. Откуда мы взяли 180 километров, когда это неизвестно? Тем не менее, дав себе эти неизвестные данные, мы продумали алгоритм и довели задачу до ответа. Осталось формализовать это решение, так чтобы не использовать то, что не дано. Обозначим наши 180 километров за S, и опишем всё, что мы делали раньше, только вместо цифр используем буквы.

Получается, что зная ход решения “в цифрах”, мы переводим его в буквенные обозначения. И тут главное не остановиться на полдороги, не смущаться, что нам неизвестно расстояние. Ведь оно в конце сократилось, и средняя скорость оказалась независящей от расстояния (что вполне логично). И от школьника здесь требуются уже алгебраические умения – складывать дроби, переворачивать их.

Если подобная задача встретилась в тесте, где требуется только ответ, можно вообще не заморачиваться – так как средняя скорость в данной задаче не зависит от расстояния, можно посчитать при любом удобном расстоянии. По крайней мере, это лучше, чем сидеть и ломать голову, не зная, как подступиться к решению. Если же требуется оформление – тут числовое решение может помочь как переходный этап, чтобы понять, что именно делать с формулами, как их крутить-вертеть.

Школьникам часто бывает трудно переходить на новый уровень абстракции – от чисел к переменным, которые могут принимать разные числовые значения. В алгебре это тренируют, но там одна переменная икс, и иногда игреки встречаются. А в физике этих переменных пруд пруди, в каждой задаче они разные, и если ученик не освоил этот уровень, то физика кажется ему супер-трудной. Кроме того, в школе переход от чисел к переменным часто упускают, в программе отдельных навыков работы с формулами нет.

2. Средняя скорость по графику пути

Пусть нам дан график зависимости координаты от времени. Требуется определить среднюю скорость.

По графику видно, что движение состоит из четырех этапов:

1. Тело стартует в нуле и через 2 секунды оказывается на координате 2 м.
2. Тело останавливается, и в течение 4 секунд покоится в точке с координатой 2 м.
3. Тело начинает движение, и через 2 секунды оказывается в точке 6 м.
4. Тело движется в обратном направлении, и через 2 секунды оказывается в точке 5 м.

Проговорить, понять все эти этапы – важная часть решения. А дальше многие школьники начинают вычислять скорости движения на каждом этапе: На первом – 1 м/с, на втором – 0, на третьем – 2 м/с, на четвертом – 0,5 м/с. Вот это действие как раз лишнее. Для того, чтобы вычислить среднюю скорость, вовсе не обязательно знать скорости на каждом этапе!

Вспомним определение средней скорости – это весь путь, поделить на всё время. Поэтому просто по графику считаем весь путь – 6 метров “туда” и 1 метр “обратно”, в сумме 7 метров. Общее время движения – 10 секунд. Делим 7 метров на 10 секунд, получаем 0,7 м/с.

3. Средняя скорость по графику скорости

Бывает так, что нам дан график зависимости скорости от времени, и требуется определить среднюю скорость. Вот, к примеру, такой график.

Читаем график. Движение состоит из трёх этапов

1. С начала движения до момента времени 2 с тело движется с постоянной скоростью 2 м/с
2. От 2 до 6 с тело движется со скоростью 6 м/с
3. В последние 4 секунды от 6 до 10 с тело замедляется, снижая свою скорость до нуля.

Попытки что-то сделать со значениями скорости самими по себе здесь обречены на провал. Опять надо найти весь путь и всё время движения. Путь по графику скорости определяется как площадь под графиком, причем если график идет ниже нуля, то соответствующие участки складываются.

Считаем площадь фигуры – два прямоугольника на первых двух этапах и треугольник на третьем. Первый этап – 4 м, второй этап – 24 м, третий этап – 12 м. Значит, весь путь будет 40 метров. Всё время 10 секунд, значит, средняя скорость 4 м/с.

Общие рекомендации для решения задач на среднюю скорость

1. Средняя скорость – это всегда весь путь делить на всё время. Данные об отдельных скоростях сами по себе не дадут полной информации о средней скорости. Используем только эту формулу.

2. Следует проанализировать конкретную ситуацию и понять, как можно применить формулу. Если кажется, что не хватает данных – не смущаться.

3. Данные по скоростям на отдельных этапах могут быть полезны для проверки готового ответа: средняя скорость должна лежать между минимальной и максимальной.

Спасибо, что прочитали до конца! Желаю школьникам хорошей учёбы, учителям – понятливых и любопытных учеников, родителям – чтобы дети радовали. Буду рада лайкам и новым подписчикам!

Была ли эта статья полезной?

План урока:

Предел функции на бесконечности

Предел функции в точке

Приращение аргумента и функции  

Средняя скорость изменения функции

Мгновенная скорость и понятие производной

Предел функции на бесконечности

Рассмотрим довольно простую функцию

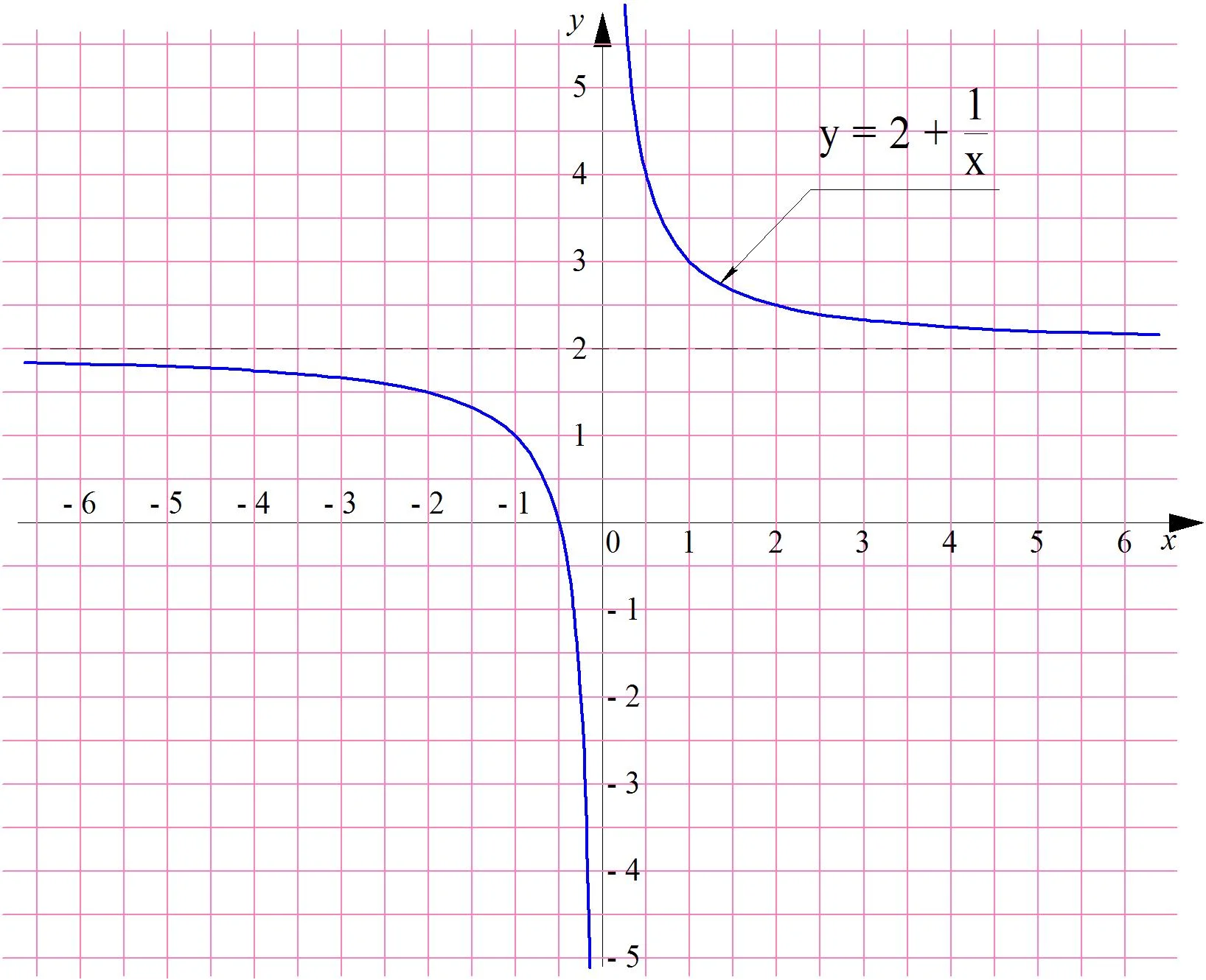
y = 1/x

Её график называется гиперболой и выглядит так:

Можно заметить, что при больших положительных значениях х график функции приближается к горизонтальной оси Ох, но не пересекает её. Действительно, если мы будем вычислять значение у при всё больших значениях х, то будем получать всё меньшие, но всё же положительные числа:

Получается, что при бесконечном росте аргумента х функция стремится к нулю. Можно ли эту особенность функции как-то записать, используя математические символы? Оказывается, можно, и выглядит это запись так:

которая означает, что х стремится к бесконечности. После символа lim записана сама функция 1/х. В целом вся запись читается так: «предел функции у = 1/х при х, стремящемся к бесконечности, равен нулю».

Вернемся к графику функции у = 1/х. Видно, что если мы будем брать всё меньшие отрицательные значения х, то функция также будет стремится к нулю. Действительно, попробуем подставлять в нее как можно меньшие значения аргумента:

Чтобы записать эту особенность функции, используется следующая запись:

который может быть получен параллельным переносом графика у = 1/х на две единицы вверх:

Очевидно, что пределы этой функции при х → + ∞ и х → – ∞ равны 2:

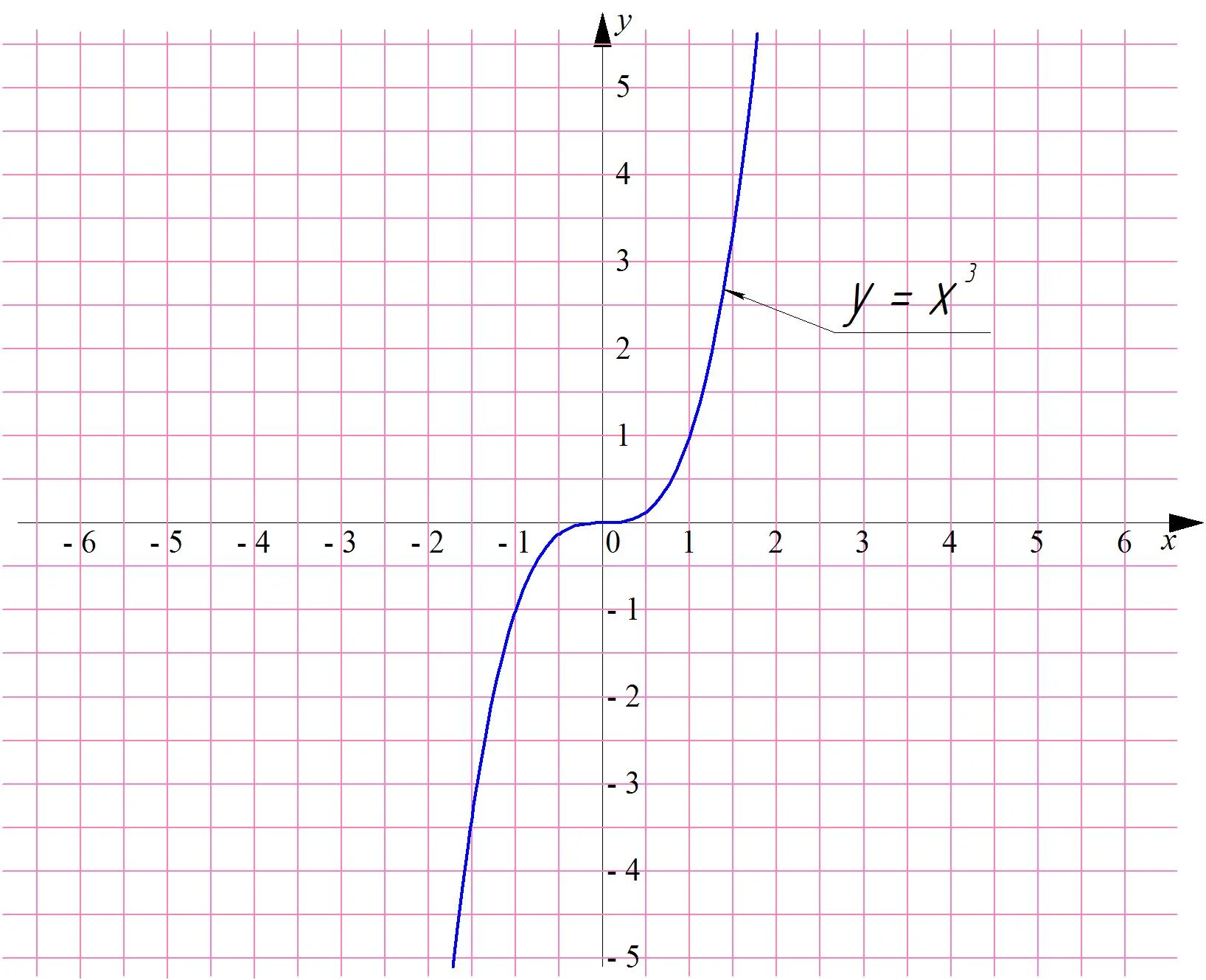
Возможны случаи, когда при бесконечном увеличении аргумента функции она не стремится к какому-то конкретному числу, а сама также неограниченно возрастает. Для примера посмотрим на график у = х³:

Видно, что при х → ∞ сама функция неограниченно растет, что можно показать расчетами:

Возникает вопрос – для всякой ли функции можно указать ее предел на бесконечности? Оказывается, что нет. Для примера рассмотрим тригонометрическую функцию у = sinx, графиком которой является синусоида:

С одной стороны, sinx явно не стремится к какому-то конкретному числу при увеличении х, он «колеблется» между числами 1 и (– 1). С другой стороны, нельзя и сказать, что он стремится к бесконечности. Получается, что у этой функции просто нет пределов на бесконечности.

Предел функции в точке

Порою нас интересует поведение функции не на бесконечности, а вблизи конкретной точки х₀. Конечно, в большинстве случае можно просто вычислить функцию в этой точке, однако иногда это невозможно сделать. Для примера рассмотрим функцию

Очевидно, что точка х = 2 не входит в ее область определения, ведь при подстановке этого значения в функцию знаменатель дроби обратится в ноль. Однако в любой другой точке значение функции будет равняться единице:

График такой функции будет выглядеть как прямая у = 1, у которой есть одна «выколотая точка», соответствующая х = 2:

Итак, функция не определена в точке х = 2, однако можно вычислить предел функции в точке х = 2. Действительно, при любом, сколь угодно близком к 2 значении х функция будет равна единице:

Попробуем также приблизиться к точке 2 с другой стороны, подставляя в функцию числа, меньшие двух:

Снова всё время получается единица. Поэтому мы можем уверенно записать, что

Значительно чаще приходится иметь дело с пределами в точке, которые равны бесконечности. Снова посмотрим на график функции у = 1/х:

Видно, график не пересекает ось Оу, ведь число х = 0 не входит в область определения функции. Однако можно заметить, что при приближении х к нулю функция неограниченно возрастает:

Обратите внимание, что под пределом мы использовали запись «х → + 0», а не «х → 0». Почему? Дело в том, что если мы будем приближаться к нулю с «противоположной» стороны, подставляя в функцию не положительные, а отрицательные числа, то функция будет стремится к – ∞:

Получается, что предел функции в точке х = 0 зависит от того, с какой стороны мы приближаемся к этой точке, слева или справа. В связи с этим в математике существует понятие односторонних пределов. Для обозначения пределов, получаемых при приближении к нулю справа, то есть со стороны бОльших чисел, перед ним ставят знак плюс, а при указании предела слева, то есть со стороны мЕньших чисел – знак минус:

Предел и односторонние пределы – это два разных понятия. Считается, что функция имеет предел в точке только тогда, когда оба односторонних предела в этой точке совпадают.

В качестве ещё одного примера предела функции в точке можно привести зависимость у = tg х, график которой выглядит следующим образом:

В точке х = π/2 функция не определена. Однако видно, что при приближении к этой точке слева функция неограниченно возрастает, а при приближении справа – неограниченно убывает. Это записывается следующим образом:

До этого мы вычисляли пределы функций в точках, где сами функции не определены. Однако пределы можно вычислять и в тех точках, где функция определена. В большинстве случаев (но не всегда) они как раз равны значению функции в этой точке. Например, найдем предел

В точке х = 2 значение функции будет равно 4:

Будут ли односторонние пределы в этой точке также равняться 4? Сначала проверим предел справа

Действительно, получаем значения у, всё более близкие к 4. Аналогично можно убедиться, что и предел слева также равен 4:

Приведем несколько искусственный пример функции, у которой предел в точке не совпадает со значением функции в этой точке. Пусть функция задается с помощью такого графика

Он представляет собой параболу у = х² с выколотой точкой (2; 4). При этом функция определена в точке х = 2, но имеет там значение, равное единице. Аналитически эту функцию можно описать так:

Понятно, что у(2) = 1, однако попытаемся приблизиться к точке х = 2 справа и слева и посмотрим, что получится:

Мы видим, что при х→2 функция и справа, и слева стремится к четверке, а не к единице. То есть получается, что предел функции в точке х = 2 не совпадает со значением функции этой функции в этой же точке. Такая ситуация произошла именно из-за того, что точка х = является выколотой.

Сразу заметим, что непосредственно в практических задачах пределы почти не используются. В связи с этим эта тема изучается в школьном курсе довольно поверхностно, не дается строгое определение предела функции (предполагается, что это понятие интуитивно понятно), а также не рассматриваются примеры на вычисление пределов функций. С другой стороны, на понятии предела построены почти все строгие рассуждения и доказательства в математическом анализе. В частности, определение понятие производной (которая имеет огромное практическое применение) дается именно с помощью предела. Поэтому полностью исключить пределы из школьного курса нельзя.

Приращение аргумента и функции

Часто нас интересует, как изменяется функция при изменении аргумента. Например, известно, что объем куба вычисляется по формуле

где а – ребро куба. Предположим, что мы провели измерения какого-то куба и выяснили, что длина его ребра равна 2 см. Тогда объем куба составит 2³ = 8 см³. Но ведь любое измерение производится не с абсолютной точностью, а с некоторой погрешностью. Как оценить погрешность вычисления объема, если известна погрешность измерения его ребра?

Пусть с учетом погрешности линейки, составляющей 0,1 см, известно, что длина ребра находится в диапазоне от 2 до 2 + 0,1 = 2,1 см. Тогда максимально возможный объем куба составит 2,1³ = 9,261 см³. Получается, что погрешность в измерении объема куба составляет 9,261 – 8 = 1,261 см³.

С точки зрения математического анализа мы в данном случае рассматривали поведение функции у = х³ в точке х = 2. Мы допустили некоторое изменение величины х, которое называют приращением аргумента и обозначают как ∆х. Далее мы высчитали, какое изменение величины у, или приращение функции, обозначаемое как ∆у, соответствует этому приращению аргумента. Выяснилось, что приращению ∆х = 0,1 соответствует приращение ∆у = 1,261.

В более общем случае произвольной функции у = f(x) можно дать некоторое приращение ∆х в некоторой точке х₀. В результате этого изменится и само значение f(x), причем величину этого изменения обозначают как ∆у. Это можно проиллюстрировать графически:

Задание. Дана функция у = 3х² + х + 4. Вычислите приращение функции в точке х₀ = 5, если ∆х = 1.

Решение. Сначала вычислим новое значение аргумента функции, с учетом данного ему приращения:

Далее вычислим значения функции, соответствующие старому и новому аргументу:

Задание. Радиус круга, измеренный с погрешностью не более 0,5 см в меньшую сторону, равен 10 см. Оцените погрешность вычисления его площади.

Решение. Площадь круга рассчитывается по формуле:

Средняя скорость изменения функции

Часто в физике и других естественнонаучных дисциплинах одни величины характеризуют изменение других величин. Классический случай – это скорость, которая характеризует, насколько быстро изменилось положение тела (или материальной точки в пространстве). Рассмотрим пример. Пусть пешеход движется по прямой улице с постоянной скоростью 2 м/с. Попытаемся построить график, который иллюстрирует зависимость пройденного пешеходом пути и его скорости от времени. Известно, что при равномерном прямолинейном движении пройденный путь можно найти по формуле:

S = v*t

Где s – путь;

V – скорость;

t – время.

Так как скорость равна 2 м/с, то зависимость пути от времени будет выглядеть так:

s(t) = 2t

которая является прямой пропорциональностью. Поэтому ее график будет прямой линией:

Так как скорость во время всего движения остается равной 2 м/с, то зависимость скорости от времени будет иметь вид v = 2, а выглядеть она будет как горизонтальная линия:

В данном случае найти зависимости s(t) и v(t) было очень легко. Но теперь усложним задачу. Пусть зависимость s(t) задается не прямой линией, а некоторой кривой:

Можно ли теперь что-то сказать о скорости движения пешехода?

Ясно, что в различные моменты времени скорость пешехода различна. Но мы можем найти среднюю скорость пешехода в какой-то момент времени. Например, рассмотрим промежуток времени со 2-ой по 10-ую секунду.

Его протяженность, очевидно, равна 10 – 2 = 8 секундам. Если первый момент времени обозначить как t₁, а второй как t₂, то протяженность этого промежутка времени (∆t) можно вычислить по формуле

Судя по графику, к моменту времени t₁ пешеход прошел только 1 метр, а на момент t₂он преодолел уже 9,5 м. Сколько же метров он прошел за промежуток времени ∆t? Если первое расстояние обозначить как s₁, а второе как s₂, то пройденное расстояние (∆s) можно рассчитать так:

Тогда средняя скорость на рассматриваемом участке можно вычислить, поделив ∆s на ∆t

В данной ситуации мы рассматривали функцию, которая задает зависимость между перемещением пешехода и временем. Средняя скорость характеризует, как быстро двигается пешеход, то есть как быстро функция s(t) меняет своё значение. Очевидно, что в данном случае величина ∆t – это некоторое приращение аргумента функции s(t), в то время как ∆s– это приращение самой функции. Получается, что с помощью приращений можно вычислять среднюю скорость объектов.

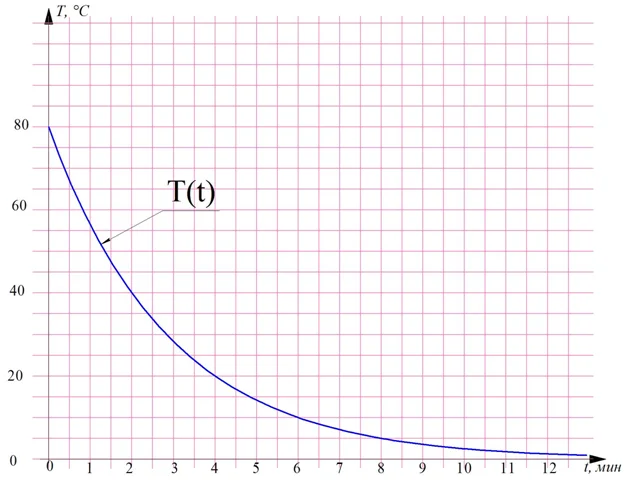
Однако в физике рассматривается не только скорость перемещения вточек пространстве. Например, можно говорить о скорости остывания горячего чайника. Пусть его температура меняется по закону, график которого представлен на рисунке:

Можно ли узнать, с какой средней скоростью остывал чайник на промежутках от 2-ой до 4-ой минуты? Да, для этого надо в точке t = 2 мин дать приращение аргумента ∆t = 2мин и посмотреть, какое приращение ∆T получит сама функция:

Пусть t₁ = 2 мин, а t₂ = 4 мин. Тогда

По графику видно, что в момент t₁ температура чайника составляет Т₁ = 40°С. Через две минуты она уже упала до отметки Т₂ = 20°С. Получается, что за промежуток ∆t функция T(t) получила приращение

Обратите внимание, что приращение оказалось отрицательным. Дело в том, что температура чайника падала, то изменялась в меньшую сторону. Знак минус указывает именно на направление изменения функции. Если бы чайник нагревался, то приращение оказалось бы положительным.

Теперь мы можем вычислить среднюю скорость остывания чайника на промежутке между 2-ой и 4-ой минутой:

Знак минус указывает на то, что температура на этом промежутке времени уменьшается, а не возрастает.

В более общем случае, когда у нас есть произвольная функция у = f(x), с помощью приращений можно вычислить среднюю скорость её изменения на каком-нибудь промежутке. Пусть первая точка промежутка обозначается как х₀, а его протяженность составляет ∆х. Тогда первой точке соответствует значение функции у(x₀), а концу промежутка – значение у(x₀ + ∆x):

Тогда средняя скорость изменения функции на промежутке [x₀;x₀ + ∆x] рассчитывается по формуле:

Мгновенная скорость и понятие производной

Итак, зная функцию, можно вычислить среднюю скорость ее изменения на любом промежутке. Но, когда автомобиль едет по шоссе, его спидометр показывает не среднее, а конкретное значение скорости в каждый момент времени. Другими словами, у автомобиля есть мгновенная скорость, и именно ее показывает спидометр. Как же узнать ее?

Пусть у нас есть функция s(t), определяющая пройденной машиной путь, и нам требуется найти мгновенную скорость в некоторый момент времени t₁. Мы можем дать функции s(t) приращение ∆t, а потом найти и среднюю скорость на промежутке [t₁; t₁ + ∆t]. Естественно, она будет являться лишь некоторым приближением, с помощью которого мы оцениваем мгновенную скорость в момент t₁. Однако далее мы можем уменьшить промежуток ∆t. Тогда у нас получится иное значение средней скорости, которое будет более близким к мгновенной скорости. Чем меньший промежуток ∆t мы возьмем, тем ближе к мгновенной скорости в точке t₀ будет полученное нами значение средней скорости.

Например, пусть путь, пройденный машиной, задается функций s = t². Нас интересует скорость автомобиля в момент t₁ = 5 сек. Мы можем найти среднюю скорость на интервале от 5-ой до 6-ой секунды. Так, к пятой секунде машина успеет проехать 5² = 25 метров, а к шестой секунде она проедет 6² = 36 метров. Получится, что за промежуток ∆t, равный 6 – 5 = 1 секунде, машина проедет путь ∆s = 36 – 25 = 11 метров. Тогда средняя скорость на промежутке составит

Теперь возьмем более короткий промежуток ∆t, равный всего лишь 0,1 с. То есть мы рассмотрим период времени между моментом t₁ = 5 cи t₂ = 5,1 c. Снова-таки, к 5-ой секунде машина проедет 25 метров, а к моменту 5,1 сона пройдет 5,1² = 26,01 м. То есть за 0,1 с автомобиль преодолеет 26,01 – 25 – 1,01 м, а средняя скорость при этом составит

Ещё раз уменьшим промежуток ∆t. Пусть теперь он составляет всего 0,01с. Тогда средняя скорость будет определяться так:

Видно, что при уменьшении промежутка ∆t средняя скорость стремится к величине 10 м/с. Поэтому логично считать именно эту величину мгновенной скоростью машины в момент времени t = 5 c. Однако возникает вопрос – уверены ли мы, что мгновенная скорость стремится именно к 10 м/с, а не, скажем, к 10,001 м/с? Как точно определить это число? Здесь как раз помогают пределы. Можно записать, что мгновенная скорость – это предел отношения ∆s/∆t при ∆t, стремящемся к нулю. То есть

Получили, что мгновенная скорость в момент t₁ = 5 действительно равна 10 м/с.

Задание. Вычислите мгновенную скорость разгоняющегося самолета через 10 секунд после начала разгона, если пройденное им расстояние задается законом s(t) = 5t².

Решение. За 10 секунд самолет успеет преодолеть

Дадим функции s(t) приращение ∆t и обозначим как t₁ момент времени, когда со старта прошло 10 секунд. Тогда к моменту t₁ + ∆t самолет успеет пройти

Решая данную задачу, мы дали функции s(t) приращение ∆t и записали отношение ∆s/∆t. Далее мы устремили величину ∆t к нулю и посмотрели, к какому числу устремится отношение ∆s/∆t. Это число и оказалось мгновенной скоростью. В более общем случае произвольной функции у = f(x)в точке х₀ можно дать приращение аргумента ∆х, которому будет соответствовать некоторое приращение функции ∆у. Далее можно вычислить предел отношения ∆у/∆х, который будет характеризовать, как быстро в точке х₀ функция меняет свое значение. Этот предел называют производной функции в точке х₀. Для обозначения производной над функцией ставят штрих.

В общем случае алгоритм вычисления производной в некоторой точке следующий:

1.Фиксируем точку х₀, вычисляем для нее значение функции у(х). Это значение будет конкретным числом

1. Даем функции приращение аргумента ∆х, переходим в новую точку х₀ + ∆х, вычисляем в ней значение функции у(х₀ + ∆х). Это значение будет не числом, а выражением, содержащим переменную ∆х.
2. Находим приращение функции ∆у, используя формулу

Это приращение также должно содержать величину ∆х.

1. Составляем соотношение ∆у/∆х.
2. Находим предел этого отношения при ∆х→0. Этот предел и есть значение производной.

Задание. Найдите производную функции у = 4х² + 7х в точке х₀ = 2.

Решение. Сначала вычислим значение функции в точке х₀:

Далее определяем величину у(х₀ + ∆х) (это будет не конкретное число, а некоторое выражение, содержащее переменную ∆х):

Задание. Найдите производную функции у = 1/х в точке х₀ = 5.

Решение. Высчитаем у(х₀):

Пусть у функции есть приращение ∆х, тогда в точке х₀ + ∆х ее значение составит:

В рассмотренных примерах для вычисления производной мы использовали ее определение. Однако на практике такой метод почти не используется. В будущем мы узнаем более эффективные способы для нахождения производной.

Мы уже убедились, что использование производной помогает находить мгновенную скорость тел. По этой причине понятие производной функции играет огромную роль в механике (разделе физике, изучающем движение). Однако этим ее практическое применение не ограничивается. По сути, она является основой для всей классической физики, и именно ее появление в XVII в. обеспечило выдающийся прогресс в науке вплоть до конца XIX в. При этом производная используется и в геометрии для анализа графиков функций. Более подробно ее применение будет также рассмотрено позже.