-
Радиус-вектор, путь перемещения материальной точки
Радиус-вектор
![]()
точки
Μ
— направленный отрезок прямой, соединяющий
начало отсчета О
с точкой Μ
(рис.
2).

Путь
s
— скалярная физическая величина,
определяемая длиной траектории, описанной
телом за некоторый промежуток времени.
Путь всегда положителен: s
> 0.
Перемещение
![]()
тела
за определенный промежуток времени —
направленный отрезок прямой, соединяющий
начальное (точка M0)
и конечное (точка М)
положение тела (см. рис. 2):
![]()
где
и
![]()
—
радиусы-векторы тела в эти моменты
времени.
Проекция
перемещения на ось Ox:
![]()
,
где x0
и x
— координаты тела в начальный и конечный
моменты времени.
Модуль
перемещения не может быть больше пути:
![]()
.
Знак
равенства относится к случаю прямолинейного
движения, если направление движения не
изменяется.
Зная
перемещение и начальное положение тела,
можно найти его положение в момент
времени t:
![]()
![]()
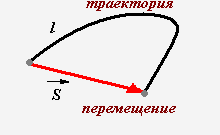
Траектория
– линия, вдоль которой движется тело.
Путь
– длина траектории.
Перемещение
– вектор, соединяющий начальное и конечное
положения тела.
Положение
тела в пространстве задается радиус
– вектором
или тремя его проекциями
на оси
координат.

![]()
Следовательно
закон движения – это зависимость
радиус-вектора от времени или зависимость
координат во времени.
где
![]()
-радиус-вектор,
x,
y,
z
–
координаты тела.
6. Средняя путевая и средняя скорость перемещения. Мгновенная линейная скорость.
Средняя
(путевая) скорость —
это отношение длины пути,
пройденного телом, ко времени,
за которое этот путь был пройден:
![]()
Средняя
путевая скорость, в отличие от мгновенной
скорости
не является векторной величиной.
Средняя
скорость равна среднему
арифметическому
от скоростей тела во время движения
только в том случае, когда тело двигалось
с этими скоростями одинаковые промежутки
времени.
В
то же время если, например, половину
пути автомобиль двигался со скоростью
180 км/ч, а вторую половину со скоростью
20 км/ч, то средняя скорость будет 36 км/ч.
В примерах, подобных этому, средняя
скорость равна среднему
гармоническому
всех скоростей на отдельных, равных
между собой, участках пути.
Средняя
скорость по перемещению
Можно
также ввести среднюю
скорость по перемещению,
которая будет вектором,
равным отношению перемещения
ко времени, за которое оно совершено:
![]()
Средняя
скорость, определённая таким образом,
может равняться нулю даже в том случае,
если точка (тело) реально двигалась (но
в конце промежутка времени вернулась
в исходное положение).
Если
перемещение происходило по прямой
(причём в одном направлении), то средняя
путевая скорость равна модулю средней
скорости по перемещению.
Мгновенная
скорость
– предел средней скорости за бесконечно
малый промежуток времени. Мгновенная
скорость направлена по касательной к
траектории движения в данной точке
траектории.
Средняя
скорость
перемещения
равна отношению полного перемещения к
промежутку времени, за которое это
перемещение совершено.
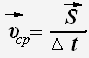
где![]()
ср
-средняя
скорость перемещения,
![]()
–
перемещение, ∆
t
– интервал
времени.
Средняя
путевая скорость
равна отношению полного пути к промежутку
времени, за который этот путь пройден.

где
υср
– средняя путевая скорость ,
l
–
путь.
Мгновенная
скорость
– скорость в заданный момент времени.
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Средняя скорость, теория и онлайн калькуляторы
Средняя скорость
Перемещение материальной точки
Пусть материальная точка совершает движение по оси X все время в одном направлении. Тогда перемещением этой материальной точки за отрезок времени $Delta t=t_2-t_1$ будет отрезок $Delta x=x_2-x_1$. Если материальная точка все время своего движения перемещалась в одном направлении, то пройденный путь ($Delta s$) равен по модулю величине перемещения:
[Delta s=left|Delta xright|left(1right).]
Если точка движется сначала в одном направлении, затем останавливается и движется в противоположном направлении, (например, так движется тело брошенное вертикально вверх) то путь равен сумме модулей перемещений в обоих направлениях:
[Delta s=left|Delta x_1right|+left|Delta x_2right|+dots left(2right).]
Определение средней скорости
Определение
Средней скоростью ($leftlangle vrightrangle $) материальной точки за промежуток времени $Delta t$ называют физическую величину, которая равна отношению перемещения, которое совершило тело к этому промежутку времени:
[leftlangle vrightrangle =frac{Delta x}{Delta t}left(3right).]
Направление средней скорости такое же, как у перемещения.
Единицей скорости является скорость такого движения, при котором перемещение точки в единицу времени равно единице длины:
[left[vright]=frac{left[xright]}{left[tright]}.]
Единица измерения скорости (в том числе и средней скорости) в Международной системе единиц (СИ) является метр в секунду:
[left[vright]=frac{м}{с}.]
Средняя скорость при переменном движении
При неравномерном движении величина средней скорости сильно зависит от выбора промежутка времени движения тела.
Рассмотрим движение тела, которое свободно падает вниз. Закон движения при этом:
[x=4,9t^2left(4right).]
Для моментов времени $t_1=0,1 $c координата тела (подставим время $t_1$ в формулу (4)) равна: $x_1=0,049 $м; для $t_2=0,2 $c$ x_2=0,196$ м, тогда $leftlangle vrightrangle $в промежутке времени от $t_1=0,1$ с до $t_2=0,2 $c будет:
[leftlangle vrightrangle =frac{0,196-0,049}{0,2-0,1}=1,47 left(frac{м}{с}right).]
Если взять для того же свободно падающего тела промежуток времени от $t_1=0,7$ с до $t_2=0,8 $c, то средняя скорость получится равной $leftlangle vrightrangle =7,4frac{м}{с}$.
Средняя скорость равномерного движения
Только при равномерном движении средняя скорость является постоянной величиной и не зависит от выбора промежутка времени, в который движется тело. При равномерном движении материальной точки по оси X кинематические уравнения для перемещения запишем как:
[x=x_0+vt left(5right).]
Тогда:
[x_1left(t_1right)=x_0+vt_1;; x_2left(t_2right)=x_0+vt_2left(6right).]
Найдем среднюю скорость движения, используя определение (3) и выражения (6):
[leftlangle vrightrangle =frac{x_0+vt_2-x_0-vt_1}{t_2-t_1}=vfrac{t_2-t_1}{t_2-t_1}=v.]
Для оценки численной величины средней скорости на практике используют следующее определение $leftlangle vrightrangle $: средняя скорость равна отношению пройдённого пути (s) ко времени (t), которое было затрачено на движение:
[leftlangle vrightrangle =frac{s}{t}left(7right).]
Определяемая таким образом средняя скорость является скалярной величиной.
Примеры задач с решением
Пример 1
Задание. Пешеход, потратил первую половину времени своего движения, двигаясь со скоростью $v_1=5frac{км}{ч}$, вторую половину времени он шел со скоростью $v_3=3frac{км}{ч}$. Какова средняя скорость движения человека?
Решение. Сделаем рисунок.
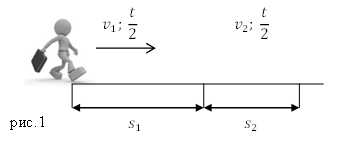
Для решения задачи используем формулу, определяющую среднюю скорость:
[leftlangle vrightrangle =frac{s}{t} left(1.1right),]
где путь складывается из двух участков движения:
[s=s_1+s_2left(1.2right).]
Причем по условию задачи:
[s_1=v_1t_1=v_1frac{t}{2}left(1.3right) и ]
[s_2=v_2t_2=v_2frac{t}{2}left(1.4right).]
Подставим в определение средней скорости (1.1) правые части выражений (1.2) – (1.4), и учтем, что $t=t_1+t_2$ имеем:
[leftlangle vrightrangle =frac{v_1frac{t}{2}+v_2frac{t}{2}}{t}=frac{v_1+v_2}{2}.]
Вычислим среднюю скорость пешехода:
[leftlangle vrightrangle =frac{5+3}{2}=4 (frac{м}{с}).]
Ответ. $leftlangle vrightrangle =4frac{м}{с}$
Пример 2
Задание. Какова средняя скорость, которую имела материальная точка за промежуток времени $tau $, если уравнение ее скорости имеет вид:
[vleft(tright)=A+Bt+Ct^2 left(0le tle tau right)left(2.1right).]
Решение. В качестве основы для решения задачи используем формулу ($t=tau $):
[leftlangle vrightrangle =frac{s}{t} left(2.1right).]
Найдем путь материальной точки, учитывая уравнение скорости из данных задачи:
[s=intlimits^{tau }_0{vdt=intlimits^{tau }_0{(A+Bt+Ct^2)dt=}}Atau +Bfrac{{tau }^2}{2}+Cfrac{{tau }^3}{3}left(2.2right).]
Подставим правую часть выражения (2.2) в (2.1), имеем:
[leftlangle vrightrangle =frac{Atau +Bfrac{{tau }^2}{2}+Cfrac{{tau }^3}{3}}{tau }=A+frac{Btau }{2}+frac{C{tau }^2}{3}.]
Ответ. $leftlangle vrightrangle =A+frac{Btau }{2}+frac{C{tau }^2}{3}$
Читать дальше: статика.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Сегодня разберем с вами очередной сложный момент, который ломает мозг не только ученикам 9-11 класса, но и студентам, которые запустили тему кинематики и подзабыли основные определения…
Средняя скорость в физике — один из подвохов, на котором попадаются учащиеся. По аналогии со средним арифметическим школьники и студенты частенько просто берут, складывают, делят пополам. Но в задачах по физике и математике на среднюю скорость так работает далеко не всегда. Предлагаю вам подумать над тем, почему не всегда работает среднее арифметическое двух скоростей, если у нас есть первая половина пути, где тело двигалось с постоянной скоростью v₁ и есть вторая половина пути, на которой тело двигалось с постоянной скоростью v₂. Почему средняя скорость на всём пути не равна среднему арифметическому ? Свой ответ напишите в комментариях. А сегодня мы рассматрим более интересную и редко встречающуюся задачку.
А пока прошу вас подписаться на мой канал в telegram IT mentor. Там я делюсь более короткими постами, рассказываю некоторые интересные случаи из жизни, непосредственно связанные с физикой, математий и IT.
Задача
Двигаясь равноускорено по прямой из состояния покоя, тело проходит некоторый путь. Чему равно отношение средней скорости тела на второй половине пути к средней скорости на первой половине пути?
Попробуйте на этом этапе остановиться, взять черновик с карандашом и решить задачку самостоятельно. Ваши ответы, комментарии, идеи и мнение о задаче обязательно напишите в комментариях. Так я лучше понимаю что интересно моим дорогим читателям 🤗
Решение:
Сделаем небольшой рисунок, уточняющий что происходит в задаче:
Для начала определим средние скорости на каждой части. Уже в этой части задачи нужно кое-что понимать. Обычно, под средней скоростью подразумевают именно среднюю путевую скорость. В то же время есть и просто средняя скорость. И две эти величины, в общем случае, отличаются. Давайте вспоминать определения.
Средняя путевая скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.
Средняя скорость — это скорость, определяемая отношением перемещения (S) при неравномерном движении к промежутку времени, за который это перемещение произошло.
Чувствуете подвох? Просто средняя скорость вполне может обнулиться, если вы попадете в момент, когда перемещение становится нулевым. В круговом движении или периодических колебаниях это реализуемо. А вот средняя путевая скорость всегда величина ненулевая, если тело прошло хоть какое-то расстояние. В нашей задаче будем иметь в виду именно среднюю путевую скорость.
1 способ
Средняя скорость на первой половине пути:
Здесь учитывается, что тело стартует с нулевой начальной скоростью.
Средняя скорость на второй половине пути:
Здесь уже учитывается, что начальная скорость для этого участка ненулевая. И находится она из времени разгона на предыдущем участке. Конечная скорость первого участка есть начальная скорость для второго участка. В полученном квадратном уравнении относительно нужного нам момента времени, корень будем выбирать заведомо положительный, т.к. нелогично предполагать, что время получится отрицательной величиной):
Отсюда средняя скорость на данном участке получается:
А теперь мы можем посчитать конечное отношение средней скорости на второй части пути к средней скорости на первой части пути:
Итак, у нас появился первый ответ на задачу. Логичный ли он? Похож ли на правду? А может нам второй способ бахнуть? 😎
2 способ
Хотите второй способ решения задачи? Для любителей хардкорных формул математического анализа я приведу альтернативное решение.
Мы помним общую формулу скорости для движения с постоянным ускорением:
Интегральное обобщенное определение средней скорости можно записать в виде:
Определим моменты времени t₁ и t₂ :
Получили точно такой же ответ, какой был в первом способе решения задачи. Задача решена. И похоже, что решена верно 😊
Краткое решение двумя способами
Какой способ решение вам больше понравился? Напишите в комментариях!
Понравилась статья? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в telegram
Средняя скорость


4.6
Средняя оценка: 4.6
Всего получено оценок: 167.
Обновлено 13 Июля, 2021
4.6
Средняя оценка: 4.6
Всего получено оценок: 167.
Обновлено 13 Июля, 2021
Важнейшей характеристикой тела в кинематике является скорость, с которой оно движется. Движение с нулевой скоростью фактически вообще не является движением. Однако скорость можно измерять различными методами и получать различные значения. Например, можно находить среднюю скорость. Рассмотрим эту тему подробнее: дадим определение средней скорости, приведем формулу средней скорости.
Движение и его скорость
Движение — это изменение координаты материальной точки со временем. Для вычисления быстроты изменения координаты используется такая физическая величина, как скорость (для обозначения используется символ $v$):
$$v={Delta x over Delta t}$$
Если движение происходит равномерно, то это отношение всегда будет одинаковым, независимо от выбора момента времени.
Например, если автомобиль движется со скоростью 36 км/ч, то за время $Delta t = 5c$ он пройдет расстояние $Delta x = 50м$, а за время $Delta t = 60c$ он пройдет расстояние $Delta x = 600м$.
Отношение пройденного расстояния ко времени перемещения в обоих случаях будет одинаковым и равным $v=10$м/с. Это и есть скорость движения автомобиля в данном примере.

Равномерное и неравномерное движение
Заметим, что автомобиль в приведенном примере на рассматриваемом промежутке времени $Delta t$ двигается равномерно. Но такое движение встречается довольно редко.
Тот же автомобиль когда-то стоял на месте, затем начал разгон и лишь потом двигался равномерно. А если рассмотреть ситуацию дальше — то рано или поздно автомобиль начнет замедление и остановится.
Получается, что скорость движения в рассматриваемом промежутке времени может изменяться. Движение с изменяемой скоростью называется неравномерным.
Средняя скорость
Как можно сравнивать скорости неравномерных движений?
Один из способов решения этой задачи — использование в физике такого понятия, как средняя скорость.
Идея состоит в том, чтобы пренебречь изменением скорости во время рассматриваемого промежутка времени, а рассматривать только начальный и конечный момент. Такое измерение удобно, если нам необходимо оценить общий результат движения.
В самом деле, как правило, целью движения является прибытие в конечный пункт к необходимому моменту времени. Как именно это достигнуто, зачастую неважно. Тело могло начать движение сразу и равномерно достигнуть конечного пункта. Могло, как автомобиль, сперва разогнаться, а потом затормозить в конечном пункте к тому же моменту времени. Наконец, тело могло двигаться «рывками», делая ряд остановок во время перемещения, но прибыть в конечный пункт, опять же, к тому же моменту времени.
Во всех трех приведенных случаях важно то, что тело начало и закончило движение в одни и те же моменты и переместилось за время движения на одно и то же расстояние. Что происходило во время движения, не рассматривается.
Скорость, рассчитываемая только по начальному и конечному моменту движения, называется средней. Для нахождения средней скорости необходимо найти отношение общего перемещения материальной точки ко времени, за которое это перемещение произошло.
$$v_{ср}={Delta x_{общ} over Delta t_{общ}}$$
Например, если автомобиль начал разгон в нулевой момент времени с нулевой скорости, разогнался до 50 км/ч, потом притормозил до 40 км/ч, и потом, через минуту, остановился в 600 м от начального пункта, то для нахождения средней скорости его движения необходимо 600 м поделить на 60 с. Средняя скорость составит 10 м/с.


Что мы узнали?
Одним из способов оценки скорости неравномерного движения является средняя скорость. При расчете средней скорости исходят только из начального и конечного моментов движения. А изменениями скорости между этими моментами пренебрегают. Средняя скорость удобна, если необходимо оценить общий результат движения, не обращая внимания на мелкие детали.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 167.
А какая ваша оценка?
В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.
Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.
Траектория, радиус-вектор, закон движения тела
Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.
Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.
Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.
Радиус-вектор – вектор, задающий положение точки в пространстве.
Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.
Перемещение и путь
Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.

В системе СИ перемещение и длина пути измеряются в метрах.
Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.
Скорость и ускорение
Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.
Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

В системе СИ скорость измеряется в метрах в секунду
Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.
Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.
Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Здесь R – радиус окружности, по которой движется тело.

Закон равноускоренного движения
Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Здесь – x нулевое- начальная координата. v нулевое – начальная скорость. Продифференцируем по времени, и получим скорость

Производная по скорости от времени даст значение ускорения a, которое является константой.
Пример решения задачи
Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.
Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.
Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.
