Как найти среднюю скорость по уравнению координаты

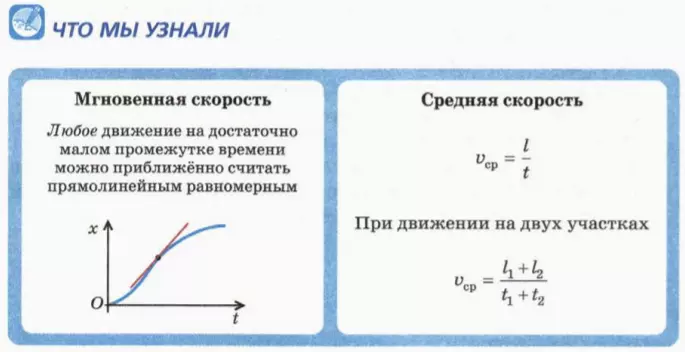
Мгновенная и средняя скорость

Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.

Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.

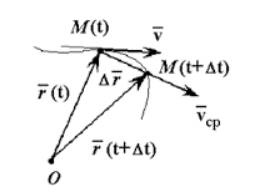
Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения ” open=” υ = ∆ r ∆ t ; ” open=” υ ↑ ↑ ∆ r .

Рисунок 1 . Средняя скорость сонаправлена перемещению

Модуль средней скорости по пути равняется ” open=” υ = S ∆ t .

Мгновенная скорость точки. Формулы

Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.

Мгновенной скоростью называют предел, к которому стремится средняя скорость ” open=” υ при стремлении промежутка времени ∆ t к 0 :

υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ .

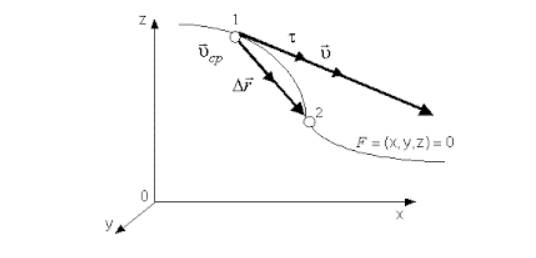
Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение d r совпадает с бесконечно малым элементом траектории d s .

Рисунок 2 . Вектор мгновенной скорости υ

Имеющееся выражение υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ в декартовых координатах идентично ниже предложенным уравнениям:

υ x = d x d t = x ˙ υ y = d y d t = y ˙ υ z = d z d t = z ˙ .

Перемещение и мгновенная скорость

Запись модуля вектора υ примет вид:

υ = υ = υ x 2 + υ y 2 + υ z 2 = x 2 + y 2 + z 2 .

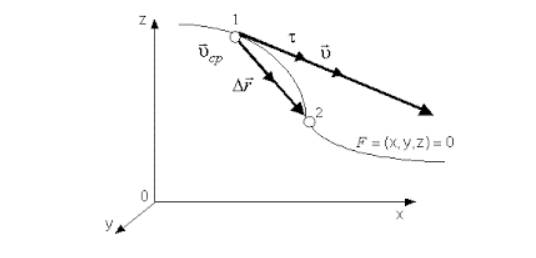
Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r = r q 1 , q 2 , q 3 , тогда значение скорости запишется как:

υ = d r d t = ∑ i = 1 3 ∂ r ∂ q i ∂ q i ∂ r = ∑ i = 1 3 ∂ r ∂ q i q ˙ i .

Рисунок 3 . Перемещение и мгновенная скорость в системах криволинейных координат

При сферических координатах предположим, что q 1 = r ; q 2 = φ ; q 3 = θ , то получим υ , представленную в такой форме:

υ = υ r e r + υ φ e φ + υ θ φ θ , где υ r = r ˙ ; υ φ = r φ ˙ sin θ ; υ θ = r θ ˙ ; r ˙ = d r d t ; φ ˙ = d φ d t ; θ ˙ = d θ d t ; υ = r 1 + φ 2 sin 2 θ + θ 2 .

Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением d r = υ ( t ) d t

Дан закон прямолинейного движения точки x ( t ) = 0 , 15 t 2 – 2 t + 8 . Определить ее мгновенную скорость через 10 секунд после начала движения.

Решение

Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:

υ ( t ) = x ˙ ( t ) = 0 . 3 t – 2 ; υ ( 10 ) = 0 . 3 × 10 – 2 = 1 м / с .

Ответ: 1 м / с .

Движение материальной точки задается уравнением x = 4 t – 0 , 05 t 2 . Вычислить момент времени t о с т , когда точка прекратит движение, и ее среднюю путевую скорость ” open=” υ .

Решение

Вычислим уравнение мгновенной скорости, подставим числовые выражения:

υ ( t ) = x ˙ ( t ) = 4 – 0 , 1 t .

4 – 0 , 1 t = 0 ; t о с т = 40 с ; υ 0 = υ ( 0 ) = 4 ; ” open=” υ = ∆ υ ∆ t = 0 – 4 40 – 0 = 0 , 1 м / с .

Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0 , 1 м / с .

Средняя скорость

Перемещение материальной точки

Пусть материальная точка совершает движение по оси X все время в одном направлении. Тогда перемещением этой материальной точки за отрезок времени $Delta t=t_2-t_1$ будет отрезок $Delta x=x_2-x_1$. Если материальная точка все время своего движения перемещалась в одном направлении, то пройденный путь ($Delta s$) равен по модулю величине перемещения:

[Delta s=left|Delta xright|left(1right).]

Если точка движется сначала в одном направлении, затем останавливается и движется в противоположном направлении, (например, так движется тело брошенное вертикально вверх) то путь равен сумме модулей перемещений в обоих направлениях:

[Delta s=left|Delta x_1right|+left|Delta x_2right|+dots left(2right).]

Определение средней скорости

Средней скоростью ($leftlangle vrightrangle $) материальной точки за промежуток времени $Delta t$ называют физическую величину, которая равна отношению перемещения, которое совершило тело к этому промежутку времени:

[leftlangle vrightrangle =frac<Delta x><Delta t>left(3right).]

Направление средней скорости такое же, как у перемещения.

Единицей скорости является скорость такого движения, при котором перемещение точки в единицу времени равно единице длины:

Единица измерения скорости (в том числе и средней скорости) в Международной системе единиц (СИ) является метр в секунду:

Средняя скорость при переменном движении

При неравномерном движении величина средней скорости сильно зависит от выбора промежутка времени движения тела.

Рассмотрим движение тела, которое свободно падает вниз. Закон движения при этом:

Для моментов времени $t_1=0,1 $c координата тела (подставим время $t_1$ в формулу (4)) равна: $x_1=0,049 $м; для $t_2=0,2 $c$ x_2=0,196$ м, тогда $leftlangle vrightrangle $в промежутке времени от $t_1=0,1$ с до $t_2=0,2 $c будет:

Если взять для того же свободно падающего тела промежуток времени от $t_1=0,7$ с до $t_2=0,8 $c, то средняя скорость получится равной $leftlangle vrightrangle =7,4frac<м><с>$.

Средняя скорость равномерного движения

Только при равномерном движении средняя скорость является постоянной величиной и не зависит от выбора промежутка времени, в который движется тело. При равномерном движении материальной точки по оси X кинематические уравнения для перемещения запишем как:

Найдем среднюю скорость движения, используя определение (3) и выражения (6):

Для оценки численной величины средней скорости на практике используют следующее определение $leftlangle vrightrangle $: средняя скорость равна отношению пройдённого пути (s) ко времени (t), которое было затрачено на движение:

[leftlangle vrightrangle =fracleft(7right).]

Определяемая таким образом средняя скорость является скалярной величиной.

Примеры задач с решением

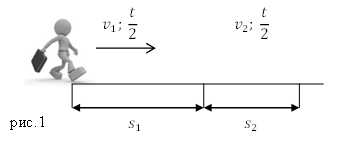
Задание. Пешеход, потратил первую половину времени своего движения, двигаясь со скоростью $v_1=5frac<км><ч>$, вторую половину времени он шел со скоростью $v_3=3frac<км><ч>$. Какова средняя скорость движения человека?

Решение. Сделаем рисунок.

Для решения задачи используем формулу, определяющую среднюю скорость:

[leftlangle vrightrangle =frac left(1.1right),]

где путь складывается из двух участков движения:

Причем по условию задачи:

[s_1=v_1t_1=v_1frac<2>left(1.3right) и ] [s_2=v_2t_2=v_2frac<2>left(1.4right).]

Подставим в определение средней скорости (1.1) правые части выражений (1.2) – (1.4), и учтем, что $t=t_1+t_2$ имеем:

Вычислим среднюю скорость пешехода:

[leftlangle vrightrangle =frac<5+3><2>=4 (frac<м><с>).]

Ответ. $leftlangle vrightrangle =4frac<м><с>$

Задание. Какова средняя скорость, которую имела материальная точка за промежуток времени $tau $, если уравнение ее скорости имеет вид:

[vleft(tright)=A+Bt+Ct^2 left(0le tle tau right)left(2.1right).]

Решение. В качестве основы для решения задачи используем формулу ($t=tau $):

[leftlangle vrightrangle =frac left(2.1right).]

Найдем путь материальной точки, учитывая уравнение скорости из данных задачи:

Подставим правую часть выражения (2.2) в (2.1), имеем:

Ответ. $leftlangle vrightrangle =A+frac<2>+frac^2><3>$

Неравномерное прямолинейное движение. Средняя скорость

п.1. График скорости при неравномерном прямолинейном движении

Прямолинейное и равномерное движение возможно лишь на участке пути.
Любое тело со временем меняет свою скорость, как по величине, так и по направлению.

Для описания неравномерного движения его можно разбить на участки, на которых скорость постоянна, и свести задачу к уже известному нам равномерному прямолинейному движению.

Например, пусть велосипедист добрался из города A в город B за 1 час. Первые полчаса он ехал со скоростью 9 км/ч, а потом проколол шину, и вторые полчаса шел пешком со скоростью 3 км/ч.
Направим ось ОХ также от A к B и получим значения проекций скоростей: $$ v_=9 text<км/ч>, v_=3 text <км/ч>$$ Построим график скорости для этого случая:

п.2. Как найти путь и перемещение по графику скорости?

Мы уже знаем, что путь равен площади прямоугольника, который образуется между отрезком графика скорости и отрезком (triangle t) на оси (t) (см. §8 данного справочника).

В таком случае, путь велосипедиста в нашем примере:
begin s=v_cdot triangle t_1+v_cdot triangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text <(км)>end Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км.
Общий путь велосипедиста равен 6 км. Расстояние между городами 6 км.

Если принять город A за начало отсчета с (x_0=0), то координата велосипедиста в конце пути: $$ x_<к>=x_0+s=0+6=6 text <(км)>$$ Перемещение по оси ОХ: (triangle x=x_<к>-x_0=6 text<(км)>).

Теперь рассмотрим другую ситуацию. Пусть велосипедист выехал из A в B и двигался со скоростью 9 км/ч в течение получаса. Но, после того как проколол шину, он развернулся и пошел пешком назад в A. Где будет находиться велосипедист через полчаса после разворота?
Снова направим ось ОХ от A к B и получим значения проекций скоростей: $$ v_=9 text<км/ч>, v_=-3 text <км/ч>$$ Построим график скорости для этого случая:

Путь велосипедиста по-прежнему будет равен сумме площадей прямоугольников, которые образует ломаная (v_x(t)) с осью (t): begin x=v_cdot triangle t_1+|v_|cdottriangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text <(км)>end
Если мы учтем знак (v_) и уберем модуль, то получим величину перемещения по оси ОХ: begin triangle x=v_cdot triangle t_1+v_cdot triangle t_2\ triangle x=9cdot 0,5-3cdot 0,5=4,5-1,5=3 text <(км)>end Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км в обратном направлении.
Конечная координата: $$ x_<к>=x_0+triangle x=0+3=3 text <(км)>$$
Ответ на вопрос задачи найден. Через полчаса после разворота велосипедист будет находиться в точке D в 3 км от города A.

п.3. Средняя скорость и средняя путевая скорость

В нашем примере с велосипедистом, который все время двигался в одну сторону и дошел до города B, получаем: begin |overrightarrow>|=frac<|overrightarrow|>=frac<triangle x>=frac 61=6 text<(км/ч)>\ v_=frac st=frac 61=6 text <(км/ч)>end Величина средней скорости равна средней путевой скорости.

А вот для случая, когда велосипедист развернулся и пошел обратно: begin |overrightarrow>|=frac<|overrightarrow|>=frac<triangle x>=frac 31=3 text<(км/ч)>\ v_=frac st=frac 61=6 text <(км/ч)>end Величина средней скорости меньше средней путевой скорости.

п.4. Задачи

Задача 1. По графику скоростей найдите среднюю скорость и среднюю путевую скорость движения.

a)

Все движение можно разделить на три участка с постоянной скоростью:
begin triangle t_1=3-0=3 c, v_=5 text<м/с>\ triangle t_2=5-3=2 c, v_=1 text<м/с>\ triangle t_3=7-5=2 c, v_=2 text<м/с>\ end Общий путь: begin s=|v_|cdot triangle t_1+|v_|cdot triangle t_2+|v_|cdot triangle t_3\ s=5cdot 3+1cdot 2+2cdot 2=21 text <(м)>end Все проекции скоростей положительны, тело двигалось в одном направлении, общее перемещение равно общему пути: (triangle x=s=21) (м)
Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (с)
Величина средней скорости равна средней путевой скорости: $$ |overrightarrow>|=v_=frac st=frac<21><7>=3 text <(м/с)>$$ Ответ: (|overrightarrow>|=v_=3 text<(м/с)>)

б)

Все движение можно разделить на три участка с постоянной скоростью:
begin triangle t_1=3-0=3 c, v_=5 text<м/с>\ triangle t_2=5-3=2 c, v_=-2 text<м/с>\ triangle t_3=7-5=2 c, v_=1 text<м/с>\ end Общий путь: begin s=|v_|cdot triangle t_1+|v_|cdot triangle t_2+|v_|cdot triangle t_3\ s=5cdot 3+2cdot 2+1cdot 2=21 text <(м)>end Проекции скоростей имеют разные знаки, тело двигалось вперед и назад.
Общее перемещение будет меньше общего пути: begin triangle x=v_cdot triangle t_1+v_cdot triangle t_2+v_cdot triangle t_3\ triangle x=5cdot 3-2cdot 2+1cdot 2=13 text <(м)>end Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (c)
Величина средней скорости: $$ |overrightarrow>|=frac<triangle x>=frac<13><7>approx 1,86 text <(м/с)>$$ Средняя путевая скорость: $$ v_=frac st=frac<21><7>=3 text <(м/с)>$$ Ответ: (|overrightarrow>|approx 1,86 text<(м/с)>; v_=3 text<(м/с)>)

Задача 2. Мотоциклист проехал расстояние между двумя пунктами со скоростью 40 км/ч. Потом увеличил скорость до 80 км/ч и проехал расстояние в два раза меньше. Найдите среднюю скорость мотоциклиста за все время движения.

Мотоциклист двигался все время в одном направлении, величина средней скорости равна средней путевой скорости: (v_=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:

Скорость, км/ч	Время, ч	Расстояние, км
1й участок	40	(frac<2d><40>=frac<20>)	(2d)
2й участок	80	(frac<80>)	(d)
Сумма	–	(t=frac<20>+frac<80>)	(s=2d+d=3d)

Упростим сумму дробей: $$ t=frac<20>+frac<80>=frac<4d+d><80>=frac<5d><80>=frac <16>$$ Получаем: $$ v_=frac st=frac<3d>=3cdot 16=48 text <(км/ч)>$$
Ответ: 48 км/ч

Задача 3. Автомобиль проехал первую половину пути по шоссе со скоростью 90 км/ч, а вторую половину – по грунтовой дороге со скоростью 30 км/ч. Найдите среднюю скорость автомобиля.

Величина средней скорости равна средней путевой скорости:
(v_=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:

Скорость, км/ч	Время, ч	Расстояние, км
1й участок	90	(frac<2cdot 90>=frac<180>)	(frac s2)
2й участок	30	(frac<2cdot 30>=frac<60>)	(frac s2)
Сумма	–	(t=frac<180>+frac<60>)	(s)

Задача 4*. Туристы прошли по маршруту со средней скоростью 32 км/ч. Маршрут был разделен на три участка, первый участок преодолевался пешком, второй – на автобусе, третий – на катере. Найдите скорость на каждом участке, если длины этих участков относятся как 1:4:45, а соответствующие интервалы времени как 4:1:20.

Величина средней скорости равна средней путевой скорости:
(v_=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:

Скорость, км/ч	Время, ч	Расстояние, км
1й участок	(frac<4t>)	(4t)	(d)
2й участок	(frac<4d>)	(t)	(4d)
3й участок	(frac<45d><20t>)	(20t)	(45d)
Сумма	–	(25t)	(50d)

По условию средняя скорость: $$ v_=frac st=frac<50d><25t>=2cdot frac dt=32Rightarrow frac dt=16 $$ Получаем: begin v_1=frac<4t>=frac<16><4>=4 text<(км/ч)>\ v_2=frac<4d>=4cdot 16=64 text<(км/ч)>\ v_3=frac<9d><4t>=frac<9><4>cdot 16=36 text <(км/ч)>end
Ответ: 4 км/ч, 64 км/ч и 36 км/ч

Задача 5*. Первую половину маршрута турист проехал на попутном автомобиле в 10 раз быстрее по сравнению с ходьбой пешком, а вторую половину – на попутном возу в 2 раза медленней. Сэкономил ли турист время на всем маршруте по сравнению с ходьбой пешком?

Пусть (v) – скорость туриста при ходьбе пешком.
Найдем среднюю путевую скорость (v_) и сравним ее со скоростью (v).
Если (v_gt v), то турист выиграл время.
Заполним таблицу:

Скорость, км/ч	Время, ч	Расстояние, км
1й участок	(10v)	(frac<2cdot 10v>=frac<20v>)	(frac s2)
2й участок	(frac<2>)	(frac<2cdot v/2>=frac sv)	(frac s2)
Сумма	–	(t=frac<20v>+frac sv)	(s)

Упростим сумму дробей: $$ t=frac<20v>+frac sv=frac svleft(frac<1><20>+1right)=frac<21><20>cdot frac sv $$ Средняя скорость: $$ v_=frac<frac<21><20>cdotfrac sv>=frac<20><21>vgt v $$Средняя скорость поездки оказалась меньше пешей скорости туриста.
Значит, он не выиграл по времени.
Ответ: нет

п.5. Лабораторная работа №3. Определение средней скорости движения тела

Цель работы
Научиться определять среднюю скорость движения тела по данным измерений на разных участках. Научиться вычислять абсолютные и относительные погрешности при подстановке данных измерений в формулы.

Теоретические сведения
В лабораторной работе изучается движение тела (шарика) по двум участкам (желобам) с различной скоростью.

Длина участков измеряется с помощью мерной ленты с ценой деления (triangle=1) см,
инструментальная погрешность равна: (d=frac<triangle><2>=0,5) см
Абсолютная погрешность измерений при работе с мерной лентой равна инструментальной погрешности, поэтому: (triangle s_1=triangle s_2=d=0,5) см
Погрешность суммы двух длин: (triangle(s_1+s_2)= triangle s_1+triangle s_2=2d=1) см

Измерение времени на каждом участке проводится в сериях их 5 измерений по методике, описанной в Лабораторной работе №2 (см. §4 данного справочника).
Погрешность суммы двух измерений: (triangle(t_1+t_2)=triangle t_1+triangle t_2)

Относительная погрешность частного равна сумме относительных погрешностей делимого и делителя: $$ delta_>=delta_+delta_ $$ Абсолютная погрешность определения средней скорости: $$ triangle v_=v_cdot delta_> $$

Приборы и материалы
Два желоба (не менее 1 м каждый), шарик, мерная лента, секундомер.

Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Соберите установку, как показано на рисунке. Установите один желоб под углом, другой – горизонтально, закрепите, поставьте в конце горизонтального участка упор. Подберите длину желобов и наклон так, чтобы движение по каждому участку было не менее 1 с.

3. Измерьте фактическую длину каждого участка движения в готовой установке с помощью мерной ленты.
4. Найдите относительную погрешность суммы двух длин (delta_=frac<triangle(s_1+s_2)>)
5. Проведите серии по 5 экспериментов для определения (t_1) и (t_2) с помощью секундомера.
6. Найдите (triangle t_1, triangle t_2, triangle(t_1+t_2), delta_)
7. По результатам измерений и вычислений найдите (v_, delta_>) и (triangle v_).
8. Сделайте выводы о проделанной работе.

Результаты измерений и вычислений

1) Измерение длин
Цена деления мерной ленты (triangle =1) см
Инструментальная погрешность мерной ленты (d=frac<triangle><2>=0,5) см
Результаты измерений:
(s_1=112) cм
(s_2=208) cм
Сумма длин участков: (s_1+s_2=112+208=320) (см)
Абсолютная погрешность суммы: (triangle (s_1+s_2)=triangle s_1+triangle s_2=2d=1) см
Относительная погрешность суммы: $$ delta_=frac<triangle (s_1+s_2)>=frac<1><320>=0,3125% $$

2) Измерение времени
Цена деления секундомера (triangle =0,2) с
Инструментальная погрешность секундомера (d=frac<triangle><2>=0,1) с

Время движения по наклонному желобу

№ опыта	1	2	3	4	5	Сумма
(t_1) c	1,5	1,6	1,5	1,4	1,4	7,4
(triangle) c	0,02	0,12	0,02	0,08	0,08	0,32

Найдем среднее время спуска с наклонного желоба: $$ t_1=frac<1,5+1,6+1,5+1,4+1,4><5>=frac<7,4><5>=1,48 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_1): $$ triangle_1=|1,5-1,48|=0,02; triangle_2=|1,6-1,48|=1,02 text <и т.д.>$$ Среднее абсолютное отклонение: $$ triangle_=frac<0,02+0,12+0,02+0,08+0,08><5>=frac<0,32><5>=0,064 text $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_1=maxleft\right>=maxleft<0,1;0,064right>=0,1 text $$ Округляем полученное значение времени до десятых. begin t_1=(1,5pm 0,1) text\ delta_=frac<0,1><1,5>=frac<1><15>approx 6,7text <%>end Время движения по горизонтальному желобу

№ опыта	1	2	3	4	5	Сумма
(t_2) c	2,3	2,4	2,2	2,2	2,4	11,5
(triangle) c	0	0,1	0,1	0,1	0,1	0,4

Найдем среднее время движения по горизонтали: $$ t_2=frac<2,3+2,4+2,2+2,2+2,4><5>=frac<11,5><5>=2,3 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_2): $$ triangle_1=|2,3-2,3|=0; triangle_2=|2,4-2,3|=0,1 text <и т.д.>$$ Среднее абсолютное отклонение: $$ triangle_=frac<0+0,1+0,1+0,1+0,1><5>=frac<0,4><5>=0,08 text $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_2=maxleft\right>=maxleft<0,1;0,08right>=0,1 text $$ Получаем: begin t_2=(2,3pm 0,1) text\ delta_=frac<0,1><2,3>=frac<1><23>approx 4,4text <%>end

3) Расчет погрешности суммы интервалов времени
Сумма интервалов времени: $$ t_1+t_2=1,5+2,3=3,8 text <(c)>$$ Абсолютная погрешность суммы: $$ triangle(t_1+t_2)=triangle t_1+triangle t_2=0,1+0,1=0,2 text <(c)>$$ Относительная погрешность суммы: $$ delta_=frac<triangle (t_1+t_2)>=frac<0,2><3,8>=frac<1><19>approx 5,3text <%>$$

4) Расчет средней скорости $$ v_=frac=frac<320><3,8>approx 84,2 left(frac<text<см>><text>right) $$ Относительная ошибка частного: $$ delta_>=delta_+delta_=frac<1><320>+frac<1><19>approx 0,003125+0,0526approx 0,0557approx 0,056=5,6text <%>$$ (оставляем две значащие цифры).
Абсолютная ошибка: $$ v_=v_cdotdelta_>=84,2cdot 0,056approx 4,7 left(frac<text<см>><text>right) $$ Получаем: begin v_=(84,2pm 4,7) text<см/с>\ delta_>=5,6text <%>end

Выводы
На основании проделанной работы можно сделать следующие выводы.

Измерения длин проводились с помощью мерной ленты. Ошибка измерений равна инструментальной ошибке 0,5 см.
Измерения времени проводились с помощью секундомера. По результатам серий экспериментов ошибка была принята равной инструментальной 0,1 с.
Получена величина средней скорости: begin v_=(84,2pm 4,7) text<см/с>\ delta_>=5,6text <%>end

[spoiler title=”источники:”]

http://www.webmath.ru/poleznoe/fizika/fizika_33_srednjaja_skorost.php

http://reshator.com/sprav/fizika/7-klass/neravnomernoe-pryamolinejnoe-dvizhenie-srednyaya-skorost/

[/spoiler]

Средняя скорость считается так: весь путь поделить на всё время движения. Формула одна и очень простая, но почему-то школьники часто путаются в задачах на среднюю скорость. Разберу три характерные задачи и основные ошибки. Возможно, статья будет полезна учителям и репетиторам, а также школьникам.

1. Половина пути

Первую половину пути поезд ехал со скоростью 60 км/ч, а вторую – 90 км/ч. С какой средней скоростью ехал поезд на всём пути?

Первым делом школьник захочет сложить эти две скорости и поделить пополам. Логично? Да. Но, к сожалению, неправильно.

Объясняю, почему. Поскольку первую половину пути поезд ехал с меньшей скоростью, то времени было затрачено больше, чем на вторую. А значит, вклад отдельных скоростей неравнозначен, и нельзя так просто делить пополам.

Тут школьник может впасть в панику. Что делать? Умножать? Делить? Непонятно. Воспользоваться напрямую формулой “расстояние поделить на время” не получится – ни расстояние, ни время нам неизвестно.

Для школьников, только начинающих изучать основы физики, бывает трудно оперировать с неизвестными величинами. Нам не дано ничего, кроме скоростей, как же быть? В качестве маленькой ступеньки к освоению неизвестности могу предложить следующий ход – сначала додумать неизвестные данные. Возьмём и сами решим, пусть поезд пройдет 180 километров, цифру возьмем так, чтобы легко делилась.

Тогда половина пути будет 90 километров. Поезд пройдет её за 1,5 часа. Вторую половину пути – за 1 час. Это легко посчитает любой школьник. Значит, общее время в пути будет 2,5 часа. Делим общее расстояние 180 километров на 2,5 часа, и получаем 72 км/ч.

Это просто и понятно, но учитель такую задачу не примет. Откуда мы взяли 180 километров, когда это неизвестно? Тем не менее, дав себе эти неизвестные данные, мы продумали алгоритм и довели задачу до ответа. Осталось формализовать это решение, так чтобы не использовать то, что не дано. Обозначим наши 180 километров за S, и опишем всё, что мы делали раньше, только вместо цифр используем буквы.

Получается, что зная ход решения “в цифрах”, мы переводим его в буквенные обозначения. И тут главное не остановиться на полдороги, не смущаться, что нам неизвестно расстояние. Ведь оно в конце сократилось, и средняя скорость оказалась независящей от расстояния (что вполне логично). И от школьника здесь требуются уже алгебраические умения – складывать дроби, переворачивать их.

Если подобная задача встретилась в тесте, где требуется только ответ, можно вообще не заморачиваться – так как средняя скорость в данной задаче не зависит от расстояния, можно посчитать при любом удобном расстоянии. По крайней мере, это лучше, чем сидеть и ломать голову, не зная, как подступиться к решению. Если же требуется оформление – тут числовое решение может помочь как переходный этап, чтобы понять, что именно делать с формулами, как их крутить-вертеть.

Школьникам часто бывает трудно переходить на новый уровень абстракции – от чисел к переменным, которые могут принимать разные числовые значения. В алгебре это тренируют, но там одна переменная икс, и иногда игреки встречаются. А в физике этих переменных пруд пруди, в каждой задаче они разные, и если ученик не освоил этот уровень, то физика кажется ему супер-трудной. Кроме того, в школе переход от чисел к переменным часто упускают, в программе отдельных навыков работы с формулами нет.

2. Средняя скорость по графику пути

Пусть нам дан график зависимости координаты от времени. Требуется определить среднюю скорость.

По графику видно, что движение состоит из четырех этапов:

1. Тело стартует в нуле и через 2 секунды оказывается на координате 2 м.
2. Тело останавливается, и в течение 4 секунд покоится в точке с координатой 2 м.
3. Тело начинает движение, и через 2 секунды оказывается в точке 6 м.
4. Тело движется в обратном направлении, и через 2 секунды оказывается в точке 5 м.

Проговорить, понять все эти этапы – важная часть решения. А дальше многие школьники начинают вычислять скорости движения на каждом этапе: На первом – 1 м/с, на втором – 0, на третьем – 2 м/с, на четвертом – 0,5 м/с. Вот это действие как раз лишнее. Для того, чтобы вычислить среднюю скорость, вовсе не обязательно знать скорости на каждом этапе!

Вспомним определение средней скорости – это весь путь, поделить на всё время. Поэтому просто по графику считаем весь путь – 6 метров “туда” и 1 метр “обратно”, в сумме 7 метров. Общее время движения – 10 секунд. Делим 7 метров на 10 секунд, получаем 0,7 м/с.

3. Средняя скорость по графику скорости

Бывает так, что нам дан график зависимости скорости от времени, и требуется определить среднюю скорость. Вот, к примеру, такой график.

Читаем график. Движение состоит из трёх этапов

1. С начала движения до момента времени 2 с тело движется с постоянной скоростью 2 м/с
2. От 2 до 6 с тело движется со скоростью 6 м/с
3. В последние 4 секунды от 6 до 10 с тело замедляется, снижая свою скорость до нуля.

Попытки что-то сделать со значениями скорости самими по себе здесь обречены на провал. Опять надо найти весь путь и всё время движения. Путь по графику скорости определяется как площадь под графиком, причем если график идет ниже нуля, то соответствующие участки складываются.

Считаем площадь фигуры – два прямоугольника на первых двух этапах и треугольник на третьем. Первый этап – 4 м, второй этап – 24 м, третий этап – 12 м. Значит, весь путь будет 40 метров. Всё время 10 секунд, значит, средняя скорость 4 м/с.

Общие рекомендации для решения задач на среднюю скорость

1. Средняя скорость – это всегда весь путь делить на всё время. Данные об отдельных скоростях сами по себе не дадут полной информации о средней скорости. Используем только эту формулу.

2. Следует проанализировать конкретную ситуацию и понять, как можно применить формулу. Если кажется, что не хватает данных – не смущаться.

3. Данные по скоростям на отдельных этапах могут быть полезны для проверки готового ответа: средняя скорость должна лежать между минимальной и максимальной.

Спасибо, что прочитали до конца! Желаю школьникам хорошей учёбы, учителям – понятливых и любопытных учеников, родителям – чтобы дети радовали. Буду рада лайкам и новым подписчикам!

Скорости и ускорения как производные координаты

Зная координату тела (закон, по которому она изменяется) можно очень многое о движении  этого тела узнать. Например, скорость – первая производная  от координаты. А ускорение – вторая производная, или первая производная скорости.  Если в задаче дано еще и время движения тела – то можно полностью описать движение и найти все его характеристики для данного момента времени.

Задача 1.

Точка движется по прямой согласно закону , где м/с, м/c. Определить: среднюю скорость точки в интервале времени от с до с, координату точки в тот момент времени, когда скорость тела будет равна нулю.

Средняя скорость – это отношение пройденного пути ко времени. Время движения очевидно: с. А путь можно определить как :

Чтобы определить скорость, возьмем производную координаты по времени:

Если скорость равна 0, то

Откуда с и м.

Ответ: м/с, м.

Задача 2.

Точка движется вдоль оси по закону . Найти направление движения в моменты времени: а) с; б) с. Чему будут равны ускорения в эти моменты времени?

Чтобы определить направление движения, нам надо узнать знак скорости в данные моменты времени. Определим сначала скорость тела как производную координаты:

Тогда

Поэтому в момент времени тело движется в положительном направлении, а в момент времени – в отрицательном.

Определим ускорение как вторую производную от координаты, или первую производную скорости по времени:

Ответ: м/с, движение по оси, м/с, м/с, движение против оси, м/с.

Задача 3.

Тело движется прямолинейно, причем скорость зависит от времени по закону: . Определить зависимость ускорения от времени . Каково значение ускорения при с?

Чтобы найти ускорение, возьмем производную скорости:

При имеем:

Ответ: , м/с.

1. Мгновенная скорость

В этом параграфе мы будем рассматривать неравномерное движение. Однако при этом нам пригодится то, что мы знаем о прямолинейном равномерном движении.

На рисунке 4.1 показаны положения разгоняющегося автомобиля на прямом шоссе с интервалом времени 1 с. Стрелка указывает на зеркальце заднего вида, положение которого мы рассмотрим далее более подробно.

Мы видим, что за равные интервалы времени автомобиль проходит разные пути, то есть движется неравномерно.

Уменьшим теперь последовательные интервалы времени в 20 раз – до 0,05 с – и проследим за изменением положения автомобиля в течение половины секунды (это нетрудно сделать, например, с помощью видеосъемки).

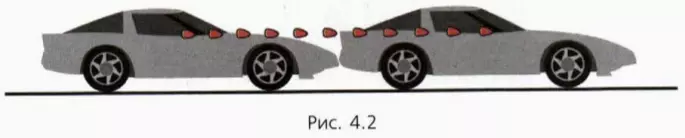
Чтобы не загромождать рисунок 4.2, на нем изображены только два положения автомобиля с промежутком времени 0,5 с. Последовательные положения автомобиля с интервалом 0,05 с отмечены положением его зеркальца заднего вида (показано красным цветом).

Мы видим, что когда последовательные равные промежутки времени достаточно малы, то пути, проходимые автомобилем за эти промежутки времени, практически одинаковы. А это означает, что движение автомобиля в течение столь малых промежутков времени можно с хорошей точностью считать прямолинейным равномерным.

Оказывается, этим замечательным свойством обладает любое движение (даже криволинейное): если рассматривать его за достаточно малый промежуток времени Δt, оно очень похоже на прямолинейное равномерное движение! Причем чем меньше промежуток времени, тем больше это сходство.

Скорость тела за достаточно малый промежуток времени и называют его скоростью в данный момент времени t, если этот момент времени находится в промежутке Δt. А более точное ее название – мгновенная скорость.

Насколько малым должен быть промежуток времени Δt, чтобы в течение этого промежутка движение тела можно было считать прямолинейным равномерным, зависит от характера движения тела.

В случае разгона автомобиля это доли секунды. А, например, движение Земли вокруг Солнца можно с хорошей точностью считать прямолинейным и равномерным даже в течение суток, хотя Земля за это время пролетает в космосе больше двух с половиной миллионов километров!

Говоря далее о скорости, мы будем (если это особо не оговорено) подразумевать обычно мгновенную скорость.

? 1. По рисунку 4.2 определите мгновенную скорость автомобиля. Длину автомобиля примите равной 5 м.

Значение мгновенной скорости автомобиля показывает спидометр (рис. 4.3).

Как найти мгновенную скорость по графику зависимости координаты от времени

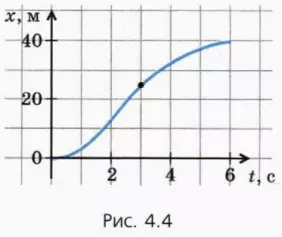
На рисунке 4.4 изображен график зависимости координаты от времени для автомобиля, который движется по прямолинейному шоссе.

Мы видим, что он движется неравномерно, потому что график зависимости его координаты от времени – это кривая, а не отрезок прямой.

Покажем, как определить по этому графику мгновенную скорость автомобиля в какой-либо момент времени – скажем, при t = 3 с (точка на графике).

Для этого рассмотрим движение автомобиля за столь малый промежуток времени, в течение которого его движение можно считать прямолинейным равномерным.

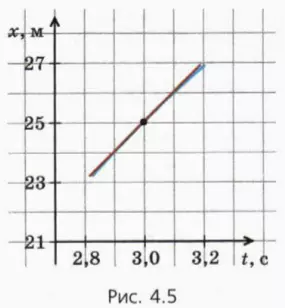
На рисунке 4.5 показан интересующий нас участок графика при десятикратном увеличении (см., например, шкалу времени).

Мы видим, что этот участок графика практически неотличим от отрезка прямой (красный отрезок). За последовательные равные промежутки времени по 0,1 с автомобиль проходит практически одинаковые расстояния – по 1 м.

2. Чему равна мгновенная скорость автомобиля в момент t = 3 с?

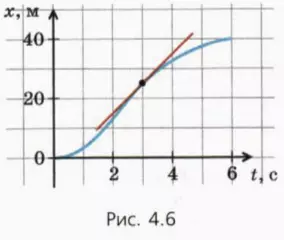
Возвращаясь к прежнему масштабу чертежа, мы увидим, что прямая красного цвета, с которой практически совпадал малый участок графика, – касательная к графику зависимости координаты от времени в данный момент времени (рис. 4.6).

Итак, о мгновенной скорости тела можно судить по угловому коэффициенту касательной к графику зависимости координаты от времени: чем больше угловой коэффициент касательной, тем больше скорость тела. (Описанный способ определения мгновенной скорости с помощью касательной к графику зависимости координаты от времени связан с понятием производной функции. Это понятие вы будете изучать в курсе «Алгебра и начала аиализа».) А в тех точках графика, где угол наклона касательной равен нулю, то есть касательная параллельна оси времени t, мгновенная скорость тела равна нулю.

? 3. Рассмотрите рисунок 4.6.
а) В каких точках графика угол наклона касательной наибольший? наименьший?
б) Найдите наибольшую и наименьшую мгновенную скорость автомобиля в течение первых 6 с его движения.

2. Средняя скорость

Во многих задачах используют среднюю скорость, связанную с пройденным путем:

v_ср = l/t.     (1)

Определенная таким образом средняя скорость является скалярной величиной, так как путь – это скалярная величина. (Иногда во избежание недоразумений ее называют средней путевой скоростью.)

Например, если автомобиль в течение трех часов проехал по городу 120 км (при этом он мог разгоняться, тормозить и стоять на перекрестках), то его средняя скорость равна 40 км/ч.

? 4. Насколько уменьшится средняя скорость только что упомянутого автомобиля, если из-за остановок в пробках общее время движения увеличится на 1 ч?

Средняя скорость на двух участках движения

Во многих задачах рассматривается движение тела на двух участках, на каждом из которых движение можно считать равномерным. В таком случае, согласно определению средней скорости (1), можно записать:

v_ср = (l₁ + l₂)/(t₁ + t₂),     (2)

где l₁ и t₁ – путь и время для первого участка, а l₂ и t₂ – для второго. Рассмотрим примеры.
Саша выехал из поселка на велосипеде со скоростью 15 км/ч и ехал в течение часа. А потом велосипед сломался, и Саша еще час шел пешком со скоростью 5 км/ч.

? 5. Найдите:
а) путь, пройденный Сашей за все время движения;
б) общее время движения Саши;
в) среднюю скорость Саши.

В рассмотренном случае средняя скорость оказалась равной среднему арифметическому скоростей, с которыми Саша ехал и шел. Всегда ли это справедливо? Рассмотрим следующий пример.
Пусть Саша ехал на велосипеде в течение часа со скоростью 15 км/ч, а потом прошел такое же расстояние пешком со скоростью 5 км/ч.

? 6. Найдите:
а) путь, который Саша прошел пешком;
б) путь, пройденный Сашей за все время движения;
в) общее время движения Саши;
б) среднюю скорость Саши.

Рассмотрев этот случай, вы увидите, что на этот раз средняя скорость не равна среднему арифметическому скоростей езды и ходьбы. А если присмотреться еще внимательнее, то можно заметить, что во втором случае средняя скорость меньше, чем в первом. Почему?

? 7. Сравните промежутки времени, в течение которых Саша ехал и шел пешком в первом и втором случаях.

Обобщим рассмотренные выше ситуации.

Рассмотрим сначала случай, когда тело двигалось с разными скоростями в течение равных промежутков времени.

Пусть первую половину всего времени движения тело двигалось со скоростью v₁, а вторую половину – со скоростью v₂. Можно ли найти среднюю скорость движения на всем участке, если не известны ни общее время движения, ни путь, пройденный телом за все время движения?

Можно: для этого введем обозначения для всех нужных нам величин независимо от того, известны они или неизвестны. Это распространенный прием при решении многих задач.

Обозначим все время движения t, весь путь l, а пути, пройденные за первую и вторую половину времени движения, обозначим соответственно) l₁ и l₂.

? 8. Выразите через v₁, v₂ и t:
a) l₁ и l₂; б) l; в) среднюю скорость.

Найдя ответы на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках с разными скоростями в течение равных промежутков времени, то его средняя скорость на всем пути равна среднему арифметическому скоростей движения на двух участках.

Рассмотрим теперь случай, когда тело двигалось с разными скоростями первую и вторую половину пути.

Пусть теперь первую половину всего пути тело двигалось со скоростью v₁, а вторую половину – со скоростью v₂. Обозначим снова все время движения t, весь путь l, а промежутки времени, в течение которых тело двигалось на первом и втором участке, обозначим соответственно t₁ и t₂.

? 9. Выразите через v₁, v₂ и l:
а) t₁ и t₂; б) t; в) среднюю скорость.

Ответив на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках равной длины с разными скоростями, то его средняя скорость на всем пути не равна среднему арифметическому этих скоростей.

? 10. Докажите, что средняя скорость тела, которое двигалось на двух участках равной длины с разными скоростями, меньше, чем если бы оно двигалось на двух участках с теми же скоростями в течение равных промежутков времени.
Подсказка. Выразите для каждого из двух случаев среднюю скорость через скорости на первом и втором участках и сравните полученные выражения.

? 11. На первом участке пути тело двигалось со скоростью v₁, а на втором – со скоростью v₂. Чему равно отношение длин этих участков, если средняя скорость движения оказалась равной среднему арифметическому v₁ и v₂?

Дополнительные вопросы и задания

12. Одну треть всего времени движения поезд ехал со скоростью v₁, а оставшееся время – со скоростью v₂.
а) Выразите пройденный поездом путь через v₁, v₂ и все время движения t.
б) Выразите среднюю скорость поезда через v₁ и v₂.
в) Найдите числовое значение средней скорости при v₁ = 60 км/ч, v₂ = 90 км/ч.

13. Автомобиль ехал три четверти всего пути со скоростью v₁, а оставшийся участок пути – со скоростью v₂.
а) Выразите все время движения автомобиля через v₁, v₂ и весь пройденный путь l.
б) Выразите среднюю скорость движения автомобиля через v₁ и v₂.
в) Найдите числовое значение средней скорости при v₁ = 80 км/ч, v₂ = 100 км/ч.

14. Автомобиль ехал 2 ч со скоростью 60 км/ч. Сколько времени после этого он должен ехать со скоростью 80 км/ч, чтобы его средняя скорость на всем пути стала равной 66,7 км/ч?

15. Перенесите в тетрадь (по клеточкам) график зависимости координаты автомобиля от времени, изображенный на рисунке 4.4. Считайте, что автомобиль едет вдоль оси x.
а) Определите графически среднюю скорость за 6 с.
б) Используя касательную, определите, в какие примерно моменты времени мгновенная скорость автомобиля была равна его средней скорости за 6 с.

16. Тело движется вдоль оси x. Зависимость координаты тела от времени выражается формулой x = 0,2 * t².
а) Выберите удобный масштаб и изобразите график зависимости x(t) в течение первых 6 с.
б) С помощью этого графика найдите момент времени, в который мгновенная скорость тела была равна средней скорости за все время движения.

В ситуации, когда координаты изменяют свое положение относительно оси, следовательно, их материальная точка будет находится в процессе движения.

Средняя скорость — это величина векторного типа, которая имеет определенное числовое равенство относительно перемещения совершаемого  в конкретную единицу времени, и направлена совместно я с векторным  перемещением.

Средняя скорость – довольно простое понятие в разделе кинематика.

[v_{mathrm{cp}}=frac{S}{t}]

Основные моменты, на которые следует уделить внимание при определении средней скорости:

• Необходимое время, которое учитывается, когда тело в процессе движения может делать кратковременные остановки;
• Определение правильной величины средней скорость тела, которое начинает движение в пункте А и оканчивает его в пункте В. Но в процессе движения, может повернуть несколько раз обратно, а затем снова продолжает движение в заданном направлении, двигаясь в пункт В.

Модуль для определения средней скорости движения вычисляется по следующей формуле: V=s/t.

Мгновенная скорость, как правило, характеризует заданное движение точки в конкретный и определенный момент времени.

Для любой категории характерно бесконечное количество точек. Потому что каждый временной интервал включает в себя бесконечное количество мгновений.

Когда сам временной интервал стремится к нулевому значению, то он автоматически преобразуется в мгновение.

Стоит отметить, что мгновенная скорость – это величина, которая изображена как вектор. Она равняется отношению движения к временному интервалу. А именно: промежуток времени, за который данное перемещение происходит, при условии, что временной интервал стремится к нулевому значению.

Временной интервал движения тела –  это всегда скляр с положительным значением. Поэтому мгновенная скорость и ее векторное значение,  всегда сонаправлено с перемещением, которое имеет значение стремящееся к нулю.

Направление и перемещение действия средней и мгновенной скорости относительно координатной оси

Средняя скорость всегда направлена вместе с перемещением:

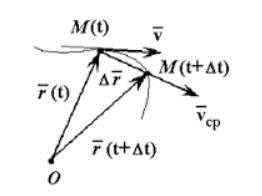
Для мгновенной скорости характерно движение в конкретный момент времени.

Направление векторной скорости, которая обозначается как: υ расположено по касательной, относительно криволинейной траектории.

Так как непрерывное малое перемещение однозначно совпадает с бесконечно малым элементом траектории.

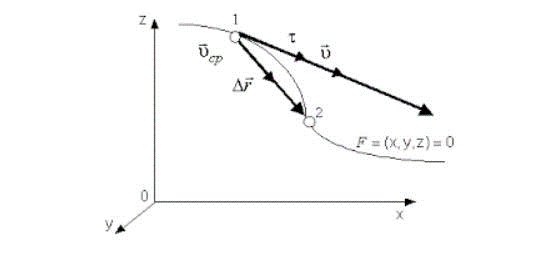
Примеры решения задач по определению мгновенной и средней скорости

Пример №1:

Имеет ли способность мгновенная скорость, изменять свое значение только относительно направления, при этом не меняя модульную величину.

Используя основные термины и формулы, решим данную задачу. При решении необходимо рассмотреть пример:

• Движение тела происходит по криволинейной траектории. На ней необходимо обозначить начальный и конечный пункты, а именно: точки А и В.
• Далее нужно обозначить основное направление мгновенной скорости в заданных ранее точках.
• Следует помнить, что мгновенная скорость имеет направление относительно касательной по траектории.
• Расстояние и скорость имеют одинаковые значения  по модулю и, следовательно, равны 5 м/с.

[left|vec{V}_{A}right|=left|vec{V}_{B}right|=5 frac{м}{c}]

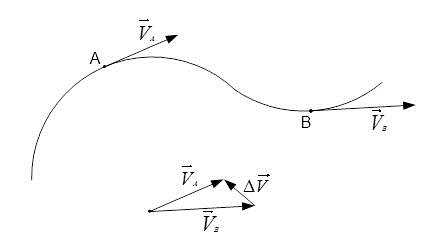
Следующее равенство вида: [vec{V}_{A}=vec{V}_{B}] будет неверным. Так как скорость – является векторной величиной. Поэтому очень важно задать не только числовое значение, но направление по которому будет осуществляться движение.

В случае, когда [vec{V}_{A}=vec{V}_{B}] можно составить равенство следующего вида:[vec{V}_{A}-vec{V}_{B}=0] однако определив вектор разности значений [Delta vec{V}], можно сделать вывод, что его значение не равно нулевому.

Следовательно, [vec{V}_{A} neq vec{V}_{B}], другими словами мгновенная скорость может быть равна нулевому значению и быть равной по модулю. Однако, при этом различаться по основному направлению движения.

Пример №2:

Возможно ли изменение по модульному значению мгновенной скорости, но при этом направление остается неизменным.

Алгоритм решения:

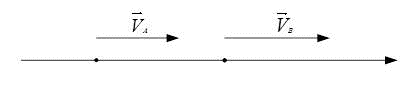
Рассмотрев рисунок, который приведен выше, можно сделать вывод, что:

• в точке А и в точке В направление движения мгновенной скорости одинаково;
• рассматриваемое тело, которое осуществляет   движение, делает это   с равным ускорением, следовательно:

[vec{V}_{A}=vec{V}_{B}]