Средняя скорость, теория и онлайн калькуляторы
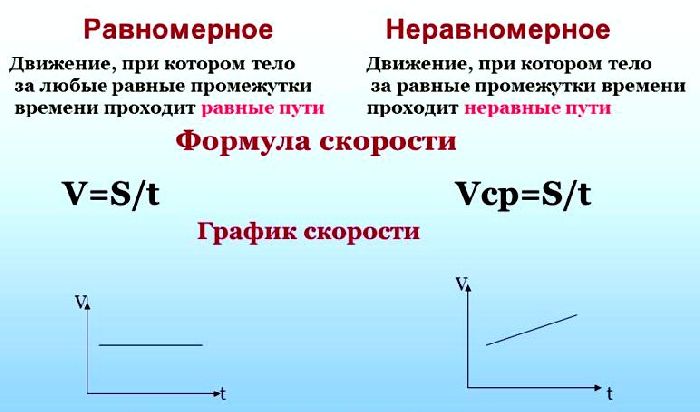
Средняя скорость
Перемещение материальной точки
Пусть материальная точка совершает движение по оси X все время в одном направлении. Тогда перемещением этой материальной точки за отрезок времени $Delta t=t_2-t_1$ будет отрезок $Delta x=x_2-x_1$. Если материальная точка все время своего движения перемещалась в одном направлении, то пройденный путь ($Delta s$) равен по модулю величине перемещения:
[Delta s=left|Delta xright|left(1right).]
Если точка движется сначала в одном направлении, затем останавливается и движется в противоположном направлении, (например, так движется тело брошенное вертикально вверх) то путь равен сумме модулей перемещений в обоих направлениях:
[Delta s=left|Delta x_1right|+left|Delta x_2right|+dots left(2right).]
Определение средней скорости
Определение
Средней скоростью ($leftlangle vrightrangle $) материальной точки за промежуток времени $Delta t$ называют физическую величину, которая равна отношению перемещения, которое совершило тело к этому промежутку времени:
[leftlangle vrightrangle =frac{Delta x}{Delta t}left(3right).]
Направление средней скорости такое же, как у перемещения.
Единицей скорости является скорость такого движения, при котором перемещение точки в единицу времени равно единице длины:
[left[vright]=frac{left[xright]}{left[tright]}.]
Единица измерения скорости (в том числе и средней скорости) в Международной системе единиц (СИ) является метр в секунду:
[left[vright]=frac{м}{с}.]
Средняя скорость при переменном движении
При неравномерном движении величина средней скорости сильно зависит от выбора промежутка времени движения тела.
Рассмотрим движение тела, которое свободно падает вниз. Закон движения при этом:
[x=4,9t^2left(4right).]
Для моментов времени $t_1=0,1 $c координата тела (подставим время $t_1$ в формулу (4)) равна: $x_1=0,049 $м; для $t_2=0,2 $c$ x_2=0,196$ м, тогда $leftlangle vrightrangle $в промежутке времени от $t_1=0,1$ с до $t_2=0,2 $c будет:
[leftlangle vrightrangle =frac{0,196-0,049}{0,2-0,1}=1,47 left(frac{м}{с}right).]
Если взять для того же свободно падающего тела промежуток времени от $t_1=0,7$ с до $t_2=0,8 $c, то средняя скорость получится равной $leftlangle vrightrangle =7,4frac{м}{с}$.
Средняя скорость равномерного движения
Только при равномерном движении средняя скорость является постоянной величиной и не зависит от выбора промежутка времени, в который движется тело. При равномерном движении материальной точки по оси X кинематические уравнения для перемещения запишем как:
[x=x_0+vt left(5right).]
Тогда:
[x_1left(t_1right)=x_0+vt_1;; x_2left(t_2right)=x_0+vt_2left(6right).]
Найдем среднюю скорость движения, используя определение (3) и выражения (6):
[leftlangle vrightrangle =frac{x_0+vt_2-x_0-vt_1}{t_2-t_1}=vfrac{t_2-t_1}{t_2-t_1}=v.]
Для оценки численной величины средней скорости на практике используют следующее определение $leftlangle vrightrangle $: средняя скорость равна отношению пройдённого пути (s) ко времени (t), которое было затрачено на движение:
[leftlangle vrightrangle =frac{s}{t}left(7right).]
Определяемая таким образом средняя скорость является скалярной величиной.
Примеры задач с решением
Пример 1
Задание. Пешеход, потратил первую половину времени своего движения, двигаясь со скоростью $v_1=5frac{км}{ч}$, вторую половину времени он шел со скоростью $v_3=3frac{км}{ч}$. Какова средняя скорость движения человека?
Решение. Сделаем рисунок.
Для решения задачи используем формулу, определяющую среднюю скорость:
[leftlangle vrightrangle =frac{s}{t} left(1.1right),]
где путь складывается из двух участков движения:
[s=s_1+s_2left(1.2right).]
Причем по условию задачи:
[s_1=v_1t_1=v_1frac{t}{2}left(1.3right) и ]
[s_2=v_2t_2=v_2frac{t}{2}left(1.4right).]
Подставим в определение средней скорости (1.1) правые части выражений (1.2) – (1.4), и учтем, что $t=t_1+t_2$ имеем:
[leftlangle vrightrangle =frac{v_1frac{t}{2}+v_2frac{t}{2}}{t}=frac{v_1+v_2}{2}.]
Вычислим среднюю скорость пешехода:
[leftlangle vrightrangle =frac{5+3}{2}=4 (frac{м}{с}).]
Ответ. $leftlangle vrightrangle =4frac{м}{с}$
Пример 2
Задание. Какова средняя скорость, которую имела материальная точка за промежуток времени $tau $, если уравнение ее скорости имеет вид:
[vleft(tright)=A+Bt+Ct^2 left(0le tle tau right)left(2.1right).]
Решение. В качестве основы для решения задачи используем формулу ($t=tau $):
[leftlangle vrightrangle =frac{s}{t} left(2.1right).]
Найдем путь материальной точки, учитывая уравнение скорости из данных задачи:
[s=intlimits^{tau }_0{vdt=intlimits^{tau }_0{(A+Bt+Ct^2)dt=}}Atau +Bfrac{{tau }^2}{2}+Cfrac{{tau }^3}{3}left(2.2right).]
Подставим правую часть выражения (2.2) в (2.1), имеем:
[leftlangle vrightrangle =frac{Atau +Bfrac{{tau }^2}{2}+Cfrac{{tau }^3}{3}}{tau }=A+frac{Btau }{2}+frac{C{tau }^2}{3}.]
Ответ. $leftlangle vrightrangle =A+frac{Btau }{2}+frac{C{tau }^2}{3}$
Читать дальше: статика.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Средняя скорость считается так: весь путь поделить на всё время движения. Формула одна и очень простая, но почему-то школьники часто путаются в задачах на среднюю скорость. Разберу три характерные задачи и основные ошибки. Возможно, статья будет полезна учителям и репетиторам, а также школьникам.
1. Половина пути
Первую половину пути поезд ехал со скоростью 60 км/ч, а вторую – 90 км/ч. С какой средней скоростью ехал поезд на всём пути?
Первым делом школьник захочет сложить эти две скорости и поделить пополам. Логично? Да. Но, к сожалению, неправильно.
Объясняю, почему. Поскольку первую половину пути поезд ехал с меньшей скоростью, то времени было затрачено больше, чем на вторую. А значит, вклад отдельных скоростей неравнозначен, и нельзя так просто делить пополам.
Тут школьник может впасть в панику. Что делать? Умножать? Делить? Непонятно. Воспользоваться напрямую формулой “расстояние поделить на время” не получится – ни расстояние, ни время нам неизвестно.
Для школьников, только начинающих изучать основы физики, бывает трудно оперировать с неизвестными величинами. Нам не дано ничего, кроме скоростей, как же быть? В качестве маленькой ступеньки к освоению неизвестности могу предложить следующий ход – сначала додумать неизвестные данные. Возьмём и сами решим, пусть поезд пройдет 180 километров, цифру возьмем так, чтобы легко делилась.
Тогда половина пути будет 90 километров. Поезд пройдет её за 1,5 часа. Вторую половину пути – за 1 час. Это легко посчитает любой школьник. Значит, общее время в пути будет 2,5 часа. Делим общее расстояние 180 километров на 2,5 часа, и получаем 72 км/ч.
Это просто и понятно, но учитель такую задачу не примет. Откуда мы взяли 180 километров, когда это неизвестно? Тем не менее, дав себе эти неизвестные данные, мы продумали алгоритм и довели задачу до ответа. Осталось формализовать это решение, так чтобы не использовать то, что не дано. Обозначим наши 180 километров за S, и опишем всё, что мы делали раньше, только вместо цифр используем буквы.
Получается, что зная ход решения “в цифрах”, мы переводим его в буквенные обозначения. И тут главное не остановиться на полдороги, не смущаться, что нам неизвестно расстояние. Ведь оно в конце сократилось, и средняя скорость оказалась независящей от расстояния (что вполне логично). И от школьника здесь требуются уже алгебраические умения – складывать дроби, переворачивать их.
Если подобная задача встретилась в тесте, где требуется только ответ, можно вообще не заморачиваться – так как средняя скорость в данной задаче не зависит от расстояния, можно посчитать при любом удобном расстоянии. По крайней мере, это лучше, чем сидеть и ломать голову, не зная, как подступиться к решению. Если же требуется оформление – тут числовое решение может помочь как переходный этап, чтобы понять, что именно делать с формулами, как их крутить-вертеть.
Школьникам часто бывает трудно переходить на новый уровень абстракции – от чисел к переменным, которые могут принимать разные числовые значения. В алгебре это тренируют, но там одна переменная икс, и иногда игреки встречаются. А в физике этих переменных пруд пруди, в каждой задаче они разные, и если ученик не освоил этот уровень, то физика кажется ему супер-трудной. Кроме того, в школе переход от чисел к переменным часто упускают, в программе отдельных навыков работы с формулами нет.
2. Средняя скорость по графику пути
Пусть нам дан график зависимости координаты от времени. Требуется определить среднюю скорость.
По графику видно, что движение состоит из четырех этапов:
- Тело стартует в нуле и через 2 секунды оказывается на координате 2 м.
- Тело останавливается, и в течение 4 секунд покоится в точке с координатой 2 м.
- Тело начинает движение, и через 2 секунды оказывается в точке 6 м.
- Тело движется в обратном направлении, и через 2 секунды оказывается в точке 5 м.
Проговорить, понять все эти этапы – важная часть решения. А дальше многие школьники начинают вычислять скорости движения на каждом этапе: На первом – 1 м/с, на втором – 0, на третьем – 2 м/с, на четвертом – 0,5 м/с. Вот это действие как раз лишнее. Для того, чтобы вычислить среднюю скорость, вовсе не обязательно знать скорости на каждом этапе!
Вспомним определение средней скорости – это весь путь, поделить на всё время. Поэтому просто по графику считаем весь путь – 6 метров “туда” и 1 метр “обратно”, в сумме 7 метров. Общее время движения – 10 секунд. Делим 7 метров на 10 секунд, получаем 0,7 м/с.
3. Средняя скорость по графику скорости
Бывает так, что нам дан график зависимости скорости от времени, и требуется определить среднюю скорость. Вот, к примеру, такой график.
Читаем график. Движение состоит из трёх этапов
- С начала движения до момента времени 2 с тело движется с постоянной скоростью 2 м/с
- От 2 до 6 с тело движется со скоростью 6 м/с
- В последние 4 секунды от 6 до 10 с тело замедляется, снижая свою скорость до нуля.
Попытки что-то сделать со значениями скорости самими по себе здесь обречены на провал. Опять надо найти весь путь и всё время движения. Путь по графику скорости определяется как площадь под графиком, причем если график идет ниже нуля, то соответствующие участки складываются.
Считаем площадь фигуры – два прямоугольника на первых двух этапах и треугольник на третьем. Первый этап – 4 м, второй этап – 24 м, третий этап – 12 м. Значит, весь путь будет 40 метров. Всё время 10 секунд, значит, средняя скорость 4 м/с.
Общие рекомендации для решения задач на среднюю скорость
1. Средняя скорость – это всегда весь путь делить на всё время. Данные об отдельных скоростях сами по себе не дадут полной информации о средней скорости. Используем только эту формулу.
2. Следует проанализировать конкретную ситуацию и понять, как можно применить формулу. Если кажется, что не хватает данных – не смущаться.
3. Данные по скоростям на отдельных этапах могут быть полезны для проверки готового ответа: средняя скорость должна лежать между минимальной и максимальной.
Спасибо, что прочитали до конца! Желаю школьникам хорошей учёбы, учителям – понятливых и любопытных учеников, родителям – чтобы дети радовали. Буду рада лайкам и новым подписчикам!
В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.
Определение средней скорости
Средней скоростью движения 
тела называется отношение пути 
, пройденного телом, ко времени 
, в течение которого двигалось тело:
![[ upsilon_{cp} = frac{s}{t}. ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-3ef4719c781f9011e08fb55b5c271fd0_l3.png "Rendered by QuickLaTeX.com")
Научимся ее находить на примере следующей задачи:
Тело двигалось 3 мин. со скоростью 5 м/с, после чего 7 мин. двигалось со скоростью 3 м/с. Найти среднюю скорость движения тела.
Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей 
и 
, которое равно:
м/с.
Частные случаи нахождения средней скорости
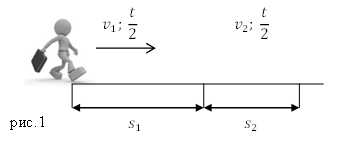
1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.
![[ upsilon_{cp} = frac{s}{t_1+t_2} = frac{s}{frac{s}{2upsilon_1}+frac{s}{2upsilon_2}} = frac{2upsilon_1upsilon_2}{upsilon_1+upsilon_2}. ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-7360def65faa837f59240afaf124708c_l3.png "Rendered by QuickLaTeX.com")
2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.
![[ upsilon_{cp} = frac{s_1+s_2}{t} = frac{upsilon_1frac{t}{2}+upsilon_2frac{t}{2}}{t} = frac{upsilon_1+upsilon_2}{2}. ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-98e13b71ea8c002dffee60fcb598f94f_l3.png "Rendered by QuickLaTeX.com")
Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.
Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.
Пройденный телом путь составляет: 
м. Можно найти также путь, который прошло тело за последние 
с своего движения: 
м. Тогда за первые 
с своего движения тело преодолело путь в 
м. Следовательно, средняя скорость на этом участке пути составила:
м/с.
Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!
Репетитор по физике на Юго-Западной
Сергей Валерьевич
Средняя скорость
- Главная
- /
- Физика
- /
- Средняя скорость
Чтобы найти среднюю скорость воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Средняя скорость на протяжении всего пути
Расстояние (путь)
S =
Время
t =
Средняя скорость
Vср =
0
/
Округление ответа:
Средняя скорость через несколько скоростей
Средняя скорость
Vср =
0
Округление ответа:
Просто введите значения скоростей на разных участках пути и получите среднюю скорость. Для того чтобы добавить в ряд более двух чисел воспользуйтесь зелёной кнопкой “+”.
Теория
Как найти среднюю скорость зная расстояние (путь) и время
Чему равна средняя скорость Vср если известны путь S и время t за которое этот путь преодолён?
Формула
Vср = S⁄t
Пример
К примеру, поезд преодолел расстояние в 1000 км за 16 часов. Посчитаем с какой средней скоростью он двигался:
Vср = 1000/16 = 62.5 км/ч
Как найти среднюю скорость зная скорости на участках пути
Чтобы найти среднюю скорость Vср на протяжении всего пути, зная показатели скорости на его участках (V1 , V2 , … Vn), следует найти среднее гармоническое этих скоростей.
Формула
| Vср | = | n |
| 1⁄V1 + 1⁄V2 + … + 1⁄Vn |
Пример
Средняя скорость через две скорости
Автомобиль проехал некий путь, при этом первые полпути он ехал со скоростью 80 км/ч, а вторые полпути – со скоростью 20 км/ч. Определим среднюю скорость этого автомобиля:
| Vср | = | 2 | = | 2 | = 32 |
| 1⁄80 + 1⁄20 | 0.0125 + 0.05 |
Средняя скорость автомобиля равна 32 км/ч.
Средняя скорость
4.6
Средняя оценка: 4.6
Всего получено оценок: 167.
Обновлено 13 Июля, 2021
4.6
Средняя оценка: 4.6
Всего получено оценок: 167.
Обновлено 13 Июля, 2021
Важнейшей характеристикой тела в кинематике является скорость, с которой оно движется. Движение с нулевой скоростью фактически вообще не является движением. Однако скорость можно измерять различными методами и получать различные значения. Например, можно находить среднюю скорость. Рассмотрим эту тему подробнее: дадим определение средней скорости, приведем формулу средней скорости.
Движение и его скорость
Движение — это изменение координаты материальной точки со временем. Для вычисления быстроты изменения координаты используется такая физическая величина, как скорость (для обозначения используется символ $v$):
$$v={Delta x over Delta t}$$
Если движение происходит равномерно, то это отношение всегда будет одинаковым, независимо от выбора момента времени.
Например, если автомобиль движется со скоростью 36 км/ч, то за время $Delta t = 5c$ он пройдет расстояние $Delta x = 50м$, а за время $Delta t = 60c$ он пройдет расстояние $Delta x = 600м$.
Отношение пройденного расстояния ко времени перемещения в обоих случаях будет одинаковым и равным $v=10$м/с. Это и есть скорость движения автомобиля в данном примере.
Равномерное и неравномерное движение
Заметим, что автомобиль в приведенном примере на рассматриваемом промежутке времени $Delta t$ двигается равномерно. Но такое движение встречается довольно редко.
Тот же автомобиль когда-то стоял на месте, затем начал разгон и лишь потом двигался равномерно. А если рассмотреть ситуацию дальше — то рано или поздно автомобиль начнет замедление и остановится.
Получается, что скорость движения в рассматриваемом промежутке времени может изменяться. Движение с изменяемой скоростью называется неравномерным.
Средняя скорость
Как можно сравнивать скорости неравномерных движений?
Один из способов решения этой задачи — использование в физике такого понятия, как средняя скорость.
Идея состоит в том, чтобы пренебречь изменением скорости во время рассматриваемого промежутка времени, а рассматривать только начальный и конечный момент. Такое измерение удобно, если нам необходимо оценить общий результат движения.
В самом деле, как правило, целью движения является прибытие в конечный пункт к необходимому моменту времени. Как именно это достигнуто, зачастую неважно. Тело могло начать движение сразу и равномерно достигнуть конечного пункта. Могло, как автомобиль, сперва разогнаться, а потом затормозить в конечном пункте к тому же моменту времени. Наконец, тело могло двигаться «рывками», делая ряд остановок во время перемещения, но прибыть в конечный пункт, опять же, к тому же моменту времени.
Во всех трех приведенных случаях важно то, что тело начало и закончило движение в одни и те же моменты и переместилось за время движения на одно и то же расстояние. Что происходило во время движения, не рассматривается.
Скорость, рассчитываемая только по начальному и конечному моменту движения, называется средней. Для нахождения средней скорости необходимо найти отношение общего перемещения материальной точки ко времени, за которое это перемещение произошло.
$$v_{ср}={Delta x_{общ} over Delta t_{общ}}$$
Например, если автомобиль начал разгон в нулевой момент времени с нулевой скорости, разогнался до 50 км/ч, потом притормозил до 40 км/ч, и потом, через минуту, остановился в 600 м от начального пункта, то для нахождения средней скорости его движения необходимо 600 м поделить на 60 с. Средняя скорость составит 10 м/с.
Что мы узнали?
Одним из способов оценки скорости неравномерного движения является средняя скорость. При расчете средней скорости исходят только из начального и конечного моментов движения. А изменениями скорости между этими моментами пренебрегают. Средняя скорость удобна, если необходимо оценить общий результат движения, не обращая внимания на мелкие детали.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 167.
А какая ваша оценка?
